Baixado 77 vezes
Carregado porJuliano van Melis
Tabelas e gráficos
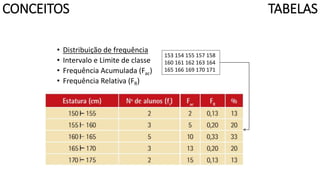
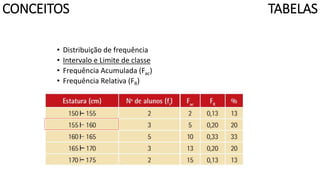
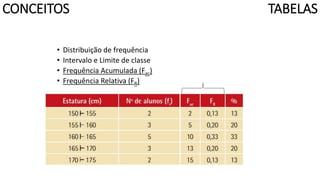
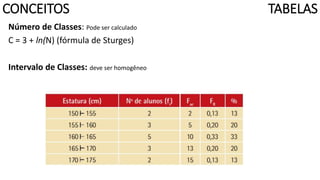
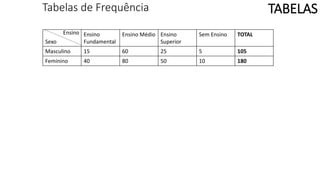
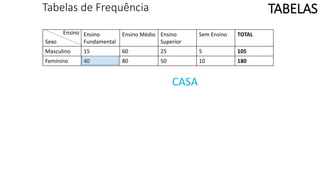
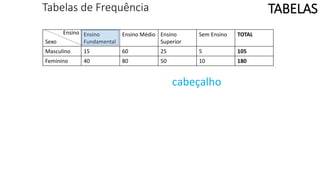
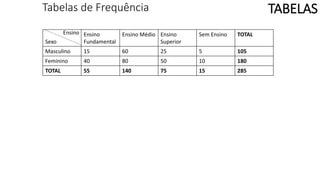
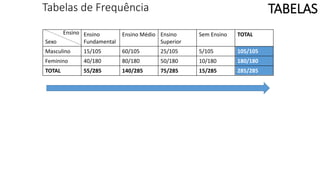
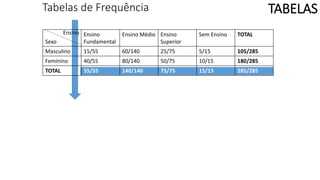
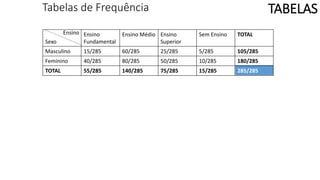
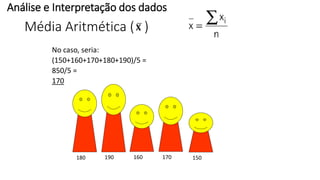
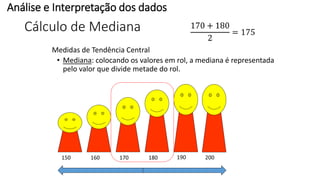
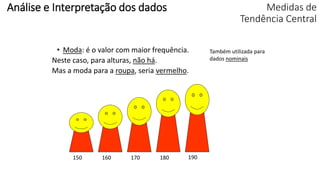
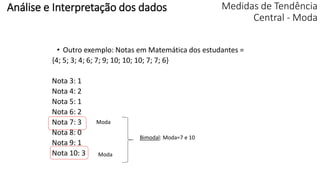
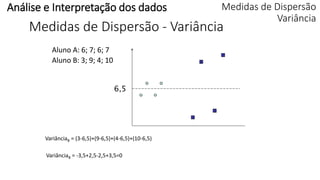
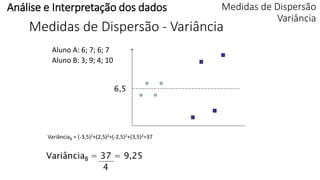
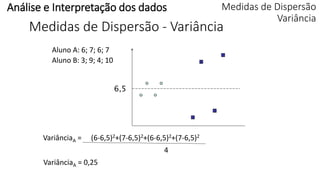
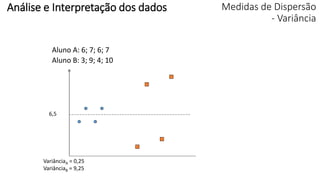
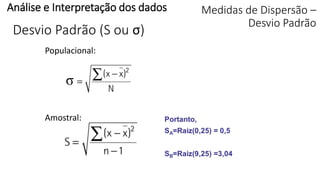
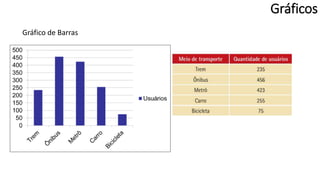
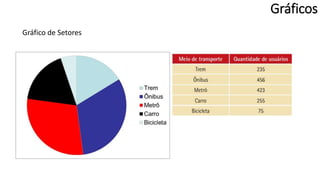
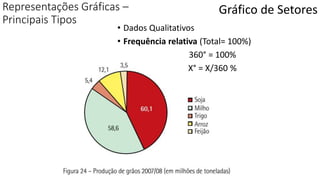
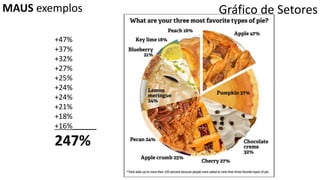
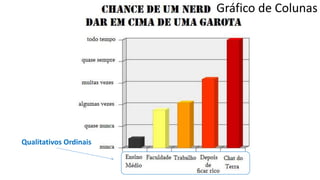
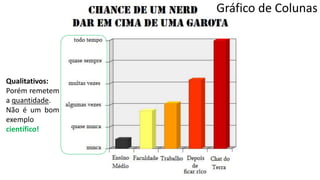
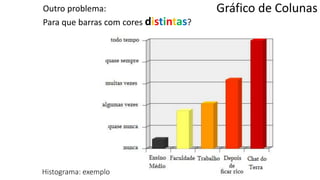
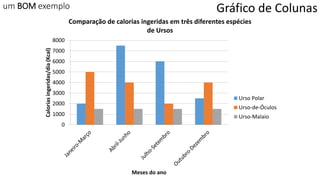
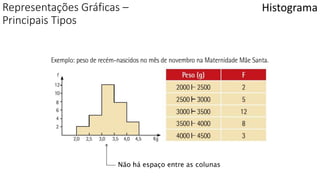
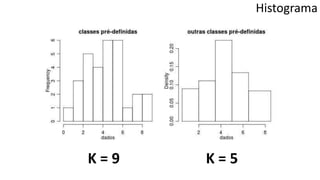
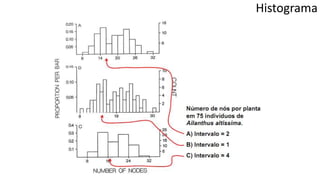
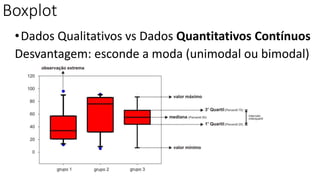
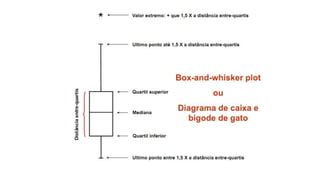
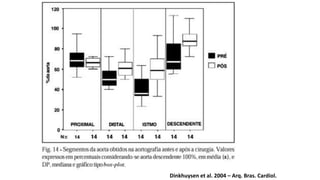
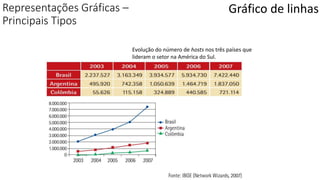
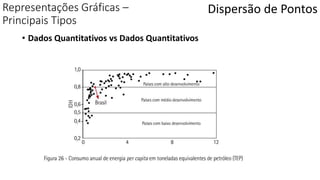
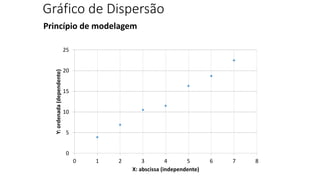
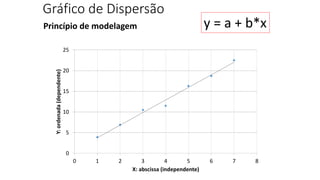
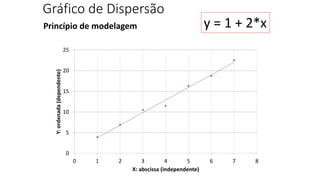
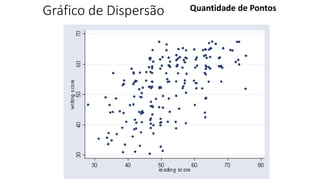
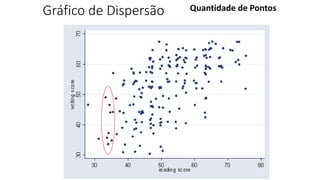
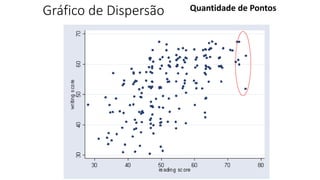
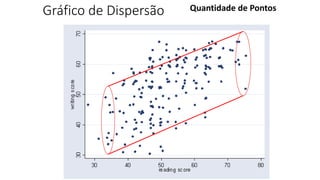
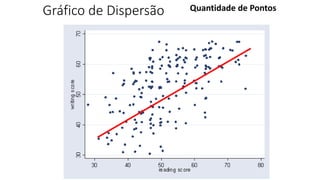
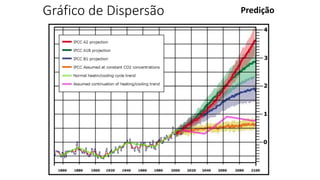
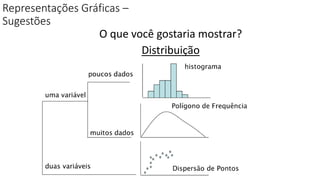
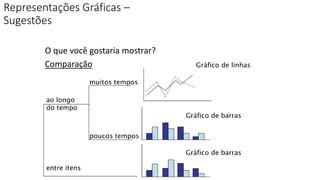
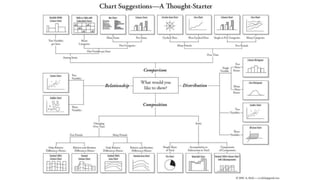
O documento apresenta os conceitos e objetivos da análise exploratória de dados, incluindo representações tabulares e gráficas. Discute tabelas, medidas de tendência central, medidas de dispersão e os principais tipos de gráficos como histograma, diagrama de dispersão e gráfico de barras.
Mais conteúdo relacionado
![Estatistica[1]](https://cdn.slidesharecdn.com/ss_thumbnails/estatistica1-120719160006-phpapp01-thumbnail.jpg?width=640&height=640&fit=bounds)
Tabelas e gráficos
- 1. Análise Exploratória dosDados “Eu posso explicar tudo” Prof. Juliano van Melis “Conhecendo melhor os seus dados”
- 2. Objetivos Aprender oque é e como fazer a análise exploratória dos dados; Aprender a fazer representações tabulares e suas normas; Aprender as principais representações gráficas, suas normas e principais utilizações.
- 3. TABELASAspectos básicos - Todatabela deve ser simples, clara e objetiva ; - Toda tabela deve ser autoexplicativa; - Nenhuma célula deve ficar em branco; - Deve ser mantida a uniformidade de casas decimais
- 4. CONCEITOS • Dados brutos •Rol • Amplitude total • Distribuição de frequência • Intervalo e Limite de classe • Frequência Acumulada (Fac) • Frequência Relativa (FR) 158 154 153 160 157 171 170 166 165 169 155 161 162 164 163 Altura dos estudantes TABELAS
- 5. CONCEITOS • Dados brutos •Rol • Amplitude total • Distribuição de frequência • Intervalo e Limite de classe • Frequência Acumulada (Fac) • Frequência Relativa (FR) Altura dos estudantes TABELAS 153 154 155 157 158 160 161 162 163 164 165 166 169 170 171
- 6. CONCEITOS • Dados brutos •Rol • Amplitude total • Distribuição de frequência • Intervalo e Limite de classe • Frequência Acumulada (Fac) • Frequência Relativa (FR) Altura dos estudantes TABELAS 153 154 155 157 158 160 161 162 163 164 165 166 169 170 171 Amplitude = 171-153 = 18
- 7. • Distribuição defrequência • Intervalo e Limite de classe • Frequência Acumulada (Fac) • Frequência Relativa (FR) 153 154 155 157 158 160 161 162 163 164 165 166 169 170 171 TABELASCONCEITOS
- 8. • Distribuição defrequência • Intervalo e Limite de classe • Frequência Acumulada (Fac) • Frequência Relativa (FR) TABELASCONCEITOS
- 9. • Distribuição defrequência • Intervalo e Limite de classe • Frequência Acumulada (Fac) • Frequência Relativa (FR) TABELASCONCEITOS
- 10. TABELASCONCEITOS Número de Classes:Pode ser calculado C = 3 + ln(N) (fórmula de Sturges) Intervalo de Classes: deve ser homogêneo
- 11. Tabelas de Frequência •Qualquer tipo de variável (qualitativa/quantitativa) • Linhas e Colunas • Fundamental para se criar os gráficos • Frequências = Nº de ocorrências (pode ser em %) TABELAS
- 12. Tabelas de Frequência SexoEnsino Fundamental Ensino Médio Ensino Superior Sem Ensino Masculino 15 60 25 5 Feminino 40 80 50 10 TABELAS
- 13. Tabelas de Frequência Sexo Ensino Fundamental EnsinoMédio Ensino Superior Sem Ensino TOTAL Masculino 15 60 25 5 105 Feminino 40 80 50 10 180 TABELAS Ensino
- 14. Tabelas de Frequência Sexo Ensino Fundamental EnsinoMédio Ensino Superior Sem Ensino TOTAL Masculino 15 60 25 5 105 Feminino 40 80 50 10 180 TABELAS CASA Ensino
- 15. Tabelas de Frequência Sexo Ensino Fundamental EnsinoMédio Ensino Superior Sem Ensino TOTAL Masculino 15 60 25 5 105 Feminino 40 80 50 10 180 TABELAS cabeçalho Ensino
- 16. Tabelas de Frequência Sexo Ensino Fundamental EnsinoMédio Ensino Superior Sem Ensino TOTAL Masculino 15 60 25 5 105 Feminino 40 80 50 10 180 TOTAL 55 140 75 15 285 TABELAS Ensino
- 17. Tabelas de Frequência Sexo Ensino Fundamental EnsinoMédio Ensino Superior Sem Ensino TOTAL Masculino 15/105 60/105 25/105 5/105 105/105 Feminino 40/180 80/180 50/180 10/180 180/180 TOTAL 55/285 140/285 75/285 15/285 285/285 TABELAS Ensino
- 18. Tabelas de Frequência Sexo Ensino Fundamental EnsinoMédio Ensino Superior Sem Ensino TOTAL Masculino 15/55 60/140 25/75 5/15 105/285 Feminino 40/55 80/140 50/75 10/15 180/285 TOTAL 55/55 140/140 75/75 15/15 285/285 TABELAS Ensino
- 19. Tabelas de Frequência Sexo Ensino Fundamental EnsinoMédio Ensino Superior Sem Ensino TOTAL Masculino 15/285 60/285 25/285 5/285 105/285 Feminino 40/285 80/285 50/285 10/285 180/285 TOTAL 55/285 140/285 75/285 15/285 285/285 TABELAS Ensino
- 20. Análise e Interpretaçãodos dados São calculados os parâmetros como: • Média • Mediana • Moda • Proporções • Percentis • Variância e Desvio padrão TABELAS
- 21. Média Aritmética () No caso, seria: (150+160+170+180+190)/5 = 850/5 = 170 150160 170180 190 Análise e Interpretação dos dados
- 22. Medidas de TendênciaCentral • Mediana: colocando os valores em rol, a mediana é representada pelo valor que divide metade do rol. 150 160 170 180 190 Análise e Interpretação dos dados
- 23. Cálculo de Mediana Medidasde Tendência Central • Mediana: colocando os valores em rol, a mediana é representada pelo valor que divide metade do rol. 150 160 170 180 190 200 Análise e Interpretação dos dados
- 24. Medidas de Tendência Central •Moda: é o valor com maior frequência. Neste caso, para alturas, não há. Mas a moda para a roupa, seria vermelho. 150 160 170 180 190 Também utilizada para dados nominais Análise e Interpretação dos dados
- 25. Medidas de Tendência Central- Moda • Outro exemplo: Notas em Matemática dos estudantes = {4; 5; 3; 4; 6; 7; 9; 10; 9; 10; 7; 7; 6} Nota 3: 1 Nota 4: 2 Nota 5: 1 Nota 6: 2 Nota 7: 3 Nota 8: 0 Nota 9: 2 Nota 10: 2 Moda Análise e Interpretação dos dados
- 26. Medidas de Tendência Central- Moda • Outro exemplo: Notas em Matemática dos estudantes = {4; 5; 3; 4; 6; 7; 9; 10; 10; 10; 7; 7; 6} Nota 3: 1 Nota 4: 2 Nota 5: 1 Nota 6: 2 Nota 7: 3 Nota 8: 0 Nota 9: 1 Nota 10: 3 Moda Moda Bimodal: Moda=7 e 10 Análise e Interpretação dos dados
- 27. Medidas de Tendência Central- Resumo •Média: Valores razoavelmente homogêneos •Mediana: Valores heterogêneos •Moda: Quando ocorrem muitas repetições Análise e Interpretação dos dados
- 28. Medidas de Dispersão ouvariabilidade Os dados podem estar muito ou pouco dispersos. Para isso, podemos usar os seguintes parâmetros: •Variância •Desvio padrão •Coeficiente de variação Podem ser relativos a população ou a amostra. Análise e Interpretação dos dados
- 29. Medidas de Dispersão- Variância Aluno A: 6; 7; 6; 7 Aluno B: 3; 9; 4; 10 Média Aluno A: (6+7+6+7)/4 = 6,5 Média Aluno B: (3+9+4+10)/4 = 6,5 Análise e Interpretação dos dados Medidas de Dispersão Variância
- 30. Medidas de Dispersão- Variância Aluno A: 6; 7; 6; 7 Aluno B: 3; 9; 4; 10 VariânciaB = (3-6,5)+(9-6,5)+(4-6,5)+(10-6,5) VariânciaB = -3,5+2,5-2,5+3,5=0 Análise e Interpretação dos dados Medidas de Dispersão Variância
- 31. Medidas de Dispersão- Variância Aluno A: 6; 7; 6; 7 Aluno B: 3; 9; 4; 10 VariânciaB = (-3,5)2+(2,5)2+(-2,5)2+(3,5)2=37 Análise e Interpretação dos dados Medidas de Dispersão Variância
- 32. Medidas de Dispersão- Variância Aluno A: 6; 7; 6; 7 Aluno B: 3; 9; 4; 10 VariânciaA = (6-6,5)2+(7-6,5)2+(6-6,5)2+(7-6,5)2 4 VariânciaA = 0,25 Análise e Interpretação dos dados Medidas de Dispersão Variância
- 33. Aluno A: 6;7; 6; 7 Aluno B: 3; 9; 4; 10 6,5 VariânciaA = 0,25 VariânciaB = 9,25 Análise e Interpretação dos dados Medidas de Dispersão - Variância
- 34. Variância (S² ouσ2) Populacional: Amostral: Análise e Interpretação dos dados σ2 Medidas de Dispersão - Variância
- 35. Problema: a variânciaestá elevada ao quadrado, portanto, a variância de variáveis como: • Metros (m): média em metros e variância em m² • Litros (l): média em litros e variância em l² • etc.. Análise e Interpretação dos dados Medidas de Dispersão - Variância Variância (S² ou σ2)
- 36. Medidas de Dispersão– Desvio Padrão Populacional: Amostral: Análise e Interpretação dos dados σ Desvio Padrão (S ou σ)
- 37. Laboratório! Tabule os seusdados (requisitados na última aula), colocando: • Frequência dos dados qualitativos • Frequência dos dados quantitativos (dividindo em classes) • Média e desvio padrão amostral dos dados quantitativos • Moda dos dados qualitativos
- 38. Gráficos Análise Exploratória dosDados “Uma imagem vale mais que mil palavras”
- 39. Regras •Estética • Eixos semelhantes. •Ordem •Abscissas (Horizontal): valores aumentam da esquerda pra direita • Ordenadas (Vertical): valores aumentam de baixo para cima •Informação • Nomes dos eixos e variáveis (com escala) •Autoria • Fonte dos dados
- 40.
- 41.
- 42. Representações Gráficas – PrincipaisTipos Gráfico de Setores • Dados Qualitativos • Frequência relativa (Total= 100%) 360° = 100% X° = X/360 %
- 43. Gráfico de SetoresTambémchamado de Gráfico de Torta (Pie Chart) ou Gráfico de Pizza
- 44. Gráfico de setores- exemplo
- 45. Título Legenda Gráfico de setores- exemplo
- 46.
- 47. MAUS exemplos ? Gráfico deSetores
- 48. MAUS exemplos Por queeu uso 3D? Preguiça É mais bonito Enganar o professor e mostrar que sei utilizar a Tecnologia AVATAR! Gráfico de Setores
- 49. Representações Gráficas – PrincipaisTipos Gráfico de Colunas
- 50. Representações Gráficas – PrincipaisTipos Gráfico de Colunas • Dados Qualitativos • Quantidade dos dados Qualitativos
- 51.
- 52.
- 53. Qualitativos: Porém remetem a quantidade. Nãoé um bom exemplo científico! Gráfico de Colunas
- 54. Histograma: exemplo Outro problema: Paraque barras com cores distintas? Gráfico de Colunas
- 55. um BOM exemplo 0 1000 2000 3000 4000 5000 6000 7000 8000 Caloriasingeridas/dia(Kcal) Mesesdo ano Comparação de calorias ingeridas em três diferentes espécies de Ursos Urso Polar Urso-de-Óculos Urso-Malaio Gráfico de Colunas
- 56. Representações Gráficas – PrincipaisTipos Histograma
- 57. Representações Gráficas – PrincipaisTipos Polígono de Frequência
- 58. K = 9K = 5 Histograma
- 59.
- 60. Boxplot •Dados Qualitativos vsDados Quantitativos Contínuos Desvantagem: esconde a moda (unimodal ou bimodal)
- 62.
- 63. Dinkhuysen et al.2004 – Arq. Bras. Cardiol.
- 64.
- 65. Representações Gráficas – PrincipaisTipos Gráfico de linhas Evolução do número de hosts nos três países que lideram o setor na América do Sul.
- 66. Representações Gráficas – PrincipaisTipos Dispersão de Pontos • Dados Quantitativos vs Dados Quantitativos
- 67. Gráfico de Dispersão Princípiode modelagem 0 5 10 15 20 25 0 1 2 3 4 5 6 7 8 Y:ordenada(dependente) X: abscissa (independente)
- 68. Gráfico de Dispersão Princípiode modelagem y = a + b*x 0 5 10 15 20 25 0 1 2 3 4 5 6 7 8 Y:ordenada(dependente) X: abscissa (independente)
- 69. Gráfico de Dispersão Princípiode modelagem y = 1 + 2*x 0 5 10 15 20 25 0 1 2 3 4 5 6 7 8 Y:ordenada(dependente) X: abscissa (independente)
- 70. Gráfico de Dispersão Princípiode modelagem
- 71. Gráfico de DispersãoQuantidade de Pontos
- 72. Gráfico de DispersãoQuantidade de Pontos
- 73. Gráfico de DispersãoQuantidade de Pontos
- 74. Gráfico de DispersãoQuantidade de Pontos
- 75. Gráfico de DispersãoQuantidade de Pontos
- 76. Gráfico de DispersãoPredição
- 77. Gráfico de DispersãoPredição
- 78. Representações Gráficas – Sugestões Oque você gostaria mostrar? Distribuição
- 79. Representações Gráficas – Sugestões Oque você gostaria mostrar? Composição
- 80. Representações Gráficas – Sugestões Oque você gostaria mostrar? Comparação
- 82. Objetivos foram cumpridos? Aprendeusobre as principais normas para construção de tabelas? Consegue construir uma tabela de frequência? Aprendeu a calcular as medidas de dispersão (variância e desvio padrão) e de tendência central (média, moda, mediana)? Aprendeu as principais normas para a construção de gráficos? Possui instrução necessária para saber qual é o gráfico mais indicado para a sua apresentação?