Este documento apresenta conceitos básicos sobre estatística descritiva e inferencial, incluindo: (1) variáveis quantitativas e qualitativas, (2) medidas de tendência central e dispersão, (3) distribuições de frequências. Também mostra como organizar e resumir dados no software R, como criar tabelas, histograma e calcular frequências.

1. +
Bioestatística - Universidade Católica de Brasília
O Programa R
Prof. Dr. Gabriel da Rocha Fernandes
Universidade Católica de Brasília
gabrielf@ucb.br - fernandes.gabriel@gmail.com

2. + 2
O Ambiente R
R é uma aplicação de distribuição gratuita (http://
cran.rproject.org/).
 Conjuntointegrado de programas para manipulação de
dados, cálculos e gráficos.
 manipulação e armazenamento efetivo de dados.
 operadores para cálculos sobre variáveis indexadas.
 vasta coleção de ferramentas para análises de dados.
 capacidade gráfica para análise exploratória.
 linguagem de programação simples e eficiente.

3. + 3
Conceitos
 Estatística descritiva: apresentação de dados.
 Estatística
inferencial: conclusão sobre conjuntos maiores
de dados, quando estudamos apenas partes.
 Unidadeexperimental: menor unidade a fornecer
informação.
 Dados: informações obtidas de uma unidade experimental.
 Variável:
característica observada em uma unidade
experimental que pode variar de um indivíduo para outro.

4. + 4
Conceitos
 Variáveis
quantitativas: dados são valores numéricos que
expressam quantidade.
 Discretas:
dados somente podem apresentar determinados valores
(números inteiros).
 Contínuas: dados podem apresentar qualquer valor dentro de um
intervalo de variação possível.
 Variáveis qualitativas: dados de natureza não numérica.
 Nível
nominal: diferencia uma categoria da outra pela
denominação.
 Nível ordinal: graus de intensidade, permite uma ordenação.

5. + 5
Conceitos
 População:todo conjunto de unidades experimentais que
apresenta características em comum.
 Amostra: qualquer fração de uma população.
 Representar uma população.
 Mesmas características.
 Representativa e não-tendenciosa.

6. + 6
Organização de dados
quantitativos
 Estatística
descritiva é imprescindível como um passo
prévio a interpretação dos resultados de uma investigação.
 Tabelas e gráficos.
 Medidas de tendência central e de dispersão.
 Distribuições de frequências.
 Amostra:
5.1 4.9 4.9 5.1 4.7
5.0 5.0 5.0 5.1 5.4
5.2 5.2 4.9 5.3 5.0
4.5 5.4 5.1 4.7 5.5
4.8 5.1 5.3 5.3 5.0

7. + 7
Tabela
Albumina (x) f fr F Fr
4.5 1 0.04 1 0.04
4.6 0 0 1 0.04
4.7 2 0.08 3 0.12
4.8 1 0.04 4 0.16
4.9 3 0.12 7 0.28
5 5 0.2 12 0.48
5.1 5 0.2 17 0.68
5.2 2 0.08 19 0.76
5.3 3 0.12 22 0.88
5.4 2 0.08 24 0.96
5.5 1 0.04 25 1
Soma 25 1 - -

8. + 8
Tabela: intervalo de classe
Peso (Kg) f fr
40 |- 45 9 0.03515625
45 |- 50 36 0.140625
50 |- 55 78 0.3046875
55 |- 60 55 0.21484375
60 |- 65 53 0.20703125
65 |- 70 11 0.04296875
70 |- 75 7 0.02734375
75 |- 80 5 0.01953125
80 |- 85 1 0.00390625
85 |- 90 1 0.00390625
Soma 256 1

9. + 9
Histograma
80
60
Frequência
40
20
0
40 45 50 55 60 65 70 75 80 85
Peso (Kg)

10. + 10
Histograma: Frequencia relativa
40
30
Frequência (%)
20
10
0
40 45 50 55 60 65 70 75 80 85
Peso (Kg)

11. + 11
Medidas de tendência central
 Média:
 Fácil de calcular.
 Fácil de interpretar.
 Muito útil para inferências.
 Valor esperado, ou esperança matemática.
 Mediana:
divide uma série ordenada de dados em dois
subgrupos de tamanho igual.
 Moda: valor mais frequente de uma série de valores.

12. + 12
No R
 Dados pertecem ao pacote MASS, e devem ser pre-
carregados antes de usar.
> library(MASS) # load the MASS package
> painters
Composition Drawing Colour Expression School
Da Udine 10 8 16 3 A
Da Vinci 15 16 4 14 A
Del Piombo 8 13 16 7 A
Del Sarto 12 16 9 8 A
Fr. Penni 0 15 8 0 A
Guilio Romano 15 16 4 14 A
.................

13. + 13
No R
 Nacoluna School contém a informação da classificação da
escola de cada um dos pintores. Elas são nomeadas como
A, B, C,... etc. E School é uma variável qualitativa.
> painters$School
[1] A A A A A A A A A A B B B B B B C C C C C C D D D D
[27] D D D D D D E E E E E E E F F F F G G G G G G G H H
[53] H H
Levels: A B C D E F G H
 Para
mais informações pode pedir uma ajuda sobre o
pacote.
> help(painters)

14. + 14
Distribuição da frequência de
dados qualitativos
A frequencia da distribuição de uma variável é o resumo da
ocorrência dos dados em um conjunto de categorias.
 Nos dados de “painters”, a distribuição da frequência da
variável School é o resumo do número de pintores em cada
escola.
> library(MASS) # carrega o pacote
> school = painters$School # School de painters
> school.freq = table(school) # aplica a função table
> cbind(school.freq) # coloca em tabela vertical

15. + 15
Distribuição da frequencia
relativa de dados qualitativos
> library(MASS) # carrega o pacote
> school = painters$School # School de painters
> school.freq = table(school) # aplica a função table
> school.relfreq = school.freq / nrow(painters)
> cbind(school.relfreq) # coloca em tabela vertical
> options(digits=1) # numeros decimais além de 1
> cbind(school.relfreq)
school.relfreq
A 0.19
B 0.11
C 0.11
D 0.19
E 0.13
F 0.07

16. + 16
Gráfico de barras
> barplot(school.freq) # aplica a função barplot
> colors = c("red", "yellow", "green", "violet", "orange", "blue"
, "pink", "cyan")
> barplot(school.freq, col=colors) # barplot com
cores

17. + 17
Gráfico de pizza
> pie(school.freq) # aplica a função pie
> colors = c("red", "yellow", "green", "violet", "orange", "blue"
, "pink", "cyan")
> pie(school.freq, col=colors) # pie com cores

18. + 18
Estatística em uma categoria
 Qual escola tem a maior média de composições?
#Criar um índice lógico para School C
> c_school = school == "C" # the logical index vector
#Encontrar os subdados de pintores onde a School = C
> c_painters = painters[c_school, ] # seleciona subdados
#Encontrar a média da composição para School C
> mean(c_painters$Composition)
[1] 13.167
 Aoinvés de calcular a média para cada School, podemos
usar a função tapply
> tapply(painters$Composition, painters$School, mean)

19. + 19
Dados Quantitativos
 Dados da variável faithful.
 Uma observação, chamada eruptions, é a duração das
erupções de um geiser do Parque Yellowstone.
A outra, chamada waiting, é o tempo esperado até a
próxima erupção.
> head(faithful)
eruptions waiting
1 3.600 79
2 1.800 54
3 3.333 74
4 2.283 62
5 4.533 85
6 2.883 55

20. + 20
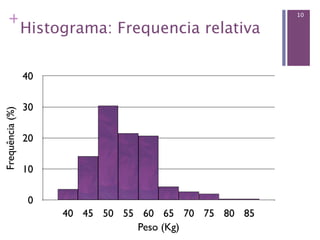
Distribuição de frequências de
dados quantitativos
 Saber a amplitude da duração das erupções.
> duration = faithful$eruptions
> range(duration)
[1] 1.6 5.1
 Dividir essa amplitude em intervalos.
> breaks = seq(1.5, 5.5, by=0.5) # sequência de meio ponto
> breaks
[1] 1.5 2.0 2.5 3.0 3.5 4.0 4.5 5.0 5.5
 Classificar as durações das erupções de acordo com os
intervalos.
> duration.cut = cut(duration, breaks, right=FALSE)
 Calcular a frequência das erupções dentro dos intervalos.
> duration.freq = table(duration.cut)

21. + 21
Histograma
> duration = faithful$eruptions
> hist(duration, right=FALSE) # função para histogramas
> colors = c("red", "yellow", "green", "violet", "orange",
"blue", "pink", "cyan")
> hist(duration, # Função hist
+ right=FALSE, # intervalos fechados somente a
esquerda
+ col=colors, # definir cores
+ main="Old Faithful Eruptions", # Titulo principal
+ xlab="Duration minutes") # Titulo do eixo X

22. + 22
Distribuição da frequencia
relativa de dados quantitativos
> duration.relfreq = duration.freq / nrow(faithful)
> duration.relfreq
duration.cut
[1.5,2) [2,2.5) [2.5,3) [3,3.5) [3.5,4) [4,4.5)
0.187500 0.150735 0.018382 0.025735 0.110294 0.26838
2
[4.5,5) [5,5.5)
0.224265 0.014706
> cbind(duration.freq, duration.relfreq)
duration.freq duration.relfreq
[1.5,2) 51 0.19
[2,2.5) 41 0.15
[2.5,3) 5 0.02
[3,3.5) 7 0.03
[3.5,4) 30 0.11
[4,4.5) 73 0.27

23. + 23
Distribuição da frequência
cumulativa
> duration.cumfreq = cumsum(duration.freq)
> duration.cumfreq
[1.5,2) [2,2.5) [2.5,3) [3,3.5) [3.5,4) [4,4.5) [4.5,5)
51 92 97 104 134 207 268
[5,5.5)
272
> cbind(duration.cumfreq)
duration.cumfreq
[1.5,2) 51
[2,2.5) 92
[2.5,3) 97
[3,3.5) 104
[3.5,4) 134
[4,4.5) 207
[4.5,5) 268
[5,5.5) 272

24. + 24
Gráfico da frequência acumulada
> cumfreq0 = c(0, cumsum(duration.freq))
> plot(breaks, cumfreq0, # Plotar os dados
+ main="Old Faithful Eruptions", # Titulos principal
+ xlab="Duration minutes", # Titulo do eixo x
+ ylab="Cumumlative Eruptions") # Titulo do eixo y
> lines(breaks, cumfreq0) # conecta os pontos

25. + 25
Distribuição da frequência
relativa acumulada
> duration.cumrelfreq = duration.cumfreq / nrow(faithful)
> duration.cumrelfreq
[1.5,2) [2,2.5) [2.5,3) [3,3.5) [3.5,4) [4,4.5) [4.5,5)
0.18750 0.33824 0.35662 0.38235 0.49265 0.76103 0.985
29
[5,5.5)
1.00000
> cbind(duration.cumfreq, duration.cumrelfreq)
duration.cumfreq duration.cumrelfreq
[1.5,2) 51 0.19
[2,2.5) 92 0.34
[2.5,3) 97 0.36
[3,3.5) 104 0.38
[3.5,4) 134 0.49
[4,4.5) 207 0.76
[4.5,5) 268 0.99

26. + 26
Gráfico da frequencia relativa
acumulada
> Fn = ecdf(duration) # Calcula a relfreq
> plot(Fn, # plot Fn
+ main="Old Faithful Eruptions",
+ xlab="Duration minutes",
+ ylab="Cumumlative Proportion")

27. + 27
Gráfico de pontos
> duration = faithful$eruptions # duração das erupções
> waiting = faithful$waiting # intervalo de espera
> plot(duration, waiting, # plotar as variáveis
+ xlab="Eruption duration", # titulo eixo x
+ ylab="Time waited") # titulo eixo y
> abline(lm(waiting ~ duration))

28. + 28
Media, mediana, quartil,
percentil, distância interquartil,
> mean(duration)
[1] 3.4878
> median(duration)
[1] 4
> quantile(duration)
0% 25% 50% 75% 100%
1.6000 2.1627 4.0000 4.4543 5.1000
> quantile(duration, c(.32, .57, .98))
32% 57% 98%
2.3952 4.1330 4.9330
> IQR(duration)
[1] 2.2915
> boxplot(duration, horizontal=TRUE)