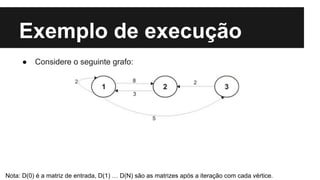
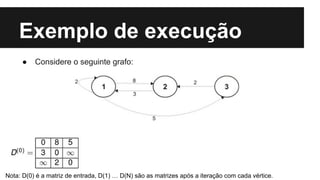
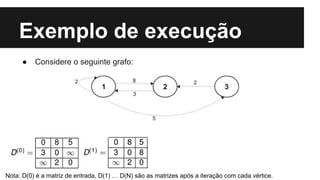
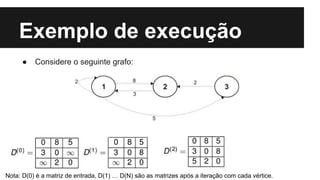
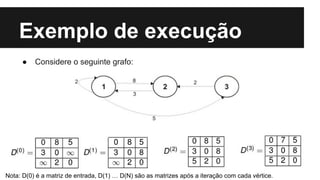
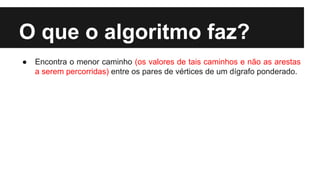
O algoritmo de Floyd-Warshall encontra os caminhos mínimos entre todos os pares de vértices de um grafo ponderado. Ele preenche uma matriz com os tamanhos dos menores caminhos, iterando sobre cada vértice e atualizando a matriz. Sua complexidade é O(n3), onde n é o número de vértices do grafo.

1. Complexidade do
Algoritmo
Caminho Mínimo de Floyd - Warshall

2. Componentes
● Lucas Vinícius
● Luiz Ricardo
● Pedro Santos

3. Roteiro da apresentação
● Explicação do algoritmo
● Pseudocódigo
● Exemplo de execução
● Dedução da complexidade

4. O que o algoritmo faz?
● Encontra o menor caminho (os valores de tais caminhos e não as arestas
a serem percorridas) entre os pares de vértices de um dígrafo ponderado.

5. Explicação do algoritmo
● O algoritmo preenche um matriz bidimensional,
caminho[][], onde caminho[i][j] é o tamanho do menor
caminho entre os nodos i e j:
○ Assume-se que a matriz está inicialmente preenchida com o
valor de cada aresta ou infinito (caso não haja uma aresta
entre dois vértices).

6. Explicação do algoritmo
● Fixa-se um vértice k do grafo; para cada par (i,j) de
vértices, é verificado se o menor caminho j conhecido
entre (i, j) supera a soma do tamanho do caminho de i
para k com o de k para j. Caso supere, o tamanho do
menor caminho passa a ser essa soma.

7. Pseudocódigo
FUNC FLOYD_WARSHALL (CAMINHO[][])
FOR K = 1 TO N
FOR I = 1 TO N
FOR J = 1 TO N
CAMINHO[I][J] = MIN(CAMINHO[I][J], CAMINHO[I][K]+CAMINHO[K][J])

8. Exemplo de execução
● Considere o seguinte grafo:
Nota: D(0) é a matriz de entrada, D(1) … D(N) são as matrizes após a iteração com cada vértice.

9. Exemplo de execução
● Considere o seguinte grafo:
Nota: D(0) é a matriz de entrada, D(1) … D(N) são as matrizes após a iteração com cada vértice.

10. Exemplo de execução
● Considere o seguinte grafo:
Nota: D(0) é a matriz de entrada, D(1) … D(N) são as matrizes após a iteração com cada vértice.

11. Exemplo de execução
● Considere o seguinte grafo:
Nota: D(0) é a matriz de entrada, D(1) … D(N) são as matrizes após a iteração com cada vértice.

12. Exemplo de execução
● Considere o seguinte grafo:
Nota: D(0) é a matriz de entrada, D(1) … D(N) são as matrizes após a iteração com cada vértice.

13. Dedução de complexidade
● Cada laço for pode ser convertido em um somatório com o mesmo
valor inicial e final. Considerando a decisão do valor mínimo entre
dois números (min(a, b)) como operação elementar e as
atribuições e acessos a matrizes como tempo constante, a
complexidade do algoritmo de Floyd-Warshall é dada por:

14. Dedução de complexidade
● Pode-se converter o somatório da variável j em n, pois o resultado deste é
a soma n vezes do valor 1, e isolar este termo, que não depende da
variável j, resultando no seguinte somatório:
● Ao repetir a dedução usada anteriormente com os somatórios das
variáveis i e k, encontra-se o seguinte resultado:

15. Dedução de complexidade
● Com a dedução anterior é perceptível que o algoritmo de
Floyd-Warshall possui complexidade O(n³), onde n é o número de
vértices do grafo fornecido.

16. Referências
● http://pt.slideshare.net/johnnatan20/caminhos-mnimos-fl
oyd?next_slideshow=1
● http://www.inf.ufrgs.br/~cgdaudt/inf05515/art1.pdf