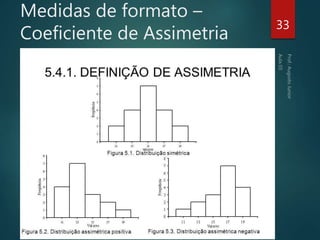
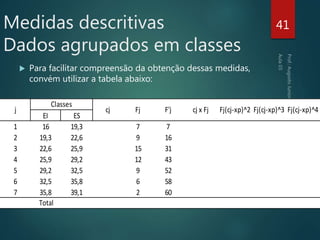
O documento descreve medidas estatísticas descritivas utilizadas para resumir e analisar conjuntos de dados numéricos. Ele discute medidas de localização como média, mediana e moda, que indicam tendências centrais nos dados. Também cobre medidas separatrizes como quartis, que dividem os dados em porcentagens. Por fim, aborda medidas de dispersão como amplitude e variância, que quantificam a variabilidade dos dados em relação à média ou mediana.

1. Probabilidade e
Estatística
ESTATÍSTICA DESCRITIVA
MEDIDAS DESCRITIVAS E ANÁLISE DE DADOS
1

2. Medidas descritivas
 Objetivo: Reduzir o conjunto de dados observados (numéricos) a
um pequeno grupo de valores.
 Classificadas em quatro grupos:
 Medidas de localização (tendência central ou posição)
 Indicam um ponto central onde, em muito dos casos, está localizada a
maioria das observações.
 Medidas separatrizes
 Indicam limites para proporções de observações de um conjunto;
 Podem ser utilizadas para construir medidas de dispersão.
 Medidas de variação (dispersão)
 Informam sobre a variabilidade dos dados
 Medidas de formato
 Informam o modo como os valores distribuem-se;
 Medidas de assimetria: indicam se a maior proporção de valores está no
centro, ou nas extremidades;
 Medidas de curtose: Descreve o grau de achatamento da distribuição.
2

3. Medidas descritivas
Devido a enorme quantidade de tipos de medidas descritivas, muitas
delas que competem entre si, é importante saber escolher a medida
mais adequada.
 Guia geral: Para escolher o(s) tipo(s) de medida mais adequado(s),
responda às perguntas abaixo:
 Com que objetivo a medida está sendo obtida?
 A medida é fácil de interpretar? É intuitiva?
 Existem valores atípicos que podem afetá-la exageradamente?
 O propósito da análise é meramente descritivo, ou planeja-se fazer
inferências?
 Uma medida descritiva deverá, sempre que possível:
 Ser representativa;
 Ser de fácil interpretação;
 Prestar-se bem a tratamento matemático e/ou estatístico em etapas
posteriores.
3

4. Medidas de localização -
Média
 Média aritmética
 Medida de localização mais utilizada;
 Pode ser simples, ou ponderada.
 Média aritmética simples ( 𝑥)
 Todas as observações participam com o mesmo peso.
𝑥 =
𝑖=1
𝑛
𝑥𝑖
𝑛
 Exemplo:
Se X = tempo (h), e para 𝑥𝑖 = 9, 7, 5, 10, 4, temos:
𝑥 =
𝑥𝑖
𝑛
=
9 + 7 + 5 + 10 + 4
5
=
35
5
= 7ℎ
4

5. Medidas de localização -
Média
 Média aritmética ponderada ( 𝑥 𝑝)
 As observações participam com pesos diferentes entre si.
𝑥 𝑝 =
𝑖=1
𝑛
𝑥𝑖 𝑝𝑖
𝑖=1
𝑛
𝑝𝑖
 Exemplo:
Para 𝑥𝑖 = 7, 8, 6, 10 temos os respectivos pesos 𝑝𝑖 = 10, 10, 8, 2:
𝑥 =
𝑥𝑖 𝑝𝑖
𝑝𝑖
=
7𝑥10 + 8𝑥10 + 6𝑥8 + (10𝑥2)
10 + 10 + 8 + 2
=
218
30
= 7,02
5

6. Medidas de localização -
Média
 Propriedades matemáticas da média aritmética
 1º - A média de um conjunto de dados que não variam (constante) é ela
própria;
 2º - Ao somar, ou subtrair, o conjunto de dados por uma constante “c”, a
média também sofre a mesma alteração e de mesmo valor;
 3º - Ao multiplicar, ou dividir, o conjunto de dados por uma constante
“c”, a média também sofre a mesma alteração e de mesmo valor;
 4º - A soma de todos desvios, em relação à média, dará o resultado igual
a zero;
(𝑥𝑖 − 𝑥) = 0
 5º - A soma do quadrado dos desvios em relação a uma constante “c”,
(𝑥𝑖 − 𝑐)2
, é mínima quando 𝑐 = 𝑥.
6

7. Medidas de localização –
Mediana (Md)
 Medida que divide um conjunto de dados
ordenados em duas partes iguais:
 50% dos valores abaixo da mediana;
 50% dos valores acima da mediana.
 Existem dois casos diferentes para o cálculo
da mediana:
 Números de dados observados (n) é ímpar;
 Números de dados observados (n) é par;
7

8. Medidas de localização –
Mediana (Md)
 Número de dados (n) ímpar
 Determinar a posição mais central (p) do conjunto de dados
ordenado;
𝑝 =
𝑛 + 1
2
A mediana será o valor do conjunto de dados que ocupa a
posição “p”, ou seja Md = 𝑥 𝑝.
Exemplo - Se X = tempo (h), e 𝑥𝑖 = 4, 5, 7, 9, 10, temos que:
𝑝 =
𝑛 + 1
2
=
5 + 1
2
= 3
Logo:
𝑀𝑑 = 𝑥 𝑝 = 𝑥3 = 7ℎ
8

9. Medidas de localização –
Mediana (Md)
 Número de dados (n) par
 Neste caso, temos duas posições centrais no conjunto de
dados ordenado, chamadas de 𝑝1e 𝑝2.
 Ao determinar a posição mais central (p) do conjunto de
dados ordenado, a expressão 𝑝 =
𝑛+1
2
gera um valor não
inteiro.
 As posições 𝑝1e 𝑝2 são os dois inteiros mais próximos do
valor de p.
 A mediana será a média aritmética simples dos valores
que ocupam as posições 𝑝1e 𝑝2.
𝑀𝑑 =
𝑥 𝑝1
+ 𝑥 𝑝2
2
9

10. Medidas de localização –
Mediana (Md)
Exemplo:
Seja X = tempo (h);
Para 𝑥𝑖 = 4, 5, 7, 9, 10, 12, temos:
𝑝 =
𝑛 + 1
2
=
7
2
= 3,5
𝑝1 = 3 e 𝑝2 = 4
Logo:
𝑀𝑑 =
𝑥 𝑝1
+ 𝑥 𝑝2
2
=
𝑥3 + 𝑥4
2
=
7 + 9
2
= 8ℎ
10

11. Medidas de localização –
Moda (Mo)
 É o valor de maior ocorrência num conjunto de dados.
 É a única medida que pode não existir e, existindo, pode não
ser a única.
Exemplos:
X = peso (em Kg)
1- Para 𝑥𝑖 = 2, 3, 7, 5, 7, 5, 8, 7, 9, temos Mo = 7 Kg;
2- Para 𝑥𝑖 = 1, 3, 4, 5, 4, 8, 6, 8, temos Mo = 4 Kg e 8 Kg
(conjunto bimodal);
3- Para 𝑥𝑖 = 5, 7, 8, 3, 9, 1, 4, não existe Mo (conjunto amodal);
4- Para 𝑥𝑖 = 1, 3, 4, 4, 5, 1, 3, 5, não existe Mo (conjunto amodal).
11

12. Medidas separatrizes
 Delimitam proporções de uma variável.
 Estabelecem limites para uma determinada proporção de
observações.
 São intuitivas e de fácil interpretação.
 Considerando um conjunto de dados ordenado, representado
como 𝑦(1), 𝑦(2), 𝑦(3), ... , 𝑦(𝑛), pressupondo uma ordenação
ascendente, de modo que 𝑦(1) é o menor valor e 𝑦(𝑛) é o maior
valor do conjunto.
 Em todas as medidas separatrizes é importante conhecer a
“profundidade”.
 Posição ocupada por um dado ordenado relação à extremidade
mais próxima.
 A profundidade do máximo e do mínimo é igual a 1. O
segundo menor e o segundo maior têm profundidade 2, e
assim por diante.
 A profundidade cresce no sentido do centro até um certo
ponto, quando começa a decrescer.
12

13. Medidas separatrizes
 Se o número de observações é ímpar, então existe no
conjunto um valor cuja profundidade é máxima.
 Mediana: divide o conjunto de dados em duas partes.
 A partir daí, surgem novas divisões:
 Quartil: Dividir cada metade surgida pela mediana em duas
partes;
 Oitavo: Dividir cada parte surgida pelos quartis em duas partes;
 Percentil: Delimitação de porções que expressam uma
percentagem de dados do conjunto ordenado.
 Estudaremos as medidas separatrizes mais utilizadas
 Mediana (já visto anteriormente);
 Quartis.
13

14. Medidas separatrizes –
Quartis (𝑄𝑖)
 Três medidas que dividem um conjunto de dados
ordenados em quatro partes iguais.
 Primeiro quartil (𝑄1): 25% dos valores ficam abaixo e 75% dos
valores ficam acima desta medida;
 Segundo quartil (𝑄2): 50% dos valores ficam abaixo e 50% dos
valores ficam acima desta medida.
 Corresponde à mediana (𝑄2 = 𝑀𝑑).
 Terceiro quartil (𝑄3): 75% dos valores ficam abaixo e 25% dos
valores ficam acima desta medida.
 Observações importantes:
 O primeiro quartil é o percentil 0,25, o segundo quartil
(mediana) é o percentil 0,5 e o terceiro quartil é o percentil
0,75.
14

15. Medidas separatrizes –
Quartis (𝑄𝑖)
 O processo de obtenção dos quartis obedecem à mesma
regra de obtenção da mediana.
 Primeiro ordenar os dados e;
 Determinar a posição do “p” do quartil no conjunto de dados
ordenado.
 Existem dois casos diferentes para a determinação de “p”:
 Quando o “n” é ímpar;
 Quando o “n” é par.
15

16. Medidas separatrizes –
Quartis (𝑄𝑖)
 1º caso: Quando “n” é ímpar.
Para 𝑄1, temos: 𝑝 =
𝑛+1
4
;
Para 𝑄2, temos: 𝑝 =
2(𝑛+1)
4
;
Para 𝑄3, temos: 𝑝 =
3(𝑛+1)
4
;
16
 2º caso: Quando “n” é par.
Para 𝑄1, temos: 𝑝 =
𝑛+2
4
;
Para 𝑄2, temos: 𝑝 =
2𝑛+2
4
;
Para 𝑄3, temos: 𝑝 =
3𝑛+2
4
;

17.  O quartil 𝑄𝑖 será o valor do conjunto de dados que ocupa a
posição “p”.
𝑄𝑖 = 𝑥 𝑝
 Se “p” não for um número inteiro, o quartil será a média
aritmética simples dos dois valores que ocupam as posições
correspondentes ao menor e ao maior número inteiro mais
próximo de “p”.
 Exercício proposto:
Com base nos dados ordenados abaixo, definir os quartis.
a) 3, 3, 4, 6, 7, 9, 9, 11, 12;
b) 3, 3, 4, 6, 7, 9, 9, 11, 12, 14.
17Medidas separatrizes –
Quartis (𝑄𝑖)

18. Medidas de dispersão
 Também chamadas de medidas de variação;
 Complementam as medidas de localização.
 Indicam quanto as observações diferem entre si, ou;
 Grau de afastamento das observações em relação à
média.
 Medidas de dispersão mais utilizadas:
 Amplitude;
 Variância;
 Desvio padrão;
 Coeficiente de variação.
18

19. Medidas de dispersão –
Amplitude
 1º - Amplitude total ( 𝑎 𝑡): Diferença entre o maior e o
menor valor de um conjunto de dados.
𝑎 𝑡 = 𝐸𝑆 − 𝐸𝐼, onde:
ES = Extremo superior do conjunto de dados;
EI = Extremo inferior do conjunto de dados.
 É uma medida pouco precisa.
 Bastante influenciada por valores discrepantes.
Exemplo: Para os dados de tempo (em horas) listados a seguir
– 9, 7, 5, 10, 4 – temos:
𝑎 𝑡 = 𝐸𝑆 − 𝐸𝐼 = 10 − 4 = 6ℎ
Significado: Todos os valores do conjunto de dados diferem,
no máximo, em 6h.
19

20. Medidas de dispersão –
Amplitude
 2º - Amplitude interquatílica ( 𝑎 𝑞): Diferença entre o
primeiro quartil (𝑄1) e o terceiro quartil (𝑄3).
𝑎 𝑞 = 𝑄3 − 𝑄1
 Apesar de pouco utilizada, é uma medida que traz um
resultado mais consistente.
 Não sofre nenhuma influência de valores discrepantes.
Exemplo: Com base no exercício proposto, letra (a), temos:
𝑄1 = 3,5 e 𝑄3 = 10
Com isso, temos que:
𝑎 𝑞 = 𝑄3 − 𝑄1 = 10 − 3,5 = 6,5𝐾𝑔
Significado: 50% dos valores (mais centrais) estão dentro desse
intervalo, diferindo entre si, no máximo, em 6,5Kg.
20

21. Medidas de dispersão –
Variância (𝑠2
)
 Definição: É a média dos quadrados dos desvios em relação à média aritmética
𝑠2
=
(𝑥𝑖 − 𝑥)2
𝑛 − 1
Onde: n-1 = Grau de liberdade ou desvios independentes.
 O “Porquê” da utilização do denominador n-1:
 1 - Como a soma dos desvios é nula, existe n-1 desvios independentes, isto é,
conhecidos n-1 desvios o último está automaticamente determinado, pois a soma é
zero;
 2 – O divisor n-1 faz com que a variância possua melhores propriedades estatísticas.
 Quando a variância for utilizada para descrever a variação de uma população,
então pode ser calculada com o denominador igual a “n”.
 Se for para descrever o fenômeno numa amostra, o denominador deverá ser “n-
1”
 Medida de dispersão mais utilizada
 Facilidade de compreensão e cálculo;
 Possibilidade de emprego na inferência estatística.
21

22. Medidas de dispersão –
Variância (𝑠2
)
Exemplo:
Se X = tempo (h)
Para 𝑥𝑖 = 9, 7, 5, 10, 4, onde 𝑥 = 7ℎ, temos
𝑠2 =
(𝑥𝑖 − 𝑥)2
𝑛 − 1
=
(9 − 7)2+(7 − 7)2+(5 − 7)2+(10 − 7)2+(4 − 7)2
5 − 1
=
4 + 0 + 4 + 9 + 9
4
=
26
4
= 6,5ℎ2
22

23. Medidas de dispersão –
Variância (𝑠2
)
 Propriedades matemáticas
1º - A variância de um conjunto de dados que não varia é igual a zero;
2º - Se somarmos uma constante “c” a todos os valores de um conjunto
de dados, a variância não se altera;
3º - Se multiplicarmos todos os valores de um conjunto de dados por
uma constante “c”, a variância desses dados fica multiplicada pelo
quadrado dessa constante.
 Desvantagens da variância
 Como é calculada a partir da média, é uma medida que pode ser
muito influenciada pela discrepância dos valores;
 Como a unidade de medida fica elevada ao quadrado, a sua
interpretação fica mais difícil.
23

24. Medidas de dispersão –
Desvio padrão (s)
 Surgiu para solucionar o problema de interpretação da variância.
 É a raiz quadrada da variância: 𝑠 = 𝑠2
Tendo como base o exemplo anterior: 𝑠2 = 6,5ℎ2
Logo, temos como desvio padrão:
𝑠 = 𝑠2 = 6,5ℎ2 = 2,55h
Observamos que o valor do desvio padrão se apresenta na mesma
unidade de medida dos dados, o que facilita a sua interpretação.
 Geralmente, o desvio padrão é apresentado junto com a média
de dados da seguinte forma: 𝑥 ± 𝑠.
 Desta forma, temos a indicação da variação média dos dados em
torno da média aritmética.
24

25. Medidas de dispersão –
Coeficiente de Variação
 Representado por “CV”, é a medida mais utilizada
quando existe interesse em comparar variabilidades de
diferentes conjuntos de dados.
 Devemos utilizar o CV nas situações em que as médias
dos conjuntos comparados são muito desiguais, ou as
unidades de medida são diferentes.
 É definido como a proporção da média representada
pelo desvio padrão.
𝐶𝑉 =
𝑠
𝑥
𝑥 100
25

26. Medidas de dispersão –
Coeficiente de Variação
No exemplo anterior, vimos que 𝑥 = 7ℎ e 𝑠 = 2,55ℎ.
Com base nesses resultados, temos como coeficiente de variação (CV):
𝐶𝑉 =
𝑠
𝑥
𝑥 100 =
2,55ℎ
7ℎ
𝑥 100 = 36,4%
 As vantagens do coeficiente de variação
 É desprovido de unidade de medida (é expresso em percentagem);
 É uma medida relativa, ou seja, que relaciona o desvio padrão (s) com a
sua respectiva média aritmética ( 𝑥).
 Melhora a interpretação do resultado do desvio padrão, no sentido de
entender se os dados obtidos estão muito variados, ou não, em relação à
média aritmética.
26

27. Medidas de dispersão –
Coeficiente de Variação
Exemplo 1:
Consideremos que 𝑥1𝑖 e 𝑥2𝑖 são conjuntos de valores referentes a
produção diária de leite (em Kg) de vacas das raças Holandesa e Jersey,
respectivamente.
Foram obtidas as seguintes medidas
Holandesa - 𝑥1 = 25𝐾𝑔, 𝑠1 = 4,2𝐾𝑔, 𝐶𝑉1 = 16,8%
Jersey - 𝑥2 = 13𝐾𝑔, 𝑠2 = 3,4𝐾𝑔, 𝐶𝑉2 = 26,2%
27

28. Medidas de dispersão –
Coeficiente de Variação
Observamos que se utilizarmos somente o desvio padrão para
comparar as variações, concluiríamos que o grupo das vacas
holandesas é o mais variável.
Entretanto, devemos fazer a seguinte consideração:
1- O desvio padrão de 4,2 mesmo sendo o maior, quando
relacionado com à média 25, representa uma porção menor deste
valor do que 3,4 quando relacionado com à média 13.
 Quando as médias são muito desiguais, devemos utilizar na
comparação dos conjuntos de valores o CV, que é uma medida
relativa.
28

29. Medidas de dispersão –
Coeficiente de Variação
Exemplo 2:
Consideremos que 𝑥𝑖 e 𝑦𝑖 são conjuntos de valores referentes a altura
(em cm) e peso (em Kg), respectivamente, de um grupo de estudantes.
Foram obtidas as seguintes medidas
Altura - 𝑥 = 165 𝑐𝑚, 𝑠 𝑥 = 30 𝑐𝑚, 𝐶𝑉𝑥 = 18,2%
Peso - 𝑦 = 58 𝐾𝑔, 𝑠 𝑦 = 9 𝐾𝑔, 𝐶𝑉𝑦 = 15,5%
Neste caso, verificamos que a comparação entre conjuntos de valores
expressos em unidades de medida diferentes o CV é a única medida
que pode ser utilizada, por ser desprovida de unidade de medida.
Se utilizássemos qualquer outra medida de variação estaríamos
comparando centímetros com quilogramas, o que não é possível, por
tratar-se de grandezas não comparáveis entre si.
29

30. Medidas de formato
 É um aspecto importante de uma distribuição.
 Relaciona-se com as idéias de simetria e curtose.
 Embora mudanças em uma medida variação alterem o
aspecto visual também da distribuição.
 Principais cálculos
 Momentos;
 Assimetria;
 Curtose.
30

31. Medidas de formato -
Momentos
 Medidas calculadas com o propósito de estudar a distribuição.
 Delas é que sabemos os dados de assimetria e curtose.
 Tanto mais conhecemos uma distribuição quanto mais conhecermos
sobre os seus momentos.
 O momento de ordem “r” centrado num valor “a” é dado pela seguinte
expressão
𝑚 𝑟 =
(𝑥𝑖 − 𝑎) 𝑟
𝑛
 Dois valores de “a” geram momentos importantes num conjunto de
dados:
 Quando a=0, temos os momentos centrados na origem, denominados
momentos ordinários de ordem r e representados por 𝑚 𝑟
′ .
 Quando a= 𝑥, temos os momentos de ordem r centrados na média.
31

32. Medidas de formato –
Coeficiente de Assimetria
 Denotado por "𝑎3", informa se a maioria dos valores estão à
esquerda, ou à direita, ou uniformemente distribuídos em torno
da média aritmética.
 Indica o grau e o sentido do afastamento da simetria e é obtida
utilizando o segundo e o terceiro momentos centrados na
média, através da seguinte expressão:
𝑎3 =
𝑚3
𝑚2 𝑚2
 Se 𝑎3 < 0, assimétrica negativa: Maioria dos valores são maiores
que a média; localizam-se à direita da média;
 Se 𝑎3 = 0, simétrica: Valores uniformemente distribuídos em
torno da média;
 Se 𝑎3 > 0, assimétrica positiva: Maioria dos valores são menores
que a média; localizam-se à esquerda da média
32

33. Medidas de formato –
Coeficiente de Assimetria
33

34. Medidas de formato –
Coeficiente de Curtose
 Denotado por "𝑎4", indica o grau de achatamento de uma
distribuição.
 Relacionada com o grau de concentração das observações no centro
e nas caudas da distribuição.
 Não tem interpretação tão intuitiva quanto a simetria.
 Calculado a partir do segundo e quarto momentos centrados na
média, através da seguinte expressão:
𝑎4 =
𝑚4
𝑚2
2
 Se 𝑎4 <3, distribuição platicúrtica: Baixa concentração de valores no
centro, tornando a distribuição mais achatada que a distribuição
normal;
 Se 𝑎3 = 3, distribuição mesocúrtica: Concentração de valores
semelhante a de uma distribuição normal;
 Se 𝑎3 > 3, distribuição leptocúrtica: Alta concentração de valores no
centro e nas extremidades, o que provoca um pico maior que o da
distribuição normal.
34

35. Medidas de formato –
Coeficiente de Curtose
35

36. Medidas descritivas
Dados agrupados em classes
 Essas medidas podem ser calculadas
quando os dados estão agrupados por
classes.
 Quando calculadas por meio de tabelas de
distribuição de frequências de variáveis
contínuas, essas medidas, em geral, são
apenas aproximações das medidas obtidas a
partir de dados não agrupados.
36

37.  Média aritmética
 Distribuição de frequência de variáveis contínuas não existem
valores individuais.
 O melhor representante dos valores de uma classe é o centro da
classe ( 𝑐𝑗).
 Portanto, a média da distribuição será a média ponderada (pelas
frequências absolutas) dos centros de classe.
𝑥 𝑝 =
𝑗=1
𝑘
𝑐𝑗 𝐹𝑗
𝑗=1
𝑘
𝐹𝑗
=
𝑗=1
𝑘
𝑐𝑗 𝐹𝑗
𝑛
 O valor da média dessa distribuição é obtido com um erro,
provocado pelo agrupamento dos dados.
 O erro será menor quanto maior for a simetria dos valores de
cada classe em relação ao seu ponto médio.
37
Medidas descritivas
Dados agrupados em classes

38.  Classe mediana e classe modal
 Classe mediana
 Aquela onde está compreendida a mediana.
 É a classe onde a frequência absoluta acumulada ( 𝐹𝑗
′
) é
maior, ou igual, ao valor de “p” (posição da mediana).
𝑝 =
𝑛 + 1
2
 Classe modal
 Aquela que possui a maior frequência acumulada ( 𝐹𝑗
′
).
 Não é, necessariamente, a classe que compreende a moda do
conjunto de valores.
38
Medidas descritivas
Dados agrupados em classes

39.  Variância
 Devido a inexistência de valores individuais na distribuição de
frequências, devemos utilizar para o cálculo da variância a
seguinte expressão:
𝑠2 =
𝐹𝑗(𝑐𝑗 − 𝑥 𝑝)2
𝑛 − 1
 A variância pode ser entendida como uma medida de extensão
de um histograma, ou de um polígono de frequências, sobre o
eixo horizontal.
 Desvio padrão e coeficiente de variação
 São obtidos da mesma forma antes explicada para dados não
agrupados.
𝑠 = 𝑠2 e CV =
𝑠
𝑥 𝑝
𝑥 100
39
Medidas descritivas
Dados agrupados em classes

40.  Medidas de formato
 As expressões que definem os coeficientes de assimetria e de curtose também
permanecem as mesmas que para os dados não agrupados.
 São elas (assimetria e curtose), respectivamente:
𝑎3 =
𝑚3
𝑚2 𝑚2
𝑒 𝑎4 =
𝑚4
𝑚2
2
 Os momentos centrados da média, utilizado para esses coeficientes, pelas
mesmas razões já mencionadas para a variância e á média, são assim definidos:
𝑚2 =
𝐹𝑗(𝑐𝑗 − 𝑥 𝑝)2
𝑛
; 𝑚3 =
𝐹𝑗(𝑐𝑗 − 𝑥 𝑝)3
𝑛
; 𝑚4 =
𝐹𝑗(𝑐𝑗 − 𝑥 𝑝)4
𝑛
40Medidas descritivas
Dados agrupados em classes

41.  Para facilitar compreensão da obtenção dessas medidas,
convém utilizar a tabela abaixo:
41Medidas descritivas
Dados agrupados em classes
EI ES
1 16 19,3 7 7
2 19,3 22,6 9 16
3 22,6 25,9 15 31
4 25,9 29,2 12 43
5 29,2 32,5 9 52
6 32,5 35,8 6 58
7 35,8 39,1 2 60
Fj(cj-xp)^2 Fj(cj-xp)^3 Fj(cj-xp)^4
Total
Classes
j cj Fj F'j cj x Fj

42. Exercícios propostos
1- Os valores que seguem são os tempos (em
segundos) da reação de um alarme de incêndio,
após a liberação de fumaça de uma fonte fixa:
12 9 11 7 9 14 6 10
Calcule as medidas de localização (média, mediana e
moda)e as medidas de dispersão (amplitude total,
variância, desvio padrão e coeficiente de variação)
para o conjunto de dados.
42

43. Exercícios propostos
2- Foram registrados os tempos de frenagem (em
segundos) para 21 motoristas que dirigiam a 65
Km/h. Os valores obtidos foram:
69 58 70 80 46 61 65 74 75 55 67
56 70 72 61 66 58 68 70 68 58
Para esse conjunto de valores, calcule os quartis e a
amplitude interquartílica e interprete os resultados
obtidos.
43

44. Exercícios propostos
3- O Gerente de um restaurante self-service fez uma análise, no
intuito de verificar se o molho especial para salada, único no mercado,
está com boa receptividade pelos clientes.
Para isso, fez uma contagem, durante um dia inteiro, da quantidade
de molhos retirados por cliente.
Com base nos dados observados, calcular as medidas descritivas.
44
j Classes Fj
1 0 7
2 1 9
3 2 19
4 3 10
5 4 3
6 5 2
50Total

45. Análise exploratória de
dados
 Vimos que a média aritmética e a variância são muito utilizadas
para representar, respectivamente, a tendência central e a
dispersão de um conjunto de valores.
 Apresentam boas propriedades matemáticas e estatísticas.
 Entretanto, elas descrevem de forma ótima somente as
distribuições de frequência unimodais, simétricas e
mesocúrticas.
 Limitação importante do uso indiscriminado da média e da
variância na descrição de um conjunto de dados.
 Numa distribuição assimétrica, essa medidas teriam valores
fortemente afetados pela discrepância dos valores observados.
45

46. Análise exploratória de
dados
 Em 1970, Jonh Tukey propôs
algumas técnicas que contornavam
esse problema;
 Ao conjunto dessa técnicas, deu-se
o nome de Análise Exploratória de
Dados;
 O enfoque proposto era de obter
medidas resistentes e robustas.
46

47. Análise exploratória de
dados
 Medidas resistentes são aquelas que se mostram
pouco sensíveis à presença de valores discrepantes do
centro da distribuição.
 Principal exemplo: Mediana.
 Medidas robustas são aquelas que apresentam pouca
sensibilidade diante dos desvios aos pressupostos
básicos, inerentes aos modelos probabilísticos.
 Exemplo: Tipos de formato da distribuição.
47

48. Análise exploratória de
dados
 As técnicas exploratórias dão uma visão distinta, prévia, mas
complementar às técnicas de Inferência. Ajudam:
 A comprovar as condições de aplicação dos testes de
hipóteses (Inferência Estatística);
 A detectar erros ou valores discrepantes;
 A buscar a melhor transformação de dados quando houver
necessidade.
 Abordaremos três dessas técnicas:
 O resumo de cinco números;
 O gráfico em caixa (“box plot”);
 O diagrama de ramos e folhas.
48

49. Análise exploratória –
Resumo de cinco números
 Descreve o conjunto de dados através de cinco valores:
 Mediana (Md);
 Os quartis primeiro e terceiro ( 𝑄1 𝑒 𝑄3, 𝑟𝑒𝑠𝑝𝑒𝑐𝑡𝑖𝑣𝑎𝑚𝑒𝑛𝑡𝑒);
 Extremos Inferior e Superior (EI e ES, respectivamente).
 A partir desses valores, calculamos:
 Amplitude interquartílica ( 𝑎 𝑞): Diferença entre os quartis;
 Dispersão Inferior (DI): Diferença entre a mediana e o EI;
 Dispersão Superior (DS): Diferença entre a mediana e o ES.
O resumo de cinco números fornece uma idéia acerca da simetria
da distribuição porque o percentual de observações compreendido
dentro de cada um desses intervalos é conhecido (25%)
49

50. Análise exploratória –
Resumo de cinco números
 A distribuição será simétrica quando a diferença entre o primeiro
quartil e o extremo inferior é aproximadamente igual à diferença
entre o extremo superior e o terceiro quartil (𝑄1 − 𝐸𝐼 ≅ 𝐸𝑆 − 𝑄3) e
a diferença entre a mediana e o primeiro quartil for
aproximadamente igual à diferença entre o terceiro quartil e a
mediana (Md − 𝑄1 ≅ 𝑄3 − 𝑀𝑑).
 Se não atender uma dessas duas condições, então, a distribuição
será assimétrica.
 Assimétrica Positiva:
 Dispersão superior for muito maior que a inferior;
 Maior concentração de dados entre o extremo inferior e a mediana.
 Assimétrica Negativa:
 Dispersão inferior muito maior que a superior;
 Maior concentração de dados entre o extremo superior e a mediana.
50

51. Resumos de cinco números:
Simétrica
51
EI 𝑄1 𝑄3 ESMd
25% 25% 25% 25%
EI ESMd
EI ESMd𝑄1 𝑄3
25% 25% 25% 25%
25% 25% 25% 25%𝑄1 𝑄3
𝑎 𝑞 < 𝐷𝐼 = 𝐷𝑆
𝑎 𝑞 = 𝐷𝐼 = 𝐷𝑆
𝑎 𝑞 > 𝐷𝐼 = 𝐷𝑆

52. Resumos de cinco números:
Assimétrica negativa 52
EI 𝑄1 𝑄3 ESMd
25% 25% 25% 25%
𝑄1 𝑄3EI ESMd
25% 25% 25% 25%
𝐷𝐼 = 𝐷𝑆
𝑎 𝑞
50%
𝐷𝐼 𝐷𝑆
50% 50%
𝑎 𝑞
50%
𝐷𝐼 𝐷𝑆
50% 50%
𝐷𝐼 > 𝐷𝑆

53. Resumos de cinco números:
Assimétrica positiva 53
EI 𝑄1 𝑄3 ESMd
25% 25% 25% 25%
𝑄1 𝑄3EI ESMd
25% 25% 25% 25%
𝐷𝐼 < 𝐷𝑆
𝑎 𝑞
50%
𝐷𝐼 𝐷𝑆
50% 50%
𝑎 𝑞
50%
𝐷𝐼 𝐷𝑆
50% 50%
𝐷𝐼 < 𝐷𝑆

54. Tomemos a seguinte variável:
X = peso ao nascer (em Kg) de 60 bovinos machos,
para qual os valores observados (e já ordenados)
foram:
16, 17, 17, 18, 18, 18, 19, 20, 20, 20, 20, 20, 21,
21, 22, 22, 23, 23, 23, 23, 23, 23, 23, 23, 23, 25,
25, 25, 25, 25, 25, 26, 26, 27, 27, 27, 27, 28, 28,
28, 29, 29, 29, 30, 30, 30, 30, 30, 30, 30, 31, 32,
33, 33, 33, 34, 34, 35, 36, 39, 45.
54
Resumos de cinco números:
Exemplo

55. O resumo de cinco número permite verificar que a distribuição não é
simétrica, assumindo um caráter assimétrico positivo.
55
25% 25% 25% 25%
𝑎 𝑞 = 8
Resumos de cinco números:
Exemplo
16 22 25 30 45
EI 𝑄1 𝑄3 ESMd
22 30
𝑄1 𝑄3
EI ESMd𝐷𝐼 = 9
16 25 45
𝐷𝑆 = 20

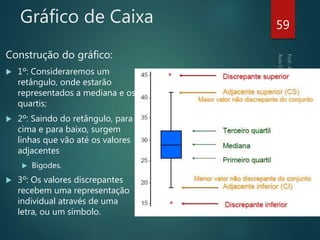
56.  Formato mais objetivo: Utilização das medidas “Cerca Inferior”
e “Cerca Superior”.
 CERCA INFERIOR
𝐶𝐼 = 𝑄1 − 1,5𝑎 𝑞
 CERCA SUPERIOR
𝐶𝑆 = 𝑄3 + 1,5𝑎 𝑞
 Serão considerados discrepantes os valores que estiverem fora
do seguinte intervalo:
[𝐶𝐼; 𝐶𝑆]
 Valores menores que a CI são considerados discrepantes
inferiores, e os maiores que a CS são considerados discrepantes
superiores.
56
Identificação de valores
discrepantes

57.  Levando em consideração os dados encontrados no exemplo
anterior, temos que:
 CERCA INFERIOR
𝐶𝐼 = 𝑄1 − 1,5𝑎 𝑞 = 22 − 1,5 𝑥 8 = 10
 CERCA SUPERIOR
𝐶𝑆 = 𝑄3 + 1,5𝑎 𝑞 = 30 + 1,5 𝑥 8 = 42
 Com isso, verificamos que o valor 45, do conjunto de dados,
ultrapassa a cerca superior, sendo classificado como discrepante
superior.
57
Identificação de valores
discrepantes

58. Gráfico de Caixa
 Uma forma de apresentar a informação dada pelo
resumo de cinco números.
 Antes de construir o gráfico, precisamos definir os
valores adjacentes.
 Maior e menor valores que não são discrepantes de um
conjunto de dados.;
 Ou seja, o maior valor que não ultrapassa a cerca
superior e o menor valor que não ultrapassa a cerca
inferior.
 SE, NUM CONJUNTO DE DADOS, NENHUM VALOR
É CONSIDERADO DISCREPANTE, OS VALORES
ADJACENTES SERÃO OS PRÓPRIOS EXTREMOS.
58

59. Gráfico de Caixa
Construção do gráfico:
 1º: Consideraremos um
retângulo, onde estarão
representados a mediana e os
quartis;
 2º: Saindo do retângulo, para
cima e para baixo, surgem
linhas que vão até os valores
adjacentes
 Bigodes.
 3º: Os valores discrepantes
recebem uma representação
individual através de uma
letra, ou um símbolo.
59

60. Gráfico de Caixa
60

61. Diagrama de ramos e folhas
 Ferramenta útil para descrever um pequeno grupo de
dados.
 Já nos dá uma idéia de como poderá comportar-se a sua
distribuição.
 Fornece boa visão geral dos dados sem que haja perda
de informação detectável.
 Cada valor retém a sua identidade, perdendo somente a
organização inicial.
 Uma boa opção quando temos em mãos somente os
dados, caneta e papel.
61

62. Diagrama de ramos e folhas
- Exemplo
 Dados relativos à nota de 40 alunos em
uma prova da matéria X.
78 59 86 94 43 56 78 84 57 49
96 68 67 65 75 73 67 87 84 45
56 94 87 56 85 76 86 79 78 77
59 76 68 49 86 87 83 94 85 96
62

63.  1º Passo: Separação dos dados, juntando os valores
que tem o mesmo número inicial.
43 49 45
59 56 57 56 56 59
68 67 65 67 68
78 78 75 73 76 79 78 77 76
86 84 89 87 84 87 85 86 86 87 83 85
94 96 94 94 96
63Diagrama de ramos e folhas
- Exemplo

64.  2º Passo: Mostrar o primeiro dígito para cada linha, à
esquerda, e separar os outros dígitos por uma linha
vertical.
4 3 9 5
5 9 6 7 6 6 9
6 8 7 5 7 8
7 8 8 5 3 6 9 8 7 6
8 6 4 9 7 4 7 5 6 6 7 3 5
9 4 6 4 4 6
64Diagrama de ramos e folhas
- Exemplo

65.  3º Passo: Organizar os números do lado direito, de
forma ascendente, ou descendente.
4 3 5 9
5 6 6 6 7 9 9
6 5 7 7 8 8
7 3 5 6 6 7 8 8 8 9
8 3 4 4 5 5 6 6 6 7 7 7 9
9 4 4 4 6 6
65Diagrama de ramos e folhas
- Exemplo

66. Diagrama de ramos e folhas
RAMO:
 Cada linha que corresponde aos dados
com o mesmo dígito inicial.
FOLHA:
 Cada número do ramo à esquerda da
linha vertical.
66

67. EXERCÍCIOS PROPOSTOS
1- Os dados abaixo, em rol, referem-se aos valores gastos (em reais)
pelas primeiras 50 pessoas que entraram em um determinado
supermercado, no dia 01/01/2000:
3,11 8,88 9,26 10,81 12,69 13,78 15,23 15,62 17,00 17,39
18,36 18,43 19,27 19,50 19,54 20,16 20,59 22,22 23,04 24,47
24,58 25,13 26,24 26,26 27,65 28,06 28,08 28,38 32,03 36,37
38,64 38,98 39,16 41,02 42,97 44,08 44,67 45,40 46,69 48,65
50,39 52,75 54,80 59,07 61,22 70,32 82,70 85,76 86,37 93,34
Para esses dados:
a) Obtenha o resumo de cinco números;
b) Verifique se existem valores discrepantes;
c) Construa o gráfico em caixa;
d) Com base no gráfico, classifique a distribuição quanto à simetria.
Justifique a sua resposta.
67

68. EXERCÍCIOS PROPOSTOS
2- As durações (em horas de uso contínuo) de 25 componentes
eletrônicos selecionados de um lote de produção são:
834 919 784 865 839
912 888 783 655 831
886 842 760 854 939
961 826 954 866 675
760 865 901 632 718
Construa um diagrama de ramos e folhas com rótulos de ramos
com um dígito e folhas de dois dígitos.
Use esse diagrama de ramos e folhas para decidir sobre a simetria
desses dados.
68