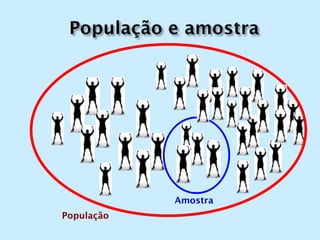
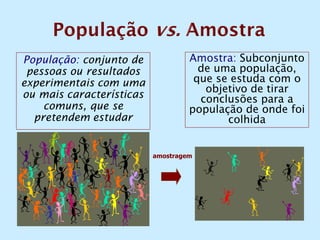
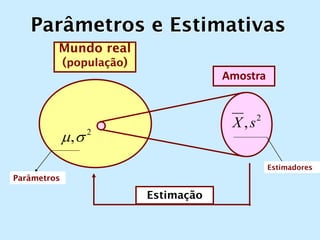
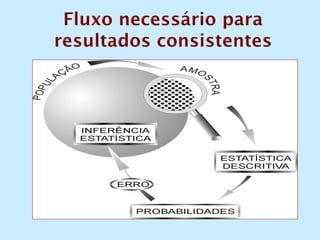
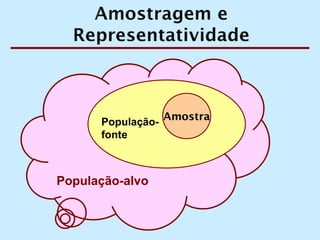
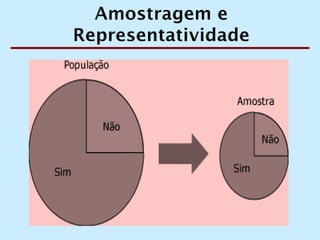
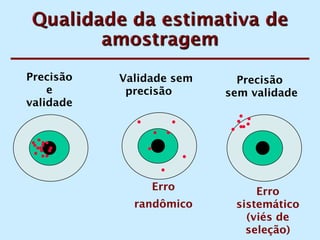
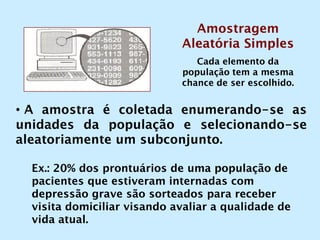
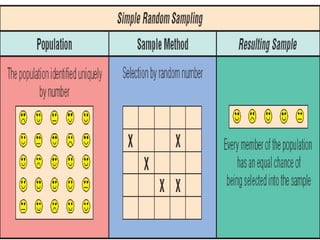
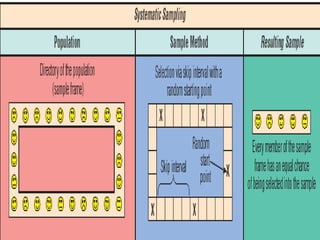
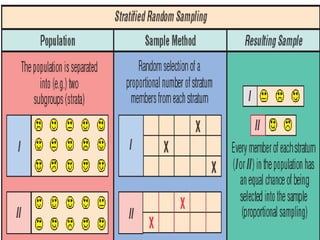
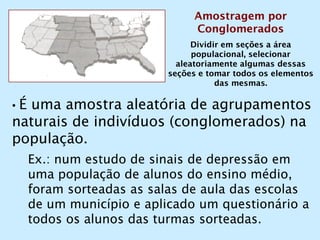
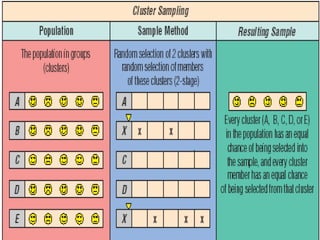
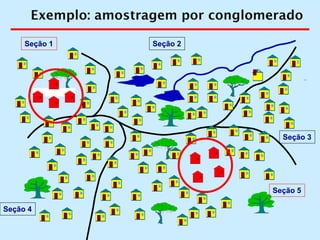
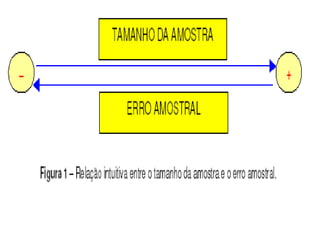
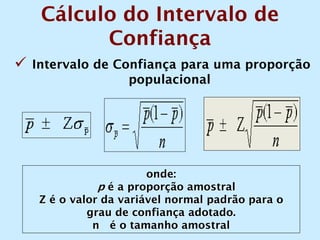
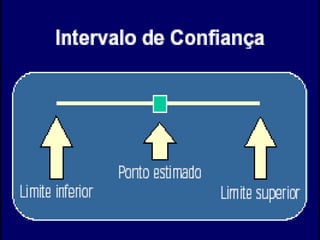
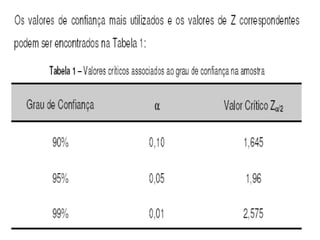
O documento discute os conceitos de amostragem simples e amostragem estratificada. A amostragem estratificada deve ser usada quando a população pode ser dividida em subconjuntos, para que a amostra reflita proporcionalmente cada subconjunto. Um exemplo ilustra como estratificar uma amostra com base no sexo para que seja representativa da população total.

2. 
 ç

 é
 á

5. amostragem

6. Amostra
2
, 
2
,X s

10. 


11. ç
ç




12. é
ç
ç

13. 


14. 
ç
á ç
í


15. 




16. População-alvo
População-
fonte

18. 
ç
ç é
ç
 ç
ç
ç

19. 
ç
ç é
ç
 ç
ç
ç

20. 
é í
ç
í ú

é ç
é
ó

21. 



22.  á é
é í
ç
 é ç
 é ç


24. •
•
•
•
•

25. 




26. 





27. 







28. •

31. 



33. •



35. Um Exemplo:
Em uma população de 200 alunos, há 120 meninos e 80 meninas.
Extraia uma amostra representativa de 10% dessa população.
Nesse exemplo, há uma característica que permite identificar 2
subconjuntos, a característica sexo.
SEXO
POPULAÇÃO
AMOSTRA
(10%)
Masculino 120 12
Feminino 80 8
Total 200 20
- A amostra deve conter 12 alunos do sexo masculino e 8 do
sexo feminino, totalizando 20 alunos, que correspondem a 10%
da população.

36. Amostragem Estratificada
Quando a população possui características que permitem a
criação de subconjuntos, as amostras extraídas por
amostragem simples são menos representativas = Neste
caso, é mais adequado utilizar a amostragem estratificada
Neste tipo de amostragem, os elementos da amostra serão
proporcionais ao número de elementos desses subconjuntos
na população

38. •

40. Seção 4
Seção 5
Seção 3
Seção 2Seção 1

42. 



44. 



46. 

47. 


48. 


49.  ç
ç

í
“ é ç


 ç á
ç

50. 


51. 



53. 53
nX

 
1N
nN
.
nX




54.  




55. 


56. 


57. 

58. 

n
Ze



59. 

n
Ze



62. •
•
•
•

64. 


65. 


66. 

67. 1

N
nN

69. 

70. 

71.   