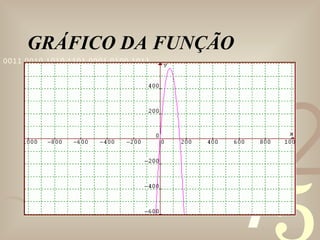
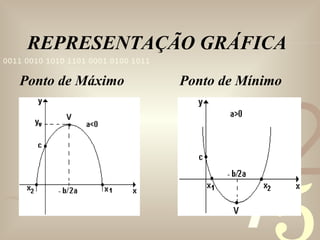
O documento explica como calcular os pontos máximo e mínimo de uma função do segundo grau através da localização do vértice da parábola. Apresenta exemplos de aplicações desses pontos em física e administração e resolve dois problemas, um sobre lançamento de projéteis e outro sobre lucro máximo de uma empresa.



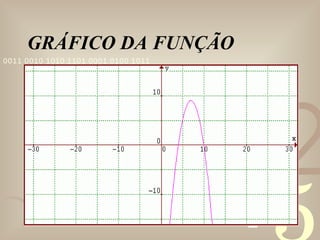
![EXEMPLO 1 - FÍSICA LANÇAMENTO DE PROJÉTEIS Uma bala é atirada de um canhão. A trajetória da bala descreve uma parábola de equação: y = -0,1x2 15x (onde x e y são medidos em metros). a) Determine, em metros, a altura máxima atingida pela Bala; b) Calcule , em metros, o alcance do disparo. Solução: a) O valor máximo (ou mínimo) desta função é o y do vértice da parábola, ou seja, y = - /4a , onde = b2 - 4ac. Então, a altura máxima da bala é: y = -[152 - 4(-0,1)(0)] / 4(-0,1) = -(225 - 0) / (-0,4) = -225 / -0,4 = 2250 / 4 = 562,5 m. b) O alcance do disparo é a diferença entre as raízes da equação -0,1x2 + 15x = 0. Vem que: -0,1x2 + 15x = x(-0,1x + 15) = 0. Então, x = 0 , ou , -0,1x + 15 = 0. Logo as raízes são: x = 0 , ou , x = 15 / 0,1 = 150. Assim, o alcance do disparo é de 150 - 0 = 150 m.](https://image.slidesharecdn.com/pontomximoepontomnimo-091215125013-phpapp02/85/Ponto-MaXimo-E-Ponto-MiNimo-5-320.jpg)