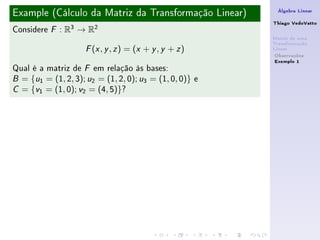
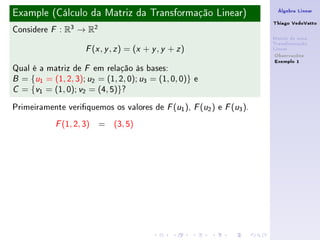
Este documento discute a definição de matriz de uma transformação linear. Ele explica que dadas bases para os espaços vetoriais de entrada e saída, os coeficientes da combinação linear dos vetores de saída em termos da base de saída formam uma matriz que representa a transformação linear entre as bases.

1. Álgebra Linear
Thiago VedoVatto
Curso de Álgebra Linear
Matriz de uma Transformação Linear
Prof. Esp.: Thiago VedoVatto
Universidade Federal de Goiás
Campus Jataí
Coordenação de Matemática
24 de novembro de 2011

2. Álgebra Linear
Thiago VedoVatto
Matriz de uma
Transformação
Linear
Parte I
Observações
Exemplo 1
Matriz de uma Transformação Linear

3. Objetivos da Aula Álgebra Linear
Thiago VedoVatto
Matriz de uma
Transformação
Linear
Observações
Exemplo 1

4. Álgebra Linear
Denição Thiago VedoVatto
Sejam U e V espaços vetoriais sobre R de dimensão m e n
Matriz de uma
respectivamente Transformação
Linear
Observações
Exemplo 1

5. Álgebra Linear
Denição Thiago VedoVatto
Sejam U e V espaços vetoriais sobre R de dimensão m e n
Matriz de uma
respectivamente. Consideremos uma transformação linear Transformação
Linear
F :U→V Observações
Exemplo 1

6. Álgebra Linear
Denição Thiago VedoVatto
Sejam U e V espaços vetoriais sobre R de dimensão m e n
Matriz de uma
respectivamente. Consideremos uma transformação linear Transformação
Linear
F : U → V . Dadas as bases B = { u1 , . . . , un } de U e Observações
Exemplo 1
C = {v1 , . . . , vm } de V

7. Álgebra Linear
Denição Thiago VedoVatto
Sejam U e V espaços vetoriais sobre R de dimensão m e n
Matriz de uma
respectivamente. Consideremos uma transformação linear Transformação
Linear
F : U → V . Dadas as bases B = {u1 , . . . , un } de U e Observações
Exemplo 1
C = {v1 , . . . , vm } de V , então cada um dos vetores
F (u1 ), . . . , F (un ) está em V e consequentemente é combinação
linear da base C

8. Álgebra Linear
Denição Thiago VedoVatto
Sejam U e V espaços vetoriais sobre R de dimensão m e n
Matriz de uma
respectivamente. Consideremos uma transformação linear Transformação
Linear
F : U → V . Dadas as bases B = {u1 , . . . , un } de U e Observações
Exemplo 1
C = {v1 , . . . , vm } de V , então cada um dos vetores
F (u1 ), . . . , F (un ) está em V e consequentemente é combinação
linear da base C :
( )
F u1 = α11 v1 + ... + αm1 vm
. . . .
. . . .
. . . .
( n)
F u = α1n v1 + ... + αmn vm

9. Álgebra Linear
Denição Thiago VedoVatto
Sejam U e V espaços vetoriais sobre R de dimensão m e n
Matriz de uma
respectivamente. Consideremos uma transformação linear Transformação
Linear
F : U → V . Dadas as bases B = {u1 , . . . , un } de U e Observações
Exemplo 1
C = {v1 , . . . , vm } de V , então cada um dos vetores
F (u1 ), . . . , F (un ) está em V e consequentemente é combinação
linear da base C :
( )
F u1 = α11 v1 + ... + αm1 vm
. . . .
. . . .
. . . .
( n)
F u = α1n v1 + ... + αmn vm
Deste modo a matriz m ×n sobre R

10. Álgebra Linear
Denição Thiago VedoVatto
Sejam U e V espaços vetoriais sobre R de dimensão m e n
Matriz de uma
respectivamente. Consideremos uma transformação linear Transformação
Linear
F : U → V . Dadas as bases B = {u1 , . . . , un } de U e Observações
Exemplo 1
C = {v1 , . . . , vm } de V , então cada um dos vetores
F (u1 ), . . . , F (un ) está em V e consequentemente é combinação
linear da base C :
( )
F u1 = α11 v1 + ... + αm1 vm
. . . .
. . . .
. . . .
( n)
F u = α1n v1 + ... + αmn vm
Deste modo a matriz m × n sobre R:
α11 . . . α1n
 
 . . . 
 ..
.
.
. 
.
αm1 . . . αmn

11. Álgebra Linear
Denição Thiago VedoVatto
Sejam U e V espaços vetoriais sobre R de dimensão m e n
Matriz de uma
respectivamente. Consideremos uma transformação linear Transformação
Linear
F : U → V . Dadas as bases B = {u1 , . . . , un } de U e Observações
Exemplo 1
C = {v1 , . . . , vm } de V , então cada um dos vetores
F (u1 ), . . . , F (un ) está em V e consequentemente é combinação
linear da base C :
( )
F u1 = α11 v1 + ... + αm1 vm
. . . .
. . . .
. . . .
( n)
F u = α1n v1 + ... + αmn vm
Deste modo a matriz m × n sobre R:
α11 . . . α1n
 
 . . . 
 ..
.
.
. 
.
αm1 . . . αmn
é chamada Matriz de F em relação às bases B e C

12. Álgebra Linear
Denição Thiago VedoVatto
Sejam U e V espaços vetoriais sobre R de dimensão m e n
Matriz de uma
respectivamente. Consideremos uma transformação linear Transformação
Linear
F : U → V . Dadas as bases B = {u1 , . . . , un } de U e Observações
Exemplo 1
C = {v1 , . . . , vm } de V , então cada um dos vetores
F (u1 ), . . . , F (un ) está em V e consequentemente é combinação
linear da base C :
( )
F u1 = α11 v1 + ... + αm1 vm
. . . .
. . . .
. . . .
( n)
F u = α1n v1 + ... + αmn vm
Deste modo a matriz m × n sobre R:
α11 . . . α1n
 
 . . . 
 ..
.
.
. 
.
αm1 . . . αmn
é chamada Matriz de F em relação às bases B e C . Usaremos
para indicar essa matriz a notação (F )B ,C

13. Álgebra Linear
Thiago VedoVatto
Matriz de uma
Transformação
Linear
Observações
Exemplo 1
Se F é um operador linear e considerarmos B=C, então
diremos apenas matriz de F em relação à base B para indicar
a matriz acima denida e usaremos a notação (F )B para
representá-la;

14. Álgebra Linear
Thiago VedoVatto
Matriz de uma
Transformação
Linear
Observações
Exemplo 1
Se F é um operador linear e considerarmos B=C, então
diremos apenas matriz de F em relação à base B para indicar
a matriz acima denida e usaremos a notação (F )B para
representá-la;
Sempre que não haja dúvidas quanto ao par de bases que
estamos considerando escreveremos apenas (F ) em relação a
esse par de bases.

15. Example (Cálculo da Matriz da Transformação Linear) Álgebra Linear
Thiago VedoVatto
Considere F : R3 → R2
Matriz de uma
Transformação
( , , ) = (x + y , y + z )
F x y z Linear
Observações
Exemplo 1
Qual é a matriz de F em relação às bases:
B = {u1 = (1, 2, 3); u2 = (1, 2, 0); u3 = (1, 0, 0)} e
C = {v1 = (1, 0); v2 = (4, 5)}?

16. Example (Cálculo da Matriz da Transformação Linear) Álgebra Linear
Thiago VedoVatto
Considere F : R3 → R2
Matriz de uma
Transformação
( , , ) = (x + y , y + z )
F x y z Linear
Observações
Exemplo 1
Qual é a matriz de F em relação às bases:
B = {u1 = (1, 2, 3); u2 = (1, 2, 0); u3 = (1, 0, 0)} e
C = {v1 = (1, 0); v2 = (4, 5)}?
Primeiramente veriquemos os valores de F (u1 ), F (u2 ) e F (u3 )

17. Example (Cálculo da Matriz da Transformação Linear) Álgebra Linear
Thiago VedoVatto
Considere F : R3 → R2
Matriz de uma
Transformação
( , , ) = (x + y , y + z )
F x y z Linear
Observações
Exemplo 1
Qual é a matriz de F em relação às bases:
B = {u1 = (1, 2, 3); u2 = (1, 2, 0); u3 = (1, 0, 0)} e
C = {v1 = (1, 0); v2 = (4, 5)}?
Primeiramente veriquemos os valores de F (u1 ), F (u2 ) e F (u3 ).
F (1, 2, 3) = (3, 5)

18. Example (Cálculo da Matriz da Transformação Linear) Álgebra Linear
Thiago VedoVatto
Considere F : R3 → R2
Matriz de uma
Transformação
( , , ) = (x + y , y + z )
F x y z Linear
Observações
Exemplo 1
Qual é a matriz de F em relação às bases:
B = {u1 = (1, 2, 3); u2 = (1, 2, 0); u3 = (1, 0, 0)} e
C = {v1 = (1, 0); v2 = (4, 5)}?
Primeiramente veriquemos os valores de F (u1 ), F (u2 ) e F (u3 ).
F (1, 2, 3) = (3, 5)
F (1, 2, 0) = (3, 2)

19. Example (Cálculo da Matriz da Transformação Linear) Álgebra Linear
Thiago VedoVatto
Considere F : R3 → R2
Matriz de uma
Transformação
( , , ) = (x + y , y + z )
F x y z Linear
Observações
Exemplo 1
Qual é a matriz de F em relação às bases:
B = {u1 = (1, 2, 3); u2 = (1, 2, 0); u3 = (1, 0, 0)} e
C = {v1 = (1, 0); v2 = (4, 5)}?
Primeiramente veriquemos os valores de F (u1 ), F (u2 ) e F (u3 ).
F (1, 2, 3) = (3, 5)
F (1, 2, 0) = (3, 2)
F (1, 0, 0) = (1, 0)

20. Example (Cálculo da Matriz da Transformação Linear) Álgebra Linear
Thiago VedoVatto
Considere F : R3 → R2
Matriz de uma
Transformação
( , , ) = (x + y , y + z )
F x y z Linear
Observações
Exemplo 1
Qual é a matriz de F em relação às bases:
B = {u1 = (1, 2, 3); u2 = (1, 2, 0); u3 = (1, 0, 0)} e
C = {v1 = (1, 0); v2 = (4, 5)}?
Primeiramente veriquemos os valores de F (u1 ), F (u2 ) e F (u3 ).
F (1, 2, 3) = (3, 5)
F (1, 2, 0) = (3, 2)
F (1, 0, 0) = (1, 0)
Agora escrevamos os vetores obtidos como combinação linear dos
vetores da base C

21. Álgebra Linear
Thiago VedoVatto
Para tanto: Matriz de uma
Transformação
Linear
Observações
(3, 5) = x (1, 0) + y (4, 5) Exemplo 1

22. Álgebra Linear
Thiago VedoVatto
Para tanto: Matriz de uma
Transformação
Linear
Observações
(3, 5) = x (1, 0) + y (4, 5) Exemplo 1
= (x , 0) + (4y , 5y )

23. Álgebra Linear
Thiago VedoVatto
Para tanto: Matriz de uma
Transformação
Linear
Observações
(3, 5) = x (1, 0) + y (4, 5) Exemplo 1
= (x , 0) + (4y , 5y )
= (x + 4y , 5y )

24. Álgebra Linear
Thiago VedoVatto
Para tanto: Matriz de uma
Transformação
Linear
Observações
(3, 5) = x (1, 0) + y (4, 5) Exemplo 1
= (x , 0) + (4y , 5y )
= (x + 4y , 5y )
Deste modo obtemos o sistema linear:
x + 4y = 3

25. Álgebra Linear
Thiago VedoVatto
Para tanto: Matriz de uma
Transformação
Linear
Observações
(3, 5) = x (1, 0) + y (4, 5) Exemplo 1
= (x , 0) + (4y , 5y )
= (x + 4y , 5y )
Deste modo obtemos o sistema linear:
x + 4y = 3
5y = 5

26. Álgebra Linear
Thiago VedoVatto
Para tanto: Matriz de uma
Transformação
Linear
Observações
(3, 5) = x (1, 0) + y (4, 5) Exemplo 1
= (x , 0) + (4y , 5y )
= (x + 4y , 5y )
Deste modo obtemos o sistema linear:
x + 4y = 3
5y = 5
Cuja solução será x = −1 e y =1

27. Álgebra Linear
Thiago VedoVatto
Para tanto: Matriz de uma
Transformação
Linear
Observações
(3, 5) = x (1, 0) + y (4, 5) Exemplo 1
= (x , 0) + (4y , 5y )
= (x + 4y , 5y )
Deste modo obtemos o sistema linear:
x + 4y = 3
5y = 5
Cuja solução será x = −1 e y = 1.
Logo:
(3, 5) = −1(1, 0) + 1(4, 5)

28. Example (Cálculo da Matriz da Transformação Linear) Álgebra Linear
Thiago VedoVatto
Considere F : R3 → R2
Matriz de uma
Transformação
( , , ) = (x + y , y + z )
F x y z Linear
Observações
Exemplo 1
Qual é a matriz de F em relação às bases:
B = {u1 = (1, 2, 3); u2 = (1, 2, 0); u3 = (1, 0, 0)} e
C = {v1 = (1, 0); v2 = (4, 5)}?
Primeiramente veriquemos os valores de F (u1 ), F (u2 ) e F (u3 ).
F (1, 2, 3) = (3, 5) = − 1(1, 0) + 1(4, 5)
F (1, 2, 0) = (3, 2)
F (1, 0, 0) = (1, 0)
Agora escrevamos os vetores obtidos como combinação linear dos
vetores da base C .

29. Álgebra Linear
Thiago VedoVatto
Para tanto: Matriz de uma
Transformação
Linear
(3, 2) = x (1, 0) + y (4, 5) Observações
Exemplo 1

30. Álgebra Linear
Thiago VedoVatto
Para tanto: Matriz de uma
Transformação
Linear
(3, 2) = x (1, 0) + y (4, 5) Observações
Exemplo 1
= (x , 0) + (4y , 5y )

31. Álgebra Linear
Thiago VedoVatto
Para tanto: Matriz de uma
Transformação
Linear
(3, 2) = x (1, 0) + y (4, 5) Observações
Exemplo 1
= (x , 0) + (4y , 5y )
= (x + 4y , 5y )

32. Álgebra Linear
Thiago VedoVatto
Para tanto: Matriz de uma
Transformação
Linear
(3, 2) = x (1, 0) + y (4, 5) Observações
Exemplo 1
= (x , 0) + (4y , 5y )
= (x + 4y , 5y )
Deste modo obtemos o sistema linear:
x + 4y = 3

33. Álgebra Linear
Thiago VedoVatto
Para tanto: Matriz de uma
Transformação
Linear
(3, 2) = x (1, 0) + y (4, 5) Observações
Exemplo 1
= (x , 0) + (4y , 5y )
= (x + 4y , 5y )
Deste modo obtemos o sistema linear:
x + 4y = 3
5y = 2

34. Álgebra Linear
Thiago VedoVatto
Para tanto: Matriz de uma
Transformação
Linear
(3, 2) = x (1, 0) + y (4, 5) Observações
Exemplo 1
= (x , 0) + (4y , 5y )
= (x + 4y , 5y )
Deste modo obtemos o sistema linear:
x + 4y = 3
5y = 2
7 2
Cuja solução será x = 5 e y = 5

35. Álgebra Linear
Thiago VedoVatto
Para tanto: Matriz de uma
Transformação
Linear
(3, 2) = x (1, 0) + y (4, 5) Observações
Exemplo 1
= (x , 0) + (4y , 5y )
= (x + 4y , 5y )
Deste modo obtemos o sistema linear:
x + 4y = 3
5y = 2
7 2
Cuja solução será x = 5 e y = 5.
Logo:
7 2
(3, 2) = (1, 0) + (4, 5)
5 5

36. Example (Cálculo da Matriz da Transformação Linear) Álgebra Linear
Thiago VedoVatto
Considere F : R3 → R2
Matriz de uma
Transformação
( , , ) = (x + y , y + z )
F x y z Linear
Observações
Exemplo 1
Qual é a matriz de F em relação às bases:
B = {u1 = (1, 2, 3); u2 = (1, 2, 0); u3 = (1, 0, 0)} e
C = {v1 = (1, 0); v2 = (4, 5)}?
Primeiramente veriquemos os valores de F (u1 ), F (u2 ) e F (u3 ).
F (1, 2, 3) = (3, 5) = − 1(1, 0) + 1(4, 5)
7 2
F (1, 2, 0) = (3, 2) = (1, 0) + (4, 5)
5 5
F (1, 0, 0) = (1, 0)
Agora escrevamos os vetores obtidos como combinação linear dos
vetores da base C .

37. Álgebra Linear
Thiago VedoVatto
Para tanto: Matriz de uma
Transformação
Linear
Observações
(1, 0) = x (1, 0) + y (4, 5) Exemplo 1

38. Álgebra Linear
Thiago VedoVatto
Para tanto: Matriz de uma
Transformação
Linear
Observações
(1, 0) = x (1, 0) + y (4, 5) Exemplo 1
= (x , 0) + (4y , 5y )

39. Álgebra Linear
Thiago VedoVatto
Para tanto: Matriz de uma
Transformação
Linear
Observações
(1, 0) = x (1, 0) + y (4, 5) Exemplo 1
= (x , 0) + (4y , 5y )
= (x + 4y , 5y )

40. Álgebra Linear
Thiago VedoVatto
Para tanto: Matriz de uma
Transformação
Linear
Observações
(1, 0) = x (1, 0) + y (4, 5) Exemplo 1
= (x , 0) + (4y , 5y )
= (x + 4y , 5y )
Deste modo obtemos o sistema linear:
x + 4y = 1

41. Álgebra Linear
Thiago VedoVatto
Para tanto: Matriz de uma
Transformação
Linear
Observações
(1, 0) = x (1, 0) + y (4, 5) Exemplo 1
= (x , 0) + (4y , 5y )
= (x + 4y , 5y )
Deste modo obtemos o sistema linear:
x + 4y = 1
5y = 0

42. Álgebra Linear
Thiago VedoVatto
Para tanto: Matriz de uma
Transformação
Linear
Observações
(1, 0) = x (1, 0) + y (4, 5) Exemplo 1
= (x , 0) + (4y , 5y )
= (x + 4y , 5y )
Deste modo obtemos o sistema linear:
x + 4y = 1
5y = 0
Cuja solução será x =1e y =0

43. Álgebra Linear
Thiago VedoVatto
Para tanto: Matriz de uma
Transformação
Linear
Observações
(1, 0) = x (1, 0) + y (4, 5) Exemplo 1
= (x , 0) + (4y , 5y )
= (x + 4y , 5y )
Deste modo obtemos o sistema linear:
x + 4y = 1
5y = 0
Cuja solução será x =1e y = 0.
Logo:
(1, 0) = 1(1, 0) + 0(4, 5)

44. Example (Cálculo da Matriz da Transformação Linear) Álgebra Linear
Thiago VedoVatto
Considere F : R3 → R2
Matriz de uma
Transformação
( , , ) = (x + y , y + z )
F x y z Linear
Observações
Exemplo 1
Qual é a matriz de F em relação às bases:
B = {u1 = (1, 2, 3); u2 = (1, 2, 0); u3 = (1, 0, 0)} e
C = {v1 = (1, 0); v2 = (4, 5)}?
Primeiramente veriquemos os valores de F (u1 ), F (u2 ) e F (u3 ).
F (1, 2, 3) = (3, 5) = − 1(1, 0) + 1(4, 5)
7 2
F (1, 2, 0) = (3, 2) = (1, 0) + (4, 5)
5 5
F (1, 0, 0) = (1, 0) = 1(1, 0) + 0(4, 5)
Agora escrevamos os vetores obtidos como combinação linear dos
vetores da base C .

45. Example (Cálculo da Matriz da Transformação Linear) Álgebra Linear
Thiago VedoVatto
Considere F : R3 → R2
Matriz de uma
Transformação
( , , ) = (x + y , y + z )
F x y z Linear
Observações
Exemplo 1
Qual é a matriz de F em relação às bases:
B = {u1 = (1, 2, 3); u2 = (1, 2, 0); u3 = (1, 0, 0)} e
C = {v1 = (1, 0); v2 = (4, 5)}?
Primeiramente veriquemos os valores de F (u1 ), F (u2 ) e F (u3 ).
F (1, 2, 3) = (3, 5) = − 1(1, 0) + 1(4, 5)
7 2
F (1, 2, 0) = (3, 2) = (1, 0) + (4, 5)
5 5
F (1, 0, 0) = (1, 0) = 1(1, 0) + 0(4, 5)
Agora escrevamos os vetores obtidos como combinação linear dos
vetores da base C . Deste modo a Matriz da Transformação Linear
F em relação as bases B e C será:
7
−1 5 1
(F )B ,C = 2
1 5 0