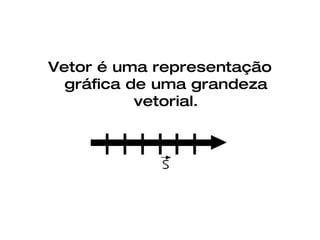
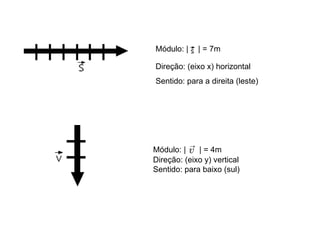
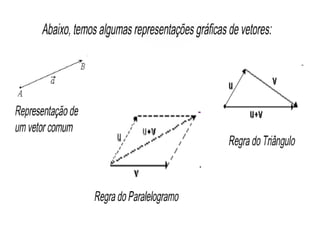
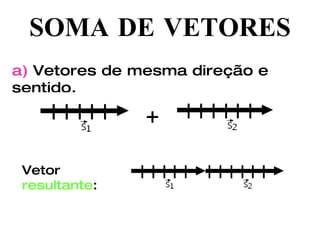
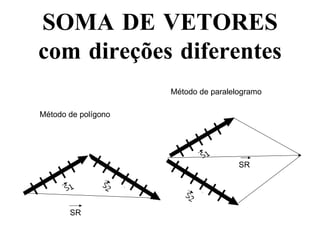
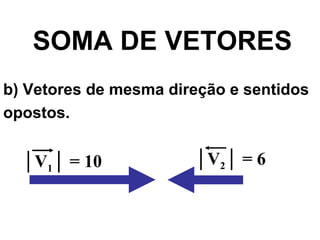
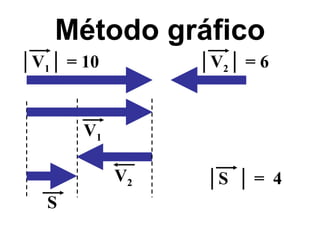
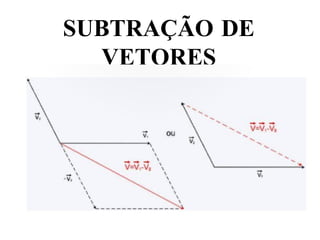
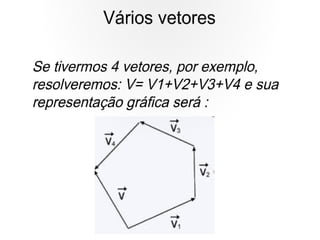
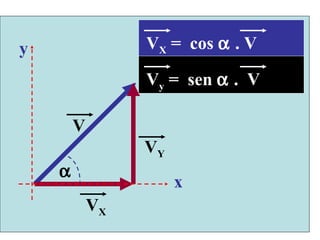
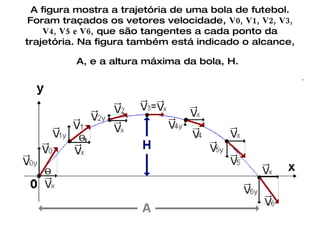
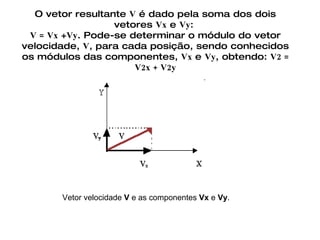
O documento discute vetores e lançamento de projéteis. Explica que vetores dependem de número, direção e sentido, enquanto escalares dependem apenas de valor numérico. Descreve como somar e subtrair vetores e decompor um vetor em componentes. Também explica a trajetória de um projétil lançado com um ângulo, com vetores de velocidade e como calcular as componentes da velocidade inicial.

1. VETORES

2. Grandezas Vetoriais dependem de - Número - Direção - Sentido Grandezas Escalares dependem só do - Valor numérico (Por ex.: Tenho 60 k, ou São 11 horas.)

3. Vetor é uma representação gráfica de uma grandeza vetorial.

4. Módulo: | | = 7m Direção: (eixo x) horizontal Sentido: para a direita (leste) Módulo: | | = 4m Direção: (eixo y) vertical Sentido: para baixo (sul)

6. SOMA DE VETORES a) Vetores de mesma direção e sentido. + Vetor resultante :

7. Método algébrico S = 6 + 7 │ S │ = 13 S = V 1 + V 2

8. SOMA DE VETORES com direções diferentes Método de polígono Método de paralelogramo SR SR

9. SOMA DE VETORES b) Vetores de mesma direção e sentidos opostos. │ V 1 │ = 10 │ V 2 │ = 6

10. Método algébrico S = 10 + (- 6 ) │ S │ = 4 S = V 1 + V 2

11. Método gráfico S V 1 V 2 │ V 1 │ = 10 │ V 2 │ = 6 │ S │ = 4

12. SUBTRAÇÃO DE VETORES

14. DECOMPOSIÇÃO DE VETORES Um vetor V pode ser decomposto em dois vetores componentes: V x (componente horizontal) e V y (componente vertical), de modo que:

15. V V Y V X  x y V X = cos  . V V y = sen  . V

16. LANÇAMENTO DE PROJÉTEIS

17. A figura mostra a trajetória de uma bola de futebol. Foram traçados os vetores velocidade, V0, V1, V2, V3, V4, V5 e V6, que são tangentes a cada ponto da trajetória. Na figura também está indicado o alcance, A, e a altura máxima da bola, H.

18. Estes vetores velocidade apresentam as componentes, Vx e Vy, para cada posição, nas direções X e Y. Na direção X o movimento é uniforme, o valor da componente Vx será constante. Na direção Y o movimento é uniformemente variado, portanto cada componente Vy terá um valor. Observe que, vetorialmente, o valor de Vy diminui na subida, anula-se no vértice da parábola (altura máxima) e aumenta na descida. A bola foi lançada a partir de O (origem), fazendo um ângulo com a horizontal. Para determinar as componentes Vx e V0y , sendo conhecidos o ângulo e a velocidade V0 , basta projetar o vetor V0 nas duas direções X e Y, obtendo: V0y = V0 sen θ V0x = V0 cos θ

19. O vetor resultante V é dado pela soma dos dois vetores Vx e Vy : V = Vx + Vy . Pode-se determinar o módulo do vetor velocidade, V , para cada posição, sendo conhecidos os módulos das componentes, Vx e Vy , obtendo: V2 = V2x + V2y Vetor velocidade V e as componentes Vx e Vy .

20. Sites de informação sobre as fórmulas http://www.algosobre.com.br/fisica/balistica-e-lancamento-de-projetil.html http://www.fisica.ufpb.br/prolicen/Cursos/Curso1/mr35lp.html http://prolina.df.ibilce.unesp.br/walter/fis_geral/proj/projetil2.html

21. Formulário Queda Livre: V=Vo+gt Sy=Soy+Voy.t+gt²/2 V²=Vo²+2gΔs Lançamento vertical para cima: Sy=Soy+Voy.t-gt²/2 Vy²=Voy²+2(-g)Δsy Vt=Voy-gt

22. Lançamento “oblíquo” Sy=Soy+Voy.t-gt²/2 hmáx= voy²/2g Sy=Sx.tgθ – g/2 (sx/vox)² R= 2.voy.vox g vox=vo.cos θ voy=vo.sen θ v= raiz de (vox²+vy²) Vy²=Voy²-2.g.Δsy Sx=vox.t Vy=voy-gt Lançamento horizontal Sy=sox+vox.t Vy²=Voy²+2.g.Δsy Vy=voy+gt v= raiz de (vox²+vy²)

23. Vídeos sobre Vetores http://www.youtube.com/watch?v=dFB5sz0PWVE http://www.youtube.com/watch?v=mtNIaRk1XOE http://www.youtube.com/watch?v=qvWh2Gf3PPw

24. Informações sobre Vetores http://educar.sc.usp.br/fisica/vetores.html http://pt.wikipedia.org/wiki/Vetor_%28espacial%29 http://efisica.if.usp.br/mecanica/universitario/vetores/ http://www.mspc.eng.br/matm/vetor110.shtml

25. Simuladores de vetores http://fisica.ufpr.br/ntnujava/vector/vector.html http://www.frontiernet.net/~imaging/vector_calculator.html http://www.fisica.ufpb.br/prolicen/Applets/Applets1/Vetores/SomaVet.html

26. Simuladores de lançamento de Projéteis http://portal.if.uff.br/applets/projeteis http://www.walter-fendt.de/ph14br/projectile_br.htm

27. Natalie Bang e Mariana Meleiro 2ºC