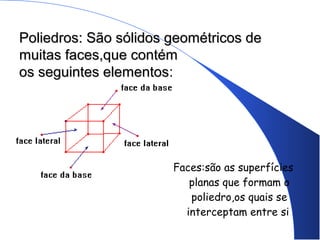
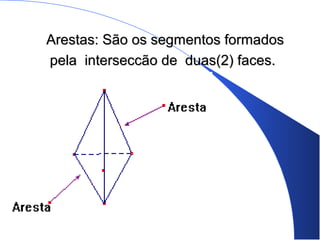
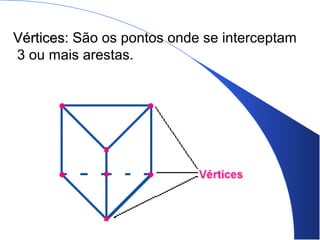
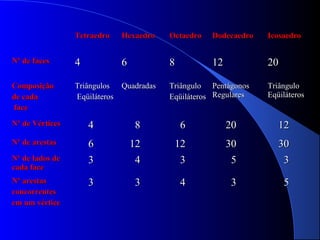
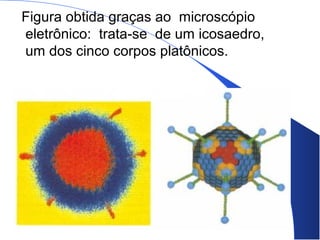
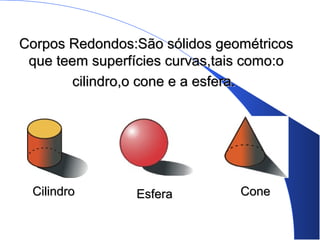
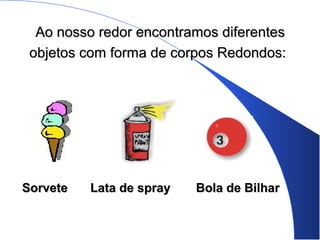
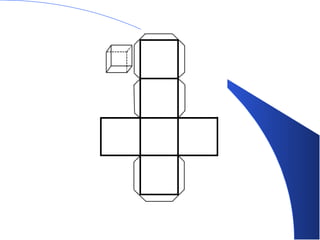
O documento lista os componentes de um grupo de estudos e fornece informações sobre poliedros e corpos geométricos. Descreve os elementos dos poliedros como faces, arestas e vértices e lista os cinco poliedros regulares. Também discute corpos redondos como cilindros, cones e esferas e fornece exemplos de como esses objetos aparecem na vida cotidiana.

1. • Irani Aparecida B. da SilvaIrani Aparecida B. da Silva
• Elaine Gomide Silva DejaviteElaine Gomide Silva Dejavite
• Juliano César OdorissioJuliano César Odorissio
• Denise Cristina C. B. LucianoDenise Cristina C. B. Luciano
• Renato Ferreira da SouzaRenato Ferreira da Souza
• João Francisco SilvaJoão Francisco Silva
Componentes do GrupoComponentes do Grupo

2. Poliedros: São sólidos geométricos dePoliedros: São sólidos geométricos de
muitas faces,que contémmuitas faces,que contém
os seguintes elementosos seguintes elementos:
Faces:são as superfícies
planas que formam o
poliedro,os quais se
interceptam entre si.

3. Poliedros regulares,Poliedros regulares, são aquelessão aqueles
cuja faces são polígonos regularescuja faces são polígonos regulares
congruentes entre si(de igual medida)congruentes entre si(de igual medida)
e cujo ângulos poliédricos são iguais.e cujo ângulos poliédricos são iguais.
Existe apenas 5 poliedros regulares:Existe apenas 5 poliedros regulares:
Tetraedro,.Hexaedro,Octaedro,Dode-Tetraedro,.Hexaedro,Octaedro,Dode-
caedro,Icosaedro.caedro,Icosaedro.

4. Para os Matemáticos Gregos conhecedoresPara os Matemáticos Gregos conhecedores
de Geometria, o estudo dos poliedros foide Geometria, o estudo dos poliedros foi
muito importante para conhecimento damuito importante para conhecimento da
existência desses cincos únicos sólidosexistência desses cincos únicos sólidos
regulares,cujos descobrimento foramregulares,cujos descobrimento foram
Atribuídos alguns, ao próprio Pitágoras,Atribuídos alguns, ao próprio Pitágoras,
onde Platão recorreu para explicar a criaçãoonde Platão recorreu para explicar a criação
do universo.do universo.

5. Leonhard EulerLeonhard Euler fez una famosafez una famosa
demonstração em 1752.demonstração em 1752.
Euler demonstrou que, se somado o númeroEuler demonstrou que, se somado o número
de faces e o número de vértices de umde faces e o número de vértices de um
poliedro convexo e, do valor obtido, subtraindo-poliedro convexo e, do valor obtido, subtraindo-
se então o número de arestas, e o resultado ése então o número de arestas, e o resultado é
sempre igual a 2.sempre igual a 2.
Deste resultado, válido para todo poliedroDeste resultado, válido para todo poliedro
convexo, se deduz facilmente a existênciaconvexo, se deduz facilmente a existência
unicamente de cinco poliedros regulares.unicamente de cinco poliedros regulares.

6. Sem censura,não consta, que
conheceram importantes resultados
relativos aos números de
Vértices,arestas,e faces de um
poliedro convexo, observado por
Descartes e o matemático suiço
Leonhard Euler

7. Arestas: São os segmentos formadosArestas: São os segmentos formados
pela interseccão de duas(2) faces.pela interseccão de duas(2) faces.

8. VérticesVértices: São os pontos onde se interceptam
3 ou mais arestas.

9. TetraedroTetraedro HexaedroHexaedro OctaedroOctaedro DodecaedroDodecaedro IcosaedroIcosaedro
Nº de facesNº de faces 44 66 88 1212 2020
ComposiçãoComposição
de cadade cada
faceface
TriângulosTriângulos
EqüiláterosEqüiláteros
QuadradasQuadradas TriânguloTriângulo
EqüiláterosEqüiláteros
PentágonosPentágonos
RegularesRegulares
TriânguloTriângulo
EqüiláterosEqüiláteros
Nº de VérticesNº de Vértices 44 88 66 2020 1212
Nº de arestasNº de arestas 66 1212 1212 3030 3030
Nº de lados deNº de lados de
cada facecada face
33 44 33 55 33
Nº arestasNº arestas
concorrentesconcorrentes
em um vérticeem um vértice
33 33 44 33 55

10. Os corpos geométricos podem ser:Os corpos geométricos podem ser:
Poliedros e Corpos Redondos.Poliedros e Corpos Redondos.

11. Em diferentes lugares do planeta, tanto naEm diferentes lugares do planeta, tanto na
natureza, como em construcões feitas pelosnatureza, como em construcões feitas pelos
homens, podemos encontrar diferenteshomens, podemos encontrar diferentes
Corpos GeométricosCorpos Geométricos
Torres do castelo deTorres do castelo de
World DisneyWorld Disney
Pirâmides do EgitoPirâmides do Egito

12. ParqueParque MontanhasMontanhas

13. Poliedro de CaracasPoliedro de Caracas

14. Utilidade: A maioria dos poliedros sãoUtilidade: A maioria dos poliedros são
figuras que existe na realidade. Umfiguras que existe na realidade. Um
exemplo deles são as pirâmides e osexemplo deles são as pirâmides e os
vírus.vírus.
Graças ao microscópio eletrônico tem sidoGraças ao microscópio eletrônico tem sido
possível visualizar a estrutura dos vírus.possível visualizar a estrutura dos vírus.
O corpo geométrico que veremos , noO corpo geométrico que veremos , no
próximo slide,é a imagem realizada porpróximo slide,é a imagem realizada por
um observador,de um adenovirus a partirum observador,de um adenovirus a partir
da micrografiada micrografia..

15. Figura obtida graças ao microscópio
eletrônico: trata-se de um icosaedro,
um dos cinco corpos platônicos.

16. Corpos Redondos:São sólidos geométricosCorpos Redondos:São sólidos geométricos
que teem superfícies curvas,tais como:oque teem superfícies curvas,tais como:o
cilindro,o cone e a esfera.cilindro,o cone e a esfera.
CilindroCilindro EsferaEsfera ConeCone

17. Em nossas vidas cotidiana existe objetosEm nossas vidas cotidiana existe objetos
que tem forma de corpos redondos,comoque tem forma de corpos redondos,como
por exemplo:os tanques para líquidos epor exemplo:os tanques para líquidos e
gases.gases.

18. Ao nosso redor encontramos diferentesAo nosso redor encontramos diferentes
objetos com forma de corpos Redondos:objetos com forma de corpos Redondos:
SorveteSorvete Lata de sprayLata de spray Bola de BilharBola de Bilhar

19. .
CuboCubo
Traça-se quatro(4) quadrados iguais,umTraça-se quatro(4) quadrados iguais,um
seguidamente ao outro.seguidamente ao outro.
2.- Em seguida distribua-se dois(2)2.- Em seguida distribua-se dois(2)
quadrados, porém a cada lado dos quequadrados, porém a cada lado dos que
existem anteriormente.existem anteriormente.
3.- Lembre-se que se devem traçar suas3.- Lembre-se que se devem traçar suas
respectivas dobras para assim construirrespectivas dobras para assim construir
todo o corpo geométrico e formar a figura.todo o corpo geométrico e formar a figura.
Nota: A longitude dos quadrados devemNota: A longitude dos quadrados devem
ser de igual medida em todos osser de igual medida em todos os
quadrados.quadrados.

21. ConeCone:
1 – Trace-se um círculo,que será a1 – Trace-se um círculo,que será a
base.base.
2. – Em seguida distribua-se um2. – Em seguida distribua-se um
triângulo cuja base deve ser emtriângulo cuja base deve ser em
forma de arcoforma de arco
3. – As dobras devem ser cortadas3. – As dobras devem ser cortadas
Na base do triângulo.Na base do triângulo.

22. Pirâmide Triangular:
1.- Se traçam três (3) triângulos iguais, um
em continuação ao outro.
2.- Em seguida distribua-se outro triângulo
menor,no qual servirá como base debaixo
de algum dos traçados anteriormente.
3.- Lembre-se de recortar as dobras.

23. Pirâmide Triangular
1.- Se traçam três (3) triângulos
iguais, um em continuação ao
outro.
2.- Em seguida distribua-se outro
triângulo menor,no qual servirá
como base debaixo de algum dos
traçados anteriormente.
3.- Lembre-se de recortar as
dobras.

24. Considerações GeraisConsiderações Gerais
A escola deve formar cidadãos que se
posicionem diante de questões sociais e que
estejam inseridos no trabalho e na cultura. O que
temos de preocuparmos não é somente o que se
deve aprender, mais como aprender ,o porquê e
para que. Deve-se sempre ter em mente que para
a formação do cidadão é de grande importância à
valorização da natureza, às artes, à tecnologia, às
construções e edificações, às maravilhas do
mundo representas pelas pirâmides que
marcaram as existências de civilizações antigas,
um verdadeiro marco da História.

25. • Levar o educando a criar sentidos,da
fundamentação de ação no seu ambiente
cultural, de modo que haja coerência,
harmonia no sentir e pensar e o fazer. O
sentido e o simbolismo, portanto, se articulam
e se completam e faz com que se conheça o
mundo.
• De acordo com as considerações acima
propomos que o conteúdo descrito abaixo seja
fruto de melhor observação por parte do
educando ,que a matemática não objetive
apenas o cálculo e que sirva de análise nas
atividades do nosso cotidiano e de teor prático
em nossas vidas..

26. BibliografiaBibliografia
Na Internet você poderá ter acesso a diversos
sites. O referido trabalho foi pesquisado nos
sites:
http://www.profesorenlinea.cl/geometria/cuerposgeometricos.htm
http://www.ue.nsc.com/cuerposgeometrico.html
http://www.profesorenlinea.cl
Você poderá acessar ainda:
http://www.geoeuclidiana.hpg.ig.com.br/prismas.htm,
Neste site encontrará definições e resoluções de
problemas.