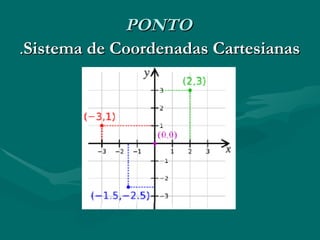
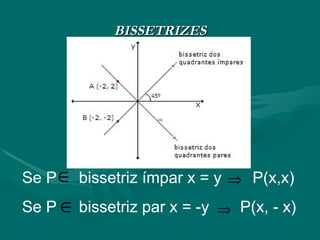
O documento descreve os conceitos básicos de geometria analítica, incluindo a origem da geometria analítica com René Descartes, a representação de pontos em um sistema de coordenadas cartesianas com pares ordenados (x, y), e a definição de bissetrizes de quadrantes ímpares e pares.

1. GEOMETRIA ANALÍTICA: PONTO E RETA Profª.: Marlúcia Brasil Colégio Manoel Novaes

2. ORIGEM A geometria analítica foi concebida por René Descartes. Aliando a álgebra à geometria, ela possibilita o estudo das figuras geométricas,associando-as a um sistema de coordenadas; desse modo as figuras podem ser representa- das por meio de pares ordenados,equa- ções ou inequações.

3. PONTO . Sistema de Coordenadas Cartesianas

4. EIXO COORDENADOS . Eixo Ox: abscissa do ponto P; . Eixo Oy: ordenada do ponto P; Representação: P(x p, y p ) Se P eixo Ox P(x,0) Se P eixo Oy P(0,y)

5. Sistema de Coordenadas Cartesianas . Quadrantes

6. BISSETRIZES Se P bissetriz ímpar x = y P(x,x) Se P bissetriz par x = -y P(x, - x)

7. Resolução de Exemplos: 1)Determine o valor de n,de forma que o ponto (10,2n – 4) pertençam à bissetriz dos quadrantes ímpares. 2)Obtenha o valor de p,de tal forma que o ponto (8, 3 + )pertençam à bissetriz dos quadrantes pares. ATIVIDADE PROPOSTA : Lista complementar