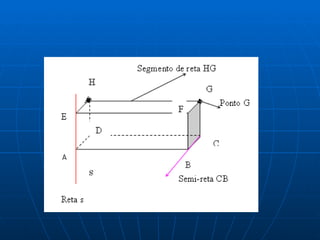
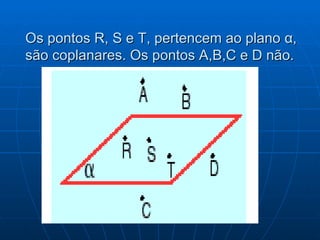
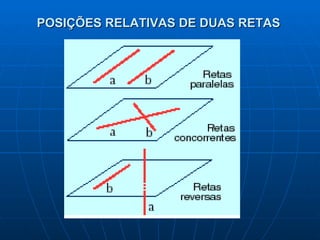
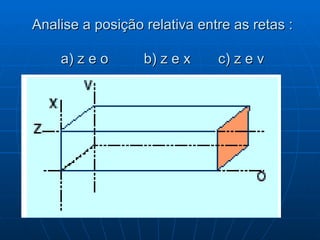
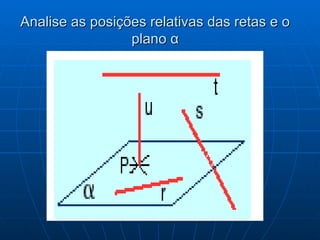
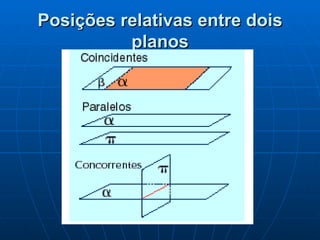
Este documento discute conceitos fundamentais de geometria de posição, incluindo pontos, retas, planos e suas posições relativas. Ele define planos como determinados por três pontos não-colineares ou duas retas paralelas/concorrentes, e discute posições de pontos e retas em relação a planos, como paralelas, contidas ou secantes. Também aborda perpendicularidade entre retas, retas e planos e planos.

1. GEOMETRIA DE POSIÇÃO A geometria de posição estuda as figuras geométricas quanto à sua forma e sua posição, e a geometria métrica as estuda em relação às sua medidas.

2. CONCEITOS FUNDAMENTAIS DA GEOMETRIA DE POSIÇAÕ: . Ponto . Reta . Semi-reta . Segmento de reta

4. DETERMINAÇÃO DE UM PLANO .Três pontos não-colineares determinam um plano. .Duas retas paralelas distintas. .Duas retas concorrentes. .Uma reta e um ponto não pertencente a ela.

5. Dado um plano no espaço,existem infinitos pontos que pertencem a ele. Posições relativas de pontos no espaço: .Eles são ou não pontos colineares ; .Eles são ou não pontos coplanares;

6. Os pontos R, S e T, pertencem ao plano α , são coplanares. Os pontos A,B,C e D não.

7. POSIÇÕES RELATIVAS DE DUAS RETAS

8. Analise a posição relativa entre as retas : a) z e o b) z e x c) z e v

9. Posições relativas entre reta e plano : . Reta paralela ao plano . Reta está contida no plano .Reta secante (ou concorrente) ao plano

10. Analise as posições relativas das retas e o plano α

11. Posições relativas entre dois planos

12. PERPENDICULARIDADE . Entre retas : Duas retas são perpendiculares se,e somente se,são concorrentes e formam ângulos retos entre si. . Entre reta e plano: Uma reta é perpendicular a um plano α se,e somente se,todas as retas do plano α que concorrem com a reta r são perpendiculares a r . . Entre planos: Dois planos são perpendiculares se,e somente se, existe uma reta contida em um deles e perpendicular ao outro.

13. ATIVIDADE PROPOSTA: 1.Lista de exercício complementar disponível no xerox do colégio (01 página) 2.Livro adotado,página 379, apenas o exercício 01 Profª Marlúcia Brasil Colégio Manoel Novaes