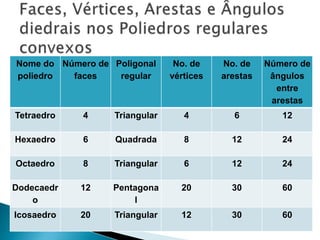
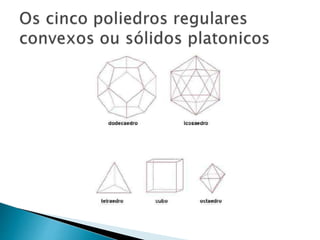
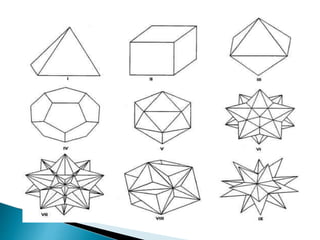
O documento discute polígonos e poliedros, incluindo suas definições e exemplos. Polígonos são figuras planas com três ou mais lados, enquanto poliedros são figuras sólidas delimitadas por planos. Os cinco poliedros regulares são o tetraedro, cubo, octaedro, dodecaedro e icosaedro.

1. Polígonos
Em geometria, uma figura plana (duas dimensões)
com três ou mais lados. Os polígonos comuns têm
nomes que definem o número de lados (por exemplo,
triângulo, quadrilátero, pentágono).

2.  Triângulo - 3 lados
 Quadrilátero – 4 lados

3.  Pentágono - 5 lados
 Hexágono - 6 lados Octágono - 8 lados
Obs. Estas figuras são regulares.

4. Estes são todos polígonos
convexos, sem nenhum ângulo
interno maior do que 180º;. A soma
dos ângulos internos de um polígono
com n lados é dada pela fórmula (2n
- 4) x 90º; então, quanto mais lados
um polígono tiver, maior a soma dos
seus ângulos internos e, no caso de
um polígono convexo, mais se
aproxima de um círculo.

5. Em geometria, uma figura plana de três lados, cuja
soma dos ângulos interiores totaliza 180º. Os
triângulos podem ser classificados pelo
comprimento relativo dos seus lados. Um
triângulo escaleno tem três lados de
comprimentos diferentes; um triângulo isósceles
tem pelo menos dois lados iguais; um triângulo
equilátero tem três lados iguais (e três ângulos
iguais de 60º).

6. Um triângulo retângulo tem um ângulo
de 90º. Se o comprimento de um lado de
um triângulo for "b" e a distância
perpendicular daquele lado ao vértice
oposto "a" (a altura do triângulo), a sua
área A = ½* b * a.
 Regular
Diz-se das figuras geométricas que têm
todos os ângulos e todos os lados iguais.
Diz-se, também, dos sólidos em que as
bases são polígonos regulares.

7.  Definição
 Poliedro é um sólido limitado externamente por planos no
espaço R3. As regiões planas que limitam este sólido são
as faces do poliedro.
 As interseções das faces são as arestas do poliedro.
 As interseções das arestas são os vértices do poliedro.
 Poliedros convexos são aqueles cujos ângulos diedrais
formados por planos adjacentes têm medidas menores do
que 180o. Outra definição: Dados quaisquer dois pontos
de um poliedro convexo, o segmento que tem esses
pontos como extremidades, deverá estar inteiramente
contido no poliedro.

8.  Se V é o número de vértices, F é o número de
faces, A é o número de arestas e M é o número
de ângulos entre as arestas de um poliedro
convexo, então:
V + F = A + 2
M = 2 A

9.  Um poliedro é dito regular se todas as suas faces
são regiões poligonais regulares com n lados, o
que significa que o mesmo número de arestas se
encontram em cada vértice.
 Existem algumas características gerais que são
válidas para todos os poliedros regulares. Se n é
o número de lados da região poligonal, a é a
medida da aresta A e z=M/V é a divisão do
número de ângulos diedrais pelo número de
vértices, então:

10. Nome do
poliedro
Número de
faces
Poligonal
regular
No. de
vértices
No. de
arestas
Número de
ângulos
entre
arestas
Tetraedro 4 Triangular 4 6 12
Hexaedro 6 Quadrada 8 12 24
Octaedro 8 Triangular 6 12 24
Dodecaedr
o
12 Pentagona
l
20 30 60
Icosaedro 20 Triangular 12 30 60

11. Em geometria, uma figura sólida com quatro ou
mais lados planos. Quanto mais faces um poliedro
tiver, mais se aproxima de uma esfera. O
conhecimento das propriedades de um poliedro é
necessária em cristalografia e estereoquímica
para determinar as formas dos cristais e das
moléculas.

12.  Os cinco tipos de poliedros regulares
convexos mais conhecidos (com todas as
faces com o mesmo tamanho e forma), tal
como havia já sido deduzido pelos
matemáticos gregos; são o tetraedro (quatro
faces triangulares equiláteras), o cubo (seis
faces quadradas), o octaedro (oito triângulos
equilaterais), o dodecágono (12 pentágonos
regulares) e o icosaedro (20 triângulos
equiláteros).

14.  Em geometria, outro nome para um poliedro
regular, uma das cinco possíveis figuras
tridimensionais com todas as faces com o mesmo
tamanho e forma.
 Tetraedro
 Em geometria, uma figura sólida (poliedro) com
quatro faces triangulares; isto é, uma pirâmide com
uma base triangular. Um tetraedro regular tem
como faces triângulos equiláteros.
 Em química, um tetraedro descreve as faces de
algumas moléculas e cristais; por exemplo, os
átomos de carbono num cristal de diamante
encontram-se no espaço como um conjunto de
tetraedros regulares inter-relacionados.

15.  Sólido regular com 12 faces pentagonais e 12
vértices. É um dos cinco poliedros regulares, ou
sólidos platónicos.

16. Sólido regular com oito faces, sendo cada
uma um triângulo equilátero. É um dos
cinco poliedros regulares ou sólidos
platónicos. A figura formada pela união
dos pontos médios das faces é um cubo
perfeito e os vértices do octaedro são eles
próprios os pontos médios das faces de
um cubo envolvente. Por esta razão, o
cubo e o octaedro denominam-se sólidos
duais.

18.  Os cinco poliedros regulares
convexos: I - Tetraedro, II - Cubo, III -
Octaedro, IV - Dodecaedro e V-
Icosaedro são conhecidos desde a
Antiguidade, como já referimos.
 Deve-se a Kepler (1571-1630) a
descoberta do primeiro poliedro
regular côncavo - o dodecaedro
estrelado de faces regulares
representado na figura (VI).

19.  O dentista Francis Louis Poinset (1777-1859)
acrescentou a esta lista, em 1809, três novos
poliedros regulares não convexos (VII, VIII e IX).
Foi, no entanto, Cauchy quem demonstrou que
somente existem estes nove poliedros regulares.
 Note-se que cada poliedro regular côncavo resulta
do prolongamento das faces de um poliedro
regular convexo que lhe serve de núcleo, como é
visível no dodecaedro estrelado de Kepler (VI)
que resulta do prolongamento do dodecaedro (IV).