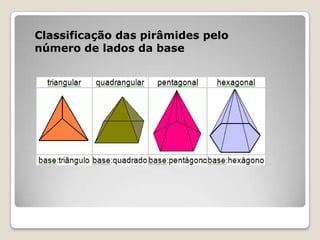
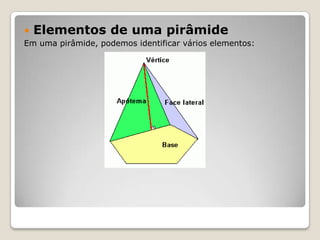
1) O documento discute o conceito de pirâmides, seus elementos e classificações. 2) As pirâmides têm vértice, base, altura e faces laterais triangulares. Sua área é a soma da área da base com a área das laterais. 3) O volume de uma pirâmide é um terço da área da base multiplicada pela altura.

1. Seminario de Matematica
Tema: Pirâmides
Equipe : Nathália Medeiros
Maciel Cosmo
Helio Santos
Assis

2.  O conceito de Pirâmide
 Consideremos um polígono contido em um plano (por
exemplo, o plano horizontal) e um ponto V localizado fora
desse plano. Uma Pirâmide é a reunião de todos os
segmentos que têm uma extremidade em P e a outra num
ponto qualquer do polígono. O ponto V recebe o nome de
vértice da pirâmide.
Exemplo: As pirâmides do Egito, eram utilizadas para sepultar
faraós, bem como as pirâmides no México e nos Andes, que
serviam a finalidades de adoração aos seus deuses. As formas
piramidais eram usadas por tribos indígenas e mais recentemente
por escoteiros para construir barracas.

3.  Elementos de uma pirâmide
Em uma pirâmide, podemos identificar vários elementos:

4.  Base: A base da pirâmide é a região plana poligonal
sobre a qual se apoia a pirâmide.
Vértice: O vértice da pirâmide é o ponto isolado P
mais distante da base da pirâmide.
 Eixo: Quando a base possui um ponto central, isto é,
quando a região poligonal é simétrica ou regular, o
eixo da pirâmide é a reta que passa pelo vértice e
pelo centro da base.
Altura: Distância do vértice da pirâmide ao plano da
base.
 Faces laterais: São regiões planas triangulares que
passam pelo vértice da pirâmide e por dois vértices
consecutivos da base.

5.  Arestas Laterais: São segmentos que têm um
extremo no vértice da pirâmide e outro extremo
num vértice do polígono situado no plano da
base.
 Apótema: É a altura de cada face lateral.
 Superfície Lateral: É a superfície poliédrica
formada por todas as faces laterais.
 Aresta da base: É qualquer um dos lados do
polígono da base.

6. Classificação das pirâmides pelo
número de lados da base

7.  Área da superfície
Para o cálculo da área da superfície de uma pirâmide,
calcularemos a área da base (Ab), a área das laterais
(Al), e somaremos as duas, formando a área total (At).
Quando sabe-se que os triângulos das laterais são
equiláteros, usamos a fórmula dos triângulos
equiláteros, mas caso não tenha sido dada nenhuma
informação sobre esses triângulos, usaremos a fórmula
de um triângulo qualquer que é onde b, é a base do
triângulo, e h é a altura do triângulo, lembrando que, a
altura do triângulo corresponde a apótema lateral da
pirâmide

8.  Para descobrir as medidas que não temos na
pirâmide, mas são necessárias, usaremos
suas características (raio, apótema da base,
aresta da base, aresta lateral, altura da
pirâmide, aresta lateral), para descobrir a
medida dos outros através do teorema de
Pitágoras, pois, poderemos observar a
formação de triângulos retângulos na base da
pirâmide, verticalmente dentro de uma
pirâmide.

9.  Volume de uma Pirâmide
 O volume de uma pirâmide pode ser obtido como um terço do
produto da área da base pela altura da pirâmide, isto é:
Volume = (1/3) A(base) h
 Exemplo: Juliana tem um perfume contido em um frasco com a forma
de uma pirâmide regular com base quadrada.
A curiosa Juliana quer saber o volume de perfume
que o frasco contém. Para isso ela usou uma régua e
tirou duas informações: a medida da
aresta da base de 4cm e a medida da aresta lateral de 6cm
Como V(pirâmide)=A(base).h/3, devemos calcular a área da
base e a medida da altura. Como a base tem forma quadrada de
lado a=4cm, temos que
A(base)=a²=4cm.4cm=16 cm².

10. Como V(pirâmide)=A(base).h/3, devemos calcular a
área da base e a medida da altura. Como a base tem
forma quadrada de lado a=4cm, temos que
A(base)=a²=4cm.4cm=16 cm².
A altura h da pirâmide pode ser obtida como a medida
de um cateto de um triângulo retângulo cuja
hipotenusa é dada pela altura L=6cm da aresta
lateral e o outro cateto Q=2×R[2] que é a metade
da medida da diagonal do quadrado. Dessa forma
h²=L²-Q², se onde segue que h²=36-8=28 e assim
temos que h=2R[7] e o volume será dado por
V=(1/3).16.2R[7]=(32/3)R[7].