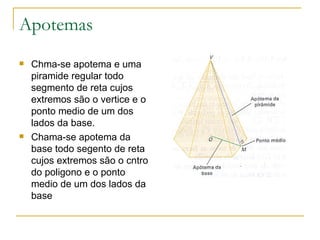
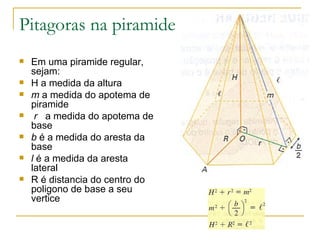
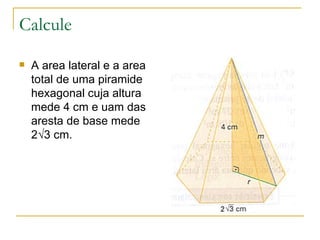
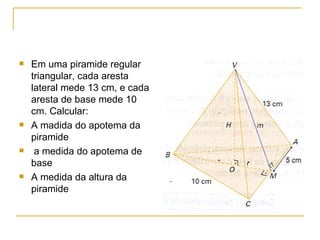
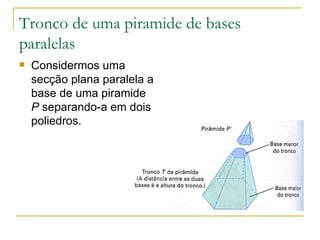
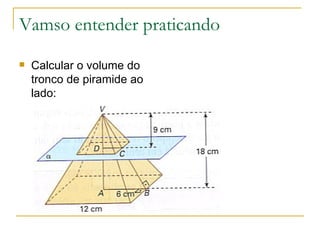
O documento descreve os elementos e classificação de pirâmides, incluindo vértice, base, faces laterais e altura. Explica como calcular a área lateral e total de pirâmides regulares usando o Teorema de Pitágoras e a fórmula do volume de uma pirâmide.

1. Pirâmides Considere uma região poligonal convexa e um ponto V que não pertence ao plano da região poligonal. Considere também todos os segmentos de reta com um extremo em um dos vértices da região poligonal e outro extremo no ponto V Junta tudo e tem uma Pirâmide

2. Elementos de pirâmide O ponto V é chamado de vértice da pirâmide A região poligonal é chamada de base Os vértices da região poligonal são os vértices da base E o polígono é o polígono de base As demais faces, que não a base, são chamadas de faces laterais As arestas não pertencentes a base, são arestas laterais A distancia entre o vértice V e o plano da base é a altura da pirâmide A soma das áreas das faces laterais é a área lateral E a soma da área da base com a área lateral é a área total

3. Classificação A Pirâmide é denominada de acordo com o numero de arestas de base pirâmide reta. É aquela em que a projeção do vértice sobre o plano de base é o centro do polígono da base Pirâmide regular, é a pirâmide reta e seu polígono de base é regular.

4. Apotemas Chma-se apotema e uma piramide regular todo segmento de reta cujos extremos são o vertice e o ponto medio de um dos lados da base. Chama-se apotema da base todo segento de reta cujos extremos são o cntro do poligono e o ponto medio de um dos lados da base

5. Pitagoras na piramide Em uma piramide regular, sejam: H a medida da altura m a medida do apotema de piramide r a medida do apotema de base b é a medida do aresta da base l é a medida da aresta lateral R é distancia do centro do poligono de base a seu vertice

6. Calcule A area lateral e a area total de uma piramide hexagonal cuja altura mede 4 cm e uam das aresta de base mede 2√3 cm.

7. Em uma piramide regular triangular, cada aresta lateral mede 13 cm, e cada aresta de base mede 10 cm. Calcular: A madida do apotema da piramide a medida do apotema de base A medida da altura da piramide

8. Volume Dessa vez, não tm como entender, então aceitem: Volume da piramide é igual a ⅓ do produto da area de base pela altua da piramide. V = ⅓ BH

9. Tronco de uma piramide de bases paralelas Considermos uma secção plana paralela a base de uma piramide P separando-a em dois poliedros.

10. Vamso entender praticando Calcular o volume do tronco de piramide ao lado:

11. Pronto CHEEEGA!!! Até semana que vem com ‘Corpos redondos’