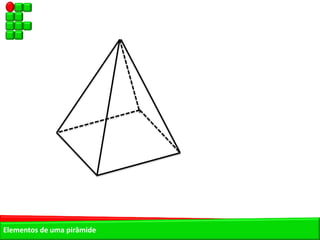
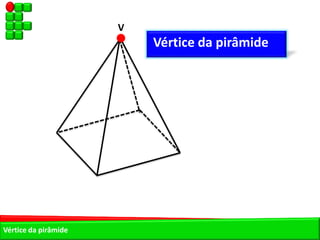
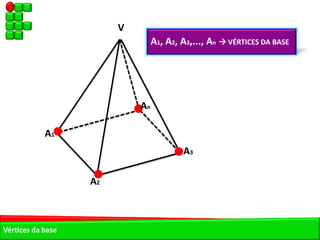
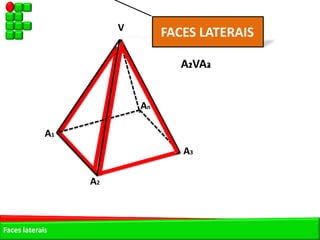
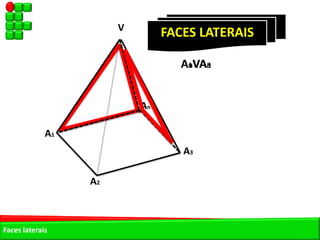
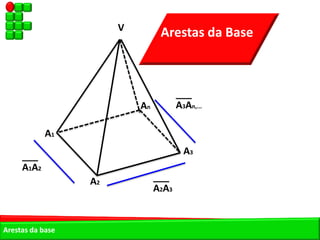
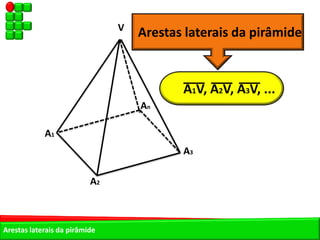
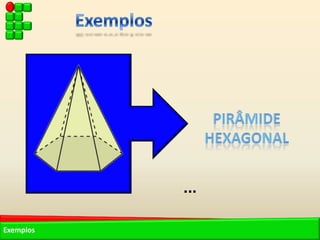
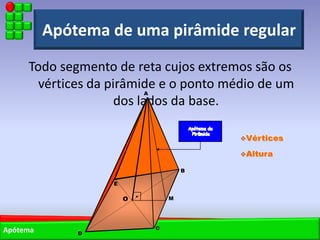
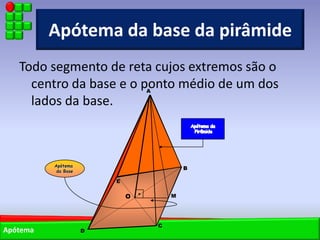
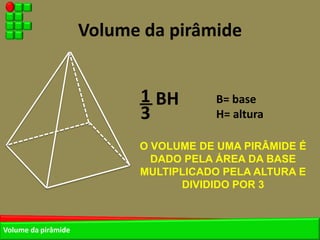
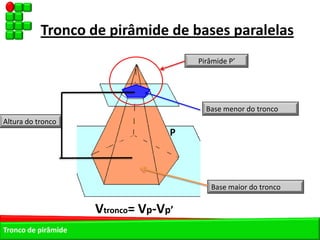
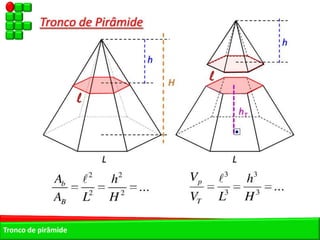
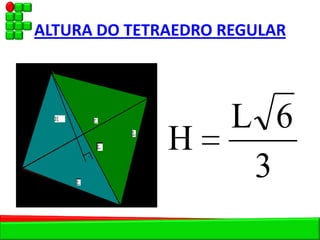
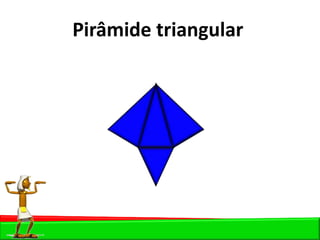
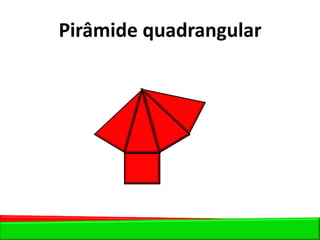
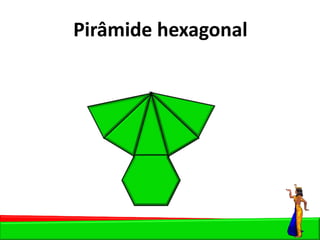
O documento descreve as pirâmides do Egito Antigo, monumentais tumbas construídas há cerca de 4.500 anos para os faraós e suas rainhas. As pirâmides eram construídas de forma hermética para garantir a vida eterna aos faraós após a morte. A maior pirâmide é a do faraó Khufu, com 147 metros de altura.