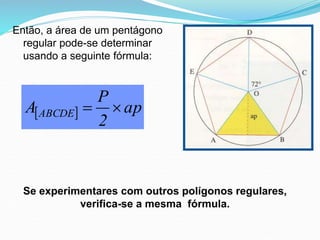
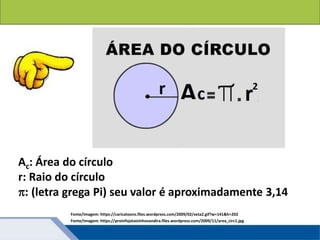
O documento discute o cálculo da área de figuras planas regulares e circulares. Explica que a área de um polígono regular pode ser calculada dividindo-o em triângulos iguais e somando suas áreas, ou usando a fórmula que envolve a apótema e o lado do polígono. Também apresenta a fórmula para calcular a área de um círculo, que envolve o raio elevado ao quadrado multiplicado por pi. Fornece exemplos ilustrativos de cálculos de áreas de círculos.
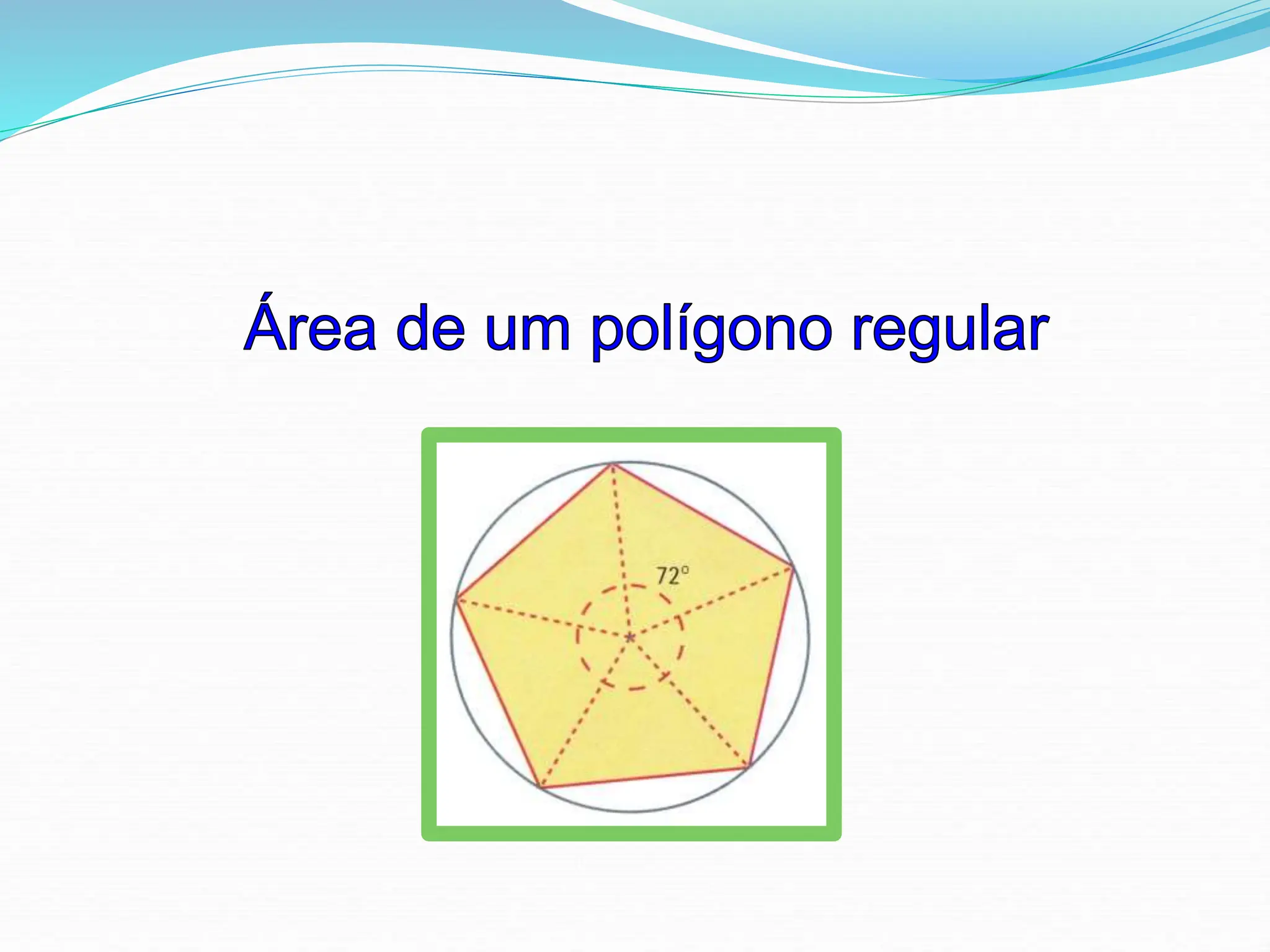
![Áreas de Polígonos
Em cada um dos polígonos regulares, traçou-se o segmento
de reta [OT], que une o centro da circunferência ao ponto
médio T do lado, sendo-lhe perpendicular.
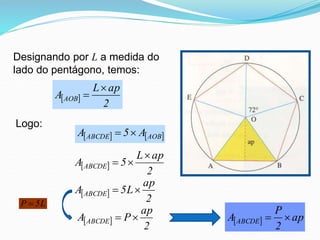
Chama-se apótema de um polígono regular
ao segmento de reta que une o centro do
polígono com o ponto médio de qualquer um
dos lados.
A apótema é perpendicular a esse lado.](https://image.slidesharecdn.com/areadeumpoligonoregularedocrculo-231109200839-decb7ccc/85/Area-de-um-poligono-regular-e-do-circulo-ppt-2-320.jpg)