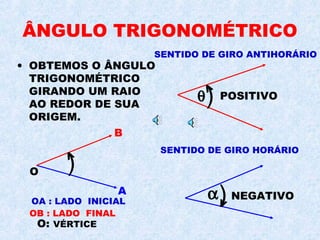
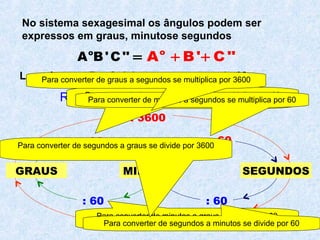
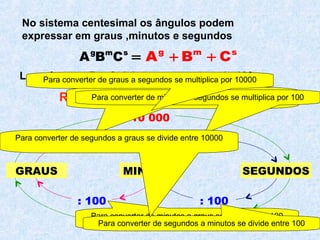
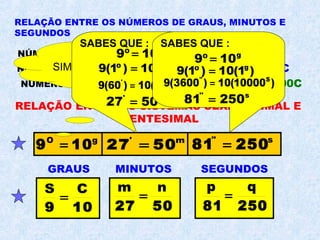
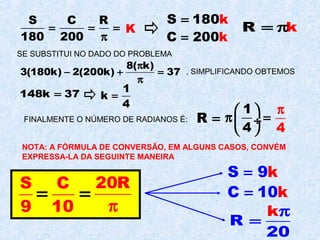
O documento descreve os três principais sistemas de medição angular: o sistema sexagesimal, o sistema centesimal e o sistema radial. Explica as equivalências entre graus, minutos e segundos nos sistemas sexagesimal e centesimal e como converter entre esses sistemas e o sistema radial medido em radianos. Também fornece fórmulas para conversão entre os sistemas.

1. MEDIÇÃO DE ANGULOS
SISTEMA SEXAGESIMAL CENTESIMAL

2. ÂNGULO TRIGONOMÉTRICO
• OBTEMOS O ÂNGULO
TRIGONOMÉTRICO
GIRANDO UM RAIO
AO REDOR DE SUA
ORIGEM.
SENTIDO DE GIRO HORÁRIO
SENTIDO DE GIRO ANTIHORÁRIO
OA : LADO INICIAL
)O
A
B
<
)
<
θ POSITIVO
)
<
α NEGATIVO
OB : LADO FINAL
O: VÉRTICE

3. SISTEMAS DE MEDIÇÃO
ANGULAR
• SISTEMA SEXAGESIMAL (SISTEMA INGLÊS)
o
1GRADO: MINUTO:
'
1 SEGUNDO:
"
1
'o
601 = "'
601 = "o
36001 =
1 volta =
o
360
EQUIVALÊNCIAS

4. No sistema sexagesimal os ângulos podem ser
expressos em graus, minutose segundos
o
A B'C'' o
A B' C ''+= +
Los números B y C deben ser menores de 60
RELACIONES DE CONVERSIÓN
GRAUS MINUTOS SEGUNDOS
x 60 x 60
x 3600
: 60 : 60
: 3600
<
<
<<
<
<
<
<
<
<
< <
Para convertir de grados a minutos se multiplica por 60
Para converter de minutos a graus se divide por 60
Para converter de minutos a segundos se multiplica por 60
Para converter de segundos a minutos se divide por 60
Para converter de graus a segundos se multiplica por 3600
Para converter de segundos a graus se divide por 3600

5. EXEMPLO:
o
20 36' 45''θ =
EXPRESSAR EM GRAUS SEXAGESIMAISθ
o ' ''
20 36 45θ = + +
o o
o 36 45
20
60 3600
θ = + +
o o
o 3 1
20
5 80
= + +
o
1649
80
θ =CONCLUSIÓN:
RELACÃO ENTRE OS NÚMEROS DE GRAUS, MINUTOS E
SEGUNDOS
NÚMERO DE GRAUS SEXAGESIMAIS = S
NÚMERO DE MINUTOS SEXAGESIMAIS ( m ) = 60 S
NÚMERO DE SEGUNDOS SEXAGESIMAIS ( p ) = 3600 S
Ao número 36 se divide por 60 e
Ao número 45 se divide por 3600

6. EXEMPLO
Calcular a medida de um ângulo no sistema sexagesimal,
sabendo que seu número de minutos sexagesimais mais o
dobro de seu número de grados sexagesimais é igual a 155.
SOLUÇÃO
Seja S = número de graus sexagesimais
Então o número de minutos sexagesimais = 60 S
Dado :
155 5(31)
S
62 2(31)
= =
60S 2S 155+ = 62S 155=
5
S
2
=
O ângulo mede:
5º 4º 60'
2
2 2
º 30'= =

7. SISTEMAS DE MEDIÇÃO
ANGULAR
• SISTEMA CENTESIMAL (SISTEMA FRANCÊS)
g
1GRAU: MINUTO:
m
1 SEGUNDO:
s
1
g m
1 100=
m s
1 100= g s
1 10000=
1volta =
g
400
EQUIVALÊNCIAS

8. No sistema centesimal os ângulos podem
expressar em graus ,minutos e segundos
g m s
A B C g m s
A B C= + +
Los números B y C deben ser menores de 100
RELACIONES DE CONVERSIÓN
GRAUS MINUTOS SEGUNDOS
x 100 x 100
x 10 000
: 100 : 100
: 10 000
<
<
<<
<
<
<
<
<
<
< <
Para convertir de grados a minutos se multiplica por 100
Para converter de minutos a graus se divide entre 100
Para converter de minutos a segundos se multiplica por 100
Para converter de segundos a minutos se divide entre 100
Para converter de graus a segundos se multiplica por 10000
Para converter de segundos a graus se divide entre 10000

9. RELAÇÃO ENTRE OS NÚMEROS DE GRAUS, MINUTOS E
SEGUNDOS
NÚMERO DE GRAUS CENTESIMAIS = C
NÚMERO DE MINUTOS CENTESIMALES ( n ) = 100C
NÚMERO DE SEGUNDOS CENTESIMAIS ( q ) = 10 000C
RELAÇÃO ENTRE OS SISTEMAS SEXAGESIMAL E
CENTESIMAL
gO
109 = m'
5027 = s"
25081 =
GRAUS MINUTOS SEGUNDOS
109
CS
=
5027
nm
=
25081
qp
=
SABEMOS QUE
SIMPLIFICANDO SE OBTIENE
g
180º 200=
g
9º 10=
SABES QUE :
g
9(1º ) 10(1 )=
' m
9(60 ) 10(100 )=
g
9º 10=
' m
27 50=
SABES QUE :
g
9º 10=
g
9(1º ) 10(1 )=
'' S
9(3600 ) 10(10000 )=
'' s
81 250=

10. SISTEMAS DE MEDIÇÃO
ANGULAR
• SISTEMA RADIAL (SISTEMA CIRCULAR)
UM RADIANO É A
MEDIDA DO
ÂNGULO CENTRAL
QUE SUBTENDE
EM QUALQUER
CIRCUNFERÊNCIA
UM ARCO DE
LONGITUDE IGUAL
AO RAIO.
.. 1rad
1vuelta 2 rad= π
o ' ''
1rad 57 17 45=
R
R
R)
NESTE SISTEMA A
UNIDADE DE MEDIDA
É OL RADIANO.

11. RELAÇÃO ENTRE OS TRÊS SISTEMAS
0 g
180 200 rad= = π
ESTA RELAÇÃOSE USA PARA CONVERTERDE UM
SISTEMA A OUTRO.
EM CADA UM DOS SIGUINTES CASOS CONVERTER A RADIANOS
0
A) 54θ =
O
54 o
rad
180
π 
 ÷
 
=
3
rad
10
π
g
B) 125φ =
g
rad
200
π 
 ÷
 
=
5
rad
8
πg
125
EXEMPLOS
SABES QUE O ÂNGULO DE UMA
VOLTA MEDE :
SIMPLIFICANDO SE OBTÉM:
g
360º 400 2 rad= = π

12. EM CADA UMO DOS SIGUINTES CASOS CONVERTER AO SISTEMA
SEXAGESIMAL
A)
2
rad
3
π
...........
o
2(180 )
3
= o
120
g
B)70 .................
g
70
o
g
9
10
 
 ÷
 
= o
63
EM CADA UM DOS SIGUINTES CASOS CONVERTEIR AO SISTEMA
CENTESIMAL
A)
3
rad
4
π
...........
g
3(200 )
4
= g
150
o
B)27 ................ o
27
g
o
10
9
 
 ÷
 
= g
30

13. FACTORES DE CONVERSÃO
DE GRAUS SEXAGESIMAIS A
RADIANOS
DE GRAUS SEXAGESIMAIS A
CENTESIMAIS
DE GRAUS CENTESIMAIS A
RADIANOS
DE GRAUS CENTESIMAIS A
SEXAGESIMAIS
DE RADIANOS A GRAUS
SEXAGESIMAIS
DE RADIANOES A GRAUS
CENTESIMAIS
o
rad
180
π
g
o
10
9
g
rad
200
π
o
g
9
10
o
rad 180π =
g
rad 200π =

14. ESTÃO
ENTENDENDO?
NÃO REPITA POR FAVOR

15. FÓRMULA DE CONVERSÃO
S
180
=
C
200
=
R
π
S : NÚMERO DE GRAUS SEXAGESIMAIS
C : NÚMERO DE GRAUS CENTESIMAIS
R : NÚMERO DE RADIANES
EXEMPLO
CALCULAR O NÚMERO DE RADIANOS DE UM ÂNGULO, SE:
8R
3S 2C 37− + =
π
NESTE TIPO DE PROBLEMA SE DEVE USAR A FÓRMULA DE CONVERSÃO
SOLUÇÃO

16. S C R
180 200
= = =
π
K
S k180=
C k200=
R k= π
SE SUBSTITUI NO DADO DO PROBLEMA
8( k)
3(180k) 2(200k) 37
π
− + =
π
, SIMPLIFICANDO OBTEMOS
148k 37= 1
k
4
=
FINALMENTE O NÚMERO DE RADIANOS É: R =
1
4
 
π = ÷
  4
π
S k9=
C k10=
R
0
k
2
π
=
NOTA: A FÓRMULA DE CONVERSÃO, EM ALGUNS CASOS, CONVÉM
EXPRESSA-LA DA SEGUINTE MANEIRA
S
9
=
C
10
=
20R
π

17. OUTRAS RELAÇÕES IMPORTANTES
* ÂNGULOS COMPLEMENTARES SOMAM: o g
90 100 rad
2
π
∨ ∨
* ÂNGULOS SUPLEMENTARES SOMAM:
O g
180 200 rad∨ ∨ π
* EQUIVALÊNCIAS USUAIS:
o
rad 60
3
π
= o
rad 30
6
π
=
o
rad 45
4
π
=
SISTEMA
SEXAGESIMAL
CENTESIMAL
RADIAL
COMPLEMENTO SUPLEMENTO
S
C
R
90 - S 180 - S
100 - C 200 - C
R
2
π
− Rπ −

18. EXERCÍCIOS
1. CALCULAR :
g
45º rad
12E
50 33º
π
+
=
−
SOLUÇÃO
Para resolver este exercício a idéia é converter cada um
dos valores dados a um só sistema, escolhemos o
SISTEMA SEXAGESIMAL
rad
12
π
=
180º
12
=15º g
50; 45º
Substituindo em E
45º 15º
E
45º 33º
+
= =
−
60º
12º
= 5
g
9º
( )
10
=

19. 2. O número de graus sexagesimais de um ângulo mais
o triplo de seu número de graus centesimais é 78,
calcular seu número de radianos
SOLUÇÃO
Seja S = número de graus sexagesimais
C = número de graus centesimais
Sabes que: S C
9 10
= = K y
Dado: S + 3C = 78
S = 9K C = 10K
9K + 3( 10K ) = 78 39K = 78 K = 2
O número de radianos é:
k
R
20
π
=
2
R
20
π
= =
10
π