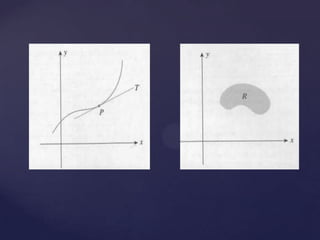
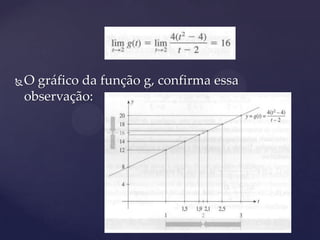
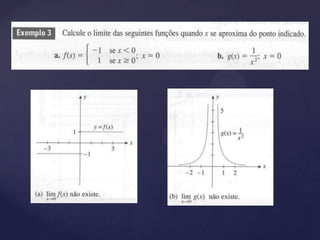
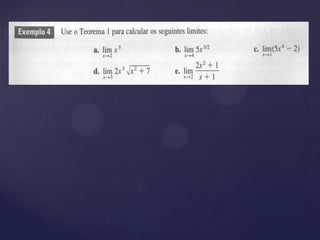
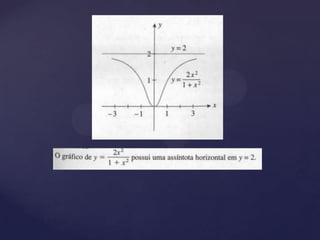
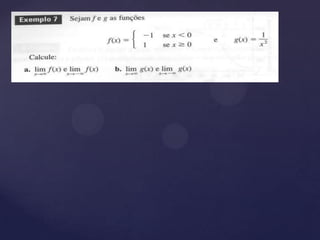
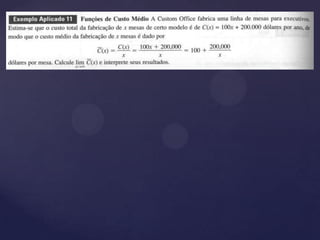
1) O documento discute o desenvolvimento do cálculo no século XVII por Newton e Leibniz através da investigação de problemas como a reta tangente e área sob curva. 2) Explica conceitos fundamentais do cálculo como derivada, integral, limite e suas aplicações práticas em problemas como velocidade e taxas de variação. 3) Apresenta definições e propriedades de limite de funções e estratégias para calcular formas indeterminadas, incluindo limites no infinito.

1. LIMITE
MATEMÁTICA APLIC. À ADM
{ 2º PERÍODO ADM FACEMA 2012.2
PROF. ARISTÓTELES MENESES LIMA

2.  Isaac Newton ( 1642 – 1727)
 Gottfried Wilhelm Leibniz (1646 – 1716)
Investigação dos seguintes problemas:
 Encontrar a reta tangente a uma curva em dado ponto
da curva;
 Encontrar a área da região plana limitada por uma
curva arbitrária.
Introdução ao Cálculo

4.  Foi precisamente a descoberta da relação entre esses
dois problemas que alavancou o desenvolvimento do
cálculo no século XVII, transformando-o em uma
ferramenta indispensável para a solução de
problemas práticos. Alguns exemplos práticos:
 Encontrar a velocidade de um objeto .
 Encontrar a taxa de variação de uma população de
bactérias em relação ao tempo .
 Encontrar a taxa de variação do lucro de uma
companhia em relação ao tempo.
 Encontrar a taxa de variação do faturamento de uma
agência de viagens em relação ao gasto da
publicidade.

5.  O estudo do problema da reta tangente levou à criação
do cálculo diferencial, que baseia no conceito de
derivada de uma função.
 O estudo do problema da área levou a criação do
cálculo integral , que baseia no conceito de
antiderivada ou integral de uma função.
 Tanto a derivada de uma função quanto a integral de
uma função são definidas em termos de um conceito
mais fundamental – o de limite, nosso próximo tópico.

6.  Considere a função g definida por
Suponhamos que temos que determinar o valor de g(t)
quando t se aproxima do número 2.
Se tomamos uma sequência de valores de t se
aproximando de 2 pela direita, e pela esquerda . Vejamos
as tabelas:
Definição intuitiva de
limite

7.  Observe que g(t) se aproxima do número 16 quando t se
aproxima de 2 – dessa vez pelo lado esquerdo. Em outras
palavras, quando t se aproxima de 2 de qualquer lado,
g(t) se aproxima de 16. Nessa situação, dizemos que o
limite de g(t) quando t se aproxima de 2 é 16, e
escrevemos:

8.  O gráfico da função g, confirma essa
observação:

9. Limite de uma função -
definição

10. Calculando o limite de
uma função

12. Propriedades de limites

14. Formas indeterminadas

15.  1. Substitua a função dada por outra mais
apropriada que assuma os mesmos valores que a
função original em todos os pontos, exceto em x=a.
 2. Calcule o limite dessa função quando x se
aproxima de a.
Exemplos 5 e 6 ilustra essas estratégias.
Estratégia para calcular
formas indeterminadas

17. Limites no infinito

20. Definição

22. Teorema 2