1. O documento descreve a equação de Schrödinger, que fornece uma descrição ondulatória da mecânica quântica. 2. É explicado que as equações envolvidas na descrição quântica, assim como a equação de onda, devem envolver derivadas parciais, diferentemente da mecânica newtoniana que envolve derivadas totais. 3. O documento introduz a equação de Lagrange, que fornece uma descrição equivalente à mecânica newtoniana em qualquer sistema de coordenadas

1. 1 A Equação de Schrödinger
Como vimos no caso da quantização de Sommerfeld, a descrição da Mecânica
Clássica (MC) adequada para se introduzir um processo de quantização não é
a formulação de Newton. Isso é verdade em geral. Tanto para os processos
da velha mecânica quântica, quanto da nova até a sua evolução relativística (a
Teoria Quântica de Campos). Um primeiro ponto que podemos salientar é que,
tendo como base uma descrição ondulatória, as equações envolvidas no processo
de descrição quântica devem, assim como a equação de onda, envolver derivadas
parciais. Enquanto a mecânica de Newton envolve derivadas totais. Além disso,
como veremos a seguir, existe uma semelhança muito grande (notada bem antes
do advento da MQ) entre estas outras descrições da MC (Hamilton, Lagrange
etc) e a descrição das características da luz na óptica geométrica. De uma
forma geral, não só nesta parte do curso como na segunda parte (Moderna II) é
impossível apreciar o processo de surgimento e evolução da MQ sem um conhec-
imento (ainda que enciclopédico) da descrição clássica da Mecânica Analítica.
Destarte, dedicaremos algum tempo para ganharmos uma certa familiaridade
com os termos e expressões envolvidos na Mecânica Analítica.
1.1 Preliminar
Se f = f (a; b) é uma função de duas variáveis a; b então
df =
@f
@a
da +
@f
@b
db
e, da mesma forma, se
df = g:da + h:db =) f = f (a; b)
não importando de quais variáveis depende g e h. Pois, independente desta
variáveis, a função f só varia quando alteramos a e b.
1.2 Equações de Euler-Lagrange
Partindo da equação de Newton temos
Fi = m
d2
xi
dt2
(1)
Para forças conservativas
Fi =
@V
@xi
= m
d
dt
_xi (2)
A energia cinética em coordenadas cartesianas é dada por (onde, assim como na
notação da relatividade, estamos admitindo que sempre existe uma somatória
implícita quando dois índices se repetem)
T =
1
2
( _xk)
2
; ( _xk)
2
=
X
i
_x2
k
1

2. com isso temos
@T
@ _xi
=
m
2
@
@xi
( _xk) ( _xk) =
1
2
@ _xk
@ _xi
_xk + _xk
@ _xk
@ _xi
=
m
2
[( ik) _xk + _xk ik] = m _xi
Voltando em (2)
@U
@xi
=
d
dt
m _xi =
d
dt
@T
@ _xi
=)
d
dt
@T
@ _xi
+
@U
@xi
= 0 ; i = 1; 2; 3: (3)
Para siatema conservativos a energia potencial depende apenas das coordenadas
U = U (xi; t). Enquanto a energia cinética é, em coordenadas cartesianas1
, uma
função apenas das velocidades, T = T ( _xi). Podemos com isso de…nir uma
função que depende de x e _x
L (xi; _xi; t) = T ( _xi) U (xi; t)
com isso
@L
@ _xi
=
@T
@ _xi
;
@L
@xi
=
@U
@xi
Substituindo em (3) temos
d
dt
@L
@ _xi
@L
@xi
= 0
A função L é chamada de lagrangiana do sistema e as (3) equações acima as
equações de Lagrange.
1.2.1 Coordenadas generalizadas
Pela construção acima vemos que as equações diferenciais parciais de Lagrange
são equivalente a equações de Newton. A princípio equações diferenciais parciais
são mais complicadas que EDO. Entretanto, existe uma grande vantagem nas
equações de Lagrange.
Suponha que você queira resolver o problema de pêndulo sob a ação da
gravidade. O ideal, neste caso, é usar a coordenada polar . Para obter as
equações do movimento na mecânica de Newton você deve escrever
x = R cos ; y = R sin ;
calcular •x e •y, substituir na equação de Newton e usar o vínculo
x2
+ y2
= R2
:
1 Em coordenadas polares, por exemplo, a energia cinética
T =
1
m
_r2
+ _r2 _2
;
depende da coordenada 6 r.
2

3. Vamos ver como obter as equações do movimento na mecânica de Lagrange.
Primeiro nos obtemos a energia cinética
T =
1
2
mv2
; v = R _ =) T =
1
2
mR2 _2
enquanto a energia potencial é dada por
V ( ) = mgR (1 cos )
Com isso temos
L = T V =
1
2
mR2 _2
mgR (1 cos )
Se esquecermos por um instante que estamos usando coodenadas polares e us-
armos as equações de Lagrange (trocando x por ) temos
@L
@
=
@
@
1
2
mR2 _2
mgR (1 cos ) = mgR
@
@
(cos ) = mgR sin
@L
@ _
=
@
@ _
1
2
mR2 _2
mgR (1 cos ) = mR2 _
com isso,
d
dt
@L
@ _
@L
@
=
d
dt
mR2 _ + mgR sin
= mR2 •+ mgR sin = 0
ou ainda
•+
g
R
sin = 0 :
Que é precisamente a equação que seria obtida a partir da equação de Newton
e o laborioso processo descrito acima.
Este resultado pode ser provado de forma geral usando uma transformação
geral de coordenadas.
Assim, utilizando as equações de Lagrange temos uma liberdade completa
na escolha das coordenadas do sistema, o que pode ser utilizado explorando as
simetrias do problema. Ou seja, a principal vantagem das equações de Lagrange
é que elas independem do sistema de coordenadas usados. Com isso, se qi é um
conjunto qualquer de coordenadas que descrevem um sistema mecânico, este
sistema deve obedecer as equações de Lagrange
d
dt
@L
@ _qi
@L
@qi
= 0 : (4)
As coordenadas qi são chamadas de coordenadas generalizadas.
Remark 1 Mais uma vez, enquanto a equação de Newton (1) só tem esta forma
em coordenadas cartesianas, as equações de Lagrange (4) têm esta forma em
qualquer sistema de coordenadas.
Exercise 2 Uma conta (miçanguinha) de massa m pode se mover livremente
numa barra rígida e reta que gira com velocidade constante !. Escreva a equação
do movimento da conta.
3

4. 2 Transformada de Legendre
Em uma série de problemas em física é importante mudarmos as variáveis que
usamos num problema. Por exemplo, na termodinâmica uma quantidade muito
importante é a energia interna de um sistema U (S; V ). Um inconveniente
desta quantidade é que ela depende da entropia S, uma quantidade que não
pode ser medida diretamente com nenhum instrumento. Entretanto, pelas leis
da termodinâmica, sabemos que a temperatura T de um corpo é a variação da
sua energia interna com a entropia
T =
@U
@S
: (5)
Vamos então de…nir uma nova quantidade F como
F = T:S U (6)
Diferenciando esta quantidade temos
dF = TdS + SdT dU ;
Sabendo que U = U (S; V ) temos
dU =
@U
@S
dS +
@U
@V
dV ; (7)
com isso
dF = TdS + SdT
@U
@S
dS
@U
@T
dT
= T
@U
@S
dS + SdT
@U
@V
dV
O fato importante na de…nição de F é que, usando (5), temos
dF = SdT
@U
@V
dV ; (8)
ou seja, a função (6) assim de…nida não depende da entropia
F = F (T; V )
Com isso
dF =
@F
@T
dT +
@F
@V
dV ;
comparando com (8) temos
S =
@F
@T
;
@F
@V
=
@U
@V
:
O importante da quantidade F, chamada energia livre de Helmholtz, é que ela
depende da temperatura e do volume, ambas quantidades que, diferente da
entropia, podem ser medidas com instrumentos usuais.
4

5. Ou seja, podemos determinar F estudando as variações das característica
do sistema com respeito ao seu volume e a sua temperatura.
O procedimento acima é um exemplo de um procedimento mais geral chamado
de transformada de Legendre. De forma geral, se f = f (x1; x2; :::; y1; y2; :::)
podemos de…nir uma nova função
g = piyi f
(somatória em i) onde
pi =
@f
@yi
com isso
dg = (dpi:yi + pi:dyi) df
= (dpi:yi + pi:dyi)
@f
@xi
dxi +
@f
@yi
dyi
= pi
@f
@yi
dyi + dpi:yi
@f
@xi
dxi
que, pela de…nição de pi,
dg = yi:dpi
@f
@xi
dxi
Ou seja a função g não depende mais de yi, mas sim de um novo conjunto de
variáveis pi.
3 Equações de Hamilton
Nosso objetivo agora é usar a transformada de Legendre nas equações de La-
grange. Primeiramente lembramos que, pela de…nição acima
L = L (qi; _qi) ;
ou seja, a Lagrangiana depende das posições e das velocidades.
Agora vamos de…nir a quantidade
H = pi _qi L (9)
onde
pi =
@L
@ _qi
é chamado momento conjugado da variável qi (i.e., para q = x temos um mo-
mento linear, para q = um momento angular e, no caso geral, um momento
5

6. conjugado). Das equações de Lagrange temos que, se uma determinada coorde-
nada qm não aparece na Lagrangiana (chamada de coordenada cíclica)
@L
@qm
= 0 =)
d
dt
@L
@ _qi
= _pi = 0 =) pi = const:
então o momento associado a esta coordenada se conserva (e.g., para uma
partícula livre L = T o momento linear em qualquer direção se conserva).
Seguindo o procedimento da seção anterior temos
dH = dpi: _qi + pi:d _qi dL :
Lembrando que L = L (q; _q) temos
dL =
@L
@qi
dqi +
@L
@ _qi
d _qi ;
com isso
dH = dpi: _qi + pi:d _qi
@L
@qi
dqi +
@L
@ _qi
d _qi ;
= pi
@L
@ _qi
d _qi + _qi:dpi
@L
@qi
dqi ;
e pela de…nição de pi
dH = _qi:dpi
@L
@qi
dqi (10)
e, como esperávamos, a função H assim obtida é uma função de q e p e não mais
de _q, H = H (q; p). A quantidade H assim de…nida é chamada de Hamiltoniana.
Sabendo que H = H (q; p) temos
dH =
@H
@qi
dqi +
@H
@pi
dpi :
Lembrando agora que q e p são coordenadas independentes em H (assim como
q e _q eram em L, i.e, obviamente _q depende de q, mas é exatamente está relação
que queremos encontrar ao resolver a equações de Lagrange) e comparando com
(10) temos
@H
@pi
= _qi ;
@H
@qi
=
@L
@qi
Se usarmos agora as equações de Lagrange temos
@L
@qi
=
d
dt
@L
@ _qi
Lembrando a de…nição de p
pi =
@L
@ _qi
=)
@L
@qi
=
d
dt
pi = _pi
6

7. Com o que
@H
@pi
= _qi ;
@H
@qi
= _pi : (11)
Estas são as chamadas equações de Hamilton (EH).
Qual a vantagem destas equações?
Uma vantagem prática destas equações é que elas possuem apenas derivadas
de primeira ordem. Como a equação de Newton, a equação de Lagrange pos-
sui derivadas das velocidades o que resulta em derivadas de segunda ordem na
posição. Obviamente perdemos algo ao ganharmos esta facilidade. O ponto é
que temos dois pares de EH, ou seja, usando a transformada de Legendre con-
seguimos transformar um sistema de n equações diferenciais de segunda ordem
num sistema de 2n equações diferenciais de primeira ordem2
.
3.0.2 Signi…cado físico da Hamiltoniana
No caso geral, a energia cinética de um sistema é uma função quadrática das
velocidades generalizadas
T = aij _qi _qj ; aij = aij (q)
(somatória em i e j) no caso de coordenadas cartesianas aij = ij
1
2 m. Diferen-
ciando a expressão acima temos
@T
@ _qk
=
X
aij
@ _qi
@ _qk
_qj + aij _qi
@ _qj
@ _qk
=
X
(aij ik _qj + aij _qi jk)
=
X
ij
aij ik _qj +
X
ij
aij _qi jk
=
X
j
akj _qj +
X
i
aik _qi
=
X
i
aki _qi +
X
i
aik _qi
Multiplicando por _qk e efetuando uma somatória em k temos
X
k
@T
@ _qk
_qk =
X
i;k
aki _qi _qk +
X
i;k
aik _qi _qk
= T + T = 2T
2 Na verdade, esta não é a maior vantagem da EH, mas sim que, além de todo o conjunto de
transformações de coordenadas disponíveis na formulação de Lagrange, tempos agora um con-
junto muito maior de transformações a nossa disposição. Voltaremos a isso quando falarmos
em transformações canônicas.
7

8. Este resultado é conhecido como teorema de Euler. Se usarmos agora este
resultado na de…nição de H temos
H =
X
i
pi _qi L
=
X
i
@L
@ _qi
_qi (T U)
=
X
i
@T
@ _qi
_qi (T U)
= 2T T + U
= T + U :
Ou seja, a hamiltoniana é a energia total do sistema.
Observe que, diferente da Lagrangiana (T U) a energia total do sistema é
uma quantidade que pode ser medida e, além disso, é uma quantidade
conservada para um sistema isolado. Esta é outra vantagem da teoria de
Hamilton. Assim, utilizando a mecânica de Hamilton podemos, a partir da
energia total do sistema e de um sistema de 2n equações de primeira ordem,
estudar a dinâmica dos corpos.
3.1 Princípio variacional
Um problema importante e comumente encontrado é o seguinte: dada uma
função y = f (x) para quais valores de x a função f, e conseqüente y, possui
valores máximos e mínimos (estes valores são chamados de extremos da função).
A resposta, obviamente, são os pontos onde a derivada de f se anula.
Um problema bem mais complicado, e interessante, é o seguinte: considere
a integral
I =
Z b
a
F (y (x) ; y0
(x) ; x) dx
onde F é uma dada função de y (x), y0
= dy=dx e x. Assim, para cada função
y (x) diferente I assume um valor diferente. Para quais funções y(x) a integral
I é um extremos?
Antes um pouco de nomenclaturas. Dada uma certa função y(x) podemos
calcular o valor de I. A quantidade I, que depende de uma função, e não apenas
de um número, é chamada de funcional. Outro ponto importante é que dado dos
valores y(x0) = a1 e y0(x0) = a2 é sempre possível encontrar uma função y(x)
que satisfaça esta condição. Neste sentido, as variáveis y e y0 são tratadas em
F como sendo independentes. Agora, para calcular I nós não podemos dar
apenas o valor de y(x) num dado ponto x0, mas sim o valor desta função em todo
o intervalo x 2 [a; b], ou seja, precisamos dar toda uma curva y(x). Dada uma
curva o valor da derivada desta curva está completamente determinada. Assim,
em I não é possível se especi…car separadamente o valor de y e y0. Resumindo
enquanto F é uma função de y, y0 e x
F = F (y; y0
; x)
8

9. Figure 1: Figura retirada do Marion.
enquanto I é um funcional apenas de y
I = I [y] :
Nosso problema de encontrar a função y para a qual I é um extremo é um
problema do chamado cálculo variacional.
Por que a derivada de uma função é nula nos extremos? Isso ocorre porque a
variações do parâmetro (x) em torno deste ponto não geram variações na função
y(x) (pelo menos até primeira ordem em dx). O mesmo acontece com uma
função de duas variáveis (o que pode ser visualizado facilmente) ou com funções
com um número qualquer de variáveis (o que não é tão simples de visualizar). Ou
seja, se estivermos num ponto extremo da função, ao deslocarmos o argumento
uma quantidade in…nitesimal não haverá variação da nossa função. A idéia por
detrás do cálculo variacional é exatamente a mesma. Se tivermos encontrado
a função y(x) para a qual nosso funcional I [y] é um extremos, esperamos que
ao variamos um pouco esta função (ou seja, pegarmos uma curva y(x) muito
próxima a y (x)) o valor do nosso funcional não irá variar (Figura).
Suponha que y (x) é a função que resolve este problema (obviamente esta é
a função que queremos encontra). O fato de y (x) ser um extremo de I signi…ca
então que com pequenas variações em torno de y (x) o valor do integrando não
varia apreciavelmente (de forma análoga ao cálculo ordinário). Vamos então
analisar como I varia se substituímos y pela função (Figura)
y (x) = y (x) + " (x)
9

10. para uma função (x) que, apesar de arbitrária, vamos supor dada, i.e., vamos
variar apenas o valor de ". Como queremos estudar todas as funções que passam
pelo mesmo ponto inicial e …nal devemos ter
y (a) = y (a) ; y (b) = y (b) =) y (a) = y (b) = 0 :
Para a variação acima (onde y e são funções conhecidas) nosso integrando I
passa a ser uma função (pois " é um número) de "
I [y] ! I (") =
Z b
a
F (y + " ; y0
+ " 0
; x) dx :
O ponto é que agora, como é uma função, podemos usar o resultado do cálculo
usual é dizer que para " = 0 a nossa função I é um extremo e, consequentemente,
sua derivada é nula, ou seja,
dI
d" "=0
= 0 : (12)
Tudo que precisamos agora é de…nir a diferencial dI=d". Fazemos isso da forma
usual
dI
d"
= lim
"!0
I [y + "] I [y]
"
= lim
"!0
1
"
"Z b
a
F (y + " ; y0
+ " 0
; x) dx
Z b
a
F (y; y0
; x) dx
#
= lim
"!0
1
"
Z b
a
[F (y + " ; y0
+ " 0
; x) F (y; y0
; x)] dx
=
Z b
a
lim
"!0
[F (y + " ; y0
+ " 0
; x) F (y; y0
; x)]
"
dx :
Agora
F (y + " ; y0
+ " 0
; x) = F (y; y0
; x) +
@F
@y
" +
@F
@y0
" 0
+ O "2
ou seja
lim
"!0
F (y + " ; y0
+ " 0
; x) F (y; y0
; x)
"
=
@F
@y
+
@F
@y0
0
com isso
dI
d"
=
Z b
a
@F
@y
+
@F
@y0
0
dx : (13)
Lembrando que 0
= d =dx podemos integrar o segundo membro da expressão
acima por partes
Z b
a
@F
@y0
d
dx
dx =
@F
@y0
b
a
Z b
a
d
dx
@F
@y0
dx : (14)
Agora usamos o fato de que a função (x) (apesar de arbitrária) deve se anular
nos extremos (a) = (b) = 0
Z b
a
@F
@y0
d
dx
dx =
Z b
a
d
dx
@F
@y0
dx :
10

11. Substituindo em (13) temos
dI
d"
=
Z b
a
@F
@y
d
dx
@F
@y0
dx
=
Z b
a
@F
@y
d
dx
@F
@y0
dx : (15)
Voltando agora para (12) temos
dI
d" "=0
= 0 =
Z b
a
@F
@y
d
dx
@F
@y0
dx
Para qualquer função (x). Isso só é possível se o integrando for zero
@F
@y
d
dx
@F
@y0
= 0 :
Para F uma função de várias variáveis este resultado tem de ser válido inde-
pendentemente para cada variação
@F
@yi
d
dx
@F
@y0
i
= 0 (16)
Esta é a chamada equação de Euler.
Observe que, no …nal, a nossa expressão (15) não depende de ". Além disso,
para lembrar que não estamos falando do cálculo usual, as pessoas inventam um
novo símbolo para a derivada (mas é apenas um símbolo)
dI
d"
I [y] =
Z b
a
F (y; y0
; x) dx :
E lesse a variação funcional de I. Ou ainda, se mudarmos a notação para y
e usarmos a notação acima, (15) pode ser escrita como
dI
d"
I [y] =
Z b
a
@F
@y
d
dx
@F
@y0
y dx (17)
e, em analogia com o cálculo ordinário de uma função f (x), costuma-se escrever
df =
df
dx
dx ! I [y]
Z b
a
I
y
y dx =
Z b
a
@F
@y
d
dx
@F
@y0
y dx ;
ou seja,
I
y
=
@F
@y
d
dx
@F
@y0
e lesse, a derivada funcional de I [y] em relação a função y (x). Mais uma vez,
isso é apenas uma notação3
, mas é importante que você a conheça porque ela é
muito usada em livros e artigos.
3 Obviamente existe muito mais por trás do cálculo variacional. Mas se trabalharmos apenas
com funções bem comportadas (e.g., diferenciáveis em todos os pontos), na grande maioria
dos casos podemos encarar apenas como uma notação.
11

12. Figure 2: Figura retirada do Marion de Mecânica.
Com isso, nesta simbologia, a nossa expressão …ca
I [y] =
Z b
a
F (y; y0
; x) dx = 0 =)
I
y
=
d
dx
@F
@y0
i
@F
@yi
= 0 :
e lesse que, o fato da derivada funcional de I ser um extremo implica na equação
de Euler.
3.1.1 Exemplo: a braquistocrôna.
Um problema variacional bastante famoso, proposto em numa revista ciêntí…ca
por Bernoulli em 1696, é o chamado problema da braquistocrôna (do grego,
o tempo mais curto). Imagine dois pontos num plano, (x1; y1) e (x2; y2), se
uma força constante for aplicada na direção x e uma partícula de massa m se
mover do primeiro ponto ao segundo sob ação desta força, qual o caminho que
esta partícula deve percorrer para efetua o trajeto no menor tempo possível?
Imagine que você quer colocar um cano para guiar o movimento de uma bolinha
e quer saber a forma do cano para minimizar o tempo de percurso. A resposta
do problema acima é exatamente a trajetória que a sua pedra terá de fazer.
Ou ainda, imagine que você pendure uma corrente entre os dois pontos acima
(onde a força é, novamente, a gravidade), que curva esta corrente irá desenhar
(esta curva se chama catenária)? Todos estes exemplos se referem ao mesmo
problema. Vamos então a sua solução. Para fazer uma referência mais natural
a força gravitacional, colocamos os eixos como na …gura abaixo
Sabemos que a energia total do sistema T + U se conserva. Colocando o
zero do potencial no ponto de início (x1; y1) e considerando que a partícula
foi lançada do repouso na direção x (podemos ignorar qualquer velocidade na
direção y pois, como não há forças nesta direção, ela se conserva) temos que no
12

13. ponto inicial
Ei = T + U = 0
Seguindo a analogia da força gravitacional temos
F = mg =
@U
@x
) U = mgx
T =
1
2
mv2
A conservação de energia nos dá
T + U = 0 =) v =
p
2gx
Com isso
ds
dt
= v ) dt =
1
v
ds ) t =
Z (x2;y2)
(x1;y1)
1
v
ds
onde
(ds)
2
= (dx)
2
+ (dy)
2
Finalmente, o tempo vale
t =
Z (x2;y2)
(x1;y1)
1
p
2gx
q
(dx)
2
+ (dy)
2
=
Z (x2;y2)
(x1;y1)
s
1 + y02
2gx
dx =
1
p
2g
Z (x2;y2)
(x1;y1)
r
1 + y02
x
dx
y0
=
dy
dx
Ou seja, o nosso problema se reduz a minimizar a integral (como (2g)
1=2
é
uma constante)
I =
Z (x2;y2)
(x1;y1)
F (y0
; x) dx ; F (y0
; x) =
s
1 + y02
2gx
Onde, neste caso, a função F não depende explicitamente de y. A solução do
nosso problema é, então, a função y que obedece a equação de Euler (16)
@F
@y
d
dx
@F
@y0
= 0
Como, neste caso, F não depende explicitamente de y
@F
@y
= 0 )
d
dx
@F
@y0
= 0 )
@F
@y0
= C
@F
@y0
=
@
@y0
r
1 + y02
x
=
y0
p
x (1 + y02)
= C
13

14. Assim, a curva que a partícula deve seguir y (x) deve ser solução da equação
y0
p
x (1 + y02)
= C ) y02
= xC2
+ xy02
C2
) y0
=
s
xC2
(1 xC2)
;
ou ainda,
dy
dx
=
s
xC2
(1 xC2)
) y =
Z x2
x1
x
p
(2ax x2)
dx ;
2a = 1=C2
Fazendo
x = a (1 cos ) ) dx = a sin d
temos
y =
Z
a (1 cos ) d =
ou seja, a curva procurada é
y = a ( sin ) + const.
Com isso, a nossa curva obedece
x = a (1 cos ) ; y = a ( sin )
que são as equações paramétricas de uma curva chamada ciclóide.
Se a sua partícula for uma conta guiada por um …o (com massa) e você
prender o …o nos pontos acima o …o assumirá exatamente esta a forma que
levará a partícula entre os dois pontos no menor tempo, i.e., o …o formará uma
catenária.
A parte da curva entre o ponto (x1; y1) até o seu mínimo é chamada de curva
tautocrônica (como muito bem observado pela senhorita Palma), i.e., é a curva
na qual o tempo gasto por um objeto para deslizar sem fricção em gravidade
uniforme até seu ponto de mínimo é independente de seu ponto de partida (este
problema foi resolvido por Christiaan Huygens em 1659).
3.1.2 Equações de Euler-Lagrange
O ponto importante para nós no desenvolvimento acima é o seguinte: suponha
que a nossa variável é o tempo (x ! t) e que a função que procuramos seja a
trajetória de uma partícula com coordenada generalizada q(t) (y (x) ! q (t)).
Alem disso, suponha que a função F que estamos integrando seja exatamente a
lagrangiana L do sistema. Com isso
Z b
a
F (y; y0
; x) dx !
Z b
a
L (q; _q; t) dt
14

15. Figure 3: Figura retirada do Marion de Mecânica.
e a expressão (15) toma a forma:
Z b
a
L (q; _q; t) dt = 0 =)
d
dt
@L
@ _qi
@L
@qi
= 0 :
Que é exatamente a equação de Lagrange obtida anteriormente. Por isso estas
equações são chamadas de equações de Euler-Lagrange (EL).
A integral Z
L (q; _q; t) dt S [q]
é chamada de ação. Usando a linguagem do cálculo funcional, podemos obter
as equações de EL se impusermos que a derivada funcional da ação seja um ex-
tremo. Esta exigência recebe o nome de princípio da mínima ação (ou princípio
de Hamilton).
Neste sentido as equações de Lagrange e, consequentemente, toda a mecânica,
podem ser construídas a partir do princípio da mínima ação e esta construção
é equivalente a mecânica de Newton (perceba que este é um caminho diferente
do seguido no início deste texto).
O fato da mecânica de Lagrange ser uma conseqüência do princípio da mín-
ima ação tem uma conseqüência crucial na questão do comportamento ondu-
latório ou corpuscular da luz. Porque todos os resultados da óptica geométrica
podem ser obtidos a partir de um princípio muito semelhante chamado princí-
pio de Fermat do tempo mínimo. Este princípio estabelece que ao atravessar
meios diferentes, dentre todos os caminhos possíveis o feixe luminoso escolhe
aquele que minimiza o tempo da sua trajetória. Este princípio determina todos
15

16. os efeitos de refração e re‡exão. Como analogia, imagine que você está de
bicicleta na praia e quer atravessar a avenida da orla para chegar num ponto
a 45o
da normal à avenida. Qual caminho você deve seguir para chegar mais
rápido? O menor caminho é, obviamente, uma linha reta. Mas, como a bi-
cicleta se move com maior facilidade no asfalto é conveniente que você passe
menos tempo na areia. Porém, se você se mover na direção normal na praia a
distância percorrida será muito maior. Encontrar o caminho que minimize este
tempo é um problema de cálculo variacional. Assim, a trajetória tanto da
luz como das partículas pode ser obtida por um princípio de mínimo
de um funcional.
Falar sobre Variáveis de ângulo-ação.
3.2 Equação de Hamilton-Jacob
Considere novamente o problema variacional da ação S da seção anterior, mas
de um ponto de vista diferente. Primeiro considere que, na variação do cam-
inho, você não exige mais que os trajetos variados comecem e terminem no
mesmo ponto. Lembre que isso foi necessário para eliminar o termo de
fronteira na integral por partes em (14).
Assim, se os extremos do caminho puderem variar, teremos novamente a
expressão (17), mas agora com o termo de fronteira:
S =
@L
@ _qi
qi
t2
t1
+
Z t2
t1
@L
@qi
d
dt
@L
@ _qi
qi dt
onde nossa partícula saiu do ponto q(t1) e chegou no ponto q(t2).
Suponha agora que, por um outro método (e.g., a mecânica de Newton), você
resolveu o problema mecânico em questão, ou seja, você conhece a trajetória
qi (t) das partículas.
Uma vez que estas trajetórias são reais, elas devem respeitar as equações
de Lagrange (que são equivalentes as equações que você resolveu). Com isso,
podemos a…rmar que o último termo da expressão acima se anula. Ao variamos
os pontos iniciais e …nais certamente estaremos variando o percurso das partícu-
las. Assim, se calcularmos a variação da ação de uma partícula com relação a
sua posição inicial e …nal teremos usando apenas as trajetórias legítimas
S =
@L
@ _qi
qi
t2
t1
= [pi qi]
t2
t1
Uma vez que conhecemos as trajetórias, neste caso S não é mais um funcional
de q (t), mas apenas uma função ordinária de q(t), ou seja, dado um valor
de t podemos calcular q, _q e L (q (t) ; _q (t)) calcular a derivada parcial acima e
multiplicar pela distância entre os dois pontos escolhido q.
Com isso, a variação funcional descrita acima se torna apenas a variação
usual de uma função. Assim, podemos escrever
@S
@qi
= pi (18)
16

17. Agora, pela de…nição de S e pelo teorema fundamental do cálculo, sabemos
que a derivada total de S com relação ao tempo vale
S =
Z
L dt =)
dS
dt
= L (19)
Além disso, como S = S (q; t) (agora S depende não só da curva q, mas também
nos limites do tempo da integral acima) podemos escrever
dS
dt
=
@S
@t
+
@S
@qi
dqi
dt
=
@S
@t
+
@S
@qi
_qi
Usando (18)
dS
dt
=
@S
@t
+ pi _qi : (20)
Substituindo (19) em (20) temos
@S
@t
= L pi _qi :
Lembrando agora a de…nição do hamiltoniano (9)
H = pi _qi L =) L = pi _qi H
temos
@S
@t
= pi _qi H pi _qi = H =)
@S
@t
+ H = 0 :
Explicitando a dependência de H = H (qi; pi; t)
@S
@t
+ H (qi; pi; t) = 0
e usando novamente (18)
@S
@t
+ H qi;
@S
@qi
; t = 0 (21)
Ou seja, se pegarmos H (qi; pi; t), substituirmos todos os momentos por @S=@qi e
depois subrtituirmos na expressão acima, o que obtemos é uma equação diferen-
cial parcial para a função (agora desconhecida) S (q; t). Resolver esta equação
é equivalente a encontrar as trajetórias reais, ou físicas (chamado de setor
físico) do problema em questão. Isto é, resolvendo esta equação encontramos
S em função de q(t) e, conseqüentemente, q(t). A equação diferencial acima se
chama equação de Hamilton-Jacob.
Este é mais um método que pode ser usado para resolver problemas em
mecânica clássica. Infelizmente, da forma que foi apresentado, …ca parecendo
que não ganhamos nada nesta nova formulação. Isso não é verdade, mas o de-
senvolvimento completo do método de Hamilton-Jacob foge ao escopo da nossa
discussão. Tudo que precisaremos é da forma explicita da equação diferencial
acima.
17

18. 3.3 Óptica geométrica
A equação da óptica que descreve a propagação de uma onda num meio é dada
por
r2 n2
c2
@2
@t2
= 0 (22)
onde é uma função escalar, c a velocidade da luz no vácuo e n o índice de
refração do meio. Em geral n = n (x) depende do meio onde a luz se propaga.
Para n constante uma solução da equação acima pode ser escrita como
(x; t) = 0 exp [i (k:x !t)]
onde o número de onda k = jkj e a freqüência angular estão relacionadas por
k =
2
=
n!
c
:
Exercise 3 Veri…que que a função acima é solução da equação de onda.
Por simplicidade, tomemos uma onda plana que se propaga na direção z
= 0 exp [i (kz !t)]
de…nindo
k = k0n ;
onde k0 é número de onda no vácuo, temos
= 0 exp [i (kz !t)] = 0 exp [ik0 (nz ct)] :
Estamos aqui interessados no caso da chamada óptica geométrica. Isto é, no
caso em que o comprimento de onda da luz é muito menor que as dimensões
espaciais envolvidas no sistema. Em especial, as características do meio não
variam apreciavelmente com distância da ordem de alguns comprimentos de
onda.
Neste caso, apesar de n não ser constante, podemos a…rmar que ele varia
lentamente no espaço. Neste caso, obviamente, a onda plana não é mais uma
solução da equação de onda, uma vez que as variações do meio destorcem a
onda. Vamos procurar por uma solução da equação de onda na forma
= (xi) exp [ik0 (L (xi) ct)] ;
com
(xi) = exp (A (xi)) =) = exp [A (xi) + ik0 (L (xi) ct)] :
As quantidades A e L funções reais a serem determinadas. Vemos que A con-
trola a amplitude da onda. Como para n constante L ! nz esta quantidade
18

19. é chamada de comprimento de onda óptico, ou ainda a eikonal. Calculando o
laplaciano de temos
r = r exp [A (xi) + ik0 (L (xi) ct)] = r [A + ik0L] ;
r2
=
n
r2
[A + ik0L] + [r (A + ik0L)]
2
o
;
e a derivada temporal
@
@t
=
@
@t
exp [A (xi) + ik0 (L (xi) ct)] = ik0c ;
@2
@t2
= (k0c)
2
:
Substituindo na equação de onda (22) e isolando parte real e imaginária temos
r2
A + (rA)
2
+ k2
0 n2
(rL)
2
= 0 ;
r2
L + 2L (rA rL) = 0 :
Usando agora a aproximação da óptica geométrica, de que o compri-
mento de onda é muito menor que a variação do meio, temos que o termo
proporcional a k2
0 = 4 2
= 2
0 é o mais signi…cativo da expressão acima. Em
especial, a variação espacial de A (xi) é, por hipótese, pequena.
Sendo todos os termos quadráticos (positivos), então todos os termos da
primeira igualdade acima devem se anular. Assim, sendo o último termo da
primeira igualdade o mais signi…cativo (na nossa aproximação), para garantir
que este termo se anule o temos que exigir que
(rL)
2
= n2
=) jrLj = n : (23)
Esta equação é conhecida como equação de eikonal da óptica geométrica. A
superfície onde L (xi) possui o mesmo valor é uma frente de onda e esta onda
se desloca na direção da normal desta superfície.
3.4 Mecânica e a óptica geométrica
Considere um sistema conservativo onde o hamiltoniano não depende do tempo.
Neste caso podemos escrever:
H (qi; pi) =
1
2m
p2
i + V (qi) = E
Usando agora (18)
pi =
@S
@qi
(24)
podemos escrever
1
2m
@S
@qi
2
+ V (qi) = E =)
@S
@qi
2
= 2m (E V )
19

20. Assim, a equação de HJ para este sistema pode ser escrita como
@S
@qi
2
= 2m (E V )
Para coordenadas cartesianas (qi = xi) podemos ainda escrever
(rS)
2
= 2m (E V ) : (25)
Esta equação é formalmente igual a equação eikonal (23) para um meio com
índice de refração
n =
p
2m (E V )
Esta semelhança foi percebida muito antes do surgimento da MQ.
Vamos explorar um pouco mais esta semelhança associando o nosso sistema
mecânico (uma partícula) com uma onda. Mas que onda é esta? Bem, com-
parando diretamente a equação acima com a equação eikonal da óptica, vemos
que a analogia seria tratar uma superfície com um dado valor de S como
a frente de uma onda. Seguindo esta analogia, associamos então a partícula
de massa m num potencial V uma “onda” cuja frente de onda são os pontos
onde S(x; t0) possui os mesmos valores num dado instante t0.
Como S depende do tempo esta frente de onda se deforma e se propaga com
uma certa velocidade u
u =
ds
dt
onde ds é o deslocamento in…nitesimal normal a superfície de valor constante.
Estamos interessados em determinar esta velocidade u.
Voltando na expressão de HJ (21) e usando o fato do nosso hamiltoniano
não depender do tempo temos
@S
@t
+ H qi;
@S
@qi
; t = 0 =)
@S
@t
= E
de onde podemos escrever
@S
@t
= E =) S (x; t) = W (x) Et : (26)
onde W (x) é a solução da nossa equação (25)
(rS)
2
= 2m (E V ) =) (rW)
2
= 2m (E V )
A função W não depende do tempo. Assim, os valores de x que de…nem um
certo valor de W (x) = a representam uma superfície constante do espaço.
Podemos então dividir o nosso espaço em superfícies com valores …xo de W.
Queremos seguir uma superfície com um valor constante S = a
(i.e., seguir a nossa frente de onda). A expressão (26) nos diz que em cada
instante …xo do tempo a superfície S constante coincide com alguma superfície
20

21. Figure 4: Figura retirada do Goldstein
W constante (se S = a num instante t1 então, neste instante, S coincide com a
superfície W = a+Et1). Assim, suponde que em t = 0 temos S = W = a depois
de um tempo dt a expressão (26) nos diz que S irá coincidir com a superfície
t = 0 : S (0) = W = a =) S (dt) = W Edt =) S + Edt = W = a + Edt
Assim, se em t = 0 a superfície S coincide com W = a, depois de um intervalo
dt, S irá coincidir com uma outra superfície W = a + Edt de onde temos que
a variação de S num intervalo dt corresponde a diferençã entre duas superfícies
W onde
dW = (a + Edt a) = Edt :
Por outro lado, sendo W uma função apenas das posições temos
dW =
@W
@xi
dxi = rW ds = jrWj :ds
onde, pela de…nição do gradiente, ds é o deslocamento normal a superfície W e,
consequentemente, a S. Igualando as duas expressões acima temos
Edt = jrWj :ds =)
ds
dt
=
E
jrWj
= u (27)
ou seja, num instante de tempo dt a frente de onda se desloca uma quantidade
ds. Em outras palavras, u é a velocidade da nossa onda.
Usando agora a relação (25) e (26) podemos escrever
(rS)
2
= (rW)
2
= 2m (E V ) =) jrWj =
p
2m (E V ) :
com o que temos
u =
E
p
2m (E V )
(28)
21

22. Ou seja, a nossa partícula, ou uma coleção de partículas não interagentes de
mesma massa, pode ser descrita por uma onda que se propaga num potencial
V com a velocidade u acima.
A região de valor constante de uma onda é exatamente a de…nição da fase
da onda. Assim, se estamos seguindo uma onda onde a frente de onda tem
valor constante S (q; t) isso signi…ca que estamos seguindo a onda cuja fase é
proporcional a iS
= exp
i
~
S = exp
i
~
(W (qi) Et) (29)
onde h é apenas uma constante de proporcionalidade. Isso signi…ca que a nossa
onda tem uma frequencia
!t =
E
~
t =) 2 =
1
~
E =) E = 2 ~ =) E = h : (30)
Além disso, lembrando da relação clássica (24) temos
pi =
@S
@qi
=) p = OS = OW (31)
Com o que a relação (27) se torna
u =
E
jrWj
=
E
p
(32)
com p o módulo do momento linear da partícula.
O seguinte resultado da óptica nos permite relacionar a frequência da onda
e seu comprimento com a sua velocidade de propagação u
= u =) =
u
usando (30) e (32)
=
u
=
E=p
E=h
=) =
h
p
(33)
As relações (32) e (33) relacionam a energia e o momento da partícula com
a sua frequência e o seu comprimento de onda. Esta analogia tem a sua origem
em trabalhos de Hamilton de 1825, para tratar problemas de óptica. Porém,
nesta época, não havia nenhum resultado experimental que pudesse dar uma in-
dicação do valor da constante h e, especialmente, nenhuma razão para crer que
esta constante não era zero para uma partícula (uma quantidade cujo compor-
tamento corpuscular fosse indubitável). Mesmo assim, Hamilton teve sucesso
em usar este desenvolvimento para a luz, num tipo de tratamento corpuscular, e
obter todos os resultados de refração e re‡exão obtidos por outros métodos da
ótpica geométrica. Isso mostrava que, pelo menos em certos limites, a descrição
corpuscular de Newton era complemente equivalente a descrição ondulatória de
Huygens. Entretanto, como este método não trazia facilidades práticas para o
22

23. tratamento de problemas (em relação aos demais métodos da óptica geométrica)
ele foi praticamente esquecido por décadas.
Porém, com o surgimento de hipóteses de um caráter dual (onda-partícula),
não apenas da luz, mas também das partículas massivas, estes resultados foram
redescobertos por Erwin Schroedinger em 1925.
3.5 A equação de Schroedinger independente do tempo
Primeiramente é necessário lembrar que os resultados acima mostram uma com-
patibilidade entre a mecânica e a óptica apenas para o limite de curtos compri-
mentos de onda (onde a equação da onda se torna a equação de eikonal que é
idêntica a equação de HJ). Desta igualdade Schrödinger supôs que a equação de
HJ pudesse ser o limite para curtos comprimentos de onda de uma equação mais
geral que descrevesse o comportamento ondulatório das partículas massivas.
Para tentar encontrar esta equação mais geral, ele voltou a equação de onda
1
u2
@2
@t2
r2
= 0
em seguida ele supôs que, pelo menos para comprimentos de onda curtas, a
velocidade da onda associada a partícula deveria ser a velocidade (28) obtida
na seção anterior
u2
=
E2
2m (E V )
Assim, nossa equação de onda se torna
2m (E V )
E2
@2
@t2
= r2
(34)
Seguindo o procedimento usual para a solução de equações parciais, podemos
separar as variáveis da nossa função de onda
(xi; t) = (xi) exp ( i!t)
Vamos agora supor que a nossa onda tem uma energia bem de…nida. Se
usarmos agora a hipótese de De Broglie (ou a equação (30)) temos
E = h ) E = ~! ) (xi; t) = (xi) exp i
E
~
t : (35)
Substituindo na equação de onda
r2
+
2m
~2
(E V ) = 0 =)
~2
2m
r2
+ V = E : (36)
Esta é a celebrada equação de Schroedinger independente do tempo. Ela descreve
as funções de onda (os estados) das partículas quando a sua energia está bem
de…nida, i.e., ela descreve os estados estacionários. Com ela podemos obter a
maioria dos resultados da mecânica quântica não-relativística, como o espectro
de energia do átomo de hidrogênio. A maior (e talvez mais importante) parte
deste curso será o estudo das soluções da equação acima.
23

24. Se o sistema é conservativo, a sua energia pode variar com o
tempo?
O que signi…ca dizer que o sistema tem uma energia bem de…nida?
Lembre-se que a descrição quântica do sistema é uma descrição probabilís-
tica. Assim, ao calcularmos uma quantidade qualquer (e.g., a energia), o que
obtemos, em geral, é a probabilidade de numa medida desta quantidade obter-
mos o valor calculado. Ou seja, em geral o sistema não possui o valor bem
determinado de nenhuma quantidade física. Mas se o sistema é um só, como
uma quantidade pode não estar determinada, será que a quantidade está bem
determinada, mas nós apenas não a conhecemos? Seria tudo isso como, por
exemplo, colocar um dado numa caixa fechada e sacolejá-la? Antes de abrir a
caixa e ver o resultado, cada número tem a chance de 1=6 de ser sorteado. Mas
o número já está lá dentro, só que você não sabe. Pelas interpretações da MQ as
coisas não são assim. A idéia é que, antes de abrir a caixa, o dado efetivamente
não possui nenhum valor de…nido. Apenas a sua observação fará com que ele
adquira efetivamente este valor. A diferença entre você não saber e o sistema
não ter é que este sistema (A) pode in‡uenciar outro (B) através do valor deste
observável e, como veremos, se o valor de um observável não está determinado
(ou seja, você não fez nenhuma medida) todos os valores possíveis desta medida
in‡uenciam B (com uma in‡uência maior ou menor dependendo da probabil-
idade). Este é um fenômeno de interferência comum na teoria ondulatória,
mas que desa…a o senso comum numa teoria corpuscular.
Assim, a…rmar que o sistema tem um valor bem de…nido E de um observável
signi…ca que, se …zemos uma medida desta quantidade, obteremos sempre (in-
dependente de quando), o valor E.
Como é possível a…rmar que um observável tem seu valor bem
de…nido, antes de fazemos a medida?
O ponto é que se …zemos uma medida de um certo observável (futuramente
de…niremos melhor este termo) e não perturbamos mais o sistema (i.e., deixamos
ele isolado) o valor deste observável não murará. Podemos garantir assim que,
se alguém …zer uma medida futura, obterá o valor que nós medimos. Chamamos
a isso de preparar o sistema num certo estado conhecido.
Mas e o dado na caixa, está numa superposição de todos os valores?
O ponto é que o dado é um sistema grande o su…ciente para o seu comporta-
mento ser completamente determinado pelas leis da mecânica clássica. Assim,
mesmo que não tenhamos aberto a caixa, é possível, num ambiente controlado
o su…ciente, saber o valor do resultado. Num certo sentido, sistemas clássicos
são sempre sistemas quânticos preparados.
Remark 4 Se um sistema está num valor indeterminado de uma grandeza. É
completamente impossível saber qual o valor desta grandeza antes da medida ser
feita.
24

25. 3.6 A partícula numa caixa
Vamos ilustrar a aplicação da ES tratando o caso de uma partícula livre numa
caixa. Ou seja, fora o fato de ser con…nada dentro da caixa, nenhuma outra
força age sobre esta partícula. Assim, vamos usar as idéias da seção anterior
para quantizar o sistema unidimensional de uma partícula de massa m num
intervalo. Um ponto importante é que este sistema em duas ou três dimensões
representa, grosso modo, apenas a aplicação do tratamento a ser desenvolvido
para cada dimensão separadamente. Ou seja, nosso sistema não é arti…cial.
Inicialmente estamos interessados em estudar os níveis de energia que esta
partícula pode ter. Estado livre, a energia desta partícula é puramente cinética.
Classicamente, uma ver que a partícula pode ter qualquer velocidade dentro
da caixa, ela também pode assumir qualquer valor de energia. Além disso, a
partícula pode estar em qualquer lugar dentro da caixa. Na descrição quântica,
entretanto, veremos que as coisas são um pouco diferentes.
Como estamos interessados em estados de energia bem de…nidos, o problema
que devemos resolver é a ES independente do tempo:
~2
2m
r2
+ V = E
Uma vez que, dentro do intervalo (caixa), a partícula está livre, V = 0, e estamos
trabalhando em uma dimensão, temos:
~2
2m
d2
dx2
= E
onde E é a energia da partícula. Podemos escrever esta equação como
d2
dx2
= k2
; k2
=
2m
~2
E (37)
Esta é uma equação de segunda ordem, logo ela deve ter duas soluções LI e
duas constantes de integração. Estas soluções podem ser escritas como
1 (x) = A exp (ikx) ; 2 (x) = B exp ( ikx)
com A e B constantes. Assim, a solução geral do nosso problema é
(x) = Aeikx
+ Be ikx
Como determinamos as constantes A e B?
Estas constantes estão relacionadas com a chamada condição de contorno
do problema. Ou seja, precisamos especi…car o comportamento da nossa função
nos extremos. Até agora, além de fazer V = 0 (uma condição física), tudo
que …zemos foi resolver um problema matemático, mas agora, na …xação destas
condições, entram as características físicas do problema.
25

26. Para isso precisamos lembrar o signi…cado da função de onda. A quantidade
j (x)j
2
signi…ca a probabilidade de encontrar a nossa partícula na posição x. Sabendo
que a nossa partícula está presa na caixa temos
j (x)j
2
= 0 para x fora da caixa.
Primeiro precisamos colocar um eixo cartesiano no nosso problema e dizer
onde está a nossa caixa. Por exemplo, podemos dizer que as paredes da caixa
estão em L e L (obviamente isso não in‡uencia no resultado).
Exigindo que a partícula esteja con…nada no intervalo de L até L e que
a função seja contínua temos (por (37) vemos que descontinuidades da função
estariam relacionadas com energias in…nitas e não queremos tais casos.)
(L) = ( L) = 0
temos
(L) = 0 =) AeikL
+ Be ikL
= 0 =) AeikL
= Be ikL
A (cos kL + i sin kL) = B (cos kL i sin kL) :
Podemos satisfazer esta igualdade de duas formas
sin kL = 0 =) kL = n ) A (cos kL) = B (cos kL) ) A = B ;
cos kL = 0 =) kL = n +
1
2
) A (i sin kL) = B ( i sin kL) ) A = B :
Ou seja, o nosso problema possui dois tipos de soluções estacionárias
n (x) = N sin kn x ; kn =
L
n ) En =
~2
2m
n
L
2
+
n (x) = N+
cos k+
n x ; k+
n =
L
n +
1
2
) E+
n =
~2
2m L
n +
1
2
2
(38)
O resultado acima nos mostra que, dentro da caixa, a partícula só pode
assumir os níveis de energia En e E+
n .
Exercise 5 Obtenha as constantes de normalização N+
e N .
Além disso, existe um nível mínimo de energia que o sistema pode assumir
que é E+
0 . A partícula nunca pode ter energia cinética nula (observe que E0 = 0
implica 0 (x) = 0 e a partícula não está mais na caixa).
26

27. Mais ainda, se esta partícula interagir com alguma coisa (e.g., fótons) ela
só poderá absorver e emitir energias que sejam proporcionais a diferença entre
dois níveis
En !n = E+
n Em
Esta é a chamada energia de transição de n para m.
Por exemplo, imagine que a partícula está no estado fundamental e você o
ilumina com uma luz de freqüência , se
h < E+
0 E1 =
3
4
~2
2m L
2
;
os fótons simplesmente irão passar pelo sistema (o sistema será transparente).
Já se
= [ E+
0 E1 =
3
4
~2
2m L
2
o sistema irá absorver este fotos e mudar de nível (ele será opaco para esta
freqüência).
Observe também que, de forma geral,
E
~
L
2
:
Ou seja, se o tamanho da caixa vai para in…nito (partícula livre) a diferença
dos níveis de energia vão a zero e, conseqüentemente, a partícula pode assumir
qualquer valor de energia.
Da mesma forma, se tomamos o limite clássico ~ ! 0 o sistema passa a
adotar o comportamento clássico de poder assumir qualquer valor de energia.
Remark 6 Observe como a limitação da partícula no intervalo tornou os níveis
de energia discretos. Este é o fenômeno por trás do comportamento dos chama-
dos pontos quânticos (QD).
Aqui é interessante ver como a realização do nosso espaço depende muito de
qual parte do sistema nos interessa. Se no exemplo acima a distância L for muito
pequena, os níveis de energia vão estar tão espaçados que para sofrer uma tran-
sição de nível precisaríamos fornecer uma quantidade muito grande de energia.
Podemos garantir assim que o sistema não sofra nenhuma transição indesejada
(e.g., térmica) e as únicas transições possíveis são aquelas que nós provocamos.
Neste caso, apenas alguns níveis de energia são relevantes e podemos tratar o
sistema como um problema de n níveis. Ao fazemos isso nosso sistema passa a
ter um número …nito de estados e passa a ser descrito por uma matriz. Esta
descrição matricial é a chamada mecânica quântica de Heisenberg, que veremos
no futuro.
27

28. 3.6.1 Números quânticos
Ainda sobre o problema da partícula numa caixa, todas as quantidades asso-
ciadas ao sistema, exceto a energia, estão indeterminadas, ou possuem a sua
determinação associada a uma probabilidade. Ademais, uma vez especi…-
cada a energia da partícula, sabemos construir a sua função de onda,
da qual retiramos todas as informações que a MQ pode nos dar sobre o sis-
tema (e acreditamos que este seja a teoria que mais informações pode nos dar).
Dizemos assim que a energia especi…ca o estado do sistema. Dentro da
notação utilizada, chamamos de En a energia associada ao sistema. Ou seja,
dado o valor de n podemos determinar a energia do sistema e, conseqüente-
mente, o seu estado. A quantidade n, que especi…ca completamente o estado
do sistema é chamada de número quântico. Se tivéssemos trabalhado com uma
caixa bidimensional, teríamos uma energia associada ao movimento na direção
x, com uma energia En, e outra associada com o movimento na direção y, que
poderíamos chamar de Em. Assim, neste caso, o sistema possui dois números
quânticos. O mesmo acontecia com a descrição das órbitas elípticas de Som-
merfeld, onde precisávamos de 2 números para conhecer o estado do sistema.
Remark 7 Assim, números quânticos são quantidades (discretas) que precisam
ser especi…cadas para se estabelecer o estado do sistema.
3.6.2 Valores médios
Sendo j (x)j
2
a probabilidade de encontrar o sistema numa certa posição,
podemos também calcular o valor médio da posição do sistema. Basta para
isso usarmos a de…nição usual de média multiplicarmos o valor da variável (no
caso, a posição) pela probabilidade do sistema possuir aquele valor desta var-
iável. Assim, a posição média do sistema dentro da caixa vale
hxi =
Z
x j (x)j
2
dx =
Z
(x) x (x) dx
Onde, por razões que se tornarão claras no futuro, usamos a última forma para
a expressão. De forma geral, se f(r) é uma função qualquer da posição da
partícula (considerada agora em 3D), o valor médio de f pode ser calculado
como
hfi =
Z
V
(r) f (r) (r) d3
V (39)
onde V é o volume onde o se deseja calcular a média.
Como veremos em detalhes no futuro, um dos postulados da MQ é que
as quantidades clássicas observadas nada mais são do que valores médios das
quantidades quânticas do sistema.
3.6.3 Preparação de sistemas e superposição
Vamos preparar um sistema com um valor especí…co de energia. Imagine para
isso um espectrômetro de massa onde atiramos partículas de massa m e carga
28

29. q conhecidas. Dependendo da velocidade, ou do momento da partícula, ela
sofrerá uma certa in‡uência do campo e se chocará com a parede do dispositivo.
Conhecendo a energia cinética da partícula, sambemos exatamente onde ela
se chocará. Podemos então fazer um furo que seria alcançado apenas pelas
partículas que tivessem uma determinada energia, digamos, E2 ,
E2 =
~2
2m
n
L
2
; n = 2 :
Em frente ao furo temos uma caixa para capturar a partícula. As paredes do
dispositivo podem ter sensores que detectem a partícula no caso de um choque.
Neste experimento vamos jogando partículas com energia desconhecida dentro
do dispositivo e, sempre que esta partícula colide com a parede, ouvimos um
clique. Quando, não ouvimos este clique é porque a partícula passou pelo bu-
raco. Neste caso sabemos que temos aprisionado em nossa caixa uma partícula
no estado
2 (x) = N sin k2 x ; kn = 2
L
:
Desta forma podemos preparar o sistema num determinado estado.
Imagine agora que fazemos dois furos na parede, uma na posição de energia
E+
1 e outra na posição de energia E2 . Suponha ainda que, pelas dimensões
dos componentes do sistema, estes dois furos estão bem próximos, de sorte que
podemos colocar uma única caixa para capturar uma partícula que passe por
qualquer buraco.
Qual o estado do sistema na caixa neste caso?
Neste caso, a partícula entrará na caixa num estado descrito pela função:
(x) = c1
+
1 (x) + c2 2 (x) ; c1; c2 2 C : (40)
Ou seja, ela não terá mais uma energia bem de…nida. Além disso, pelos
princípios da MQ o módulo quadrado dos coe…cientes c1 e c2 acima são dados
pela probabilidade do sistema ser detectado com energia E+
1 e E2 , respecti-
vamente. Além disso, como estes módulos são probabilidade e sabemos que o
sistema estará (com certeza) num estado ou no outro
jc1j
2
+ jc2j
2
= 1
Por exemplo, se o experimento foi desenvolvido (depende basicamente de quão
aleatório é a velocidade das partículas lançadas) para que a partícula tenha
exatamente a mesma probabilidade de estar no estado E+
1 ou E2 , podemos
então a…rmar que
jc1j
2
= jc2j
2
=
1
2
Obviamente, isso não …xa o valor destes coe…cientes, pois
jc1j
2
=
1
2
=) c1 =
exp (i )
p
2
; Re = 0 (41)
29

30. A quantidade é chamada de fase do coe…ciente. Futuramente trataremos da
determinação destes coe…cientes.
Observe que estamos frisando que a partícula entra na caixa no estado acima.
Isso porque, como a energia da partícula não é mais bem determinada ela não
está mais num estado estacionário.
Na obtenção da ES independente do tempo, usamos a seguinte separação de
variáveis (35)
(x; t) = (x) exp i
E
~
t
e, com isso, obtivemos a ES. Ou seja, o que estamos chamando de é, na
verdade, apenas a função (x) acima.
Isso signi…ca que a função de onda completa do nosso sistema com uma
energia E2 conhecida é
(x; t) = 2 (x) exp i
E2
~
t :
Agora, a probabilidade desta partícula ser encontrar numa posição x num in-
stante t vale
j (x; t)j
2
= 2 (x)
2
exp i
E2
~
t
2
= 2 (x)
2
:
E não depende do tempo. Por isso, estados com energia bem de…nida são
chamados de estados estacionários.
Agora, para uma partícula no estado (40) acima, temos a seguinte evolução
temporal
(x) = c1
+
1 (x)+c2 2 (x) =) (x; t) = c1
+
1 (x) exp i
E+
1
~
t +c2 2 (x) exp i
E2
~
t
Usando que a probabilidade inicial do sistema ter uma ou outra energia é a
mesma (41) temos
(x; t) =
1
p
2
+
1 (x) exp i
E+
1
~
t + 1 + c2 2 (x) exp i
E2
~
t + 2
=
1
p
2
exp i
E+
1
~
t + 1
"
+
1 (x) + c2 2 (x) exp
"
i
E2 E+
1
~
t + ( 2 1)
!##
A probabilidade de encontrar este sistema na posição x num instante t vale
j (x; t)j
2
=
1
2
+
1 (x) + c2 2 (x) exp
"
i
E2 E+
1
~
t + ( 2 1)
!# 2
:
(42)
onde a dependência temporal não mais desaparece. Assim, esta probabilidade
varia com o tempo e o sistema não está mais num estado estacionário. Observe
30

31. também que esta probabilidade depende da diferença de fase ( 2 1). Esta
quantidade não possui um análogo clássico e, na verdade, não pode ser me-
dida por nenhum instrumento. Mesmo assim, como veremos, ela pode produzir
efeitos mensuráveis. Por causa desta fase, esta descrição difere da probabili-
dade clássica (que seria apenas a soma das probabilidades). Veja novamente a
discussão no capítulo Ondas e Partículas.
O que acontece se …zemos um furo numa região que não corresponde a nen-
hum dos valores de En, por exemplo, entre os valores de E2 e E+
1 ?
A princípio pode-se imaginar que nunca capturaremos uma partícula. Ou
seja, sempre ouviremos o clique da partícula se chocando com a parede do
dispositivo. Mas isso não é verdade.
Observe que, se não colocamos a caixa (ou seja, apenas o espectrômetro)
detectaríamos o choque de partículas em todas as posições da parede, inclusive
na posição correspondente a energia E. Assim, o fato de termos ou não colocado
a caixa naquele ponto não deve alterar o comportamento das partículas dentro
do espectrômetro. Por isso deveríamos realmente esperar que alguma partícula
entrasse na caixa. Entretanto, nosso problema e entender como uma partícula
que classicamente tem energia E será detectada na caixa apenas com energia
E+
1 e E2 .
Quando não ouvirmos o clique saberemos que capturamos uma partícula
na caixa e, mais ainda, esta partícula estará num estado inicial aproximada-
mente da forma (40). Onde o módulo quadrado dos coe…cientes será tão maior
quão mais próximo o furo estiver do estado de energia de…nido. Por exemplo,
conforme o furo se aproxima de E+
1 , o jc1j
2
cresce até que, quando o furo estiver
exatamente em E+
1 temos
jc1j
2
= 1 ; jc2j = 0 :
Além disso, o sistema (que não está num estado estacionário, pois sua energia
não está bem determinada), evoluirá no tempo com a forma aproximadamente
(42).
Isso signi…ca que mesmo que, classicamente, a partícula só possa passar
entrar na caixa se ela tiver uma energia entre E1 e E2, quanticamente ela tem
uma probabilidade de entrar (e, ocasionalmente, entrará) se a sua energia não
for bem determina, mas compatível com o fato dela entrar na caixa. Neste
experimento, sempre que abrirmos a caixa e medirmos a energia da partícula
obteremos (sempre) os valores E+
1 ou E2 e nunca entre estes valores. Mas se
detectamos o valor E2 e para passar pelo furo ela teria de ter uma energia
E < E2 , para onde foi a diferença de energia? Não foi para lugar nenhum!
Pense no pior: ela foi detectada na caixa com uma energia E+
1 < E. Como a
partícula conseguiu passar pelo furo se ela não tinha energia pra isso? O que
acontece com a conservação de energia? O ponto aqui é a descrição quântica
jamais a…rma que a partícula passou pelo furo, mas apenas que ela está dentro
da caixa. Ou seja, a única forma de saber se ela passou pelo furo é colocando
um detector lá dentro. Sem fazer isso, tudo que sabemos é que uma partícula
entrou na caixa. O problema está em que toda a nossa descrição anterior se
31

32. baseia na idéia da trajetória seguida pela partícula e, quanticamente, tal idéia
dependeria de colocarmos detectores em todos os pontos do espaço e medirmos
(e, conseqüentemente, interferirmos) na partícula em cada instante de tempo.
Ou seja, na MQ não existe a idéia de trajetória de uma partícula. Além
disso, o fato da partícula ter entrado na caixa com uma energia E+
1 menor
que a energia clássica necessária para passar pelo furo, não viola nenhuma lei de
conservação, pois, em nem um momento, a partícula teve a energia bem de…nida
E (nunca demos esta energia para ela). O fato de sistemas quânticos fazerem
coisas que são classicamente proibidas devido a sua energia é bem comum em
MQ. Este fenômeno é observado corriqueiramente em laboratório e recebe o
nome de tunelamento. Voltaremos a este fenômeno no futuro.
Exercise 8 Mas então, como uma partícula que classicamente tem energia E
pode ser detectada com energia E+
1 ou E2 ?
O ponto aqui é que, na verdade, como o estado inicial da partícula é descon-
hecido, a MQ nos diz que esta partícula está no estado
=
X
n
c+
n
+
n + cn n
De sorte que ela terá uma maior probabilidade de entrar na caixa quanto maior
for c+
1
2
e c2
2
. Além disso, ao entrar na caixa, o estado da partícula não foi
alterado. Assim, se ela inicialmente, além de um coe…ciente c+
1 e c2 auto tiver
também um coe…ciente c+
8 (obviamente pequeno) haverá também a probabili-
dade c+
8
2
de se detectar esta partícula com uma energia E+
8 bem maior que
E2 .
Exercise 9 Mas e se colocarmos uma caixa com tamanho diferente?
Neste caso a decomposição acima não irá mais corresponder ao estado das
partículas permitidas dentro da caixa e, para fazer a descrição acima, teremos
de uma outra decomposição
=
X
n
cn n ;
com n 6= +
n ; n .
Exercise 10 Mas qual das decomposições acima descreve a partícula?
Ambas! Na verdade, observando explicitamente as funções +
n ; n (38) ve-
mos que as decomposições acima nada mais são que a série de Fourie da função
e existem in…nitas formas de se decompor a mesma função em séries diferentes.
Exercise 11 Mas como a energia clássica E se relaciona com todas estas de-
composições?
32

33. Como veremos mais tarde, as partículas capturadas tem uma energia média
igual a E
E = hEi =
X
n
E+
n c+
n
2
+ En cn
2
:
Além disso, mesmo no caso dos dois furos nas posições correspondentes as
energias E+
1 e E2 , a MQ não apóia a idéia de que a partícula passou por um
ou pelo outro furo.
Remark 12 Observe que a fase d em (41) não interfere nos valores médios
(39).
Gato de Schroedinger
Superposição
Decomposição e série de Fourie.
3.7 A equação de Schroedinger dependente do tempo
Nosso objetivo agora é encontrar uma equação que descreva não apenas a parte
espacial , mas a função completa , ou seja, nós queremos a versão dependente
do tempo da expressão acima.
A equação (36) só funciona (só é compatível com a equação de onda) para
ondas com uma só freqüência (monocromáticas), mas gostaríamos de ter uma
maior liberdade na dependência temporal do nosso problema. Para isso pre-
cisamos eliminar E (E = h ) da nossa equação.
Para isso, primeiro multiplicamos a equação (36)
~2
2m
r2
+ V = E :
por exp ( iEt=~) e voltamos para a função de onda completa
~2
2m
r2
+ V = E ;
(mas esta equação só é válida para as nossas ondas monocromáticas).
Se operarmos em ambos os lados desta equação com o operador ~2
=2m r2
+ V
temos
~2
2m
r2
+ V
~2
2m
r2
+ V =
~2
2m
r2
+ V E = E2
;
ou seja,
~2
2m
r2
+ V
2
= E2
: (43)
Agora derivamos duas vezes a equação (35)
33

34. (xi; t) = (xi) exp i
E
~
t ;
em relação ao tempo
• =
E2
~2
exp i
E
~
t =
E2
~2
=) E2
= ~2 • :
Substituindo na equação (43)
~2
2m
r2
+ V
2
= ~2 • : (44)
Esta equação fornece a equação correta para o caso monocromático, mas, por
não depender de E, possui também outras soluções. Entretanto, esta equação
possui o terrível inconveniente de ser uma equação de quarta ordem nas co-
ordenadas espaciais. Isso signi…ca que as soluções desta equação exigem uma
quantidade enorme de condições iniciais e condições de contorno que di…cilmente
poderiam ser associadas com parâmetros físicos do sistema.
Vamos então reescrever a equação anterior na forma
^H2
= ~2 @2
@t2
;
onde introduzimos o operador
^H =
~2
2m
r2
+ V : (45)
Nossa equação pode ainda ser escrita como
^H ^H = i~
@
@t
i~
@
@t
:
Soluções desta equação pode ser construídas com funções que respeitem
^H = i~
@
@t
)
~2
2m
r2
+ V = i~
@
@t
(46)
Esta é a equação de Schrödinger dependente do tempo. Esta equação, diferente
da equação de onda usual, é de primeira ordem no tempo e de segunda ordem
nas derivadas espaciais.
Ao trabalhar com ondas (equações de ondas) é comum usarmos uma função
complexa e, no …nal, atribuirmos uma realidade física apenas a parte real. En-
tretanto o caso aqui é um pouco diferente, pois a nossa equação é, na verdade,
(44). Se dividirmos em sua parte real e imaginária
= P + iQ ;
34

35. e substituirmos em (46) temos
i~
@P
@t
~
@Q
@t
=
~2
2m
r2
+ V P + i
~2
2m
r2
+ V Q
comparando as partes reais e imaginárias desta equação temos
~
@P
@t
=
~2
2m
r2
+ V Q
~
@Q
@t
=
~2
2m
r2
+ V P
Podemos agora eliminar P ou Q diferenciando uma das equações acima com
relação ao tempo e substituindo na segunda. O que obteremos com isso é que
tanto Q como P respeitam a equação (44). Ou seja, temos uma equação de
quarta ordem para funções reais, ou uma equação de segunda ordem para uma
função complexa, cujas partes não podem ser separadas. Mas, neste último
caso, precisamos das relações acima, o que mostra que, neste formalismo, nós
precisamos da função completa = P + iQ, i.e., não podemos atribuir um
signi…cado físico separadamente para a parte real ou a imaginária.
Voltemos agora na relação com a óptica geométrica. Lembre que obtivemos
os resultados da seção anterior seguindo uma frente de onda de…nida pela função
S. Além disso, como vimos anteriormente, a nossa onda se relaciona com S
por (29)
= exp
i
~
S (47)
com isso temos
@
@t
=
i
~
@S
@t
;
@
@xi
=
i
~
@S
@xi
Substituindo na equação de Schrödinger (46)
1
2m
(rS)
2 ~2
2m
i
~
r2
S + V =
@S
@t
ou seja, S respeita a equação
1
2m
(rS)
2
+ V +
@S
@t
=
i~
2m
r2
S (48)
Vamos comparar este resultado com a equação de HJ (??)
@S
@t
+ H qi;
@S
@qi
; t = 0
Lembrando que H é o Hamiltoniano da partícula podemos escrever
H =
p2
2m
+ V (49)
35

36. usando (18)
rS = p =) H =
(rS)
2
2m
+ V =)
1
2m
(rS)
2
+ V +
@S
@t
= 0 (50)
As equações (48) e (50) são idênticas a menos do último termo em (48). Lem-
brando que h = 2 ~ é a constante de proporcionalidade que introduzimos em
(29). Mais uma vez, a semelhança acima já havia sido percebida por Hamilton.
Mas a inexistência de qualquer evidência experimental do comportamento ondu-
latório das partículas o levou (talvez) a pensar que h fosse zero para partículas
massivas. Além disso, ao se tratar sistemas mecânicos usuais, o fato de h ser
muito pequeno, em relação às demais quantidades do sistema, faz com que a
presença do termo a direita em (47) não in‡uencie apreciavelmente a dinâmica
do sistema. Podemos ainda dizer que a equação de HJ representa um limite
da equação de Schrödinger quando todas as quantidades envolvidas são muito
grandes em relação à h. Isso normalmente é chamado de tomar o limite quando
h tende a zero. Obviamente, como h é uma constante, isso deve ser entendido
no contexto acima de comparações de grandezas. Além disso, tomar o limite
h ! 0 é chamado de tomar o limite clássico do sistema quântico. Como, neste
caso, a equação que descreve o sistema (ES) se torna a equação HJ, todas as
quantidades calculadas através da ES (e.g., energia) deve se tornar os resultados
calculados pela mecânica clássica.
Falar sobre o operador Hamiltoniano.
3.7.1 A quantização de Schrödinger e de Sommerfeld
Dado um sistema mecânico (clássico) sujeito a um potencial V , a ES nos permite
construir a descrição quântica deste sistema, i.e., construir a equação de onda
que rege o comportamento quântico do sistema clássico em questão. Assim,
este é um processo de quantização que podemos considerar como o primeiro
processo de quantização geral. Este processo é mais geral de o que Sommerfeld
por prescindir da existência de uma variável periódica no sistema. Além disso,
este novo processo nos permite construir não apenas certas quantidades clássicas
(e.g., energia), mas sim a própria função de onda que descreve o sistema (de
onde podemos tirar muito mais informações).
Lembrando agora que a quantização de Sommerfeld pode ser considerada
como uma generalização dos processos de quantização anteriores (de Bohr e
de Planck), será que a quantização de Schroedinger estaria relacionada com a
quantização de Sommerfeld? A resposta é sim.
Dado um sistema com uma coordenada periódica, por exemplo, um ângulo
, pontos no espaço com coordenada e + 2 representam o mesmo ponto.
Com isso, seria de se esperar que qualquer função f( ) que represente uma
característica de um sistema físico tenha um único valor de…nido neste ponto,
i.e., f( ) = f( + 2 ). Neste caso dizemos que a função f tem valor único, ou
que ela respeita uma condição de unicidade.
36

37. Por exemplo, a função f ( ) = exp (in ), n 2 N, respeita esta condição no
intervalo de 0 a 2 , pois
f ( + 2 ) = exp [in ( + 2 )] = exp i (n ) exp i (2 n) = exp i (n ) = f ( ) :
Entretanto, isso não ocorre com a função f ( ) = exp (i =2), neste mesmo inter-
valo,
f ( + 2 ) = exp i
+ 2
2
= exp i
2
exp i ( ) = exp i
2
= f ( ) :
De forma geral, se q é uma variável periódica, podemos testar se uma função
f (q) = exp [ig (q)] é de valor único calculando a variação da fase num período
completo I
dg
e exigindo que este valor seja proporcional a 2 ,
I
dg = 2 n ; n 2 N : (51)
Por exemplo,
f ( ) = ein
=) g = g ( ) = n =)
I
dg =
Z 2
0
nd = 2n ;
f ( ) = ei =2
=) g = g ( ) =
2
=)
I
dg =
Z 2
0
1
2
d = 6= 2n :
Lembre-se agora que a ES foi obtida tomando que a partícula obedece a uma
equação de onda na forma (47) temos
= exp
i
~
S
Para um sistema conservativo temos
= exp
i
~
(W (qi) Et) = exp
i
~
W (qi) exp
i
~
Et :
Como estamos interessados só na variação da parte espacial, temos
g (qi) =
1
~
W (qi) =)
I
dg =
I
1
~
dW
Lembrando que W = W (qi) temos
dW =
@W
@qi
dqi
37

38. usando (31)
pi =
@W
@qi
=) dW =
X
i
pi dqi
com o que I
dg =
I
1
~
dW =
1
~
X
i
I
pi dqi
Usando agora a condição de unicidade (51) temos
1
~
X
i
I
pi dqi = 2 n =)
X
i
I
pi dqi = 2 ~n =)
X
i
I
pi dqi = hn :
como as variáveis são independentes, podemos respeitar a igualdade acima se,
para cada variável I
pi dqi = hn :
Que é a regra de quantização de Sommerfeld. Resumindo:
Remark 13 A regra de quantização de Sommerfeld é uma conseqüência da
unicidade da função de onda.
Na teoria de Schrödinger esta unicidade é introduzida à mão, através do es-
tabelecimento das condições de contorno do problema. Ou seja, impor a quan-
tização de Sommerfeld é equivalente a impor condições de contorno
que garantam a unicidade da função de onda na teoria de Schrödinger.
Como vimos na seção anterior, a discretização nos níveis de energia de uma
partícula são uma conseqüência do con…namento da posição da partícula, i.e.,
das condições de contorno do problema.
Além disso, assim como a quantização de Sommerfeld permitiu generalizar
as orbitas circulares para elípticas. A ES permite impor novas condições de
contorno.
Condições de contorno são cruciais para se determinar as características
quânticas do sistema. Efeitos curiosíssimos, como o surgimento de forças (men-
suráveis) como a possibilidade de se detectar efeitos provenientes da energia do
vácuo, uma conseqüência do chamado efeito Casimir, são resultados do estudo
das condições de fronteira do sistema. Características gerais da matéria, como o
número de prótons do elemento mais pesado, podem estar ligadas aos problemas
de condições de contorno.
4 Limite clássico
Voltemos, mais uma vez, ao problema da partícula numa caixa de tamanho L.
Vamos inicialmente analisar este problema do ponto de vista da física clássica.
Neste caso, a partícula sempre teria uma velocidade constante e sua posição
será dada por
x = x0 + vt :
38

39. Figure 5: Figura retirada do Libof
Suponha agora que você não conhece a posição inicial x0 da partícula. Qual
a chance de encontrar a particular numa certa posição da caixa?
Ou seja, classicamente quanto vale P (x) dx?
Se a velocidade da partícula variasse, poderíamos esperar que, onde ela …ca
mais lenta (ou seja, a região onde ela gasta mais tempo para atravessar) teria
um valor maior de P(x). Como a nossa partícula tem uma velocidade constante,
a probabilidade de encontrá-la em qualquer intervalo dx é simplesmente o valor
deste intervalo dividido pelo tamanho da caixa (o valor da variável, dividira pelo
total de valores que ela pode ter)
P dx =
1
L
dx
Ou seja, a probabilidade é uma constante. Isso signi…ca que, se …zermos uma
série de cópias da nossa caixa e as abrirmos encontraremos as partículas dis-
tribuídas igualmente por toda a caixa.
Como vimos anteriormente, a descrição quântica é bem diferente. Existindo
pontos onde a partícula pode estar com maior probabilidade e pontos onde
ela não pode estar. Entretanto, na descrição quântica, conforme o valor da
energia aumenta, surgem mais picos de probabilidade de onde a partícula pode
estar. Num caso de energia muito alta para qualquer intervalo dx que tomarmos
teremos sempre o mesmo número de picos dentro deste intervalo. Assim, neste
caso, a probabilidade de encontrar a partícula em qualquer região dx é, assim
como no caso clássico, uma constante.
Assim, para o caso em que n ! 1, a descrição quântica concorda com a
descrição clássica. Mais ainda, para sistemas cuja energia seja muito maior que
a ordem de grandeza de h, esperamos um comportamento clássico. Em todo
sistema quântico, existe um limite para o qual o comportamento do sistema
tende àquela prevista pela teoria clássica. Usualmente este limite está associ-
ado ao regime de altas energias. Mas, de forma geral, basta que as grandezas
envolvidas sejam muito grandes, em comparação a h. A existência deste limite
clássico é chamada de princípio da correspondência de Bohr.
39

40. Outra característica importante para se analisar este limite é o comprimento
de onda de De Broglie. Por exemplo, num gás com densidade a distância média
das partículas vale aproximadamente 1=3
. Assim, para o regime
1=3
>> ;
devemos esperar que o comportamento deste gás seja descrito pela mecânica es-
tatística clássica. Mas, para o caso em que 1=3
' , uma mecânica estatística
quântica deve ser aplicada (este é um assunto da segunda parte do curso).
As comparações acima nos mostrar que, se um certo resultado quântico não
contem h, este resultado deve ser mesmo que o obtido por uma teoria clássica.
O exemplo mais famoso é a seção de choque de espalhamento coulombiano. Um
tratamento quântico detalhado fornece um resultado que não depende de h e é
exatamente igual ao resultado obtido por Rutherford usando teorias clássicas.
5 A equação de continuidade
Lembrando a lei da continuidade da carga para o eletromagnetismo temos
r J =
@
@t
:
onde é a densidade de carga e J a densidade de corrente. A leitura desta
equação nos diz que toda a corrente que ‡ui para fora de uma região é igual a
carga que esta região perdeu.
Desde sua origem os testes e aplicações da MQ se referem ao problema do
espalhamento de partículas. Ou seja, partículas vindas “livremente”do in…nito
interagem momentaneamente com um certo potencial (e.g., outra partícula) e
voltam a se propagar livremente. Lembre-se, por exemplo, dos experimentos
de Rutherford. Todos os problemas estudados em aceleradores de partículas
são desta forma. A interação momentânea da partícula teste com o potencial
é chamada de espalhamento. Usualmente neste tipo de processo a forma exata
do potencial de espalhamento não é conhecida. Mas este é modelado por certas
características principais.
Por exemplo, podemos modelar a interação de um elétron com um neutro
supondo que o nêutron é uma esfera impenetrável de raio R e usando o potencial:
V (r) =
0 ; r R
1 ; r < R
;
chamado de potencial de caroço duro. A quantização deste potencial fornece
bons resultados desde que a energia do elétron não seja muito grande.
Na maioria dos processos observamos uma partícula, ou um feixe de partícu-
las, e queremos saber o comportamento deste feixe. Assim, como veremos mais
adiante, neste tipo de problema o conceito de conservação da partícula é
muito importante (obviamente para os casos onde ela não se desintegra). Por
isso é importante buscar por uma lei de conservação semelhante a do eletromag-
netismo.
40

41. A dinâmica de uma partícula é descrita pela ES dependente do tempo
^H = i~
@
@t
=)
@
@t
=
i
~
^H
Usando o mesmo desenvolvimento feito para obter a equação acima, mas partindo
do complexo conjugado da função de onda
= exp
i
~
S ! = exp
i
~
S
é fácil mostrar que obedece a equação
^H = i~
@
@t
=)
@
@t
=
i
~
^H
Observe agora que
@ j j
2
@t
=
@
@t
=
@
@t
+
@
@t
usando as duas ES acima temos
@ j j
2
@t
=
i
~
^H +
i
~
^H
Para um problema unidimensional
^H =
~2
2m
@2
@x2
+ V (x)
temos
@ j j
2
@t
=
i
~
~2
2m
@2
@x2
+ V (x) +
i
~
~2
2m
@2
@x2
+ V (x)
= i
~
2m
@2
@x2
@2
@x2
= i
~
2m
@
@x
@
@x
@
@x
ou ainda
@ j j
2
@t
+
@
@x
i
~
2m
@
@x
@
@x
= 0
Em 3 dimensões temos
@ j j
2
@t
+ r i
~
2m
( r r ) = 0
Se de…nirmos as quantidades
J = i
~
2m
( r r ) ; = j j
2
(52)
41

42. temos a equação exatamente uma equação de continuidade. De…nimos assim o
conceito quântico de densidade e corrente de partículas.
Além do fato da densidade das partículas estar relacionada com a proba-
bilidade de onde a partícula está, existe também uma corrente associada a ela.
Pelos princípios da MQ esta corrente não pode ser associada diretamente ao
movimento da partícula.
Por exemplo, uma partícula numa caixa, com energia bem de…nida E é
descrita por uma função na forma
(x) = N sin (kx) exp i
E
~
t
e possui uma densidade
(x; t) = j j
2
= jNj
2
sin2
(kx)
e uma corrente
J = i
~
2m
@
@x
@
@x
= 0 =
@
@t
Ou seja, mesmo que classicamente pensemos numa partícula andando de um
lado para o outro da caixa (consequentemente um ‡uxo na forma Jc = v (x)),
quanticamente não há ‡uxo algum. Além disso, classicamente a nossa densidade
seria diferente de zero apenas num ponto ( c = (x)), mas quanticamente, ela
se espalha por toda a caixa.
Por exemplo, um elétron de um átomo de hidrogênio in‡uencia a sua viz-
inhança como se fosse uma distribuição de carga dada por = j (r)j
2
e não
como uma distribuição de carga clássica de uma única partícula c = q (r).
Obviamente, como sempre acontece em MQ, existem regimes onde os con-
ceitos clássicos e quânticos concordam.
6 Barreira de potencial …nita
Vamos agora analisar o problema de uma barreira de potencial …nita. Imagine,
por exemplo, um circuito como o da …gura abaixo:
42

43. Onde as grades es-
tão ligadas a uma bateria. Na região I temos um potencial constante, que
podemos chamar de U = 0. E na Região II temos, novamente um potencial
constante U = V > 0. Uma carga se movendo em qualquer uma destas regiões
não sofrerá a in‡uência de nenhuma força.
Agora, se uma carga (positiva) tentar se mover na Região III entre as placas,
sofrerá uma força constante F = qE, dada por um potencial U = Ex. O grá…co
deste potencial seria algo como:
Classicamente uma carga na Região I só poderia penetrar na Região II se
ela tiver energia su…ciente para vencer a barreira de potencial, ou seja, apenas
se ela possui uma energia E > V . Se uma carga com E < V viaja pela Região
I, ao chegar na Região III ela seria desacelerada até ser re‡etida de volta.
Além disso, toda a carga com E > V passaria pelo potencial.
Vejamos agora o que nos diz a descrição quântica deste problema.
Para simpli…car bastante o nosso problema, nós jogamos as duas placas
externas para o in…nito e fazemos D ! 0 ou, o que dá no mesmo, fazemos
V >> D. Com isso, o potencial tem a forma da …gura abaixo
43

44. Então
agora temos apenas duas regiões. A Região I será aquela onde o potencial vale
zero, U = 0, enquanto na Região II , temos U (x) = V . Assim, nesta descrição,
temos também duas ES, uma para cada região.
Assim como no caso da partícula livre, imaginemos que a partícula possui
uma energia bem de…nida, i.e., vamos estudar a ES independente do tempo para
este problema.
Na Região I:
~2
2m
d2
dx2
+ U = E !
~2
2m
00
I = E I =) 00
I = k2
1 I ;
k2
1 =
2m
~2
E : (53)
A solução deste problema é o mesmo da partícula livre, ou seja, podemos
escrever a solução como:
I = A exp (ikIx) + B exp ( ikIx) :
As duas soluções acima representam ondas viajando na direção x (kI = ^x)
e x ( kI = ^x).
44

45. Já para a Região II temos:
~2
2m
d2
dx2
+ U = E !
~2
2m
d2
dx2
+ V II = E II
00
II = k2
2 ; k2
2 =
2m
~2
(E V ) : (54)
Note que, apesar de ambos serem constante, kI 6= kII. Assim, a solução da
equação diferencial acima é a mesma da anterior, mas, como veremos, o com-
portamento destas soluções é bem diferente. Ou seja,
II (x) = C exp (ik2x) + D exp ( ik2x) :
Nosso objetivo é saber o que acontece com uma partícula que vem da região
I, viajando para a direita, quando esta encontra a barreira de potencial. Assim,
podemos simpli…car ainda mais o nosso problema fazendo D = 0. Observe que
a partícula pode vir pela direita, ser re‡etida pela barreira e voltar viajando
para a esquerda, por isso não fazemos B = 0. Com isso, as soluções procuradas
têm a forma
I (x) = A exp (ik1x) + B exp ( ik1x)
II (x) = C exp (ik2x)
As soluções acima representam a composição de 3 onde distintas:
1. i = A exp (ik1x) descreve uma onda plana que vem do in…nito ( 1) em
direção a barreira (nossa partícula inicial).
2. t = C exp (ik2x) descreve uma onda que atravessou a barreira e se move
para a direita.
3. r = B exp ( ik1x) descreve uma onda para a esquerda. Como inicial-
mente só temos partículas vindas da direita, esta onda só pode descrever
uma onda (ou uma partícula) que foi re‡etida pela barreira.
45

46. Da descrição acima vemos que jCj
2
é a probabilidade da nossa partícula
atravessar a barreira (pois se jCj
2
= 0 ) j IIj = 0 e não há partícula na
região II), enquanto jBj
2
é a probabilidade da nossa partícula ser re‡etida pela
barreira. Se a partícula foi re‡etida ela volta com a mesma energia E e se ela
atravessou ela agora terá uma energia E V .
Podemos associar ao sistema então uma corrente Ji da partícula (ou das
partículas) incidentes. Usando (52)
Ji = i
~
2m
i
@ i
@x i
@ i
@x
= i
~
2m
2ik1 jAj
2
=
~
m
k1 jAj
2
Lembrando que, pela relação de De Broglie (ou pela de…nição de k)
p =
h
=
h
2
k = ~k
a quantidade ~k1 é o momento da nossa partícula incidente. Assim, se associ-
amos a partícula uma velocidade (clássica), v = p=m, a quantidade Ji pode ser
escrita como
Ji =
~k1
m
jAj
2
(^x) =
p1
m
jAj
2
(^x) = v1 jAj
2
(^x) :
Além disso, lembrando a nossa de…nição quântica para a densidade de partículas
= j j
2
) i = jAj
2
temos
Ji = v1 i
Que é exatamente a expressão clássica para a corrente de uma distribuição
com densidade e velocidade v. É necessário ter em mente que, apesar das
descrições baterem, a interpretação por detrás destas equações é bem diferente.
Enquanto classicamente esperamos ter uma in…nidade de partículas distribuídas
uniformemente no eixo x (pois i é constante), e cada uma com velocidade v.
Quanticamente podemos ter apenas uma partícula com momento ~k que possui
a mesma probabilidade de ser encontrada em qualquer lugar do eixo
x. Lembre-se que a solução com energia de…nida é uma onda estacionária que
ocupa (sempre) todo o espaço.
Entretanto, levando adiante esta analogia, podemos ainda de…nir uma cor-
rente para as partículas re‡etidas Jr
Jr =
~
m
k1 jBj
2
( ^x)
O coe…ciente de re‡exão R de um meio mede exatamente a fração da corrente
incidente (ou da intensidade da onda incidente) que este meio é capaz de re‡etir.
Assim:
R =
jJrj
jJij
=
jAj
2
jBj
2
46

47. Se pensarmos apenas em termos de ondas (como eletromagnéticas) a expressão
acima simplesmente nos diz que o coe…ciente de re‡exão de um meio é a razão
entre a intensidade da onda re‡etida e da onda incidente.
Da mesma forma, podemos de…nir uma corrente transmitida Jt
Jt =
~k2
m
jCj
2
(^x)
e determinar o coe…ciente de transmissão do nosso potencial
T =
jJtj
jJij
=
k2
k1
jCj
2
jBj
2
Se o nosso sistema consiste numa in…nidade de partículas, emitidas uma após
a outras, os coe…cientes acima nos dizem a proporção destas partículas que irá
atravessa ou será re‡etida pela barreira. Estes efeitos são facilmente observa-
dos com a luz em meios translúcidos. Mas veja que agora, a expressões acima
são válidas para uma única partícula (massiva, ou um fóton). Esta descrição é
completamente diferente da clássica que a…rma: se partícula tem energia
maior que a barreira ela passa, caso contrário ela não passa. Falando
novamente sobre fótons, vemos que o comportamento clássico (observado em
meios translúcidos) é esperado para um sistema constituído com um grande
número de partículas. Neste sentido a teoria clássica da luz funciona perfeita-
mente bem para intensidades altas, mas, para baixas intensidades, precisamos
da teoria quântica. Baixas intensidade (apenas alguns, ou mesmo um único
fóton) só foram alcançados em equipamentos mais modernos. Vemos que, no
caso da luz, o limite clássico está relacionado com altas intensidades.
Bem, voltemos agora a nossa descrição quântica. Para determinarmos os
coe…cientes R e T da nossa barreira, precisamos obter as razões entre as intensi-
dades da nossa função de onda, ou seja, determinar a razão entre as constantes
da nossa equação diferencial. Assim como no caso da partícula na caixa, para
determinar as constantes acima precisamos impor condições de contorno no
problema.
Mais uma vez, não queremos descontinuidades na função de onda (pois isso
estaria associado com uma energia in…nita). Além disso, como ES indepen-
dente do tempo envolve uma derivada segunda, pela mesma razão não queremos
uma descontinuidade na primeira derivada da função de onda. Matematica-
mente estas exigências são necessárias para que as equações diferen-
ciais façam sentido.
Assim, devemos impor as condições
I (0) = II (0) ; 0
I (0) = 0
II (0) ;
Com isso
A + B = C
ik1 (A B) = ik2C =) A B =
k2
k1
C
47

48. Resolvendo para C=A e B=A temos
C
A
=
2
h
1 + k2
k1
i ;
B
A
=
1 k2
k1
1 + k2
k1
Com isso, nossos coe…cientes se tornam
T =
4k2=k1
1 + k2
k1
2 ; R =
1 k2=k1
1 + k2=k1
2
Usando (53) e (54)
k2
k1
=
r
1
V
E
Vamos primeiro analisar o caso em que E V
E V )
V
E
1 ) 0
k2
k1
1
Primeiramente note que, como era de se esperar
T + R =
1
1 + k2
k1
2
h
2k2=k1 + 1 + (k2=k1)
2
i
= 1
Para o caso especial E = V
T = 0 ; R = 1
temos uma re‡exão total da partícula. Conforme E cresce o coe…ciente de
transmissão vai aumentando enquanto o de re‡exão vai diminuindo.
Observe que, apesar do coe…ciente de transmissão aumenta com a energia
(o que é natural), o comportamento é completamente diferente do esperado
classicamente. Pois, mesmo que a partícula tenha uma energia E > V
ela tem uma probabilidade de ser re‡etida pela barreira. Ou seja, se
jogarmos várias partículas com uma energia E > V detectaremos algumas sendo
re‡etidas pela barreira. No nosso exemplo da carga atravessando o campo, a
nossa partícula tem energia cinética su…ciente para vencer o campo,
mas, mesmo assim, ela é re‡etida.
Vejamos agora o que ocorre quando E < V .
Neste caso, a ES na região II se torna
d2
dx2 II =
2m
~2
(E V ) II =
d2
dx2 II =
2m
~2
(V E) II
00
II = 2
II ; 2
=
2m
~2
(V E) > 0
Cuja solução vale
48

49. Figure 6: Libo¤
II (x) = C exp ( x) + C0
exp (+ x)
Qual dos sinais acima usar?
A resposta para esta pergunta permite analisar uma série de características
(físicas e formais) da MQ.
Vamos considerar que a solução geral seja uma combinação linear dos dois
sinais.
o sinal positivo (+). Neste caso, conforme nossa onda se aproxima do in…nito
teremos:
II (x ! 1) ' C exp ( x) ! 1
(A partícula sempre estaria no in…nito)
Fisicamente isso signi…ca que a partícula sempre seria encontrada no in-
…nito, ou seja, a probabilidade dela estar no in…nito (e conseqüentemente ser
transmitida seria sempre maior que qualquer outra probabilidade …nita). Obvi-
amente isso não acontece, o que nos permite (com argumentos físicos) escolher
o sinal de menos na exponencial. Matematicamente o mesmo argumento
a…rma que uma função de onda este fato está relacionado com não podermos
normalizar a função de onda acima. Assim, entre os postulados da MQ, temos
que os estados físicos do sistema são dados por funções de onda que respeitam
Z 1
1
j (x)j
2
dx < 1
Ou seja, cuja probabilidade de serem encontrada em todo o espaço seja …nita.
Dizemos que as funções permitidas são de quadrado integrável, ou, mais tecni-
camente, que elas pertencem ao espaço de Hilbert.
49

50. Podemos continuar usando todos os resultados anteriores fazendo
00
II = 2
= (i )
2
II
e substituindo k2 por i . Com isso
B
A
=
1 i
k1
1 + i
k1
Se de…nirmos
z = 1 + i
k1
lembrando que =k1 2 R, temos
B
A
=
z
z
=) R =
B
A
2
=
z
z
2
= 1
Para obter o coe…ciente R vamos usar,
T + R = 1 ) T = 0 :
Entretanto, precisamos ver que este resultado continua válido para E < V
(lembre-se que, para obter o resultado acima, usamos explicitamente E V ).
Neste caso é necessário notar que no processo de espalhamento que estamos estu-
dando todas as correntes são constantes. O que, pela equação de continuidade,
signi…ca que
r J =
@
@t
)
@
@t
= 0 :
Para o caso de uma partícula, este resultado não é nada intuitivo com a nossa
visão clássica. Pois não podemos imaginar a partícula entrando nem
saindo de nenhuma região. Mas lembres-se que, enquanto você não detectar
a partícula ela é uma onda no espaço todo. O resultado acima nos diz que
@Jx
@x
@J
@x
= 0 ;
com isso Z 1
1
@J
@x
dx = J1 J 1 = 0 :
Mas sabemos que
J 1 = Ji Jr
J1 = Jt
com isso
Jt Ji + Jr = 0 =)
Jt
Ji
+
Jr
Ji
= 1 =) T + R = 1 :
Assim este resultado é válido para qualquer corrente estacionária.
50

51. Com isso, para E < V , temos
R = 1 =) T = 0
Ou seja, para energias menores que a barreira todas as partículas são re‡etidas.
Este último resultado concorda plenamente com o esperado classicamente.
Podemos obter este resultado também diretamente da solução
II (x) = C exp ( x) =) II (1) = 0
Ou seja, não podemos encontrar nossa partícula muito longe da barreira e,
consequentemente, não há corrente Jt nesta região. Além disso, como a corrente
é estacionária, Jt 0.
6.1 Comportamento dentro da barreira
Uma atenção especial deve ser dada para o comportamento da função de onda
na região dentro da barreira
II (x) = C exp ( x)
Onde o valor de C está relacionado com as demais constantes pelas condições de
contorno e pela normalização. Observe que agora a probabilidade de encontrar
a partícula no interior da barreira (apesar de não ser nula) cai exponencialmente
II (x ! 1) ' Ce x
! 0
Mas, a previsão da MQ, é que existe uma probabilidade não nula da partícula
ser encontrada numa região classicamente proibida.
Observe, entretanto, que nesta região a partícula teria uma energia total
negativa (E V < 0). Um tal estado não é considerável …sicamente possível,
porque não saberíamos que tipo de dispositivo físico poderia medir esta energia
(não há um análogo clássico para isso). Entretanto, o ponto importante é que,
se a barreira tiver uma largura …nita, de sorte que a função não seja zero no
…nal da barreira, uma partícula com uma energia E < V poderia atravessar esta
barreira.
7 Barreira quadrada
Vamos analisar agora um problema um pouco mais complicado, mas muito mais
interessante. Imagine agora que o nosso potencial não continua constante até o
in…nito, mas volta a cair num certo ponto. Ou seja, a nossa partícula vem livre
até x < a (U (x < a) = 0), sofre a ação de um potencial em x = a (U = V ),
mas a in‡uência deste potencial torna a desaparecer numa certa distância a
(U (x > a) = 0).
51

52. Figure 7: Libo¤
Temos agora 3 regiões de interesse e, para cada região, temos a seguinte ES
independente do tempo
I (x) = Aeik1x
+ Be ik1x
; k2
1 =
2mE
~2
; x < a
II (x) = Ceik2x
+ De ik2x
; k2
2 =
2m
~2
(E V ) ; a < x < a
III (x) = Feik1x
; x > a
Onde, na última função de onda, usamos novamente que estamos interessados
apenas no espalhamento de uma partícula vinda da esquerda.
Mais uma vez, estamos interessados no estudo dos coe…cientes de transmissão
T e re‡exão R deste potencial
T =
F
A
2
; R =
B
A
2
Mais uma vez, os coe…cientes estão relacionados pela continuidade da função
e sua derivada nos pontos a
e ik1a
+
B
A
eik1a
=
C
A
e ik2a
+
D
A
eik2a
k1 e ik1a B
A
eik1a
= k2
C
A
e ik2a D
A
eik2a
52

53. e a,
C
A
eik2a
+
D
A
e ik2a
=
F
A
eik1a
k2
C
A
eik2a D
A
e ik2a
= k1
F
A
eik1a
Resolvendo estas equações para F=A, B=A temos:
F
A
= e2ik1a
cos (2k2a)
i
2
k2
1 + k2
2
k1k2
sin (2k2a)
1
B
A
=
i
2
F
A
k2
2 k2
1
k1k2
sin (2k2a)
Exercise 14 Obtenha as expressões acima.
Usando a segunda das relações acima podemos escrever
B
A
2
=
F
A
2
1
4
k2
2 k2
1
k1k2
2
sin2
(2k2a)
e suando a relação
T + R =
F
A
2
+
B
A
2
= 1 =)
B
A
2
= 1
F
A
2
temos
1
T
=
A
F
2
=
1
4
k2
2 k2
1
k1k2
2
sin2
(2k2a) + 1
7.1 Primeiro caso E > V
Para E > V temos
k2
1 =
2mE
~2
; k2
2 =
2m
~2
(E V )
k2
1 k2
2 =)
k2
2 k2
1
k1k2
2
=
k2
1 k2
2
k1k2
2
=
E (E V )
V 2
com isso
T =
4E (E V )
V 2 sin2
g
p
E V + 4E (E V )
; E > V
g = 2a
r
2m
~2
(55)
Onde agrupamos todas as características da partícula e da espessura da barreira
na constante g.
53

54. Além disso, a transmissão é total (T = 1) sempre que a diferença entre a
energia e o potencial valer:
E V =
~2
2m
n
2a
2
=) T =
4E (E V )
4E (E V )
= 1
Ou seja, quando a barreira respeita a relação acima ela se torna transparente
para as partículas. Usando a relação de De Bloglie
2ak2 = n =) 2a = n
2
quando o comprimento de onda da partícula é metade do tamanho da barreira.
Esta relação pode ser usada para medir a espessura da barreira.
Para energias muito altas
T = 1 ; E ! 1 :
Mais uma vez temos o comportamento descrito anteriormente de que, mesmo
para energias mais altas que V , a partícula pode ser re‡etida pelo potencial.
Quando E ! V temos
E !
+
V ; sin g
p
E V ! g
p
E V ;
T !
1
g
2
2
V + 1
< 1 :
Agora temos que para energias próximas ao valor do potencial o coe…ciente de
transmissão não mais se anula. Além disso, para uma barrira in…nita (V ! 1),
ou uma barreira muito longa (g ! 1, que é o caso analisado anteriormente),
temos (como esperado) T = 0.
7.2 Segundo caso E < V
Analisemos agora o caso para E < V . Novamente podemos aproveitar toda a
álgebra desenvolvida anteriormente fazendo a substituição
k2
2 =
2m
~2
(E V )
2
=
2m
~2
(V E) = k2
2 ) i = k2
com isso
II (x) = Ce x
Observe então que antes e depois da barreira temos ondas (oscilantes) en-
quanto dentro da barreira a função de onda decai exponencialmente. Assim,
devemos esperar um comportamento como o da …gura abaixo. Onde a ampli-
tude da onda depois da barreira e tão menor quanto mais longa a barreira.
54

55. Libo¤
Com isso temos:
1
T
=
1
4
(i )
2
k2
1
k1i
2
sin2
(2i a) + 1
=
1
4
2
k2
1
k1i
2
sinh2
(2 a) + 1
=
1
4
2
+ k2
1
k1
2
sinh2
(2 a) + 1
usando
2
+ k2
1
k1
=
V
p
E (V E)
temos
T =
4E (V E)
V 2 sinh2
g
p
V E + 4E (V E)
; E < V
O principal ponto deste resultado é que, mesmo para E < V (classicamente
nossa partícula não tem energia para atravessar o potencial), temos T 6= 0. Este
fenômeno é chamado de tunelamento quântico, ou simplesmente, tunelamento.
Este processo esta por trás do Scanning tunneling microscope. De acordo com
este efeito, sistemas quânticos fazem coisas que eles não teriam energia pra fazer
(mas isso, de forma alguma, viola a conservação de energia). Uma das primeiras
aplicações do tunelamento, foi para explicar o decaimento radioativo de certos
átomos. No núcleo atômico a forca de repulsão coulombiana entre os prótons e
compensada pela atração nuclear entre os nucleons. Entretanto, como a força
nuclear é de curto alcance, enquanto a força de Coulomb é de longo alcance,
conforma aumentamos o tamanho do átomo, prótons mais distantes continuam
55

56. se repelindo pela força eletromagnética, mas são atraídos apenas pelos nucleons
a sua volta. Vamos tendo assim um aumento gradual da repulsão, enquanto
a atração permanece a mesma. Se tentarmos montar um átomo muito grande
a repulsão colombiana simplesmente despedaçará o nosso átomo. Mas, para
átomos não tão grandes (e.g., urânio-238), a força de atração ainda é maior (mas
pouco maior) que a repulsão. Assim, classicamente este átomo seria estável.
Entretanto, devido ao processo de tunelamento, pedaços do núcleo que não
teriam energia (devido a repulsão) para escaparem da atração, conseguem fazê-
lo. Assim, alguns pedaços do núcleo (e.g., dois prótons e dois nêutrons, chamado
de partícula alfa) escapam do átomo de urânio. Este problema foi tratado com
esta abordagem de tunelamento por Gamow, Condon e Gurney em 1928.
Atualmente uma série de dispositivos eletrônicos (junção de Josephson e
diodos de tunelamento) funciona através deste processo de tunelamento, neste
caso, envolvendo elétrons.
Vemos que para E < V temos T < 1. E para E ! 0
T !
0
h
V 2 sinh2
g
p
V
i = 0 ;
O comportamento geral do sistema pode ser visto na …gura abaixo
O coe…ciente (e, conseqüentemente, a probabilidade) de transmissão vai au-
mentando com a energia E, até atingir um valor máximo (T = 1) que depende
das características da barreira (g). Depois este valor oscila próximo ao máximo,
de sorte que num certo range, se aumentarmos a energia diminuímos a trans-
missão (um comportamento bastante inesperado). Depois, para energias muito
altas, a transmissão passa a valer sempre 1.
8 Poço …nito
O poço de potencial quadrado, apesar de mais complicado que os potenciais
anteriores, fornece uma forma simples de entender alguns dos mais importantes
problemas tratados pela MQ. Ente eles, a estrutura do átomo de hidrogênio e a
condução eletrônica tanto em metais e em semicondutores.
A con…guração deste problema pode ser descrita por um potencial na forma
56

57. Figure 8: Figura tirada do Libo¤, para g = 4.
57

58. Libo¤
Neste problema podemos continuar usando as mesmas equações do problema
anterior
I (x) = Aeik1x
+ Be ik1x
; k2
1 =
2mE
~2
; x < a
II (x) = Ceik2x
+ De ik2x
; k2
2 =
2m
~2
(E V ) ; a < x < a
III (x) = Feik1x
; x > a (56)
apenas com a modi…cação
k2
2 =
2m
~2
(E V ) ! k2
2 =
2m
~2
(E + jV j)
com isso, para E 0 (que equivale ao caso E V ) o coe…ciente de transmissão
(55)
T =
4E (E V )
V 2 sin2
g
p
E V + 4E (E V )
; E > V ; g = 2a
r
2m
~2
se torna
T =
4E (E + jV j)
V 2 sin2
g
p
E + jV j + 4E (E + jV j)
58

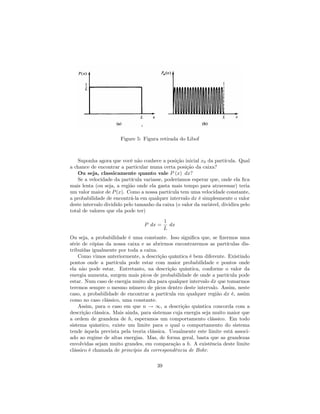
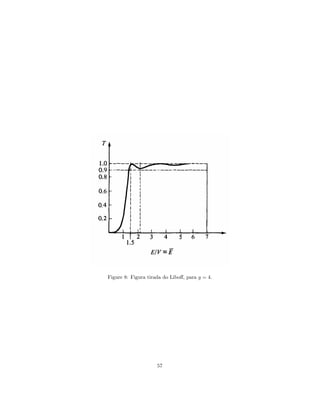
59. Para este potencial temos
T ! 1 para E ! 1
T = 0 para E = 0
Além disso, temos, novamente, um máximo de transmissão para
g
p
E + jV j = 2ak2 = n
O principal ponto a se notar agora que este potencial, diferente do anterior, é
um potencial atrativo.
Classicamente, é impossível para um potencial atrativo re‡etir uma partícula.
Entretanto, no caso quântico, vemos que tal efeito pode acontecer. Nesta teoria,
podemos imaginar um elétron sendo atirado contra um núcleo, temos que este
elétron pode ser re‡etido pelo núcleo. Além disso, para valores de energia acima
(2ak2 = n ), o núcleo é completamente transparente para o elétron (este é o
efeito Ramsauer).
Neste caso, como nos anteriores, a partícula pode assumir qualquer
valor de energia, i.e., o espectro de energia forma um contínuo.
8.0.1 Energia negativa.
Vamos agora procurar por soluções da ES com E < 0. Neste caso temos (lembre
que agora a região classicamente proibida é jxj > a)
d2
I
dx2
= 2
I ; 2
=
2m
~2
jEj > 0 =) I (x) = A exp ( x)
d2
II
dx2
= k2
2 II ; 2
2 =
2m
~2
(jV j jEj) > 0 =) II (x) = B exp (ik2x) + C exp ( ik2x)
d2
III
dx2
= 2
III ; =) I (x) = D exp ( x) (57)
Onde, pela condição de normalização, em I usamos apenas o sinal de + e em
II o sinal de . E usamos novas letras para as constantes multiplicativas.
Nesta escolha implicitamente estamos escolhendo a raiz positiva de
2
=
r
2m
~2
jEj =) = +
r
2m
~2
jEj > 0 :
Novamente impomos as condições de continuidade da função e sua derivada
nos pontos a
A exp ( a) = B exp ( ik2a) + C exp (ik2a)
A exp ( a) = ik2 [B exp ( ik2a) C exp (ik2a)]
59

60. e a
B exp (ik2a) + C exp ( ik2a) = D exp ( a)
ik2 [B exp (ik2a) C exp ( ik2a)] = D exp ( a)
coletando estas equações temos
Ae a
Be ik2a
Ceik2a
= 0 ;
Beik2a
+ Ce ik2a
De a
= 0 ;
A e a
Bik2e ik2a
+ Cik2eik2a
= 0 ;
Bik2eik2a
Cik2e ik2a
+ D e a
= 0 :
As equações acima podem ser escritas na seguinte forma matricial
Mv = 0
onde
M =
0
B
B
@
e a
e ik2a
eik2a
0
0 eik2a
e ik2a
e a
e a
ik2e ik2a
ik2eik2a
0
0 ik2eik2a
ik2e ik2a
e a
1
C
C
A ; v =
0
B
B
@
A
B
C
D
1
C
C
A
Se a matriz M for inversível, podemos escrever
v = M 1
0 ) A = B = C = D = 0 :
Assim, a única forma da equação acima ter uma solução não trivial, é a matriz
M não ser inversível. Ou seja,
det M = 0 ;
(esta é a regra de Kramer para que um sistema de equações tenha solução não-
trivial).
Manipulando a matriz temos
1. Multiplicando a primeira linha por e subtraindo com a terceira; multi-
plicando a segunda por e somando da quarta; multiplicar primeira linha
por 1
0
B
B
@
0 G G 0
0 G G 0
e a
ik2e ik2a
ik2eik2a
0
0 ik2eik2a
ik2e ik2a
e a
1
C
C
A
0
B
B
@
A
B
C
D
1
C
C
A ;
onde
G ( + ik2) eik2a
:
60

61. 2. Trocar primeira coluna com a segunda (observe que estamos reorganizando
o sistema e precisamos rede…nir v)
0
B
B
@
G 0 G 0
G 0 G 0
ik2e ik2a
e a
ik2eik2a
0
ik2eik2a
0 ik2e ik2a
e a
1
C
C
A
0
B
B
@
B
A
C
D
1
C
C
A
e depois segunda com a terceira
0
B
B
@
G G 0 0
G G 0 0
ik2e ik2a
ik2eik2a
e a
0
ik2eik2a
ik2e ik2a
0 e a
1
C
C
A
0
B
B
@
B
C
A
D
1
C
C
A
Se calcularmos agora o determinante da matriz acima temos
det M =
2
k2
2
G2
(G )2
e2( a )
Exercise 15 Calcule o determinante da matriz acima.
Com isso, a condição de Kronecker se torna
det M = 0 ) G2
= (G )2
) G = G (58)
Lembrando que um número complexo pode ser escrito na forma polar
z = + ik2 = jzj ei
; jzj =
q
k2
2 + 2 ; tan =
k2
temos
G = jGj exp (i [k2a + ])
Assim, (58) se torna
G = G ) exp (i [k2a + ]) = exp ( i [k2a + ])
Para as raízes positivas
G = +G =) exp (i [k2a + ]) = exp ( i [k2a + ]) =) k2a + = 0
ou ainda
k2a + = 0 =) tan (k2a) = tan =
k2
=) tan (k2a) = k2
ou ainda
=
cos (k2a)
sin (k2a)
k2 = k2 cot (k2a) ;
G
G
= 1 (59)
61

62. Para a raiz negativa fornece
G = G =) exp (i [k2a + ]) = exp ( i [k2a + ]) = exp ( i [k2a + ])
k2a + = k2a + =) k2a + =
2
ou ainda
tan =
k2
= tan
2
k2a = cot (k2a)
que pode ser colocada na forma
k2 tan k2a = ;
G
G
= 1
Retornando estas soluções em
0
B
B
@
G G 0 0
G G 0 0
e ik2a
eik2a
ik2
e a
0
eik2a
e ik2a
0 ik2
e a
1
C
C
A
0
B
B
@
B
C
A
D
1
C
C
A = 0 (60)
temos
G B + GC = 0 =)
B
C
=
G
G
GB + G C = 0 =)
B
C
=
G
G
com isso, para cada uma das raízes (58) e (59) temos
B
C
=
G
G
= 1 =) B = C ; k2 tan k2a = ;
G
G
= 1 ;
B
C
=
G
G
= 1 =) B = C ; = k2 cot (k2a) ;
G
G
= 1 :
8.0.2 Raiz negativa, primeira igualdade
Substituindo a segunda igualdade B = C nas duas outras últimas equações em
(60) temos
e ik2a
B Ceik2a
ik2
e a
A = 0 =) A = 2
k2
B sin (k2a) e a
eik2a
B + Ce ik2a
ik2
e a
D = 0 =) D = 2
k2
B sin (k2a) e a
Substituindo nas funções de onda (57) temos
I (x) = A exp ( x) =) I (x) = 2
k2
B sin (k2a) exp [ (x + a)] ;
II (x) = B exp (ik2x) + C exp ( ik2x) =) II = 2B cos (k2x) ;
III (x) = D exp ( x) =) III (x) = 2
k2
B sin (k2a) exp ( (x a)) ;
k2 tan k2a = : (61)
62

63. Que, pela dependência na coordenada na forma do cosseno, são chamada de
soluções pares.
Para determinar a constante B em ambas as soluções acima, basta nor-
malizar as função Z 1
1
j j
2
dx = 1
temos assim a solução completa do nosso problema.
A relação entre k2 e na equação (61) determinam os valores possíveis de
energia do nosso problema. Entretanto, esta é uma equação transcendental e
não podemos encontrar uma forma algébrica fechada para as soluções (i.e., não
podemos encontrar uma relação simples entre estas quantidades).
Vamos primeiro estudas as pares (61). Fazendo mudança de variáveis (para
variáveis adimensionais)
= k2a ; = a =) tan = (62)
Lembrando que escolhemos a raiz positiva de e que a > 0 temos
> 0 :
Pela de…nição de k2 e temos
2
=
2m
~2
jEj ; k2
2 =
2m
~2
(jV j jEj) =) 2
+k2
2 =
2m
~2
jEj+
2m
~2
(jV j jEj) =
2m
~2
jV j
ou ainda
2
+ 2
= a2 2m
~2
jV j 2
ou seja, para dados valores de a,m e V a relação acima descreve um círulo de
raio no plano .
Ou seja, para um dado poço de tamanho a, profundidade V e uma partícula
de massa m, a ES do nosso problema terá soluções não-triviais, apenas se as
seguintes equações forem (simultaneamente) satisfeitas
= tan ; = +
p
2 2 ;
(E) = a =
a
~
p
2m jEj > 0 (63)
onde, novamente, escolhemos o sinal de + para porque já haviamos escolhido
a raiz positiva de . Esta é uma restrição nas energias (para soluções
estacionárias pares) permitidas para o nosso sistema.
Para encontrar estes valores possíveis de energia, podemos usar métodos
numéricos, ou simplesmente plotar num grá…co as duas equações (63) e procu-
rarmos pelas intersecções destas …guras.
Um exemplo, para um dado valor de < , é mostrado na …gura abaixo.
63

64. Libo¤
Ou seja, para
< =) jV j <
~2
2m a
2
estas curvas se encontrar apenas uma vez no ponto 1 da …gura. Assim, para
este valor de potencial, temos apenas um possível valor de k2 e que respeita as
condições de contorno do nosso problema. A energia deste estado é dada pelo
valor de
1 = 1a =) jE1j =
~2
2m
2
1 =) E1 =
~2
2m
1
a
2
Este é um estado estacionário (par) permitido para o sistema (como é a solução
da ES independente do tempo, o estado deve ser estacionário). Lembrando que
os estados estacionários são estados de energia determinada, nestas condições
o sistema tem apenas um valor permitido de energia. Este é um estado esta-
cionário em que a partícula está presa dentro do posso. Ou seja, a região
permitida para a partícula é limitada no espaço. Um estado estacionário (de
energia bem de…nida) limitado no espaço é chamado de um estado ligado (em
contradição aos estados não ligados onde a partícula de energia bem de…nida
pode ir para o in…nito).
Observe que, se aumentarmos a profundidade do poço (i.e., aumentar a força
de atração jV j), de forma que
< < 2 =) <
r
a2
2m
~2
jV j < 2
64

65. teremos dois estados ligados para o sistema. Ou seja, dois estados de energia
permitidos. Além disso, o número de estados ligados aumenta com a largura
do poço a. Outro ponto a se observar é que para qualquer valor de energia
E < 0 existe pelo menos um estado ligado par. Ou seja, assim como no caso
clássico, um poço de potencial quântico sempre pode capturar uma partícula
com E < 0. A diferença é que classicamente esta partícula é sempre capturada
enquanto quanticamente ela tem uma probabilidade de ser capturada dada pelo
coe…ciente de re‡exão.
8.0.3 Raiz positiva, segunda igualdade
Substituindo a segunda igualdade B = C nas duas outras equações temos
B
C
= 1 =)
A
B
=
D
B
= 2i sin (k2a) e a
e ik2a
B Ceik2a
ik2
e a
A = 0 =) A = 2
ik2
e a
B cos (k2a)
eik2a
B + Ce ik2a
ik2
e a
D = 0 =) D = 2
ik2
Be a
cos (k2a)
Substituindo nas funções de onda (57) temos
I (x) = A exp ( x) =) I (x) = 2
ik2
B cos (k2a) exp ( (x + a)) ;
II (x) = B exp (ik2x) + C exp ( ik2x) =) II (x) = 2B sin (k2x)
III (x) = D exp ( x) =) III (x) = 2
ik2
B cos (k2a) exp ( (x a)) ;
k2 cot (k2a) = : (64)
Estas são as soluções impares do nosso problema.
O desenvolvimento segue de forma completamente análoga ao caso da raiz
negativa (ondas pares). Neste caso, novamente, temos a condição:
2
+ 2
= a2 2m
~2
jV j 2
; = k2a ; = a
mas agora devemos procurar por intersecções deste circulo com a curva:
= cot (k2a)
O grá…co desta curva tem a forma:
Ou seja, para valores
2
< <
3
2
temos apenas um estado ligado. Diferente das soluções pares, para < =2
(i.e., jV j < ~2
2m a
2
) não temos nenhum estado ligado ímpar.
65

66. Figure 9: Libo¤
Obviamente, os estados ligados disponíveis para a partícula no poço são a
soma dos estados pares e impares. Entretanto, com o veremos na segunda parte
deste curso, esta característica de paridades estão diretamente relacionadas com
a natureza das partículas con…nadas dentro do poço.
Os dois primeiros estados ligados do sistema têm a forma:
Observe que, novamente, existe uma probabilidade da partícula ser detectada
na região classicamente proibida fora do poço. Além disso, se o poço é muito
profundo (jV j ! 1) teremos estados ligados com energia E << 0 (jEj >> 0)
e conseqüentemente >> 0. Neste caso (o poço de profundidade in…nita)
qualquer estado com energia …nita terá um decaimento muito rápido fora da
barreira. Ou seja, a probabilidade de ser encontrada fora do poço é
nula. Assim, quando a profundidade do poço tende a in…nito, voltamos a ter o
problema da partícula na caixa, com as mesmas soluções e energias encontradas
anteriormente.
8.0.4 Espectro contínuo e discreto
O desenvolvimento matricial permite ver com mais facilidade a diferença en-
tre o problema para o espectro contínuo E > 0 e o espectro discreto E < 0.
Para o espectro contínuo do caso do espalhamento, as condições de fronteira do
66

67. Figure 10: Libo¤
problema nos dão
B
A
eik1a
+
C
A
e ik2a
+
D
A
eik2a
= e ik1a
B
A
eik1a
+
k2
k1
C
A
e ik2a k2
k1
D
A
eik2a
= e ik1a
C
A
eik2a
+
D
A
e ik2a F
A
eik1a
= 0
k2
k1
C
A
eik2a k2
k1
D
A
e ik2a F
A
eik1a
= 0
onde, como temos agora cinco variáveis, podemos eliminar uma delas escrevendo
todas as quantidades em relação a razão ?=A, uma vez que o número de condições
de fronteira é o mesmo temos o mesmo número de equações. Além disso, como
estamos interessados num problema de espalhamento de partículas lançadas de
1 (as funções de onda foram montadas com esta suposição), sabemos que
sempre teremos A 6= 0.
67

68. Com isso podemos escrever o nosso sistema na forma
B0
eik1a
+ C0
e ik2a
+ D0
eik2a
= e ik1a
B0
eik1a
+
k2
k1
C0
e ik2a k2
k1
D0
eik2a
= e ik1a
C0
eik2a
+ D0
e ik2a
D0
eik1a
= 0
k2
k1
C0
eik2a k2
k1
D0
e ik2a
F0
eik1a
= 0
Onde as quantidades com linha são as originais divididas por A.
Novamente, podemos colocar as equações acima na forma matricial
Mv = u
onde
M =
0
B
B
@
eik1a
e ik2a
eik2a
0
eik1a k2
k1
e ik2a k2
k1
eik2a
0
0 eik2a
e ik2a
eik1a
0 k2
k1
eik2a k2
k1
e ik2a
eik1a
1
C
C
A ; v =
0
B
B
@
B0
C0
D0
F0
1
C
C
A ; u = e ik1a
0
B
B
@
1
1
0
0
1
C
C
A
O que obtemos agora é uma equação não homogenia (u 6= 0) nas nossas
incógnitas. Neste caso a solução geral do nosso problema não está restrita a
condição de Kronecker (ou, seja, não impomos mais que M não seja inversível).
Na verdade, tudo que temos de fazer agora e inverter a matriz M e podemos
determinar (de forma unívoca) o vetor v
v = M 1
u
Se você …zer isso, irá obter exatamente as relações calculadas anteriormente. Ou
seja, neste caso não precisamos impor nenhum vínculo no sistema para obter
uma solução não trivial (i.e., para obter v 6= 0). A constante A que sobra pode
agora ser determinada pelas condições de normalização.
Este problema é importante porque mostra bem a diferença entre estados
ligados e não-ligados, e para modelar a física da condução em metais de semi-
condutores. Entretanto, como veremos, ele é bastante arti…cial, especialmente
porque matematicamente alguns observáveis não estão bem de…nidos.
9 Estrutura formal da MQ
A fenomenologia da MQ surge nos trabalhos de Planck e Einstein (1895-1915).
A estrutura formal da MQ nasce com o processo de quantização de Bohr-
Sommerfeld e dos postulados de De Broglie (1910-1923). Esta é a chamada velha
MQ. Esta estrutura é modi…cada pela estrutura envolvendo variáveis intrinse-
camente complexa, presente nos trabalhos de Schroedinger e a estrutura não-
comutativa (matricial) dos trabalhos Heisenberg, Born e Jordan (1925-1930).
68

69. Estas duas estruturas foram posteriormente uni…cadas por Schroedinger dentro
dos conceitos da análise funcional. Nasce aqui a nova MQ. Este trabalho foi
avançado numa estrutura formal ainda mais consistente pelos trabalhos de Von
Neumann (análise complexa), Weyl (teoria de grupos) e Dirac (tudo!).
Nos trabalhos iniciais de Bohr-Sommenrfelde e De Broglie, a MQ é pensada
como uma “releitura”da física clássica. Ou seja, a interpretação de quantidades
clássicas mensuráveis não como uma característica intrínseca dos sistemas, mas
como probabilidades que o sistema assuma tais valores. Entretanto, como vi-
mos, a teoria de Schroedinger a…rma que a descrição completa de um sistema
físico envolve quantidades complexas que estão fora do alcance dos aparelhos
de medida. Ou seja, a descrição anterior da mecânica, baseada em variáveis
reais e no espaço de fase, não pode comportar a realidade dos sistemas
físicos. Foi necessário então desenvolver uma nova estrutura matemática para
descrever de forma satisfatória esta nova teoria quântica. Esta nova estrutura
envolve conceitos da análise funcional como espaços de Hilbert e o espectro
de operadores. E é em termos desta estrutura matemática que os postula-
dos da MQ são estabelecidos. Ou seja, é impossível ter uma idéia da estrutura
atual da MQ sem um conhecimento, ainda que (bem) super…cial, da estrutura
matemática envolvida nesta teoria. Por isso vamos fazer um pequeno passeio
por alguns conceitos da análise funcional complexa.
9.1 Espaços vetoriais e operadores
Um espaço vetorial V é qualquer conjunto de elementos onde de…nimos uma
regra de composição entre estes elementos, que simbolizamos geralmente pelo
sinal de soma (+). Ou seja, dado dois elementos quaisquer v1; v2 2 V , sabemos
realizar a composição:
8 v1; v2 2 V : v1 + v2 = v3 2 V ;
Ademais estabelecesse uma outra regra, chamada de produto com um escalar
( ), da composição dos elementos deste conjunto sobre o corpo dos reais (ou dos
complexos). Ou seja:
8 v1 2 V; a 2 R : a:v1 = av1 = v3 2 V ;
Além disso, esta operação de soma deve respeitar (lembre-se que podemos
de…nir diferentes somas, e.g., soma de setas, de matrizes.):
1. (a) Associativa: v1 + (v2 + v3) = (v1 + v2) + v3.
(b) Comutativa: v1 + v2 = v2 + v1.
(c) Elemento identidade: 9 0 2 V : v + 0 = v; 8 v 2 V .
(d) Elemento inverso: 8 v 2 V; 9 v 2 V : v + ( v) = 0 :
(e) Distributiva pelo produto com um escalar: a (v1 + v2) = av1 + av2.
69

70. (f) Distributiva pela soma escalar: (a1 + a2) v = a1v + a2v
(g) compatível com a multiplicação escalar dos campo: a1 (a2v) = (a1a2) v
Um exemplo simples e bem conhecido de um espaço vetorial seria o con-
junto de setas num plano. Ou seja, quantidades com um certo comprimento
que apontam em determinada direção e sentido (mas que não estão …xas em
nenhum ponto). Com isso, V é o conjunto de todas as setas. Para que este
conjunto se torne um espaço vetorial precisamos primeiro de…nir como estas
setas são multiplicadas por um número real. Fazemos isso de…nindo que
~v2 = a~v1 ; ~v1; 2 V ; a 2 R ; a 0
é uma nova seta ~v2 2 V (também no plano) que aponta na mesma direção de
~v1, mas tem o comprimento a vezes maior. Da mesma forma,
~v3 = a~v1 ; ~v1 2 V ; a 2 R ; a < 0
tem o mesmo módulo e sentido de ~v2, mas aponta na direção contrária (tem
sentido contrário).
Precisamos agora de…nir como se somam estas. Fazemos isso de…nindo
~v3 = ~v1 + ~v2 ; ~v1;~v2 2 V
como uma nova seta ~v3 2 V obtida levando a origem de ~v1 na ponta de ~v2 e
ligamos a extremidade de ~v1 com a ponta de ~v2 (ou fazemos o mesmo invertendo
~v1 com ~v2).
Com isso, é fácil ver que V é um espaço vetorial.
9.2 Produto interno
Dentro do espaço vetorial, podemos ainda (mas não é uma condição necessária
para a sua construção) de…nir uma operação de produto entre os elementos
do espaço. Esta operação, no caso geral, associa a dois vetores quaisquer um
número. Ou seja, esta operação é um mapa
V V V 2
! R ;
O símbolo usual para esta operação é o seguinte:
(~v1;~v2) = v ; ~v1;~v2 2 V ; v 2 R
Esta operação é chamada de produto vetorial, ou, de forma mais geral, de produto
interno. Ela pode ser de…nida de várias formas diferentes, precisando apenas
respeitar as seguintes regras (no corpo dos reais):
(~v1;~v2) = (~v2;~v1) (simétrico)
(a~v1 + b~v2;~v3) = (a~v1;~v3) + (b~v2;~v3) (linear)
(~v;~v) 0 ; (~v;~v) = 0 =) ~v = ~0 (positivo de…nido)
70

71. onde ~0 é o vetor identidade do espaço vetorial, usualmente denotamos ~0 0,
mas lembre-se que 0 2 V .
Como exemplo, no nosso espaço de setas podemos de…nir:
(~v1;~v2) = j~v1j j~v2j cos
Onde jvj 2 R é o tamanho da nossa seta e é o menor ângulo entre as setas.
Num espaço vetorial geral, este tamanho é chamado de norma do vetor e pode
ser escrito como
(~v;~v) = j~vj j~vj cos 0 = j~vj
2
:
Ou seja, uma vez de…nido o produto interno sabemos calcular a norma
dos vetores.
O produto interno fornece uma forma bastante conveniente de fazemos refer-
ências as nossas setas (sem termos de fazer desenhos ou guardamos a seta, cuida-
dosamente para não girar, numa gaveta). Imagine que todas as pessoas que irão
trabalhar com estas setas concordam em usar duas setas especiais ~e1 e ~e2, ou
seja, duas setas que todos sabem o tamanho e a direção que apontam (apenas
estas duas nós guardamos na gaveta). Feito isso, podemos associar a uma seta
qualquer ~v os números:
v1 = (~v;~e1) ; v2 = (~v;~e2) (65)
Dado estes dois números, qualquer pessoa que conheça as setas ~e1 e ~e2 pode
reconstruir ~v. Estes dois vetores formam uma base do nosso espaço de setas.
A única exigência é que estes não sejam setas que apontem na mesma direção
(co-lineares).
Como reconstruímos o vetor ~v? O que temos de fazer é procurar por um
vetor cujo produto interno com ~e1 e ~e2 forneça os números acima. Feito isso,
este vetor será único.
Agora, seria muito conveniente se pudéssemos sistematizar a reconstrução de
~v numa álgebra simples. Por exemplo, seria bastante conveniente se púdessemos
reconstruir ~v apenas fazendo
~v = v1~e1 + v2~e2 (66)
Isso é válido para qualquer base (~e1;~e2)? A resposta é não.
Quais as característica devemos impor para a nossa base para podermos usar
a expressão (66)?
Tomemos novamente o produto interno do nosso vetor (66) com ~e1
(~v;~e1) = (v1~e1 + v2~e2;~e1) = v1 (~e1;~e1) + v2 (~e2;~e1)
Usando agora (65) devemos ter
v1 (~e1;~e1) + v2 (~e2;~e1) = v1
71

72. para um vetor ~v qualquer do nosso espaço. Esta igualdade só é válida para
vetores ~e1 e ~e2 que respeitam
(~e2;~e1) = 0 (ortogonal)
(~e1;~e1) = 1 (normalizado)
A primeira igualdade nos diz que os nossos vetores de base são ortogonais e a
segunda que o vetor ~e1 está normalizado. Da mesma fora, se tivéssemos feito
o produto com ~e2 teríamos
(~e1;~e2) = 0 ; (~e2;~e2) = 1 :
Ou seja, dada uma base e um vetor ~v estes só estarão relacionados pela expressão
(66) se
(~ei;~ej) = ij : (67)
Uma base que respeita a igualdade (67) é chamada de ortonormal.
Remark 16 Observer que bases não-ortonormais também são legítimas para
descrever o espaço. Entretanto, para bases ortonormais as expressões e manip-
ulações dos vetores toma uma forma bastante simples.
Como veremos a seguir, existe um procedimento geral para, dado um espaço,
obtermos uma base ortogonal. Entretanto, esta base usualmente não é nor-
malizada. Contudo, num espaço vetorial com o produto interno de…nido, dados
dois vetores ~e1 e ~e2 que sejam ortogonais ((~e1;~e2) = 0), mas não normalizados,
podemos facilmente de…nir novos vetores
^ei =
~ei
j~eij
=
~ei
p
(~ei;~ei)
que serão obviamente normais
(^ei; ^ei) = 1
Este processo é chamado de normalização dos vetores de base. Usamos o chapél
para indicar que a base foi normalizada.
A base ortonormal nos dá uma forma também muito conveniente de de…nir-
mos a soma dos nossos elementos (mais uma vez, sem precisarmos apelar para
desenhos). Vimos que, dada uma base ortonormal, a representação dos nossos
vetores nesta base assume a forma
~v = v1^e1 + v2^e2 ; vi = (~v; ^ei)
Podemos agora escolher uma representação matricial para os nossos ve-
tores da base. Uma escolha possível é a seguinte:
^e1
1
0
= ^e1 ; ^e2
0
1
= ^e2 (68)
72

73. Com isso,
~v = v1^e1 + v2^e2 v1^e1 + v2^e2 =
v1
v2
:
Feito isso, a soma e a multiplicação por escalar se resume a álgebra usual de
matrizes
v + av0
=
v1
v2
+ a
v0
1
v0
2
=
v1 + av0
1
v2 + av0
2
No lugar de (68) poderíamos ter escolhido qualquer base ortonormal para o
espaço das matrizes. Ou seja, qualquer par de matrizes que fossem ortogonais
e normalizadas. Por exemplo:
^e1
1
p
2
1
1
= ^e0
1 ; ^e2
1
p
2
1
1
= ^e0
2 (69)
Mas, neste caso, a forma matricial dos nossos vetores não seria tão simples
v1^e0
1 + v2^e0
2 = v1
1
p
2
1
1
+ v2
1
p
2
1
1
=
1
p
2
v1 + v2
v1 v2
A base (68) se chama base canônica.
A igualdade acima é válida para qualquer base ortonormal. Ou
seja, se escolhermos uma base diferente da canônica, ainda podemos encontrar
as componentes dos vetores na base original através do produto interno
vi = (v;^ei) = (~v; ^ei) :
Por exemplo, dado o vetor
v =
0
1
:
As componentes vi deste vetor na base canônica é, obviamente, v1 = 0 ; v2 = 1.
Entretanto, se tivéssemos escolhido a base (69), teríamos
v1 = (v;^e0
1) = 0 1
1
p
2
1
1
=
1
p
2
v2 = (v;^e0
1) = 0 1
1
p
2
1
1
=
1
p
2
Assim, sempre que temos um vetor na forma matricial, precisamos saber em
que base este vetor foi escrito. Usualmente, e quando nada for especi…cado,
estaremos falando da base canônica.
Como veremos, algumas vezes é conveniente trabalhar numa base diferente
da canônica.
73

74. 9.2.1 Representação dual
Poderíamos também ter escolhido representar nossos vetores (na base canônica)
por matrizes linha
~v = v1 v2 :
Observe que o próprio conjunto das matrizes n m (para qualquer valor
de m e n) com a de…nição usual de soma e multiplicação por escalar já forma
um espaço vetorial. Ou seja, no procedimento acima estamos identi…cando
um espaço vetorial com outro. Para com isso aproveitarmos as características
algébricas já conhecidas do outro espaço (das matrizes).
Neste processo podemos identi…car, ou representar, o vetor ~v com a matriz
n 0 ou com a matriz 0 n. A representação n 0 é chamada de dual da
representação 0 n (e vice-versa).
Dada uma base ortonormal f^eig e as componentes de dois vetores nesta
base
~v = v1^e1 + v2^e2 ; ~g = g1^e1 + g2^e2 ;
o produto interno entre eles pode ser calculado como
(~v;~g) = (v1^e1 + v2^e2; g1^e1 + g2^e2)
= v1g2 (^e1; ^e2) + v1g1 (^e1; ^e1) + v2g1 (^e2; ^e1) + v2g2 (^e2; ^e2)
= v1g1 + v2g2 =
2X
i=1
vigi :
Na representação matricial esta igualdade toma a forma
(~v;~g) = v1g1 + v2g2 = v1 v2
g1
g2
= vT
g
onde vT
é a transposta de v. Ou seja, podemos realizar o produto interno
convencionando que o elemento a direita em (:; :) representa o vetor, enquanto
o elemento a esquerda, representa o dual do vetor.
74

75. Recapitulando:
1. Partimos de um conjunto de objetos (setas) e de…nimos neste conjunto
uma operação de soma entre os elementos e a multiplicação destes ele-
mentos por um número real. De…nimos assim um espaço vetorial V
sobre os reais.
2. Em seguida selecionamos dois elementos ortogonais deste conjunto (duas
setas que formam um ângulo de 90o
) e normalizados (setas de comprimento
unitário) e formamos uma base ortonormal f^eig.
3. Passamos então a identi…car as setas com as suas componentes nesta base
~v 2 V : ~v ! fv1; v2g.
4. Em seguida organizamos estas componentes em matrizes. E passamos a
não mais olhar para o espaço original das setas, mas sim para o espaço
das matrizes associadas a cada elemento ~v 2 V : ~v ! fv1; v2g ! v.
Dizemos com isso que estamos escolhendo uma representação matricial para
o nosso espaço vetorial.
9.3 Mudança de base
Como vimos anteriormente, a forma explicita das componentes do vetor depen-
dem de qual base escolhemos.
Se numa certa base f^e1; ^e2g um vetor ~v tem componentes
~v = v1^e1 + v2^e2
numa outra base f^e0
1; ^e0
2g ele terá outras componentes
~v = v0
1^e0
1 + v0
2^e0
2
Se você escolher uma certa base ortonormal f^e1; ^e2g, como comparar suas
quantidades com os de alguém que ecolheu outra base f^e0
1; ^e0
2g? Ou seja, como
vi se relaciona com v0
i?
Para saber isso basta lembrar que todos estes vetores formam uma base do
espaço. Assim, podemos escrever
^e1 = a11^e0
1 + a12^e0
2
^e2 = a21^e0
1 + a22^e0
2
onde, pela de…nição dos nossos coe…cientes de expansão (65), temos a11 =
(^e1; ^e0
1), ou, de forma geral
aij = ^ei; ^e0
j :
^ei =
2X
j=1
aij ^e0
j =
2X
j=1
^ei; ^e0
j ^e0
j (70)
75

76. Assim, se você tem um vetor qualquer
~v = v1^e1 + v2^e2 =
2X
i=1
vi^ei
podemos usar (70) e escrever
~v =
2X
i=1
vi^ei =
2X
i=1
2X
j=1
vi ^ei; ^e0
j ^e0
j =
2X
j=1
2X
i=1
vi ^ei; ^e0
j ^e0
j
Ou seja, se vi são as componentes de ~v na base f^eig as componentes v0
i deste
mesmo vetor na base fe0
ig são
v0
j =
2X
i=1
vi ^ei; ^e0
j
As quantidades ^ei; ^e0
j também podem ser organizadas numa matriz quadrada
com linha i e coluna j. Esta matriz é chamada de matriz de mudança da base
f^eg para a base fe0
g.
Vemos assim como é conveniente identi…carmos nossos vetores com matrizes.
De forma geral, todas as quantidades com um único índice podem ser vistos
como uma matriz coluna de 2 elementos e qualquer quantidade com dois índices
como uma matriz 2 2.
9.4 Notação de Dirac
Observe que estamos trabalhando com duas quantidades, os elementos do con-
junto que formam o espaço vetorial V e os elementos do conjunto dos reais R.
Por isso usamos uma notação especial para diferenciar os elementos destes dois
conjuntos. No caso, uma seta sobre os vetores para as setas, ou um negrito para
as matrizes. Poderíamos também usar letras gregas para vetores e romanas para
números. O importante é sabermos, numa expressão, diferenciar os vetores dos
números.
A seta usada anteriormente nos lembra que estamos trabalhando com um
conjunto de setas. Como queremos trabalhar com diferentes espaços vetoriais,
vamos apenas introduzir uma notação mais abstrata e geral. Para diferenciar o
número a 2 R de um vetor a 2 V , usaremos o seguinte símbolo:
V 3 a jai :
Ou seja, colocar a letra dentro do símbolo (j i) acima, chamado de ket, apenas
indica que esta quantidade é um vetor.
Dentro da nossa representação matricial devemos identi…car jai com uma
matriz a. Nesta representação podemos também de…nir o símbolo para o dual
do vetor
aT
haj :
76

77. chamado de bra. Esta é a notação de Dirac.
A vantagem desta notação é que ela nos permite representar diretamente o
produto escalar dos vetores
(b; a)
como o produto de um vetor jai pelo dual de hbj
(b; a) hbj jai hbj ai
onde o símbolo h:j :i é chamado de braket (parênteses). Ou seja, a notação
de Dirac divide o símbolo (:; :) em paren j) e teses (j que juntos formam um
parênteses (esta foi a notação original que posteriormente mudou para h:j e j:i)
9.5 Operadores
Podemos também realizar operações nos nossos vetores. Por exemplo, se nosso
vetor é uma seta que aponta numa certa direção, você pode querer saber o
que acontece com esta seta se ela for girada de um certo ângulo. Ou seja,
queremos de…nir a operação de rotação nos nossos vetores. Se nosso vetor tem
componentes
jvi =
v1
v2
Quais as novas componentes, ou novo vetor jv0
i, se este vetor for girado no sen-
tido anti-horário, de um ângulo . Como vimos na primeira parte do curso, na
representação matricial, estas novas componentes se relacionam com as anteri-
ores por
jv0
i =
v0
1
v0
2
=
cos sin
sin cos
v1
v2
;
ou ainda simbolicamente
jv0
i = ^R jvi ; ^R =
cos sin
sin cos
:
^R, que nosso caso é uma matriz 2 2, é um operador no nosso espaço de
vetores de dimensão 2. Ou seja, no nosso espaço vetorial 2 0 um operador é
uma matriz 2 2.
As componentes de matriz n n podem ser identi…cadas através de dois
índices Rij. Na notação de Dirac um operador pode ser representado como
Rij jii hjj
Se encararmos jii como um vetor (uma matriz 2 0), vemos que a quantidade
acima representa um “produto”entre o vetor jii e o dual do vetor jii. Ou seja,
para dois vetores jai ; jbi 2 V , podemos de…nir dois tipos de produtos entre um
e o dual do outro
haj jbi haj bi (produto interno)
jbi haj jbi haj (produto externo)
77

78. o primeiro, como vimos, é o produto interno. O segundo é chamado de produto
externo, ou produto tensorial.
Ou seja o produto tensorial leva um par de vetores em V (matrizes 2 0)
em um elemento do espaço V V = V 2
(matrizes 2 2).
Ou de um ket 2 0 com um bra 0 2 leva a 2 2. Lembrando que o
conjunto das matrizes m n formam um espaço vetorial, este é uma mapa (ou
uma relação entre espaços vetoriais).
Este é o mesmo produto tensorial estudado na primeira parte do curso.
Como vimos, a sua realização no espaço das matrizes pode ser feito através do
produto de Kronecker.
jbi haj = b1 b2
a1
a2
= b1
a1
a2
b2
a1
a2
=
a1b1 a1b2
a2b1 a2b2
que é igual a matriz jji hij = bjai (compare com a equação (1.11) da primeira
parte do curso).
Remark 17 Lembre-se que haj bi é um número, mas jai hbj é uma matriz.
Na notação de Dirac, a atuação do operador jai hbj 2 V 2
num vetor jvi 2 V
é de…nida como
(jai hbj) jvi = jai (hbj jvi) = jai hbj vi 2 V
Ou seja, a atuação do operador jai hbj no vetor jvi gerou um novo vetor que é o
produto do vetor jai com o número hbj vi.
Escrevendo
jbi = b1 j^e1i + b2 j^e2i
jai = a1 j^e1i + a2 j^e2i
temos
jai hbj = b1a1 j^e1i h^e1j + b2a1 j^e1i h^e2j + b1a2 j^e2i h^e1j + b2a2 j^e2i h^e2j
=
2X
i;j=1
biaj j^eii h^ejj
ou seja, se ai e bi são as componentes de jai e jbi então as componentes do
produto tensorial jai hbj são aibj na base (de V 2
) j^eii h^ejj.
Todo o operador (matriz), pode ser decomposto nesta base. Em especial, a
nossa matriz de rotação tem a forma
^R =
2X
i;j=1
Rij j^eii h^ejj
78

79. (o chapéu indica que R é um operador), com Rij números reais. Com isso
jv0
i = ^R jvi ! jv0
i =
0
@
2X
i;j=1
Rij j^eii h^ejj
1
A
2X
k=1
vk j^eki
!
=
2X
i;j=1
2X
k=1
Rij j^eii vk h^ejj j^eki
=
2X
i;j=1
2X
k=1
Rij j^eii vk jk
=
2X
i;j=1
Rijvj j^eii
Da mesma forma, na representação matricial, num espaço de dimensão N
um vetor é uma matriz linha de N elementos e operadores são matrizes N N.
79

80. 9.6 Autovalores e autovetores
Uma relação entre operadores e vetores que é de especial interesse é quando a
aplicação de um operador sobre um vetor resulta num vetor na mesma direção
(i.e., proporcional) ao vetor original. Isso é, quando:
^M jxi = a jxi ; a 2 R ; jxi 6= 0:
Neste caso, dizemos que jxi é um autovetor do operador ^M e que a é o autovalor
do autovetor jxi.
Por exemplo, se aplicarmos o operador ^P (que troca o eixo x por x, ou
seja, coloca um espelho no nosso sistema) no vetor
jp1i =
0
1
teremos
^P jp1i =
1 0
0 1
0
1
=
0
1
= jp1i :
Ou seja, o vetor jp1i é um autovetor de ^P com autovalor 1. Já o vetor
jp2i =
1
0
)
1 0
0 1
1
0
=
1
0
=
1
0
= jp2i :
Assim, jp2i é outro autovetor de ^P, mas com auto valor 1: Já o vetor
jp3i =
1
1
)
1 0
0 1
1
1
=
1
1
6= a jp3i
então, jp3i não é auto vetor de ^P. Da mesma forma, qualquer vetor é autovetor
de ^R ( ) com autovalor 1, pois
^R ( ) jxi =
1 0
0 1
x1
x2
=
x1
x2
= jxi
Além disso, o operador ^R ( =2) não possui nenhum autovetor.
9.6.1 Espaço euclidiano de dimensão …nita RN
Apesar dos exemplos explícitos dados anteriormente envolverem apenas espaços
bidimensionais, toda as discussões e de…nições apresentadas são igualmente vál-
idas para um espaço com uma dimensão N arbitrária. Neste caso, obviamente,
as somatórias devem ir até N. Por exemplo, num espaço de dimensão N existe
uma base fjeiig ; i = 1; 2; 3:::; N que podemos escolher ortonormal e, qualquer
vetor do nosso espaço pode ser escrito como
j i =
NX
i=1
ci jeii :
80

81. Onde ci são as componentes do vetor j i na base fjeiig.
Na representação matricial, os vetores serão matrizes N 1, os duais matrizes
1 N e os operadores matrizes N N. Obviamente, neste caso, as di…culdades
algébricas crescem com o valor de N, mas nenhuma di…culdade conceitual está
envolvida neste processo.
9.7 Espaço de Hilbert
Nosso objetivo aqui é obter uma generalização dos resultados da seção anterior.
O primeiro ponto é lembrar que nossos vetores, e os números que multiplicam
estes vetores, são todos reais. Assim, a primeira generalização que podemos fazer
é de…nir um vetor num espaço de dimensão n é qualquer seqüência de números
complexos 1; 2; :::; n ( i 2 C) e que nossos vetores podem se multiplicados
também por números complexo
j i + j i = j i ; ; 2 C
com
i = i + i :
Até aqui nada mudou. O ponto agora é que devemos lembrar que se é um
número complexo, podemos ter
2
< 0
(e.g., para = i). Isso implica que a somatória do quadrado de números
complexo não é uma quantidade positiva de…nida e, consequentemente, a norma
de…nida anteriormente pode nos dar valores negativos. Não queremos ter vetores
de norma negativa (isso é, na verdade, contra a de…nição do que é uma norma).
Podemos resolver este problema lembrando que
: 0; 8 2 C
onde, além disso
: = 0 ) = 0 :
Assim, podemos recuperar a característica de positividade da nossa norma se,
no lugar de (??) de…nirmos o produto interno como
h j i = 1 1 + 2 2 + ::: + n n =
nX
i=0i
i i ; (71)
com isso temos, novamente,
j j
2
= h j i =
nX
i=0
i i 0
com
j j
2
= 0 =) j i = 0 :
81

82. A única diferença neste produto interno é que, no lugar da simetria, temos
agora uma simetria conjugada
h j i =
nX
i=0i
i i =
nX
i=0
( i i) =
nX
i=0
i i
!
= h j i :
Já para o produto externo entre os vetores j i e j i, temos agora duas opções.
Podemos de…nir o operador
^M = j i h j
com componentes
Mij = i j
Ou podemos formar também o transposto conjugado do operador
^M+
= j i h j = ^MT
com
M+
ij = i j = j i = (Mji)
ou seja
^M+
= ^MT :
Da mesma forma, no que se refere a representação matricial, continuamos
representando nossos vetores por matrizes coluna
j i =
0
B
B
B
@
1
2
...
n
1
C
C
C
A
mas, para ser compatível com o produto interno (71), devemos de…nir o dual de
j i, não apenas como o transposto, mas como o transposto conjugado
h j = 1 2 n
A segunda generalização que vamos fazer é permitir que a dimensão do
espaço assuma qualquer valor, incluindo o in…nito. Ou seja, vamos admitir
espaços com n = 1. Esta é, na verdade, a motivação deste desenvolvimento.
Neste caso, obviamente não podemos mais representar nossos vetores por ma-
trizes. Mas podemos continuar usando todas as expressões anteriores (fazendo
n = 1). A grande diferença é que antes, bastava que cada elemento do nosso ve-
tor estivesse bem de…nido (não fosse in…nito) e, certamente, todas as expressões
também estariam bem de…nidas.
Agora, para n = 1, pode acontecer de cada elemento do nosso vetor estar
bem de…nido e, mesmo assim, não conseguirmos calcular quantidades como, por
exemplo, o produto interno. Ou seja, agora precisamos exigir que as somatórias
de…nidas anteriormente convirjam.
82

83. Por exemplo, podemos de…nir as componentes do nosso “vetor”como
xk =
1
k1=2
; k 2 N
Cada componente está bem de…nida. Em especial, para n ! 1
x1 =
1
(1)
1=2
= 0
Entretanto, se desejarmos calcular a norma deste “vetor”teremos4
jxj
2
=
1X
k=1
1
k1=2
1
k1=2
=
1X
k=1
1
k
! 1 :
E não podemos utilizar para estas componentes a noção de norma que é indis-
pensável em todas as nossas análises. Destarte, se quisermos de…nir um espaço
vetorial tratável, devemos exigir que os vetores do nosso espaço respeitem a
restrição
1X
k=1
j kj < 1 :
Ou seja, para nós agora, vetores são toras as seqüência, …nitas e in…nitas, sobre
o corpo dos complexos, tal que a soma do módulo quadrado convirja.
Um espaço vetorial de dimensão arbitrária (incluindo in…nito) sobre o corpo
dos complexos onde (para todo elemento) está de…nido um produto interno é
chamado de espaço de Hilbert.
Todos os conceitos desenvolvidos anteriormente, incluindo a noção de ortog-
onalidade e base, são válidos no EH. A diferença é que agora a nossa base pode
conter in…nitos termos.
Um caso especial de espaço de Hilbert com dimensão in…nita é o espaço das
funções de quadrado integrável. Neste caso, nossos vetores representam funções
nos reais dentro de um certo intervalo. Ou seja, à função
f (x) ; x 2 [a; b]
corresponde a um vetor jfi 2 H onde jfi indica a coleção de todos os valores
possíveis da função f(x), assim como j i indicava todos os valores de uma
sequência k. Neste caso o “índice”que identi…ca estes valores (x) é um índice
contínuo, ao invés do índice xk anterior que era discreto. Podemos facilmente
generalizar os resultados anteriores trocando as somatórias dos índices discretos
por integrais sobre os índices contínuos. Assim, o produto interno se torna:
h j i =
nX
i=0i
i i ! hfj gi =
Z b
a
f (x) g (x) dx :
4 Lembre que
1X
n=1
1
ns
diverge para s 1.
83

84. Novamente, para que o produto interno acima esteja de…nido, devemos exigir
que
hfj fi < 1 :
O conjunto de todas as funções que respeitam a restrição acima é um espaço de
Hilbert chamado espaço das funções de quadrado integrável no intervalo [a; b],
ou L2
(a; b).
Assim, daqui pra frente, quando escrevermos um vetor j i 2 H podemos
estar falando de uma matriz coluna de tamanho N, de uma seqüência in…nita
k, ou mesmo de uma função (x) dentro de um intervalo. Para todas estas
quantidades as expressões anteriores são idênticas (a menos do produto interno
das funções que envolve integrais e não somatórias).
Por exemplo, para o espaço L2
( ; ), podemos de…nir uma base ortonormal
fjekig dada pelas funções
ek (x) =
1
p
2
exp (ikx)
Exercise 18 Veri…que que estas funções pertencem ao espaço de Hilbert L2
( ; ).
Exercise 19 Veri…que que estas funções são ortonormais.
Assim, para qualquer função f (x) ; x 2 [ ; ] o vetor correspondente jfi 2
H pode ser escrito como
jfi =
1X
k= 1
ck jeki
onde, por ser uma base ortonormal,
ck = hekj fi =
1
p
2
Z
exp ( ikx) f (x) dx
e jfi representa a coleção de todos os valores da função
f (x) =
1
p
2
1X
k= 1
ck exp (ikx)
A decomposição acima, nesta base fjekig é chamada de série de Fourie da
função f. Como veremos, existem várias outras decomposições (i.e., outras
bases) possíveis.
9.8 Operadores hermitianos
Como vimos anteriormente um operador pode ser visto como o produto externo
de dois vetores j i e j i5
. Se um operador ^M é de…nido como
^M = j i h j
5 Isso não é válido para todo operador.
84

85. então, seu hermitiano conjugado ^M+
será
^M+
= j i h j
Para o caso do espaço de dimensão …nita, este operador é apenas o transposto
conjugado da matriz ^M, mas a nomenclatura continua para o caso de dimen-
são in…nita. Neste caso podemos imaginar nossos operadores como matrizes
quadradas in…nitas.
O produto interno do vetor jzi = ^M jxi com o vetor jyi vale
hyj zi = hyj ^M jxi
podemos eliminar o parênteses acordando que o operador sempre age no vetor a
direita (o que é equivalente a acordar que o conjugado do operador age no dual
do vetor a esquerda, hyj zi = hwj xi com jwi = ^M+
jyi, mas basta convencionar
que ele age a direita). Com isso, temos
hyj ^M jxi = hyj i h j xi = h j yi hxj i = hxj i h j yi = hxj ^M+ jyi (72)
onde usamos
hyj i = h j yi :
Um operador é dito simétrico, ou hermitiano se
^M = ^M+
) j i h j = j i h j
ou seja, para espaços de dimensão …nita são matrizes cuja transposto conjugado
é igual a ela mesma. Por exemplo, qualquer matriz na forma
0
B
B
B
@
a11 a12 a13
a12 a22 a23
a13 a23 a33
...
...
...
...
1
C
C
C
A
; aii 2 R ; i = 1; 2; 3::
Para operadores hermitianos a propriedade (72) fornece
hyj ^M jxi = hxj ^M jyi : (73)
Propriedades dos operadores hermitianos:
Imagine agora que você encontrou um autovetor j i de um operador her-
mitiano ^M com autovalor , ou seja,
^M j i = j i
observe que estamos usando a mesma letra apenas por conveniência, mas 2 C
enquanto j i 2 H.
85

86. Com isso a propriedade (73) acima fornece
hyj ^M jxi = hxj ^M jyi =)
h j ^M j i = h j j i = h j j i = h j M j i = h j j i = h j j i
Mas
h j i = h j i
com isso
h j i = h j i
como
h j i 6= 0 ; h j i < 1,
temos
= ) 2 R :
Ou seja, todos os autovalores de um operador hermitiano são reais.
Exemplo: Num espaço de dimensão 2 o operador
^2 =
0 i
i 0
:
(em MQ este é um dos operadores associados ao spin das partículas). É hermi-
tiano.
Vamos encontrar seus autovalores. O processo geral é o seguinte: En-
contrar um autovetor signi…ca resolver a equação
^M j i = j i ) ^M I j i = 0 :
A quantidade ^M I é um novo operador. Para um espaço de dimensão …nita,
este operador é uma nova matriz. Vamos chamar esta nova matriz de
^T = ^M I
Nossa equação …ca
^T j i = 0
Se ^T é uma matriz inversível, podemos calcular ^T 1
e multiplicar pelos dois
lados da expressão acima
^T 1 ^T j i = ^T 1
0 ) j i = 0
Ou seja, se ^T é inversível, o vetor j i é único e vale j i = 0. Assim, ^M não terá
autovetor. Portanto: A única forma de ^M ter autovetor é que ^T = ^M I
não tenha inversa. Para que uma matriz não tenha inversa, basta que
det ^T = det ^M I = 0 :
86

87. Para o nosso caso
^M = ^2
Logo devemos exigir que
det (^2 I ) =
0 i
i 0
1 0
0 1
=
i
i
= 0 ;
ou seja,
2
( i:i) = 2
1 = 0 =) 2
= 1 =) = 1 :
Vemos então que ^2 tem dois autovaloes 1 = 1 e 2 = 1 e, como esperado,
ambos são reais.
Suponha agora que temos dois autovetores de um operador hermitiano
^M j i = j i ; ^M j i = j i
com
6= :
Para estes vetores podemos calcular
h j ^M j i = h j j i = h j j i ;
h j ^M j i = h j j i = h j j i
além disso, usando (72) temos
h j ^M j i = h j ^M j i =) h j i = h j i = h j i = h j i
onde usamos que ; 2 R. Com isso
[ ] h j i = 0
Se usarmos agora 6= a igualdade acima implica
h j i = 0
Ou seja, autovetores correspondentes a autovalores distintos são or-
togonais.
O resultado acima fornece uma forma prática e bastante útil de encontramos
bases ortogonais para um espaço qualquer. Bastando para isso encontrarmos
operadores hermitianos neste espaço.
Exemplo: Voltemos a nossa matriz
2 =
0 i
i 0
Sendo esta matriz hermitiana, devemos esperar que seus auto vetores sejam
ortogonais. Encontremos então estes autovetores. Voltando a equação de auto-
valores,
( 2 I) j i = 0 )
i
i
1
2
= 0
87

88. sabemos que = 1. Para = 1 temos
1 i
i 1
1
2
= 0 ) 1 i 2 = 0
i 1 2 = 0
Primeiro note que, se multiplicarmos a primeira equação por i temos
i 1 2 = 0
que é idêntica a segunda equação. Assim, na verdade, temos apenas uma
equação e duas incógnitas. Isso nada mais é do que uma conseqüência do
fato da matriz
1 i
i 1
não possuir inversa (ou ter determinante nulo). Lembre-se que construímos os
valores de impondo esta exigência. Assim, usando a única equação que temos
i 1 2 = 0 ) i 1 = 2
Ou seja, o nosso autovetor tem a forma
j +i = 1
i 1
= 1
1
i
para qualquer valor 1 2 C.
Isso é uma característica geral destes problemas. Para um sistema qualquer
de dimensão N, construímos seus autovalores de um operador ^M exigindo
que a matriz ^M I não tenha inversa. Isso faz com que, para estes valores
de , tenhamos um sistema de N 1 equações para N incógnitas. Com isso
sempre teremos uma parâmetro livre nos nossos autovetores. É a existência
deste parâmetro que nos permite normalizar nossos vetores. Ou seja, escolhemos
este parâmetro de forma que nossos vetores tenham norma 1.
Com isso, o autovetor associado ao autovalor 1 vale
+ = +1 ; j +i = 1
1
i
:
Da mesma forma, encontramos o autovetor associado ao auto-valor = 1
1 i
i 1
1
2
= 0 ) 1 i 2 = 0
i 1 + 2 = 0
:
Onde já sabemos que podemos usar apenas uma destas equações. Assim, usando
a segunda equação,
i 1 + 2 = 0 ) i 1 = 2
Ou seja, o autovetor associado ao auto-valor = 1 vale
= 1 ; j i = 1
1
i
:
88

89. Como vimos, uma vez que + 6= devemos esperar que os vetores j i e j +i
sejam ortogonais. De fato
h +j i = 1 1 i 1
1
i
= j 1j
2
(1 1) = 0 :
Assim, fj +i ; j ig formam uma base ortogonal do nosso espaço. Podemos
ainda normalizar esta base fazendo
je i =
j i
p
h j i
=
1
j 1j
p
1 + 1
1
1
i
=
1
p
2
1
j 1j
1
i
=
1
p
2
ei 1
i
; 2 R:
Ou seja, a nossa normalização também está de…nida a menos de uma
constante. Como veremos, os princípios da MQ nos permitem …xar arbitrari-
amente esta constante. Escolhendo o caso mais simples = 0 temos
je i =
1
p
2
1
i
Da mesma forma, podemos de…nir o vetor normalizado
je+i =
1
p
2
1
i
estes vetores respeitam
he+j e i = 0 ; he+j e+i = he j e i = 1
e, consequentemente, formam uma base ortonormal do nosso espaço.
Este resultado é geral. Para um espaço de Hilbert H de dimensão N qual-
quer, inclusive in…nito, dado um operador hermitiano ^M neste espaço, os auto-
vetores deste operador formam uma base deste espaço. Assim, qualquer vetor
j i 2 H pode ser escrito como
j i =
NX
k=1
ck j ki
onde
^M j ki = k j ki :
9.9 Postulados da Mecânica Quântica
Os estados de um sistema físico podem ser (completamente) representados por
vetores (normalizados) no espaço de Hilbert. Ou seja, uma vez identi…cado o
vetor em H que representa o nosso sistema, sabemos tudo que é possível saber
sobre este sistema.
89

90. Na teoria de Schroedinger o sistema quântico é representado por uma função,
chamada de função de onda. Uma exigência da interpretação probabilística
da MQ é que estas funções de onda sejam normalizáveis e, consequentemente,
possuam norma …nita Z
j (x)j
2
dx < 1 :
Ou seja, as funções de onda devem pertencer ao espaço de Hilbert L2
. Da
mesma forma, na teoria de Heisenberg, os estados do sistema são representados
por matrizes coluna. Pela mesma razão, estas matrizes têm de ser de quadrado
somável. Ou seja, nesta teoria os estados do sistema são vetores no espaço de
Hilbert RN
. O postulado acima nos diz que qualquer teoria quântica trabal-
hará com vetores em algum EH. Escolher o espaço signi…ca escolher como os
estados do sistema físico serão representados. Nos exemplos acima temos então
a representação de Schroedinger e a representação de Heisenberg.
Além disso, vetores que di…ram apenas por uma fase (global) representam o
mesmo estado físico. Ou seja, o estado do sistema é representado por vetores
em H a menos de uma fase. Assim, os vetores
j i ; j 0
i = ei
j i
representam o mesmo estado físico do sistema.
Isto está relacionado com o fato das quantidades …sicamente mensuráveis
do sistema estarem relacionados com as médias, ou com o produto interno, dos
vetores e os dois vetores acima fornecem o mesmo valor.
h 0
j 0
i = h j e i
ei
j i = h j i
Remark 20 É por isso que, no processo de normalização, podemos escolher
arbitrariamente a fase dos vetores.
Um ponto importante é observar que a fase referida acima deve ser global.
Como vimos, na descrição quântica um sistema pode estar numa superposição
de dois estados
j i = a j 1i + b j 2i
o estado acima é equivalente ao estado
j 0
i = ei
[a j 1i + b j 2i] ;
mas não é equivalente ao estado
j 00
i = ei
a j 1i + b j 2i
A fase não-global presente no estado j 00
i gera fenômenos de interferência
que permitem (…sicamente) distinguir este estado de j i.
Uma vez preparado um sistema no laboratório, este sistema “será”um vetor
no espaço de Hilbert. Precisamos agora saber como descrever (dentro da teoria)
90

91. a manipulação, a evolução temporal e as possíveis medidas que fazemos
neste sistema.
Quando um sistema no estado j i sofre qualquer tipo de modi…cação ele
passa a ser descrito por um novo vetor j 0
i. Ou seja modi…cações no sistema
são transições
j i ! j 0
i
Estas transições podem ser descritas por operadores agindo em H,
j 0
i = ^M j i
Assim, tudo que acontece com o sistema pode ser representado por
um operador agindo em H.
Um tipo muito especial destes operadores são exatamente as medidas que
podemos fazer no sistema (e.g., sua energia), ou seja, o que podemos observar
do sistema. Estas quantidades são chamadas de observáveis.
Outro postulado da MQ a…rma que todo o observável corresponde a um
operador hermitiano no espaço de Hilbert. Assim, se um sistema possui
uma certa característica observável, por exemplo spin, existe um operador ^S
agindo em H correspondente a este observável.
Para entendermos melhor este postulado, precisamos ainda de um terceiro
postulado: Se ^M é um operador (hermitiano) relacionado com um observável
m (i.e., m é o valor que o aparelho que mede esta quantidade pode marcar), e
se no laboratório efetuarmos uma medida deste observável os únicos valores
possíveis de se obter são os auto-valores do operador ^M (ou seja, o valor
m marcado no aparelho é um autovalor de ^M).
Um exemplo disso já nos é conhecido. Voltemos para a teoria de Schroedinger
e tomemos o operador hamiltoniano (45)
^H =
~2
2m
r2
+ V (x) :
Pela teoria de Schroedinger (baseada na mecânica analítica) sabemos que este
operador está relacionado com o hamiltoniano do sistema, que por sua vez está
(classicamente) relacionado com a energia do sistema.
A primeira pergunta que surge é: Será que ^H é hermitiano?
Primeiramente é necessário dizer em qual espaço de Hilbert estamos tra-
balhando. Vamos escolher, por exemplo, uma partícula presa numa caixa de
tamanho a. Ou seja, nosso EH é H = L2
(0; a). Dos resultados anteriores,
sabemos que, se um operador é hermitiano, ele respeita a igualdade (73)
hyj ^M jxi = hxj ^M jyi : (74)
Lembrando que estamos no espaço das funções e, consequentemente, nosso pro-
91

92. duto interno se realiza por uma integral, temos
h j ^H j i =
Z a
0
(x)
h
^H (x)
i
dx =
Z a
0
(x)
~2
2m
d2
dx2
+ V (x) (x) dx
=
~2
2m
Z a
0
d2
dx2
+
Z a
0
V dx (75)
onde e são dois estados quaisquer do nosso sistema, ou seja
j i ; j i 2 H :
Já para o segundo termo de (74) temos
h j ^M j i =
Z a
0
(x)
~2
2m
d2
dx2
+ V (x) dx
=
Z a
0
(x)
~2
2m
d2
dx2
+ V (x) dx
=
~2
2m
Z a
0
d2
dx2
+
Z a
0
V dx (76)
Ser ou não hermitiano depende de (76) ser, ou não, igual a (75).
Analisemos primeiro o último membro de cada igualdade. Para (76) temos
Z a
0
(x) V (x) dx =
Z a
0
(x) V (x) (x) dx
que, obviamente, é igual ao último termo de (75).
Vejamos agora o primeiro termo de (75). Fazendo uma integral por partes
temos
Z a
0
d2
dx2
dx =
d
dx
a
0
Z a
0
d
dx
d
dx
dx
=
d
dx
a
0
d
dx
a
0
Z a
0
d2
dx2
dx
=
d
dx
a
0
d
dx
a
0
+
Z a
0
d2
dx2
dx
que (multiplicado por ~2
=2m) seria exatamente igual ao primeiro termo de
(76) se não fossem os dois primeiros termos de fronteira.
Devemos lembrar agora que nem todos os vetores em L2
(0; a) descreve um
estado físico do nosso sistema. Em especial, para resolvermos o problema da
partícula na caixa, tivemos de impor as condições de fronteira
(0) = (a) = 0 :
Ou seja, os vetores do nosso espaço não são todos os vetores em L2
(0; a), mas
apenas os vetores
2 L2
(a; b) ; (0) = (a) = 0 :
92

93. Com esta imposição temos
d
dx
a
0
=
d
dx
(a)
d
dx
(0) = 0
d
dx
a
0
=
d
dx
(a)
d
dx
(0) = 0
e, com isso,
h j ^H j i = h j ^H j i
e o operador ^H é hermitiano.
Remark 21 Vemos agora como a imposição física de que a partícula não pen-
etre nas paredes da caixa, se traduz no formalismo matemática da MQ como
uma exigência de que a energia do sistema seja um observável (i.e., que ^H seja
hermitiano).
Para sistemas mais complicados nem sempre é possível estabelecer as condições
de contorno do sistema através de argumento físicos (como …zemos com a
partícula na caixa). Assim o resultado acima é bastante prático e geral: as
condições de contorno do sistema devem ser impostas de forma que os ob-
serváveis de interesse (no geral a energia) sejam hermitianos.
Em seguida, no desenvolvimento do nosso problema, encontramos os autove-
tores de ^H,
^H n = En n
(ou seja, resolvemos a ES independente do tempo) e encontramos n e En. O
que o postulado acima sobre os autovalores nos diz é que, numa medida da
energia do sistema, podemos obter apenas um dos valores En acima.
Lembre ainda que uma característica peculiar a MQ é que o sistema pode
estar numa superposição de estados. Ou seja, nossa partícula na caixa pode
estar, por exemplo, num estado (x) na forma
(x) = a0 0 (x) + a2 2 (x) :
O que o postulado sobre autovalores nos diz é que, mesmo num caso como este,
ao medirmos a energia da partícula encontraremos apenas ou E0 ou E2.
Uma extensão do postulado acima a…rma que, se …zermos uma medida da
energia e obtivermos o resultado E2, isso garante que, após a medida, o
sistema tem energia E2. Ou seja, o estado após a medida não é mais o estado
(x) acima, mas o estado 0
(x)
0
(x) = 2 (x)
Dizemos assim que o sistema que estava numa superposição de ondas (ou
num pacote de ondas) colapsou para uma das ondas do pacote. Este efeito é
chamado de colapso da função de onda.
93

94. O fato de um sistema poder existir numa superposição de vários estados
possíveis, mas apresentar (colapsar para) apenas um destes estados quando uma
medida é feita, dá origem a pergunta: se o sistema está num certo estado qual
a probabilidade de, numa medida deste sistema, ele ser encontrado no estado .
Por exemplo, suponha que ^L representa o operador de momento angular do
sistema. Num certo instante o sistema é preparado no estado
j i = a1 j 1i + a2 j 2i + a3 j 3i ;
(com ai conhecidos) onde
^L j ni = ln j ni :
Se efetuamos uma medida do momento angular e obtivermos o valor l = 2
sabemos que, após esta medida, o sistema estará no estado j 2i. Assim, a
pergunta acima seria: qual a probabilidade do sistema no estado j i ser
encontrado no estado j 2i. A resposta para esta pergunta é mais um postulado
da MQ.
Se um sistema se encontra num determinado estado, dado por um vetor j i,
a probabilidade de que este sistema seja encontrado num estado j i é dado por:
jh j ij
2
=
PN
i=1 i iR 1
1
(x) (x) dx
:
Por exemplo,voltemos ao estado que uma superposição dos estados de mo-
mento ângular
j i = a1 j 1i + a2 j 2i + a3 j 3i :
Qual a probabilidade de numa medida deste sistema ele ser encontrado no
estado de momento angular j 2i?
Este valor é dado por:
jh 2j ij
2
= jh 2j (a1 j 1i + a2 j 2i + a3 j 3i)j
2
= j(a1 h 2 j 1i + a2 h 2 j 2i + a3 h 2 j 3i)j
2
Entra aqui o fato (já visto) que os autovetores de um operador hermi-
tiano são ortogonais, com isso (lembrando que nossas funções estão normal-
izadas)
jh 2j ij
2
= jh 2j (a1 j 1i + a2 j 2i + a3 j 3i)j
2
= ja2 h 2 j 2ij
2
= ja2j
2
:
Um outro fato, que vamos aceitar sem provar (isso não é um postulado),
é que, além de ortogonais, os autovetores de um operador hermitiano forma uma
base do espaço. Ou seja, se ^M é um operador hermitiano, com autovetor j ni
e autovalor mn,
^M j ni = mn j ni
94

95. qualquer estado do nosso sistema pode ser escrito como:
j i =
X
n
cn j ni ;
Além disso, sendo a nossa base ortonormal sabemos que
cn = h n j i =) jh n j ij
2
= jcnj
2
e jcnj
2
é, no caso geral, a probabilidade de, numa medida do observável ^M,
obermos o valor mn.
Vemos assim que o signi…cado físico dos autovetores de um operador her-
mitiano serem ortogonais está relacionado com o fato de que, se …zemos uma
medida obtemos apenas um valor. Ou seja, se após uma medida obtivermos o
valor j 2i a probabilidade de, após esta medida, o sistema ser encontrado no
estado j 3i deve ser nulo:
h 3 j 2i = 0 :
E o fato destes vetores j ni formarem uma base signi…ca que nosso sistema pode,
em princípio assumir qualquer valor do observável, com uma certa probabilidade
jcnj
2
.
Além disso, o fato de operadores hermitianos terem apenas autovalores reais
está relacionado com medidas nos darem apenas valores reais.
Dada uma in…nidade de cópias idênticas do sistema, podemos nos perguntar
sobre o valor médio de algum observável. Ou seja, pegamos uma in…nidade
de exemplares desta coleção de sistema, efetuamos em cada um a medida de
um certo observável M e tiramos a média deste valor para obter hMi. Esta
quantidade é também chamada de valor esperado do observável.
Classicamente, se cada exemplar do nosso sistema tem uma probabilidade
Pi de que o observável M forneça o valor mi, esta média pode ser calculada
como
hMi =
X
i
Pimi
somado para todos os valore mi possíveis do observável M. No caso de m ser
uma variável contínua, temos
hMi =
Z
mP (m) dm
onde P (m) é a probabilidade do sistema ter o valor medido entre m e m + dm.
O próximo postulado da MQ a…rma que, se o sistema está no estado j i, o
valor esperado de observável ^M é dado por:
hMi = h j ^M j i =
Z 1
1
(x; t) ^M (x; t) dt : (77)
Esta expressão está diretamente relacionada a noção clássica de média. Sendo
^M um observável, podemos escrever:
j i =
X
i
ci j ii
95

96. onde
^M j ii = mi j ii
Substituindo em (77) temos
h j ^M j i =
2
4
X
j
h jj cj
3
5 ^M
"
X
i
ci j ii
#
=
X
j
X
i
cjci h jj ^M j ii
=
X
j
X
i
cjci h jj mi j ii =
X
j
X
i
micjci ij
=
X
i
jcij
2
mi =
X
i
Pimi
onde usamos que jcij
2
é a probabilidade de se obter o valor mi numa medida de
^M.
O ponto importante deste postulado está no fato de geralmente, em exper-
iências, não estamos tratando apenas com uma entidade, mas sim uma coleção
destas entidades. Por exemplo, uma corrente de elétrons, um feixe de laser
(vários fótons), ou um feixe de partículas. Assim, o que nossos aparelhos reg-
istram pode não ser o valor possível do observável, mas sim uma média destes
valores. Com isso, o valor esperado de um observável quântico está diretamente
relacionado com o limite clássico no valor deste observável. Ou seja, se temos
um feixe de partículas (e.g., elétron) no estado
j i = c1 j 1i + c2 j 2i
onde
^H j ii = Ei j ii
são autoestados da energia, se medirmos a energia do feixe (não de um único
elétron) nosso aparelho clássico mostrará o valor
E = hHi = h j ^H j i = E1 jc1j
2
+ E2 jc2j
2
:
Nosso último postulado diz respeito a evolução temporal do sistema. E
a…rma que: a evolução temporal de um sistema dado por uma função
de onda (x; t) é dado pela equação de Schroedinger
i~
@
@t
= ^H ; ^H =
~2
2m
r2
+ V (x)
Este postulado pode ser convertido na linguagem de operadores agindo em
H e, com isso, generalizado para qualquer descrição quântica (e.g., Heisenberg).
Para isso basta introduzirmos o chamado operador de evolução temporal ^U6
^U (t) = exp
i
~
^Ht
6 Este é o caso especial em que ^H não depende do tempo.
96

97. onde ^H é o hamiltoniano do sistema e
exp
i
~
^Ht =
X 1
n!
i
~
^Ht
n
= 1
i
~
t ^H
1
2~2
t2 ^H2
+ :::
ou seja, cada termo ^Hn
é a aplicação de n vezes o operador ^H. Com esta
de…nição de ^U temos
j ti = ^U (t) j 0i
onde j 0i é o vetor (estado) do sistema no instante inicial e j ti seu estado num
instante t posterior. Usando a ES temos
i
@
@t
j ti = i
@
@t
^U (t) j 0i = i
@ ^U (t)
@t
j 0i = i
@
@t
exp
i
~
^Ht j 0i
usando
@
@t
exp
i
~
^Ht =
@
@t
X 1
n!
i
~
^Ht
n
=
@
@t
1
i
~
t ^H
1
2~2
t2 ^H2
+ :::
=
i
~
^H
1
~2
t ^H2
+ :::
=
i
~
^H 1
1
~
t ^H + :::
=
i
~
^H exp
i
~
^Ht
temos
i
@
@t
j ti = i
@
@t
exp
i
~
^Ht j 0i = i
i
~
^H exp
i
~
^Ht j 0i
=
1
~
^H exp
i
~
^Ht j 0i
=
1
~
^H j ti
ou seja, o vetor j ti obedece a equação
i~
@
@t
j ti = ^H j ti :
Por exemplo. Suponha que num instante inicial o sistema com hamiltoni-
ano ^H está preparado estar no estado (x; 0) dado por
(x; 0) =
1
p
2
[ 1 (x) + 2 (x)] ;
97

98. onde
^H i = Ei i :
Qual o estado do sistema num instante t posterior? Neste caso, como temos
a condição inicial escrita em termos dos autovetores de ^H, podemos apenas
aplicar o operador de evolução temporal
(x; t) = ^U (t) (x; 0) =
1
p
2
exp
i
~
^Ht 1 (x) + exp
i
~
^Ht 2 (x)
o importante aqui é observar que
exp
i
~
^Ht i (x) =
X 1
n!
i
~
^H
n
i (x) =
= 1
i
~
t ^H
1
2~2
t2 ^H2
+ ::: i (x)
= 1
i
~
tEi
1
2~2
t2
E2
i + ::: i (x)
= exp
i
~
Eit i (x)
com isso
(x; t) =
1
p
2
exp
i
~
E1t 1 (x) + exp
i
~
E2t 2 (x) :
Com o exemplo acima podemos ver porque geralmente não precisamos re-
solver a equação de Schroedinger dependente do tempo, mas apenas a indepen-
dente (i.e., apenas encontrar os autovalores e autovetores de ^H). Neste caso a
di…culdade se transfere em decompor o estado inicial nos autovetores de ^H. Ou
seja, se o sistema está num estado inicial (x; 0) precisamos escrever
(x; 0) =
X
cn n (x) ;
o que equivale a calcular
cn = h nj i =
Z
n (x) (x) dx
Temos assim a opção de resolver uma equação diferencial parcial (a ES depen-
dente do tempo), ou calcular as in…nitas integrais acima.
Resumindo nossos postulados temos:
1. O estado de um sistema físico é completamente descrito por um vetor
(normalizado) no espaço de Hilbert. E vetores que di…ram apenas por
uma fase representam o mesmo estado físico;
2. A todo o observável esta relacionado um operador hermitiano;
98

99. 3. Uma medida do observável ^M pode fornecer apenas autovalores deste
operador e, após uma medida em que se obteve o valor mn o sistema
estará no estado n.
4. Se o sistema se encontra no estado j i, o valor médio de um observável
^M é dado por:
hMi = h j ^M j i =
Z
(x; t) ^M (x; t) dt :
5. A evolução temporal de um sistema no estado inicial j 0i é dado por (no
caso geral de ^H (t))
j ti = U (t) j 0i ; ^U (t) = exp
i
~
Z
^H dt
que é equivalente a ES
i~
@
@t
= ^H :
9.10 O operador de momento
Vejamos agora alguns operadores hermitianos e a que observáveis estes estão
associados. Um caso já visto é o operador hamiltoniano, cujos autovalores cor-
respondem a energia do sistema. Se introduzirmos agora o operador
^p = i~r
podemos escrever
^H =
~2
2m
r2
+ V (x)
como
^H =
^p2
2m
+ V (x)
Que, comparando com a forma clássica do hamiltoniano justi…ca chamar ^p de
operador de momento. Ou seja, seus autovalores estão associados com o
momento que a partícula pode assumir. Obviamente a semelhança com a
forma clássica do hamiltoniano não é a única justi…cativa para isso.
Uma partícula livre, que pode se mover em todo espaço, é descrita quanti-
camente pela onda plana
(x) = N exp (ikx)
Lembrando que, por de…nição, o comprimento de uma onda é a distância
para a qual ela volta a assumir o mesmo valor, o comprimento de onda do estado
acima pode ser calculado como
(x) = (x + ) ) exp (ikx) = exp (ik (x + )) ) exp (ik ) = 1
99

100. com isso
k = 2 ) k =
2
:
A aplicação do operador de momento neste estado fornece
^p = i~
d
dx
N exp (ikx) = k~N exp ( ikx) = ~k
Ou seja, o estado acima é autovetor de ^p com autovalor ~k. Se usarmos agora
k = 2 e a relação de De Broglie p = h= temos
^p = k~ = k
h
2
=
2 h
2
=
h
= p
Ou seja, a relação de De Broglie nos permite associar os autovalores
do operador
^p = i~
d
dx
com o valor do momento do sistema clássico.
100

101. Como era de se esperar por argumentos clássicos, apenas partículas livres
tem um valor de momento bem que não se altera com o tempo. Mesmo a
partícula numa caixa tem seu momento alternado e, conseqüentemente, os au-
tovetores de energia da partícula na caixa não são autovetores do momento.
O fato do sistema estar num estado que é autovetor de um operador qualquer
^M signi…ca que a aplicação de ^M não altera o estado do sistema. Ou seja, assim
que efetuamos esta operação o sistema estará num estado
j 0
i = ^M j i = m j i
Mas para ser um estado legítimo j 0
i precisa ser normalizado e, uma vez que
j i já estava normalizado,
j 0
i = j i :
Se lembrarmos agora que a aplicação do operador é a descrição quântica da
medida do observável, vemos que se o sistema está num auto-estado de um
operador qualquer, podemos fazer a medida deste observável sem perturbar
o sistema (ou seja, após a medida o sistema colapsa para o próprio estado).
Dizemos com isso que o sistema possui esta quantidade bem de…nida.
Isso porque, se o sistema estiver num estado j i que não é autovetor de ^M
ao aplicarmos o operador o sistema irá colapsar para um estado j 0
i 6= j i e
a aplicação do operador (ou a medida da quantidade) perturbou o sistema, de
sorte que não temos mais acesso ao sistema original. Além disso, o valor
obtido corresponde apenas a uma, dentre várias, probabilidade de se obter os
valores deste observável. Agora, quando o sistema está num autovalor
de um operador, podemos sempre medir o observável correspondente sem
perturbar o sistema e, pelos postulados introduzidos, obteremos sempre o
mesmo valor deste observável.
9.11 Quantização
Com a introdução do operador de momento, podemos de…nir um outro processo
de quantização completamente compatível com a quantização de Schroedinger
(ou seja, o procedimento que nos permite identi…car o hamiltoniano clássico H
com o operador ^H).
Dado um hamiltoniano clássico
H (p; x) =
p2
2m
+ V (x)
podemos quantizar este hamiltoniano fazendo
p ! ^p = i~r ;
x ! ^x = x ;
onde a última igualdade indica que o operador ^x é simplesmente a multiplicação
por x, ou seja
^x (x0
) = x0
(x0
) :
101

102. ou seja, para qualquer função f
f (^x) = f (x) :
Com isso
H (p; x) ! ^H (^p; ^x) =
^p2
2m
+ V (^x) =
~2
2m
r2
+ V (x) :
que é o hamiltoniano quântico obtido na teoria de Schroedinger.
Este procedimento de quantização permite quantizar qualquer quantidade
clássica que dependa da posição e do momento, por exemplo, o operador de
momento angular pode ser obtido através do momento angular clássico L =
x p, fazendo
L = x p ! ^L = ^x ^p :
Em componentes,
Li = "ijkxjpk ! ^Li = "ijk ^xj ^pk = "ijkxj i~
@
@xk
= i~"ijkxj
@
@xk
ou
^L = i~x r
Vamos, por exemplo, calcular o momento angular de uma partícula livre,
^LiN exp (ikixi) = N i~"ijkxj
@
@xk
exp (ikixi)
= N ( i~"ijkxj) exp (ikixi)
@ (ikjxj)
@xk
= N ( i~"ijkxj) exp (ikixi) ikj
@xj
@xk
= N ( i~"ijkxj) exp (ikixi) ikj jk
= N ( i~"ijkxj) exp (ikixi) ikk
= N ("ijkxj (~kk)) exp (ikixi)
= N ("ijkxj (pk)) exp (ikixi)
ou seja, para a partícula livre,
^L = x p
(onde p não é mais um operador, mas o momento clássico). Assim, para uma
partícula quântica livre o momento angular é uma quantidade bem de…nida é
tem o mesmo valor esperado classicamente.
É importante notar que nem todos os observáveis podem ser quantizados
pelo procedimento acima. Existem quantidades, por exemplo, o spin, que não
se relacionam com os operadores ^p e ^x. Quando isso ocorre dizemos que este
observável só existe na MQ, ou ainda, que este observável não possui um
análogo clássico.
102

103. 9.12 O problema do ordenamento
Um dos problemas que surge no processo de quantização acima (e, de uma
certa forma, em todos os processos de quantização), é o chamado problema do
ordenamento. Dado um observável clássico que envolva o produto (o momento
angular é um exemplo)
xp ;
quanticamente podemos associar a este observável os operadores
^M = ^x^p ; ^M0
= ^p^x
onde
^M0
= ^p^x = i~
d
dx
x = i~ i~x
d
dx
= i~ + ^x^p
= ^M i~ = ^M i~
ou ainda
^M0
= ^M i~
Ou seja, os dois operadores acima dizem respeito a mesma quantidade clássica
xp. Isso ocorre porque, diferente da MC, na MQ os observáveis não são
números, mas sim operadores. Assim, para um observável clássico pode
estar relacionado mais de um operador quântico.
Um ponto a se observar é que, assim como no exemplo acima, no problema
de ordenamento os operadores sempre diferem por uma quantidade proporcional
a ~n
. Lembrando que uma das formas de tomarmos o limite clássico do nosso
sistema é fazer ~ ! 0, vemos que os dois operadores ^M e ^M0
possuem o mesmo
limite clássico. Assim, teorias quânticas que di…ram por um problema
de ordenamento possuem o mesmo limite clássico. Ou de outra forma,
para o mesmo sistema clássico podemos ter várias teorias quânticas
diferentes. Entretanto, apesar de todas terem o mesmo limite clássico, estas
teorias podem gerar resultados puramente quânticos (e.g., supercondutividade)
bastante diferentes.
9.13 Observáveis compatíveis
Uma questão crucial em MQ é quando uma medida perturba o sistema, ou
ainda, quando um observável tem um valor bem de…nido. Como vimos, para
que a medida de uma quantidade ^A não perturbe o sistema, este deve estar
num auto-estado de ^A. Assim, ^A não irá perturbar um sistema que esteja num
auto-estado
^A j i = a j i :
Suponha agora que, depois de efetuada uma medida de ^A desejamos efetuar
uma medida de outro observável ^B. Isso só será possível, sem perturbar o
103

104. sistema, se o vetor obtido após a aplicação de ^A em j ai também for um
autovetor de ^B, ou seja, se
^B ^A j i = b0 ^A j i = b0
a j i = b j i ; b = b0
a
ou seja, j ai tem de ser simultaneamente autovetor dos dois operadores ^A e ^B.
^A j i = a j i
^B j i = b j i
Mas, se isso é verdade, temos
^A ^B j i = ab j i
^B ^A j i = ba j i = ab j i
ou ainda h
^A ^B ^B ^A
i
j i = 0
Para qualquer auto-vetor simultâneo de ^A e ^B.
A quantidade acima é chamada de comutador entre os operadores ^A e ^B
h
^A; ^B
i
= ^A ^B ^B ^A :
Além disso, se todo o autovetor de ^A for também autovetor de ^B temos
h
^A; ^B
i
j ni = 0 ; ^A j ni = n j ni
e sabemos que qualquer vetor pode ser escrito como
j i =
X
n
cn j ni
temos que
h
^A; ^B
i
j i =
h
^A; ^B
i X
n
cn j ni =
X
n
cn
h
^A; ^B
i
j ni = 0
Ou seja, se
h
^A; ^B
i
= 0 para qualquer vetor j i do nosso espaço, então ^A
e ^B tem uma base de auto-vetores em comum. Mais ainda, podemos efetuar
medidas de um dos operadores sem alterar o valor do outro.
(Podem ser medidos simultaneamente)
Ou ainda, os dois observáveis podem ser medidos simultaneamente. Quando
h
^A; ^B
i
= 0
dizemos que ^A e ^B comutam, ou ainda, que estes observáveis são compatíveis.
104

105. Remark 22 Apenas observáveis compatíveis podem ser medidos simultanea-
mente em MQ.
Por exemplo: Para uma partícula livre, os operadores de momento e ener-
gia são
^H =
^p2
2m
; ^p = i~
d
dx
calculando os comutadores temos
h
^H; ^p
i
= ^H ^p ^p ^H =
^p2
2m
^p ^p
^p2
2m
=
1
2m
^p2
^p ^p^p2
=
1
2m
^p3
^p3
= 0
Assim, para qualquer partícula livre (x) (não só para os autoestados de ^p e
^H) h
^H; ^p
i
(x) = 0
e o momento e a energia podem ser medidos simultaneamente. Além disso, todo
auto-vetor de ^H e também auto-vetor de ^p.
Exercise 23 Explique por que para o problema de uma partícula numa caixa
os auto-vetores de ^H não são auto-vetores de ^p.
Segundo exemplo: Como vimos, os operadores de momento e posição são
dados por
^p = i~
d
dx
; ^x = x
calculando os comutadores temos
[^x; ^p] (x) = ^x^p (x) ^p^x (x)
= x i~
d
dx
(x) i~
d
dx
[x (x)]
= i~ x
d
dx
dx
dx
(x) + x
d
dx
= i~ [ (x)] = i~ (x)
Ou seja, para qualquer função (x)
[^x; ^p] = i~
E, consequentemente, momento e posição não podem ser medidos simultanea-
mente. O que já sabíamos pelo princípio da incerteza de Heisenberg.
Os resultados acima nos dizem quando devemos esperar uma incerteza rela-
cionada a medida de dois observáveis quaisquer.
Por exemplo, podemos efetuar uma medida da posição da partícula na
direção x e medirmos o seu momento na direção y, pois
[^x; ^py] = i~ x;
@
@y
= i~ x
@
@y
@
@y
x = i~x
@
@y
@
@y
= 0
105

106. logo
[^x; ^py] = 0 ;
ou ainda
[^xi; ^pj] = i~ ij ;
da mesma forma
[^xi; ^xj] = [^pi; ^pj] = 0 :
106

107. Um exemplo mais fácil de visualizar é o caso do spin da partícula. Classica-
mente
U = B
Força
F = r ( B)
Para B = B^z
F = r ( zB) = z
@B
@z
O momento magnético sofre um torque
= B
O torque o faz precessionar (Einstein–de Haas).
Assim, um feixe de partículas clássicas com todas as orientações de momento
magnético seria espelhado continuamente.
Se efetuarmos uma medida do spin de uma partícula de spin 1
2 em qualquer
direção, obteremos sempre os valores +1 ou 1, ou seja, a partícula tem o
spin na direção medida, ou contrária a esta direção. Esta medida pode ser
realizada através de um experimento de Stern-Gerlach que consistem em passar
a partícula por um campo magnético não uniforme e esta partícula se deslocará
para cima se seu spin for +1 e para baixo se for 1.
j+i ; j i
j i = c1 j+i + c2 j i
Lembre que j i é um vetor no espaço de Hilbert. Este espaço possui dois
elementos na base e, consequentemente, tem dimensão 2.
Mas para trabalhar precisamos de uma representação para esta quantidade.
Neste caso temos uma total liberdade na escolha desta representação e, em
especial, na base desta representação. Vamos então escolher uma direção, por
exemplo z, é dizer que j+i é o spin nesta direção e j i na direção contrária.
Para deixar isso mais explicito, vamos mudar a notação
j i ! jz i
Como nosso espaço tem dimensão 2 podemos escolher qualquer matriz (nor-
malizada) para representar o nosso estado, a escolha mais simples é
jz+i =
1
0
e para jz i um vetor normalizado ortogonal a jz+i
jz i =
0
1
107

108. Sabemos que existe um operador, que é uma matriz 2x2 relacionada ao spin.
Ou seja, seus autovalores são os possíveis valores do spin. Pela de…nição dos
vetores acima temos:
3 jz+i = +1 jz+i
3 jz i = 1 jz i
Com isso, podemos escrever
3 =
1 0
0 1
O operador de spin na direção z é apenas de…nido proporcional a este operador
com constantes que acerte as unidades
^S3 =
~
2
3
Por razões não podemos esclarecer agora (esta é a teoria de Pauli que veremos
na segunda parte do curso), os operadores de spin nas direções x,y,z são dados
por:
^Si =
~
2
i ; 1 =
0 1
1 0
; 2 =
0 i
i 0
; 3 =
1 0
0 1
:
Vamos então à descrição de uma série de medidas do spin de uma partícula.
Suponha que você alinhou o aparato de SG na direção z, ou seja, efetuou uma
medida de ^S3 e obteve o valor +1 (a partícula subiu). Com isso, pelos postulados
vistos, sabemos que a partícula, após a medida, está num auto-estado de ^S3 com
valor +1:
jz+i =
1
0
:
Exercise 24 Veri…que que este estado é auto-estado de ^S3 com autovalor +1.
Suponha agora que, depois desta medida, você alinha o aparato da direção
x efetua uma nova medida.
Qual a probabilidade de você obter o valor +1 novamente?
Bem, após esta segunda medida o sistema irá colapsar num dos autovetores
de ^S1
jx+i =
1
p
2
1
1
; jx i =
1
p
2
1
1
:
Exercise 25 Veri…que que estes vetores são autovetores de ^S1 com auto valor
+1 e 1.
108

109. A questão é a seguinte: você sabe que o seu sistema está no estado jz+i
(pois você mediu o spin na direção z) e que saber, por exemplo, a probabilidade
de, numa medida do spin na direção x obter o valor +1. Pelos postulados
vistos anteriormente, sabemos que a probabilidade P (x+) encontrar o sistema
no estado jx+i sabendo que ele está no estado jz+i vale
P (x+) = jhx+ jz+ij
2
= 1 0
1
p
2
1
1
2
=
1
2
Da mesma forma
P (x ) = jhx jz+ij
2
=
1
2
ou seja, você tem uma incerteza total na medida do spin na direção x.
(Depois da medida em x)
Agora, se você efetuou a medida na direção x (do estado jz+i) e obteve o
valor +1 (a partícula foi para a direita), você sabe que após a medida a partícula
está no estado
jx+i =
1
p
2
1
1
Se você …zer novamente uma medida do spin na direção z, a probabilidade de
obter novamente +1 vale
P (z+) = jhz+ jx+ij
2
=
1
p
2
1 1
1
0
2
=
1
2
Da mesma forma P (z ) = 1=2. Ou seja, após a medida na direção x você
perdeu toda a informação do spin na direção z.
Uma forma clara de ver isso é notando que
jx+i =
1
p
2
1
1
=
1
p
2
1
0
+
0
1
=
1
p
2
jz+i +
1
p
2
jz i
E uma partícula no estado jx+i tem 50% de chance de apresentar, numa medida
do spin da direção z, o valor +1 e 1.
O ponto aqui é que a medida de um dos observáveis perturbou o valor do
outro. Ou seja, não podemos medir, simultaneamente, Sx e Sz.
Isso já era de se esperar pelo resultado anterior, pois estes operadores não
comutam:
h
^Sx; ^Sz
i
=
~
2
0 1
1 0
;
~
2
1 0
0 1
=
~
2
2
0 2
2 0
=
~2
2
0 1
1 0
= i
~2
2
0 i
i 0
= i
~2
2
S2 6= 0
109

110. 9.13.1 Relações de incerteza
Uma quantidade clássica muito usada para caracterizar a incerteza de uma
medida A é o desvio quadrado médio
2
A = A2
hAi
2
Pelos postulados da MQ sabemos que, o valor médio de um observável ^A num
estado vale
hAi = h j ^A j i
e a versão quântica para o desvio padrão pode ser escrita como
2
A ( ) = h j ^A2
j i h j ^A j i
2
se …zemos
^A = ^A h j ^A j i
podemos escrever
2
A ( ) = h j ^A2
j i
Exercise 26 Veri…que a a…rmação acima.
Considere agora dois observáveis ^A e ^B.
Um resultado conhecido como desigualdade de Schwarz nos diz que para
qualquer operador ^A e qualquer vetor j i (não necessariamente normalizado)
h j ^A2
j i h j ^B2
j i h j ^A ^B j i
2
com isso temos
2
A ( ) 2
B ( ) = h j ^A2
j i h j ^B2
j i h j ^A ^B j i
2
(78)
Além disso, apesar de serem hermitianos, o produto ^A ^B nem sempre o será.
Com isso a quantidade
2
A ( ) 2
B ( )
será, em geral, complexa
h j ^A ^B j i
2
=
h
Re h j ^A ^B j i
i2
+
h
Im h j ^A ^B j i
i2 h
Im h j ^A ^B j i
i2
(79)
Podemos agora calcular
Im h j ^A ^B j i =
1
2i
h j ^A ^B j i h j ^A ^B j i
Mas,
h j ^A ^B j i = h j ^A ^B
+
j i = h j ^B+ ^A+
j i = h j ^B ^A j i
110

111. onde, na última igualdade, usamos a hermiticidade de de ^A e ^B. Com isso
Im h j ^A ^B j i =
1
2i
h j ^A ^B j i h j ^B ^A j i
=
1
2i
h j ^A ^B ^B ^A j i
=
1
2i
h j
h
^A ; ^B
i
j i
usando h
^A ; ^B
i
=
h
^A h j ^A j i ; ^B h j ^B j i
i
=
h
^A; ^B
i
temos
Im h j ^A ^B j i =
1
2i
h j
h
^A; ^B
i
j i (80)
Usando (78), (79), (80) temos
2
A ( ) 2
B ( ) h j ^A ^B j i
2 h
Im h j ^A ^B j i
i2
=
1
2i
h j
h
^A; ^B
i
j i
2
:
Com isso
A ( ) B ( )
1
2
h j
h
^A; ^B
i
j i
ou seja, o produto da incerteza de qualquer medida é proporcional ao comutador
dos operadores correspondentes.
Para o caso especial de posição e momento temos
[^x; ^p] = i~ ) x p ( )
~
2
que é a relação de incerteza de Heisenberg.
9.14 O oscilador harmônico
São incontáveis os sistemas e aplicações em física que podem ser modelados
pelo problema do oscilador harmônico (OH). Uma das razões para isso é que
um potencial V (x) qualquer (dado por uma função analítica) sempre pode ser
expandido em sua série de Taylor
V (x) = V0 +
dV
dx x0
x +
1
2
d2
V
dx2
x0
x2
+
1
3!
d3
V
dx3
x0
x3
+ ::::
Além disso, em muitos problemas em física estamos interessados no comporta-
mento do sistema perto da condição de equilíbrio. Nesta condição
dV
dx x0
= 0
111

112. e nosso potencial se torna
V (x) =
1
2
kx2
+ O x3
k =
d2
V
dx2
x0
onde usamos que uma constante no potencial não altera o comportamento do
sistema. Assim, próximo do equilíbrio, qualquer potencial pode ser aproximado
por um OH.
Vamos introduzir os seguintes operadores diferenciais lineares
^L ^H =
~2
2m
d2
dx2
+
1
2
m!2
^x2
;
^p = i~
d
dx
D (^p) = D ^H = ; 0
2 L2
; a:c:
aqui ^H é o operador hamiltoniano de um oscilador harmônico. A solução do
problema quântico se obtém pela solução da ES estacionária, i.e., através da
solução do problema de autovalores de ^H,
^H = E =)
~2
2m
d2
dx2
+
1
2
m!2
^x2
= E
Esta equação não é nada simples de se resolver.
Vamos tentar então um método alternativo. Primeiro observe que, para
qualquer função 2 D (^p) temos
x^p ^p (x ) = x i~
d
dx
i~
d
dx
(x )
= i~x
d
dx
+ i~
d
dx
(x )
= i~x
d
dx
+ i~ ( ) + i~x
d
dx
= i~ (81)
Se usarmos a notação
x^p ^p (x ) = [x^p ^px] [x; ^p] ;
onde
[x; ^p] [x^p ^px]
é chamado o comutador de x com ^p, lembrando que o operador atua em tudo que
estiver a sua direita e que (81) é válida para toda função , podemos escrever
simbolicamente
[x; ^p] = i~ (82)
112

113. ou seja, sempre que aparecer o comutador entre x e ^p podemos sub-
stituir por i~. Lembre que a quantidade acima é um operador enquanto a
quantidade à direita da igualdade é um número.
Remark 27 Assim, esta igualdade só faz sentido quando ambos os lados atuam
numa função qualquer.
Vamos agora de…nir os seguintes operadores diferenciais
^a = p
2
x +
i^p
m!
; ^a+
= p
2
x
i^p
m!
x =
1
p
2
^a + ^a+
; ^p = i~p
2
^a+
^a (83)
=
r
m!
~
Com estes novos operadores o Hamiltoniano pode ser escrito como (veri…que):
^H = ~2
2
2
(^a+
^a)
2
2m
+
1
2
1
22
m!2
^a + ^a+ 2
=
1
4
!~
h
^a + ^a+ 2
^a+
^a
2
i
=
1
4
!~
h
^a2
+ ^aa+
+ a+
^a + a+ 2
^a2
^aa+
a+
^a a+ 2
i
=
1
2
!~ ^aa+
+ a+
^a
^H =
^p2
2m
+
1
2
m!2
^x2
= ~! ^a+
^a +
1
2
(84)
As regras de comutação (82) implicam que (veri…que):
^a; ^a+
=
2
2
x +
i^p
m!
; x
i^p
m!
=
2
2
x +
i^p
m!
; x
i^p
m!
=
2
2
x +
i^p
m!
x
i^p
m!
x
i^p
m!
x +
i^p
m!
=
2
2
"
x2
x
i^p
m!
+
i^p
m!
x
i^p
m!
2
x2
x
i^p
m!
+
i^p
m!
x +
i^p
m!
2
#
= i
2
2
2
m!
[x; ^p]
= 1
[x; ^p] = i~ =) ^a; ^a+
= 1 : (85)
113

114. ^a^a+
= 1 + ^a+
^a
H =
1
2
!~ ^aa+
+ a+
^a
= !~
1
2
+ a+
^a
Suponha agora que n (x) é uma auto função qualquer de ^H, ou seja,
^H n = En n
Agora uma característica muito mais do que importante dos oper-
adores (83): Usando a regra de comutação (85) vemos que
^H^a n = ~! ^a+
^a +
1
2
^a n = ~! ^a+
^a ^a +
1
2
^a n
= ~! ^a^a+
1 ^a +
1
2
^a n
= ^a~! ^a+
^a 1 +
1
2
n
= ^a~! ^a+
^a +
1
2
1 n
= ^a
h
^H ~!
i
n
= ^a [En ~!] n
= ~!
En
~!
1 ^a n :
fazendo
En
~!
= n =) ^H n = ~! n n
temos
^H^a n = ~! ( n 1) ^a n :
Ou seja, se n é autovetor de ^H com autovalor ~! n, então ^a n é outro
autovetor de ^H, mas com autovalor ~! ( n 1) diminuindo de uma unidade.
Simbolicamente podemos chamar este vetor de n 1;
^a n n 1 ; ^H n 1 = ~! n 1 n 1 ; n 1 n 1 :
114

115. Da mesma forma
^H^a+
n = ~! ^a+
^a +
1
2
^a+
n
= ~! ^a+
^a^a+
+ ^a+ 1
2
n
= ~! ^a+
1 + ^a+
^a + ^a+ 1
2
n
= ^a+
~! 1 + ^a+
^a +
1
2
n
= ^a+
~! 1 + ^H n
= ^a+
~! (1 + n) n
= ~! (1 + n) ^a+
n
Ou seja, se n é autovetor de ^H com autovalor ~! n, então ^a+
n é outro au-
tovetor de ^H, mas com autovalor ~! ( n + 1) acrescido de uma unidade. Sim-
bolicamente podemos chamar este vetor de n+1;
^a+
n n+1 ; ^H n+1 = ~! n+1 n+1 ; n+1 n + 1 : (86)
Por isso estes operadores são chamados de operadores de criação a+
e aniquilação
a.
Vamos usar agora que a energia do sistema é uma quantidade positiva7
h j ^H j i 0
num estado n qualquer
h nj ^H j ni = h nj ~! n j ni = ~! n h nj ni = ~! n 0 : (87)
(onde supusemos que n está normalizado).
Se a energia é positiva deve haver um estado de energia fundamental, i.e.,
um estado cuja energia não possa ser reduzida. Podemos chamar este estado
simbolicamente de 0 com energia 0 min ( n).
Mas a existência do operador ^a garante que sempre podemos baixar a energia
do sistema. Ou seja, o vetor = ^a 0 teria uma energia 0 1 < 0, a menos
que (x) = 0, ou seja,
^a 0 = 0 :
7 Isso pode ser visto observando que para qualquer autovetor normalizado n temos
h nj ^a+
^a j ni =
Z b
a
[ n (x)] a+
a n (x) dx
=
Z b
a
[a n (x)] [a n (x)] dx
= h^a nj j^a ni 0 :
115

116. Voltando agora para os nossos operadores originais (x; ^p) temos:
^a 0 = 0 =) p
2
^x +
i^p
m!
0 = 0
x 0 +
~
m!
d 0
dx
= 0
fazendo
k =
~
m!
temos
d 0
dx
=
1
k
x 0 =)
1
0
d 0
dx
=
d
dx
ln 0 =
x
k
;
Fácil ver que a equação acima é bem mais fácil de resolver que a nossa
equação original (??). Sua solução vale
ln 0 =
x2
2k
+ C =) 0 (x) = N exp
x2
2k
:
com N uma constante (normalização).
A exigência ^a 0 = 0, nos permite ainda determinar a energia deste estado
fundamental. Partido da eq. (84)
^H n = ~! n n
~! ^a+
^a +
1
2
0 = ~! 0 0
~! ^a+
(^a 0) +
1
2
0 = ~! 0 0
~!
1
2
0 = ~! 0 0
0 =
1
2
Então já temos o estado fundamentas e a sua energia (auto-valor).
Observe que a descrição quântica do OH implica na existência de uma energia
mínima (o oscilador nunca para de oscilar).
Como construir os outros estados n?
Para isso, basta usar a propriedade (86)
^a+
n = n+1 =) ^a+
0 = 1 =) p
2
^x
i^p
m!
0 = 1
E1 = ~! ( 0 + 1) = ~!
1
2
+ 1
116

117. explicitamente
p
2
x 0
~
m!
d
dx
0 = 1
1 (x) = p
2
x 1 +
~
~
m! m!
!
0
1 (x) = 2p
2
x 0 = N
2
p
2
x exp
x2
2k
Da mesma forma, podemos obter todos os outros estados (não-normalizados)
n
n = ^a+ n
0
n (x) = N p
2
x
~
m!
d
dx
n
0 (x)
Com autovalor
En = ~! n +
1
2
9.14.1 Normalização
As funções n (x) não estão normalizadas, i.e., após a aplicação do operador ^a+
n vezes, precisamos calcular N. Isso pode ser simpli…cado supondo que, se n
é um vetor normalizado, queremos obter N e N+
para que
^a n N n 1
^a+
n N+
n+1
^a n e ^a+
n também já estejam normalizados.
^H j ni = En j ni
~! ^a+
^a +
1
2
j ni = ~! n +
1
2
j ni
^a+
^a j ni = n j ni
multiplicando pelo dual de j ni temos
h nj ^a+
^a j ni = n h nj j ni = n (88)
Agora observe que, pela de…nição de adjunto
h j ^A j i = h j ^A+ j i
temos Z
^A dx =
Z
(A+ ) dx =
Z
(A+ ) dx
117

118. ou seja, podemos calcular h j ^A j i como o produto do dual de j i com ^A j i,
ou como o produto de j i com o dual de ^A+
j i. Com isso
h nj ^a+
^a j ni =
Z
n a+
(a n) dx =
Z
^a n (^a n) dx
se …zemos
j ni = ^a j ni
a expressão acima se torna
Z
( n) ( n) dx = h nj j ni = j nj
2
= j^a nj
2
usando (88)
j^a nj
2
= n )
^a n
p
n
2
= 1
ou seja, se quisermos um vetor normalizado não devemos de…nir ^a n = n 1,
mas sim
^a n
p
n
n 1 ) ^a n =
p
n n 1
Da mesma forma
h nj ^a^a+
j ni = h nj 1 + ^a+
^a j ni = 1 + h nj ^a+
^a j ni = 1 + n = N+ 2
^a+
n =
p
n + 1 n+1
Ou, fazendo m = n + 1,
^a+
m 1 =
p
m m
com isso
m =
^a+
m 1
p
m
=
^a+
p
m
^a+
p
m 1
^a+
p
m 2
m 3
=
^a+
p
m
^a+
p
m 1
^a+
p
m 2
:::
^a+
p
m m
m m
=
(^a+
)
m
p
m!
0 :
Assim, a formula para a n-ésima autofunção do hamiltoniano do OH se torna
n (x) =
N0
p
n!
p
2
x
~
m!
d
dx
n
0 (x)
onde N0 é a normalização do estado 0 .
As funções n assim construídas são chamadas de funções de Hermite.
118

119. Exercise 28 Use a integral gaussiana
Z 1
1
e x2
dx =
p
e ache a normalização N0.
Exercise 29 Construa a função de Hermite 4 (x).
10 Potenciais centrais
Até aqui tratamos praticamente todos os exemplo em 1D e argumentamos que a
extensão destes resultados para 3D não envolvia nenhuma di…culdade conceitual
mais profunda.
Vamos agora considerar o momento angular orbital de um sistema, ou seja,
uma característica que exige que nosso sistema tenha mais de 2D. O momento
angular que vamos tratar aqui é chamado de momento angular orbital. Este
representa a quantização, nos moldes introduzidos anteriormente, do observável
clássico momento angular
L = x p ! ^L = i~x r :
Esta distinção é necessária porque em MQ temos ainda um outro tipo de
momento angular, chamado spin, que representa uma característica interna das
partículas (a seguir veremos a diferença). Este último não representa a quanti-
zação de nenhum observável clássico e, mais ainda, não possui nenhum análogo
em MC.
O operador de momento angular respeita a seguinte regra de comutação
h
^Lj; ^Lk
i
= i~"ijk
^Li
e, conseqüentemente, não podemos esperar medir suas três componentes
simultaneamente (não são compatíveis). Portanto escolhemos uma destas
componentes para caracterizar o sistema,usualmente ^Lz.
Exercise 30 Veri…que a regra de comutação acima.
Entretanto, apesar de não podemos medir simultaneamente as 3 compo-
nentes do momento angular, podemos de…nir um operador relacionado com o
módulo (ou o valor total do momento angular)
^L2
= ^L2
1 + ^L2
2 + ^L2
3 :
(na verdade, a raiz quadrada do autovalor do operador acima). Este operador
comuta com todas as componentes do momento angular
h
^L2
; ^Li
i
= 0
119

120. Exercise 31 Veri…que explicitamente que
h
^L3; ^L2
i
= 0.
Assim, podemos caracterizar (medir simultaneamente) tanto o momento an-
gular numa dada direção (e.g., ^L3), quanto o seu módulo. Ou seja, podemos
procurar por autofunções simultâneas destes dois operadores. Vamos chamar
estas autofunções de Km e, por conveniência, vamos escrever seus autovalores
como
^L2
Km = ~2
K2
Km
^L3 Km = ~m Km
Os índices K; m caracterizam nosso estado físico. Índices que caracterizam
um estado físico em MQ são chamados de números quânticos. Ou seja, dizer que
nosso sistema esta no estado l;m signi…ca dizer que ele tem momento angular
na direção z igual a ~m e o módulo do vetor momento angular vale ~K.
Remark 32 Qualquer outra tentativa para especi…car melhor o valor do vetor
L irá destruir as informações obtidas anteriormente.
Uma visão clássica para o nosso sistema (que ajuda a desenvolver alguns
raciocínios) é que, após uma medida de L3 e L2
o vetor momento angular está
precessionando em torno do eixo z. Mas este imagem não deve ser levada
tão à sério. O resultado mais preciso, mas que é difícil de visualizar, é que,
após a medida de L3, nosso sistema está numa superposição de todos os valores
possíveis de Lx e Ly, compatíveis com o valor de L2
.
10.1 Autovalores e autovetores do momento angular
Vamos agora discutir os possíveis valores dos autovalores e a forma dos autove-
tores de ^L3 e ^L2. Estes operadores são, obviamente, operadores diferenciais e a
obtenção destas quantidades representa a resolução do problema de autovalores
para estas equações. Entretanto, no lugar de resolvermos diretamente estas
equações, podemos usar um método completamente análogo ao desenvolvido
para resolver o problema do oscilador harmônico. Neste caso, introduzamos os
operadores
^L+ = ^L1 + i^L2 :
^L = ^L1 i^L2 = ^L+
+
:
Estes operadores fazem às vezes de ^a e ^a+
neste problema e obedecem as
seguintes regras de comutação
h
^L3; ^L+
i
= ~^L+
h
^L3; ^L
i
= ~^L
[L+; L ] = 2~L3
h
^L2
; ^L
i
= 0
120

121. Exercise 33 Veri…que as leis de comutação acima
Assim como …zemos no caso do OH, imagine que você encontrou um autove-
tor m do operador ^L3
^L3 m = ~m m :
Usando as regras de comutação acima é possível mostrar que
^L3
^L+ m = ~ (m + 1) ^L+ m
^L3
^L m = ~ (m 1) ^L m
Ou seja, o operador ^L+ (^L ) permite construir um novo autovetor com o auto-
valor aumentado (diminuído) de uma unidade. Por isso este operador é chamado
de operador de levantamento (abaixamento).
Exercise 34 Veri…que as igualdades acima.
Uma vez que ^L2
comuta com ^L3, podemos esperar que o autovetor m acima
seja também autovetor de ^L2
^L2
m = ~2
K2
m :
Além disso, como
h
^L ; ^L2
i
temos
^L2
(L m) = L ^L2
m = L ~2
K2
m = ~2
K2
(L m)
Ou seja, os autovetores construídos acima são também autovetores de ^L2
como
o mesmo autovalor. Assim, os operadores ^L abaixam e levantam a projeção
do momento angular no eixo z sem mudar o valor do módulo do vetor.
Fazer desenho
Assim como ^H do OH, o operador ^L2
é positivo de…nido, com isso,
D
^L2
E
m
0 ) K2
0 :
Além disso, temos
D
^L2
E
m
=
D
^L2
1
E
m
+
D
^L2
2
E
m
+
D
^L2
3
E
m
=
D
^L2
1
E
m
+
D
^L2
2
E
m
+ ~2
m2
;
ou seja
jKj jmj ) K < m < K
Que obviamente signi…ca apenas que o módulo de um vetor é maior ou igual
qualquer uma de suas componentes.
Entretanto, o fato de podermos sempre aumentar o valor da projeção com
o operador ^L+ leva a uma contradição com a igualdade acima (assim como no
121

122. caso da energia mínima do OH). Por isso, se mmax K é o maior valor possível
para a projeção do momento angular na direção z, devemos exigir que
^L+ mmax = 0 : (89)
Pela mesma razão
^L mmin = 0 : (90)
O operador ^L2
pode ser escrito como
^L2
= ^L2
1 + ^L2
2 + ^L2
3
= ^L ^L+ + ^L2
3 + ~^L3
= ^L+
^L + ^L2
3 ~^L3
Exercise 35 Veri…que as igualdades acima.
Usando a relação acima, podemos escrever (89) como
^L2
mmax = ~2
K2
= ^L ^L+ + ^L2
3 + ~^L3 mmax
= ^L2
3 + ~^L3 mmax = ~2
m2
max + ~2
mmax mmax
ou seja
K2
= mmax (mmax + 1)
Da mesma forma
K2
= mmin (mmin 1)
Com isso
mmax (mmax + 1) = mmin (mmin 1)
m2
max + mmax = m2
min mmin
que implica
mmax = mmin
Ou seja, os valores possíveis de m variam de uma em uma unidade e
se distribuem simetricamente em torno de 0.
A simetria da distribuição acima, nos mostra que temos apenas duas possi-
bilidades para os valores de mmax
mmax = inteiro ) m = f mmax; mmax + 1; ::; 0; ::; mmaxg
mmax = semi-inteiro ) m = f mmax; mmax + 1; ::; mmaxg
no segundo caso m 6= 0. Qualquer outro valor de mmax não teria a simetria
necessária para que mmax = mmin.
Os dois tipos de valores para mmax caracterizam os dois tipos diferentes de
momento angular mencionados anteriormente. Para mmax um semi-inteiro, ^L
é um momento angular intrínseco, i.e., um spin (e.g., férmions tem spin 1=2).
122

123. Como veremos mais pra frente, para o caso do momento angular orbital, nec-
essariamente devemos ter mmax inteiro8
.
Vamos chamar
l mmax = mmin
Ou seja, os valores de m variam de uma em uma unidade desde l até l. Com
a de…nição acima temos
K2
= mmax (mmax + 1) = l (l + 1)
Ou seja, os autovalores deL3 e ^L2
são
^L2
m;l = ~2
l (l + 1) m;l ; l = 0; 1; 3:::
^L3 m;l = ~m m;l ; m = l; l + 1; :::; 0; :::; l
Para cada valor de m temos 2l + 1 valores de m.
Por razões que se tornarão claras futuramente, l é chamado de número quân-
tico orbital, enquanto m é chamado de número quântico azimutal (ou número
quântico magnético).
Vemos que o valor máximo da projeção é sempre menor que o módulo do
vetor, ou seja, o vetor nunca está projetado inteiramente no eixo z. Se
isso fosse possível, teríamos um estado com L3 bem de…nido e com L1 = L2 = 0,
ou seja, haveria um estado em que conheceríamos as 3 componentes do momento
angular.
Observe que a MQ nos diz que as partículas podem ter apenas valores inteiros
e semi-inteiros de l. Desta forma, temos 3 casos distintos:
1. o momento angular orbital, com l inteiro;
2. o momento angular intrínseco (spin) com l inteiro e semi-inteiro. No que
se refere ao spin,
(a) partículas com spin inteiro são chamados de bósons e
(b) partículas com spin semi-inteiro são chamados de férmions.
Esta característica pode ser observada num experimento de EG.
Da mesma forma como no caso do OH, temos agora uma equação diferencial
mais simples pra resolver
^L+ l;l = 0
Uma vez obtida esta solução, podemos construir as demais soluções baixando o
auto-valor de m
l;l 1 = ^L l;l
e assim até l; l onde, obviamente
^L l; l = 0 :
8 Não estamos a…rmando que mmax inteiro não pode ser um valor de spin, mas apenas que
o momento angular orbital tem, obrigatoriamente, um valor inteiro de mmax.
123

124. Para resolver este problema o ideal é trabalhamos em coordenadas esféricas
x = r sin cos
y = r sin sin
z = r cos
Nestas coordenadas temos
^L = ^Lx + i^Ly = ~e i
i cot
@
@
@
@
^L2
=
1
sin
@
@
sin
@
@
+
1
sin2
@2
@ 2
(91)
Em especial, o operador ^L3 assume uma forma bem simples
^L3 = i~
@
@
:
Assim, as funções procuradas obedecem a equação (fazendo l;m = Y m
l )
^L3Y m
l = imY m
l ;
Y m
l = Y m
l ( ; )
fazendo uma separação de variáveis
Y m
l ( ; ) = m ( ) m
l ( )
temos
^L3Y m
l = imY m
l ) m ( ) =
1
p
2
exp (im ) :
Onde o fator 1=
p
2 é, obviamente, a normalização.
Observe que a condição de unicidade da solução exige que
m ( ) = m ( + 2 ) ) eim2
= 1 ) m = 0; 1; 2; ::
Ou seja, m deve ser inteiro. Como a…rmamos para o caso do momento
angular orbital.
Assim, nossas soluções têm a forma
Y m
l ( ; ) =
1
p
2
m
l ( ) exp (im ) ; m 2 Z :
Voltando agora para a nossa equação
^L+Y l
l = 0 ) ~ei
i cot
@
@
+
@
@
1
p
2
l
l ( ) exp (il ) = 0
ou seja
@
@
l
l ( ) = l cot l
l ( )
124

125. que possui a solução
l
l ( ) = Nl sinl
) Y l
l ( ) =
Nl
p
2
exp (im ) sinl
onde Nl é uma normalização. As demais soluções são obtidas pela aplicação do
operador ^L
Y l m
l ( ; ) = ^L
m
Y l
l ( ; ) = Nl m ~e i
i cot
@
@
@
@
m
sinl
; m 2l
As funções Y l m
l assim construídas, e devidamente normalizadas, são chamadas
de harmônicos esféricos. Com isso
^L2
Y m
l = ~2
l (l + 1) Y m
l ; l 2 N:::
^L3Y m
l = ~mY m
l ; m = l; l + 1; :::; 0; :::; l
hY m
l Y m0
l0 i =
Z
Y m
l ( ; ) Y m0
l0 ( ; ) d d = mm0
ll0
Os harmônicos esféricos são funções tabeladas e também podem ser escritos
como
Y m
l ( ; ) =
2l + 1
4
(l m)!
(l + m)!
1=2
Pm
l (cos ) eim
onde
Pm
l ( ) = ( 1)
m
1 2 m=2 dm
Pl ( )
d m
Pl ( ) =
1
2ll!
dl
d l
2
1
l
onde Pl são conhecidos como os polinômios de Legendre e Pm
l os polinômios
associados de Legendre.
10.2 O átomo de hidrogênio
Partindo do hamiltoniano da partícula livre
H =
~2
2m
r2
e escrevendo o laplaciano em coordenadas esféricas temos
H =
^p2
r
2m
+
^L2
2mr2
com
^pr =
1
r
@
@r
r
^L2
=
1
sin
@
@
sin
@
@
+
1
sin2
@2
@ 2
125

126. onde ^L2
é o operador de momento angular introduzido anteriormente (91) e ^pr é
chamado de momento radial. Assim, para o caso de um potencial que dependa
apenas da coordenada radial, i.e., um potencial central, temos que o operador
hamiltoniano se torna
^H =
^p2
r
2m
+
^L2
2mr2
+ V (r)
Para o caso de um sistema ligado de um próton e um elétron (i.e., um átomo
de hidrogênio) temos que o potencial do elétron devido ao próton vale
V (r) =
e2
r
com o que nosso hamiltoniano …ca
^H =
^p2
r
2m
+
^L2
2mr2
e2
r
Remark 36 Lembre que, na verdade, sendo um sistema de dois corpos, deve-
mos usar a massa reduzida
=
memp
me + mp
' me ;
reveja o capítulo sobre o átomo de Bohr.
Assim, na teoria de Schroedinger, o problema dos estados estacionário (es-
tados com energia de…nida) do átomo de hidrogênio, consiste em encontrar os
autoestados do operador acima
^H = jEj :
Além disso, como estamos interessados em estados ligados, estamos interessados
no caso E < 0 (pois, como no problema usual do potencial acima, estamos
colocando o zero de energia no in…nito).
O problema acima pode ser facilitado usando, novamente, uma separação de
variáveis. Entretanto, observe que
h
^H; ^L2
i
=
h
^H; ^L3
i
= 0 ;
ou seja, podemos procurar por autofunções simultâneas de ^H; ^L2
e ^L3 (ou ainda,
podemos medir simultaneamente ^H; ^L2
e ^L3). Com isso, vamos procurar as
nossas soluções na forma
= R (r) Y m
l ( ; ) :
Substituindo a solução na forma acima na ES temos:
~2
2m
1
r
d2
dr2
r +
~2
l (l + 1)
2mr2
e2
r
+ jEj R (r) = 0
126

127. Esta equação pode ser simpli…cada fazendo
u rR
com o que
d2
dr2
r +
l (l + 1)
r2
2me2
~2r
+
2m jEj
~2
u (r) = 0
que pode ser colocada numa forma ainda mais simples através das variáveis
2 r ;
~2 2
2m
= jEj ; =
RH
jEj
RH =
~2
2ma2
0
; a0 =
~2
me2
onde RH é a constante de Rydberg e a0 o raio de Bohr introduzidos na seção
sobre o átomo de Bohr. Nestas novas variáveis temos
d2
u
d 2
l (l + 1)
2
u +
1
4
u = 0
Nosso trabalho se resume, obviamente, em resolver a equação diferencial acima.
Assim como nos casos anterior existem técnicas especí…cas para encontrar a
solução desta equação. Após a aplicação destas técnicas, as soluções do prob-
lema acima podem ser escritos como:
un;l ( ) =
2
exp
2
l+1
Fnl ( )
onde
Fnl ( ) =
n l 1X
i=0
( 1)
i
[(n + l)!]
2 i
i! (n l 1 i)! (2l + 1 + i)!
; n 2 N
são os polinômios associados de Laguerre. Para que estas funções sejam de
quadrado integrável, devemos ter9
n l 1 0 ) l n 1 ) l < n
Assim, a solução do problema do átomo de hidrogênio pode ser escrito como
n;l;m (r; ; ) = Rn;l (r) Y m
l ( ; ) ;
Rn;l (r) =
1
r
un;l ( ) ; 2 r
un;l ( ) = exp
2
l+1
Fnl ( ) :
9 Podemos de…nir os polinômios acima para valores negativos do fatorial usando a função
. Entretanto, ( m)) = 1 para m inteiro positivo.
127

128. com os autovalores
En =
RH
n2
que são exatamente os mesmos obtidos pela quantização de Bohr.
A solução da parte radial do problema (como era de se esperar) introduziu
o novo número quântico n nas nossas soluções. Chamado de número quântico
principal.
Remark 37 A energia depende apenas do número quântico principal.
As restrições acima impõem
l < n :
e as restrições obtidas anteriormente
jmj < l :
Assim, para um dado valor de l temos 2l + 1 estados e, para um dado valor de
n temos n2
estados com a mesma energia.
Na notação usada em química, os valores de n rotulam os chamados orbitais.
Os valores de l são chamados, em seqüência, s; p; d etc. E para cada um destes
valores, temos m = 2l + 1 estados distintos.
1s1
2s1
2p3
3s1
3p3
3d5
...
A descrição completa dos orbitais atômicos depende ainda de uma carac-
terística negligenciada até aqui: o spin do elétron. Esta quantidade faz com
que cada estado possa existir em dois estados distintos de spin. Ou seja, o
número de estados de cada orbital é dobrado.
1s2
2s2
2p6
3s2
3p6
3d10
...
Além disso, a estrutura da distribuição eletrônica, bem como a estabilidade de
toda a matéria conhecida, depende diretamente da in‡uência do spin nestes
níveis eletrônicos. Ou seja, é impossível compreender a distribuição eletrônica
(em especial a tabela periódica) sem tomar em conta o spin do elétron.
Mas isso é uma outra história...
128