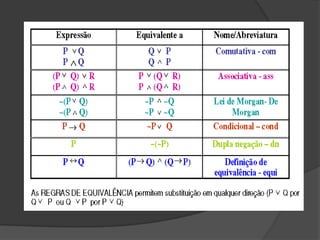
Este documento discute lógica proposicional e métodos dedutivos para provar validade de argumentos. Ele introduz representação simbólica de proposições e argumentos, regras de equivalência e inferência para lógica proposicional, e como usar suposição para provar conclusões de argumentos na forma R → S.

1. MATEMÁTICA COMPUTACIONAL
PROFESSOR: ARISTÓTELES MENESES LIMA
CURSO: ANÁLISE E DESENVOLVIMENTO DE
SISTEMAS
PERÍODO: 1º

2. Fórmula bem formulada -
fbf


3. 

4. Lógica Proposicional
 Usamos a notação da lógica formal para
representar proposições em forma simbólica
como fbf.
 O sistema formal que usa proposicionais é
chamado de lógica proposicional, ou lógica
declarativa, ou cálculo proposicional.

5. “Se meu cliente fosse culpado, a faca estaria
na gaveta. Ou a faca não estava na gaveta
ou Jason viu a faca. Se a faca não estava lá
no dia 10 de outubro, segue que Jason não
viu a faca. Além disso, se a faca estava lá no
dia 10 de outubro, então a faca estava na
gaveta e o martelo estava no celeiro. Mas
todos sabemos que o martelo não estava no
celeiro. Portanto, senhores e senhoras do
júri, meu cliente é inocente.”

6. Argumentos válidos
 Um argumento pode ser representado
em forma simbólica como:
 Rrr
 Onde são proposições dadas
chamadas de hipóteses do argumento,
e Q é a conclusão do argumento.

7. Exemplo 1:
Considere o seguinte argumento:
 Esse argumento tem duas hipóteses, e a conclusão é
que “todo dia tem 24 horas”.
 Embora cada hipótese individual, assim como a
conclusão, seja uma proposição verdadeira, não
deveríamos considerar esse argumento válido. A
conclusão é meramente um fato verdadeiro isolado, que
não está relacionado com as hipóteses.
 Portanto, para que um argumento seja válido, ele deve
ser “intrinsecamente verdadeiro”.
 Logo, um argumento é válido quando for uma tautologia.

8.  O exemplo anterior pode ser
representado da seguinte forma:
 O que evidentemente não é uma
tautologia.

9. Regras de Dedução para a
lógica Proposicional
As regras são de dois tipos:
 Equivalências
 Inferências
1 – Regras de equivalências: permitem que
fbs individuais sejam reescritas mantendo o
mesmo valor lógico. Uma fbf verdadeira
continua verdadeira se for feita uma dessas
substituições em um de seus componentes.
A tabela a seguir nos fornece uma lista de
regras de equivalências que usaremos em
nosso sistema de lógica porposicional.

11. 2 – Regras de inferência: Permitem a dedução de
novas fbfs a partir de fbfs anteriores na sequencia de
demonstração. Assim como as regras de
equivalência, também preservam os valores lógicos.

12. Exemplo 1:
Usando a lógica proposicional, prove que
o argumento abaixo é válido.

14. Métodos Dedutivos
 Supondo que o argumento que
queremos provar tenha a forma:
 Onde a conclusão é uma implicação.
 O método dedutivo nos permite
adicionar R como uma hipótese e
depois inferir S. Em outras palavras,
podemos provar

15. 

16. 

17. 

18. 

19. 