O documento discute quantificadores, predicados e validade em lógica matemática. Explica que quantificadores como "para todo" e "para algum" se referem a propriedades de objetos. Predicados descrevem essas propriedades. A validade de uma expressão lógica depende se é verdadeira sob todas as interpretações possíveis dos quantificadores e predicados.

1. Quantificadores, Predicados e
Validade
Matemática Computacional
Prof. Aristóteles Meneses
Análise e Desenvolvimento de Sistemas

2. Quantificadores, Predicados e Validade
• Quantificadores: são frases do tipo “para
todo”, ou “para cada”, ou “para algum”, isso
é, frases que dizem quantos objetos, em algum
sentido, tem uma determinada propriedade. O
quantificador universal é simbolizado por ∀
, e se lê ”para todo”, “para qualquer” ou “para
cada”.
• Predicados: é a propriedade de uma
determinada sentença. A notação é P (x).

3. • Observe a sentença: “Para todo x, x > 0”
• Essa é uma proposição verdadeira sobre os
inteiros positivos.
• Ela contém o quantificador - Para todo x , e o
predicado é x > 0. Logo a sentença acima pode
ser simbolizada por:
• (∀ x )(x > 0), mas como x > 0 é o
predicado, podemos colocar ainda numa forma
mais geral:
• (∀ x )(Px)

4. • O Valor lógico dessa expressão depende do domínio
dos objetos sobre os quais estamos nos
referindo, isso é, a coleção de objetos dentre os quais
x pode ser escolhido. Essa coleção se chama
domínio de interpretação, ou conjunto
universo.
• Exemplo 1:
• Se o conjunto universo consiste em todos os livros
em sua biblioteca municipal.
• Se (Px) é a propriedade de x ter a capa vermelha.
• Logo (∀ x )(Px) diz que:” todos os livros em sua
biblioteca municipal têm capa vermelha”.
• É claro que o valor lógico dessa expressão, com essa
interpretação, deve ser falso.

5. • Exemplos 2:
• Qual o valor lógico da expressão (∀ x )(Px) nas duas
interpretações:
• A)(Px) é a propriedade que x é amarelo e o conjunto
universo é o conjunto de todos os botões de ouro.
(verdadeira)
• B) (Px) é a propriedade que x é amarelo e o
conjunto universo é o conjunto de todas as flores.
(falsa)

6. • Quantificador existencial: é simbolizado por ∃
, e se lê “existe”, “há pelo menos um”, “existe algum”
ou “para algum”.
• Exemplo 3:
• Se o conjunto universo consiste em todos os livros
em sua biblioteca municipal.
• Se (Px) é a propriedade de x ter a capa vermelha.
• Logo (∃ x )(Px) diz que: „em sua biblioteca
municipal tem pelo menos um livro de capa
vermelha‟.
É claro que o valor lógico dessa expressão, com essa
interpretação, deve ser verdadeiro.

7. • Os predicados que vimos envolvem
propriedades de uma única variável, são os
predicados unários. Mas eles podem ser
binários, se envolvem duas
variáveis, ternários, envolvendo propriedades
de três variáveis e assim por diante.
• Exemplo: Na expressão: (∀ x) (∃ y) Q(x,y) que
é lida como “para todo x existe um y tal que
Q(x,y)”, há dois predicados para as duas
variáveis da propriedade binária.
ATENÇÂO: a ordem dos quantificadores é muito
importante, ela altera a interpretação.

8. • O QUE É NECESSÁRIO PARA UMA
INTERPRETAÇÃO:
• 1º) Uma coleção de objetos, chamada de conjunto
universo, que precisa incluir pelo menos um objeto.
• 2º) A especificação de uma propriedade dos objetos
no domínio para cada predicado na expressão.
• 3º) A atribuição de um objeto particular no conjunto
universo para cada símbolo constante na expressão.

9. • “SÍMBOLOS DE AGRUPAMENTO”, como parênteses ou
colchetes, identificam o escopo de um quantificador, a
parte da fbf à qual o quantificador se aplica.
• Exemplo 4:
• 1) P (x) v Q (x) não tem quantificadores
• 2) (∀ x)[P ( x) →Q( x)] o escopo do quantificador é P(x)
→ Q(x)
• 3) (∀ x)((∃ y)[ P ( x, y) ∧ Q( x, y)] →R( x)) o escopo de
(∃y ) é P(x,y)∧ Q( x,y),e o escopo de (∀ x) é a expressão
inteira entre parênteses.
• 4) (∃x ) S ( x ) ∨ (∀y) T(y ) o escopo de (∃x ) é S(x) e o
escopo de (∀ y) é T(y).

10. • Exemplo 5:
• Na fbf (∀ x )(∃y )[ S ( x , y ) ∧L ( y , a )]
• Considere a interpretação onde o conjunto
universo consiste em todas as cidades do Brasil,
• S(x,y) é a propriedade “x e y estão no mesmo
estado”
• L(y,z) é a propriedade “o nome da cidade y
começa com a mesma letra que a cidade z”e é
atribuído o valor Alfenas a a.
• Logo a interpretação da fbf inteira é que “para
qualquer cidade x existe uma cidade no mesmo
estado que começa com a letra A”. Com essa
interpretação, a fbf é verdadeira.

11. TRADUÇÃO
• Muitas declarações em português podem ser
expressas como fbfs predicadas.
• Exemplo:
• “Todo papagaio é feio”
• Significa, de fato, que “Dada uma coisa, se é um
papagaio, então é feio”.
• Denotando por P(x) a frase “x é um papagaio” e por
F(x) “x é feio”, a proposição pode ser simbolizada
como:
• (∀ x) [P(x) → F(x)]
• A fbf (∀ x) [P(x) ∧ F(x)] seria uma tradução
incorreta, pois diz que “Dado x, x é papagaio e é
feio”.

12. • ATENÇÃO: ∀ e → estão quase sempre
juntos.
Analogamente, “Existe um papagaio feio”
Significa que “Existe alguma coisa que é, ao mesmo
tempo, papagaio e feio”.
Simbolizando:
(∃ x) [P(x) ∧ F(x)]
ATENÇÃO: ∃ e ∧ estão quase sempre juntos.
Os advérbios “só”, “somente” e “apenas” são
particularmente problemáticos, pois sua colocação
em uma sentença pode alterar completamente o
significado.

13. Observe as três sentenças Elas podem ser reescritas como:
abaixo:
João ama apenas Maria Se João ama alguma coisa, então essa
coisa é Maria.
Apenas João ama Maria Se alguma coisa ama Maria, então essa
coisa é João.
João apenas ama Maria Se João tem alguma relação com
Maria, essa relação é amor.
Dados:
A(x) é “x é um cachorro”
B(y) é “y é um coelho”
C(x) é “x persegue y”
Observe a tabela abaixo:

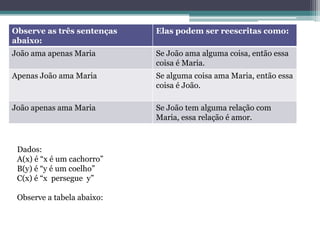
14. Declaração em Proposição Fbf
Português intermediária
1. Todos os cachorros Dada uma coisa qualquer, (∀ x)[A( x) → (∀ y) (B( y)
perseguem todos os se → C ( x, y))
coelhos. for um cachorro, então,
para qualquer outra coisa,
se essa outra coisa for um
coelho, então o cachorro
vai persegui-lo.
2. Alguns cachorros Existe uma coisa que é um (∃ x)[A( x) ∧ (∀ y) (B( y)
perseguem todos os cachorro e, para qualquer → C ( x, y))]
coelhos. outra coisa, se essa coisa é
um coelho, então o
cachorro o persegue.
3. Apenas cachorros Para qualquer coisa, se é (∀ y)[B( y) → (∀ x)
(C( x, y) → A( x))
perseguem coelhos um coelho, então, se
alguma coisa o persegue,
essa coisa é um cachorro.
A(x) é “x é um cachorro” B(y) é “y é um coelho” C(x) é “x persegue y”

15. Validade
• O valor lógico de uma fbf proposicional depende
dos valores lógicos atribuídos às letras de
proposição. O valor lógico de uma fbf predicada
depende da interpretação. Portanto, escolher uma
interpretação para uma fbf predicada é análogo a
escolher valores lógicos para um fbf proposicional.
• Uma fbf predicada é válida se ela é verdadeira
para todas as interpretações possíveis.
• Se pudermos encontrar uma única interpretação
de modo que a fbf tenha o valor falso ou não tenha
valor lógico, então a fbf não é válida.
• Não existe algoritmo para determinar se uma fbf
predicada é válida.

16. Exemplos: Vamos agora tentar
determinar a validade:
• 1. (∀ x ) P ( x ) →(∃ x ) P ( x ) (é válida)
Se todo elemento do conjunto universo tem uma
determinada propriedade, então existe um
elemento do conjunto que tem essa
propriedade. Logo sempre que o antecedente
for verdadeiro o consequente também o é, o
condicional é verdadeiro.
• 2. (∀ x ) P ( x ) →P ( a )(é válida)

17. Como todo elemento do conjunto universo tem uma
determinada propriedade, e a é um elemento particular do
conjunto universo, portanto ele tem a propriedade que todos os
elementos têm.
• 3. (∀ x )[ P ( x ) ∧Q ( x )] ↔(∀ x ) P ( x ) ∧(∀ x ) Q ( x )(é
válida)
Se P e Q forem verdadeiras para todos os elementos do
domínio, então P é verdadeira para todos os elementos e Q é
verdadeira para todos os elementos, e vice-versa.
( ↔ ; V V = V ou F F = V)
• 4. (∃x ) P ( x ) →(∀ x ) P ( x )(não é válida)
Por exemplo, como a interpretação onde o domínio é o
conjunto dos inteiros e P(x) significa que x é par, é verdade que
existe um inteiro par, mas é falso que todos os inteiros são
pares. O antecedente do condicional é verdadeiro e o
conseqüente é falso. Logo o condicional é falso.
(→ ;VF=F)