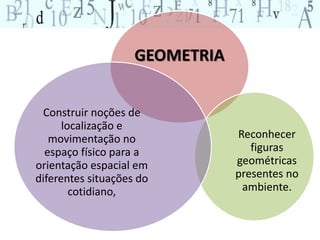
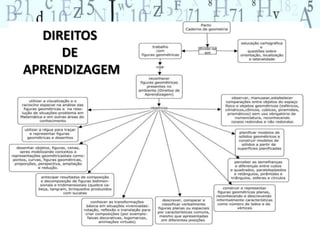
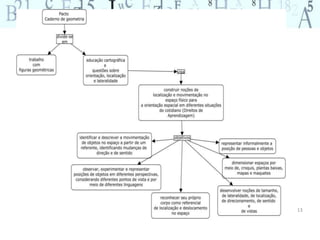
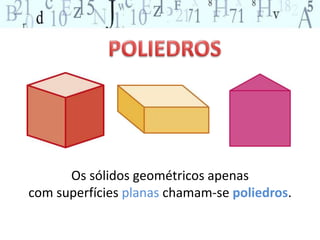
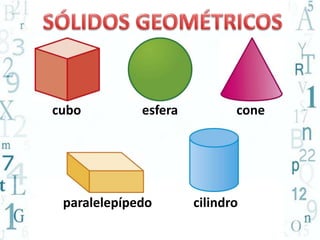
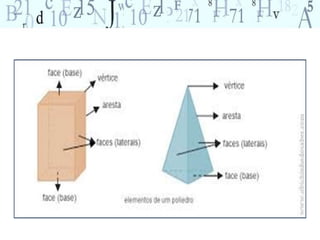
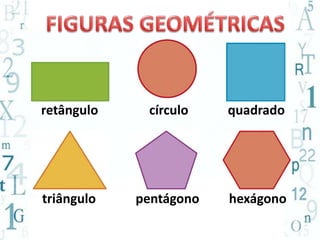
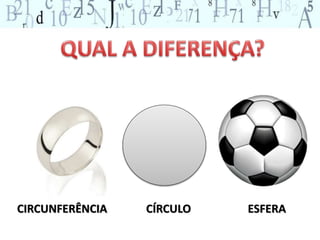
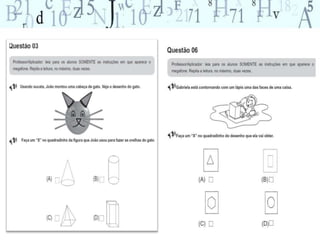
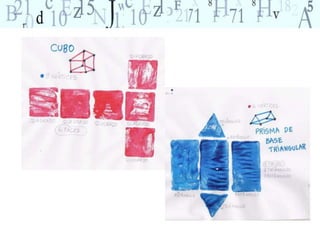
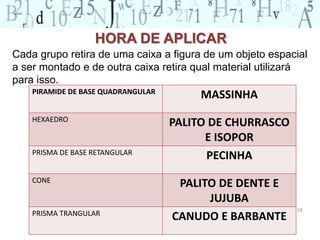
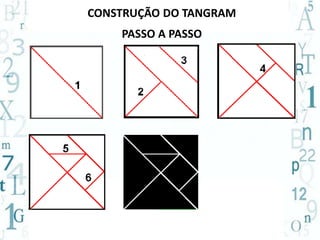
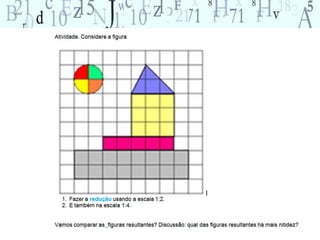
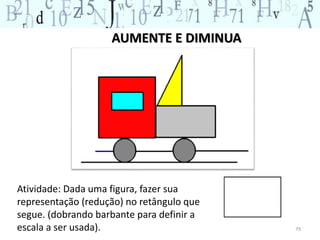
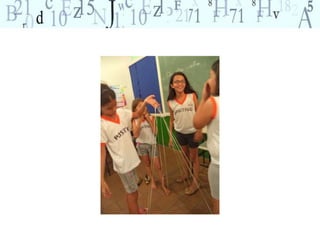O documento aborda a importância do ensino de geometria na educação, destacando suas aplicações práticas e como ela pode motivar alunos com dificuldades em matemática. Sugere atividades interativas e de exploração que envolvem a manipulação de objetos geométricos, além de discussões sobre sua relevância no cotidiano. Por fim, enfatiza a necessidade de uma abordagem que conecte figuras planas e sólidas, promovendo um ensino mais dinâmico e eficaz.

1. Orientadora Aline Manzini
PNAIC – Bertioga
Outubro/2014

2. LEITURA DE DELEITE
INTERATIVA
As três formas. Edson Luiz Kosminski
Cada dupla receberá as três partes que fazem parte dessa história...
Vamos ver quem acertará a imagem que deve formar!

5. DESAFIO MATEMÁTICO
Monte figuras utilizando palito de dente
observando as comandas:

6. QUER RACHAR UM POUCO MAIS A CUCA?
Acesse:
Jogo Online: Palitos ao quadrado
http://rachacuca.com.br/jogos/palitos-ao-quadrado/
Diversos desafios
http://rachacuca.com.br/jogos/palitos/

7. Geometria e suas aplicabilidades
em sala de aula

8. 1- O que é geometria para você?
2- A professora do vídeo afirma que o conteúdo de
geometria sempre é o ultimo do ano. Esta verdade se
aplica as suas aulas?
3- Qual a importância deste conteúdo para a vida
pratica do aluno?
4- Pensando em todos os conteúdos destinados ao 1º
ou 2º ano, defina numa escala de 0 a 10 a importância
do conteúdo de geometria. Justifique sua resposta.
5- Alguma vez você já realizou um projeto em que o
foco estivesse na geometria? Se sim, conte-nos
resumidamente seus objetivos e atividades. Se não, por
que nunca utilizou este conteúdo como norteador de
um projeto?

9. Geometria no
cotidiano
VIDEO
http://www.youtube.com/watch?v=_7yXoZnSTBM

10. O que significa Geometria?
Resulta de dois termos gregos:
Geo significa terra
Metriasignifica medir

11. GEOMETRIA
Reconhecer
figuras
geométricas
presentes no
ambiente.
Construir noções de
localização e
movimentação no
espaço físico para a
orientação espacial em
diferentes situações do
cotidiano,

12. 12
DIREITOS
DE
APRENDIZAGEM

13. 13

14. A Geometria e
o Ciclo de Alfabetização
Caderno 5 das páginas 5 a 9

15. Por que ensiná-la?
A Geometria inclui um valor intrínseco, sua estrutura
com uma lógica específica que lhe permite articular a
evidência visual com a exatidão do seu método.
Podemos, também, falar num valor estético, que se
traduz em sensibilidade para contemplar obras de arte, que
recorrem a motivos geométricos, peças de design,
arquitetura e elementos geométricos específicos e
monumentos.
Se pensarmos ainda na Geometria como currículo,
podemos considerar também o valor motivação. A
experiência mostra que os alunos que revelam mais
dificuldades na aprendizagem da Matemática, por vezes,
melhoram o seu desempenho quando se envolvem em
atividades de natureza geométrica.

16. O QUE ENSINAR?
No nosso dia-a-dia, somos confrontados com inúmeras
situações que envolvem a mobilização de capacidades e ideias
geométricas.
Ao tentarmos decifrar a informação de um manual de
instruções, ao analisarmos a planta de uma casa, ao interpretarmos
um mapa, ou mesmo ao explicarmos um caminho a alguém,
estamos usando nossa orientação espacial. Para lidar com esta
diversidade de situações, temos de recorrer às nossas capacidades
de visualização, quer no espaço quer no plano.
Existem, também, fenômenos da realidade cuja explicação
tem características geométricas. Pensemos, por exemplo, nos
motivos pelos quais a nossa sombra às vezes é “maior” e em outras
“pequena”, nas razões porque se fazem determinadas dobragens
em cartões de modo a construir caixas dentre tantas outras coisas.

17. DIVERSAS GEOMETRIAS

18. DE QUE MANEIRA ENSINAR?
Os exemplos referidos realçam o valor prático da
Geometria, dado que a “utilizamos” diariamente
quer para resolver problemas quer para
justificar fenômenos da vida real.
Para entendê-la então é necessário:
CONJECTURAR EXPERIMENTAR VALIDAR

19. CONJECTURAR
 Ato ou efeito de inferir ou deduzir que algo é provável, com base em
presunções, evidências incompletas, pressentimentos, hipóteses e
suposições.
 A orientação é que as crianças não realizem
demonstrações formais, mas que sejam
estimuladas a elaborar conjecturas a partir
de observações e experimentos.

20. EXPERIMENTAR
Pôr à prova, tentar, procurar
Após levantarem conjecturas, vem a fase
de experimentação, ou seja, de pôr à
prova o que conjecturaram.
Observar, medir, desenhar, estimar,
montar, desmontar, generalizar...

21. VALIDAR
Tornar ou declarar válido; legitimar.
Entre outros aspectos relevantes do
pensamento geométrico para VALIDAR ou
não suas conjecturas é elaborar
argumentações sobre os resultados.

22. Conjectura: Dados três segmentos é sempre
possível formar um triangulo?
Experimentação
Validar: Para construirmos um triangulo é
necessário que a medida de qualquer um dos
lados seja menor que a soma das outras duas
medidas.
22
Um exemplo:

23. Eu ouço e eu esqueço
Eu vejo e eu lembro
Eu faço e eu entendo.
Provérbio chinês

24. INICIAR POR FIGURAS
PLANAS OU SÓLIDOS?
• Em nosso dia a dia vemos isto...
• Ou isto?

25. FAZEM UM LINK COM LINGUA
PORTUGUESA...
Iniciar o ensino da geometria pelas figuras
planas é como iniciar a alfabetização
linguística pelas letras e só meses mais
tarde apresentar as palavras?!

26. ETAPAS DO TRABALHO COM AS FORMAS
LIVRO A ESCOLA É NOSSA
Figuras geométricas espaciais (reais)
Figuras geométricas espaciais (representação)
Figuras geométricas espaciais (caracterização- rola, não rola)
Figuras geométricas espaciais (vistas)
Figuras geométricas espaciais (caracterização- quadrado,
retângulo)
Figuras geométricas planas (reconhecimento nos objetos
reais)
Figuras geométricas planas (representação)

27. PROPOSTAS DE
ATIVIDADE COM OS
SÓLIDOS GEOMÉTRICOS.

28. Manipulando objetos
• Proponha aos alunos que traga para a sala de
aula caixinhas, latinhas, blocos de madeira ou
plástico, etc das mais variadas formas e
tamanhos.
• Eles exploram livremente
os objetos, fazem torres,
carrinhos, robôs,
castelos, casas, túneis, etc.

29. Em seguida, classificarão livremente os objetos:
• Por tamanho (grande, pequeno, médio);
• Pelo tipo de material (madeira, papelão, lata);
• Pela cor (verde, amarelo, azul);

30. • Proponha uma nova
classificação: pergunte as
crianças quais objetos elas
acreditam que rolam ou rodam
dos que não rolam ou não
rodam.
• Após várias tentativas (até
mesmo jogando os objetos no
chão) com erros e acertos, é
provável que vençam o desafio,
separando os que rolam (tem
partes curvas, redondas) dos
que não rolam (têm partes
“chatas”).

31. Essa classificação é muito importante do
ponto de vista matemático, pois prepara para
uma classificação mais rigorosa: a de corpos
redondos e não redondos.
VAMOS ENTÃO RELEMBRAR:

32. Os sólidos geométricos apenas
com superfícies planas chamam-se poliedros.

33. cubo esfera
paralelepípedo
cone
cilindro

34. Os sólidos geométricos com uma ou mais
superfície curvas chamam-se não poliedros.

36. As figuras limitadas por linhas
retas são polígonos.
Repara nos exemplos.

37. As figuras limitadas só por uma linha
curva ou por linhas retas e curvas
chamam-se não polígonos.
Repara nos exemplos.

38. retângulo círculo quadrado
triângulo pentágono hexágono

39. QUADRILÁTEROS
Os polígonos com quatro lados
chamam-se quadriláteros.

40. CIRCUNFERÊNCIA CÍRCULO ESFERA

41. Círculo, esfera e circunferência
• Pegue uma bola e um circulo recortado em cartolina.
Escolha uma mesa cuja tampa seja bem plana e coloque a
bola e o circulo.
• O que você observa? Ambos ficaram totalmente
encostados na superfície?
• Você deve ter notado que o circulo ficou todo encostado,
enquanto a bola não. O circulo é uma figura plana que tem
um centro e uma circunferência. A esfera é cheinha, tem
volume, é um sólido geométrico.
• Circunferência é a linha que contorna todo o circulo, é a sua
borda(anéis e arcos).
Construa duas esferas com massa de modelar. Amasse uma delas.
Uma virou circulo e outra é uma esfera. Forme o circulo com barbante.
Revista Nova escola

42. 42

44. Jogo 21 pag 59 do Caderno de jogos
DOMINÓ GEOMÉTRICO
a) Aprendizagem: Estabelecer comparações entre representações
bidimensionais de objetos do espaço físico e representações
bidimensionais de objetos geométricos espaciais.
b) Material: – 21 cartas (peças de dominó)
c) Número de jogadores: 3 ou 4 participantes.
d) Regras:
– As cartas do dominó devem ser embaralhadas e distribuídas igualmente
entre os jogadores. Caso se opte por 4 jogadores, a peça que sobrar
deverá ser colocada sobre a mesa.
– Um dos jogadores inicia a partida, escolhendo uma de suas cartas.
– Os demais colocam as peças de modo a associar corretamente o modelo
geométrico aos objetos.
– Se um jogador não tiver a peça indicada, ele deverá passar a vez.
– Vence o jogador que utilizar primeiro todas as suas cartas.
e) Problematizando:
Em primeiro lugar, é importante reconhecer que este jogo possibilita o
trabalho com representações planas de sólidos geométricos e não
efetivamente com os próprios sólidos. Dessa maneira, a intervenção do
professor é imprescindível no início deste processo.
Isto pode ser efetivado levando-se para a sala diversos sólidos de madeira,
objetos do cotidiano com formas geométricas e suas representações em papel:
44

45. Descubra o objeto
 Através da descrição, descobrir o objeto escondido na
caixa.
Apresentar vários objetos e pedir que as crianças os
observem.
Peça a uma criança, sem que os demais vejam, retirar um
destes objetos e colocar na caixa surpresa.
Cada grupo pode ir fazendo perguntas:
• É arredondado?
• Lado quadrado (Faces)?
• Quantos lados (faces)?
• Como é a parte de baixo (base)?
(podem fazer estas perguntas sem
utilizar termos matemáticos
Complexos)
Os grupos devem desenhar a embalagem e mostrar para ver
se acertaram qual embalagem está na caixa.

46. PLANIFICAÇÃO
PROBLEMATIZAÇÃO
Preciso guardar cada um destes objetos em uma
caixa de presente.
Tenho estas caixas em meu armário:
Em qual delas você colocaria os presentes?
Qual delas tem o mesmo formato dos presentes?

47. Mas tem um grande problema, só tenho uma de
cada e preciso guardar seis batons e seis cubos mágicos.
• O que fazer?
Possivelmente sairão respostas como: Coloca tudo
junto na caixa grande; Embala com papel de presente, dá
dois ou mais para cada um. Enfim, o importante é sempre
dizer que o que é preciso fazer é colocar cada presente
em uma caixa.
• Deixe problematizarem até que se chegue na resposta
que se deseja:
- Faça mais caixas.
- Peça que o ajudem dizendo como podemos fazê-las.
- Permita que cada um possa conjecturar, experimentar
e validar suas hipóteses para a construção das caixas.

48. Sugestões de trabalho com
planificação
Copiar cada face do objeto em questão (de preferencia a
objetos reais e não representação dos mesmos)

49. Carimbar cada face do objeto

51. •Alguns podem desenhar a planificação da caixa, como é mostrado a
seguir:
• Problematizações possíveis: O que está faltando em cada uma das
representações? Se dobrarmos, o que acontecerá, teremos uma
caixa?”
• Outras discussões e reflexões poderão ser levantadas, como:
Quais são as figuras geométricas representadas? Por que a caixa tem
este formato? Ela poderia ter formato diferente?
• Nesse caso a experimentação é uma ação importante para que os
alunos validem as suas ideias e percebam como podem aprimorar as
suas representações.
51

52. Construir para validar
• Apresente algumas representações da caixa-cubo.
• Peça que montem e digam quais fecham a
caixa e em quais não é possível montar a
caixa.

53. Recordar é viver:
E você professor, lembra-se quais são as 11
possíveis representações de um cubo?

54. Respostas:

56. GEOMETRIA VIRTUAL
POLY
http://www2.mat.ufrgs.br/edumatec/softwares/interfaces/poly.jpg

57. Construções com materiais diversos
É comum as crianças imaginarem situações
que incluem a construção de alguma coisa.
Construir, com lego ou outros materiais, uma
casa para um boneco ou uma garagem para um
carro são exemplos de ações que,
possivelmente, já todos nós pudemos observar
nas suas brincadeiras.

58. Cada grupo retira de uma caixa a figura de um objeto espacial
a ser montado e de outra caixa retira qual material utilizará
para isso.
58
HORA DE APLICAR
PIRAMIDE DE BASE QUADRANGULAR MASSINHA
HEXAEDRO PALITO DE CHURRASCO
E ISOPOR
PRISMA DE BASE RETANGULAR PECINHA
CONE PALITO DE DENTE E
JUJUBA
PRISMA TRANGULAR CANUDO E BARBANTE

60. Ao girar o palito rapidamente obtém-se
o formato espacial da mesma.

61. GEOPLANO 3D

62. Montagem - Poliedros

63. Animais e
as formas

64. Montagem de sólidos com
papel cartão e elástico

65. Montagem de sólidos
garrafa pet e elástico

68. PROPOSTAS DE ATIVIDADE
COM OS FIGURAS PLANAS

70. CONSTRUÇÃO DO TANGRAM
PASSO A PASSO

71. Podemos transpor de uma figura espacial para a
uma plana observando as sombras.

72. ELEFANTE COLORIDO, QUE FORMA?
• Criança 1: Elefante colorido
• Todos: Que forma?
• Criança 1: Quadrado
• Todos devem correr e tocar em um quadrado.
O ultimo a encontrar a forma, perde e assume
o lugar da criança 1.

73. • Também podemos fazê-lo desmontando
(planificando) a forma espacial.
• Por exemplo, ao desmontar um cubo de
cartolina obtemos quadrados:

74. • De modo interdisciplinar, trabalham-se as
figuras planas (retângulo, triangulo, quadrado
e círculo) recorrendo-se as placas de trânsito,
algo familiar ás crianças.

75. Construir figuras usando uma corda
Esta tarefa deve ser realizada a pares. A cada
par é fornecida uma corda atada com um nó.
O objetivo da tarefa é que, segurando
a corda, as crianças obtenham figuras
geométricas. O educador deverá começar
por propor a construção de um retângulo.
Para tal, as crianças terão de
combinar entre elas o modo como
posicionarão as mãos de maneira a que os
lados definidos pela corda entre as suas
mãos sejam iguais, ou seja, terão de as
afastar igualmente. Por outro lado, as
crianças terão de posicionar as mãos frente
a frente, de maneira a construir um
retângulo e não apenas uma figura com os
lados iguais dois a dois.

77. 77

78. 78

79. 79
AUMENTE E DIMINUA
Atividade: Dada uma figura, fazer sua
representação (redução) no retângulo que
segue. (dobrando barbante para definir a
escala a ser usada).

80. A turma será dividida em grupos de 4 crianças. Cada grupo de 4 será subdividido em duas duplas.
Um OE descreverá a figura sob a supervisão da dupla adversária para o seu parceiro, utilizando os
nomes das figuras geométricas e as posições.
80
Jogo 20 – Jogo das figuras

81. MUSICAS COM TANGRAN

82. Twister das formas geométricas

84. Corrida das formas

85. Figuras e formas

86. Batalha geométrica

87. Desenho livre com as formas

90. Trabalho com bandeiras

94. 94
Proposta de Atividade - Discussão
MATERIAIS VIRTUAIS PARA O ENSINO DA GEOMETRIA

95. PARA CASA / ESCOLA
• Nos slides 23 e 24 há o seguinte questionamento:
“Iniciar o ensino da geometria pelas figuras planas é
como iniciar a alfabetização linguística pelas letras e
só meses mais tarde apresentar as palavras?!” Você
concorda?, discorda? Por que?
• Utilizando-se de alguma sugestão ofertada nestes
slides, elabore uma sequencia didática que foque o
ensino dos sólidos geométricos e/ou as figuras
planas no cotidiano do aluno. Utilize, se achar
necessário, a interdisciplinaridade.
NÃOSERÁ NECESSÁRIO APLICAR EM SALA DE AULA.