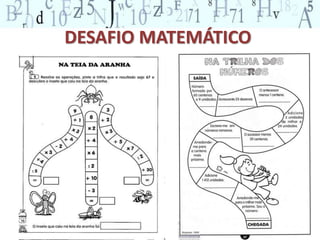
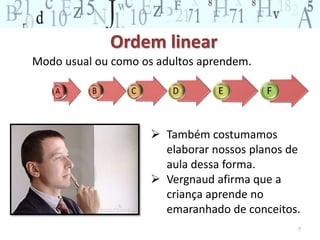
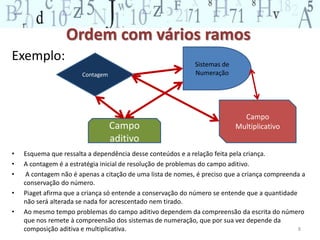
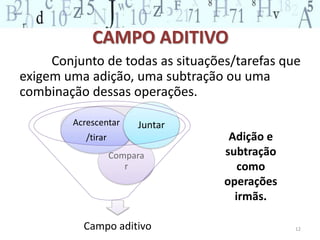
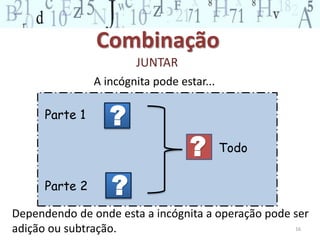
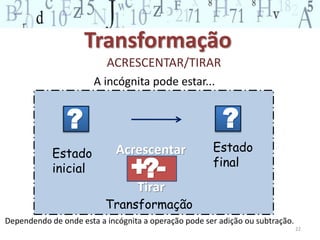
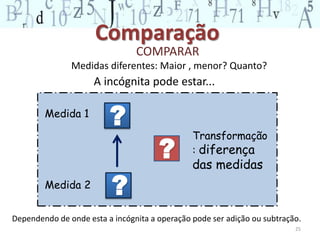
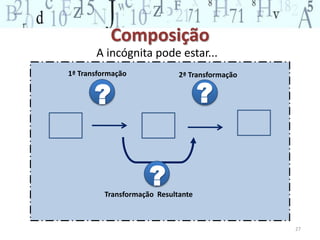
O documento descreve os principais conceitos do campo conceitual aditivo, incluindo classes de situações como combinação, transformação, comparação e composição. Explica que embora situações envolvam adição e subtração, a forma como a pergunta é formulada torna as situações cognitivamente diferentes para as crianças. Também ressalta a importância de diversificar atividades para permitir que crianças construam raciocínios adequados a cada situação.

1. Orientadora Aline Manzini
PNAIC – Bertioga
Setembro/2014

2. LEITURA DE DELEITE
Os filhotes do vovô coruja
Eun Hee Na

3. DESAFIO MATEMÁTICO

4. 4
Dica: Cada numero nos círculos, representa a
soma das duas peças imediatamente
abaixo dele.

5. O significado
das operações
VIDEO
https://www.youtube.com/watch?v=GAu4JRRjefc

6. Teoria dos Campos Conceituais
A Teoria dos Campos Conceituais foi
idealizada por Gérard Vergnaud, psicólogo
francês, discípulo de Jean Piaget e Lev
Vygotsky, ainda atuante na área.
Vergnaud investigou os processos de
aprendizagem de crianças e adolescentes.
A frase abaixo resume muito bem os
príncipios da Teoria dos Campos Conceituais.
“A ideia de Gérard Vergnaud de que se aprende na
trama, não de conceitos linearmente sequenciais, mas no
emaranhado de uma rede de muitos conceitos presentes
em situações de vida”. (Grossi, E. , 2010).
6

7. Ordem linear
Modo usual ou como os adultos aprendem.
7
 Também costumamos
elaborar nossos planos de
aula dessa forma.
 Vergnaud afirma que a
criança aprende no
emaranhado de conceitos.

8. Ordem com vários ramos
Exemplo:
Sistemas de
Numeração
Campo
Campo Multiplicativo
aditivo
Contagem
• Esquema que ressalta a dependência desse conteúdos e a relação feita pela criança.
• A contagem é a estratégia inicial de resolução de problemas do campo aditivo.
• A contagem não é apenas a citação de uma lista de nomes, é preciso que a criança compreenda a
conservação do número.
• Piaget afirma que a criança só entende a conservação do número se entende que a quantidade
não será alterada se nada for acrescentado nem tirado.
• Ao mesmo tempo problemas do campo aditivo dependem da compreensão da escrita do número
que nos remete à compreensão dos sistemas de numeração, que por sua vez depende da
composição aditiva e multiplicativa.
8

9. Campo Conceitual
• Conjunto de situações que evocam um certo conceito.
Inclui todos os problemas, tarefas cognitivas, significados e
significantes que se utilizam daquele conceito.
9
“Não se pode entender separadamente o
desenvolvimento cognitivo e o aprendizado de
um conceito. Desenvolvemos conceitos e
representamos objetos e pensamentos por meio
de suas características gerais, para enfrentar
situações. E sempre há uma variedade enorme de
situações envolvidas na formação de um conceito
e também uma variedade de conceitos
envolvidos no entendimento de uma situação.
Juntos, eles formam sistemas progressivamente
organizados”

10. Exemplificando o Campo Conceitual
10

11. 11
Revista Nova Escola

12. CAMPO ADITIVO
Conjunto de todas as situações/tarefas que
exigem uma adição, uma subtração ou uma
combinação dessas operações.
Acrescentar
Juntar
Compara
r
/tirar
Adição e
subtração
como
operações
irmãs.
Campo aditivo 12

13. CLASSES DO
CAMPO ADITIVO
13

14. COMBINAÇÃO
Situações associadas à ideia de combinar dois estados
para obter um terceiro.
Esta é uma das situações mais frequentemente
trabalhadas na escola e é comumente
identificada pelos professores com a ação de
“juntar”. Vejamos um exemplo:
• Em classe há 15 meninos e 13 meninas.
Quantas crianças há nessa classe?
14
Parte 1
TINHA
Parte 2
GANHEI/PERDI
Todo
FIQUEI
15 13 ?

15. 15
A partir dessa situação é possível formular outras
duas, mudando-se a pergunta. As novas situações
são comumente identificadas como ações de
“separar ou tirar”. Exemplos:
• Em uma classe de 28 alunos, há alguns meninos
e 13 meninas. Quantos são os meninos?
Parte 1
TINHA
Parte 2
GANHEI/PERDI
Todo
FIQUEI
? 13 28
• Em uma classe de 28 alunos, 15 são meninos.
Quantas são as meninas?
Parte 1
TINHA
Parte 2
GANHEI/PERDI
Todo
FIQUEI
15 ? 28

16. Combinação
JUNTAR
16
Parte 1
Parte 2
Todo
A incógnita pode estar...
?
?
?
Dependendo de onde esta a incógnita a operação pode ser
adição ou subtração.

17. TRANSFORMAÇÃO
Situações ligadas à ideia de transformação, ou seja, à
alteração de um estado inicial, que pode ser positiva
ou negativa.
Nestas situações é como se a criança tivesse que
observar cenas sucessivas de um acontecimento e identificar
a alteração ocorrida.
17

18. Vejamos dois exemplo:
• Numa sala de aula haviam 20 alunos. Durante o ano
chegaram 12 novos estudantes . Quantas alunos há agora
nesta sala?
• Numa sala de aula haviam 32 alunos. Durante o ano
saíram 12 estudantes . Quantas alunos há agora nesta
sala?
18
Estado inicial
TINHA
Transformação
GANHEI
Estado final
FIQUEI
20 12 ?
Transformação positiva
Estado inicial
TINHA
Transformação
PERDI
Estado final
FIQUEI
32 12 ?
Transformação negativa

19. • “É interessante observar que embora duas situações
possam ser muito similares, o tipo de pergunta
formulada, as tornam muito diferentes para as
crianças. Assim, é muito importante diversificar as
propostas de trabalho em sala de aula e em especial,
não condicionar os alunos a resolver problemas
baseados em palavras chave. O fato de no enunciado
aparecer a palavra “perder” em geral leva o aluno a
pensar em subtração, o que nem sempre é um
raciocínio correto.”
CÉLIA MARIA CAROLINO PIRES
19

20. Cada uma dessas situações pode gerar outras, mudando-se a
pergunta feita. Vejamos:
• Numa sala de aula haviam alguns alunos. Durante o ano
chegaram mais 12 estudantes e sala ficou com um total de
32 alunos. Quantas alunos havia nesta sala no inicio do ano?
• Numa sala de aula haviam 20 alunos. Durante o ano
chegaram alguns estudantes e sala ficou com um total de 32
alunos. Quantas alunos chegaram a esta sala durante o ano?
20
Estado inicial
TINHA
Transformação
PERDI/GANHEI
Estado final
FIQUEI
? 12 32
Estado inicial
TINHA
Transformação
PERDI/GANHEI
Estado final
FIQUEI
20 ? 32
Transformações positivas

21. Cada uma dessas situações pode gerar outras, mudando-se a
pergunta feita. Vejamos:
• Numa sala de aula haviam alguns alunos. Durante o ano
saíram 12 estudantes e sala ficou com um total de 20
alunos. Quantas alunos havia nesta sala no inicio do ano?
• Numa sala de aula haviam 32 alunos. Durante o ano saíram
alguns estudantes e sala ficou com um total de 20 alunos.
Quantas alunos havia nesta sala no final do ano?
21
Estado inicial
TINHA
Transformação
PERDI/GANHEI
Estado final
FIQUEI
? 12 20
Estado inicial
TINHA
Transformação
PERDI/GANHEI
Estado final
FIQUEI
32 ? 20
Transformações negativas

22. Transformação
ACRESCENTAR/TIRAR
22
A incógnita pode estar...
? ?
Estado
final
Estado
inicial
Acrescentar
+ -
?
Tirar
Transformação
Dependendo de onde esta a incógnita a operação pode ser adição ou subtração.

23. COMPARAÇÃO
Situações associadas à ideia de comparação.
• Neste grupo há uma situação já configurada e
a questão proposta implica numa
comparação. Vejamos alguns exemplos.
• Em classe há 15 meninos e 13 meninas.
Quantas meninas há a mais nessa classe?
23
Medida 1
TINHA
Medida 2
GANHEI/PERDI
Comparação
FIQUEI
15 13 ?

24. • Em classe há 15 meninos e duas meninas a menos.
Quantas meninas há nesta classe?
• Em classe há 13 meninas e dois meninos a mais.
Quantas meninos há nesta classe?
• Em classe há 15 meninos e 13. Quantas meninas precisam
chegar nesta sala, para que a quantidade de meninos e
meninas sejam iguais?
24
Medida 1
A TEM...
Medida 2
B TEM...
Comparação
DIFERENÇA
15 ? -2
Medida 1
A TEM...
Medida 2
B TEM...
Comparação
DIFERENÇA
? 13 +2
Medida 1
A TEM...
Medida 2
B TEM...
Comparação
DIFERENÇA
15 13 ?

25. Comparação
COMPARAR
Medidas diferentes: Maior , menor? Quanto?
25
Medida 1
Medida 2
A incógnita pode estar...
Transformação
: diferença
das medidas
?
?
?
Dependendo de onde esta a incógnita a operação pode ser adição ou subtração.

26. COMPOSIÇÃO
Situações de composição em que há mais de uma transformação
(positiva ou negativa)
• Neste tipo de situação há uma sequencia de
transformações e para dar a resposta não há
necessidade de se saber o que acontece no início,
mas apenas no decorrer. Esse fato provoca discussões
interessantes com os alunos. Vejamos alguns
exemplos:
• Em classe haviam 25 alunos. Durante o ano
entraram 10 e saíram 12. Quantos alunos há nesta
sala agora?
26
Inicio Decorrer Fim
25 +10 e -12 ?

27. Composição
A incógnita pode estar...
1ª Transformação 2ª Transformação
Transformação Resultante
27
? ?
?

28. • “Como podemos observar, embora todas estas situações
façam parte do campo aditivo, elas colocam em evidência
níveis diferentes de complexidade. No início da aprendizagem
escolar os alunos ainda não dispõem de conhecimentos e
competências para resolver todas elas, necessitando de uma
ampla experiência com situações-problema que os leve a
desenvolver raciocínios mais complexos por meio de
tentativas, explorações e reflexões. Evidentemente, a
categorização das situações problema é uma ferramenta
importante para o trabalho do professor no sentido de
diversificá-las e permitir ao aluno a construção de raciocínios
adequados a cada situação, mas não deve ser apresentada a
eles. Da mesma forma, os quadros que apresentamos no
corpo deste texto para explicitar cada situação analisada não
devem ser impostos aos alunos, que devem ser incentivados
a criar formas de registro que sejam significativas para eles,
como podemos ver em algumas produções. “
28

29. CAFÉ PEDAGÓGICO

30. REFERENCIAS:
Campo conceitual aditivo. Disponível em:
http://pt.slideshare.net/anaile10_amaral/campo-conceitual110615141336phpapp02-1
CÉLIA MARIA CAROLINO PIRES. ADIÇÃO, SUBTRAÇÃO E SIGNIFICADOS.
ELEMENTOS CONCEITUAIS E METODOLÓGICOS PARA DEFINIÇÃO DOS DIREITOS DE
APRENDIZAGEM E DESENVOLVIMENTO DO CICLO DE ALFABETIZAÇÃO (1º, 2º E 3º
ANOS) DO ENSINO FUNDAMENTAL Disponível em:
portal.mec.gov.br/index.php?option=com_docman&task
MEC – Ministério da Educação. Pacto Nacional pela Alfabetização na Idade Certa –
Caderno 4: Operações na resolução de problemas. Brasília: 2013