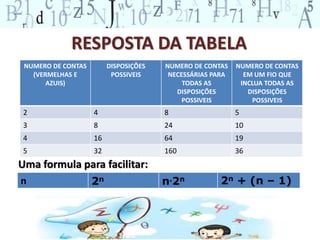
O documento discute o uso do fio de contas como material didático para o ensino de matemática na educação infantil e anos iniciais do ensino fundamental. Apresenta a origem do fio de contas, tipos comuns, materiais necessários, variações possíveis, objetivos educacionais e diversas atividades que podem ser realizadas com as crianças utilizando este material.

1. Orientadora Aline Manzini
PNAIC – Bertioga
Julho/2014

3. ORIGEM
O fio de contas é um material didático
introduzido em 1974 pelo famoso matemático
americano Hassier Whitney, do Instituto para
Estudos Avançados de Princeton, Nova Jersey, EUA.
Após ter sido reconhecido como um dos
maiores matemáticos deste século, o Professor
Whitney passou a dedicar-se exclusivamente ao
trabalho com crianças, em especial as da pré-escola
e dos anos iniciais do Ensino Fundamental.

4. TIPOS MAIS COMUNS
• Dois em dois
• Cinco em cinco
• Dez em dez

5. QUAIS MATERIAIS SERÃO UTILIZADOS?
Você precisará de:
Um pacote de miçangão nº10 com 250 grs, contem cerca de 650
unidades e custa de R$ 15,00 a R$ 20,00.
Portanto, para uma sala de 35 alunos
• Se quiser 100 contas para cada criança, será necessário 6 pacotes.
• Se quiser 50 contas para cada aluno ou se quiser 100 para cada
dupla precisará de 3 pacotes.
• Se quiser 50 para cada dupla precisará de 2 pacotes.
Utilizasse um metro de barbante para cada fio com 100 contas.

6. VARIAÇÕES

10. PARA QUE SERVE?
“Um bom material didático deve ajudar a compreensão da criança e ser como uma
extensão dela mesma. Deve também ser simples, durável, útil, facilmente conservado e,
se possível, feito pela própria criança.” Vieira
O fio de contas tem todas essas qualidades.
Este material didático é extremamente útil para trabalhar a ideia de
quantidade, construção do conceito de número, contagem e pequenos
cálculos, tornando bastante familiar à criança as quantidades e suas
representações simbólicas.
O Fio de contas dá-nos imensas
possibilidades: somar, subtrair, decompor,
compor, fazer contagens de 2 em
2, de 3 em 3 (...), situações
problemas, etc...

11. APRECIAÇÃO
Entregue fio de contas a cada aluno,
dupla ou grupo, deixando que
manuseiem livremente, explorando
o material.
COMO UTILIZAR?
CONCEITUAÇÃO
-Utilizando um fio de contas grande-
Professora: Olhando para o fio vocês sabem me dizer quantas contas tem aqui?
Crianças: Cem! Vinte! Mil!
Professora: Olha só. Vou separar as contas roxas. Quantas vocês acham que tem aqui?
Vini: Acho que tem dez!
Professora: Vamos ver se tem dez?
Fizemos a contagem em voz alta e confirmamos a hipótese de Vini. Então separei as
contas brancas e perguntei:E aqui, quantas tem?
Eri: Tem dez também, porque está do mesmo tamanho.
Professora: Será? Vamos ver se tem dez mesmo?
Relato na integra no Caderno 1 – paginas 11 a 13

12. CONSTRUÇÃO COLETIVA OU INDIVIDUAL
DO MATERIAL COM A CRIANÇA

13. Ofereça ao aluno objetos que o
auxiliem a separar as quantidades
• Eva
• Pregador
• Lápis

14. Utilize o registro (semi-concreto)
Conforme orienta FIORENTINI e MIORIM
(1996): “o registro das atividades com
material concreto deve fazer parte do
cotidiano das aulas. Os estudantes podem
fazer isso na forma de desenhos ou da
linguagem matemática. Essa estratégia é
importante para avaliação do trabalho e
definição de que momento deixar o objeto
de lado e se ater apenas ao abstrato ou
vice-versa. Para o aluno, esse momento
serve para organizar as idéias e refletir
sobre a atividade realizada.

15. Explorando a idéia de quantidade
a) Mostre 4 contas
4 é visto como 1 a menos do que 5.
b) Mostre 7 contas
7 é visto como 2 a mais do que 5.

16. • Contar 10 contas. Verificar quantos
agrupamentos de 5 existem no número 10.
• Contar 15 contas. Verificar quantos
agrupamentos de 5 existem no número 15.
• Contar 20 contas. Verificar quantos
agrupamentos de 5 existem no número 20.
• Marcar os números 5, 10, 15, 20 no colar e
assinalar no modelo do fio de contas.

17. Adição: a idéia de juntar quantidades
Com o colar de contas a criança compreende
por que, por exemplo, 6 + 5 tem de ser 11 e
não outra quantidade qualquer. Veja como:
Com um marcador, ela marca 6 (isto é fácil: 1 a
mais que 5)
Conta 5 (4 da mesma cor e 1 da outra) depois do
6 e marca com outro marcador: pronto, temos
11 (1 a mais que 10). Logo, 6 + 5 é igual a 11.

18. Subtração: a idéia de tirar uma
quantidade de outra
Como usar o colar de contas para responder a uma
pergunta como esta: se você tem 9 e tira 3,
quantos ficam? É fácil. Veja:
1 a mais que 5, ou seja, 6. Logo, 9 – 3 são 6.

19. Multiplicação: a idéia de juntar
quantidades iguais
Exemplo: Quanto é três vezes dois?
1 a mais que 5, ou seja, 6. Logo, 3 x 2 são 6.
E quatro vezes três, quanto dá?
UTILIZANDO BOLINHAS COLORIDAS DE 2 EM 2, 3
EM 3, 4 EM 4

20. Divisão: a idéia de repartir
igualmente ou a idéia de medida
Por exemplo, oito dividido por quatro: 8 : 4.
• Repartir igualmente
Ao repartir a quantidade 8 em 4 partes iguais, obtemos a quantidade 2 em
cada uma das partes. Logo, 8 : 4 = 2.
• Idéia de medida
Quantos 4 cabem em 8? Cabe 2 vezes o 4 no 8. Logo, 8 : 4 = 2.

21. Conceito unidade, dezena e centena

22. RESULTADO DE JOGOS

23. Atividade: Qual o número
• O professor ou um colega seleciona uma
quantidade e prende um clips ou separa com
lápis. A outra criança tem que descobrir qual
quantidade foi selecionada sem contar um a um,
apenas observando as dezenas e unidades.
Exemplo:
Nesta atividade
ao lado o numero
selecionado foi o
13.

24. Construção coletiva da centena
(com pregadores)

25. OUTRAS IDÉIAS PARA
UTILIZAÇÃO DAS CONTAS

26. Conceito de unidade e dezena

27. Número e quantidade

28. Professor
Vamos problematizar?
Temos aqui várias contas vermelhas e azuis. Elas podem ser dispostas em várias
sequencias diferentes.
Vamos começar com pares de contas. Quantas disposições diferentes de duas contas
são possíveis se cada conta pode ser vermelha ou azul?
Resposta:
Existem quatro disposições possíveis. Para criar todas as quatro disposições, são
necessárias 8 contas.
Mas se colocarmos as contas em um fio, é possível incluir todas as quatro disposições
usando menos de 8 contas. Este fio de cinco contas inclui todas as quatro
disposições mostradas acima.
Veja como:

29. Continue problematizando
preenchendo esta tabela:
NUMERO DE
CONTAS (UMA
VERMELHA, UMA
AZUL)
DISPOSIÇÕES
POSSIVEIS
NUMERO DE
CONTAS
NECESSÁRIAS
PARA TODAS AS
DISPOSIÇÕES
POSSIVEIS
NUMERO DE
CONTAS EM UM
FIO QUE INCLUA
TODAS AS
DISPOSIÇÕES
POSSIVEIS
2 4 8 5
4
6

30. RESPOSTA DA TABELA
NUMERO DE CONTAS
(VERMELHAS E
AZUIS)
DISPOSIÇÕES
POSSIVEIS
NUMERO DE CONTAS
NECESSÁRIAS PARA
TODAS AS
DISPOSIÇÕES
POSSIVEIS
NUMERO DE CONTAS
EM UM FIO QUE
INCLUA TODAS AS
DISPOSIÇÕES
POSSIVEIS
2 4 8 5
3 8 24 10
4 16 64 19
5 32 160 36
n 2n n.2n 2n + (n – 1)
Uma formula para facilitar:

31. TAREFA CASA/ESCOLA
Separados por ano-série, em
grupos de 3 ou 4 planeje e
aplique em sala de aula:
- Utilizando a apostila crie uma situação problema na qual os
alunos utilizarão o fio de contas para resolvê-la.
- Para isto utilize um texto ou conteúdo de outras disciplinas
(português, ciências, historia ou geografia)
- Envie o registro desta atividade no ambiente virtual até 10
de agosto.
OBS: Lembre-se de também trazer os materiais e registros
para expor em nosso encontro presencial.

32. Referências
• Colar de Contas Disponível em:
http://promatematicaibiraci.blogspot.com.br/2011/05/cola
r-de-contas-o-colar-de-contas-e-um.html
• MEC – Ministério da Educação. Pacto Nacional pela
Alfabetização na Idade Certa – Caderno 2: Quantificação,
registros e agrupamentos. Brasília: 2013
• Modelo colar de contas. Disponível em:
http://www.aprendermatematica.uevora.pt/numeros_taref
as/1ciclo/Modelo_do_colar_de_contas1.pdf
• Sentido de número e visualização no pré ‐ escolar e
primeiros anos. Disponível em:
http://setepinceladas.files.wordpress.com/2010/11/jogos-
matematica-1c2baano.pdf