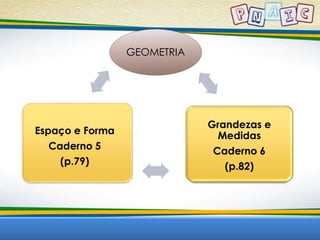
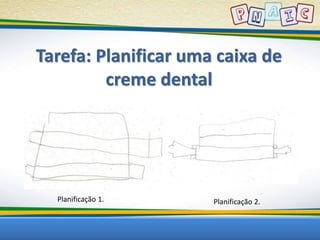
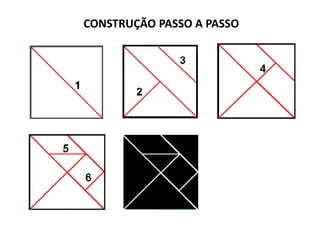
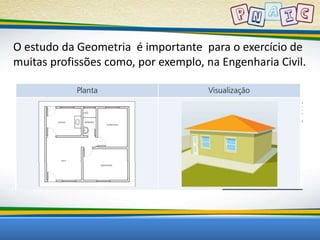
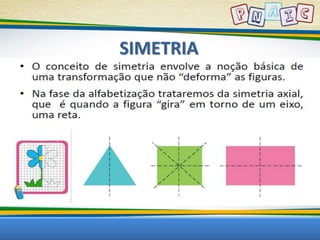
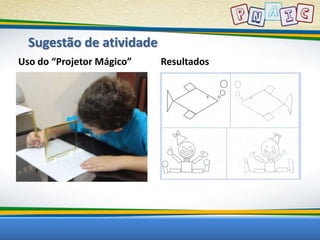
Este documento discute conceitos geométricos e atividades pedagógicas relacionadas. Inclui objetivos de aprendizagem sobre dimensão, semelhança, forma e geometria no ciclo de alfabetização. Também apresenta a lenda do Tangram e sugestões de jogos e exercícios envolvendo figuras geométricas.

1. Valquíria Queiroz Fernandes

2. 1º MOMENTO: Manhã
Leitura deleite “Clact Clact Clact”
Objetivos do caderno 5;
Conceitos de Geometria;
Dimensão, semelhança e forma;
Primeiros elementos da Geometria;
A Lenda do Tangram;
A Geometria e o Ciclo de Alfabetização;
Simetria.
PAUTA 6º ENCONTRO
27.09 .2014

3. LEITURA DELEITE
Clact ... Clact ... Clact ...

21. Objetivos gerais do caderno 5
Fornecer subsídios que permitam auxiliar o professor
a desenvolver trabalhos pedagógicos, possibilitando
às crianças: construir noções de localização e
movimentação no espaço físico para a orientação
espacial em diferentes situações do cotidiano e
reconhecer figuras geométricas presentes no
ambiente.

22. Objetivos Específicos
• Representar informalmente a posição de pessoas e objetos e dimensionar
espaços por meio de desenhos, croquis, plantas baixas, mapas e maquetes,
desenvolvendo noções de tamanho, de lateralidade, de localização, de
direcionamento, de sentido e de vistas;
• reconhecer seu próprio corpo como referencial de localização e
deslocamento no espaço;
• observar, experimentar e representar posições de objetos em diferentes
perspectivas, considerando diferentes pontos de vista e por meio de
diferentes linguagens;
• identificar e descreve a movimentação de objetos no espaço a partir de um
referente, identificando mudanças de direção e de sentido;

23. • observar, manusear, estabelecer comparações entre objetos do espaço
físico e objetos geométricos (esféricos, cilíndricos, cônicos, cúbicos,
piramidais, prismáticos) sem uso obrigatório de nomenclatura,
reconhecendo corpos redondos e não redondos;
• planificar modelos de sólidos geométricos e construir modelos de sólidos a
partir de superfícies planificadas;
• perceber as semelhanças e diferenças entre cubos e quadrados,
paralelepípedos e retângulos, pirâmides e triângulos, esferas e círculos;
• construir e representar figuras geométricas planas, reconhecendo e
descrevendo informalmente características como número de lados e de
vértices;
• descrever, comparar e classificar verbalmente figuras planas ou espaciais
por características comuns, mesmo que apresentadas em diferentes
disposições;

24. • conhecer as transformações básicas em situações vivenciadas: rotação,
reflexão e translação para criar composições (por exemplo: faixas
decorativas, logomarcas, animações virtuais);
• antecipar resultados de composição e decomposição de figuras
bidimensionais e tridimensionais (quebra-cabeça, tangram, brinquedos
produzidos com sucatas);
• desenhar objetos, figuras, cenas, seres mobilizando conceitos e
representações geométricas tais como: pontos, curvas, figuras geométricas,
proporções, perspectiva, ampliação e redução;
• utilizar a régua para traçar e representar figuras geométricas e desenhos;
• utilizar a visualização e o raciocínio espacial na análise das figuras
geométricas e na resolução de situações-problema em Matemática e em
outra áreas do conhecimento.

25. Geometria

26. GEOMETRIA
Espaço e Forma
Caderno 5
(p.79)
Grandezas e
Medidas
Caderno 6
(p.82)

27. Reflexão inicial
O que significa Geometria para você?
Como você vivenciou a Geometria na escola?
Que Geometria você aprendeu?
Qual o papel da Geometria para você?
Que Geometria você já ensinou?

28. O que significa Geometria?
Resulta de dois termos gregos:
Geosignifica terra
metriasignifica medir

29. Ampliando a discussão...
Leitura das páginas 7 à 9
Ler e grifar os conceitos de:
Dimensão, Semelhança, Simetria e forma

30. DIMENSÃO, SEMELHANÇA E
FORMA

31. DIMENSÃO

33. SEMELHANÇA

34. FORMA

36. PARA REFLETIR
As asas de uma
borboleta nos
remetem a que
conceito da
geometria?

38. PRIMEIROS ELEMENTOS DA
GEOMETRIA

39. Tarefa: Planificar uma caixa de
creme dental
Planificação 1. Planificação 2.

40. Questões para mediar a
investigação:
• O que está faltando em cada uma das
representações?
• Se a dobrarmos, o que acontecerá? Teremos
uma caixa?
• Quais são as figuras geométricas
representadas?
• Por que a caixa tem esse formato?

41. Trabalho com a caixa
• Desenhar todos os lados da caixa que você
trouxe.
• Quantos lados a sua caixa possui.
• Comparar com seus colegas para ver se todas
as caixas possuem o mesmo número de lados;
• Quais as figuras geométricas que a sua caixa
possui?
• Pode-se trabalhar: vértice, lado, figuras
geométricas, ...

42. Planificar a sua caixa
• Descolar a sua caixa e abri-la;
• Colá-la novamente, do lado avesso;
• Desenhar no avesso da sua caixa um imóvel
(utilizar giz de cera, canetinhas, cola, tesoura,
papel colorido...)

43. Construir maquete de uma cidade
• Colocar a sua caixa (imóvel), em um local destinado para
as maquetes.
• Observar, em grupo, quais os imóveis estão na mesma
rua, em ruas paralelas, à direita, à esquerda, a frente,
atrás...

44. Desenho da maquete
• Pedir para os alunos desenharem observando de vários
ângulos: oblíqua, frontal (de frente), vertical (de cima)
• Trabalhar os diferentes conceitos: atrás, na frente, ao
lado, na rua paralela...

45. Sugestão de Atividade
Em uma sacola não transparente colocam-se
vários sólidos. A criança deve pegar um
deles, de olhos fechados, e descrevê-lo:
Se tem pontas, se tem vértices, quantas
arestas, se é arredondado...
Essa atividade deve ser utilizada para a
identificação de atributos, classificação
de formas e identificação de
propriedades.

46. Atributos definidores ou invariantes
São os atributos que distinguem uma figura de outra e que são utilizados nas
definições.
Quais as características que distinguem o quadrado de outras figuras?
Um dos objetivos do ensino da geometria no ciclo de
alfabetização é levar os alunos a classificar as figuras
geométricas por meio de suas características, as quais
denominaremos de atributos definidores.

47. Atributos relevantes e irrelevantes
As cores são atributos irrelevantes.
Atributos definidores são os
relevantes.

48. Quais são os atributos relevantes de
um quadrado?
Ângulos retos, lados
iguais, quatro lados.

49. Quais são os atributos relevantes de
um triângulo?

50. Quais são os atributos relevantes de
um retângulo?
Quatro lados, ângulos
retos

51. Práticas a serem evitadas
Apresentar as figuras
geométricas:
• sempre na mesma
posição;
• sempre com a
mesma cor;
• sempre com o
mesmo tamanho. Imagem do livro Sem pé nem cabeça, de Pedro Bandeira

52. Práticas adequadas
• Uso de figuras recortadas para que a criança possa
girar, não estabelecendo relação entre cores,
tamanhos ou posições com os nomes das figuras.
• Apresentação de exemplos e contra-exemplos em
sala de aula, ou seja, falar de triângulos e não-triângulos,
quadrados e não-quadrados, e assim por
diante.

53. Práticas adequadas
• Uso do GEOPLANO

54. Práticas adequadas
• Construção de POLIEDROS com canudinhos

55. Direitos de Aprendizagem relativos à
percepção geométrica
•Observar, manusear, estabelecer relações entre figuras
planas e espaciais, compor e decompor figuras.
Sugestão de atividade: exploração do Tangram.

56. •Relacionamento de objetos do cotidiano com os sólidos
geométricos (objetos matemáticos) e vice-versa, reconhecendo
corpos redondos e não redondos (poliédricos).

57. •Planificação de modelos de sólidos geométricos e construção
de modelos de sólidos a partir de superfícies planificadas

58. Ampliando a discussão...
Leitura compartilhada das páginas 10 à 17
Leitura da lenda do Tangram – Confecção do
Tangram e Exposição dialogada.

60. História do Tangram
• Quando trabalhamos geometria com as
crianças, um dos materiais clássicos é o
tangram.

62. …um chinês que possuía um
azulejo da I Dinastia Chinesa e
que era o seu encanto.

63. Um dia, ao afagá-lo pela
vigésima quinta vez, deixou-o
cair partindo-se em sete
pedaços.

66. Apanhou-os do chão e colocou-os
sobre a mesa …

67. …e, muito triste sentou-se e chorou até
que adormeceu.

68. Os pedaços de azulejo, fartos de
formarem um quadrado, meditaram
e procuraram uma forma diferente.

69. Movimentaram-se e surgiu um
triângulo.

70. Bem, é diferente mas não gostamos!

71. Voltaram a rodopiar e surgiu, desta
vez, um retângulo.

72. Comentaram entre si:
Parece um quadrado, só que engordou
para um dos lados!

73. Moveram-se novamente e eis que
surge um gato.

74. Ah, agora sim, um gato com vida e
bem diferente do quadrado!

75. Mas o gato teve fome.

76. Construiram um barco e foram à pesca.

77. Apanharam um peixe que deram ao
gato.

78. Decidiram voar e tomaram a
forma de um pássaro e voaram.

80. Voltaram e resolveram assustar o
chinês, transformando-se na sua
figura.

82. Este ao acordar, foi buscar a
cola para colar os pedaços do
azulejo.

84. Porém, ao olhar para cima da mesa,
verificou que os pedaços do azulejo
se tinham transformado na sua
figura e, admirou-se!

86. Enervado, olhou e com receio
movimentou alguns daqueles pedaços,
aparecendo-lhe um cão.

87. - Olha que giro, estes pedaços parecem
mágicos!

88. Voltou a reunir os pedaços e …

89. ... surgiu um cisne.

90. CONSTRUÇÃO PASSO A PASSO

92. Atividade 5
PNAIC_MAT_Caderno 5_ p.74 e 75
• Relembrar conceitos relativos às
características de algumas figuras
geométricas.
• Sugerir uma sequência de atividades que
podem ser realizadas com as crianças.
Materiais:
• Uma caixa de fósforos para adultos e palitos
de picolé para crianças.
• Papel para registro.

93. PRATICANDO...
a) Forme todas as figuras possíveis com 3, 4, 5,
6, 7, e 8 palitos de fósforo.
• Registre os desenhos que obteve e os
respectivos nomes.
b) Agrupe os desenhos das figuras de acordo
com as similaridades entre elas.

94. REFLETINDO...
• Como as crianças poderiam fazer estes
agrupamentos?
• Quais conceitos podem ser trabalhados?

95. -
Relato da professora
Relações entre geografia e geometria
• Relato da professora Doutora Maria José da
Silva Fernandes, docente do Departamento de
Educação da Universidade Estadual Paulista
(UNESP/Bauru).
( PNAIC_MAT_Caderno 5_ p. 75)

96. REFLETINDO...
• Quais as possibilidades que esse trabalho
oferece?
• Quais Direitos de Aprendizagem estão
relacionados com essa atividade?

97. OBJETIVOS...
• Reconhecer seu próprio corpo como referencial
de localização no espaço (em cima e embaixo,
acima e abaixo, frente e atrás, direita e
esquerda).
• Identificar diferentes pontos de referência para a
localização de pessoas e objetos no espaço,
estabelecendo relações entre eles e expressando-as
através de diferentes linguagens: oralidade,
gestos, desenho, maquete, mapa, croqui, escrita;

98. VIVENCIANDO OS JOGOS
• Jogo 18 - na direção certa - p.50
• Jogo 19 - Trilha dos sabores - p.54
• Jogo 20 – Jogo das Figuras – p. 57
• Jogo 21 – Dominó Geométrico – p.59
• Equilíbrio Geométrico – p. 61
• Explorar: objetivos, desenvolvimento,
avaliação e questionamentos possíveis
• Apresentar à turma.

99. A GEOMETRIA E O
CICLO DE
ALFABETIZAÇÃO

100. DIREITOS DE APRENDIZAGEM DA ÁREA
DE MATEMÁTICA (BRASIL, 2012)
Objetivos a serem alcançados por meio do ensino
da Geometria/Espaço e Forma:
Possibilitar aos alunos construírem noções de
localização e movimentação no espaço físico para
orientação espacial em diferentes situações do
cotidiano e reconhecer figuras geométricas.

101. No que diz respeito ao trabalho com a movimentação e
localização, o ensino de geometria deve propiciar aos
alunos desenvolver noções de:
• Noções de lateralidade (direita e esquerda);
• Noções topológicas (dentro e fora);
Que atividades podem auxiliar os alunos
nesse sentido?

102. Registros de trajetos por
meio de:
• expressão oral;
• desenhos;
• relatos escritos.
Registros da localização
por meio de:
• desenhos;
• papel quadriculado;
• croquis;
• mapas.

103. Com o desenvolvimento da percepção geométrica,
o estudante deve ser capaz de :
• Visualizar, discriminar e classificar figuras
geométricas por meio de suas características e
identificar números de lados (faces) e vértices;
• Reconhecer padrões, regularidades e
propriedades de figuras geométricas presentes
em diferentes contextos, por exemplo: na
observação da natureza, obras de arte e
manifestações artísticas de diferentes culturas;

104. • Perceber figuras geométricas por meio de vistas
de objetos e planificação de sólidos geométricos,
por exemplo: dado um objeto, a criança
representa no papel, por meio de desenhos, o
que ela vê em diferentes perspectivas;
• Planificar sólidos geométricos;
• Ampliar e reduzir figuras;
• Compor e decompor figuras;
• Construir diferentes figuras geométrica utilizando
a régua e diferentes softwares;

105. • Resolver problemas que requeiram pensar
geometricamente;
• Relacionar objetos e situações do cotidiano
com sólidos geométricos e vice-versa,
por exemplo: bola de futebol, caixa de
sapato, caixa de leite.

106. PARA QUE SERVE A GEOMETRIA?
ONDE USAMOS OS
CONHECIMENTOS DE GEOMETRIA?

107. O estudo da Geometria é importante para o exercício de
muitas profissões como, por exemplo, na Engenharia Civil.

108. O estudo da Geometria é importante no campo, para
decidir o formato mais adequado de plantações

109. O que deve ser superado no Ensino da
Geometria:
• O ensino isolado da disciplina, no final do ano.
• O ensino da Geometria desconectado de outros
conteúdos, como Números, Grandezas e Medidas e
Estatística.
• A visão de que Geometria se resume às figuras
geométricas, esquecendo-se de que se refere também à
movimentação e localização de pessoas e objetos no
espaço.

110. Quais atividades podem ser
propostas para o trabalho com
geometria?
Atividades de observação e registro de diferentes
figuras geométricas.

111. Que tal um passeio pela cidade?
Pode-se observar
placas de trânsito,
fachadas de casas,
prédios, igrejas e
formato de
praças.

112. Ou uma visita ao museu?
Pode-se observar os
diferentes recursos
utilizados pelos
artistas, como figuras
geométricas, linhas
retas e curvas,
paralelismo,
regularidades e
padrões.

113. Ou conhecer outras comunidades?
Pode-se perceber que a Geometria está presente em
práticas sociais, como a pintura corporal, rituais e
cestarias.

114. IMPORTANTE!
Em todo esse processo, o
REGISTRO é muito importante,
seja ele escrito ou em forma de
desenhos ou diagramas.

115. SIMETRIA

116. O QUE É SIMETRIA?
De uma forma geral, uma figura é simétrica quando
podemos dividi-la em partes iguais, sendo que
coincidem perfeitamente quando sobrepostas.

117. Simetria na escola
Completar figuras sobre o papel
quadriculado, supondo-as
simétricas
Uso de espelhos planos

118. Sugestão de atividade
Uso do “Projetor Mágico” Resultados

119. Possíveis questionamentos
• O que aconteceu com as figuras desenhadas?
• Elas têm o mesmo tamanho?
• O que dizer da posição das figuras desenhadas
em relação às figuras dadas?
• Se dobrarmos o papel, uma figura ficará
sobreposta à outra?
• Quais outros aspectos e relações interessantes
podemos ver nas duas figuras?

120. A natureza é uma fonte de recursos a
serem utilizados no ensino da
Geometria.
O que é possível explorar?

121. • Reconhecer regularidades das formas, como as
figuras geométricas se justapõem;
A casca do abacaxi O favo de mel O casco da tartaruga

122. • Identificar e explorar conceitos e propriedades
geométricas;
• Desenvolver um trabalho interdisciplinar com
Ciências.
• Perceber que a proporção, o padrão e a
regularidade, a beleza e o equilíbrio das formas
encontradas na natureza são fenômenos que
atraem e envolvem o homem.

123. 1º MOMENTO: Tarde
Leitura deleite “Obras de Julian Beever em 3D”;
Simetria e Artes;
Conexão da Geometria com a arte;
Informática na Educação;
Jogos educativos e virtuais;
Localização e movimento no espaço;
Para casa.
PAUTA 6º ENCONTRO
27.09 .2014

124. DELEITE
Obras de Julian Beever em 3D

133. CONEXÕES DA GEOMETRIA
COM A ARTE

134. A geometria e as artes
As conexões entre as artes e as geometrias, além
do estudo de diversos conteúdos geométricos,
dá a oportunidade aos alunos de conhecerem a
vida e a obra de diferentes artistas, contribuindo
para o seu enriquecimento cultural e para
mostrar que a geometria está presente em
diferentes contextos.

135. O QUE SE PODE OBSERVAR?
Nas obras de Oscar Niemeyer?

136. Teatro Paiol - Curitiba
Ponto de ônibus - Curitiba

137. Nas obras de Alfredo Volpi, pintor italiano que
viveu no Brasil?

138. Nas obras de Escher, o artista gráfico holandês ?
O que há de curioso nesta
obra de Escher?

139. E na obra de Piet
Mondrian, nascido
em 1872?
Mondrian, Composição com vermelho,
amarelo e azul, ano de 1921
Podemos observar uma
exploração bastante criativa
das figuras geométricas.
Uma obra de Mondrian é mais
adequada ao ciclo de
alfabetização do que uma obra
de Escher. Esse fato deve ser
levado em conta no uso das
obras de arte em sala de aula.

140. As crianças podem
ser estimuladas a
criar os seus
“Mondrians”.
Ao lado, vemos um
destes desenhos
feitos por crianças
do primeiro ano do
ciclo de
alfabetização.

141. Agora é sua vez!
Aprecie a obra de arte de Mondrian (1906)
- Destaque os
elementos
geométricos usados
por Mondrian.
- Que tal criar uma
“obra de arte” com
esses mesmos
elementos
geométricos?

143. KIRIGAMI
Kirigami (do japonês: de kiru, "recortar", e kami, "papel")
é a arte tradicional japonesa de recorte o papel, criando
representações de determinados seres ou objetos.

146. KIRIGAMI
Vamos fazer toalhinhas para enfeitar a janela utilizando a técnica
KIRIGAMI?

154. INFORMATICA NA EDUCAÇÃO
“VIVIANE MOZÉ”

155.  JOGOS EDUCATIVOS E
VIRTUAIS
“De cá pra lá, de lá pra cá”

156.  Leitura individual das páginas
46 e 47.

157. LOCALIZAÇÃO E MOVIMENTO
NO ESPAÇO

161.  Para casa:
Obrigada a todas
e ótima semana!!!