Baixado 176 vezes
Carregado porLeonardo Mannini
Grécia e a geometria
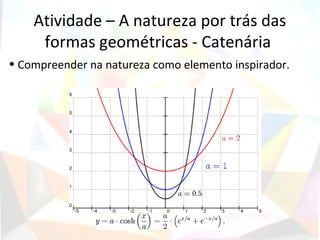
O documento descreve a história da geometria no Egito e na Grécia Antiga, com ênfase nos principais pensadores e descobertas geométricas nesses períodos, como o Papiro de Ahmes, Tales de Mileto, Pitágoras, Platão, Aristóteles, Euclides e Arquimedes. Também aborda a importância do ensino da geometria na educação básica e sugere atividades lúdicas para trabalhar conceitos geométricos de forma prazerosa.
Mais conteúdo relacionado
Semelhante a Grécia e a geometria
![Vc6 final[1]](https://cdn.slidesharecdn.com/ss_thumbnails/vc6final1-141010111949-conversion-gate02-thumbnail.jpg?width=640&height=640&fit=bounds)
Grécia e a geometria
- 1.
- 2. História da Geometria Egito
- 3. A geometria navida cotidiana • Papiro de Ahmes; • Como se deu a elaborada as primeiras regras para obtenção das áreas de um triangulo e trapézio; • Pontos fracos da geometria egípcia; • Legado de maior valor da geometria egípcia.
- 4. Grécia • Grécia doséc. 7 a.C. - geometria como ciência dedutiva • Geometria grega - régua e compasso • Gregos herdam dos egípcios • Criaram leis e regras acerca do espaço
- 5. Grécia e aGeometria • Mais antigas Histórias da Matemática - Eudemos de Rodes, por volta de 320 aC., aluno de Aristóteles • Primeiro registro: Comentário ao primeiro livro de Os Elementos de Euclides - Proclus Diadchus (410-485 dC). É tudo o que sabemos sobre Tales e Pitágoras
- 6. Grécia e aGeometria • Tales de Mileto (624 - 546 a.C.) - introdutor da geometria na Grécia • Pitágoras de Samos (572 - 497 a.C.) - esfericidade Terra, Lua, outros corpos celestes - céu = cosmos - “Teorema de Pitágoras”
- 7. Grécia e aGeometria • Platão (427 – 347 a.C) - Escreve “Timeu”, 5 figuras cósmicas perfeitas • Aristóteles de Estagira (384-322 a.C.) - explicou fases da Lua e eclipses - Universo e esférico e finito - Esfericidade da Terra • Heraclides de Pontus (388-315 a.C.) - propôs Terra gira diariamente sobre seu próprio eixo
- 8. Grécia e aGeometria • Euclides (360 – 295 a.C.) - Criador da famosa geometria euclidiana - “Os Elementos” – dividida em 13 volumes (5 de geometria plana, 3 de geometria no espaço) • Aristarco de Samos (310-230 a.C.) - 1° Terra se movia em volta do Sol, antecipando Copérnico em quase 2000 anos - distâncias relativas do Sol, Lua à Terra - tamanhos relativos da Terra, Sol e Lua
- 9. Grécia e aGeometria •Eratóstenes de Cirênia (276-194 a.C.) - primeiro a medir o diâmetro da Terra - Siena e Alexandria - ângulo 7 graus circunferência da Terra = 1% do valor correto
- 10. • Hiparco deNicéia (160 - 125 a.C.) - catalogo com posição no céu de 850 estrelas; - razão tamanho sombra Terra x tamanho Lua: 8/3; - Lua 59 vezes o raio da Terra de distância (correto 60); - duração do ano com margem de erro de 6 minutos; • Ptolomeu (85 d.C. - 165 d.C.) - último astrônomo importante da antiguidade; - compilou o Almagesto, maior fonte de conhecimento sobre a astronomia na Grécia
- 11. PRINCIPAIS PROBLEMAS COM GEOMETRIAPLANA: POR QUE ENSINAR GEOMETRIA?
- 12. • É atravésda geometria que o homem lida com sua realidade concreta, interage com seu meio e estabelece relações com o mundo. • Desenvolver capacidade de abstração, de generalização e a possibilidade de projeção. • A geometria exige do aluno uma maneira específica de raciocinar (LORENZATO, 1995).
- 13. Por que ensinarGeometria? • Ser bom conhecedor de Aritmética ou de Álgebra não é suficiente para resolver problemas de Geometria (LORENZATO, 1995). • EXEMPLO 1: Compare as áreas dos retângulos escurecidos. Figura 1 Adaptado de (LORENZATO, 1995).
- 14. Por que ensinarGeometria? • EXEMPLO 2: Quantos triângulos você vê? Figura 2 Adaptado de (LORENZATO, 1995). • Em ambos exemplos não há presença de números ou medidas.
- 15. Por que ensinarGeometria? • A Geometria demanda uma leitura diferente da Aritmética ou da Álgebra, na medida em que para resolver o problema é preciso ter “percepção geométrica, raciocínio geométrico e linguagem geométrica, fatores estes essenciais na relação real/forma” (LORENZATO, 1995, p.5).
- 16. Por que ensinarGeometria? • A Geometria pode auxiliar na compreensão de outras formas de raciocínio matemático. • Exemplo de problema: entre coelhos e galinhas tenho 7 cabeças e 20 pés, no total. Quantos coelhos e quantas galinhas possuo?
- 17. Por que ensinarGeometria? • Solução Aritmética: • Equação dos pés: 2 × galinhas + 4 × coelhos = 20 • Equação das cabeças: 1 × galinhas + 1 × coelhos = 7 Resultado: tenho 3 coelhos e 4 galinhas.
- 18. Por que ensinarGeometria? • Solução Geométrica: • “Cada bicho tem sua casinha...são 7” • “2 pernas para cada bicho...sobraram” • “6 pernas...tem que ser dos coelhos“ • “2 pernas mais para cada casinha” • “São 3 coelhos e 4 galinhas” (LORENZATO, 1995).
- 19. Por que ensinarGeometria? • “Apresentação da Geometria como elemento fortemente presente no meio ambiente da criança; portanto, o conhecimento geométrico escolar inicial é natural e familiar”. • “As formas são reproduzidas e investigadas, independentemente de serem bi ou tridimensionais”. • “Transformação de formas, por divisão, ou por combinação de artefatos”. • “Favorecer o desenvolvimento do senso espacial da criança” (LORENZATO, 1995).
- 20. A GEOMETRIA NOENSINO FUNDAMENTAL: CONTEÚDO E MODOS DE ENSINO ORIENTAÇÕES DO PCN.
- 21. No ensino da Matemática, destacam-se dois aspectos básicos: um consiste em relacionar observações do mundo real com representações (esquemas, tabelas, figuras); outro consiste em relacionar essas representações com princípios e conceitos matemáticos. Nesse processo, a comunicação tem grande importância e deve ser estimulada, levando-se o aluno a “falar” e a “escrever” sobre Matemática, a trabalhar com representações gráficas, desenhos, construções, a aprender como organizar e tratar dados. (p.18) (...) o ponto de partida da atividade matemática não é a definição, mas o problema. (p32)
- 22. Década de 60/70– A matemática moderna Década de 80 – doc. “Agenda para Ação” - Etnomatemática • importância do desempenho de um papel ativo do aluno na construção do seu conhecimento; • ênfase na resolução de problemas, na exploração da Matemática a partir dos problemas vividos no cotidiano e encontrados nas várias disciplinas; • importância de se trabalhar com um amplo espectro de conteúdos, incluindo-se, já no ensino fundamental, elementos de estatística, probabilidade e combinatória, para atender à demanda social que indica a necessidade de abordar esses assuntos; • necessidade de levar os alunos a compreenderem a importância do uso da tecnologia e a acompanharem sua permanente renovação. (p.21)
- 23. Temas Transversais •Meio Ambiente- recursos naturais, desperdício — terá ferramentas essenciais em conceitos (médias, áreas, volumes); •Saúde - desenvolvimento físico (altura, peso, musculatura); •educação do consumidor (medidas, porcentagem, sistema monetário). Trabalho coletivo Jogo: “é uma atividade natural no desenvolvimento dos processos psicológicos básicos; supõe um “fazer sem obrigação externa e imposta”, embora demande exigências, normas e controle”.
- 24. Blocos de conteúdos • Números e Operações; • Espaço e Forma; • Grandezas e Medidas; • Tratamento da Informação;
- 25. ESPAÇO E FORMA Os conceitos geométricos constituem parte importante do currículo de Matemática no ensino fundamental, porque, por meio deles, o aluno desenvolve um tipo especial de pensamento que lhe permite compreender, descrever e representar, de forma organizada, o mundo em que vive. A Geometria é um campo fértil para se trabalhar com situações-problema e é um tema pelo qual os alunos costumam se interessar naturalmente. O trabalho com noções geométricas contribui para a aprendizagem de números e medidas, pois estimula a criança a observar, perceber semelhanças e diferenças, identificar regularidades e vice-versa. Além disso, se esse trabalho for feito a partir da exploração dos objetos do mundo físico, de obras de arte, pinturas, desenhos, esculturas e artesanato, ele permitirá ao aluno estabelecer conexões entre a Matemática e outras áreas do conhecimento. (p.39)
- 26. • Localização depessoas ou objetos no espaço, com base em diferentes pontos de referência e algumas indicações de posição. • Movimentação de pessoas ou objetos no espaço, com base em diferentes pontos de referência e algumas indicações de direção e sentido. • Descrição da localização e movimentação de pessoas ou objetos no espaço, usando sua própria terminologia. • Dimensionamento de espaços, percebendo relações de tamanho e forma. • Interpretação e representação de posição e de movimentação no espaço a partir da análise de maquetes, esboços, croquis e itinerários.
- 27. • Observação deformas geométricas presentes em elementos naturais e nos objetos criados pelo homem e de suas características: arredondadas ou não, simétricas ou não, etc. • Estabelecimento de comparações entre objetos do espaço físico e objetos geométricos — esféricos, cilíndricos, cônicos, cúbicos, piramidais, prismáticos — sem uso obrigatório de nomenclatura. • Percepção de semelhanças e diferenças entre cubos e quadrados, paralelepípedos e retângulos, pirâmides e triângulos, esferas e círculos. • Construção e representação de formas geométricas.
- 28.
- 29. Atividade pode serrealizada com: •1º, 2º e 3º do ciclo I. Material utilizado: •Tesoura sem ponta; •Papel sulfite; •Lápis de cor ou giz de cera; •Cola; Objetivos: •Reconhecer as formas geométricas (triângulo, quadrado, séculos e retângulo); •Delimitar seu espaço e diferenciar as diferentes dimensões das formas geométricas; •Estabelecer paralelo com o cotidiano.
- 33. • Atividade podeser realizada com: • 3º e 4º do ciclo I. • Material utilizado: • Lápis de cor ou giz de cera; • Pode-se utilizar o Paint Brush ou outro software para colorir o desenho; • Objetivos: • Reconhecer as formas geométricas mais simples (triângulo, quadrado, séculos e retângulo) e as mais complexas (losângulo, pentágono, paralelograma e trapézio) • Delimitar seu espaço e diferenciar as diferentes dimensões das formas geométricas;
- 36. Atividade – Apreciaçãodo espaço urbano • Verificar no espaço urbano diferentes formas geométricas.
- 37. Atividade 1 –Apreciação do espaço urbano
- 38. Atividade – Apreciaçãodo espaço urbano
- 39. Atividade – Anatureza por trás das formas geométricas - Catenária • Compreender na natureza como elemento inspirador.
- 40. Atividade 2 –A natureza por trás das formas geométricas - Catenária Missouri - Estados Unidos: Homenagem ao presidente Thomas Jefferson
- 41. Atividade – Anatureza por trás das formas geométricas - Catenária
- 42. Atividade – Combinaçãode Formas geométricas • Compor material didático através das diferentes formas geométricas.
- 43. Bibliografia • LORENZATO, S.Por que não ensinar Geometria?, Educação em Revista –Sociedade Brasileira de Educação Matemática – SBM, ano 3, n. 4, p. 4 – 13, 1o sem. 1995. • PCN – Parâmetros Curriculares Nacionais – Matemática – Ciclo I • SCHMTZ, Carmen e outros. Geometria de 1a a 4a série uma brincadeira séria. R.S. Ed. Unisinos.1994.
Notas do Editor
- #7 Tales - O grande impulsionador da geometria na Grécia, trazidos do Egito. Das suas principais proposições destaca-se a demonstração da altura da pirâmide através da sua sombra
- #8 Platão - Profundo admirador de proporção e geometria. Escreve o “Timeu” em 400 a.C. explicando a origem do universo através de 5 figuras cósmicas perfeitas (Ar – octaedro, Fogo – tetraedro, Universo – dodecaedro, Terra – cubo, Água – icosaedro) Aristóteles de Estagira - explicou que as fases da Lua,também, os eclipses. Afirmava que o Universo e esferico e finito. Aristoteles argumentou a favor da esfericidade da Terra, ja que a sombra da Terra na Lua durante um eclipse lunar e sempre arredondada. Heraclides de Pontus - propôs que a Terra gira diariamente sobre seu próprio eixo
- #9 Euclides – Criador da famosa geometria euclidiana, demonstra nela postulados como “Todos os ângulos rectos são iguais”; “Juntando igual com igual os totais são iguais”; “O todo é maior do que a parte”, etc. Faz das obras mais importantes na história da geometria “Os Elementos” – dividida em 13 volumes (5 de geometria plana, 3 de geometria no espaço) Aristarco de Samos - primeiro a propor a Terra se movia em volta do Sol, antecipando Copérnico em quase 2000 anos. Entre outras coisas, desenvolveu um método para determinar as distâncias relativas do Sol e da Lua à Terra e mediu os tamanhos relativos da Terra, do Sol e da Lua.
- #10 Ele notou que, na cidade egipcia de Siena (atualmente chamada de Aswan), no primeiro dia do verao, ao meio-dia, a luz solar atingia o fundo de um grande poco, ou seja, o Sol estava incidindo perpendicularmente a Terra em Siena. Ja em Alexandria, situada ao norte de Siena, isso nao ocorria; medindo o tamanho da sombra de um bastao na vertical, Eratostenes observou que em Alexandria, no mesmo dia e hora, o Sol estava aproximadamente sete graus mais ao sul. A distancia entre Alexandria e Siena era conhecida como de 5000 estadios. Um estadio era uma unidade de distancia usada na Grecia antiga. Um camelo atravessa 100 estadios em um dia, e viaja a cerca de 16 km/dia. Como 7 graus corresponde a 1/50 de um circulo (360 graus), Alexandria deveria estar a 1/50 da circunferencia da Terra ao norte de Siena e a circunferencia da Terra deveria ser 50×5000 estadios. Infelizmente, nao e possivel se ter certeza do valor do estadio usado por Eratostenes, ja que os gregos usavam diferentes tipos de estadios. Se ele utilizou um estádio equivalente a 1/6 km, o valor esta a 1% do valor correto de 40000 km.
- #11 Hiparco de Nicéia - compilou um catalogo com a posicao no ceu e a magnitude de 850 estrelas. também deduziu o valor correto de 8/3 para a razão entre o tamanho da sombra da Terra e o tamanho da Lua e também que a Lua estava a 59 vezes o raio da Terra de distância; o valor correto é 60. Ele determinou a duração do ano com uma margem de erro de 6 minutos. Ptolomeu - último astrônomo importante da antiguidade que compilou uma série de treze volumes sobre astronomia, conhecida como o Almagesto, que é a maior fonte de conhecimento sobre a astronomia na Grécia.