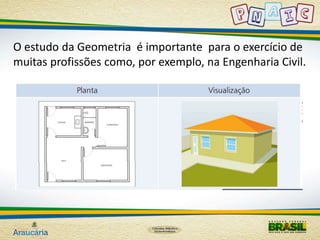
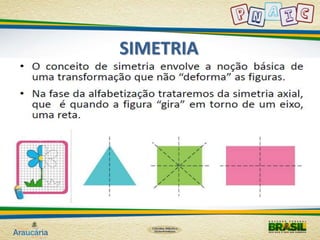
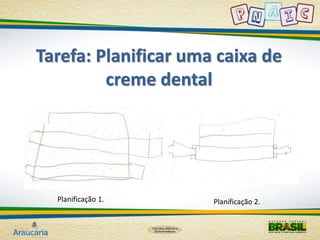
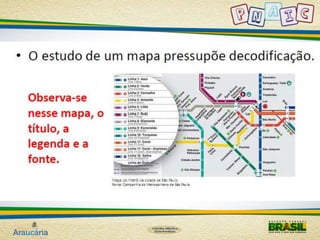
Este documento fornece diretrizes pedagógicas para o ensino de geometria no ciclo de alfabetização, com foco em desenvolver a percepção espacial e reconhecimento de figuras geométricas. Ele discute atividades como observação da natureza, arte, mapas e jogos que podem auxiliar nesse processo, sempre enfatizando a importância do registro das atividades.

1. CADERNO 5
GEOMETRIA
CAMILA RIBEIRO

2. LEITURA DELEITE

3. Objetivos gerais do caderno:
Fornecer subsídios que
permitam auxiliar o professor a
desenvolver trabalhos
pedagógicos, possibilitando às
crianças: construir noções de
localização e movimentação no
espaço físico para a orientação
espacial em diferentes
situações do cotidiano e
reconhecer figuras geométricas
presentes no ambiente.

4. A GEOMETRIA E O
CICLO DE
ALFABETIZAÇÃO
Andréia Aparecida da Silva Brito Nascimento
Evandro Tortora
Gilmara Aparecida da Silva
Giovana Pereira Sander
Juliana Aparecida Rodrigues dos Santos Morais
Nelson Antonio Pirola
Thais Regina Ueno Yamada

5. DIREITOS DE APRENDIZAGEM DA ÁREA
DE MATEMÁTICA (BRASIL, 2012)
Objetivos a serem alcançados por meio do ensino da
Geometria/Espaço e Forma:
Possibilitar aos alunos construírem noções de
localização e movimentação no espaço físico para
orientação espacial em diferentes situações do
cotidiano e reconhecer figuras geométricas.

6. No que diz respeito ao trabalho com a movimentação e
localização, o ensino de geometria deve propiciar aos
alunos desenvolver noções de:
• Noções de lateralidade (direita e esquerda);
• Noções topológicas (dentro e fora);
Que atividades podem auxiliar os alunos
nesse sentido?

7. Registros de trajetos por
meio de:
• expressão oral;
• desenhos;
• relatos escritos.
Registros da localização
por meio de:
• desenhos;
• papel quadriculado;
• croquis;
• mapas.

8. Com o desenvolvimento da percepção geométrica,
o estudante deve ser capaz de :
• Visualizar, discriminar e classificar figuras
geométricas por meio de suas características e
identificar números de lados (faces) e vértices;
• Reconhecer padrões, regularidades e
propriedades de figuras geométricas presentes
em diferentes contextos, por exemplo: na
observação da natureza, obras de arte e
manifestações artísticas de diferentes culturas;

9. • Perceber figuras geométricas por meio de vistas
de objetos e planificação de sólidos geométricos,
por exemplo: dado um objeto, a criança
representa no papel, por meio de desenhos, o
que ela vê em diferentes perspectivas;
• Planificar sólidos geométricos;
• Ampliar e reduzir figuras;
• Compor e decompor figuras;
• Construir diferentes figuras geométrica utilizando
a régua e diferentes softwares;

10. • Resolver problemas que requeiram pensar
geometricamente;
• Relacionar objetos e situações do cotidiano
com sólidos geométricos e vice-versa,
por exemplo: bola de futebol, caixa de
sapato, caixa de leite.

11. PARA QUE SERVE A GEOMETRIA?
ONDE USAMOS OS
CONHECIMENTOS DE GEOMETRIA?

12. O estudo da Geometria é importante para o exercício de
muitas profissões como, por exemplo, na Engenharia Civil.

13. O estudo da Geometria é importante no campo, para
decidir o formato mais adequado de plantações

14. O que deve ser superado no Ensino da
Geometria:
• O ensino isolado da disciplina, no final do ano.
• O ensino da Geometria desconectado de outros
conteúdos, como Números, Grandezas e Medidas e
Estatística.
• A visão de que Geometria se resume às figuras
geométricas, esquecendo-se de que se refere também à
movimentação e localização de pessoas e objetos no
espaço.

15. Quais atividades podem ser
propostas para o trabalho com
geometria?
Atividades de observação e registro de diferentes
figuras geométricas.

16. Que tal um passeio pela cidade?
Pode-se observar
placas de trânsito,
fachadas de casas,
prédios, igrejas e
formato de
praças.

17. Ou uma visita ao museu?
Pode-se observar os
diferentes recursos
utilizados pelos
artistas, como figuras
geométricas, linhas
retas e curvas,
paralelismo,
regularidades e
padrões.

18. Ou conhecer outras comunidades?
Pode-se perceber que a Geometria está presente em
práticas sociais, como a pintura corporal, rituais e
cestarias.

19. IMPORTANTE!
Em todo esse processo, o
REGISTRO é muito importante,
seja ele escrito ou em forma de
desenhos ou diagramas.

20. DIMENSÃO, SEMELHANÇA E
FORMA
Carlos Roberto Vianna
Emerson Rolkouski
Iole de Freitas Druck

21. DIMENSÃO

25. SEMELHANÇA

26. FORMA

28. PARA REFLETIR
As asas de uma
borboleta nos
remetem a que
conceito da
geometria?

29. SIMETRIA

30. O QUE É SIMETRIA?
De uma forma geral, uma figura é simétrica quando
podemos dividi-la em partes iguais, sendo que
coincidem perfeitamente quando sobrepostas.

31. Simetria na escola
Completar figuras sobre o papel
quadriculado, supondo-as
simétricas
Uso de espelhos planos

32. Sugestão de atividade
Uso do “Projetor Mágico” Resultados

33. Possíveis questionamentos
• O que aconteceu com as figuras desenhadas?
• Elas têm o mesmo tamanho?
• O que dizer da posição das figuras desenhadas
em relação às figuras dadas?
• Se dobrarmos o papel, uma figura ficará
sobreposta à outra?
• Quais outros aspectos e relações interessantes
podemos ver nas duas figuras?

34. A natureza é uma fonte de recursos a
serem utilizados no ensino da
Geometria.
O que é possível explorar?

35. • Reconhecer regularidades das formas, como as
figuras geométricas se justapõem;
A casca do abacaxi O favo de mel O casco da tartaruga

36. • Identificar e explorar conceitos e propriedades
geométricas;
• Desenvolver um trabalho interdisciplinar com
Ciências.
• Perceber que a proporção, o padrão e a
regularidade, a beleza e o equilíbrio das formas
encontradas na natureza são fenômenos que
atraem e envolvem o homem.

37. KIRIGAMI
Kirigami (do japonês: de kiru, "recortar", e kami, "papel")
é a arte tradicional japonesa de recorte o papel, criando
representações de determinados seres ou objetos.

40. KIRIGAMI
Vamos fazer toalhinhas para enfeitar a janela utilizando a técnica
KIRIGAMI?

41. PRIMEIROS ELEMENTOS DA
GEOMETRIA
Andréia Aparecida da Silva Brito Nascimento
Evandro Tortora
Gilmara Aparecida da Silva
Giovana Pereira Sander
Juliana Aparecida Rodrigues dos Santos Morais
Nelson Antonio Pirola
Thais Regina Ueno Yamada

42. Tarefa: Planificar uma caixa de
creme dental
Planificação 1. Planificação 2.

43. Questões para mediar a
investigação:
• O que está faltando em cada uma das
representações?
• Se a dobrarmos, o que acontecerá? Teremos
uma caixa?
• Quais são as figuras geométricas
representadas?
• Por que a caixa tem esse formato?

44. Trabalho com a caixa
• Desenhar todos os lados da caixa que você
trouxe.
• Quantos lados a sua caixa possui.
• Comparar com seus colegas para ver se todas
as caixas possuem o mesmo número de lados;
• Quais as figuras geométricas que a sua caixa
possui?
• Pode-se trabalhar: vértice, lado, figuras
geométricas, ...

45. Planificar a sua caixa
• Descolar a sua caixa e abri-la;
• Colá-la novamente, do lado avesso;
• Desenhar no avesso da sua caixa um imóvel
(utilizar giz de cera, canetinhas, cola, tesoura,
papel colorido...)

46. Construir maquete de uma cidade
• Colocar a sua caixa (imóvel), em um local destinado
para as maquetes.
• Observar, em grupo, quais os imóveis estão na mesma
rua, em ruas paralelas, à direita, à esquerda, a frente,
atrás...

47. Desenho da maquete
• Pedir para os alunos desenharem observando de vários
ângulos: oblíqua, frontal (de frente), vertical (de cima)
• Trabalhar os diferentes conceitos: atrás, na frente, ao
lado, na rua paralela...

48. Sugestão de Atividade
Em uma sacola não transparente colocam-se
vários sólidos. A criança deve pegar um deles,
de olhos fechados, e descrevê-lo:
Se tem pontas, se tem vértices, quantas
arestas, se é arredondado...
Essa atividade deve ser utilizada para a
identificação de atributos, classificação de
formas e identificação de propriedades.

49. Atributos definidores ou invariantes
São os atributos que distinguem uma figura de outra e que são utilizados nas
definições.
Quais as características que distinguem o quadrado de outras figuras?
Um dos objetivos do ensino da geometria no ciclo de
alfabetização é levar os alunos a classificar as figuras
geométricas por meio de suas características, as quais
denominaremos de atributos definidores.

50. Atributos relevantes e irrelevantes
As cores são atributos irrelevantes.
Atributos definidores são os
relevantes.

51. Quais são os atributos relevantes de
um quadrado?
Ângulos retos, lados
iguais, quatro lados.

52. Quais são os atributos relevantes de
um triângulo?
Três lados

53. Quais são os atributos relevantes de
um retângulo?
Quatro lados, ângulos
retos

54. Práticas a serem evitadas
Apresentar as figuras
geométricas:
• sempre na mesma
posição;
• sempre com a
mesma cor;
• sempre com o
mesmo tamanho.
Imagem do livro Sem pé nem cabeça, de Pedro Bandeira

55. Práticas adequadas
• Uso de figuras recortadas para que a criança possa
girar, não estabelecendo relação entre cores,
tamanhos ou posições com os nomes das figuras.
• Apresentação de exemplos e contra-exemplos em
sala de aula, ou seja, falar de triângulos e não-triângulos,
quadrados e não-quadrados, e assim por
diante.

56. Práticas adequadas
• Uso do GEOPLANO

57. Práticas adequadas
• Construção de POLIEDROS com canudinhos

58. Direitos de Aprendizagem relativos à
percepção geométrica
•Observar, manusear, estabelecer relações entre figuras
planas e espaciais, compor e decompor figuras.
Sugestão de atividade: exploração do Tangram.

59. •Relacionamento de objetos do cotidiano com os sólidos
geométricos (objetos matemáticos) e vice-versa, reconhecendo
corpos redondos e não redondos (poliédricos).

60. •Planificação de modelos de sólidos geométricos e construção
de modelos de sólidos a partir de superfícies planificadas

61. CONEXÕES DA GEOMETRIA
COM A ARTE
Andréia Aparecida da Silva Brito Nascimento
Evandro Tortora
Gilmara Aparecida da Silva
Giovana Pereira Sander
Juliana Aparecida Rodrigues dos Santos Morais
Nelson Antonio Pirola
Thais Regina Ueno Yamada

62. A geometria e as artes
As conexões entre as artes e as geometrias, além
do estudo de diversos conteúdos geométricos,
dá a oportunidade aos alunos de conhecerem a
vida e a obra de diferentes artistas, contribuindo
para o seu enriquecimento cultural e para
mostrar que a geometria está presente em
diferentes contextos.

63. O QUE SE PODE OBSERVAR?
Nas obras de Oscar Niemeyer?

64. Teatro Paiol - Curitiba
Ponto de ônibus - Curitiba

65. Nas obras de Alfredo Volpi, pintor italiano que
viveu no Brasil?

66. Nas obras de Escher, o artista gráfico holandês ?
O que há de curioso nesta
obra de Escher?

67. Podemos observar uma
exploração bastante criativa
das figuras geométricas.
Uma obra de Mondrian é mais
adequada ao ciclo de
alfabetização do que uma obra
de Escher. Esse fato deve ser
levado em conta no uso das
obras de arte em sala de aula.
E na obra de Piet
Mondrian, nascido
em 1872?
Mondrian, Composição com vermelho,
amarelo e azul, ano de 1921

68. As crianças podem
ser estimuladas a
criar os seus
“Mondrians”.
Ao lado, vemos um
destes desenhos
feitos por crianças
do primeiro ano do
ciclo de
alfabetização.

69. Agora é sua vez!
Aprecie a obra de arte de Mondrian (1906)
- Destaque os
elementos
geométricos usados
por Mondrian.
- Que tal criar uma
“obra de arte” com
esses mesmos
elementos
geométricos?

70. LOCALIZAÇÃO E MOVIMENTO
NO ESPAÇO
Antônio Vicente Marafioti Garnica
Maria Edinéia Martins - Salandim

74. CARTOGRAFIAS
Antônio Vicente Marafioti Garnica
Maria Edinéia Martins - Salandim

76. COMO O USO DOS MAPAS
PODE SERVIR DE RECURSO
DIDÁTICO PARA AS
NOSSAS
SALAS DE AULA?

83. A LATERALIDADE E OS
MODOS DE VER E
REPRESENTAR
Antônio Vicente Marafioti Garnica
Maria Edinéia Martins - Salandim

100. SUGESTÃO DE ATIVIDADE COM MAPAS
MAPA DO TESOURO

101. SUGESTÃO DE ATIVIDADE COM MAPAS
Decida o "formato" da sua caça ao tesouro.
- Pense em uma caça ao tesouro incluindo mapas e bússolas, ou algo em
que as crianças precisem se fantasiar.
- Você pode dividir as crianças em dois times e fazer com que corram pelo
tesouro. (Certifique-se de que as crianças têm idade e maturidade o
suficiente para isso.)
- Você quer que a caça tenha um final específico?
Uma ideia é uma "caça ao quebra cabeças" na qual cada localização
tem uma peça. No final, as crianças montam o quebra cabeças, viram
cuidadosamente e veem a localização do tesouro escrita no verso.
Caças ao tesouro também podem ser feitas numa tarde de culinária,
em que cada localização tem um ingrediente para uma certa receita
"secreta" que será feita no final.

102. SUGESTÃO DE ATIVIDADE COM MAPAS
Comece fazendo as pistas!
Use fotos como pistas. Desenhe ou tire fotos dos lugares que devem
ser investigados.
Faça rimas. "Para encontrar a primeira pista, olhe o pé do dentista."
Você pode usar charadas. Ex.: "Tem chapéu mas não tem cabeça.
Tem boca mas não fala. Tem asa mas não voa. (Um bule.)
Você também pode usar códigos secretos que você encontre na
internet e tinta invisível. (A maneira mais fácil de fazer tinta invisível é
escrever algo com giz de cera branco e deixar as crianças cobrirem
com grifa texto.) Uma outra ideia é tirar uma foto bem de perto de um
objeto e fazer as crianças adivinharem o que é e irem para lá.
Além disso, você pode vendar uma das crianças e dar instruções
verbais para a próxima pista.

103. SUGESTÃO DE ATIVIDADE COM MAPAS
Escolha uma forma de entregar a primeira pista para as crianças.
-A ideia geral é que a primeira pista leve a um local diferente, com outra
pista para um novo local e por aí vai até que cheguem ao tesouro.
Faça um bom tesouro! Coloque o tesouro em
um local bem escondido e depois faça com que
a última pista leve a ele. Decore uma caixa com
fotos ou papel de parede, depois encha com
doces, moedas ou brinquedos.
Crianças adoram se gabar! Inclua um troféu ou
medalha para o vencedor.
Se forem crianças menores, certifique-se de
incluir alguns prêmios de consolação.

104. TAREFA DE CASA
• PARA 30/09 (NOITE) - Trazer um relato de
experiência com uma atividade interdisciplinar
envolvendo GEOMETRIA .

105. • Slides organizados pela
orientadora do
PNAIC/Araucária,
Camila Ribeiro, a partir dos slides
das professoras da UFPR
despactando.blogspot.com