Baixar para ler offline
Carregado porEliana Gonçalves Pereira
Vc6 final[1]
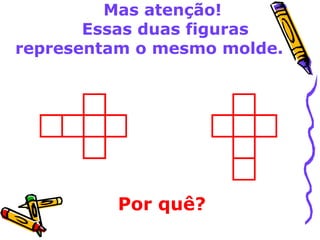
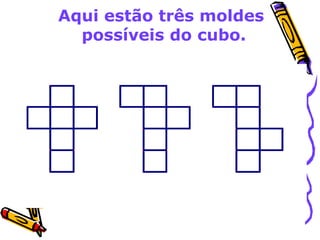
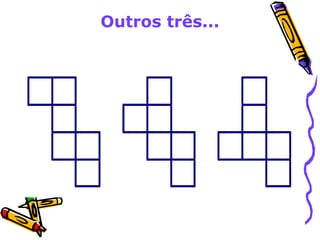
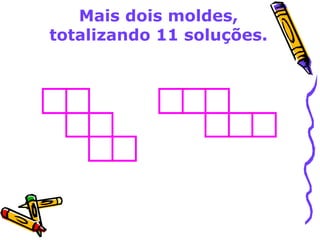
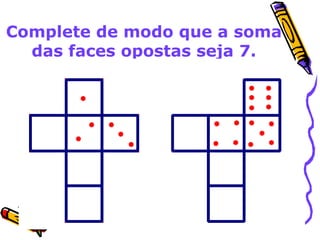
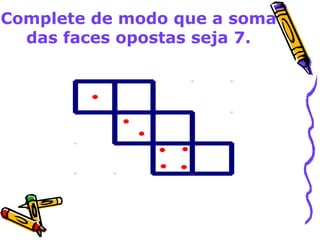
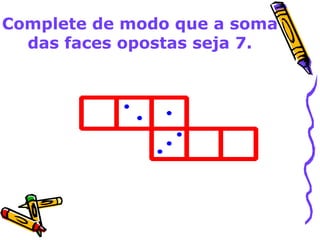
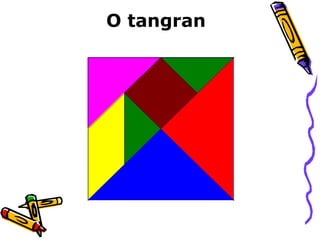
Este documento discute o ensino de geometria nas séries iniciais, abordando sua importância, atividades recomendadas e evolução histórica. Apresenta reflexões sobre como as crianças constroem noções geométricas através de experiências concretas com objetos do espaço. Também fornece exemplos de atividades que desenvolvem conceitos como localização espacial, reconhecimento de formas tridimensionais e propriedades de figuras planas.
Mais conteúdo relacionado
Vc6 final[1]
- 1. 1 PPrroojjeettoo:: EEnnssiinnaarrMMaatteemmááttiiccaa nnaass sséérriieess iinniicciiaaiiss CCEENNPP//SSEEEE--SSPP
- 2. 2 TTeemmaa 55 UUnniiddaaddee 55..55 MMaatteemmááttiiccaa
- 3. vídeo conferência 6 Espaço e Forma
- 4. Pauta • Apresentaçãode algumas atividades de cálculo mental (com ou sem calculadora). • Discussão sobre o ensino e aprendizagem de geometria nos anos iniciais do EF. • Competências matemáticas. • Conexões possíveis com geometria.
- 5. Objetivos • Refletirsobre sua prática em relação ao ensino de geometria. • Refletir sobre a importância do ensino de geometria nas quatro primeiras séries do EF. • Compreender como se dá a construção de relações espaciais pelas crianças.
- 6. • Analisar atividadesgeométricas identificando algumas competências matemáticas trabalhadas, como experimentar, conjecturar, representar, relacionar, comunicar, argumentar e validar.
- 7. • Identificar conexõesentre geometria, natureza e arte analisando de que modo elas fornecem a construção dos conhecimentos geométricos.
- 8. Apresentação de atividades • Algumas DEs apresentam atividades de cálculo mental (utilizando ou não calculadora) desenvolvidas pelos professores após a VC5 – 15 minutos.
- 9. Tarefa 1 •Cada DE vai se subdividir em grupos para analisar as 3 próximas questões e socializar as discussões - 10 minutos. • Apresentação de 3 DEs inscritas e finalização pelo especialista - 15 minutos.
- 10. Tarefa 1 •Como foi sua formação em Geometria? Dê exemplos • Você acha importante ensinar Geometria? Por quê? Dê exemplos. • O que você costuma ensinar de Geometria a seus alunos?
- 11. A Geometria esuas histórias • A Geometria é um dos ramos mais antigos da Matemática e se desenvolveu em função de necessidades humanas. • As civilizações da época pré-histórica utilizavam regras para medir comprimentos, superfícies e volumes.
- 12. • Nas diferentescivilizações – egípcia, babilônica, grega etc. – a Geometria sempre esteve presente.
- 13. Ensino de Geometria- 1956 a 1965 a) Aprendizagem da nomenclatura de linhas (curvas, retas, mistas, quebradas e pontilhadas) e figuras; b) Cálculo de perímetros, áreas e volumes apoiado na memorização de fórmulas sem justificativas.
- 14. 1966 a 1975 Movimento Matemática Moderna · Aspectos geométricos pouco enfatizados; · Trabalho com pontos, retas e planos dentro do quadro da teoria dos conjuntos.
- 15. 1966 a 1975 Os problemas que envolviam aspectos métricos eram pouco explorados, assim como as construções geométricas.
- 16. 1966 a 1975 Década de 70: começaram a surgir propostas de trabalho apoiadas em experiências feitas pelos alunos, a partir das quais eles construíam sus noções geométricas. “Geometria Experimental” (PROJETO PREMEM -MEC/IMECC/UNICAMP, 1972).
- 17. 1976 a 1998 Propostas curriculares e artigos ressaltam a importância do ensino de geometria. Atenção para o desenvolvimento de um pensamento geométrico de tanta relevância para o aluno quanto o pensamento aritmético ou algébrico.
- 18. 1976 a 1998 Propagam-se trabalhos inspirados na teoria de Van Hiele, propostas com tangrans, malhas, poliminós, padrões etc. Piaget contribuiu para a compreensão de como as crianças constroem suas idéias sobre o espaço e as formas.
- 19. Geometria nos PCN 1998 a 2004 Bloco de conteúdo que deve ser trabalhado articuladamente com outros temas. Vivenciando experiências sobre os objetos do espaço em que vive, as crianças constroem conhecimentos relativos à localização e orientação.
- 20. Geometria nos PCN 1998 a 2004 Esse trabalho vai permitir que as crianças penetrem no domínio da representação dos objetos e, assim, construam seu pensamento geométrico.
- 21. A localização ea movimentação no espaço • Tarefa 2 - 15 minutos. • Fazer um esboço da sala onde estão, indicando sua posição na sala. • Algumas DEs apresentam o esboço na câmara-doc.
- 22. Atividades que podemser feitas com as crianças • Minha sala de aula; • Colocando o rabo no burro; • Visitando a escola; • Fotos e percursos; • Caça ao tesouro; • Construção de maquetes.
- 23. As respostas dascrianças • Cubo: dado, aparelho de TV; • Paralelepípedo: caixa de sapato, caixa de remédio, caixa de leite; • Pirâmide: cabana, chapéu, pirâmide da sorte.
- 24. Os objetos tridimensionais Com quem me pareço? • Esfera: bola; • Cone: casca de sorvete, chapéu de palhaço; • Cilindro: lata de óleo, garrafa, copo, osso.
- 25. A passagem dotridimensional para o bidimensional Atividades • Faces dos sólidos – desenhar as faces dos sólidos; • Desmontar caixas e desenhar os moldes.
- 26. A passagem dobidimensional para o tridimensional • Tarefa 3 – 20 minutos • Com 6 quadrados, todos de mesmo tamanho, obtenham diferentes moldes para se construir um cubo. • Quantos moldes diferentes poderemos obter? • Apresentação em câmara-doc.
- 27. Mas atenção! Essasduas figuras representam o mesmo molde. Por quê?
- 28. Aqui estão trêsmoldes possíveis do cubo.
- 29. Aqui estão maistrês moldes.
- 30.
- 31. Mais dois moldes, totalizando 11 soluções.
- 32. A soma dospontos das faces opostas de um dado é sempre 7. Você sabia? Tarefa 4 10 minutos- Completar com pontos as planificações do cubo que vamos apresentar, de maneira que esse fato ocorra. Mas atenção! Procure descobrir os pares de faces opostas mentalmente.
- 33. Complete de modoque a soma das faces opostas seja 7.
- 34. Complete de modoque a soma das faces opostas seja 7.
- 35. Complete de modoque a soma das faces opostas seja 7.
- 36. Semelhanças e diferenças de figuras planas • Um trabalho de observação e construção das formas levará o aluno a perceber semelhanças e diferenças entre elas.
- 37. Sugestões de atividades: contar o número de lados; compor e decompor figuras; perceber a simetria como característica de algumas figuras, e não de outras; etc.
- 38.
- 39. Simetria Para desenvolvera noção se simetria é importante que: • complete figuras (igreja, casinha, navio etc.) usando a simetria; • encontre o eixo de simetria de algumas figuras (o uso de espelhos é bastante recomendado).
- 40. O papel quadriculadoé interessante para obter uma figura simétrica a uma dada por meio de reflexão em reta.
- 41. Essa reta podeser vertical num primeiro momento.
- 42. Num outro, elapode ser horizontal.
- 43. Fazer a reflexãoem reta inclinada é mais difícil...
- 44. O trabalho comos polígonos não deve se restringir apenas à classificação quanto ao número de lados, mas também: • estabelecer semelhanças e diferenças; • encontrar eixos de simetria; • medir lados e ângulos.
- 45. Atividades que levamà classificação de quadriláteros. Quanto ao paralelismo dos lados: Nenhum par de lados paralelos Apenas um par de lados paralelos Dois pares de lados paralelos
- 46. Propor atividades para classificar os quadriláteros também quanto: • à medida dos ângulos. (Há ângulos retos? Quantos?); • à medida dos lados.
- 47. Qual o nomedesse polígono? Tem dois pares de lados paralelos. Seus quatro lados têm medidas iguais.
- 48. E desse? Temdois pares de lados paralelos. Seus quatro ângulos são retos.
- 49. Encontre, caso existam,os eixos de simetria desses quadriláteros. Quadrado Retângulo qualquer Paralelogram o qualquer
- 50. As diagonais doretângulo são eixos de simetria?
- 51. Para aprofundamento “Espaçoe forma: a construção de noções geométricas pelas crianças.” Pires, CMC. et al. Editora PROEM, 2001.