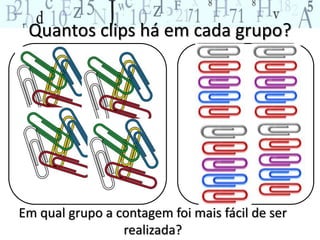
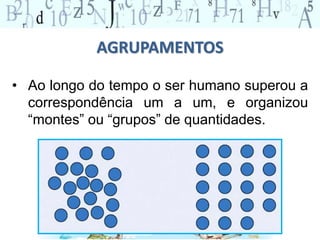
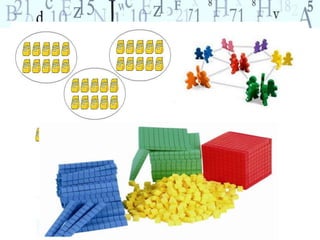
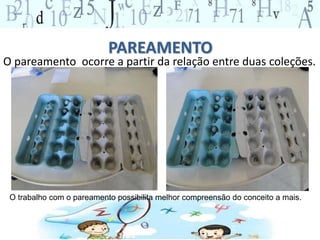
O documento discute conceitos e atividades relacionadas a números e quantificação para crianças. Ele aborda a importância de provocar reflexões sobre números no cotidiano e oferecer experiências que ajudem as crianças a desenvolver conceitos como identificar, quantificar, comparar e representar quantidades. O documento também fornece exemplos de atividades que podem ser aplicadas em sala de aula.

1. Orientadora Aline Manzini
PNAIC – Bertioga
Julho/2014

2. INTENCIONALIDADE PEDAGOGICA
• Provocar reflexões sobre a ideia de números e
seus usos em situações do cotidiano,
oferecendo subsídios para praticas
pedagógicas.

3. OBJETIVOS ESPECÍFICOS
Eixo: Números e operações
• Identificar números em diferentes contextos
e funções;
• Quantificar elementos de uma coleção,
utilizando diferentes estratégias;
• Comunicar as quantidades, utilizando a
linguagem oral, os dedos das mãos ou materiais
substitutivos aos da coleção;

4. • Representar graficamente quantidades
utilizando registros não convencionais e
notação numérica;
• Compartilhar, confrontar, validar e aprimorar
seus registros nas atividades que envolvem
a quantificação
• Reproduzir sequências numéricas em
escalas ascendentes e descendentes a partir
de qualquer número dado;

5. Números
Em todo o tempo e em todo lugar
Antes de cinco meses, os
bebês apresentam uma
sensibilidade quantitativa,
sendo capazes de
discriminar quantidades
pequenas como 1 objeto
de 2 objetos, 1 objeto de 3
objetos.

6. Qual a compreensão dos nossos
alunos sobre os números e
matemática?
Para auxiliarmos as crianças a alcançarem os
objetivos propostos no eixo: “Números e
Operações” é necessário primeiramente
sabermos quais conhecimentos já possuem para
então ofertarmos novos desafios.

7. Detetive do
numero
VIDEO
https://www.youtube.com/watch?v=5Mgnp0HJEmg

8. CORRESPONDÊNCIA “UM A UM”

9. CORRESPONDÊNCIA “UM A UM”
• Andar de ônibus (bancos e pessoas);
• No cinema (bancos e pessoas);
• Sala de aula (carteiras e alunos, materiais e
alunos, lanche e alunos e outros);
• Nas refeições (pratos e pessoas, pratos e
copos e outros);
3

11. Quantos clips há em cada grupo?
Em qual grupo a contagem foi mais fácil de ser
realizada?

12. AGRUPAMENTOS
• Ao longo do tempo o ser humano superou a
correspondência um a um, e organizou
“montes” ou “grupos” de quantidades.

13. AGRUPAMENTOS NA ORGANIZAÇÃO
DA CONTAGEM
Contar e Agrupar são ações que permitem controlar,
comparar e representar quantidades. Daí a importância de
propor atividades para seus alunos que exijam a contagem
de uma coleção de objetos por meio de seu agrupamento
em quantidades menores.

15. PAREAMENTO
O pareamento ocorre a partir da relação entre duas coleções.
O trabalho com o pareamento possibilita melhor compreensão do conceito a mais.

16. ATIVIDADE EM GRUPOS
Cada grupo fará uma lista de JOGOS,
MUSICAS e BRINCADEIRAS que
propiciem a contagem e agrupamento.

17. O NÚMERO: DA ORALIDADE PARA A
ESCRITA – um caminho a percorrer
Uma característica da contagem é a enunciação de
palavras, nomes dos números, numa determinada
sequência fixa, a começar por “um”;
Recitar a sequência numérica não é a mesma coisa
que saber contar com compreensão elementos de um
conjunto.
(p. 35)

18. QUANTOS CLIPS HÁ NO QUADRO?

19. ONDE TEM MAIS?

20. QUAL A PILHA MAIOR?

21. QUANTOS QUADRADINHOS
TERÁ A 4ª FIGURA?

22. SENSO NUMÉRICO
O senso numérico é a capacidade que
permite diferenciar, sem contar, pequenas
quantidades de grandes quantidades;
perceber onde há mais e onde há menos,
assim como permite perceber quando há
“tantos quantos”, uma situação de igualdade
entre dois grupos.

23. SENTIDO NUMÉRICO: HABILIDADE QUE PERMITE QUE O
INDIVÍDUO LIDE DE FORMA BEM SUCEDIDA E FLEXÍVEL COM
OS VÁRIOS RECURSOS E SITUAÇÕES DO COTIDIANO
DESENVOLVER UM SENTIDO NUMÉRICO E
TORNAR-SE NUMERALIZADO

24. INDICADORES DE SENTIDO NUMÉRICO:
Realizar cálculo mental flexível
Realizar estimativas e usar
pontos de referência
Fazer julgamentos
quantitativos e inferências

25. INDICADORES DE SENTIDO NUMÉRICO
ALINA GALVÃO SPINILLO (p.22)
Estabelecer relações
matemáticas
Usar e reconhecer que um
instrumento ou suporte de
representação pode ser mais útil
ou apropriado que outro.

26. CONCLUINDO...
Somente explicações não levam a criança à noção de número.
Pense em um treinador que ensina um menino a jogar futebol
da seguinte maneira: ele explica o que é drible, trave, gol, etc;
faz o menino decorar tudo isso. No dia da partida manda o
menino jogar e marcar gols.
Só com explicações, é quase impossível. Aprende-se a jogar
futebol jogando, tendo contatos, experiências com a bola.
Com as crianças e os números acontece a mesma coisa. Para
entender bem os números, as crianças precisam ter vivido
certas experiências. Só depois disso que os conceitos serão
úteis.

27. ATIVIDADE PARA CASA/ESCOLA
Separados em grupos por escolas, cada cursista deverá
aplicar em sala de aula uma das seguintes atividades:
• Caderno 2: Objetos e quantidades pags 8 a 10, Buzinaro
• O sitio animado pags. 16 a 18; José de Oliveira e Jardim
Vista Linda
• A centopeia pags. 38 e 39; e Cama de gato pags 63 e 64 Boraceia e
Vista Linda
• A fazendinha pags. 39 a 41; Ermirio e Mario Covas
• Uma coleção de lápis pags. 44 e 45 e Arrumando o armário
pg. 77; Giusfredo
• O varal pags. 46 e 47, 78 a 81; Delphino e Chacara
• O pastor e suas ovelhas pags. 73 a 76. Inacio Hora, Rio da
Granja

28. APLIQUE ESTA ATIVIDADE EM SUA SALA DE AULA REALIZANDO,
SE NECESSÁRIO AS DEVIDAS ADEQUAÇÕES.
Responda por e-mail (individualmente, até terça 29/07)
• Qual objetivo desta atividade?
• Qual direito de aprendizagem e eixo foram
contemplados?
• Foi necessário realizar adaptações?
• Planeje uma sequencia didática de atividades com o
mesmo objetivo. Exemplo: caso o foco de sua atividade
tenha sido sequencia numérica, quais outras atividades
de sequencia numérica poderiam ser trabalhadas,
auxiliando a criança a desenvolver este
conceito/habilidade.
Observação: O grupo-escola deverá apresentar e detalhar
a atividade no próximo encontro.

29. LEMBRETES
• Cronograma Portfólio da sala
• ENTREGAR
Portfólios (ano passado) e Sacolinha (1º encontro)
Apostila (intr. e caderno 1)
• Lista presença
• Lista com dados pessoais (conferir e preencher)
• Termo de compromisso

30. REFERENCIAS:
ELEMENTOS CONCEITUAIS E METODOLÓGICOS PARA DEFINIÇÃO DOS DIREITOS DE
APRENDIZAGEM E DESENVOLVIMENTO DO CICLO DE ALFABETIZAÇÃO (1º, 2º E 3º
ANOS) DO ENSINO FUNDAMENTAL Disponível em:
portal.mec.gov.br/index.php?option=com_docman&task
MEC – Ministério da Educação. Pacto Nacional pela Alfabetização na Idade Certa –
Caderno 2: Quantificação, registros e agrupamentos. Brasília: 2013
Canal Nova Escola no Youtube.