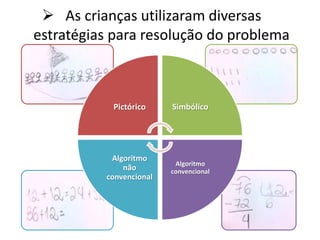
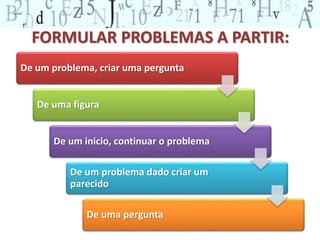
O documento aborda a importância de situações-problema no ensino da matemática, enfatizando que problemas devem ser usados como ponto de partida para a aprendizagem. Apresenta estratégias para a resolução de problemas e discute a relação entre leitura, compreensão e matemática, defendendo a diversificação de abordagens pelos professores. Além disso, sugere que alunos criem seus próprios problemas como forma de aprofundar o entendimento matemático.

1. Orientadora Aline Manzini
PNAIC – Bertioga
Setembro/2014

2. ANTES DE COMEÇAR...
Não se esqueçam do
DIA DA
MATEMÁTICA

3. LEITURA DE DELEITE
Mamãe, por que os dinossauros não vão à escola?
Quentin Gréban

4. DESAFIO MATEMÁTICO
O incrível desafio do sumiço do R$1,00
https://www.youtube.com/watch?v=wfNiIFlpjWs

5. REVELAÇAO DO DESAFIO MATEMÁTICO
O incrível desafio do sumiço do R$1,00
https://www.youtube.com/watch?v=eMEknIUsEXI

6. O QUE É UM PROBLEMA?
O QUE É UMA SITUAÇÃO-PROBLEMA?

7. SITUAÇÃO-PROBLEMA
É toda e qualquer situação onde se deseja
obter uma solução, cuja resposta exige pôr à
prova tudo o que se sabe promovendo a
construção de conceitos, procedimentos e
atitudes relacionadas a Matemática.
PROBLEMA
Algo que apresenta dificuldades para as
quais não há uma solução evidente. É o
desafio em si, a pergunta, o que é necessário
solucionar.

8. Como ensinar
ou aprender
por meio de
situações-problema.
VIDEO
https://www.youtube.com/watch?v=0EA8KGd-zJo

9. Exemplo de uma excelente
situação problema
• Texto scaneado em: http://pt.scribd.com/doc/84407113/O-Misterio-
dos-Numeros-Perdidos

10. Resolução de problemas
PCN de Matemática(1997)
“O ponto de partida da atividade
matemática não é a definição, mas o
problema. No processo de ensino e
aprendizagem, conceitos, ideias e métodos
matemáticos devem ser abordados mediante
a exploração de problemas, ou seja, de
situações em que os alunos precisem
desenvolver algum tipo de estratégia para
resolvê-las.”

11. Vídeo sobre resolução de problemas

12. Vídeo Resolução de problemas
https://www.youtube.com/watch?v=ptgvwKdAp7Y
Elenque as principais ideias apresentadas
no vídeo assistido no HTPC Virtual.

13.  As crianças utilizaram diversas
estratégias para resolução do problema
Pictórico Simbólico
Algoritmo
convencional
Algoritmo
não
convencional

14.  Houve a socialização destas estratégias
Através deste
momento o alunos
avançam em suas
hipóteses e registros
matemáticos.
Todas as estratégias
devem ser valorizadas.

15.  As intervenções da professora foram
encorajadoras e questionadoras.
Notou-se que esta professora primeiramente
estimulou as diversas estratégias de resolução, para
depois apresentar o algoritmo tradicional.
Se tivesse feito na ordem
inversa, as crianças teriam
realizado o exercício já se
utilizando do ensino da
professora como única fonte de
resolução.

16. Como
proceder?

17. Erro e seus encaminhamentos
O desafio matemático de hoje surgiu de um
“erro” de calculo. Como proceder se o
apresentador do vídeo fosse
um de nossos alunos e
utilizasse os dados e cálculos
“errados” para formular e/ou
resolver problemas?

18. Mediação de
leitura em
Matemática –
Gustavo Reis
VIDEO
https://www.youtube.com/watch?v=aBpjaM6P0Lc

19. Principais motivos que levam os
alunos a errarem
Ausência de
compreensão ou
compreensão
inadequada na leitura
Ausência ou equivoco
de compreensão
matemática

20. LEITURA, COMPREENSÃO E RESOLUÇÃO DE
PROBLEMAS MATEMÁTICOS:
Qual a relação?
Para Fonseca e Cardoso
(2005, p.64), os obstáculos
que podem surgir na interação
dos alunos com os textos, se
devem ao vocábulo exótico, à
ambiguidade de significados,
ao desconhecimento funcional
do conteúdo matemático.

21. “A percepção do problema de matemática como um gênero
textual a ser abordado constantemente nas aulas, tanto nas
atividades de leitura de diferentes gêneros textuais, quanto nas
aulas de matemática, nos momentos de reflexão dos seus
textos específicos, já que a capacidade de entender e produzir
textos é fundamental em qualquer disciplina, intensificando,
dessa forma, a importância do papel da leitura como
instrumento de aquisição de outras aprendizagens.”
(Kleiman,1997)

22. ESTRATÉGIAS PARA COMPREENSÃO DO
RACIOCÍNIO MATEMÁTICO
 O professor deve conhecer e diversificar
diferentes tipos de problemas.
Segundo Smole e Diniz: “A seleção de
diferentes tipos de problemas não
pretende ser uma classificação. O objetivo
é simplesmente auxiliar o trabalho em sala
de aula e, especialmente, permitir ao
professor que possa identificar dificuldades
ou evitar que elas existam entre seus
alunos ao trabalhar com resolução de
problemas.”

24. ATIVIDADE EM GRUPO
Cada grupo deve ler um trecho do capitulo 6:
“Conhecendo diferentes tipos de problemas”, do
livro: “Ler, escrever e resolver problemas” de
Smole e Diniz. Registre as principais idéias em
cartolina e apresentar para os demais.

25. Problemas sem solução
Problemas com mais de uma solução
Problemas com excesso de dados
Problemas de logica
Outros problemas não convencionais

26. CAFÉ PEDAGÓGICO

27. ESTRATÉGIAS PARA COMPREENSÃO DO
RACIOCÍNIO MATEMÁTICO
“Prefiro as pessoas que erram porque elas
fazem diferente, usam a criatividade, as
outras fazem sempre do mesmo jeito”
“Quanto mais livres, quanto mais se tenta,
maiores relações se estabelece com a
matemática”
“É muito ruim ser tolhido a cada ação. Se o
raciocínio utilizado for contrariado e
desprezado sempre, a criança não se arrisca
mais.

28. ESTRATÉGIAS PARA COMPREENSÃO DO
RACIOCÍNIO MATEMÁTICO
 Discutir com o grupo, por que a solução está
errada é uma das formas de trabalho que
contribui muito para que a criança reveja suas
estratégias, localize seu erro e reorganize os
dados em busca de uma solução correta.”
 “Ao identificar erros que venham acontecendo
com certa frequência, o professor pode
selecionar alguns deles e montar uma folha
para que as crianças descubram onde está o
erro e tentem corrigi-los através da discussão
com os colegas”

30. ESTRATÉGIAS PARA COMPREENSÃO DO
RACIOCÍNIO MATEMÁTICO
 Direcionar os alunos a formularem problemas
“Quando o aluno cria seus próprios
textos de problemas, ele precisa
organizar tudo que sabe e elaborar o
texto, dando-lhe sentido e estrutura
adequados. Nesse processo,
aproximam-se a língua materna e a
matemática. O aluno deixa, então, de
ser um resolvedor de problemas,
vivenciando o controle sobre o texto
e as idéias matemática” Smole e
Diniz

31. ATIVIDADE EM GRUPO
Cada grupo deve ler um trecho do capitulo 8:
“Por que formular problemas?”, do livro: “Ler,
escrever e resolver problemas” de Smole e Diniz.
Crie um novo problema e apresente para os
demais grupos.

32. FORMULAR PROBLEMAS A PARTIR:
De um problema, criar uma pergunta
De uma figura
De um inicio, continuar o problema
De um problema dado criar um
parecido
De uma pergunta

33. FORMULAR PROBLEMAS A PARTIR:
De uma palavra
De uma resposta
De uma operação
De um tema
De um determinado tipo de texto

35. REFERENCIAS:
ELEMENTOS CONCEITUAIS E METODOLÓGICOS PARA DEFINIÇÃO DOS DIREITOS DE
APRENDIZAGEM E DESENVOLVIMENTO DO CICLO DE ALFABETIZAÇÃO (1º, 2º E 3º
ANOS) DO ENSINO FUNDAMENTAL Disponível em:
portal.mec.gov.br/index.php?option=com_docman&task
MEC – Ministério da Educação. Pacto Nacional pela Alfabetização na Idade Certa –
Caderno 4: Operações na resolução de problemas. Brasília: 2013
SOLÉ, I. Estratégias de leitura. 6ª edição. POA: Artmed, 1998.
SMOLE, Kátia S. ; DINIZ, Maria I. Ler escrever e resolver problemas: habilidades básicas
para aprender. Porto Alegre: Artmed Editora,2001.