O documento apresenta conceitos sobre funções afins, como:
1) Uma função afim relaciona duas grandezas onde a variação de uma é proporcional à variação da outra.
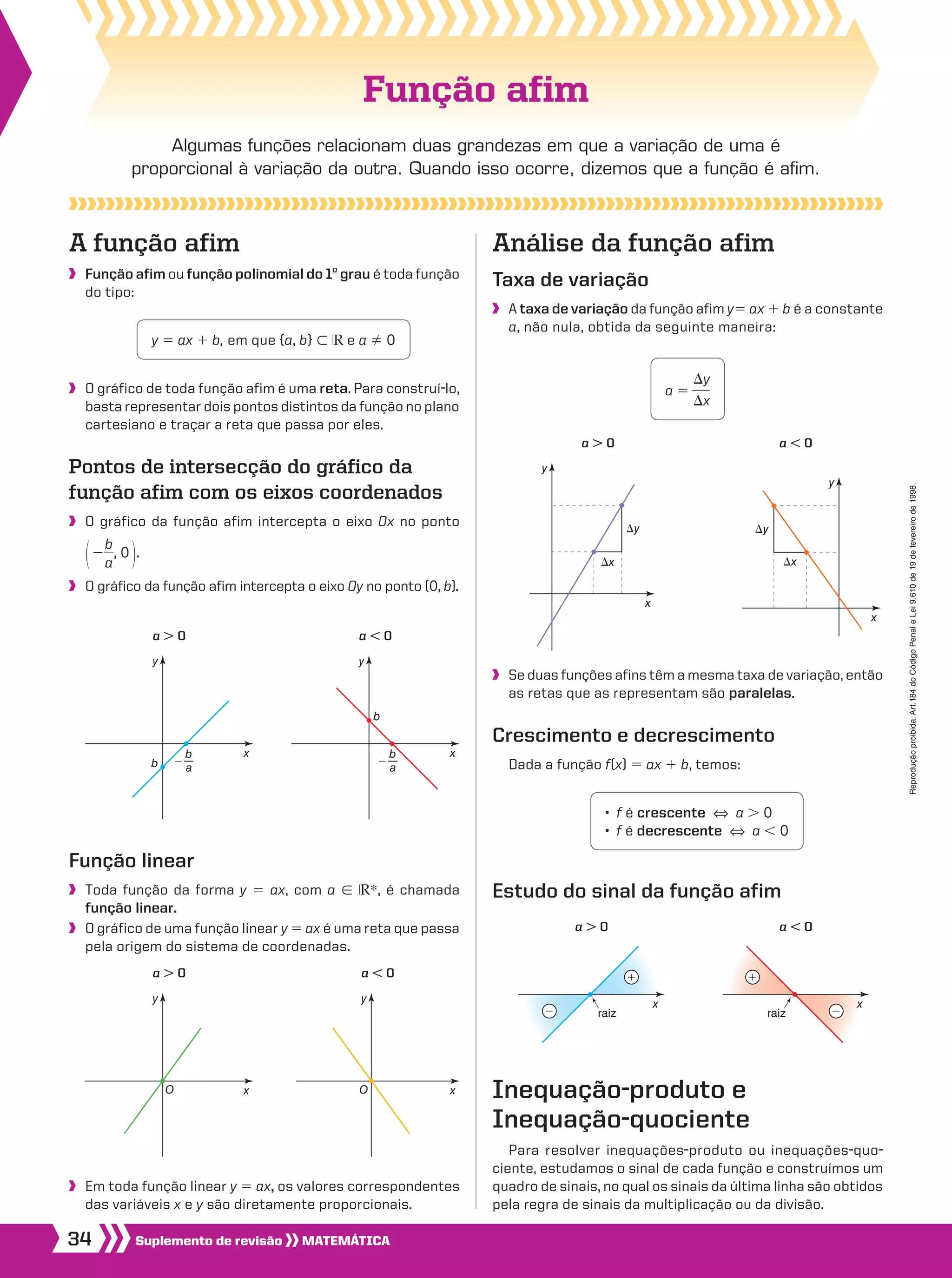
2) O gráfico de uma função afim é uma reta.
3) O gráfico de uma função afim intercepta os eixos em pontos que podem ser determinados a partir da equação da reta.
![Reproduçãoproibida.Art.184doCódigoPenaleLei9.610de19defevereirode1998.
35Função afim NO VESTIBULAR
1. (Mackenzie-SP) Os gráficos das funções y 5 x 1 2 e
y 5 2x1 6 definem, com os eixos, no primeiro quadrante,
um quadrilátero de área:
a) 12 c) 10 e) 14
b) 16 d) 8
2. (Udesc) Sabemos que a receita total RT de certo produto
produzido por uma família de agricultores é dada pela
função RT(q) 5 q 1 2, em que q é a quantidade de unida-
des do produto. Determine a função do primeiro grau,
custo total CT(q) deste produto; sabendo que, quando a
quantidade do produto é de 3 unidades, o custo total é
de R$ 4,00; e que, quando a quantidade do produto é de
4 unidades, a receita total é igual ao custo total. Faça o
esboço do gráfico das funções RT(q) e CT(q).
3. (UFPel-RS)Muitosbrasileirossonhamcomempregosformais.
Na falta destes, cada vez mais as pessoas precisam buscar
formas alternativas de conseguir uma renda.Para isso,uma
família decidiu montar uma malharia. O gráfico abaixo
mostra o custo mensal de produção dessa empresa.
No Vestibular
Função afim
Sabendo que as peças são vendidas por R$ 19,50 e que a
família almeja um lucro mensal de R$ 4.200,00, o número
de peças produzidas e vendidas, para atingir esse fim,
deverá ser:
a) 215 c) 467 e) 494
b) 400 d) 525 f) I.R.
(Nota: Admita que o custo C para x peças produzidas é
uma função afim.)
4. (Mackenzie-SP) A figura mostra os esboços dos gráficos
das funções A(x) e B(x), que fornecem os preços que as
copiadoras, A e B, cobram para fazer x cópias de uma
folha. Para fazer 360 cópias, a copiadora A cobra:
a) R$ 7,00 a menos que B.
b) R$ 5,00 a mais que B.
c) R$ 10,00 a menos que B.
d)
3
__
2
do que cobra B.
e) O mesmo preço cobrado por B.
No
de peças
Custo em real
468
441
49 52
x
B
A
R$
12
30
72
200 540 1.400
Inicialmente, vamos determinar o ponto de intersecção
dos gráficos que representam as duas funções dadas.
Para isso, resolvemos o sistema:
{
y 5 x 1 2
y 5 2x 1 6
] x 5 2 e y 5 4
Assim, obtemos o gráfico ao
lado.
A área do quadrilátero em
destaque é igual à soma da área
de um trapézio de base maior
4, base menor 2 e altura 2 com
a área de um triângulo retângulo isósceles cujos catetos
medem 4. Ou seja, a área é dada por:
(4 1 2) 3 2
_________
2
1
4 3 4
____
2
5 14
Alternativa e.
Como a receita total é igual ao custo
total, para 4 unidades temos que:
RT(4) 5 CT(4) 5 4 1 2 5 6
Assim, o gráfico da função custo total,
CT(q) 5 aq 1 b, passa pelos pontos
A(3, 4) e B(4, 6). Substituindo, temos:
{ 4 5 a 3 3 1 b
6 5 a 3 4 1 b
] a 5 2 e b 5 22
Assim, a função custo total é
CT(q) 5 2q 2 2.
Admitindo que a função custo C seja afim, temos:
C(x) 5 ax 1 b, com C(x) em real e x representando o
número de peças. Como o gráfico de C passa pelos
pontos (49, 441) e (52, 468), temos:
{ 441 5 a 3 49 1 b
468 5 a 3 52 1 b
] a 5 9 e b 5 0
Logo, C(x) 5 9x, C(1) 5 9 e, portanto, o lucro em real por
cada camiseta é 19,5 – 9 5 10,5.
Para que a família tenha um lucro de R$ 4.200,00, o
número de camisetas produzidas e vendidas deverá
ser:
4.200
_____
10,5
5 400
Alternativa b.
Exercício1Exercício2Exercício3Exercício4
Sejam A(x) e B(x), respectivamente, as funções que
fornecem os preços, em real, das copiadoras A e B em
função do número x de cópias.
Para x 9 [0, 540] a função A(x) é representada por uma
função linear com taxa de variação igual a
Sy
___
Sx
5
30 2 0
_______
540 2 0
5
1
___
18
. Assim, para esse domínio, temos
A(x) 5
x
___
18
e, portanto, A(360) 5
360
____
18
5 20.
Para x 9 [200, 1.400], a função B(x) 5 ax 1 b é
representada por uma função afim cujo gráfico passa
pelos pontos P(200, 12) e Q(1.400, 72). Assim, temos:
{ 12 5 a 3 200 1 b
72 5 a 3 1.400 1 b
] a 5 1 ___
20
e b 5 2
Logo, para esse domínio, temos B(x) 5
x
___
20
1 2 e,
portanto, B(360) 5 20.
Alternativa e.
x
y � x � 2
y � �x � 6
y
6
2
4
2 6
q
RT
CT
2
1
�2
�2
034_037_SR_MAT_PLUS_T_04.indd 35 21.10.10 14:47:07](https://image.slidesharecdn.com/funoafim-160103024200/85/Funcao-afim-2-320.jpg)

![Reproduçãoproibida.Art.184doCódigoPenaleLei9.610de19defevereirode1998.
37Função afim NO VESTIBULAR
a) Para a drogaria A, serão enviadas x caixas do depósito
D1 e, portanto, 30 2 x caixas do depósito D2. Assim, o
gasto GA com transporte será:
GA 5 10x 1 12(30 2 x) 5 22x 1 360
Para a drogaria B, serão enviadas y caixas do depósito D1
e, portanto, 40 2 y caixas do depósito D2. Assim, o gasto
GB com transporte será:
GB 5 14y 1 15(40 2 y) 5 2y 1 600
Assim, o gasto total é:
GA 1 GB 5 22x 2 y 1 960
b) Para o gasto ser mínimo, devemos encomendar todas as
caixas possíveis do depósito D1, ou seja, x 1 y 5 40 (I).
Por outro lado, como o gasto total é 890 reais, temos
2x 2 y 1 960 5 890 (II).
Resolvendo o sistema formado pelas equações I e II,
temos:
{
x 1 y 5 40
22x 2 y 5 270
] x 5 30 e y 5 10
Logo, serão enviadas 30 caixas de D1 e 0 caixa de D2 para
a drogaria A; 10 caixas de D1 e 30 caixas de D2 para a
drogaria B; e os gastos serão, respectivamente, GA 5 300
reais e GB 5 590 reais.
Exercício8Exercício9 a) Podemos admitir que, entre os anos de 1965 e 1972
e entre 1987 e 2005, o número de baleias caçadas
anualmente é nulo.
Entre 1972 e 1987, o gráfico representa um
segmento de reta; assim, sua taxa de variação é:
34.200 2 0
____________
1.987 2 1.972
5 2.280
b) Entre o final de 1987 e o final de 2005, o número de
baleias caçadas por ano pelos barcos japoneses foi:
(41.840 2 35.000)
_______________
(2.005 2 1.987)
5
6.840
_____
18
5 380
Desse modo, entre o final de 1987 e o final de 1990, o
número de baleias capturadas foi aproximadamente:
380 3 (90 2 87) 5 380 3 3 5 1.140
Somando esse valor ao que o Japão caçou entre 1965
e 1987, obtemos:
35.000 1 1.140 5 36.140
Entre 1965 e 2005, os barcos brasileiros caçaram
13.500 baleias, enquanto os barcos soviéticos
abateram 34.200 baleias.
Assim, concluímos que, entre 1965 e 2005, o número
de baleias caçadas foi aproximadamente:
13.500 1 34.200 1 36.140 5 83.840
A taxa de variação da função na empresa A é
Sy
___
Sx
5
165 2 30
________
300 2 0
5 0,45, e seu coeficiente linear é 30.
Assim, a função A(x), que representa o valor pago, em
real, em função da quilometragem x, é A(x) 5 30 1 0,45x.
A taxa de variação da função na empresa B é
Sy
___
Sx
5
250 2 50
________
500 2 0
5 0,4, e seu coeficiente linear é 50.
Assim, a função B(x), que representa o valor pago, em
real, em função da quilometragem x, é B(x) 5 50 1 0,4x.
Logo, para rodar 400 km, a empresa A cobra, em real,
A(400) 5 30 1 180 5 210, e a empresa B cobra, em real,
B(400) 5 50 1 160 5 210.
Alternativa c.
a) Como para 0 t 10 o gráfico é um segmento de
reta, o gráfico da função P(t) 5 at 1 b passa pelos
pontos A(0, 5) e B(10, 10). Substituindo, temos:
{ 5 5 a 3 0 1 b
10 5 a 3 10 1 b
] a 5
1
__
2
e b 5 5
Assim, a expressão da função para esse intervalo de
tempo t é:
P(t) 5
1
__
2
3 t 1 5 e P(6) 5 8 kg
b) Como t . 0, temos que t 1 10 . 0. Assim:
10 ,
120t 2 1.000
___________
t 1 10
70 ]
] 10t 1 100 , 120t 2 1.000 70t 1 700
} 100 , 110t 2 1.000 e 50t 1.700 ]
] t . 10 e t 34
} 10 , t 34
1
______
x 2 20
1
______
12 2 x
]
1
______
x 2 20
2
1
______
12 2 x
0
}
22x 1 32
______________
(x 2 20)(12 2 x)
0
Portanto: x , 12 ou 16 x , 20
Alternativa b.
Exercício5Exercício6Exercício7
� �
�
��
�
�
�
�
�
� ���
� � ��
12
�2x � 32
12 � x
x � 20
16
16
20
2012
�2x � 32
(x � 20)(12 � x)
65
0
A � 2.000
Númerodebaleiascaçadas
B � 4.000
85
Ano
95 0575
034_037_SR_MAT_PLUS_T_04.indd 37 21.10.10 14:47:09](https://image.slidesharecdn.com/funoafim-160103024200/85/Funcao-afim-4-320.jpg)