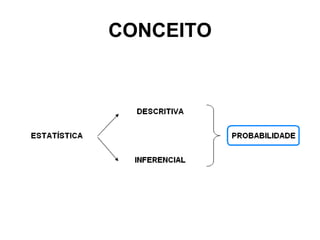
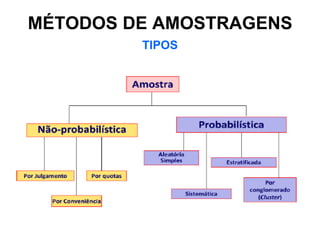
Este documento fornece informações sobre um caderno de notas sobre estatística inferencial. Ele discute conceitos como população, amostra, métodos de amostragem, variáveis, distribuição normal e estimação por ponto. O documento apresenta exemplos para ilustrar esses conceitos e exercícios para praticar cálculos estatísticos.




















































![EXERCÍCIO
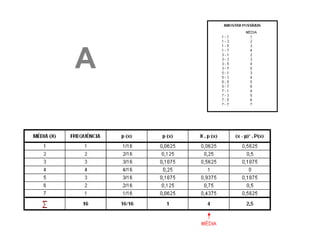
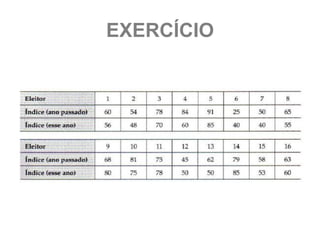
Você escreve os valores da população [1, 3, 5, 7] em
pedaços de papel e os coloca em uma caixa.
Você seleciona dois papéis aleatoriamente, com
substituições.
a) Liste todas as amostras possíveis de tamanho n = 2 e
calcule a média de cada.
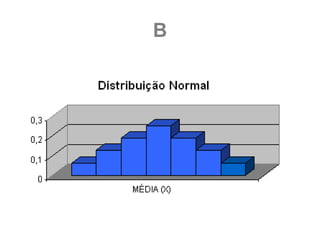
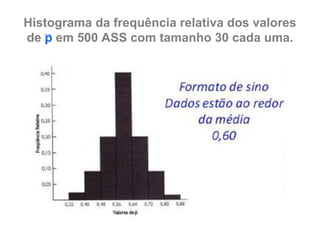
b) Represente essas médias que formam a distribuição
amostra de média das amostras em um histograma.
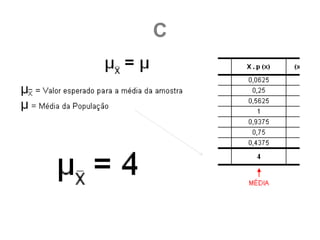
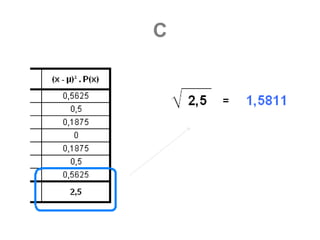
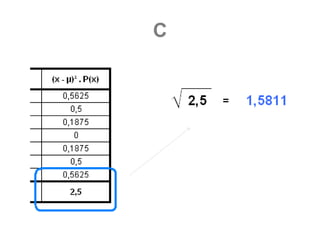
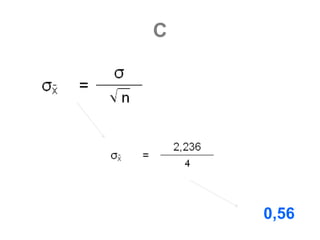
c) Encontre a média e o desvio padrão da média das
amostras. Compare seus resultados com a média μ=4 e
desvio padrão 2,236 da população.](https://image.slidesharecdn.com/estastticainferencial-111126120724-phpapp01/85/Estastitica-Inferencial-90-320.jpg)