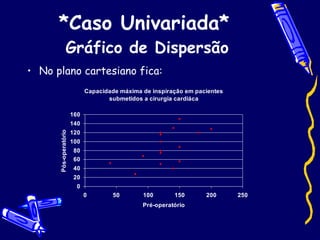
Este documento descreve os conceitos iniciais da análise de regressão linear. Ele explica que a regressão linear avalia se uma variável dependente é consequência de uma ou mais variáveis independentes e, caso seja, se essa relação é constante, crescente ou decrescente. Também descreve os tipos de variáveis envolvidas, o caso univariado com um gráfico de dispersão e linha de tendência, e os três passos da análise de regressão: correlação, regressão e testes estatísticos.

1. Inferência – Parte 4 Análise de Regressão Linear Conceitos Iniciais

2. Análise de Regressão Linear * Objetivo * Possibilitar ao pesquisador a avaliar entre variáveis pareadas se uma delas, chamada de Dependente, é ou não conseqüência de outra(s) variável (eis), denominada de independente(s);

3. Análise de Regressão Linear * Objetivo * Caso uma variável seja conseqüência das outras, avaliar se faz de forma constante, crescente ou decrescente.

4. Análise de Regressão Linear * Tipo de Variáveis * No caso de Regressão Linear, é necessário que as variáveis sejam: Pareadas; Reais, podendo ser inteira, porem não-restrita.

5. Análise de Regressão Linear * Caso Univariada* Neste caso o que se tem são duas variáveis pareadas, digamos x e y, e pelo qual deseja verificar se os valores da variável y(dependente) é ou não conseqüência da variável x (independente).

6. *Caso Univariada* Pontos Amostrais Considere que a amostra tenha fornecido os seguintes pares de valores: (x 1 , y 1 ); (x 2 ,y 2 ); . . . ; (x n ,y n ).

7. *Caso Univariada* Principio Matemático Por se tratar do modelo linear, indica que se baseia no princípio matemático de uma reta, sendo que para ter uma visão de seu comportamento tem-se o:

8. *Caso Univariada* Gráfico de Dispersão Utiliza-se do eixo cartesiano pelo qual insere nele cada par obtido na amostra, tal qual a ilustração:

9. *Caso Univariada* Gráfico de Dispersão Pesquisa: Avaliar a capacidade de respiração máxima em pacientes obesos e submetidos à cirurgia de estomago e com o auxilio da fisioterapia. Acadêmicas Renata e Joyce

10. *Caso Univariada* Gráfico de Dispersão No tocante à Pressão Inspiratória máxima a amostra coletada forneceu (mm/Hg):

11. *Caso Univariada* Gráfico de Dispersão No plano cartesiano fica:

12. * Gráfico de Dispersão* Linha de Tendência Por linha de tendência compreende como sendo a “melhor” curva matemática que se ajusta estatisticamente aos dados obtidos em uma amostra; No objetivo deste capítulo é a Reta.

13. * Gráfico de Dispersão* Linha de Tendência

14. Análise de Regressão * Passo 1 * Avaliar, de forma descritiva, se existe uma relação linear entre as variáveis criadas sendo que para isto utiliza da parte denominada de Correlação ;

15. Análise de Regressão * Passo 2 * Encontrar aquela pela qual seja a reta que se ajusta de forma mais precisa aos dados e esta parte é chamada de Regressão ou Ajustamento ;

16. Análise de Regressão * Passo 3 * Fazer testes estatísticos pelos quais visa comprovar se os valores descritivos encontrados têm valores pelos quais são estatisticamente significativos ou não.

17. Inferência – Parte 4 Análise de Regressão Linear Conceitos Iniciais FIM Prof. Gercino Monteiro Filho