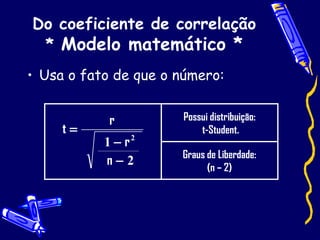
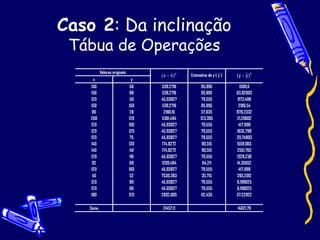
O documento descreve testes de coeficientes em análise de regressão linear, incluindo teste do coeficiente de correlação e da inclinação. O teste do coeficiente de correlação é usado para verificar se existe uma relação significativa entre variáveis, enquanto o teste da inclinação avalia se a reta ajustada é horizontal ou inclinada. Exemplos ilustram como aplicar os testes e interpretar os resultados estatisticamente.

1. Inferência – Parte 4 Análise de Regressão Linear Teste de Coeficientes

2. Teste de Coeficientes * Razão de Ser * Quando encontra os coeficientes em análise de Regressão, tem seus valores, porem não sabe precisar o grau de grandeza. Assim Testes de Coeficientes visa avaliar e comprovar suas grandezas para que em uma pesquisa, possa tirar conclusões acerca destes coeficientes quando estende o resultado de uma amostra para uma população

3. Teste de Coeficientes Objetivo Comprovar estatisticamente a significância dos valores descritivos em um modelo de regressão e de Correlação de acordo com o que pretende avaliar em uma pesquisa.

4. Teste de Coeficientes Caso 1: Do coeficiente de correlação Objetivo: Comprovar se uma das variáveis é explicada em função da outra variável de forma significativa ou não. Quadro d Hipóteses:

5. Do coeficiente de correlação * Conclusão final* Se p < 0,05, ou seja se for significativo, indicará que o coeficiente não é nulo, e assim existe relação significativa entre as variáveis; Se p > 0,05, ou seja se Não for significativo, indicará que o coeficiente é nulo, e assim a variável dependente não se avalia por valores da independente.

6. Do coeficiente de correlação * Modelo matemático * Usa o fato de que o número:

7. Do coeficiente de correlação * Exemplo* Da Pesquisa: Avaliar a capacidade de respiração máxima em pacientes obesos e submetidos à cirurgia de estomago e com o auxilio da fisioterapia. (Acadêmicas: Renata e Joyce); Faça um teste para verificar se existe relação significativa entre o pré-operatório e o pós-operatório da capacidade de inspiração.

8. Do coeficiente de correlação * Exemplo* Dados Originais

9. Do coeficiente de correlação * Exemplo 1* Solução Quadro de hipóteses: Pelos resolução do presente, em Correlação de Pearson, os valores encontrados foram: n = 18 e r = 0,588, Com estas informações, vem:

10. * Exemplo 1* Solução Na fórmula: Vem: Graus de liberdade: 18 – 2 = 16

11. * Exemplo 1* Solução – Uso da Tábua Na tabela t-Student vem que: p < 0,010 Conclusão A diferença foi significativa, isto é, capacidade de inspiração no pós-operatório está diretamente associada à do pré-operatório.

12. Teste de Coeficientes Caso 2 : Da inclinação Objetivo: Avaliar se, quando faz um ajuste, a reta identifica como sendo horizontal (valores da variável dependente como sendo constante) ou se inclinada (crescente ou decrescente)

13. Teste de Coeficientes Caso 2 : Da inclinação Quadro de Hipóteses Modelo matemático

14. Caso 2 : Da inclinação * Exemplo 2 * Dos dados da capacidade inspiratória, testar se a reta ajustada é ou não horizontal. (Em outras palavras: Testar se a relação entre Inspiração no Pré-operatório e Pós-Operatório se faz de forma constante ou não)

15. Caso 2 : Da inclinação * Exemplo 2 * Solução Quadro de hipóteses No tópico: REGRESSÃO LINEAR, foi feito o ajuste e obteve:

16. Caso 2 : Da inclinação Estimativa No modelo matemático, é necessário que seja efetuado todas as estimativas de y, baseado nos valores amostrados de x, cujo procedimento é: Substituir cada valor de x, na equação da reta de ajuste e encontrar o de y.

17. Caso 2 : Da inclinação Estimativa Assim procedendo vem: i) Para x = 150 fica: Y est = 13,795 + 0,548x150 = 95,995 ii) para x = 120 vem: Y est = 13,795 + 0,548x120 = 79,555

18. Caso 2 : Da inclinação Estimativa Procedendo da forma citada, chega que as estimativas foram:

19. Caso 2 : Da inclinação Cálculos Intermediários Devido ao fato da fórmula ser: Necessita calcular cada uma das somas dentro do radical, assim, procedendo e com o auxílio da Tábua de Operações, vem:

20. Caso 2 : Da inclinação Tábua de Operações

21. Caso 2 : Da inclinação Valor de t Com os dados da Tábua de Operações e o Resultado do ajuste, como: Chega a:

22. Caso 2 : Da inclinação Uso da tabela t-student Graus de Liberdade: 18 – 2 = 16

23. Caso 2 : Da inclinação Conclusão Com p < 0,05, conclui: A diferença foi significativa, isto é, a reta ajustada é inclinada; Como b = 0,548 (positivo) indica que ela é crescente, ou seja, aumentando a inspiração no pré-operatório, ficará aumentado no pós-operatório.

25. Regressão Linear Ajuste de Uma Reta FIM Prof. Gercino Monteiro Filho