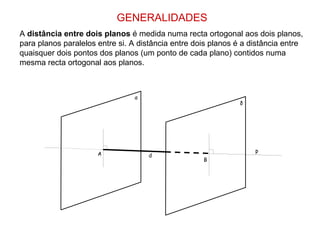
O documento descreve como calcular a distância entre dois planos em geometria descritiva. Existem vários métodos dependendo se os planos são paralelos, projectantes ou oblíquos. No caso geral, traça-se uma reta ortogonal aos planos e mede-se a distância entre os pontos de interseção com cada plano.

1. GEOMETRIA DESCRITIVA A 11.º Ano Problemas Métricos Distância entre Dois Planos

2. GENERALIDADES A distância entre dois planos é medida numa recta ortogonal aos dois planos, para planos paralelos entre si. A distância entre dois planos é a distância entre quaisquer dois pontos dos planos (um ponto de cada plano) contidos numa mesma recta ortogonal aos planos. p d A α δ B

3. O método geral para a determinação da distância entre dois planos paralelos consiste em: 1. conduzir uma recta qualquer, ortogonal aos dois planos; 2. determinar os pontos de intersecção dessa recta com ambos os planos; 3. a distância entre os dois pontos de intersecção é a distância entre os dois planos (é o comprimento do segmento de recta que tem extremos nos dois pontos).

4. Distância entre Dois Planos Projectantes Pretende-se as projecções e a V.G. da distância entre os dois planos. Primeiro, é conduzido uma recta ortogonal aos dois planos, a recta p . f α h α Depois, são determinados os pontos de intersecção da recta p com os planos. Como os planos são projectantes frontais, as intersecções são determinadas nos cruzamentos da projecção frontal da recta com os traços frontais dos planos. p 2 p 1 V.G. f δ h δ x A 1 A 2 B 1 B 2 A distância de A a B é a distância entre os dois planos. O segmento de recta [ AB ] é um segmento de recta frontal, pelo que a V.G. de AB está na projecção frontal de AB , A 2 B 2 .

5. São dados dois planos verticais, α e γ . O plano α faz um diedro de 45º (a.d.) com o Plano Frontal de Projecção. O plano γ corta o eixo x num ponto situado 4 cm para a direita do ponto de intersecção do plano α com o eixo x . Determina as projecções e a V.G. da distância entre os dois planos. f α h α f γ h γ p 1 p 2 V.G. Primeiro, é conduzido uma recta ortogonal aos dois planos, a recta p . Depois, são determinados os pontos de intersecção da recta p com os planos. Como os planos são projectantes horizontais, as intersecções são determinadas nos cruzamentos da projecção horizontal da recta com os traços horizontais dos planos. x A 1 A 2 B 1 B 2 A distância de A a B é a distância entre os dois planos. O segmento de recta [ AB ] é um segmento de recta horizontal, pelo que a V.G. de AB está na projecção horizontal de AB , A 1 B 1 .

6. Distância entre Dois Planos Oblíquos Pretende-se as projecções e a V.G. da distância entre os dois planos. Primeiro, é conduzido uma recta ortogonal aos dois planos, a recta p . f α h α Depois, são determinados os pontos de intersecção da recta p com os planos. Como nem a recta nem os planos são projectantes, as intersecções são determinadas pelos cruzamentos dos traços dos planos com as projecções da recta, através do plano auxiliar γ, que é projectante horizontal e contém a recta p . p 2 p 1 V.G. f θ h θ f γ ≡ h γ ≡ i 1 i 2 i’ 2 ≡ i’ 1 (f υ ) ≡ e 2 ≡ e 1 ≡ A r x A 1 A 2 B 1 B 2 A distância de A a B é a distância entre os dois planos. O segmento de recta [ AB ] é um segmento de recta oblíquo, pelo que a V.G. de AB tem que ser obtida pelo processo de rebatimento. F 1 F 2 H 1 H 2 H’ 1 H’ 2 B r

7. É dado um plano oblíquo α, ortogonal ao β 1,3 . O traço frontal do plano α faz um ângulo de 40º (a.e.) com o eixo x. É dado um plano μ, paralelo ao plano α. O plano μ corta o eixo x num ponto situado 8 cm para a esquerda do ponto de intersecção do plano α com o eixo x . Determina as projecções e a V.G. da distância entre os dois planos. f α h α f μ h μ Primeiro, é conduzido uma recta ortogonal aos dois planos, a recta p . p 1 p 2 Depois, são determinados os pontos de intersecção da recta p com os planos. Como nem a recta nem os planos são projectantes, as intersecções são determinadas pelos cruzamentos dos traços dos planos com as projecções da recta, através do plano auxiliar θ , que é projectante frontal e contém a recta p . ≡ f θ h θ ≡ i 2 i 1 i’ 1 (h φ ) ≡ e 1 ≡ e 2 ≡ A r V.G. ≡ i’ 2 x H 1 H 2 F 1 F 2 F’ 1 F’ 2 A 1 A 2 B 1 B 2 A distância de A a B é a distância entre os dois planos. O segmento de recta [ AB ] é um segmento de recta oblíquo, pelo que a V.G. de AB tem que ser obtida pelo processo de rebatimento. B r

8. São dados dois planos oblíquos e paralelos, θ e δ. O plano θ corta o eixo x num ponto com -4 cm de abcissa, com o seu traço horizontal a fazer um ângulo de 45º (a.e.) com o eixo x , e o seu traço frontal a fazer um ângulo de 60º (a.d.) com o eixo x. O plano δ corta o eixo x num ponto com 2 cm de abcissa. Determina as projecções e a V.G. da distância entre os dois planos. f θ h θ f δ h δ Primeiro, é conduzido uma recta ortogonal aos dois planos, a recta p . p 1 p 2 Depois, são determinados os pontos de intersecção da recta p com os planos. Como nem a recta nem os planos são projectantes, as intersecções são determinadas pelos cruzamentos dos traços dos planos com as projecções da recta, através do plano auxiliar α, que é projectante horizontal e contém a recta p . f α ≡ h α i 2 ≡ i 1 ≡ i’ 1 i’ 2 (f υ ) ≡ e 2 ≡ e 1 ≡ A r V.G. x y ≡ z H’ 1 H’ 2 H 1 H 2 F 1 F 2 A 1 A 2 B 1 B 2 A distância de A a B é a distância entre os dois planos. O segmento de recta [ AB ] é um segmento de recta oblíquo, pelo que a V.G. de AB tem que ser obtida pelo processo de rebatimento. B r

9. Distância entre Dois Planos de Rampa via Rebatimento Pretende-se as projecções e a V.G. da distância entre os dois planos. f ρ h σ h ρ f σ Primeiro, é conduzido uma recta ortogonal aos dois planos, a recta p . p1 ≡ p 2 Depois, são determinados os pontos de intersecção da recta p com os planos. Como nem a recta nem os planos são projectantes, as intersecções são determinadas pelos cruzamentos dos traços dos planos com as projecções da recta, através do plano auxiliar π, que é plano de perfil e contém a recta p . Para se determinar os pontos A e B é necessário recorrer ao processo de rebatimento. ≡ f π ≡ h π ≡ F 1 ≡ i 1 ≡ i 2 ≡ F’ 1 ≡ i’ 1 ≡ i ’ 2 ≡ e 1 ≡ h πr ≡ (e 2 ) ≡ f πr ≡ H r i r i’ r p r V.G. x H 2 H 1 F 2 F’ 2 F r F’ r A r B r A r B r é a V.G. da distância entre os dois planos. Invertendo o rebatimento do plano π, obtêm-se as projecções dos pontos A e B , e do segmento de recta [ AB ]. A 1 A 2 B 1 B 2

10. São dados dois planos de rampa paralelos ao β 2,4 , ρ e σ. O traço frontal do plano ρ tem 2 cm de cota e o traço horizontal do plano σ tem 5 cm de afastamento. Determina as projecções e a V.G. da distância entre os dois planos. f ρ h σ h ρ f σ Primeiro, é conduzido uma recta ortogonal aos dois planos, a recta p . p1 ≡ p 2 Depois, são determinados os pontos de intersecção da recta p com os planos. Como nem a recta nem os planos são projectantes, as intersecções são determinadas pelos cruzamentos dos traços dos planos com as projecções da recta, através do plano auxiliar π, que é plano de perfil e contém a recta p . Para se determinar os pontos A e B é necessário recorrer ao processo de rebatimento. ≡ f π ≡ h π ≡ F 1 ≡ i 1 ≡ i 2 ≡ F’ 1 ≡ i’ 1 ≡ i ’ 2 ≡ H’ 2 ≡ e 1 ≡ (e 2 ) ≡ h πr ≡ f πr ≡ H r i r ≡ H’ r i’ r p r V.G. x H 1 H 2 F’ 2 F 2 H’ 1 F r F’ r A r B r A r B r é a V.G. da distância entre os dois planos. Invertendo o rebatimento do plano π, obtêm-se as projecções dos pontos A e B, e do segmento de recta [ AB ]. A 1 A 2 B 1 B 2