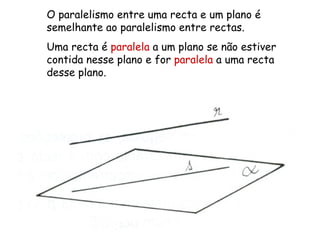
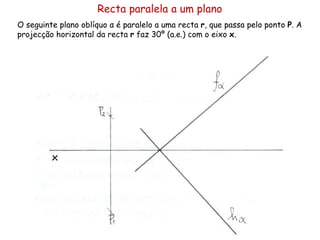
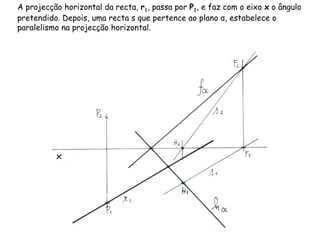
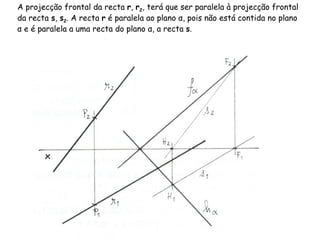
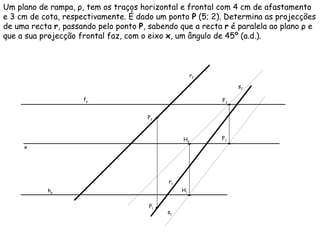
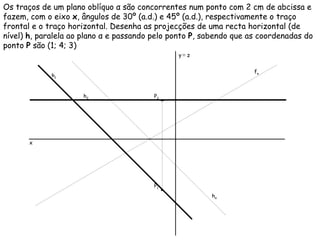
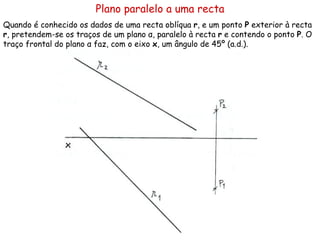
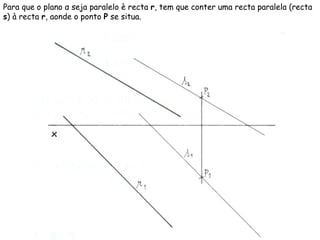
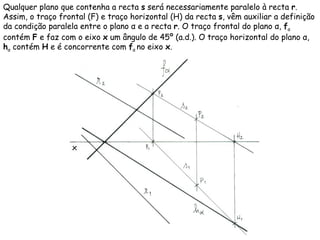
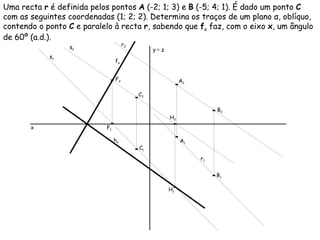
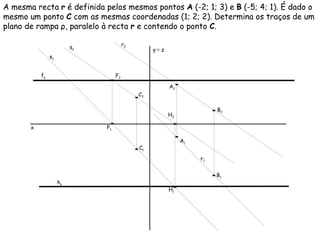
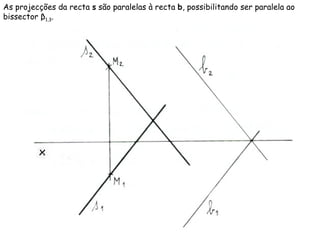
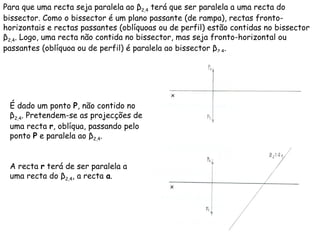
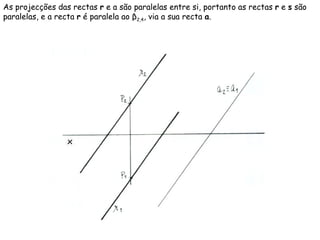
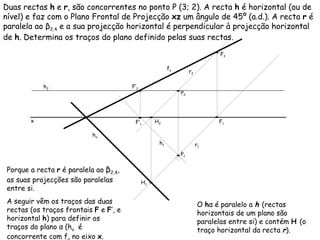
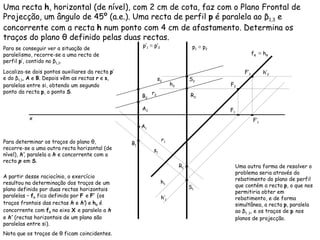
O documento descreve os conceitos de paralelismo entre retas e planos na geometria descritiva. Explica que uma reta é paralela a um plano se não estiver contida nele e for paralela a uma reta desse plano. Fornece exemplos ilustrando como determinar as projeções de retas paralelas a planos ou bissectores, utilizando retas auxiliares quando necessário.

1. GEOMETRIA DESCRITIVA A 11.º Ano Paralelismo entre Rectas e Planos © antónio de campos, 2009

2. O paralelismo entre uma recta e um plano é semelhante ao paralelismo entre rectas. Uma recta é paralela a um plano se não estiver contida nesse plano e for paralela a uma recta desse plano.

3. Recta paralela a um plano O seguinte plano oblíquo α é paralelo a uma recta r , que passa pelo ponto P . A projecção horizontal da recta r faz 30º (a.e.) com o eixo x .

4. A projecção horizontal da recta, r 1 , passa por P 1 , e faz com o eixo x o ângulo pretendido. Depois, uma recta s que pertence ao plano α , estabelece o paralelismo na projecção horizontal.

5. A projecção frontal da recta r , r 2 , terá que ser paralela à projecção frontal da recta s , s 2 . A recta r é paralela ao plano α , pois não está contida no plano α e é paralela a uma recta do plano α , a recta s .

6. Um plano de rampa, ρ , tem os traços horizontal e frontal com 4 cm de afastamento e 3 cm de cota, respectivamente. É dado um ponto P (5; 2). Determina as projecções de uma recta r , passando pelo ponto P , sabendo que a recta r é paralela ao plano ρ e que a sua projecção frontal faz, com o eixo x , um ângulo de 45º (a.d.). r 1 h ρ r 2 f ρ s 2 s 1 x P 1 P 2 F 1 F 2 H 2 H 1

7. Os traços de um plano oblíquo α são concorrentes num ponto com 2 cm de abcissa e fazem, com o eixo x , ângulos de 30º (a.d.) e 45º (a.d.), respectivamente o traço frontal e o traço horizontal. Desenha as projecções de uma recta horizontal (de nível) h , paralela ao plano α e passando pelo ponto P , sabendo que as coordenadas do ponto P são (1; 4; 3) h 2 h 1 h α f α x y ≡ z P 2 P 1

8. Plano paralelo a uma recta Quando é conhecido os dados de uma recta oblíqua r , e um ponto P exterior à recta r , pretendem-se os traços de um plano α , paralelo à recta r e contendo o ponto P . O traço frontal do plano α faz, com o eixo x , um ângulo de 45º (a.d.).

9. Para que o plano α seja paralelo è recta r , tem que conter uma recta paralela (recta s ) à recta r , aonde o ponto P se situa.

10. Qualquer plano que contenha a recta s será necessariamente paralelo à recta r . Assim, o traço frontal (F) e traço horizontal (H) da recta s , vêm auxiliar a definição da condição paralela entre o plano α e a recta r . O traço frontal do plano α , f α contém F e faz com o eixo x um ângulo de 45º (a.d.). O traço horizontal do plano α , h α contém H e é concorrente com f α no eixo x .

11. Uma recta r é definida pelos pontos A (-2; 1; 3) e B (-5; 4; 1). É dado um ponto C com as seguintes coordenadas (1; 2; 2). Determina os traços de um plano α , oblíquo, contendo o ponto C e paralelo à recta r , sabendo que f α faz, com o eixo x , um ângulo de 60º (a.d.). r 2 r 1 f α s 2 s 1 F 1 F 2 H 1 H 2 h α x y ≡ z A 1 A 2 B 1 B 2 C 1 C 2

12. A mesma recta r é definida pelos mesmos pontos A (-2; 1; 3) e B (-5; 4; 1). É dado o mesmo um ponto C com as mesmas coordenadas (1; 2; 2). Determina os traços de um plano de rampa ρ , paralelo à recta r e contendo o ponto C . r 2 r 1 f ρ s 2 s 1 F 1 F 2 H 1 H 2 h ρ x y ≡ z A 1 A 2 B 1 B 2 C 1 C 2

13. Rectas paralelas aos planos bissectores Para que uma recta seja paralela ao β 1,3 terá que ser paralela a uma recta do bissector. Como o bissector é um plano passante (de rampa), rectas fronto-horizontais e rectas passantes (oblíquoas ou de perfil) estão contidas no bissector β 1,3 . Logo, uma recta não contida no bissector, mas que seja fronto-horizontal ou passantes (oblíqua ou de perfil) é paralela ao bissector β 1,3 . Pretende-se as projecções de uma recta s oblíqua passante pelo ponto M , que seja paralela ao bissector β 1,3 . A recta b e uma recta oblíqua passante.

14. As projecções da recta s são paralelas à recta b , possibilitando ser paralela ao bissector β 1,3 .

15. Para que uma recta seja paralela ao β 2,4 terá que ser paralela a uma recta do bissector. Como o bissector é um plano passante (de rampa), rectas fronto-horizontais e rectas passantes (oblíquoas ou de perfil) estão contidas no bissector β 2,4 . Logo, uma recta não contida no bissector, mas seja fronto-horizontal ou passantes (oblíquoa ou de perfil) é paralela ao bissector β 2,4 . É dado um ponto P , não contido no β 2,4 . Pretendem-se as projecções de uma recta r , oblíqua, passando pelo ponto P e paralela ao β 2,4 . A recta r terá de ser paralela a uma recta do β 2,4 , a recta a .

16. As projecções das rectas r e a são paralelas entre si, portanto as rectas r e s são paralelas, e a recta r é paralela ao β 2,4 , via a sua recta a .

17. Um plano de rampa, ρ , têm 3cm de cota e 4 cm de afastamento. Uma recta oblíqua, a , é paralela ao β 1,3 e contém o ponto P (3; 2). A recta a faz a sua projecção horizontal com o eixo x num ângulo de 50º (a.d.). Determina as projecções do ponto de intersecção da recta a com o plano ρ . a 1 a 2 f α ≡ h α ≡ i 1 i 2 A projecção frontal da recta a tem que ter o mesmo ângulo de 50º, pois é paralela ao β 1,3 . Para obter o ponto I (ponto de intersecção da recta a com o plano ρ ), recorre-se ao método de intersecções entre rectas e planos: 1. conduzir, pela recta, um plano auxiliar (o plano α é um plano vertical que contém a recta); 2. determinar a recta de intersecção dos dois planos (a recta i , definida pelos seus traços, é a recta de intersecção do plano α com o plano ρ); 3. o ponto de intersecção das duas rectas (recta a e recta i ) é o ponto I . x P 1 P 2 f ρ h ρ F 1 F 2 H 1 H 2 I 2 I 1

18. Duas rectas h e r , são concorrentes no ponto P (3; 2). A recta h é horizontal (ou de nível) e faz com o Plano Frontal de Projecção xz um ângulo de 45º (a.d.). A recta r é paralela ao β 2,4 e a sua projecção horizontal é perpendicular à projecção horizontal de h . Determina os traços do plano definido pelas suas rectas. r 1 h 2 h 1 r 2 Porque a recta r é paralela ao β 2,4 , as suas projecções são paralelas entre si. A seguir vêm os traços das duas rectas (os traços frontais F e F ’, e horizontal h ) para definir os traços do plano α (h α é concorrente com f α no eixo x . f α h α O h α é paralelo a h (rectas horizontais de um plano são paralelas entre si) e contém H (o traço horizontal da recta r ). x P 1 P 2 F 1 F 2 F’ 1 F’ 2 H 1 H 2

19. Com rectas de perfil, é necessário a utilização de rectas auxiliares, para desenhar as projecções paralelas da recta p em relação ao β 1,3 . A recta p’ é uma recta de perfil do β 1,3 . Um ponto M não contido no β 1,3 . Pretendem-se as projecções de uma recta p , de perfil, paralela ao β 1,3 e passando pelo ponto M .

20. Rebatendo o plano α , para ver os traços paralelos da recta p , de perfil, com o β 2,4 . Um ponto A não contido no β 2,4 . Pretendem-se as projecções de uma recta p , de perfil, paralela ao β 2,4 e passando pelo ponto A . Rebatimento do plano de perfil π , juntamente com a recta de perfil p ; utilizando uma recta i , de intersecção do plano π com o β 2,4 e um ponto B da recta p , para obter a relação de paralelismo entre a recta de perfil p e o β 2,4 .

21. Uma recta h , horizontal (de nível), com 2 cm de cota, faz com o Plano Frontal de Projecção, um ângulo de 45º (a.e.). Uma recta de perfil p é paralela ao β 1,3 e concorrente com a recta h num ponto com 4 cm de afastamento. Determina os traços do plano θ definido pelas duas rectas. h 2 h 1 p 1 ≡ p 2 Para se conseguir ver a situação de paralelismo, recorre-se a uma recta de perfil p ’, contido no β 1,3 . Localiza-se dois pontos auxiliares da recta p ’ e do β 1,3 , A e B . Depois vêm as rectas r e s , paralelas entre si, obtendo um segundo ponto da recta p , o ponto S . p’ 1 ≡ p’ 2 r 1 r 2 s 1 s 2 Para determinar os traços do plano θ , recorre-se a uma outra recta horizontal (de nível), h’ , paralela a h e concorrente com a recta p em S . h’ 2 h’ 1 f θ ≡ h θ A partir desse raciocínio, o exercício resultou na determinação dos traços de um plano definido por duas rectas horizontais paralelas – f θ fica definido por F e F’ (os traços frontais das rectas h e h’ ) e h θ é concorrente com f θ no eixo X e paralelo a h e h’ (rectas horizontais de um plano são paralelas entre si). Nota que os traços de θ ficam coincidentes. Uma outra forma de resolver o problema seria através do rebatimento do plano de perfil que contém a recta p , o que nos permitiria obter em rebatimento, e de forma simultânea, a recta p , paralela ao β 1 ,3 , e os traços de p nos planos de projecção. x R 1 R 2 A 1 A 2 B 2 B 1 S 1 S 2 F 1 F 2 F’ 1 F’ 2