1. O documento apresenta soluções para exercícios de geometria descritiva sobre paralelismo. 2. As soluções fornecem explicações passo-a-passo das resoluções gráficas dos problemas com escala reduzida para evitar comparações métricas. 3. Os exercícios envolvem determinar se retas ou planos são paralelos usando propriedades geométricas como retas auxiliares e rebatimento.

1. 1
SOLUÇÕES
SOLUÇÕES DOS EXERCÍCIOS PROPOSTOS
PARALELISMO
13
NNOOTTAA:: Se bem que os dados métricos dos enunciados estejam em cceennttíímmeettrrooss, as soluções apresentadas nnããoo ccoonnssiiddeerraarraamm o centíme-
tro como unidade. De facto, no sentido do estudante, o objectivo da consulta das soluções dos exercícios deve ser a vveerriiffiiccaaççããoo ddaa ccoorrrreecc--
ççããoo dos raciocínios e dos traçados e não a ccoommppaarraaççããoo mmééttrriiccaa dos mesmos. Dessa forma, considerou-se de maior utilidade o
desenvolvimento dos relatórios e a resolução gráfica dos problemas a uma escala que evite qualquer tentativa de comparação métrica. A
escala utilizda foi de 1/2, o que significa que a cada centímetro da resolução do aluno corresponderá 0,5 cm nestas soluções.
1.
a) Em primeiro lugar, desenharam-se as projecções da recta rr, em função dos dados. Em
seguida, assinalaram-se as projecções da recta ss, coincidentes com as projecções de
nome contrário da recta rr, ou seja, ss22 (a projecção frontal da recta ss) está coincidente
com rr11, (a projecção horizontal da recta rr) e ss11 (a projecção horizontal da recta ss)está
coincidente com rr22 (a projecção frontal da recta rr). As duas rectas são ppaarraalleellaass, pois
têm as projecções homónimas paralelas entre si.
b) Em primeiro lugar, determinaram-se os traços da recta rr nos planos de projecção – FF e
HH. Em seguida, determinaram-se os traços da recta ss nos planos de projecção – FF’’ e HH’’.
O traço frontal do plano está definido por FF e FF’’ e o traço horizontal do plano está definido
por HH e HH’’,, o que resulta no facto de os dois traços do plano estarem coincidentes.
2.
3.
Em primeiro lugar, desenharam-se as projecções das rectas pp e pp’’, de acordo
com os dados (ver relatório do exercício anterior). Em seguida, uma vez que é ex-
pressamente pedido o recurso ao pprroocceessssoo ddoo rreebbaattiimmeennttoo, conduziu-se, pela
recta pp, um plano de perfil π e rebateu-se o plano para o Plano Frontal de Projec-
ção (a charneira foi ffπ). Rebatendo o plano obtiveram-se AArr e BBrr, bem como a rec-
ta pprr, definida por AArr e BBrr. Em seguida, conduziu-se, pela recta pp’’, um outro plano
de perfil π’, e rebateu-se o plano π’ também para o Plano Frontal de Projecção e
ppaarraa oo mmeessmmoo llaaddoo – note que só é possível averiguar o paralelismo entre as
duas rectas eemm rreebbaattiimmeennttoo se o rebatimento dos dois planos de perfil for eexxaacc--
ttaammeennttee o mesmo (é necessário rebater os dois planos de perfil para o mesmo
plano e no mesmo sentido de rotação). Rebatendo o plano π’ obtiveram-se os
pontos CCrr e DDrr, bem como a recta pp’’rr, definida por CCrr e DDrr. As rectas pprr e pp’’rr nnããoo
ssããoo ppaarraalleellaass, pelo que as rectas pp e pp’’ nnããoo ssããoo ppaarraalleellaass no espaço. Note que
um outro processo de resolver este exercício (mas que não é o pedido no enun-
ciado) seria o de efectuar uma mmuuddaannççaa ddoo ddiieeddrroo ddee pprroojjeeccççããoo – substituindo
o Plano Frontal de Projecção por um outro plano de projecção (ppllaannoo 44), paralelo
às duas rectas, por exemplo (transformando as duas rectas em rectas frontais),
seria possível averiguar o paralelismo entre as duas rectas sem se ter o cuidado
de garantir a semelhança entre os dois rebatimentos dos planos de perfil.
Em primeiro lugar, representaram-se as rectas pp e pp'', pelas respectivas projecções, em função
dos dados. Os pontos AA e BB têm a mesma abcissa, pois todos os pontos de uma recta de perfil
têm a mesma abcissa. Da mesma forma, os pontos CC e DD também têm a mesma abcissa. Sobre
a posição relativa das duas rectas, sabe-se imediatamente que não são concorrentes – podem
ser paralelas ou enviesadas. Uma vez que, no enunciado, se refere expressamente a não utiliza-
ção de qualquer processo geométrico auxiliar, foi necessário um raciocínio relativamente linear.
Se as rectas pp e pp’’ forem paralelas, então são complanares, pelo que quaisquer duas rectas
concorrentes com pp e pp’’ serão, também elas, complanares. Recorreu-se a duas rectas auxilia-
res, as rectas rr e ss. A recta rr é concorrente com pp em AA e com pp’’ em DD (está definida por dois
pontos). A recta ss é concorrente com pp em BB e com pp’’ em CC (também está definida por dois
pontos). As rectas rr e ss não são complanares (não são paralelas nem concorrentes), pelo que pp
e pp’’ não são complanares – logo, nnããoo ssããoo ppaarraalleellaass.

2. 2
SOLUÇÕES
4.
Em primeiro lugar, desenharam-se as projecções da recta pp e do ponto CC, em função dos dados (ver re-
latório do exercício 22). Em seguida, pelas projecções de CC conduziram-se imediatamente as projecções
da recta pp’’, a recta pedida – note que, embora as projecções da recta pedida se tivessem desenhado
imediatamente, estas não são suficientes para definir a recta em Dupla Projecção Ortogonal (a recta pp’’
está definida por um ponto e uma direcção). É necessário, então, mais um ponto da recta pp’’ (para além
de CC) para a definirmos totalmente em projecções. Como as rectas pp e pp’’ são paralelas, então são com-
planares, pelo que quaisquer duas rectas concorrentes com pp e pp’’ serão igualmente complanares. Assim,
recorreu-se a uma recta do plano definido pelas rectas pp e pp’’ – a recta aa, que está definida por BB e CC
(que são os pontos de concorrência de rr com pp e pp’’, respectivamente). Em seguida, recorreu-se a uma
outra recta, a recta bb, paralela à recta aa e concorrente com a recta pp no ponto AA – a recta bb está definida
por um ponto (ponto AA) e uma direcção (é paralela à recta aa) e é complanar com as rectas aa e pp. A recta bb
terá, também, de ser complanar com a recta pp’’, pelo que, não sendo paralela a esta, será nneecceessssaarriiaa--
mmeennttee concorrente – o ponto GG é o ponto de concorrência das rectas bb e pp’’. A recta pp’’, definida por AA e
GG, é nneecceessssaarriiaammeennttee paralela à recta pp. Sublinha-se que a recta bb poderia ser concorrente com a recta
aa – nesse caso estaria definida por dois pontos (os pontos de concorrência com as recta pp e aa). Note
que o problema poderia ter sido resolvido tanto pelo processo exposto como pelo rebatimento tanto
como, ainda, pela mudança do diedro de projecção, uma vez que o enunciado é omisso em relação ao
processo de resolução.
6.
Em primeiro lugar, representaram-se a recta pp e o ponto CC, pelas suas projecções, bem como o pla-
no ν, pelo seu traço frontal, em função dos dados. Em seguida, pelas projecções de CC conduziram-
-se imediatamente as projecções da recta pp’’, a recta paralela a pp (a recta pp’’ não fica totalmente
definida pelas suas projecções). As rectas pp e pp’’ são paralelas, pelo que são complanares – quais-
quer duas rectas concorrentes com pp e pp’’ serão igualmente complanares. Assim, recorreu-se a uma
recta do plano definido pelas rectas pp e pp’’ – a recta rr, que está definida por AA e CC (que são os pontos
de concorrência de rr com pp e pp’’, respectivamente). Em seguida, recorreu-se a uma outra recta, a
recta ss, paralela à recta rr e concorrente com a recta pp no ponto BB – a recta ss está definida por um
ponto (ponto BB) e uma direcção (é paralela à recta rr). A recta ss terá, também, de ser complanar com
a recta pp’’, pelo que, não sendo paralela a esta, será necessariamente concorrente – o ponto DD é o
ponto de concorrência das rectas ss e pp’’. A recta pp’’, definida por CC e DD, é necessariamente paralela à
recta pp. Para determinar a recta de intersecção dos dois planos, teve-se em conta que o plano ν é
projectante frontal – ii22, a projecção frontal da recta ii (a recta de intersecção dos dois planos), está
necessariamente sobre (ffν). Para definirmos a recta ii são necessários dois pontos ou um ponto e
uma direcção. Os pontos poderiam ser os pontos em que o plano ν corta as rectas pp e pp’’ (as rectas
dadas), mas a determinação desses pontos carece do recurso a processos geométricos auxiliares.
Assim, atendendo a que já temos quatro rectas do plano (as rectas pp, pp’’, rr e ss), foi suficiente recorrer
às rectas rr e ss para determinar a recta ii – o plano ν corta a recta rr no ponto MM (que é, assim, um
ponto comum aos dois planos) e corta a recta ss no ponto NN (que é um outro ponto comum aos dois
planos). A recta ii, definida por MM e NN, é a recta de intersecção entre os dois planos.
Em primeiro lugar, desenharam-se as projecções da recta pp e do ponto RR, em função dos
dados (os pontos MM e NN têm a mesma abcissa). Em seguida, pelas projecções de RR condu-
ziram-se imediatamente as projecções da recta pp’’, a recta paralela a pp (note que as projec-
ções da recta pp’’ são insuficientes para a definir – ver relatório do exercício anterior). Como as
rectas pp e pp’’ são paralelas, então são complanares, pelo que quaisquer duas rectas concor-
rentes com pp e pp’’ serão igualmente complanares. Assim, recorreu-se a uma recta do plano
definido pelas rectas pp e pp’’ – a recta ff, que está definida por MM e RR (que são os pontos de
concorrência de ff com pp e pp’’, respectivamente – a recta ff é uma recta frontal). Em seguida,
recorreu-se a uma outra recta, a recta ff’’, paralela à recta ff e concorrente com a recta pp no
ponto NN – a recta ff’’ está definida por um ponto (ponto NN) e uma direcção (é paralela à recta
ff). A recta ff’’ terá, também, de ser complanar com a recta pp’’, pelo que, não sendo paralela a
esta, será necessariamente concorrente – o ponto SS é o ponto de concorrência das rectas ff’’
e pp’’. A recta pp’’, definida por RR e SS, é necessariamente paralela à recta pp. Para determinar os
traços do plano α, poder-se-ia ter determinado os traços das rectas de perfil, o que envolve-
ria o recurso a processos geométricos auxiliares. No entanto, optou-se por um outro raciocí-
nio, mais simples – atendeu-se ao facto que já temos quatro rectas do plano α (as rectas pp,
pp’’, ff e ff’’). Assim, foi suficiente recorrer às rectas ff e ff’’ para determinar os traços do plano α. HH
é o traço horizontal da recta ff e HH’’ é o traço horizontal da recta ff’’. O traço horizontal do plano
α, hhα, está definido por HH e HH’’. O traço frontal do plano α, ffα, é concorrente com hhα no eixo XX
e é paralelo às rectas ff e ff’’ (rectas frontais de um plano são paralelas entre si e paralelas ao
traço frontal do plano, que é uma recta frontal do plano com afastamento nulo). Note que o
problema se poderia ter resolvido sem a determinação do ponto SS – de facto, com o recurso
às duas rectas auxiliares, o problema resolveu-se como se o plano estivesse definido por
três pontos não colineares, pelos quais se conduziram duas rectas do plano.
5.

3. 3
SOLUÇÕES
8.
Uma recta é paralela a um plano se e só se for paralela a uma recta do plano e não estiver contida nesse plano, ou seja, uma recta é para-
lela a um plano se pertencer a uma «família» de rectas que esteja contida no plano. De forma recíproca, um plano é paralelo a uma recta se
e só se não contiver a recta e contiver uma recta paralela à recta dada, ou seja, um plano é paralelo a uma recta se contiver a «família» de
rectas a que a recta dada pertence.
Em primeiro lugar, representaram-se o plano ρ, pelos seus traços, e o ponto PP, pelas suas
projecções, em função dos dados. Em seguida, desenhou-se a projecção frontal da recta rr
– rr22 – passando por PP22 e fazendo, com o eixo XX, o ângulo pedido. Para a recta rr ser paralela
ao plano ρ, terá de ser paralela a uma recta do plano. Para tal, recorreu-se a uma recta
auxiliar ss, pertencente ao plano e garantindo que ss seja paralela à recta rr – ss22 é paralela a
rr22. A recta ss está definida pelos seus traços (condição para que uma recta pertença a um
plano). Em seguida, conduziu-se, por PP11, a projecção horizontal da recta rr (rr11), paralela a
ss11. A recta rr é paralela ao plano ρ, pois é paralela a uma recta do plano (a recta ss).
10.
7.
Em primeiro lugar, representaram-se a recta pp e o ponto BB, pelas suas pro-
jecções, em função dos dados. A recta pp, porque é passante, é concorrente
com o eixo XX no ponto PP. Em seguida, pelas projecções de BB conduziram-se
imediatamente as projecções da recta pp’’, a recta paralela a pp (note que a rec-
ta pp’’ não fica totalmente definida em projecções – ver relatório do exercício
44). Assim, há que obter as projecções de mais um ponto da recta. Optou-se
por recorrer a uma mudança do diedro de projecção – substituiu-se o Plano
Frontal de Projecção (ppllaannoo 22) por um novo plano de projecção (ppllaannoo 44),
paralelo às duas rectas, definindo um novo diedro de projecção (o diedro for-
mado pelo ppllaannoo 11 e pelo ppllaannoo 44) no qual as rectas pp e pp’’ são rectas fron-
tais (de frente) – o novo eixo XX (eixo XX’’) é paralelo a pp11 e a pp’’11 e é a recta de
intersecção do ppllaannoo 11 com o ppllaannoo 44. As projecções de AA, BB e PP no ppllaannoo
44 determinaram-se em função das respectivas cotas, que se mantiveram. A
projecção da recta pp no ppllaannoo 44 (pp44) está definida por AA44 e por PP44. A projec-
ção da recta pp’’ no ppllaannoo 44 (pp’’44) passa por BB44 e é paralela a pp44 (o paralelismo
entre as rectas é directo no novo diedro de projecção). Determinou-se um
ponto qualquer da recta pp’’ – o ponto FF (que é o traço frontal da recta pp’’). FF11
determinou-se directamente e FF22, a projecção frontal de FF no diedro de pro-
jecção inicial, determinou-se em função da sua cota, que se manteve. A recta
pp’’, definida por BB e FF, é paralela à recta pp.
9.
Em primeiro lugar, representaram-se o plano α, pelos seus traços, e o ponto PP, pelas suas pro-
jecções, em função dos dados. Em seguida, por PP11, conduziu-se rr11, a projecção horizontal da
recta rr, fazendo o ângulo pretendido (45o a.d.) com o eixo XX. Para a recta rr ser paralela ao pla-
no α, terá de ser paralela a uma recta do plano. Para tal, recorreu-se a uma recta auxiliar ss,
pertencente ao plano e garantindo que ss seja paralela à recta rr – ss11 é paralela a rr11. A recta ss
está definida pelos seus traços (condição para que uma recta pertença a um plano). Em segui-
da, conduziu-se, por PP22, a projecção frontal da recta rr (rr22), paralela a ss22. A recta rr é paralela ao
plano α, pois é paralela a uma recta do plano (a recta ss).

4. 4
SOLUÇÕES
11.
Em primeiro lugar, representaram-se o plano α, pelos seus traços, e o ponto PP, pelas suas
projecções, em função dos dados. Em seguida, pelas projecções de PP conduziram-se ime-
diatamente as projecções da recta pp – note que não foi necessário nenhum procedimento
particular para desenhar as projecções da recta pp. A recta pp, no entanto, não está completa-
mente definida – falta-nos outro ponto para definir a recta, para além do ponto PP. Por outro
lado, há que garantir que a recta pp seja paralela ao plano α, para o que a recta pp terá de ser
paralela a uma recta do plano α (critério de paralelismo entre rectas e planos). Assim, recor-
reu-se a uma recta pp’’, qualquer, de perfil e pertencente ao plano – a recta pp’’ está definida
por dois pontos, que são os seus traços (condição para que uma recta pertença a um pla-
no). A recta pp tem de ser paralela à recta pp’’. Para garantir o paralelismo entre as rectas pp e
pp’’ recorreu-se ao raciocínio exposto no relatório do exercício 44. As rectas pp e pp’’, sendo pa-
ralelas, são complanares – recorreu-se a duas rectas do plano definido por pp e pp’’. A recta rr
é concorrente com a recta pp no ponto PP e com a recta pp’’ no ponto HH (o seu traço hori-
zontal). A recta ss é concorrente com a recta pp’’ no ponto FF (o seu traço frontal) e com a recta
rr no ponto MM. A recta ss, porque é complanar com a recta pp, é concorrente com esta num
ponto RR. A recta pp, definida por PP e RR, é paralela à recta pp’’, que é uma recta do plano α,
pelo que a recta pp é paralela ao plano α.
13.
Em primeiro lugar, representaram-se o plano γ, pelos seus traços, e o ponto PP, pelas suas
projecções, em função dos dados. Em seguida, por PP22, conduziu-se rr22, a projecção frontal
da recta rr, fazendo, com o eixo XX, o ângulo pretendido (60° a.d.). Para que a recta rr seja pa-
ralela ao plano γ, terá de ser paralela a uma recta do plano γ. Ora, uma vez que o plano γ é
projectante horizontal, sabe-se que todas as suas rectas têm a sua projecção horizontal so-
bre hhγ, pelo que desenhando rr11 paralela a hhγ (e passando por PP11) se garante que a recta rr é
paralela ao plano α (porque existe, de certeza, uma recta do plano γ que é paralela à recta rr).
Em primeiro lugar, representaram-se o plano ρ, pelos seus traços, e o ponto PP, pelas
suas projecções, em função dos dados. Sobre a determinação das projecções da recta
pp, de perfil, paralela ao plano ρ e passando por PP, ver relatório do exercício anterior.
12.
Em primeiro lugar, representaram-se o plano φ, pelos seus traços, e o ponto RR, pelas
suas projecções, em função dos dados. Para que a recta ff (a recta frontal pretendida)
seja paralela ao plano φ, a recta terá de ser paralela a uma recta de φ (critério de para-
lelismo entre rectas e planos). O traço frontal de φ (ffφ) é uma recta frontal (de frente) do
plano, com afastamento nulo – esta raciocínio permitiu-nos economizar traçado, pois não
houve necessidade de se desenharem as projecções de outra recta do plano. Assim, por
RR conduziu-se a recta ff pedida, paralela a ffφ – ff está definida por um ponto (RR) e por uma
direcção (é paralela a ffφ).
14.

5. 5
SOLUÇÕES
15.
Em primeiro lugar, representaram-se o plano δ, pelos seus traços, e o ponto PP,
pelas suas projecções, em função dos dados. Sobre a determinação das projec-
ções da recta rr, ver exercício 99 e respectivo relatório. Note que, com vista a uma
maior economia de traçados, se optou por fazer com que o traço frontal da recta
ss (a recta auxiliar do plano δ à qual a recta rr é paralela) tenha abcissa nula.
18.
Em primeiro lugar, representaram-se a recta rr pelas suas projecções, em função dos dados. Os tra-
ços do plano ρ (o plano passante paralelo à recta rr) determinaram-se imediatamente – estão am-
bos coincidentes com o eixo XX. No entanto, os traços do plano ρ, porque ssããoo uummaa úúnniiccaa rreeccttaa,
são insuficientes para definir o plano (um plano só pode estar definido por uma única recta se essa
recta for uma das suas rectas de maior declive ou uma das suas rectas de maior inclinação).
Assim, há que recorrer a mais um elemento para definir o plano ρ – esse elemento poderá ser um
ponto (caso em que o plano ρ estará definido por uma recta – o eixo XX – e um ponto exterior) ou
uma recta (caso em que o plano ρ estará definido por duas rectas). Assim, recorreu-se a uma recta
qualquer, paralela à recta rr – a recta ss. A recta ss tem nneecceessssaarriiaammeennttee de ser uma rreeccttaa ppaassssaannttee,
pois caso contrário não seria uma recta do plano ρ (o plano ρ apenas contém rectas fronto-horizon-
tais e rectas passantes – estas poderão ser oblíquas ou de perfil). Note que não se poderia recorrer
a uma recta fronto-horizontal, pois uma recta fronto-horizontal não é paralela à recta rr. Note ainda
que também não se poderia ter recorrido a uma recta de perfil passante, pois a recta rr não é de
perfil. A única hipótese é, pois, a situação apresentada – uma recta oblíqua passante, qualquer,
paralela à recta rr. O plano ρ está, assim, definido por duas rectas concorrentes – o eixo XX e a recta ss.
Em primeiro lugar, representaram-se a recta mm e o ponto AA, pelas respectivas pro-
jecções, em função dos dados. Em seguida, para que o plano pedido contenha o
ponto AA, o ponto AA tem de pertencer a uma recta do plano. Por outro lado, para
que o plano α seja paralelo à recta mm, tem de conter uma recta paralela à recta
mm. Assim, há que conduzir, por AA, uma recta paralela à recta mm, que será uma
recta do plano α – a recta rr. Determinaram-se os traços da recta rr, pois os traços
da recta têm de estar sobre os traços homónimos do plano (condição para que
uma recta pertença a um plano). Em seguida, pelo traço horizontal de rr conduziu-
-se hhα, com o ângulo pretendido (hhα está definido por um ponto e uma direcção)
– ffα é concorrente com hhα sobre o eixo XX e contém FF, o traço frontal de rr (ffα está
definido por dois pontos). O plano α é paralelo à recta mm, pois contém uma recta
paralela a mm (a recta rr). O plano α contém o ponto AA, pois AA pertence a uma recta
do plano (a recta rr).
17.
Em primeiro lugar, representaram-se a recta rr e o ponto AA, pelas respectivas pro-
jecções, em função dos dados. Sobre a determinação dos traços do plano ρ ver
relatório do exercício anterior. A recta ss, paralela à recta rr e passando por AA, foi a
recta auxiliar a que se recorreu. Os traços do plano ρ são rectas fronto-horizontais
que contêm os traços homónimos da recta ss. O plano ρ é paralelo à recta rr, pois
contém uma recta paralela a rr (a recta ss). O plano ρ contém o ponto AA, pois AA
pertence a uma recta do plano (a recta ss).
16.

6. 6
SOLUÇÕES
19.
Em primeiro lugar, representaram-se a recta ff e o ponto PP, pelas respectivas projec-
ções, em função dos dados. Sobre a determinação dos traços do plano α, ver relató-
rio do exercício 1166. A recta ff’’, paralela à recta ff e passando por PP, foi a recta auxiliar
a que se recorreu. HH’’ é o traço horizontal da recta ff’’. Uma vez que os traços do plano
α estão coincidentes, nnoo ppllaannoo ddoo ppaappeell, os dois traços têm a mesma direcção.
Assim, por HH’’11 conduziu-se hhα, o traço horizontal de α, paralelo a ff’’22 (e a ff22). O traço
frontal de α, ffα, é concorrente com hhα no eixo XX e também é paralelo a ff’’22 (e a ff22),
pelo que os traços de α ficam coincidentes (no plano do papel).
20.
Em primeiro lugar, representaram-se a recta rr e o ponto PP, pelas respectivas projecções, em
função dos dados. Para que o plano γ seja paralelo à recta rr, o plano γ, terá de conter uma
recta paralela à recta rr. Ora, uma vez que o plano γ é projectante horizontal, sabe-se que
todas as suas rectas têm a sua projecção horizontal sobre hhγ. Além disso, e uma vez que se
trata de um plano projectante horizontal, sabe-se também que todos os seus pontos têm a
sua projecção horizontal sobre hhγ. Assim, desenhando hhγ, passando por PP11 e paralelo a rr11
(a projecção horizontal de rr), está garantido o paralelismo entre o plano γ e a recta rr – note
que qualquer recta do plano (à excepção das rectas verticais) terá a sua projecção horizontal
paralela à projecção horizontal da recta rr. Note ainda que o plano γ contém o ponto PP, pois PP11
situa-se sobre hhγ. Tratando-se de um plano vertical, ffγ é uma recta vertical com afastamento
nulo, que é concorrente com hhγ no eixo XX.
22.
Em primeiro lugar, representou-se o ponto PP, pelas suas projecções, em função dos dados.
Em seguida, conduziu-se, por PP11, a projecção horizontal da recta rr (rr11), com o ângulo pretendi-
do – rr11 faz, com o eixo XX, um ângulo de 45° (a.d.). A recta rr é uma recta paralela ao β2/4, pelo
que as suas projecções são paralelas entre si – assim, por PP22 conduziu-se rr22, a projecção frontal
da recta rr, paralela a rr11.
Em primeiro lugar, representaram-se a recta rr e o ponto AA, pelas respectivas
projecções, em função dos dados. Sobre a determinação dos traços do pla-
no α, ver exercício 1166 e respectivo relatório. A recta ss é a recta auxiliar a que
se recorreu – a recta ss contém o ponto AA e é paralela à recta rr. FF’’ é o traço
frontal da recta ss e HH é o seu traço horizontal. Uma vez que os traços do
plano estão coincidentes (na folha de papel), estão coincidentes na recta
que passa por FF’’22 e por HH11.
21.

7. 7
SOLUÇÕES
23.
Em primeiro lugar, representou-se o ponto PP, pelas suas projecções, em função dos da-
dos. Em seguida, conduziu-se, por PP22, a projecção frontal da recta rr (rr22), com o ângulo
pretendido – rr22 faz, com o eixo XX, um ângulo de 30o (a.d.). A recta rr é uma recta paralela
ao β1/3, pelo que as suas projecções fazem, com o eixo XX, ângulos iguais e com o mes-
mo sentido de abertura. Assim, por PP11 conduziu-se rr11, a projecção horizontal da recta rr,
fazendo também um ângulo de 30o (a.d.) com o eixo XX.
Em primeiro lugar, representaram-se o ponto KK e a recta ff, pelas respectivas projec-
ções, em função dos dados. Em seguida, conduziu-se, por PP11, a projecção horizon-
tal da recta, rr11, com o ângulo pretendido – um ângulo de 45o (a.d.) com o eixo XX.
A recta rr é uma recta paralela ao β2/4, pelo que as suas projecções são paralelas entre
si – assim, por PP22 conduziu-se rr22, a projecção frontal da recta rr, paralela a rr11.
Em seguida, determinaram-se os traços das duas rectas e desenharam-se os traços
do plano. HH é o traço horizontal da recta rr e HH’’ é o traço horizontal da recta ff. FF é o
traço frontal da recta rr. O traço horizontal do plano α, hhα, passa por HH e HH’’ (está
definido por dois pontos). O traço frontal do plano α, ffα, é concorrente com hhα no
eixo XX e passa por FF (está também definido por dois pontos).
25.
O ponto de concorrência tem 4 cm de afastamento – atendendo a que o ponto de
concorrência (ponto PP) pertence à recta hh, que tem 2 cm de cota, sabe-se imediata-
mente que o ponto PP tem também 2 cm de afastamento. Este raciocínio permitiu-nos
desenhar as projecções da recta hh e do ponto PP. Em seguida conduziu-se, por PP11, a
projecção horizontal da recta, rr11, com o ângulo pretendido – um ângulo de 30o (a.d.)
com o eixo XX. A recta rr é uma recta paralela ao β1/3, pelo que as suas projecções
fazem, com o eixo XX, ângulos iguais e com o mesmo sentido de abertura. Assim, por
PP22 conduziu-se rr22, a projecção frontal da recta rr, fazendo também um ângulo de 30o
(a.d.) com o eixo XX. Em seguida, determinaram-se os traços das duas rectas e dese-
nharam-se os traços do plano. HH é o traço horizontal da recta rr e FF é o traço frontal da
recta hh. O traço horizontal do plano α, hhα, passa por HH e é paralelo à recta hh (rectas
horizontais de um plano são paralelas entre si e paralelas ao traço horizontal do plano,
que é uma recta horizontal do plano com cota nula). O traço frontal do plano α, ffα, é
concorrente com hhα no eixo XX e passa por FF (está definido por dois pontos).
Em primeiro lugar, representou-se o plano α, pelos seus traços, bem como o pon-
to MM e a recta aa, pelas respectivas projecções, em função dos dados. A recta aa é
uma recta paralela ao β1/3, pelo que as suas projecções fazem, com o eixo XX, ân-
gulos iguais e com o mesmo sentido de abertura – assim, aa11, a projecção horizon-
tal da recta aa, faz também um ângulo de 30o (a.e.) com o eixo XX. Para determinar
o ponto de intersecção da recta aa com o plano α, e uma vez que nem a recta nem
o plano são projectantes, recorreu-se ao mmééttooddoo ggeerraall ddaa iinntteerrsseeccççããoo ddee rreeccttaass
ccoomm ppllaannooss. Assim, tem-se: 11.. por aa conduziu-se um plano auxiliar (o plano γ, que
é um plano vertical – é o plano projectante horizontal da recta aa); 22.. determinou-se
a recta ii, a recta de intersecção dos dois planos (a recta ii está definida pelos seus
traços, pois trata-se do caso geral da intersecção entre planos); 33.. o ponto de
concorrência da recta ii com a recta aa (o ponto II) é o ponto de intersecção da rec-
ta aa com o plano α.
24.
26.

8. 8
SOLUÇÕES
28.
Em primeiro lugar, representou-se o ponto AA, pelas suas projecções, em função das
suas coordenadas. Em seguida, desenharam-se imediatamente as projecções da recta
pp – estas, no entanto, não são suficientes para definir totalmente a recta pp em Dupla Pro-
jecção Ortogonal (a recta, no espaço, está definida por um ponto e uma direcção). Por
outro lado, para que a recta pp seja paralela ao β2/4, a recta tem de ser paralela a uma
recta do β2/4. Recorreu-se a um plano de perfil π, que contém a recta pp, e determinou-se
a recta de intersecção do plano π com o β2/4 – a recta ii. A recta pp terá de ser paralela à
recta ii (critério de paralelismo entre rectas e planos). A recta ii é uma recta de perfil pas-
sante que faz, com os planos de projecção (e com os traços do plano π) ângulos de 45°.
Em seguida, rebateu-se o plano π para o Plano Frontal de Projecção (a charneira foi ffπ),
obtendo-se AArr. Em seguida, desenhou-se iirr, que é a recta ii em rebatimento. Note que o
ponto AA se situa no 1o Diedro e que a recta ii, sendo uma recta do β2/4, atravessa os 2o e
4o Diedros – assim, iirr não pode, nunca, passar pelo quadrante em que se situa AArr. Por
outro lado, sendo ii uma recta passante, o seu ponto de concorrência com o eixo XX é fixo,
pois situa-se na charneira – iirr passa pelo ponto de concorrência dos traços do plano e
faz, com ffπrr
e hhπrr
, ângulos de 45°. A recta pprr passa por AArr e é paralela a iirr. Em seguida,
determinaram-se os traços da recta pp em rebatimento – FFrr está sobre ffπrr
e HHrr está sobre
hhπrr
(condição para que uma recta pertença a um plano, que se verifica tanto no espaço
como em projecções e em rebatimento). Invertendo o rebatimento, determinaram-se as
projecções de FF (traço frontal da recta pp) e HH (traço horizontal da recta pp). Note que se
poderia ter determinado a recta ii em rebatimento, recorrendo a um ponto qualquer da
recta – seria um ponto do β2/4, pelo que teria as suas projecções coincidentes. Rebatendo
esse ponto, ter-se-ia a recta iirr definida por dois pontos.
27. a) Em primeiro lugar, representaram-se as rectas rr e ss, pelas respectivas projecções, em
função dos dados. A recta rr é paralela ao β1/3, pelo que as suas projecções fazem,
com o eixo XX, ângulos iguais e com o mesmo sentido de abertura. A recta ss é paralela
ao β2/4, pelo que as suas projecções são paralelas entre si. Em seguida, determina-
ram-se os traços das duas rectas e desenharam-se os traços do plano. FF é o traço
frontal da recta rr e FF’’ é o traço frontal da recta ss. HH é o traço horizontal da recta rr e HH’’
é o traço horizontal da recta ss. ffα passa por FF e FF’’. hhα passa por HH e HH’’ (e é concor-
rente com ffα no eixo XX).
b) A recta ii’’ é uma recta que pertence simultaneamente ao plano α (o plano dado) e ao
β1/3 – todos os seus pontos pertencem simultaneamente aos dois planos. Para definir
uma recta são necessários dois pontos ou um ponto e uma direcção. O ponto de
concorrência dos dois traços do plano (ffα e hhα) é um ponto que pertence aos dois
planos, pois situa-se no eixo XX (todos os pontos do eixo XX pertencem ao β1/3). Já temos
um ponto – falta-nos outro ponto ou uma direcção. Determinou-se QQ, o traço da
recta ss no β1/3 – QQ pertence ao plano α, pois pertence a uma recta do plano (a recta
ss) e pertence ao β1/3, pois tem as suas projecções simétricas em relação ao eixo XX.
Já temos dois pontos para definir a recta ii’’. Note que a recta rr, porque é paralela ao
β1/3, não tem traço no β1/3. Por outro lado, e uma vez que as rectas rr e ii’’ são rectas
complanares (pertencem, ambas, ao plano α), e não sendo concorrentes, são parale-
las – a recta ii’’ é paralela à recta rr (a recta ii’’ é uma recta do β1/3 e a recta rr é uma recta
paralela ao β1/3 – são rectas da mesma «família» de rectas). A recta ii’’’’ é uma recta que
pertence simultaneamente ao plano α e ao β2/4 – todos os seus pontos pertencem
simultaneamente aos dois planos. Para definir uma recta são necessários dois pontos
ou um ponto e uma direcção. O ponto de concorrência dos dois traços do plano é
um ponto que pertence aos dois planos, pois situa-se no eixo XX (todos os pontos do
eixo XX pertencem ao β2/4). Já temos um ponto – falta-nos outro ponto ou uma direc-
ção. Determinou-se II, o traço da recta rr no β2/4 – II pertence ao plano α, pois pertence
a uma recta do plano (a recta rr) e pertence ao β2/4, pois tem as suas projecções coin-
cidentes. Já temos dois pontos para definir a recta ii’’’’. Note que a recta ss, porque é
paralela ao β2/4, não tem traço no β2/4. Por outro lado, e uma vez que as rectas ss e ii’’’’
são rectas complanares (pertencem, ambas, ao plano α), e não sendo concorrentes,
são paralelas – a recta ii’’’’ é paralela à recta ss (a recta ii’’’’ é uma recta do β2/4 e a recta ss
é uma recta paralela ao β2/4 – são rectas da mesma «família» de rectas).

9. 9
SOLUÇÕES
29.
Em primeiro lugar, representou-se o ponto PP, pelas suas projecções, em função das
suas coordenadas. Em seguida, desenharam-se imediatamente as projecções da recta
pp – estas, no entanto, não são suficientes para definir totalmente a recta pp em Dupla
Projecção Ortogonal (a recta, no espaço, está definida por um ponto e uma direcção).
Por outro lado, para que a recta pp seja paralela ao β1/3, a recta tem de ser paralela a
uma recta do β1/3. Representou-se uma recta rr, de perfil, contida no β1/3 e situada no
mesmo plano de perfil da recta pp – a recta rr está definida pelo ponto AA (que é o seu
ponto de concorrência com o eixo XX) e por um ponto BB, qualquer, do β1/3 (BB tem as
suas projecções simétricas em relação ao eixo XX). Em seguida, optou-se por recorrer a
uma mudança do diedro de projecção – substituiu-se o Plano Frontal de Projecção
(ppllaannoo 22) por um novo plano de projecção (ppllaannoo 44), paralelo às duas rectas, definindo
um novo diedro de projecção (o diedro formado pelo ppllaannoo 11 e pelo ppllaannoo 44) no
qual as rectas pp e rr são rectas frontais (de frente). O novo eixo XX (eixo XX’’) é paralelo a
pp11 e a rr11 e é a recta de intersecção do ppllaannoo 11 com o ppllaannoo 44. As projecções de AA, BB e
PP no ppllaannoo 44 determinaram-se em função das respectivas cotas, que se mantiveram. A
projecção da recta rr no ppllaannoo 44 (rr44) está definida por AA44 e por BB44. A projecção da recta
pp no ppllaannoo 44 (pp44) passa por PP44 e é paralela a rr44 (o paralelismo entre as rectas é directo
no novo diedro de projecção). Em seguida, determinaram-se os traços da recta pp em
função das coordenadas conhecidas – FF11 já era conhecido no diedro de projecção ini-
cial e HH22 também. HH44 determinou-se em função da sua cota (que é nula) e FF44 determi-
nou-se em função de FF11. Invertendo a mudança do diedro de projecção, determinou-se
FF22 em função da sua cota (que é negativa e que se manteve). Note que o exercício se
poderia ter resolvido com o recurso ao rebatimento do plano de perfil que contém as
duas rectas, conforme exposto no relatório do exercício anterior.
Em primeiro lugar, desenharam-se as projecções das rectas pp e hh, concorrentes no
ponto PP, em função dos dados. Para determinar os traços do plano há que deter-
minar os traços das duas rectas nos planos de projecção – FF’’ é o traço frontal da
recta hh. Note que as projecções da recta pp se desenharam imediatamente, apesar
da recta estar definida apenas por um ponto e uma direcção (é paralela ao β2/4).
Para determinar os traços da recta pp (que são mais dois pontos da recta) é neces-
sário o recurso a um processo geométrico auxiliar – recorreu-se ao rebatimento do
plano de perfil que a contém (o plano π). Rebateu-se o plano π para o Plano Fron-
tal de Projecção (a charneira foi ffπ), obtendo-se PPrr. A recta pprr passa por PPrr e, uma
vez que a recta pp é paralela ao β2/4, sabe-se que a recta faz ângulos de 45° com os
planos de projecção (e com os traços do plano π) – os ângulos de 45° com os tra-
ços do plano estão em V.G., em rebatimento, nos ângulos que a recta pprr faz com
hhπrr
e com ffπrr
. Das duas hipóteses possíveis, apenas a apresentada garante que a
recta pp é paralela ao β2/4 (na outra situação, a recta seria paralela ao β1/3) – note
que o ponto PP se situa no 1o Diedro e que a recta, sendo paralela ao β2/4, terá de
atravessar os 2o e 4o Diedros, bem como um qualquer dos outros dois (se não
atravessasse mais nenhum Diedro, seria uma recta do próprio β2/4). Em função
das coordenadas do ponto PP, a recta pp atravessa os 2o, 1o e 4o Diedros. Note que
se poderia ter determinado a recta de intersecção do plano π com o β2/4 (recta ii) e
garantir o paralelismo da recta pp em relação à recta ii, conforme exposto no relató-
rio do exercício 2288. Em seguida, determinaram-se os traços da recta pp em rebati-
mento (ver exercício 2288 e respectivo relatório) – FF é o traço frontal da recta pp e HH é
o seu traço horizontal. ffα, o traço frontal do plano α, passa por FF e FF’’. hhα, o traço
horizontal do plano α, passa por HH, é concorrente com ffα no eixo XX e é paralelo à
recta hh (rectas horizontais de um plano são paralelas entre si e paralelas ao traço
horizontal do plano, que é uma recta horizontal do plano com cota nula).
30.

10. 10
SOLUÇÕES
32.
Em primeiro lugar, representaram-se as rectas pp e rr, pelas respectivas projecções, em
função dos dados. Uma vez que a recta rr é paralela ao β1/3, as suas projecções fazem,
com o eixo XX, ângulos iguais e com o mesmo sentido de abertura. Em seguida, deter-
minaram-se os traços frontal e horizontal da recta rr – FF e HH, respectivamente. A deter-
minação dos traços da recta pp (FF’’ e HH’’) processou-se conforme exposto no relatório do
exercício 3300. ffα, o traço frontal do plano α, está definido por FF e FF’’. hhα, o traço horizon-
tal do plano α, está definido por HH e HH’’ e é concorrente com ffα no eixo XX.
31.
Em primeiro lugar, representaram-se o plano ρ, pelos seus traços, e a recta pp, pelas suas
projecções, em função dos dados. Note que as projecções da recta pp se desenharam imedia-
tamente, apesar da recta não se encontrar completamente definida. Para determinar o ponto
de intersecção da recta pp com o plano ρ, e uma vez que nem a recta nem o plano são
projectantes, recorreu-se ao mmééttooddoo ggeerraall ddaa iinntteerrsseeccççããoo ddee rreeccttaass ccoomm ppllaannooss, como
em seguida se expõe: 11.. conduziu-se, pela recta, um plano auxiliar – o plano π (que é um
plano de perfil); 22.. determinou-se a recta de intersecção do plano π com o plano ρ (a recta ii,
que é uma recta de perfil) – a recta ii fica definida por dois pontos, que são os seus traços
(trata-se do caso geral da intersecção de planos); 33.. o ponto de concorrência das duas rec-
tas (recta pp e recta ii) é o ponto de intersecção da recta pp com o plano ρ. Uma vez que tanto
a recta pp com a recta ii são rectas de perfil, a determinação do seu ponto de concorrência só
se pode processar com o recurso a um processo geométrico auxiliar. Optou-se pelo rebati-
mento do plano π – rebateu-se o plano π para o Plano Frontal de Projecção (a charneira foi
ffπ). Rebateu-se a recta ii, pelo rebatimento dos seus traços – iirr fica definida por FFrr e HHrr. A rec-
ta pprr passa por SSrr e, uma vez que a recta pp é paralela ao β1/3, sabe-se que a recta faz ângu-
los de 45° com os planos de projecção (e com os traços do plano π) – os ângulos de 45°
com os traços do plano estão em V.G., em rebatimento, nos ângulos que a recta pprr faz com
hhπrr
e com ffπrr
. Das duas hipóteses possíveis, apenas a apresentada garante que a recta pp é
paralela ao β1/3 (na outra situação, a recta seria paralela ao β2/4, tal como se observou no
exercício anterior) – note que o ponto SS se situa no 1o Diedro e que a recta, sendo paralela
ao β1/3, terá de atravessar os 1o e 3o Diedros, bem como um qualquer dos outros dois (se
não atravessasse mais nenhum Diedro, seria uma recta do próprio β1/3). Em função das
coordenadas do ponto SS, a recta pp atravessa os 1o, 2o e 3o Diedros. Uma outra forma de
resolver a questão do paralelismo da recta pp em relação ao β1/3 seria determinar a recta de
intersecção do plano π com o β1/3 e desenhar a recta em rebatimento (à semelhança do
exposto no relatório do exercício 2288) – a recta pprr passaria por SSrr e seria paralela àquela.
O ponto de intersecção das duas rectas (recta pp e recta ii) – o ponto II – determinou-se em
rebatimento. IIrr é o ponto de concorrência de iirr e pprr. Invertendo o rebatimento, determina-
ram-se as projec-ções do ponto II que é o ponto de intersecção da recta pp com o plano ρ.
33.
Dois planos são paralelos se e só se duas rectas concorrentes de um dos planos forem paralelas a duas rectas concorrentes do outro pla-
no, ou seja, dois planos são paralelos se e só se tiverem, em comum, duas «famílias» de rectas.

11. 11
SOLUÇÕES
34.
Em primeiro lugar representaram-se o plano α, pelos seus traços, e o ponto PP, pelas suas pro-
jecções, em função dos dados. Para que dois planos sejam paralelos, duas rectas concorren-
tes de um dos planos têm de ser paralelas a duas rectas concorrentes do outro (os dois planos
têm de conter duas «famílias» de rectas em comum). Atendendo a que os traços de um plano
oblíquo são duas rectas concorrentes desse plano, para que o plano θ seja paralelo ao plano
α, basta que os seus traços sejam paralelos aos traços homónimos de α. Por outro lado, para
que o plano θ contenha o ponto PP, é necessário que PP se situe numa recta do plano θ. Assim,
em primeiro lugar há que conduzir, por PP, uma recta do plano θ – essa recta terá de ser uma
recta frontal (de frente) ou uma recta horizontal (de nível), que são as rectas do plano θ que já
conhecemos (ffθ é uma recta frontal e hhθ é uma recta horizontal). Optou-se pela primeira hipótese
– a recta ff, frontal (de frente), que passa por PP, é uma recta do plano θ pois será paralela a ffθ,
uma vez que rectas frontais (de frente) de um plano são paralelas entre si (e ffθ é paralelo a ffα,
pelo que já sabemos a direcção das rectas frontais de θ). Em seguida, determinou-se HH, o
traço horizontal de ff. Por HH conduziu-se hhθ, paralelo a hhα e ffθ é paralelo a ffα (e a ff) e con-
corrente com hhθ no eixo XX. O plano θ contém o ponto PP e é paralelo ao plano α.
36.
Em primeiro lugar, representaram-se o plano α, pelos seus traços, e o ponto PP,
pelas suas projecções, em função dos dados. Note que as projecções do pon-
to PP estão sobre os traços homónimos do plano α, mas PP nnããoo ppeerrtteennccee ao
plano α, pois não verifica a condição para que um ponto pertença a um plano
em relação ao plano α (tem de pertencer a uma recta do plano). Sobre a
determinação dos traços do plano δ, ver exercício 3344 e respectivo relatório. A
recta hh, horizontal (de nível), que passa por PP, é uma recta do plano δ pois
será paralela a hhδ, uma vez que rectas horizontais (de nível) de um plano são
paralelas entre si (e hhδ é paralelo a hhα, pelo que já sabemos a direcção das
rectas horizontais de δ). Em seguida, determinou-se FF, o traço frontal de hh. Por
FF conduziu-se ffδ, paralelo a ffα e hhδ é paralelo a hhα (e a hh) e concorrente com ffδ
no eixo XX. O plano δ contém o ponto PP e é paralelo ao plano α.
Em primeiro lugar representaram-se o plano γ, pelos seus traços, e o ponto MM, pelas
suas projecções, em função dos dados. Sobre a determinação dos traços do plano λ,
ver relatório do exercício anterior.
Em primeiro lugar representaram-se o plano θ, pelos seus traços, e o ponto PP, pelas
suas projecções, em função dos dados. Note que as projecções do ponto PP estão
sobre os traços homónimos do plano θ, mas PP nnããoo ppeerrtteennccee ao plano θ, pois não
verifica a condição para que um ponto pertença a um plano em relação ao plano θ
(tem de pertencer a uma recta do plano). Sobre a determinação dos traços do plano α,
ver exercício 3344 e respectivo relatório. A recta hh, horizontal (de nível), que passa por PP,
é a recta auxiliar a que se recorreu – será paralela a hhα. FF é o traço frontal de hh – por FF
conduziu-se ffα, paralelo a ffθ e hhα é paralelo a hhθ (e a hh) e concorrente com ffα no eixo XX.
O plano α contém o ponto PP e é paralelo ao plano θ.
35.
37.

12. 12
SOLUÇÕES
39.
A afirmação é vveerrddaaddeeiirraa. No entanto, os traços homónimos de um plano de rampa são sempre paralelos entre si, mesmo que os dois pla-
nos não sejam paralelos entre si, pois são rectas da mesma «família» de rectas. De facto, tanto o traço frontal como o traço horizontal de um
qualquer plano de rampa são, ambos, rectas fronto-horizontais, e rectas fronto-horizontais são sempre paralelas entre si. Assim, quaisquer
dois planos de rampa têm, sseemmpprree, os traços homónimos paralelos entre si, mesmo que não sejam paralelos. De facto, ao contrário das
restantes situações (todos os planos que não sejam paralelos ao eixo XX), o facto de os traços homónimos de dois planos de rampa serem
paralelos entre si (o que se verifica sempre) não nos garante o paralelismo entre os dois planos.
Em primeiro lugar representaram-se os dois planos, pelos respectivos traços, em função
dos dados. Para que os dois planos sejam paralelos, têm de conter duas «famílias» de
rectas em comum (duas rectas concorrentes de um dos planos têm de ser paralelas a
duas rectas concorrentes do outro plano). Os traços (horizontal de frontal) dos dois pla-
nos são rectas de uma mesma «família» de rectas (as rectas fronto-horizontais), pelo que
os dois planos já têm uma «família» de rectas em comum. É necessário averiguar se
existe outra «família» de rectas em comum. Para tal, recorreu-se a uma recta auxiliar qual-
quer, rr do plano ρ – a recta rr está definida por dois pontos, que são os seus traços (con-
dição para que uma recta pertença a um plano). Se os dois planos forem paralelos, a
«família» da recta rr também existe no plano σ. Assim, desenharam-se as projecções de
uma recta ss, do plano σ, tentando que ss seja paralela à recta rr – ss22, a projecção frontal
da recta ss, é paralela a rr22, a projecção frontal da recta rr. Em seguida, determinaram-se
os traços da recta ss e desenhou-se a sua projecção horizontal, ss11 (a recta ss também está
definida por dois pontos, que são igualmente os seus traços). Constata-se que, embora
as projecções frontais das duas rectas sejam paralelas entre si, as suas projecções hori-
zontais não o são, pelo que as duas rectas não são paralelas entre si (não são rectas da
mesma «família» de rectas). Então, os dois planos nnããoo ssããoo ppaarraalleellooss.
41.
Em primeiro lugar representaram-se o plano ρ, pelos seus traços, e o ponto PP, pelas
suas projecções, em função dos dados. De acordo com o exposto na resposta à
questão do exercício 3399, os traços de σ serão sempre paralelos aos traços homóni-
mos de ρ, quer os planos sejam paralelos ou não (são rectas da mesma «família» de
rectas). Assim, há que recorrer a outra «família» de rectas para garantir o paralelismo
entre os dois planos. Por outro lado, para que o plano σ contenha o ponto PP, é neces-
sário que PP pertença a uma recta do plano. Assim, desenharam-se as projecções de
uma recta rr, oblíqua, qualquer, do plano ρ. A recta rr é uma recta de uma outra «famí-
lia» de rectas qualquer (diferente da «família» de rectas dos traços do plano), que terá
de ser comum aos dois planos. Em seguida, pelas projecções de PP conduziram-se as
projecções de uma recta ss, paralela à recta rr, e determinaram-se os seus traços. Pelos
traços de ss conduziram-se os traços homónimos do plano σ. O plano σ é paralelo ao
plano ρ (pois contém duas rectas concorrentes paralelas a duas rectas concorrentes
do plano ρ) e contém o ponto PP (pois PP pertence a uma recta do plano – a recta ss).
Em primeiro lugar representaram-se o plano α, pelos seus traços, e o ponto PP, pelas suas
projecções, em função dos dados. Para que o plano γ seja paralelo ao plano α, o plano γ
tem de ter os seus traços paralelos aos traços homónimos do plano α. Por outro lado, uma
vez que se trata de planos projectantes horizontais, para que o plano γ contenha o ponto PP,
basta que hhγ passe por PP11 – um plano projectante horizontal projecta todas as suas rectas e
pontos no seu traço horizontal, e o plano γ é projectante horizontal. Assim, por PP11 conduziu-
-se hhγ, paralelo a hhα – ffγ é vertical (é paralelo a ffα) e é concorrente com hhγ no eixo XX.
38.
40.

13. 13
SOLUÇÕES
a) Em primeiro lugar representou-se o ponto PP pelas suas
projecções, em função das suas coordenadas. Sendo
dada a amplitude do diedro que o plano ρ faz com o Pla-
no Horizontal de Projecção, sabe-se que as suas rectas
de perfil fazem, com o Plano Horizontal de Projecção,
ângulos com a mesma amplitude. Assim, em primeiro
lugar conduziu-se, por PP, uma recta pp, de perfil, que
está definida por um ponto (o ponto PP) e uma direcção
(faz um ângulo de 30o com o Plano Horizontal de Pro-
jecção). Os traços do plano ρ têm de conter os traços
homónimos da recta pp. Optou-se por recorrer ao rebati-
mento do plano de perfil (plano π) que contém a recta pp
– rebateu-se o plano π para o Plano Frontal de Projecção
(a charneira foi ffπ), obtendo PPrr. O ângulo que a recta pp
faz com o Plano Horizontal de Projecção é igual (tem a
mesma amplitude) ao ângulo que a recta pp faz com hhπ,
que está em V.G. no ângulo entre pprr e hhπrr
. Assim, condu-
ziu-se pprr, por PPrr, fazendo um ângulo de 30° com hhπrr
e
garantindo que o traço horizontal da recta se situa no
SSPPHHAA (é dado que o traço horizontal do plano tem afas-
tamento positivo). Determinaram-se os traços da recta pp
em rebatimento, após o que se inverteu o rebatimento e
se determinaram as respectivas projecções. Em seguida,
por FF conduziu-se ffρ (o traço frontal do plano ρ) e por HH
conduziu-se hhρ (o traço horizontal do plano ρ).
b) Em primeiro lugar representou-se o ponto SS, pelas suas projecções. O plano σ é necessariamente um plano de rampa, pelo que já temos a
direcção dos seus traços, que são uma única «família» de rectas. Para que o plano σ seja paralelo ao plano ρ, tem de haver outra «família» de rec-
tas comum aos dois planos – essa «família» de rectas pode ser a das rectas de perfil. Assim, de forma a economizar traçado e a usar o rebati-
mento já efectuado, conduziu-se, por SS, uma recta gg, fronto-horizontal – a recta gg é nneecceessssaarriiaammeennttee uma recta do plano σ. O ponto SS’’ é o
ponto de intersecção da recta gg com o plano π. A recta pp’’, que passa por SS’’ e é paralela à recta pp, é uma recta do plano σ – note que pp’’ é a recta
de intersecção do plano π com o plano σ, tal como a recta pp era a recta de intersecção do plano π com o plano ρ. Determinou-se SS’’rr e por SS’’rr
conduziu-se pp’’rr, paralela a pprr. Determinaram-se os traços da recta pp’’ em rebatimento, após o que se inverteu o rebatimento e se determinaram as
respectivas projecções. Em seguida, por FF’’ conduziu-se ffσ (o traço frontal do plano σ) e por HH’’ conduziu-se hhσ (o traço horizontal do plano σ).
42.
Em primeiro lugar representaram-se o plano ρ, pelos seus traços, e o plano σ, pelo seu
traço frontal, em função dos dados. Os dois planos já têm uma «família» de rectas em
comum – a «família» das rectas fronto-horizontais. Para que os planos sejam paralelos,
os planos têm de conter uma outra «família» de rectas em comum. Recorreu-se a uma
recta rr, oblíqua, qualquer, do plano ρ. A recta rr é uma recta de uma outra «família» de rectas
qualquer (diferente da «família» de rectas dos traços do plano), que terá de ser comum
aos dois planos. Em seguida, desenharam-se as projecções de uma recta ss, paralela à
recta rr e pertencente ao plano σ (o traço frontal da recta ss, FF’’, tem de se situar sobre ffσ).
Determinou-se o traço horizontal da recta ss, HH’’, e por HH’’ conduziu-se o traço horizontal
do plano σ, hhσ. O plano σ é paralelo ao plano ρ, pois contém duas rectas concorrentes
paralelas a duas rectas concorrentes do plano ρ (o seu traço frontal e a recta ss, por
exemplo, que são paralelos, respectivamente, ao traço frontal do plano ρ e à recta rr).
44.
Em primeiro lugar representaram-se os planos ρ e σ pelos seus traços, em função
dos dados – note que, sendo o plano σ um plano passante, é possível definir ime-
diatamente os seus traços que, no entanto, são insuficientes para definir o plano,
pois são uma única recta (é possível definir um plano por uma única recta se e só
se essa recta for uma das suas rectas de maior declive ou uma das suas rectas de
maior inclinação). Os dois planos já têm uma «família» de rectas em comum – a
«família» das rectas fronto-horizontais. Para que os planos sejam paralelos, os pla-
nos têm de conter uma outra «família» de rectas em comum. Recorreu-se a uma
recta rr, oblíqua, qualquer, do plano ρ. A recta rr é uma recta de uma outra «família»
de rectas qualquer, que terá de ser comum aos dois planos. Em seguida desenha-
ram-se as projecções de uma recta ss, paralela à recta rr e pertencente a σ – a recta
ss é nneecceessssaarriiaammeennttee uma recta passante. O plano σ, definido por duas rectas
concorrentes (o eixo XX e a recta ss) é paralelo ao plano ρ.
43.

14. 14
SOLUÇÕES
45.
Em primeiro lugar representaram-se o plano σ, pelos seus traços (que estão
coincidentes no eixo XX) e pelo ponto PP, e o ponto AA, pelas suas projecções,
em função dos dados. Já se sabe que os traços do plano ρ (o plano pedido)
são rectas fronto-horizontais, pois trata-se de um plano de rampa – os dois
planos já têm uma «família» de rectas em comum (a «família» das rectas
fronto-horizontais). Para que os planos sejam paralelos, os planos têm de
conter uma outra «família» de rectas em comum. Por outro lado, para que o
plano ρ contenha o ponto AA, o ponto tem de pertencer a uma recta do plano.
Recorreu-se a uma recta rr, oblíqua, qualquer, do plano σ – a recta rr passa
pelo ponto PP (que é um ponto do plano σ) e é uma recta passante. Em
seguida, desenharam-se as projecções de uma recta ss, paralela à recta rr e
passando por AA – determinaram-se os traços da recta ss, pelos quais se con-
duziram os traços homónimos do plano ρ. O plano ρ é paralelo ao plano σ
(os dois planos têm duas «famílias» de rectas em comum) e contém o ponto
AA, pois o ponto AA pertence a uma recta do plano ρ (a recta ss).
46.
Em primeiro lugar representaram-se o plano γ, pelos seus traços, e o ponto PP, pelas suas
projecções, em função dos dados. Em seguida, pelas projecções de PP conduziram-se
imediatamente as projecções da recta pp – note que não foi necessário nenhum procedi-
mento particular para desenhar as projecções da recta pp. A recta pp, no entanto, não está
completamente definida – falta-nos outro ponto para definir a recta, para além do ponto
PP. Por outro lado, há que garantir que a recta pp seja paralela ao plano γ, para o que a rec-
ta pp terá de ser paralela a uma recta do plano γ (critério de paralelismo entre rectas e pla-
nos). Assim, recorreu-se a uma recta pp’’, qualquer, de perfil e pertencente ao plano – por
uma questão de economia de traçados, optou-se por fazer com que a recta pp’’ tenha
abcissa nula. A recta pp’’ está definida por dois pontos, que são os seus traços (condição
para que uma recta pertença a um plano). A recta pp tem de ser paralela à recta pp’’. Para
garantir o paralelismo entre as rectas pp e pp’’ recorreu-se ao raciocínio exposto no relatório
do exercício 44. As rectas pp e pp’’, sendo paralelas, são complanares – recorreu-se a duas
rectas do plano definido por pp e pp’’. A recta rr é concorrente com a recta pp no ponto PP e
com a recta pp’’ no ponto HH (o seu traço horizontal). A recta ss é concorrente com a recta pp’’
no ponto FF (o seu traço frontal) e é paralela à recta rr. A recta ss, porque é complanar com
a recta pp, é concorrente com esta num ponto MM. A recta pp, definida por PP e MM, é paralela
à recta pp’’, que é uma recta do plano γ, pelo que a recta pp é paralela ao plano γ.
47.
Em primeiro lugar representaram-se o plano ψ, pelos seus traços, e a recta pp,
pelas suas projecções, em função dos dados. Note que as projecções da recta pp
se desenharam imediatamente, apesar da recta não se encontrar completa-
mente definida. Para determinar o ponto de intersecção da recta pp com o plano
ψ, e uma vez que nem a recta nem o plano são projectantes, recorreu-se ao
mmééttooddoo ggeerraall ddaa iinntteerrsseeccççããoo ddee rreeccttaass ccoomm ppllaannooss, como em seguida se expõe:
11.. conduziu-se, pela recta, um plano auxiliar – o plano π (que é um plano de per-
fil); 22.. determinou-se a recta de intersecção do plano π com o plano ψ (a recta ii,
que é uma recta de perfil) – a recta ii fica definida por dois pontos, que são os
seus traços (trata-se do caso geral da intersecção de planos); 33.. o ponto de con-
corrência das duas rectas (recta pp e recta ii) é o ponto de intersecção da recta pp
com o plano ψ. Uma vez que tanto a recta pp com a recta ii são rectas de perfil, a
determinação do seu ponto de concorrência só se pode processar com o recur-
so a um processo geométrico auxiliar. Optou-se pelo rebatimento do plano π –
rebateu-se o plano π para o Plano Frontal de Projecção (a charneira foi ffπ). Reba-
teu-se a recta ii, pelo rebatimento dos seus traços – iirr fica definida por FFrr e HHrr. A
recta pprr passa por PPrr e, uma vez que a recta pp é paralela ao β2/4, sabe-se que a
recta faz ângulos de 45° com os planos de projecção (e com os traços do plano
π) – ver exercício 3300 e respectivo relatório. O ponto de intersecção das duas rec-
tas (recta pp e recta ii) – o ponto II – determinou-se em rebatimento. IIrr é o ponto de
concorrência de iirr e pprr. Invertendo o rebatimento, determinaram-se as projec-
ções do ponto II que é o ponto de intersecção da recta pp com o plano ρ.

15. 15
SOLUÇÕES
48.
Em primeiro lugar representaram-se as rectas rr e hh, pelas respectivas projec-
ções, em função dos dados. Para que o plano α seja paralelo à recta rr, tem de
conter uma recta paralela à recta rr (critério de paralelismo entre planos e rec-
tas). Assim, conduziu-se uma recta ss, paralela à recta rr e concorrente com a
recta hh – por uma questão de economia de traçados, optou-se por fazer com
que a recta ss seja concorrente com a recta hh no ponto BB. O plano definido pelas
rectas hh e rr está definido por duas rectas concorrentes e é necessariamente
paralelo à recta rr. Em seguida, determinaram-se HH, o traço horizontal da recta ss
(o seu traço frontal está fora dos limites do desenho) e FF, o traço frontal da recta
hh. hhα, o traço horizontal do plano α, passa por HH e é paralelo a à recta hh (rectas
horizontais de um plano são paralelas entre si e paralelas ao traço horizontal
do plano, que é uma recta horizontal do plano com cota nula). ffα passa por FF e
é concorrente com hhα no eixo XX.
49.
Em primeiro lugar representaram-se o plano θ, pelos seus traços, e a recta gg, pelas suas projecções, em função dos dados. Para que os
dois planos sejam paralelos, têm de conter duas «famílias» de rectas em comum – uma vez que se trata de planos de rampa, os dois planos
já têm, em comum, a «família» das rectas fronto-horizontais. É necessária uma outra «família» de rectas comum aos dois planos. Assim,
desenharam-se as projecções de uma recta rr, oblíqua, qualquer, do plano θ. A recta rr é uma recta de uma outra «família» de rectas qualquer
(não é fronto-horizontal, que é a «família» que os dois planos já têm em comum), que terá de ser comum aos dois planos – a recta rr está
definida por dois pontos, que são os seus traços. Em seguida, desenharam-se as projecções de uma recta ss, paralela à recta rr e concorrente
com a recta gg num ponto PP, e determinaram-se os seus traços. Pelos traços de ss conduziram-se os traços homónimos do plano ρ. O plano ρ
é paralelo ao plano θ, pois contém duas rectas concorrentes paralelas a duas rectas concorrentes do plano θ.

16. 16
SOLUÇÕES
50.
Duas rectas ppeerrppeennddiiccuullaarreess são duas rectas oorrttooggoonnaaiiss (que formam, entre si, quatro ângulos rectos – de 90°) que são complanares (são
ccoonnccoorrrreenntteess). Rectas oorrttooggoonnaaiiss são rectas nnããoo ccoommppllaannaarreess paralelas a duas rectas ppeerrppeennddiiccuullaarreess.
PERPENDICULARIDADE E ORTOGONALIDADE
14
51.
A afirmação é ffaallssaa. Duas rectas ortogonais podem ou não ser perpendiculares – se forem complanares, então são perpendiculares (são
concorrentes), mas se não forem complanares, as rectas serão apenas ortogonais. Já o contrário é verdade – duas rectas perpendiculares
são necessariamente ortogonais. A ortogonalidade é condição necessária para que se verifique a perpendicularidade, mas não o contrário.
52.
A afirmação é ffaallssaa. As projecções de duas rectas perpendiculares entre si nnããoo ssããoo perpendiculares entre si, a menos que uma das rectas
sseejjaa ppaarraalleellaa aa uumm ddooss ppllaannooss ddee pprroojjeeccççããoo – nesse caso, as projecções das duas rectas nneessssee ppllaannoo ddee pprroojjeeccççããoo serão sempre per-
pendiculares entre si.
53.
A afirmação é vveerrddaaddeeiirraa. De facto, e como se referiu na resposta à questão anterior, se duas rectas são perpendiculares ou ortogonais e
uummaa ddeellaass éé ppaarraalleellaa aa uumm ddooss ppllaannooss ddee pprroojjeeccççããoo, as projecções das duas rectas nneessssee ppllaannoo ddee pprroojjeeccççããoo são necessariamente
perpendiculares entre si. Assim, atendendo a que as rectas horizontais (de nível) são paralelas ao Plano Horizontal de Projecção, qualquer
recta perpendicular ou ortogonal a uma recta horizontal (de nível) terá a sua projecção horizontal (a projecção no Plano Horizontal de Pro-
jecção) perpendicular à projecção horizontal da recta horizontal (de nível).
55.
Em primeiro lugar representaram-se a recta hh e o ponto PP, pelas respectivas projec-
ções, em função dos dados. Os dados permitiram-nos, imediatamente, desenhar a pro-
jecção frontal da recta pp – pp22. Em seguida, uma vez que a recta hh é paralela ao Plano
Horizontal de Projecção, a ortogonalidade entre a recta hh e qualquer outra recta é
directa em projecção horizontal. Assim, por PP11 conduziu-se pp11, a projecção horizontal
da recta pp, perpendicular a hh11 – a ortogonalidade entre as duas rectas já está garantida.
As duas rectas não são concorrentes – são apenas ortogonais.
Em primeiro lugar representaram-se a recta hh e o ponto PP, pelas respectivas projec-
ções, em função dos dados. Em seguida, uma vez que a recta hh é paralela ao Plano
Horizontal de Projecção, sabe-se que a ortogonalidade entre a recta hh e qualquer outra
recta é directa em projecção horizontal. Assim, por PP11 conduziu-se pp11, a projecção hori-
zontal da recta pp, perpendicular a hh11 – a ortogonalidade entre as duas rectas já está
garantida. Por outro lado, é pedido que as rectas sejam ppeerrppeennddiiccuullaarreess, pelo que as
rectas terão de ser concorrentes. Em projecção horizontal, determinou-se II11, a projecção
horizontal do ponto de concorrência das duas rectas – II22 situa-se sobre hh22. A projecção
frontal da recta pp, pp22, está definida por PP22 e por II22. As rectas pp e hh são ortogonais e, uma
vez que são concorrentes, são ppeerrppeennddiiccuullaarreess.
54.

17. 17
SOLUÇÕES
Em primeiro lugar representaram-se a recta ff e o ponto PP, pelas respectivas projecções, em fun-
ção dos dados. A recta aa é frontal (de frente) e a ortogonalidade entre rectas frontais (de frente) é
directa em projecção frontal, pois ambas as rectas (ff e aa) são paralelas ao Plano Frontal de Projec-
ção. Assim, por PP22 conduziu-se, imediatamente, aa22, a projecção frontal da recta aa, perpendicular a
ff22 – aa11 é paralela ao eixo XX e passa por PP11. Já no que respeita à recta bb, que é horizontal (de nível),
teve-se em conta que não há nenhuma recta horizontal (de nível) cuja projecção frontal seja
perpendicular a ff22. No entanto, tratando-se de uma recta horizontal (de nível), que é paralela ao
Plano Horizontal de Projecção, sabe-se que a ortogonalidade é directa em projecção horizontal.
Assim, por PP11 conduziu-se bb11, perpendicular a ff11 (bb11 fica perpendicular ao eixo XX) – a partir de bb11
constatou-se que a recta bb terá de ser uma recta de topo, pois é a única recta horizontal (de nível)
cuja projecção horizontal é perpendicular ao eixo XX (uma recta de topo é um caso particular das
rectas horizontais). A projecção frontal de bb é um ponto, que está coincidente com PP22. Sublinha-se
que para desenhar as projecções da recta aa se teve em conta que a recta aa é uma rreeccttaa ffrroonnttaall
((ddee ffrreennttee)), paralela ao Plano Frontal de Projecção, pelo que aa oorrttooggoonnaalliiddaaddee éé ddiirreeccttaa eemm pprroo--
jjeeccççããoo ffrroonnttaall. Já para desenhar as projecções da recta bb, que é uma rreeccttaa hhoorriizzoonnttaall ((ddee nníívveell)),
paralela ao Plano Horizontal de Projecção, se teve em conta que aa oorrttooggoonnaalliiddaaddee éé ddiirreeccttaa eemm
pprroojjeeccççããoo hhoorriizzoonnttaall. Visualize no espaço que qualquer recta de topo é necessariamente ortogo-
nal a qualquer recta frontal (de frente).
56.
Em primeiro lugar representaram-se a recta hh e o ponto PP, pelas respectivas projecções,
em função dos dados. Sobre a determinação das projecções da recta rr, ver exercício 5555 e
respectivo relatório.
57.
58.
Em primeiro lugar representaram-se a recta tt e o ponto BB, pelas respectivas projecções,
em função dos dados. Em seguida, por BB22 conduziu-se pp22, com o ângulo pedido – pp22
faz, com o eixo XX, um ângulo de 45° (a.d.). Uma recta de topo é um caso particular das
rectas horizontais (de nível) – é paralela ao Plano Horizontal de Projecção e a ortogonali-
dade entre uma recta de topo e outra recta qualquer é directa em projecção horizontal.
Assim, por BB11 conduziu-se a projecção horizontal da recta pp, pp11, perpendicular a tt11 –
constata-se imediatamente que a recta pp é uma rreeccttaa ffrroonnttaall ((ddee ffrreennttee)). Visualize no
espaço que qualquer recta ortogonal a uma recta de topo é necessariamente uma recta
frontal (de frente), incluindo qualquer dos seus casos particulares.
Em primeiro lugar representaram-se a recta gg e o ponto PP, pelas respectivas projecções, em
função dos dados. A recta gg, porque se trata de uma recta fronto-horizontal, é simultaneamente
um caso particular das rectas frontais (de frente) e um caso particular das rectas horizontais (de
nível). Assim, para desenhar as projecções de uma recta ortogonal à recta gg, esta pode ser con-
siderada como uma recta frontal (em que a ortogonalidade é directa em projecção frontal) ou
como uma recta horizontal (em que a ortogonalidade é directa em projecção horizontal).
Optou-se pela segunda hipótese – considerando a recta gg como uma recta horizontal (de nível),
sabe-se que a ortogonalidade entre a recta gg e outra recta qualquer é directa em projecção hori-
zontal. Assim, pp11, a projecção horizontal da recta pp, é perpendicular a gg11 (e ao eixo XX) – qual-
quer que seja a projecção frontal da recta, a recta pp é necessariamente ortogonal à recta gg, pois
a ortogonalidade já está garantida. A projecção horizontal desenhada só pode corresponder a
uma recta de topo ou a uma recta de perfil. Optou-se pela primeira situação – a recta pp dese-
nhada é uma recta de topo. Caso se tivesse considerado a recta gg como um caso particular das
rectas frontais (de frente), pp22, a projecção frontal da recta pp, seria perpendicular a gg22 – nesse
caso, a recta pp poderia ser uma recta vertical ou uma recta de perfil (são as únicas rectas a que
poderia corresponder aquela projecção frontal). Assim, face ao exposto, as hipóteses de resolu-
ção que existem são três – rreeccttaass ddee ttooppoo, rreeccttaass vveerrttiiccaaiiss ou rreeccttaass ddee ppeerrffiill. Tenha em con-
ta que qualquer recta de perfil é necessariamente ortogonal a uma recta fronto-horizontal –
assim, quando se refere a recta de perfil estão incluídas as infinitas direcções de rectas de perfil.
59.

18. 18
SOLUÇÕES
60.
Em primeiro lugar representaram-se a recta gg e o ponto PP, pelas respectivas pro-
jecções, em função dos dados. De acordo com o exposto no relatório do exercí-
cio anterior, é possível começar por desenhar qualquer das projecções da recta pp
– optou-se igualmente por desenhar pp11. No entanto, ao contrário do exercício an-
terior, agora pretende-se que as duas rectas sejam ppeerrppeennddiiccuullaarreess – para tal, as
duas rectas terão de ser concorrentes. O ponto II, determinado através da sua
projecção horizontal, é o ponto de concorrência das duas rectas. A recta pp passa
por PP e por II, pelo que é nneecceessssaarriiaammeennttee uma rreeccttaa ddee ppeerrffiill que está definida
por dois pontos. Note que, caso se tivesse começado por desenhar a projecção
frontal da recta pp se chegaria à mesma resolução final, sendo que, nesse caso, o
ponto II seria determinado a partir da sua projecção frontal.
61.
Em primeiro lugar representaram-se a recta rr e o ponto PP, pelas respectivas projec-
ções, em função dos dados. As únicas rectas ortogonais à recta rr que se podem definir,
com os conhecimentos adquiridos, são rreeccttaass ffrroonnttaaiiss ((ddee ffrreennttee)) ou rreeccttaass hhoorrii--
zzoonnttaaiiss ((ddee nníívveell)). Optou-se pela segunda hipótese. Fazendo a recta pp uma recta ho-
rizontal (de nível), que é paralela ao Plano Horizontal de Projecção, a ortogonalidade
é directa em projecção horizontal. Assim, pp11 passa por PP11 e é perpendicular a rr11 – pp22
passa por PP22 e é paralela ao eixo XX. Caso se tivesse optado por fazer a recta pp uma
recta frontal (de frente), que é paralela ao Plano Frontal de Projecção (em que a orto-
gonalidade é directa em projecção frontal), pp22 seria perpendicular a rr22. Conforme se
referiu acima, a outra hipótese seria, então, uma rreeccttaa ffrroonnttaall ((ddee ffrreennttee)).
a) Em primeiro lugar representaram-se a recta gg e o ponto PP, pelas respectivas projecções, em fun-
ção dos dados. A recta rr é uma recta horizontal (de nível), paralela ao Plano Horizontal de Projec-
ção, pelo que a ortogonalidade é directa em projecção horizontal – assim, rr11 passa por PP11 e tem
de ser perpendicular a gg11 (e perpendicular ao eixo XX). A única recta horizontal (de nível) que tem a
projecção horizontal desenhada é uma recta de topo – rr é, assim, uma rreeccttaa ddee ttooppoo.
b) A recta ss é uma recta frontal (de frente), paralela ao Plano Frontal de Projecção, pelo que a ortogo-
nalidade é directa em projecção frontal – assim, ss22 passa por PP22 e tem de ser perpendicular a gg22 (e
perpendicular ao eixo XX). A única recta frontal (de frente) que tem a projecção frontal desenhada é
uma recta vertical – ss é, assim, uma rreeccttaa vveerrttiiccaall.
63.
a) Em primeiro lugar representou-se a recta rr pelas suas projecções, em função dos
dados. Em seguida, determinou-se o ponto da recta rr que tem 2 cm de cota – o
ponto PP (que é o ponto de concorrência das duas rectas). A projecção frontal da
recta hh, hh22, desenhou-se imediatamente, passando por PP22 e paralela ao eixo XX.
Uma vez que a recta hh é horizontal (de nível), que é paralela ao Plano Horizontal de
Projecção, a ortogonalidade é directa em projecção horizontal – assim, hh11 passa
por PP11 e é perpendicular a rr11.
b) Para determinar os traços do plano definido pelas duas rectas, determinaram-se os
traços destas nos planos de projecção – FF e HH são, respectivamente, o traço frontal
e o traço horizontal da recta rr e FF’’ é o traço frontal da recta hh. ffα, o traço frontal do
plano, está definido por FF e FF’’. hhα, o traço horizontal do plano, passa por HH, é con-
corrente com ffα no eixo XX e é paralelo à recta hh. A recta rr é uma rreeccttaa ddee mmaaiioorr
ddeecclliivvee do plano α, pois é perpendicular às rectas horizontais (de nível) do plano
(e ao traço horizontal do plano).
62.

19. 19
SOLUÇÕES
a) Em primeiro lugar, representou-se a recta rr pelas suas projecções, em função dos
dados. Em seguida, determinou-se o ponto da recta rr que tem 2 cm de afastamento
– o ponto PP (que é o ponto de concorrência das duas rectas). A projecção horizontal
da recta ff, ff11, desenhou-se imediatamente, passando por PP11 e paralela ao eixo XX.
Uma vez que a recta ff é frontal (de frente), que é paralela ao Plano Frontal de Projec-
ção, a ortogonalidade é directa em projecção frontal – assim, ff22 passa por PP22 e é
perpendicular a rr22.
b) Para determinar os traços do plano definido pelas duas rectas, determinaram-se os
traços destas nos planos de projecção – FF e HH são, respectivamente, o traço frontal
e o traço horizontal da recta rr e HH’’ é o traço horizontal da recta ff. hhδ, o traço hori-
zontal do plano, está definido por HH e HH’’. ffδ, o traço frontal do plano, passa por FF e
é paralelo à recta ff (note que o ponto do eixo XX que é o ponto de concorrência dos
dois traços do plano se situa fora dos limites do desenho). A recta rr é uma rreeccttaa ddee
mmaaiioorr iinncclliinnaaççããoo do plano δ, pois é perpendicular às rectas frontais (de frente) do
plano (e ao traço frontal do plano).
65.
A recta hh tem 4 cm de cota – todos os seus pontos têm 4 cm de cota. A recta ff tem 3 cm de afasta-
mento – todos os seus pontos têm 3 cm de afastamento. O ponto de concorrência das duas rectas
(ponto PP), porque pertence simultaneamente às duas rectas, tem 4 cm de cota e 3 cm de afasta-
mento. A partir do raciocínio exposto, desenharam-se as projecções das rectas ff e hh, em função
dos dados. A recta rr, sendo perpendicular à recta ff (que é paralela ao Plano Frontal de Projecção),
tem de ter a sua projecção frontal perpendicular a ff22, pois a perpendicularidade é directa em pro-
jecção frontal – rr22 passa por PP22 e é perpendicular a ff22. Por outro lado, a recta rr, sendo perpendicu-
lar à recta hh (que é paralela ao Plano Horizontal de Projecção), tem de ter a sua projecção
horizontal perpendicular a hh11, pois a perpendicularidade é directa em projecção horizontal – rr11 pas-
sa por PP11 e é perpendicular a hh11.
66.
A afirmação é ffaallssaa. Uma recta é ortogonal a um plano se e só se for ortogonal a duas rectas ccoonnccoorrrreenntteess do plano. De facto, atendendo à
situação do exercício 6633, por exemplo, a recta rr é ortogonal (e perpendicular) a duas rectas do plano α (a recta hh e hhα, o traço horizontal do
plano) mas, no entanto, a recta rr nnããoo éé ortogonal ao plano mas, sim, pertence ao plano. Tal justifica-se pelo facto de as rectas hh e hhα serem
duas rectas ppaarraalleellaass do plano α e não duas rectas ccoonnccoorrrreenntteess.
67.
O CCrriittéérriioo ddee oorrttooggoonnaalliiddaaddee eennttrree rreeccttaass ee ppllaannooss afirma que uma recta é ortogonal a um plano se e só se for ortogonal a duas rectas ccoonn--
ccoorrrreenntteess desse plano, pelo que um plano é ortogonal a uma recta se e só se contiver duas rectas ccoonnccoorrrreenntteess ortogonais à recta dada.
68.
A afirmação é vveerrddaaddeeiirraa. Segundo o TTeeoorreemmaa ddaa oorrttooggoonnaalliiddaaddee eennttrree rreeccttaass ee ppllaannooss, uma recta ortogonal a um plano é ortogonal a
ttooddaass as rectas desse plano. Assim, uma vez que os traços de um plano são duas rectas desse plano, qualquer recta ortogonal a esse pla-
no é necessariamente ortogonal aos traços do plano.
69.
Em primeiro lugar representaram-se o plano ν, pelo seu traço frontal, e o ponto PP, pelas
suas projecções, em função dos dados. Uma recta ortogonal a um plano tem de ser
ortogonal a duas rectas concorrentes desse plano. O plano ν, porque é horizontal (de
nível), contém todas as direcções das rectas horizontais (de nível). Assim, a recta pp terá
de ser uma recta qualquer, que seja ortogonal a duas rectas horizontais (de nível) quais-
quer, concorrentes – a recta pp é nneecceessssaarriiaammeennttee uma rreeccttaa vveerrttiiccaall.
70.
Em primeiro lugar representaram-se o plano ϕ, pelo seu traço horizontal, e o ponto AA, pelas suas pro-
jecções, em função dos dados. Uma recta ortogonal a um plano tem de ser ortogonal a duas rectas
concorrentes desse plano. O plano ϕ, porque é frontal (de frente), contém todas as direcções das
rectas frontais (de frente). Assim, a recta pp terá de ser uma recta qualquer, que seja ortogonal a duas
rectas frontais (de frente) quaisquer, concorrentes – a recta pp é nneecceessssaarriiaammeennttee uma rreeccttaa ddee ttooppoo.
64.

20. 20
SOLUÇÕES
Em primeiro lugar representaram-se o plano γ, pelos seus traços, e o ponto PP, pelas suas
projecções, em função dos dados. Uma recta ortogonal a um plano tem de ser ortogonal
a duas rectas concorrentes desse plano. Os traços do plano γ são dduuaass rreeccttaass ccoonnccoorr--
rreenntteess do plano – assim, basta fazer com que a recta pp seja simultaneamente ortogonal
aos traços do plano, para garantir que a recta pp seja ortogonal ao plano. O traço frontal do
plano, ffγ, é uma recta frontal (de frente) do plano (é uma recta vertical, que é um caso par-
ticular das rectas frontais), pelo que a ortogonalidade é directa em projecção frontal – por
PP22 conduziu-se pp22, perpendicular a ffγ. O traço horizontal do plano, hhγ, é uma recta hori-
zontal (de nível) do plano, pelo que a ortogonalidade é directa em projecção horizontal –
por PP11 conduziu-se pp11, perpendicular a hhγ. A recta pp é uma rreeccttaa hhoorriizzoonnttaall ((ddee nníívveell)).
71.
72.
Em primeiro lugar representaram-se o plano θ, pelos seus traços, e o ponto PP, pelas suas
projecções, em função dos dados. Uma recta ortogonal a um plano tem de ser ortogonal a
duas rectas concorrentes desse plano. Os traços do plano θ são dduuaass rreeccttaass ccoonnccoorrrreenntteess
do plano – assim, basta fazer com que a recta pp seja simultaneamente ortogonal aos traços
do plano, para garantir que a recta pp seja ortogonal ao plano. O traço horizontal do plano, hhθ,
é uma recta horizontal (de nível) do plano (é uma recta de topo, que é um caso particular das
rectas horizontais), pelo que a ortogonalidade é directa em projecção horizontal – por PP11 con-
duziu-se pp11, perpendicular a hhθ. O traço frontal do plano, ffθ, é uma recta frontal (de frente) do
plano, pelo que a ortogonalidade é directa em projecção frontal – por PP22 conduziu-se pp22, per-
pendicular a ffθ. A recta pp é uma rreeccttaa ffrroonnttaall ((ddee ffrreennttee)).
74.
Em primeiro lugar representaram-se o plano α, pelos seus traços, e o ponto PP, pelas suas projecções,
em função dos dados. Uma recta ortogonal a um plano tem de ser ortogonal a duas rectas concorrentes
desse plano. Os traços do plano α são dduuaass rreeccttaass ccoonnccoorrrreenntteess do plano – assim, basta fazer com que
a recta pp seja simultaneamente ortogonal aos traços do plano, para garantir que a recta pp seja ortogonal
ao plano. O traço horizontal do plano, hhα, é uma recta horizontal (de nível) do plano, pelo que a ortogo-
nalidade é directa em projecção horizontal – por PP11 conduziu-se pp11, perpendicular a hhα. O traço frontal do
plano, ffα, é uma recta frontal (de frente) do plano, pelo que a ortogonalidade é directa em projecção
frontal – por PP22 conduziu-se pp22, perpendicular a ffα. A recta pp é ortogonal ao plano, pois é ortogonal a
duas rectas concorrentes do plano – os traços do plano. Note que as projecções da recta pp são per-
pendiculares aos traços homónimos do plano, o que se verificou igualmente nas situações anteriores.
Em primeiro lugar representaram-se o plano π, pelos seus traços, e o ponto AA, pelas suas projec-
ções, em função dos dados. Uma recta ortogonal a um plano tem de ser ortogonal a duas rectas
concorrentes desse plano. Os traços do plano π são dduuaass rreeccttaass ccoonnccoorrrreenntteess do plano – assim,
basta fazer com que a recta pp seja simultaneamente ortogonal aos traços do plano, para garantir
que a recta pp seja ortogonal ao plano. O traço horizontal do plano, hhπ, é uma recta horizontal (de
nível) do plano (é uma recta de topo, que é um caso particular das rectas horizontais), pelo que a
ortogonalidade é directa em projecção horizontal – por AA11 conduziu-se pp11, perpendicular a hhπ.
O traço frontal do plano, ffπ, é uma recta frontal (de frente) do plano (é uma recta vertical, que é um
caso particular das rectas frontais), pelo que a ortogonalidade é directa em projecção frontal – por
AA22 conduziu-se pp22, perpendicular a ffπ. A recta pp é uma rreeccttaa ffrroonnttoo--hhoorriizzoonnttaall.
73.

21. 21
SOLUÇÕES
75.
a) Em primeiro lugar representaram-se o plano α, pelos seus traços, e o ponto PP, pelas
suas projecções, em função dos dados. Sobre a determinação das projecções da
recta pp, ver exercício anterior e respectivo relatório.
b) Para determinar o ponto de intersecção da recta pp com o plano α, e uma vez que
nem a recta nem o plano são projectantes, há que recorrer ao mmééttooddoo ggeerraall ddaa iinn--
tteerrsseeccççããoo ddee rreeccttaass ccoomm ppllaannooss. Assim, tem-se: 11.. por pp conduziu-se um plano au-
xiliar (o plano γ, que é um plano vertical – é o plano projectante horizontal da recta
pp); 22.. determinou-se a recta ii, a recta de intersecção dos dois planos (a recta ii está
definida pelos seus traços, pois trata-se do caso geral da intersecção entre planos);
33.. o ponto de concorrência da recta ii com a recta pp (o ponto II) é o ponto de inter-
secção da recta pp com o plano α.
Em primeiro lugar representaram-se o plano θ, pelos seus traços, e o ponto AA, pelas suas
projecções, em função dos dados. Sobre a determinação das projecções da recta rr, ver
exercício 7744 e respectivo relatório. Sobre a determinação do ponto II, e tendo em conta que
nem a recta nem o plano são projectantes, recorreu-se ao mmééttooddoo ggeerraall ddaa iinntteerrsseeccççããoo ddee
rreeccttaass ccoomm ppllaannooss (ver a alínea bb)) do relatório do exercício anterior). O plano γ, de topo, é o
plano auxiliar a que se recorreu – é o plano projectante frontal da recta rr.
Em primeiro lugar representaram-se o plano ρ, pelos seus traços, e o ponto PP, pelas suas
projecções, em função dos dados. Em seguida, desenharam-se imediatamente as projec-
ções da recta pp, perpendiculares aos traços homónimos de ρ. A recta pp é uma rreeccttaa ddee
ppeerrffiill, que não se encontra totalmente definida em Dupla Projecção Ortogonal, uma vez
que as suas projec-ções não verificam o Critério de reversibilidade. Assim, necessitamos de
mais um ponto da recta pp, para além do ponto PP. A recta pp, para ser ortogonal ao plano ρ,
tem de ser ortogonal a duas «famílias» de rectas do plano. A recta pp já é ortogonal às rectas
fronto-horizontais de ρ (qualquer recta de perfil é necessariamente ortogonal a uma recta
fronto-horizontal – ver relatório do exercício 5599) – é necessário que a recta pp seja ortogonal
a outra «família» de rectas do plano (às rectas de perfil do plano, por exemplo). Por pp con-
duziu-se um plano auxiliar π, de perfil. Em seguida, determinou-se a recta ii, que é a recta de
intersecção de π com ρ – a recta ii é uma recta de perfil de ρ e está definida pelos seus tra-
ços (trata-se do caso geral da intersecção entre planos). A recta pp terá de ser perpendicular
à recta ii. É necessário o recurso a um processo geométrico auxiliar – optou-se pelo rebati-
mento do plano π para o Plano Frontal de Projecção (a charneira foi ffπ), obtendo-se iirr (defi-
nida por FFrr e HHrr) e PPrr. Por PPrr conduziu-se pprr, perpendicular a iirr. Sobre pprr representou-se arbitrariamente um outro ponto, para além de PP – RRrr.
Invertendo o rebatimento, determinaram-se as projecções de RR – a recta pp, ortogonal a ρ, está definida por PP e RR. Note que o processo geomé-
trico auxiliar utilizado poderia ser, por exemplo, uma mudança do diedro de projecção.
77.
Em primeiro lugar representaram-se o plano δ, pelos seus traços, e o ponto PP, pelas suas projec-
ções, em função dos dados. Sobre a determinação das projecções da recta rr, ver exercício 7744 e
respectivo relatório. Note que a recta rr tem as suas projecções paralelas entre si – trata-se de uma
recta paralela ao β2/4.
76.
78.

22. 22
SOLUÇÕES
Em primeiro lugar, representaram-se o plano ρ, pelos seus traços, e o ponto MM, pelas
suas projecções, em função dos dados. Sobre a determinação da recta pp, ver relatório
do exercício anterior. O outro ponto da recta pp a que se recorreu para a definir em
Dupla Projecção Ortogonal foi o seu traço frontal – o ponto FF’’. A recta pp, definida por MM e
por FF’’, é ortogonal ao plano ρ.
80.
Em primeiro lugar representaram-se o plano ρ, pelo seu traço frontal (não é conhecido o seu
traço horizontal, pois é dada a orientação do plano), e o ponto PP, pelas suas projecções, em
função dos dados. Em seguida, desenharam-se imediatamente as projecções da recta pp,
que é necessariamente uma rreeccttaa ddee ppeerrffiill – a recta pp não se encontra totalmente definida
em Dupla Projecção Ortogonal, uma vez que as suas projecções não verificam o Critério de
reversibilidade. Assim, necessitamos de mais um ponto da recta pp, para além do ponto PP. A
recta pp, para ser ortogonal ao plano ρ, tem de ser ortogonal a duas «famílias» de rectas do
plano. A recta pp já é ortogonal às rectas fronto-horizontais de ρ (qualquer recta de perfil é
necessariamente ortogonal a uma recta fronto-horizontal) – é necessário que a recta pp seja
ortogonal a outra «família» de rectas do plano (às rectas de perfil do plano, por exemplo). Por
pp conduziu-se um plano auxiliar π, de perfil. Em seguida, determinou-se a recta ii, que é a rec-
ta de intersecção de π com ρ – a recta ii é uma recta de perfil de ρ e está definida pelo seu
traço frontal, FF, e pela sua direcção (faz um ângulo de 30° com o Plano Horizontal de Projec-
ção, que é um ângulo com a mesma amplitude do diedro que o plano ρ faz com o Plano Ho-
rizontal de Projecção). O ângulo que a recta ii faz com o Plano Horizontal de Projecção tem a
mesma amplitude que o ângulo que a recta ii faz com hhπ. A recta pp terá de ser perpendicular
à recta ii. É necessário o recurso a um processo geométrico auxiliar – optou-se pelo rebati-
mento do plano π para o Plano Frontal de Projecção (a charneira foi ffπ), obtendo-se PPrr e FFrr.
Por FFrr conduziu-se iirr, fazendo um ângulo de 30o com hhπrr
e garantindo que o traço horizontal da recta tem afastamento positivo (é dado que o traço
horizontal do plano ρ se situa no SSPPHHAA). Por PPrr conduziu-se pprr, perpendicular a iirr. Sobre pprr representou-se arbitrariamente um outro ponto, para
além de PP – AArr. Invertendo o rebatimento, determinaram-se as projecções de AA – a recta pp, ortogonal a ρ, está definida por PP e AA. Note que o pon-
to AA é o ponto de concorrência das duas rectas (pp e ii) e é, assim, o ponto de intersecção da recta pp com o plano ρ, mas poderia ser outro ponto
qualquer. Note ainda que não foi necessária a determinação do traço horizontal do plano ρ para a resolução do exercício, nem aquele era pedido
no enunciado. A determinação do traço horizontal da recta ii, HH, processou-se apenas para garantir que o traço horizontal do plano tem afas-
tamento positivo. Sublinha-se que o processo geométrico auxiliar utilizado poderia ser, por exemplo, uma mudança do diedro de projecção.
81.
Em primeiro lugar representaram-se o plano ρ, pelo seu traço frontal
(ver exercício anterior), e o ponto PP, pelas suas projecções, em fun-
ção dos dados. Sobre a determinação da recta, ver exercício anterior
e respectivo relatório. Note que, nesta situação, o traço horizontal da
recta ii (a recta de intersecção do plano π com o plano ρ) tem afasta-
mento negativo, pois é pedido expressamente no enunciado que o
traço horizontal do plano se situe no SSPPHHPP. O ponto AA, o outro ponto
a que se recorreu para definir a recta pp, já não foi o ponto de inter-
secção da recta pp com o plano ρ.
79.

23. 23
SOLUÇÕES
82.
Em primeiro lugar representaram-se o plano ρ, pelos seus traços (que estão
coincidentes no eixo XX) e pelo ponto PP, bem como o ponto KK, pelas suas
projecções, em função dos dados. Em seguida, passando por KK, desenha-
ram-se imediatamente as projecções da recta pp, que é necessariamente
uma rreeccttaa ddee ppeerrffiill – a recta pp não se encontra totalmente definida em
Dupla Projecção Ortogonal, uma vez que as suas projecções não verifi-
cam o Critério de reversibilidade. Assim, necessi-tamos de mais um ponto
da recta pp, para além do ponto KK. A recta pp, para ser ortogonal ao plano ρ,
tem de ser ortogonal a duas «famílias» de rectas do plano. A recta pp já
é ortogonal às rectas fronto-horizontais de ρ (qualquer recta de perfil é
necessariamente ortogonal a uma recta fronto-horizontal) – é necessário
que a recta pp seja ortogonal a outra «família» de rectas do plano (às rectas
de perfil do plano, por exemplo). Por pp conduziu-se um plano auxiliar π, de
perfil. Em seguida, determinou-se a recta ii, que é a recta de intersecção
de π com ρ – a recta ii é uma recta de perfil de ρ (é uma recta de perfil pas-
sante). Para definir a recta ii já temos um ponto – o seu ponto de concor-
rência com o eixo XX. Necessitamos de um outro ponto. Pelo ponto PP (que
é um ponto do plano ρ) conduziu-se uma recta mm, fronto-horizontal (que é
uma recta do plano ρ), e determinou-se o ponto de intersecção da recta mm
com o plano π – o ponto MM. MM é um ponto comum aos dois planos, pelo que é um outro ponto da recta ii. A recta ii já está, assim, definida
por dois pontos. A recta pp terá de ser perpendicular à recta ii. É necessário o recurso a um processo geométrico auxiliar – optou-se pelo
rebatimento do plano π para o Plano Frontal de Projecção (a charneira foi ffπ), obtendo-se KKrr e MMrr. A recta iirr fica definida por dois pontos – MMrr
e o seu ponto de concorrência com o eixo XX, que é fixo (é um ponto da charneira). Por PPrr conduziu-se pprr, perpendicular a iirr. Sobre pprr repre-
sentou-se arbitrariamente um outro ponto, para além de PP – LLrr. Invertendo o rebatimento, determinaram-se as projecções de LL – a recta pp,
ortogonal a ρ, está definida por KK e LL. Note que o processo geométrico auxiliar utilizado poderia ser, por exemplo, uma mudança do diedro
de projecção, conforme se expõe no relatório do exercício seguinte.
83.
Em primeiro lugar representaram-se o plano ρ, pelos seus traços (que estão
coincidentes no eixo XX) e pelo ponto AA, bem como o ponto PP, pelas suas projec-
ções, em função dos dados. Em seguida, passando por PP, desenharam-se
imediatamente as projecções da recta pp, que é necessariamente uma rreeccttaa ddee
ppeerrffiill – a recta pp não se encontra totalmente definida em Dupla Projecção Orto-
gonal, uma vez que as suas projecções não verificam o Critério de reversibilidade.
Assim, necessitamos de mais um ponto da recta pp, para além do ponto PP. Para
evitar a complexidade dos raciocínios dos exercícios anteriores, optou-se por
recorrer imediatamente a uma mudança do diedro de projecção, de forma a
transformar o plano ρ num plano de topo, por exemplo – com um plano de topo,
cujos traços são duas rectas concorrentes (ao contrário dos planos de rampa,
cujos traços são duas rectas paralelas – são rectas da mesma «família» de
rectas), a ortogonalidade entre rectas e planos é directa. Assim, substituiu-se o
Plano Frontal de Projecção (ppllaannoo 22) por um outro plano de projecção (ppllaannoo 44),
ortogonal ao plano ρ – o novo eixo XX (eixo XX’’) é perpendicular a hhρ e é a recta de
intersecção do ppllaannoo 11 com o ppllaannoo 44. As projecções de AA e PP no ppllaannoo 44
determinaram-se em função das respectivas cotas, que se mantiveram. O traço
do plano ρ no ppllaannoo 44, ff44ρ
, é concorrente com hhρ no eixo XX’’ e passa por AA44 (note
que, no diedro formado pelo ppllaannoo 11 e pelo ppllaannoo 44, o plano ρ é de topo, pro-
jectante frontal, pelo que projecta todos os seus pontos e rectas no seu traço no
ppllaannoo 44). Uma vez que, no novo diedro de projecção, hhρ e ff44ρ
são duas rectas
concorrentes, e tendo já pp11 perpendicular a hhρ, para que a recta pp seja ortogonal
a ρ basta que pp44 (a projecção da recta pp no ppllaannoo 44) seja perpendicular a ff44ρ
(trata-se da situação do exercício 7722). Assim, por PP44 conduziu-se pp44, perpendi-
cular a ff44ρ
. No diedro de projecção formado pelo ppllaannoo 11 e pelo ppllaannoo 44, deter-
minou-se um ponto qualquer da recta pp – o ponto BB (que é o ponto de
intersecção da recta pp com o plano ρ, mas que poderia ser um ponto qualquer). BB11 teve determinação directa, a partir de BB44. Invertendo a
mudança do diedro de projecção efectuada, determinou-se BB22 em função da cota de BB, que se manteve. A recta pp, ortogonal a ρ, está definida
por PP e BB. Note que o exercício se poderia ter resolvido pelo processo de resolução do exercício anterior.

24. 24
SOLUÇÕES
84.
Em primeiro lugar representaram-se o plano ρ, pelos seus traços (que estão coincidentes
no eixo XX) e o ponto PP, pelas suas projecções, em função dos dados. O plano ρ está defi-
nido por uma recta (o eixo XX) e pela sua orientação – é dado o diedro que o plano faz
com o Plano Frontal de Projecção. Em seguida, passando por PP, desenharam-se imedia-
tamente as projecções da recta pp, que é necessariamente uma rreeccttaa ddee ppeerrffiill – a recta pp
não se encontra totalmente definida em Dupla Projecção Ortogonal, uma vez que as suas
projecções não verificam o Critério de reversibilidade. Assim, necessitamos de mais um
ponto da recta pp, para além do ponto PP. A recta pp, para ser ortogonal ao plano ρ, tem de
ser ortogonal a duas «famílias» de rectas do plano. A recta pp já é ortogonal às rectas fron-
to-horizontais de ρ (qualquer recta de perfil é necessariamente ortogonal a uma recta
fronto-horizontal) – é necessário que a recta pp seja ortogonal a outra «família» de rectas
do plano (às rectas de perfil do plano, por exemplo). Por pp conduziu-se um plano auxiliar
π, de perfil. Em seguida, determinou-se a recta ii, que é a recta de intersecção de π com ρ
– a recta ii é uma recta de perfil de ρ (é uma recta de perfil passante), que está definida
pelo ponto MM (o seu ponto de concorrência com o eixo XX) e pela sua direcção. Note que
a recta ii faz um ângulo de 30° com o Plano Frontal de Projecção, que é um ângulo com a
mesma amplitude do diedro que o plano ρ faz com o Plano Frontal de Projecção). O ân-
gulo que a recta ii faz com o Plano Frontal de Projecção tem a mesma amplitude que o
ângulo que a recta ii faz com ffπ. A recta pp terá de ser perpendicular à recta ii. É necessário o recurso a um processo geométrico auxiliar – optou-
-se pelo rebatimento do plano π para o Plano Frontal de Projecção (a charneira foi ffπ), obtendo-se PPrr e MMrr (MM roda sobre si próprio, pois é um
ponto da charneira). A recta iirr passa por MMrr e faz, com ffπrr
, um ângulo de 30°. Note que, sendo PP um ponto do 1o Diedro, a recta iirr tem de pas-
sar pelo quadrante em que se situa PPrr. Por PPrr conduziu-se pprr, perpendicular a iirr. Sobre pprr representou-se arbitrariamente um outro ponto, para
além de PP – AArr. Note que AA é o ponto de intersecção da recta pp com o plano ρ (é o ponto de concorrência das rectas pp e ii), mas poderia ser
outro ponto qualquer. Invertendo o rebatimento, determinaram-se as projecções de AA – a recta pp, ortogonal a ρ, está definida por PP e AA. Note
que o exercício poderia ter sido resolvido com o recurso a uma mudança do diedro de projecção, à semelhança do exercício anterior.
Em primeiro lugar, representou-se o ponto PP, pelas suas projecções, em função dos da-
dos. O β2/4 está definido por uma recta (o eixo XX) e pela sua orientação – o β2/4 faz diedros
de 45o com os dois planos de projecção, pelo que esta situação é semelhante à situação
do exercício anterior (ver relatório do exercício anterior). A recta ii é a recta de intersecção
do plano π com o β2/4 – é uma recta de perfil do β2/4 (é uma recta de perfil passante). A
recta ii faz ângulos de 45o com os traços do plano π. Rebateu-se o plano π para o Plano
Frontal de Projecção (a charneira foi ffπ), obtendo-se PPrr. A recta iirr faz, com ffπrr
e hhπrr
, ângu-
los de 45o – note que, sendo PP um ponto do 1o Diedro, a recta iirr não pode passar pelo
quadrante em que se situa PPrr. O ponto a que se recorreu para definir a recta pp foi o seu
traço frontal, FF – a recta pp, ortogonal ao β2/4, está definida por PP e FF. Note que o exercício
poderia ter sido resolvido com o recurso a uma mudança do diedro de projecção, à seme-
lhança do exercício 8833.
86.
Em primeiro lugar representaram-se o plano ρ, pelos seus traços, em função dos da-
dos. Em seguida, determinou-se um ponto AA qualquer, do eixo XX (a recta pp é uma recta
passante), pelo qual se conduziu a recta pp. Note que este exercício é idêntico ao exer-
cício 7788, pelo que se aconselha a leitura do respectivo relatório. As diferenças resi-
dem, apenas, no facto de o ponto dado ser um ponto do eixo XX e no facto de os
traços do plano serem coincidentes, o que pode resultar nalguma confusão ao nível
da execução, mas tenha em conta que se mantêm todos os raciocínios expostos no
relatório do exercício 7788. O ponto BB é o ponto a que se recorreu para definir a recta pp
em Dupla Projecção Ortogonal.
85.

25. 25
SOLUÇÕES
Em primeiro lugar representaram-se a recta hh e o ponto GG, pelas respectivas projecções, em fun-
ção dos dados. Em seguida, para que o plano γ seja ortogonal à recta hh, o plano γ tem de conter
duas rectas concorrentes ortogonais à recta hh (duas «famílias» de rectas ortogonais à recta hh) –
essas rectas podem ser os seus traços. Assim, ffγ, o traço frontal do plano, porque é uma recta
frontal (de frente), tem de ser perpendicular a hh22 (a ortogonalidade é directa em projecção fron-
tal). Por seu lado, hhγ, o traço horizontal do plano γ, porque é uma recta horizontal (de nível), tem
de ser perpendicular a hh11 (a ortogonalidade é directa em projecção horizontal). Para que ffγ seja
perpendicular a hh22, que é paralela ao eixo XX, ffγ terá de ser perpendicular ao eixo XX – o plano γ é,
assim, um plano vertical (um plano projectante horizontal). Para que o plano γ contenha o ponto
GG, e uma vez que se trata de um plano projectante horizontal, basta que hhγ passe por GG11 –
assim, por GG11 conduziu-se hhγ, perpendicular a hh11. ffγ é concorrente com hhγ no eixo XX e é perpen-
dicular a hh22 (é vertical). O plano γ é ortogonal à recta hh e contém o ponto GG, pois GG11 situa-se
sobre hhγ (o plano γ é projectante horizontal). O plano γ é necessariamente um ppllaannoo vveerrttiiccaall.
Visualize a situação no espaço e constate que um plano ortogonal a uma recta horizontal (de nível)
é necessariamente um plano vertical (projectante horizontal).
87.
88.
Em primeiro lugar representaram-se a recta ff e o ponto BB, pelas respectivas projecções, em função
dos dados. Em seguida, para que o plano α seja ortogonal à recta ff, o plano α tem de conter duas
rectas concorrentes ortogonais à recta ff (duas «famílias» de rectas ortogonais à recta ff ) – essas rectas
podem ser os seus traços. Assim, ffα, o traço frontal do plano, porque é uma recta frontal (de frente),
tem de ser perpendicular a ff22 (a ortogonalidade é directa em projecção frontal). Por seu lado, hhα, o traço
horizontal do plano α, porque é uma recta horizontal (de nível), tem de ser perpendicular a ff11 (a ortogona-
lidade é directa em projecção horizontal). Para que hhα seja perpendicular a ff11, que é paralela ao eixo XX, hhα
terá de ser perpendicular ao eixo XX – o plano α é, assim, um plano de topo (um plano projectante frontal).
Para que o plano α contenha o ponto BB, e uma vez que se trata de um plano projectante frontal, basta
que ffα passe por BB22 – assim, por BB22 conduziu-se ffα, perpendicular a ff22. hhα é concorrente com ffα no eixo XX
e é perpendicular a ff11 (é de topo). O plano α é ortogonal à recta ff e contém o ponto BB, pois BB22 situa-se
sobre ffα (o plano α é projectante frontal). O plano α é necessariamente um ppllaannoo ddee ttooppoo. Visualize a
situação no espaço e constate que um plano ortogonal a uma recta frontal (de frente) é necessaria-
mente um plano de topo (projectante frontal).
Em primeiro lugar representaram-se a recta rr e o ponto PP, pelas suas projecções, em
função dos dados. Em seguida, para que o plano α seja ortogonal à recta rr, o plano
α tem de conter duas rectas concorrentes ortogonais à recta rr (duas «famílias» de
rectas ortogonais à recta rr) – essas rectas podem ser os seus traços. Por outro lado,
para que o plano α contenha o ponto PP, PP terá de pertencer a uma recta do plano α.
Assim, por PP conduziu-se uma recta hh, horizontal (de nível), pertencente ao plano α –
hh é ortogonal à recta rr, pois hh11 é perpendicular a rr11 (a ortogonalidade é directa em
projecção horizontal). Já temos uma «família» de rectas do plano α que é ortogonal à
recta rr (o traço horizontal do plano é também uma recta horizontal, que é paralela à
recta hh). Necessitamos de uma outra, que terá de ser a «família» das rectas frontais
(de frente) de α. Por FF, o traço frontal da recta hh, conduziu-se ffα, perpendicular a rr22 – ffα
é uma recta frontal (de frente) do plano α e é ortogonal à recta rr, pois a ortogonalida-
de verifica-se directamente em projecção frontal. Em seguida, desenhou-se hhα, que é
concorrente com ffα num ponto do eixo XX e é paralelo a hh11 (e perpendicular a rr11). O
plano α é ortogonal à recta rr (contém duas rectas concorrentes ortogonais à recta rr)
e passa pelo ponto PP, pois PP pertence a uma recta do plano α (a recta hh). Note que
se tem que os traços do plano α são perpendiculares às projecções homónimas da
recta rr, o que já se tinha verificado nas situações anteriores.
Em primeiro lugar representou-se a recta gg, pelas suas projecções, em função dos dados. Em seguida, para
que o plano seja ortogonal à recta gg, o plano tem de conter duas rectas concorrentes ortogonais à recta gg
(duas «famílias» de rectas ortogonais à recta gg) – essas rectas podem ser os seus traços. Assim, o traço
frontal do plano, porque é uma recta frontal (de frente), tem de ser perpendicular a gg22 (a ortogonalidade é
directa em projecção frontal). Por seu lado, o traço horizontal do plano, porque é uma recta horizontal
(de nível), tem de ser perpendicular a gg11 (a ortogonalidade é directa em projecção horizontal). Para que o
traço horizontal do plano seja perpendicular a gg11, que é paralela ao eixo XX, o traço horizontal do plano terá
de ser perpendicular ao eixo XX – o traço horizontal do plano é, assim, uma recta de topo e o plano é um plano
projectante frontal. Para que o traço frontal do plano seja perpendicular a gg22, que é paralela ao eixo XX, o traço
frontal do plano terá de ser perpendicular ao eixo XX – o traço frontal do plano é, assim, uma recta vertical e o
plano é um plano projectante horizontal. O plano pedido é, pois, um plano dduuppllaammeennttee pprroojjeeccttaannttee – trata-
-se de um ppllaannoo ddee ppeerrffiill (um plano de perfil é o único plano duplamente projectante, cujo traço frontal é
uma recta vertical e cujo traço horizontal é uma recta de topo). Visualize a situação no espaço e constate
que um plano ortogonal a uma recta fronto-horizontal é necessariamente um plano de perfil.
89.
90.

26. 26
SOLUÇÕES
91.
Em primeiro lugar representaram-se a recta mm e o ponto PP, pelas suas projecções, em função dos dados. A recta mm tem as suas projecções
paralelas entre si, pois é paralela ao β2/4. Sobre a determinação dos traços do plano α, ver exercício anterior e respectivo relatório.
92.
Em primeiro lugar representaram-se a recta pp e o ponto PP, pelas suas projecções, em função dos dados. Os pontos AA e BB têm a mesma abcissa,
pois situam-se na mesma recta de perfil. Um plano ortogonal a uma recta de perfil é necessariamente um ppllaannoo ddee rraammppaa. Assim, já sabemos
uma das «famílias» das rectas do plano (o plano σ) que são ortogonais à recta pp – as rectas fronto-horizontais. Por outro lado, para que o ponto PP
pertença ao plano σ, o ponto terá de pertencer a uma recta do plano – essa recta poderá ser uma recta fronto-horizontal. Assim, por PP conduziu-se
uma recta mm, fronto-horizontal, pertencente ao plano. Necessitamos de uma outra recta do plano σ – essa recta terá, também ela, de ser ortogonal
à recta pp. Essa recta poderá ser uma recta de perfil. Conduziu-se, pela recta pp, um plano de perfil π. A recta pp’’, de perfil, é a recta de intersecção
do plano π com o plano σ – a recta pp’’ é necessariamente ortogonal (perpendicular) à recta pp. Já temos a direcção da recta. Falta-nos um ponto
para definir a recta pp’’. O ponto PP’’ é o ponto de intersecção da recta mm (que é uma recta do plano σ) com o plano π. O ponto PP’’ é, assim, um ponto
da recta pp’’. A recta pp’’ está, assim, definida por um ponto (o ponto PP’’) e por uma direcção (é perpendicular à recta pp). Resolveu-se o problema atra-
vés do rebatimento do plano π para o Plano Frontal de Projecção. A recta pprr está definida por AArr e por BBrr. A recta pp’’rr passa por PP’’rr e é ortogonal à
recta pprr. Note que as rectas pp e pp’’ são perpendiculares, pois são concorrentes – são complanares (estão contidas no mesmo plano de perfil).
Em seguida, determinaram-se os traços da recta pp’’, em rebatimento, e inverteu-se o rebatimento. Pelos traços da recta pp’’ conduziram-se os traços
homónimos do plano σ. O plano σ é ortogonal à recta pp (pois contém duas «famílias» de rectas que são ortogonais à recta pp) e contém o ponto PP,
pois PP pertence a uma recta do plano (a recta mm). Note que este exercício poderia ter sido resolvido com o recurso a uma mudança do diedro de
projecção, à semelhança do exercício seguinte.

27. 27
SOLUÇÕES
93.
Em primeiro lugar representaram-se a recta pp e o ponto PP, pelas suas pro-
jecções, em função dos dados. A recta pp, porque é passante, é concorren-
te com o eixo XX num ponto (o ponto BB). Um plano ortogonal a uma recta
de perfil é necessariamente um ppllaannoo ddee rraammppaa. Para evitar a complexida-
de dos raciocínios do exercício anterior, optou-se por recorrer imediata-
mente a uma mudança do diedro de projecção, de forma a transformar a
recta pp numa recta frontal (de frente) – ao contrário da recta de perfil, cujas
projecções não verificam o Critério de reversibilidade, a ortogonalidade
entre uma recta frontal (de frente) e um plano é directa (um plano ortogo-
nal a uma recta frontal é um plano de topo – ver exercício 8888). Assim, subs-
tituiu-se o Plano Frontal de Projecção (ppllaannoo 22) por um outro plano de
projecção (ppllaannoo 44), paralelo à recta pp – o novo eixo XX (eixo XX’’) é paralelo
a pp11 e é a recta de intersecção do ppllaannoo 11 com o ppllaannoo 44. As projecções
de AA, BB e PP no ppllaannoo 44 determinaram-se em função das respectivas cotas,
que se mantiveram. A projecção da recta pp no ppllaannoo 44, pp44, está definida por
AA44 e BB44. No novo diedro de projecção (o diedro formado pelo ppllaannoo 11 e
pelo ppllaannoo 44), o plano ρ (o plano ortogonal à recta pp) é projectante frontal
(é um plano de topo) – ff44ρ
, o traço do plano ρ no ppllaannoo 44, passa por PP44
(o plano é projectante frontal) e é perpendicular a pp44 (a ortogonalidade é
directa). O traço do plano ρ no ppllaannoo 44 é concorrente com hhρ no eixo XX’’ – hhρ
é perpendicular ao eixo XX’’ (está definido por um ponto e uma direcção).
Para inverter a mudança do diedro de projecção efectuada e determinar o
traço frontal do plano ρ no diedro de projecção inicial recorreu-se a um
ponto qualquer do plano, cuja projecção horizontal esteja no eixo XX inicial
– o ponto FF. Por uma questão de economia de traçados, optou-se por se
situar FF na linha de chamada do ponto PP. A projecção frontal de FF (no ppllaa--
nnoo 22) determinou-se em função da sua cota, que se manteve. Por FF22 con-
duziu-se ffρ, o traço frontal do plano ortogonal à recta pp. O plano ρ é o
plano ortogonal à recta pp que contem o ponto PP.
Em primeiro lugar representaram-se a recta rr e o ponto KK, pelas suas projecções, em
função dos dados. A recta rr é paralela ao β1/3, pelo que as suas projecções fazem,
com o eixo XX, ângulos iguais e com o mesmo sentido de abertura. Em seguida, uma
vez que a ortogonalidade entre a recta rr, que é oblíqua, e a recta pp, que é também ob-
líqua, não é directa em nenhuma das projecções (nenhuma das duas rectas é paralela
a qualquer dos planos de projecção), é necessário fazer com que a recta pp esteja con-
tida num plano ortogonal à recta rr. Por outro lado, uma vez que se pretende que a rec-
ta pp contenha o ponto KK, esse plano ortogonal à recta rr tem necessariamente de
conter o ponto KK. Assim, conduziu-se, por KK, um plano α ortogonal à recta rr (para o que
se recorreu a uma recta ff, frontal) – ver exercício 9900. Todas as rectas do plano α são orto-
gonais ou perpendiculares à recta rr. A recta pp é a recta do plano α que contém KK e cuja
projecção horizontal faz, com o eixo XX, o ângulo pretendido (60°, de abertura para a di-
reita). A recta pp tem de ter os seus traços sobre os traços homónimos do plano α, para
pertencer ao plano (condição para que uma recta pertença a um plano). Determinaram-
-se os traços da recta – FF e HH’’. A recta pp está definida por HH’’, KK (a recta passa por KK)
e FF, mas poderia estar definida, apenas, por HH’’ e KK, por exemplo (bastavam dois pontos).
A recta pp passa pelo ponto KK e é ortogonal à recta rr, pois está contida num plano orto-
gonal à recta rr (o plano α, que também contém o ponto KK).
95.
Em primeiro lugar representaram-se a recta rr e o ponto MM, pelas suas projecções, em
função dos dados. Em seguida, uma vez que a ortogonalidade entre a recta rr, que é
oblíqua, e a recta pp, que é também oblíqua, não é directa em nenhuma das projec-
ções (ver exercício anterior), é necessário fazer com que a recta pp esteja contida num
plano ortogonal à recta rr, plano esse que tem de conter o ponto MM, para que a recta pp
contenha o ponto MM. Assim, conduziu-se, por MM, um plano γ, ortogonal à recta rr (para
o que se recorreu a uma recta hh, horizontal) – ver exercício 9900. Todas as rectas do
plano γ são ortogonais ou perpendiculares à recta rr. A recta pp é, assim, uma recta do
plano γ que contenha o ponto MM. Sabe-se que a recta pp é uma recta passante – qual-
quer recta passante do plano γ tem de ser concorrente com o eixo XX no ponto de con-
corrência dos traços do plano. A recta pp está, assim, definida por dois pontos – o
ponto MM e o ponto de concorrência dos traços do plano γ. A recta pp passa pelo ponto MM
e é ortogonal à recta rr, pois está contida num plano ortogonal à recta rr (o plano γ).
94.

28. 28
SOLUÇÕES
96.
Em primeiro lugar representaram-se a recta rr e o ponto PP, pelas suas projecções, em
função dos dados. Em seguida, uma vez que a ortogonalidade entre a recta rr, que é
oblíqua, e a recta pp, que é também oblíqua, não é directa em nenhuma das projec-
ções (nenhuma das duas rectas é paralela a qualquer dos planos de projecção), é ne-
cessário fazer com que a recta pp esteja contida num plano ortogonal à recta rr, plano
esse que tem de conter o ponto PP, para que a recta pp contenha o ponto PP. Assim
conduziu-se, por PP, um plano γ, ortogonal à recta rr (para o que se recorreu a uma
recta ff, frontal) – ver exercício 9900. Todas as rectas do plano γ são ortogonais ou perpen-
diculares à recta rr. A recta pp é a recta do plano γ que contém PP e cuja projecção hori-
zontal é paralela à projecção horizontal da recta rr. A recta pp tem os seus traços (FF’’ e HH)
sobre os traços homónimos do plano γ (condição para que uma recta pertença a um
plano). A recta pp está definida por FF’’, PP e HH, mas poderia estar definida, apenas, por
dois daqueles pontos. A recta pp passa pelo ponto PP e é ortogonal à recta rr.
Em primeiro lugar representaram-se a recta rr e o ponto PP, pelas suas projec-
ções, em função dos dados. Sobre a determinação da recta pp, ver relatório
do exercício anterior. Note que a recta pp, de perfil, está definida por três pon-
tos – o ponto PP (conduziram-se as projecções da recta pp pelas projecções
do ponto PP) e os seus traços nos planos de projecção, FF e HH (a recta tem de
verificar a condição para que uma recta pertença a um plano).
98.
Em primeiro lugar representaram-se a recta rr e o ponto PP, pelas suas projecções, em função
dos dados. A recta rr tem as suas projecções paralelas entre si, pois é uma recta paralela ao
β2/4. Em seguida, uma vez que a ortogonalidade entre a recta rr, que é oblíqua, e a recta pp,
que é também oblíqua, não é directa em nenhuma das projecções, é necessário fazer com
que a recta pp esteja contida num plano ortogonal à recta rr, plano esse que tem de conter o
ponto PP, para que a recta pp contenha o ponto PP. Assim conduziu-se, por PP, um plano α, orto-
gonal à recta rr (para o que se recorreu a uma recta hh, horizontal) – ver exercício 9900. Note que,
atendendo a que as projecções da recta rr são paralelas entre si, os traços do plano α (o pla-
no ortogonal à recta rr) ficam coincidentes. Todas as rectas do plano α são ortogonais ou
perpendiculares à recta rr. A recta pp é, assim, uma recta do plano α que contenha o ponto PP e
que pertença ao β1/3 – a recta pp é, então, a recta de intersecção do plano α com o β1/3. O pon-
to PP, que pertence ao plano α, é também um ponto do β1/3 – PP é um ponto comum aos dois
planos. Já temos um ponto. Falta-nos outro ponto ou uma direcção. Os traços do plano são
concorrentes no ponto MM, que é um ponto do eixo XX – todos os pontos do eixo XX pertencem
ao β1/3, pelo que o ponto MM é outro ponto que pertence simultaneamente aos dois planos. Já
temos dois pontos para definir a recta pp. A recta pp, definida por PP e por MM, é ortogonal à recta
rr e pertence ao β1/3 (é uma recta de perfil passante – é uma recta de perfil do β1/3).
99.
O CCrriittéérriioo ddee oorrttooggoonnaalliiddaaddee eennttrree ppllaannooss afirma que um plano é ortogonal a um plano dado se e só se contiver uma recta ortogonal ao
plano dado, ou seja, dois planos são ortogonais entre si se e só se um deles contiver a «família» de rectas que é ortogonal ao outro plano.
97.

29. 29
SOLUÇÕES
100.
O problema admite iinnffiinniittaass ssoolluuççõõeess. Segundo o CCrriittéérriioo ddaa oorrttooggoonnaalliiddaaddee eennttrree ppllaannooss, para que um plano seja ortogonal ao plano α,
aquele tem de conter uma recta ortogonal ao plano α. Por outro lado, para que o plano pedido contenha o ponto PP, a recta ortogonal ao
plano α terá de passar pelo ponto PP – qualquer plano que contenha essa recta contém o ponto PP e é ortogonal ao plano α. De facto, por PP é
possível, apenas, conduzir uummaa úúnniiccaa recta ortogonal ao plano α mas, no entanto, ttooddooss ooss ppllaannooss que contenham essa recta (que são in-
finitos planos) serão necessariamente ortogonais ao plano α e contêm o ponto PP.
101.
Em primeiro lugar representaram-se o plano ν, pelo seu traço frontal, e o ponto PP, pelas
suas projecções, em função dos dados. Para que um plano seja ortogonal ao plano ν,
tem de conter uma recta ortogonal ao plano ν. Por outro lado, para que o plano conte-
nha o ponto PP, o ponto tem de pertencer a uma recta do plano. Assim, em primeiro lugar
há que conduzir, pelo ponto PP, uma recta ortogonal ao plano ν – a recta pp, que é uma
recta vertical (ver exercício 6699). Qualquer plano que contenha a recta pp é necessaria-
mente ortogonal ao plano ν e contém o ponto PP. Optou-se por representar um plano γ,
vertical, qualquer, mas o problema admite iinnffiinniittaass ssoolluuççõõeess (ver a resposta à questão
do exercício anterior) – todos os planos verticais que contêm a recta pp, o plano frontal
(de frente) que contém a recta pp e o plano de perfil que contém a recta pp.
102.
Em primeiro lugar representaram-se o plano γ, pelos seus traços, e o ponto AA, pelas suas
projecções, em função dos dados. Em seguida, para que o plano α seja ortogonal ao
plano γ, o plano α tem de conter uma recta ortogonal ao plano γ. Por outro lado, para
que o plano α contenha o ponto AA, o ponto AA tem de pertencer a uma recta do plano α.
Assim, começou-se por conduzir, por AA, uma recta hh, ortogonal ao plano γ (ver exercício 7711)
– a recta pp é uma recta horizontal (de nível). Qualquer plano que contenha a recta pp é
ortogonal a γ e contém o ponto AA. Determinou-se o traço frontal da recta hh – FF. O traço
frontal do plano α, ffα, passa por FF e faz, com o eixo XX, o ângulo pedido – 60o (a.d.). O tra-
ço horizontal do plano α, hhα, é concorrente com ffα no eixo XX e é paralelo à recta hh (rectas
horizontais de um plano são paralelas entre si e paralelas ao traço horizontal do plano,
que é uma recta horizontal do plano com cota nula). O plano α é ortogonal ao plano γ
(contém uma recta ortogonal ao plano γ – a recta hh) e contém o ponto PP (PP pertence a
uma recta do plano α – a recta hh).
103.
Em primeiro lugar representaram-se o plano α, pelos seus traços, e o ponto PP, pe-
las suas projecções, em função dos dados. Em seguida, para que o plano δ seja
ortogonal ao plano α, o plano δ tem de conter uma recta ortogonal ao plano α. Por
outro lado, para que o plano δ contenha o ponto PP, o ponto PP tem de pertencer a
uma recta do plano δ. Assim, começou-se por conduzir, por PP, uma recta pp, ortogo-
nal ao plano α (ver exercício 7744) – a recta pp é uma recta oblíqua, cujas projecções
são perpendiculares aos traços homónimos do plano α. Qualquer plano que conte-
nha a recta pp é ortogonal a α e contém o ponto PP. Determinaram-se os traços da
recta pp – FF e HH. O traço frontal do plano δ, ffδ, passa por FF e faz, com o eixo XX, o ân-
gulo pedido – 65o (a.d.). O traço horizontal do plano δ, hhδ, é concorrente com ffδ no
eixo XX e passa por HH. O plano δ é ortogonal ao plano α (contém uma recta ortogo-
nal ao plano α – a recta pp) e contém o ponto PP (PP pertence a uma recta do plano δ
– a recta pp).
104.
Em primeiro lugar representaram-se o plano α, pelos seus traços, e o ponto PP, pelas
suas projecções, em função dos dados. Sobre a determinação do plano θ, ver relatório
do exercício anterior. Note que não é estritamente necessária a determinação dos traços
da recta pp nos planos de projecção, pois o plano θ é o plano projectante horizontal da
recta pp (seria possível determinar os traços de θ sem determinar os traços da recta pp).

30. 30
SOLUÇÕES
Em primeiro lugar representaram-se o plano θ, pelos seus traços, e o ponto PP, pelas
suas projecções, em função dos dados. Em seguida, para que o plano α seja ortogonal
ao plano θ, o plano α tem de conter uma recta ortogonal ao plano θ. Por outro lado, para
que o plano α contenha o ponto PP, o ponto PP tem de pertencer a uma recta do plano α.
Assim, começou-se por conduzir, por PP, uma recta pp, ortogonal ao plano θ (ver exercício 7722)
– a recta pp é uma recta frontal (de frente). Qualquer plano que contenha a recta pp é orto-
gonal a θ e contém o ponto PP. Determinou-se o traço horizontal da recta pp – HH. O traço
horizontal do plano α, hhα, passa por HH e tem de ser paralelo a pp22, para que os traços do
plano α sejam coincidentes (os dois traços, na folha de papel, têm de ter a mesma direc-
ção). O traço frontal do plano α, ffα, é concorrente com hhα no eixo XX e é paralelo à recta pp
(rectas frontais de um plano são paralelas entre si e paralelas ao traço frontal do plano,
que é uma recta frontal do plano com afastamento nulo). O plano α é ortogonal ao plano θ
(contém uma recta ortogonal ao plano θ – a recta pp) e contém o ponto PP (PP pertence a
uma recta do plano α – a recta pp).
105.
106.
Em primeiro lugar representaram-se o plano λ, pelos seus traços, e o ponto GG,
pelas suas projecções, em função dos dados. Sobre a determinação dos traços
do plano γ, ver relatório do exercício 110033. Note que, para que os traços do plano
γ sejam coincidentes (na folha de papel), aqueles têm de se situar na recta que
passa por FF22 e por HH11.
108.
Em primeiro lugar representaram-se o plano ρ, pelos seus traços, e o ponto
AA, pelas suas projecções, em função dos dados. Em seguida, para que o
plano σ seja ortogonal ao plano ρ, o plano σ tem de conter uma recta orto-
gonal ao plano ρ. Por outro lado, para que o plano σ contenha o ponto AA, AA
tem de pertencer a uma recta do plano σ. Assim, conduziu-se, por AA, uma
recta pp, ortogonal ao plano ρ (ver exercício 7788 e respectivo relatório). A recta
pp é uma recta de perfil. Qualquer plano que contenha a recta pp é ortogonal
a ρ e contém o ponto AA. Determinaram-se os traços da recta pp – FF’’ e HH’’.
Note que os traços da recta pp se determinaram previamente em rebatimento,
após cuja inversão se obtiveram as projecções de FF’’ e HH’’. Pelos traços de pp
conduziram-se os traços homónimos do plano σ. O plano σ é ortogonal ao
plano ρ (pois contém uma recta ortogonal a ρ – a recta pp) e contém o ponto
AA (pois AA pertence a uma recta de σ – a recta pp).
107.
Em primeiro lugar representaram-se o plano α, pelos seus traços, e o ponto MM, pelas
suas projecções, em função dos dados. Sobre a determinação dos traços do plano ρ,
ver relatório do exercício 110033. A recta pp é a recta ortogonal ao plano α que passa por MM
– a recta pp tem as suas projecções paralelas entre si, pelo que é uma recta paralela ao
β2/4. Pelos traços da recta pp conduziram-se os traços homónimos do plano ρ, paralelos
ao eixo XX.

31. 31
SOLUÇÕES
109.
Em primeiro lugar representaram-se o plano ρ, pelos seus traços, e o ponto DD,
pelas suas projecções, em função dos dados. Sobre a determinação dos tra-
ços do plano α, ver relatório do exercício anterior. FF’’ e HH’’ são os traços da recta
pp, a recta ortogonal ao plano ρ que passa pelo ponto DD. Por HH’’ conduziu-se hhα,
o traço horizontal do plano, fazendo, com o eixo XX, o ângulo pedido – um ân-
gulo de 60o (a.e.). O traço frontal do plano, ffα, é concorrente com hhα no eixo XX
e passa por FF’’.
110.
Em primeiro lugar representaram-se o plano ρ, pelos seus traços (que estão coincidentes no eixo XX) e pelo ponto PP, e o ponto AA, pelas suas
projecções, em função dos dados. Em seguida, para que o plano α seja ortogonal ao plano ρ, o plano α tem de conter uma recta ortogonal ao
plano ρ. Por outro lado, para que o plano α contenha o ponto AA, AA tem de pertencer a uma recta do plano α. Assim, conduziu-se, por AA, uma
recta pp, ortogonal ao plano α (ver exercício 8833 e respectivo relatório). A recta pp é uma recta de perfil. Qualquer plano que contenha a recta pp é
ortogonal a ρ e contém o ponto AA. Determinaram-se os traços da recta pp – FF e HH. Note que para a determinação dos traços da recta pp se teve
em conta que já era conhecida uma projecção de cada um – HH22 está no eixo XX (HH tem cota nula) e FF11 também está no eixo XX (FF tem afastamento
nulo). A partir destas, determinaram-se HH44 (em função da sua cota, que se manteve) e FF44 (a partir da sua projecção horizontal, que se manteve).
HH11 teve determinação imediata, a partir de HH44. Invertendo a mudança do diedro de projecção efectuada, determinou-se FF22 em função da sua
cota, que se manteve. Pelos traços de pp conduziram--se os traços homónimos do plano α, que são concorrentes num ponto com –5 de abcissa.
O plano α é ortogonal ao plano ρ (pois contém uma recta ortogonal a ρ – a recta pp) e contém o ponto AA (pois AA pertence a uma recta de α – a
recta pp). Note que o problema se poderia resolver com o recurso a um rebatimento, à semelhança do exercício seguinte.

32. 32
SOLUÇÕES
111.
Em primeiro lugar representaram-se o plano ρ,
pelos seus traços (que estão coincidentes no eixo
XX) e pelo ponto PP, e o ponto AA, pelas suas projec-
ções, em função dos dados. Em seguida, para
que o plano α seja ortogonal ao plano ρ, o plano
α tem de conter uma recta ortogonal ao plano ρ.
Por outro lado, para que o plano α contenha o
ponto AA, AA tem de pertencer a uma recta do plano
α. Assim, conduziu-se, por AA, uma recta pp, ortogo-
nal ao plano α (ver exercício 8822 e respectivo rela-
tório). A recta pp é uma recta de perfil. Qualquer
plano que contenha a recta pp é ortogonal a ρ e
contém o ponto AA. Determinaram-se os traços da
recta pp (FF e HH) em rebatimento – invertendo o re-
batimento, obtiveram-se as projecções de FF e HH.
Por HH conduziu-se ffα, o traço frontal do plano, fa-
zendo, com o eixo XX, o ângulo pedido – um ângulo
de 60o (a.e.). O traço horizontal do plano, hhα, é
concorrente com ffα no eixo XX e passa por HH. O
plano α é ortogonal ao plano ρ (pois contém uma
recta ortogonal a ρ – a recta pp) e contém o ponto
AA (pois AA pertence a uma recta de α – a recta pp).
Note que o exercício se poderia resolver com o
recurso a uma mudança do diedro de projecção,
à semelhança do exercício anterior.
113.
Em primeiro lugar desenharam-se as projecções da recta ff, em função dos dados.
Em seguida, determinou-se o traço horizontal da recta – HH. Um plano ortogonal ao
β1/3 tem os seus traços simétricos em relação ao eixo XX. Assim, por HH conduziu-se
hhα, fazendo um ângulo de 30o (a.e.) com o eixo XX (um ângulo igual e com o mesmo
sentido de abertura do ângulo entre o traço frontal e o eixo XX, que será igual ao ân-
gulo que a recta frontal faz com o Plano Horizontal de Projecção). O traço frontal do
plano α, ffα, é concorrente com hhα no eixo XX e é paralelo a ff22, pelo que os traços do
plano ficam simétricos em relação ao eixo XX.
114.
Em primeiro lugar representaram-se os planos α e ρ, pelos respectivos traços, em função
dos dados. O plano α é ortogonal ao β2/4, pelo que tem os seus traços coincidentes. O pla-
no ρ é ortogonal ao β1/3, pelo que tem os seus traços simétricos em relação ao eixo XX – ffρ
tem 4 cm de cota. Em seguida, determinaram-se as projecções da recta ii, a recta de inter-
secção dos dois planos – a recta ii fica definida por dois pontos, que são os seus traços nos
planos de projecção (trata-se do caso geral da intersecção entre planos).
112.
Em primeiro lugar desenharam-se as projecções da recta ff, em função dos
dados. Em seguida, determinou-se o traço horizontal da recta – HH. Um plano
ortogonal ao β2/4 tem os seus traços coincidentes. Assim, hhα o traço horizontal
do plano α, tem de passar por HH e, para que os traços do plano fiquem coinci-
dentes, tem de ser paralelo a ff22. O traço frontal do plano, ffα, é concorrente
com hhα no eixo XX e é paralelo a ff22, pelo que fica coincidente com hhα.

33. 33
SOLUÇÕES
116.
Em primeiro lugar representou-se o plano γ pelos seus traços, em função dos dados. O pla-
no γ é ortogonal ao β2/4, pelo que tem os seus traços coincidentes. A recta ss, porque é uma
recta de maior inclinação do plano γ, tem a sua projecção frontal perpendicular a ffγ. Por ou-
tro lado, uma vez que se trata de uma recta passante, a recta ss tem de ser concorrente com
o eixo XX no ponto de concorrência dos traços do plano. Estes dois raciocínios permitiram-
-nos desenhar imediatamente ss22, a projecção frontal da recta. No entanto, para definir a rec-
ta só temos um ponto – o seu ponto de concorrência com o eixo XX. Falta-nos outro ponto
ou uma direcção. Os dados do plano são insuficientes para definir a recta ss, pelo que é ne-
cessário o recurso a uma recta auxiliar do plano. Optou-se por recorrer a uma recta ii – ii é
uma outra recta de maior inclinação do plano (a recta ii está definida por dois pontos, que
são os seus traços). As rectas ss e ii são complanares (estão, ambas, contidas no plano γ) e
não são concorrentes, pelo que são paralelas – já temos a direcção. Em seguida, dese-
nhou-se ss11, paralela a ii11. Tenha em conta que as rectas de maior inclinação de um plano
são todas paralelas entre si, pois trata-se de uma mesma «família» de rectas do plano.
115.
Em primeiro lugar representou-se o plano α pelos seus traços, em função dos dados. O
plano α é ortogonal ao β1/3, pelo que tem os seus traços simétricos em relação ao eixo
XX. A recta rr, porque é uma recta de maior declive do plano α, tem a sua projecção hori-
zontal perpendicular a hhα. Por outro lado, uma vez que se trata de uma recta passante, a
recta rr tem de ser concorrente com o eixo XX no ponto de concorrência dos traços do
plano. Estes dois raciocínios permitiram-nos desenhar imediatamente rr11, a projecção ho-
rizontal da recta. No entanto, para definir a recta só temos um ponto – o seu ponto de
concorrência com o eixo XX. Falta-nos outro ponto ou uma direcção. Os dados do plano
são insuficientes para definir a recta rr, pelo que é necessário o recurso a uma recta auxi-
liar do plano. Optou-se por recorrer a uma recta dd – dd é uma outra recta de maior declive
do plano (a recta dd está definida por dois pontos, que são os seus traços). As rectas rr e
dd são complanares (estão, ambas, contidas no plano α) e não são concorrentes, pelo
que são paralelas – já temos a direcção. Em seguida, desenhou-se rr22, paralela a dd22.
Tenha em conta que as rectas de maior declive de um plano são todas paralelas entre si,
pois trata-se de uma mesma «família» de rectas do plano.
Em primeiro lugar representaram-se o plano α, pelos seus traços, e o ponto
PP, pelas suas projecções, em função dos dados. O plano α é ortogonal ao
β2/4, pelo que tem os seus traços coincidentes. Pelas projecções de PP con-
duziram-se as projecções da recta pp, perpendiculares aos traços homóni-
mos do plano α (ver exercício 7744) – a recta pp, porque tem as suas
projecções paralelas entre si, é uma recta paralela ao β2/4. Para determinar o
ponto de intersecção da recta pp com o plano α, e uma vez que nem a recta
nem o plano são projectantes, recorreu-se ao mmééttooddoo ggeerraall ddaa iinntteerrsseeccççããoo
ddee rreeccttaass ccoomm ppllaannooss (ver exercício 7755).
118.
Em primeiro lugar representaram-se o plano δ, pelos seus traços, e o ponto PP, pelas suas
projecções, em função dos dados. O plano δ é ortogonal ao β1/3, pelo que tem os seus tra-
ços simétricos em relação ao eixo XX. Pelas projecções de PP conduziram-se as projecções
da recta pp, perpendiculares aos traços homónimos do plano δ (ver exercício 7744) – as projec-
ções da recta pp fazem, com o eixo XX, ângulos iguais e com o mesmo sentido de abertura,
pelo que a recta pp é uma recta paralela ao β1/3. Para determinar o ponto de intersecção da
recta pp com o plano δ, e uma vez que nem a recta nem o plano são projectantes, recorreu-
-se ao mmééttooddoo ggeerraall ddaa iinntteerrsseeccççããoo ddee rreeccttaass ccoomm ppllaannooss (ver exercício 7755).
117.

34. 34
SOLUÇÕES
119.
Em primeiro lugar representaram-se o plano ρ, pelos seus traços, e o ponto PP, pelas
suas projecções, em função dos dados. O plano ρ é ortogonal ao β1/3, pelo que tem
os seus traços simétricos em relação ao eixo XX – o traço horizontal do plano tem 4 cm
de afastamento. Por PP conduziram-se as projecções da recta pp, a recta ortogonal ao
plano – pp é uma recta de perfil, que está definida por um ponto (o ponto PP) e uma di-
recção (é ortogonal ao plano ρ). Para determinar o ponto de intersecção da recta pp
com o plano ρ, e atendendo a que nem a recta nem o plano são projectantes, há que
recorrer ao mmééttooddoo ggeerraall ddaa iinntteerrsseeccççããoo ddee rreeccttaass ccoomm ppllaannooss. Assim sendo, tem-
se: 11.. por pp conduziu-se um plano auxiliar (o plano π, que é um plano de perfil); 22..
determinou-se a recta ii, a recta de intersecção dos dois planos (a recta ii está definida
pelos seus traços, pois trata-se do caso geral da intersecção entre planos – a recta ii é
uma recta de perfil do plano ρ); 33.. o ponto de concorrência da recta ii com a recta pp
(o ponto II) é o ponto de intersecção da recta pp com o plano ρ. A terceira etapa con-
clui-se com o recurso a um processo geométrico auxiliar. Optou-se pelo rebatimento
do plano π – rebateu-se o plano para o Plano Frontal de Projecção (a charneira foi ffπ).
A recta iirr fica definida por FFrr e HHrr, os seus traços em rebatimento. A recta pprr passa por
PPrr e é perpendicular à recta iirr – note que só nesta etapa é que se resolveu definitiva-
mente o problema da ortogonalidade entre a recta pp e o plano ρ, pois só agora é que
se garante que a recta pp é ortogonal a duas «famílias» de rectas do plano ρ (ver exer-
cício 7788 e respectivo relatório). O ponto IIrr é o ponto de concorrência das rectas iirr e pprr
– II é o ponto de intersecção da recta pp com o plano ρ. Invertendo o rebatimento,
determinaram-se as projecções do ponto II. Note que o problema se poderia resolver
com o recurso a uma mudança do diedro de projecção, à semelhança do exercício
seguinte.
120.
Em primeiro lugar representaram-se o plano ρ, pelos seus traços,
e o ponto PP, pelas suas projecções, em função dos dados. O pla-
no ρ é ortogonal ao β2/4, pelo que os seus traços estão coinciden-
tes. Por PP conduziram-se as projecções da recta pp, a recta
ortogonal ao plano – pp é uma recta de perfil, que está definida por
um ponto (o ponto PP) e uma direcção (é ortogonal ao plano ρ).
Para determinar o ponto de intersecção da recta pp com o plano ρ,
e atendendo a que nem a recta nem o plano são projectantes,
optou-se por recorrer a uma mudança do diedro de projecção,
transformando o plano ρ num plano projectante – um plano de
topo. Nesse sentido, substituiu-se o Plano Frontal de Projecção
(o ppllaannoo 22) por um novo plano de projecção (o ppllaannoo 44), ortogo-
nal ao plano ρ – o novo eixo XX (o eixo XX’’) é a recta de intersecção
do ppllaannoo 11 com o ppllaannoo 44 e é perpendicular a hhρ. Na mudança do
diedro de projecção efectuada, mantiveram-se as projecções hori-
zontais e as cotas. Para determinar o traço do plano ρ no ppllaannoo 44,
recorreu-se a um ponto qualquer do plano – o ponto AA, que é um
ponto com afastamento nulo. O ponto AA tem cota negativa (é um
ponto de ffρ), que se manteve – AA44 e PP44 são, respectivamente, as
projecções de AA e PP no ppllaannoo 44, e determinaram-se em função
das respectivas cotas, que se mantiveram. O traço do plano ρ no
ppllaannoo 44, ff44ρ, é concorrente com hhρ no eixo XX’’ e passa por AA44 (note
que o plano ρ, no novo diedro de projecção, é projectante frontal,
pelo que projecta todos os seus pontos e rectas no ppllaannoo 44). No
novo diedro de projecção (formado pelo ppllaannoo 11 e pelo ppllaannoo 44,
o plano ρ é um plano de topo e a recta pp, sendo ortogonal ao pla-
no, é uma recta frontal (de frente) – ver exercício 7722. Assim, por PP44
conduziu-se imediatamente pp44, perpendicular a ff44ρ. Por outro lado, atendendo a que, no novo diedro de projecção, o plano ρ é projectante
frontal, a determinação do ponto de intersecção da recta pp com o plano ρ resume-se à intersecção entre uma recta não projectante e um
plano projectante – II tem, assim, determinação imediata a partir da sua projecção no ppllaannoo 44, II44. II11 teve determinação imediata, a partir
de II44. Invertendo a mudança do diedro de projecção efectuada, e uma vez que se mantêm as cotas, determinou-se II22 em função da sua
cota (que se manteve).

35. 35
SOLUÇÕES
122.
Em primeiro lugar desenharam-se as projecções da recta hh, em função dos dados. Em
seguida, determinaram-se as projecções do ponto PP, o ponto de concorrência das
duas rectas (que tem 2 cm de afastamento). Pretende-se que a recta rr seja perpendicu-
lar à recta hh – uma vez que a recta hh é paralela ao Plano Horizontal de Projecção, sabe-
-se que a perpendicularidade é directa em projecção horizontal. Assim, por PP11
conduziu-se rr11, a projecção horizontal da recta rr, perpendicular a hh11 – rr22 é paralela a rr11,
pois a recta rr, sendo paralela ao β2/4, tem as suas projecções paralelas entre si. Em
seguida, determinaram-se os traços da recta rr nos planos de projecção, FF e HH – note
que não foi necessário determinar o traço frontal da recta hh. O traço horizontal do
plano α, hhα, passa por HH e é paralelo à recta hh (rectas horizontais de um plano são
paralelas entre si e paralelas ao traço horizontal do plano, que é uma recta horizon-
tal do plano com cota nula). O traço frontal do plano ffα, passa por FF e é concorrente
com hhα no eixo XX.
121.
Em primeiro lugar representaram-se os planos α e θ, pelos respectivos traços,
e o ponto PP, pelas suas projecções, em função dos dados. O plano α, porque é
ortogonal ao β1/3, tem os seus traços simétricos em relação ao eixo XX. O plano
θ, porque é ortogonal ao β2/4, tem os seus traços coincidentes. Pretende-se
que o plano γ contenha o ponto PP e seja ortogonal ao plano α – o plano γ terá,
então, de conter uma recta ortogonal ao plano γ que passe pelo ponto PP (ver
exercício 110033). A recta pp é a recta que passa pelo ponto PP e é ortogonal ao pla-
no α. Por outro lado, pretende-se também que o plano γ contenha o ponto PP e
seja ortogonal ao plano θ – o plano γ terá, então, de conter uma recta ortogonal
ao plano θ que passe pelo ponto PP (ver exercício 110033). A recta pp’’ é a recta que
passa pelo ponto PP e é ortogonal ao plano θ. As rectas pp e pp’’ são concorrentes
(no ponto PP), pelo que definem um plano – esse será o plano γ, simultanea-
mente ortogonal aos planos α e θ. Note que a recta pp é uma recta passante – é
concorrente com o eixo XX e é uma recta do β1/3. Determinaram-se os traços da
recta pp’’ nos planos de projecção – FF e HH. O traço frontal do plano γ, ffγ, passa
por FF e pelo ponto de concorrência da recta pp com o eixo XX. O traço horizontal
do plano γ, hhγ, passa por HH e é concorrente com ffγ no eixo XX.
123.
Em primeiro lugar desenharam-se as projecções da recta mm, em função dos dados. A
recta mm tem as suas projecções paralelas entre si, pois é paralela ao β2/4. Sobre a deter-
minação da recta pp, ver relatório do exercício 9988. O plano α é o plano ortogonal à recta rr
a que se recorreu para determinar a recta pp e a recta ff foi a recta a que se recorreu para
determinar o plano α – note que a recta ff pode ser uma recta qualquer (ortogonal à rec-
ta mm), pois não é dado nenhum ponto. A recta pp, porque pertence simultaneamente ao
plano α (para ser ortogonal à recta mm) e ao β2/4, tem de ser a recta de intersecção do
plano α com o β2/4. O ponto de concorrência dos traços do plano já é um ponto que
pertence simultaneamente ao plano α e ao β2/4. Falta-nos outro ponto ou uma direcção.
Determinou-se II, o traço da recta ff no β2/4. II pertence ao β2/4, pois tem as suas projec-
ção coincidentes, e pertence ao plano α, pois pertence a uma recta do plano – a recta ff.
Já temos dois pontos para definir a recta pp – a recta pp passa por II e é concorrente com
o eixo XX no ponto de concorrência dos traços do plano α.
Em primeiro lugar desenharam-se as projecções da recta rr, em função dos dados. Em se-
guida, sendo pedida uma recta do β1/3 que seja ppeerrppeennddiiccuullaarr à recta rr, sabe-se que as rec-
tas têm de ser ccoonnccoorrrreenntteess – o único ponto da recta rr (que é uma recta do β2/4) que
pertence ao β1/3 é o seu ponto de concorrência com o eixo XX (o ponto AA). Sabe-se, portanto,
que a recta pp terá de passar por AA. Para definir a recta pp há que conduzir, por AA, um plano
ortogonal à recta rr (ver exercício 9988). Uma vez que AA é um ponto do eixo XX, AA será também
o ponto de concorrência dos traços do plano α (o plano ortogonal à recta rr) – os traços do
plano α, perpendiculares às projecções homónimas da recta rr, têm, assim, determinação
imediata. Sabe-se que a recta pp (a recta pedida) é uma recta do β1/3 e que passa por AA – já
temos um ponto para definir a recta. Falta-nos outro ponto ou uma direcção. Recorreu-se
a uma recta hh, horizontal (de nível), auxiliar, do plano α, determinou-se o traço da recta hh
no β1/3 – o ponto QQ. A recta pp está definida por dois pontos – AA e QQ.
124.

36. 36
SOLUÇÕES
125.
Em primeiro lugar representaram-se o plano ρ, pelos seus traços, e o ponto PP,
pelas suas projecções, em função dos dados. Sobre a determinação dos traços
do plano σ, ver exercício 110088 e respectivo relatório.
126.
Em primeiro lugar representaram-se os planos α e ρ, pelos respectivos traços, em função dos
dados. O plano α é ortogonal ao β2/4, pelo que tem os seus traços coincidentes. O plano ρ tam-
bém é ortogonal ao β2/4, pelo que os seus traços também estão coincidentes. Para determinar a
recta de intersecção entre os dois planos, teve-se em conta que se trata do caso geral da inter-
secção de planos – determinaram-se os traços da recta nos planos de projecção (HH é o ponto
de concorrência dos traços horizontais dos dois planos e FF é o ponto de concorrência dos tra-
ços frontais dos dois planos). A recta de intersecção dos dois planos é uma rreeccttaa ddee ppeerrffiill que
está definida por FF e HH, os seus traços nos planos de projecção.

37. 37
SOLUÇÕES
127.
A finalidade dos processos geométricos auxiliares é a determinação de projecções mais favoráveis de um dado objecto para um determinado
estudo (em relação às projecções iniciais). De facto, é através dos processos geométricos auxiliares que é possível resolver situações que as
projecções iniciais não permitem, como, por exemplo, a determinação de verdadeiras grandezas onde estas não existem de forma imediata.
128.
Os processos geométricos auxiliares são ttrrêêss: o processo da mmuuddaannççaa ddoo ddiieeddrroo ddee pprroojjeeccççããoo, o processo da rroottaaççããoo e o processo do
rreebbaattiimmeennttoo (que consiste no caso particular de uma rroottaaççããoo).
129.
O processo da mmuuddaannççaa ddoo ddiieeddrroo ddee pprroojjeeccççããoo consiste em, mantendo fixo o objecto, introduzir novos planos de projecção, criando novos
diedros de projecção nos quais o objecto se projecte de forma mais favorável para o estudo em curso. O processo da rroottaaççããoo consiste em
rodar o objecto em torno de um eixo (uma recta), mantendo o diedro de projecção inicial, de forma a que, no diedro de projecção inicial, o objecto
se projecte de forma mais favorável para o estudo em curso. Por fim, o processo do rreebbaattiimmeennttoo é semelhante ao processo da rroottaaççããoo e,
assim, consiste também na rotação do objecto em torno de um eixo (uma recta), mantendo o diedro de projecção inicial. A diferença entre
estes dois processos (o da rroottaaççããoo e o do rreebbaattiimmeennttoo) consiste em que, no segundo (no rreebbaattiimmeennttoo), o eixo de rotação é ccoommppllaannaarr
com os objectos a rodar, enquanto que, no primeiro (na rroottaaççããoo), tal não se verifica. Resulta dessa diferença o facto de, nos rreebbaattiimmeennttooss,
os objectos a rodar terem de estar nneecceessssaarriiaammeennttee contidos em planos (para que o eixo de rotação seja complanar com o objecto) – o eixo
é, assim, uma recta do plano que contém o objecto (que tem de estar contido num plano). Já nas rroottaaççõõeess, o eixo é uma recta exterior ao
plano e podem rodar-se objectos tridimensionais (num rreebbaattiimmeennttoo só se podem rodar objectos uni ou bidimensionais – só se rebatem planos).
130.
O processo da mmuuddaannççaa ddoo ddiieeddrroo ddee pprroojjeeccççããoo consiste em introduzir nnoovvooss planos de projecção em posições mais favoráveis em relação
ao objecto a projectar, substituindo os planos de projecção iniciais e mantendo fixo o objecto, o que implica que o objecto passa a existir num
diedro de projecção diferente (de onde vem o nome deste processo) e no qual se projecta de forma mais favorável para o estudo em curso.
131.
Há que substituir o Plano Frontal de Projecção (o ppllaannoo 22) por um outro plano de projecção (o ppllaannoo 44), paralelo ao segmento – uma vez
que se mantém o Plano Horizontal de Projecção, mantêm-se todas as referências a este plano de projecção (mantêm-se as projecções hori-
zontais e mantêm-se as cotas). O novo eixo XX (eixo XX’’) é a recta de intersecção do Plano Horizontal de Projecção (o ppllaannoo 11) com o novo
plano de projecção (o ppllaannoo 44) e fica paralelo à projecção horizontal do segmento. A projecção do segmento no ppllaannoo 44 obtém-se a partir
das cotas dos extremos do segmento, que se mantêm.
132.
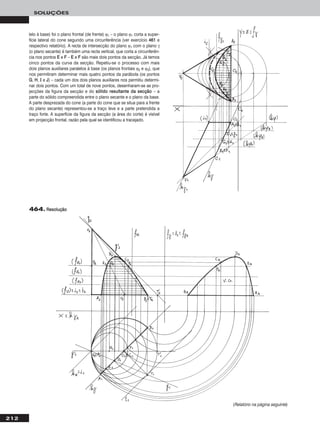
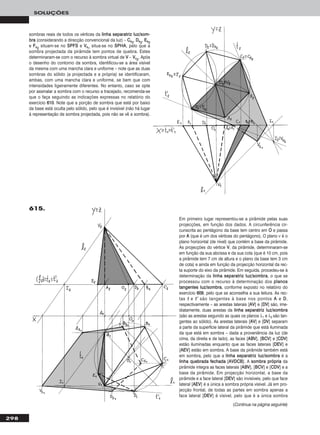
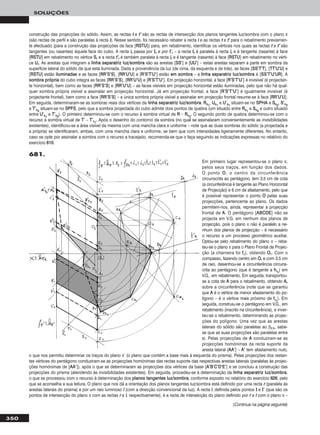
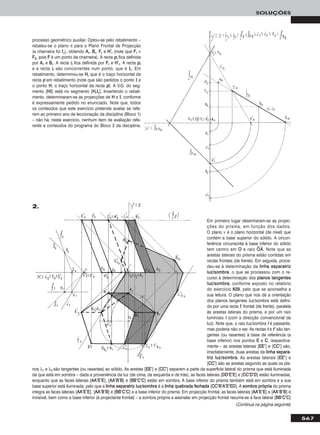
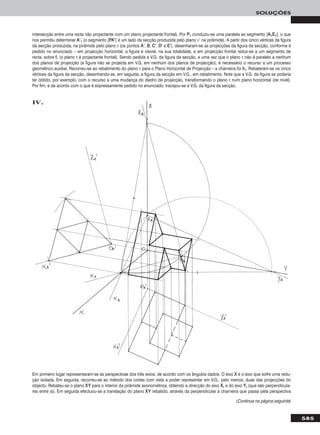
Em primeiro lugar representou-se o segmento de recta [AABB] pelas suas
projecções, em função dos dados. Em seguida, teve-se em conta que
uma recta de topo é um caso particular das rectas horizontais (de nível).
Assim, em primeiro lugar transformou-se [AABB] num segmento horizontal
(de nível) com 4 cm de cota, substituindo o Plano Horizontal de Projecção
(ppllaannoo 11) por um novo plano de projecção (o ppllaannoo 44), paralelo a [AABB] e a
4 cm deste. O novo eixo XX (o eixo XX’’) é a recta de intersecção do ppllaannoo 44
com o Plano Frontal de Projecção (o ppllaannoo 22) e é paralelo a [AA22BB22]. Man-
teve-se o Plano Frontal de Projecção, pelo que se mantiveram as projec-
ções frontais e os afastamentos dos pontos AA e BB. AA44 e BB44 são as
projecções de AA e BB no ppllaannoo 44, que se determinam em função dos afas-
tamentos dos pontos. No novo diedro de projecção, o segmento de recta
[AABB] é horizontal (de nível) e tem 4 cm de cota. Um segmento de topo é
ortogonal ao Plano Frontal de Projecção, o que ainda não se verifica no diedro de projecção criado. Assim, substituiu-se o Plano Frontal de
Projecção (ppllaannoo 22) por um novo plano de projecção (o ppllaannoo 55), ortogonal a [AABB]. O novo eixo XX (o eixo XX’’’’) é a recta de intersecção do
ppllaannoo 44 com o ppllaannoo 55 e é perpendicular à recta suporte de [AA44BB44]. Manteve-se o ppllaannoo 44, pelo que se mantiveram as projecções no ppllaannoo 44
e a cota dos pontos, que passou a ser 4 cm (e está referenciada ao ppllaannoo 44). AA55 e BB55 determinam-se em função das suas cotas, que é 4 cm.
No diedro de projecção formado pelo ppllaannoo 44 e pelo ppllaannoo 55, [AABB] é de topo e tem 4 cm de cota. A V.G. de AAෆBBෆ é AAෆ44ෆBBෆ44ෆ.
PROCESSOS GEOMÉTRICOS AUXILIARES II
15
133.
Em primeiro lugar representou-se o segmento de recta [AABB] pelas suas projecções, em função dos dados. Em seguida, teve-se em conta que
uma recta fronto-horizontal é um caso particular das rectas frontais (de frente) e das rectas horizontais (de nível). Começou-se por transformar
[AABB] num segmento frontal (de frente) com 4 cm de afastamento. Para tal substituiu-se o Plano Frontal de Projecção (o ppllaannoo 22) por um novo
(Continua na página seguinte)

38. 38
SOLUÇÕES
plano de projecção (o ppllaannoo 44), paralelo a [AABB] e a 4 cm deste. O novo eixo XX
(o eixo XX’’) é a recta de intersecção do Plano Horizontal de Projecção (o ppllaannoo 11
– o plano de projecção que se mantém) com o ppllaannoo 44 e é paralelo a [AA11BB11].
Manteve-se o Plano Horizontal de Projecção, pelo que se mantiveram as pro-
jecções horizontais e as cotas dos pontos AA e BB. AA44 e BB44 determinam-se
em função das suas cotas, que se mantêm. No novo diedro de projecção, o
segmento de recta [AABB] é frontal (de frente) e tem 4 cm de afastamento. Um
segmento fronto-horizontal é paralelo ao Plano Horizontal de Projecção.
Assim, em seguida substituiu-se o Plano Horizontal de Projecção (o ppllaannoo 22)
pelo ppllaannoo 55, paralelo a [AABB] e a 2 cm deste. O novo eixo XX (o eixo XX’’’’) é a recta
de intersecção do ppllaannoo 44 com o ppllaannoo 55 e é paralelo a [AA44BB44]. Manteve-se o
ppllaannoo 44, pelo que se mantiveram as projecções no ppllaannoo 44 e o afastamento
dos pontos, que passou a ser 4 cm (e está referenciado ao ppllaannoo 44). AA55 e BB55
determinam-se em função dos seus afastamentos, que é 4 cm. No diedro de
projecção formado pelo ppllaannoo 44 e pelo ppllaannoo 55, o segmento [AABB] é fronto-
-horizontal e tem 4 cm de afastamento e 2 cm de cota. A V.G. de AAෆBBෆ é AAෆ44ෆBBෆ44ෆ ou
AAෆ55ෆBBෆ55ෆ.
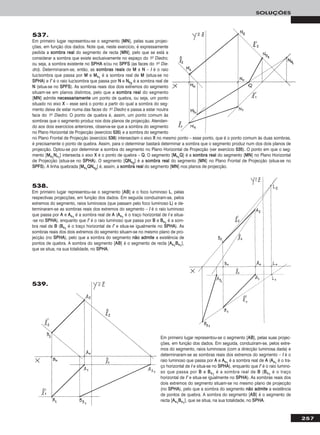
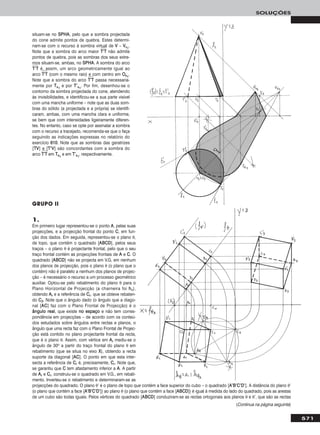
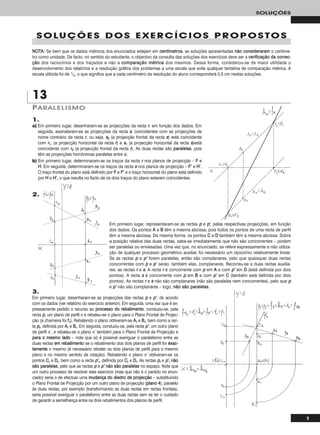
Em primeiro lugar representou-se a recta rr, pelas suas projecções, em fun-
ção dos dados – a recta rr é paralela ao β1/3, pelo que as suas projecções
fazem, com o eixo XX, ângulos iguais e com o mesmo sentido de abertura.
Em seguida teve-se em conta que uma recta vertical é um caso particular
das rectas frontais (de frente). Assim, começou-se por transformar rr numa
recta frontal (de frente) com 4 cm de afastamento. Nesse sentido, substi-
tuiu-se o Plano Frontal de Projecção (o ppllaannoo 22) por um novo plano de pro-
jecção (o ppllaannoo 44), paralelo a rr e a 4 cm desta. O novo eixo XX (o eixo XX’’) é
a recta de intersecção do Plano Horizontal de Projecção (ppllaannoo 11 – o plano
de projecção que se mantém) com o ppllaannoo 44 e é paralelo a rr11. Mantêm-se
as projecções horizontais e as cotas. AA44 determinou-se em função da sua
cota, que se mantém. Para definir a recta rr no novo diedro de projecção
necessitamos de um outro ponto para além de AA. Assim, recorreu-se a um
outro ponto de rr – HH, o seu traço horizontal. HH44 determinou-se em função
da sua cota, que é nula e se mantém – rr44 fica definida por AA44 e HH44. No novo
diedro de projecção, a recta rr é uma recta frontal (de frente). Uma recta ver-
tical é ortogonal ao Plano Horizontal de Projecção. Assim, em seguida substituiu-se o Plano Horizontal de Projecção (o ppllaannoo 11) por um novo
plano de projecção (o ppllaannoo 55), ortogonal a rr. O novo eixo XX (o eixo XX’’’’) é a recta de intersecção do ppllaannoo 44 com o ppllaannoo 55 e é perpendi-
cular a rr44. Mantêm-se as projecções no ppllaannoo 44 e os afastamentos (agora referenciados ao ppllaannoo 44) – note que, agora, todos os pontos da
recta já têm o mesmo afastamento, que é 4 cm. AA55 e HH55 determinaram-se em função dos seus afastamentos (e estão coincidentes) – rr55, a
projecção da recta rr no ppllaannoo 55, é um ponto, pois no diedro de projecção formado pelo ppllaannoo 44 e pelo ppllaannoo 55 a recta rr é vertical (projec-
tante horizontal).
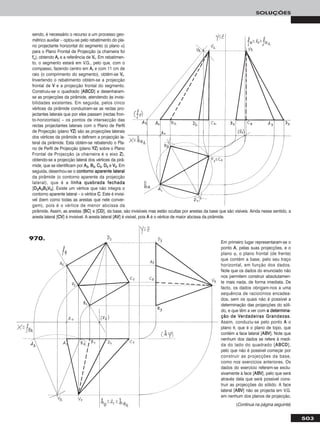
135.
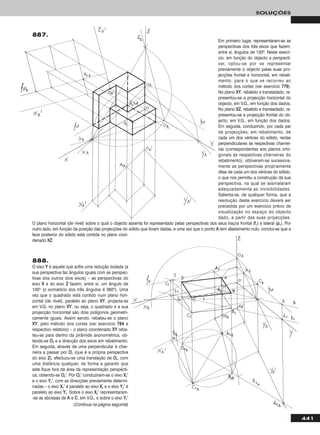
Em primeiro lugar representou-se a recta mm, pelas suas projecções, em função dos
dados – a recta mm é paralela ao β2/4, pelo que as suas projecções são paralelas
entre si. Em seguida, teve-se em conta que uma recta fronto-horizontal é simultanea-
mente um caso particular das rectas frontais (de frente) e das rectas horizontais
(de nível). Começou-se por transformar a recta mm numa recta horizontal (de nível)
com 3 cm de cota. Nesse sentido, substituiu-se o Plano Horizontal de Projecção
(o ppllaannoo 11) por um novo plano de projecção (o ppllaannoo 44), paralelo a mm e a 3 cm desta.
O novo eixo XX (o eixo XX’’) é a recta de intersecção do Plano Frontal de Projecção
(ppllaannoo 22 – o plano de projecção que se mantém) com o ppllaannoo 44 e é paralelo a mm22.
Mantêm-se as projecções frontais e os afastamentos. PP44 determinou-se em função
do seu afastamento, que se mantém. Para definir a recta mm no novo diedro de pro-
jecção necessitamos de um outro ponto para além de PP. Assim, recorreu-se a um
outro ponto de mm – FF, o seu traço frontal. FF44 determinou-se em função do seu afasta-
mento, que é nulo e se mantém – mm44 fica definida por PP44 e FF44. No novo diedro de
projecção, a recta mm é uma recta horizontal (de nível). Uma recta fronto-horizontal é
paralela ao Plano Frontal de Projecção. Assim, em seguida substituiu-se o Plano
Frontal de Projecção (o ppllaannoo 22) por um novo plano de projecção (o ppllaannoo 55), paralelo a mm. O novo eixo XX (o eixo XX’’’’) é a recta de intersec-
ção do ppllaannoo 44 com o ppllaannoo 55 e é paralelo a mm44. Mantêm-se as projecções no ppllaannoo 44 e as cotas (agora referenciadas ao ppllaannoo 44) – note
que, agora, todos os pontos da recta já têm a mesma cota, que é 3 cm. PP55 e FF55 determinaram-se em função das suas cotas – mm55, a projecção
da recta mm no ppllaannoo 55, é paralela ao eixo XX’’’’, pois no diedro de projecção formado pelo ppllaannoo 44 e pelo ppllaannoo 55 a recta mm é fronto-horizontal.
134.

39. 39
SOLUÇÕES
136.
Em primeiro lugar representou-se a recta tt, pelas suas projecções, em
função dos dados. Em seguida, para transformar a recta tt numa recta
oblíqua, há que efectuar os raciocínios expostos no relatório do exercí-
cio 113322 por ordem inversa. Assim, uma vez que uma recta de topo é
um caso particular das rectas horizontais (de nível), em primeiro lugar
há que transformar a recta tt numa recta horizontal (de nível). Para tal,
há que substituir o Plano Frontal de Projecção (o ppllaannoo 22) por um
novo plano de projecção (o ppllaannoo 44), que não seja ortogonal à recta tt
– o novo eixo XX (o eixo XX’’) é a recta de intersecção do ppllaannoo 44 com o
Plano Horizontal de Projecção (o ppllaannoo 11 – o plano de projecção que
se mantém) e é oblíquo a tt11. Manteve-se o Plano Horizontal de Projec-
ção, pelo que se mantiveram as projecções horizontais e as cotas. Para
definir uma recta são necessários dois pontos ou um ponto e uma
direcção – assim, para definir tt44 (a projecção da recta tt no ppllaannoo 44)
representaram-se previamente dois pontos da recta tt, no diedro de
projecção inicial (os pontos AA e BB). AA44 e BB44 são as projecções de AA e
BB no ppllaannoo 44, que se determinaram em função das suas cotas (que é
4 cm) e tt44, a projecção da recta tt no ppllaannoo 44, está definida por AA44 e BB44
e é paralela ao eixo XX’’. No novo diedro de projecção, a recta tt é horizon-
tal (de nível) – é paralela ao Plano Horizontal de Projecção (o ppllaannoo 11) e oblíqua ao ppllaannoo 44. Para transformar agora a recta tt numa recta oblí-
qua cuja projecção frontal faça um ângulo de 45o (a.e.) com o eixo XX (que será o novo eixo XX – o eixo XX’’’’), é necessário substituir o Plano
Horizontal de Projecção (o ppllaannoo 11) por um novo plano de projecção (o ppllaannoo 55), oblíquo a tt44 e tal que o eixo XX’’’’ faça um ângulo de 45o (a.e.)
com tt44 – o eixo XX’’’’ cumpre essas premissas e é a recta de intersecção do ppllaannoo 44 com o ppllaannoo 55. Manteve-se o ppllaannoo 44, pelo que se mantive-
ram as projecções no ppllaannoo 44 e os afastamentos dos pontos. AA55 e BB55 são as projecções de AA e BB no ppllaannoo 55, que se determinaram em função
dos seus afastamentos e tt55, a projecção da recta tt no ppllaannoo 55, está definida por AA55 e BB55. No novo diedro de projecção (formado pelo ppllaannoo 44
e pelo ppllaannoo 55), a recta tt é oblíqua e a sua projecção frontal (a projecção no ppllaannoo 44) faz um ângulo de 45o (a.e.) com o eixo XX (o eixo XX’’’’).
137.
Em primeiro lugar representou-se a recta pp, pelas suas projecções, em função dos dados – a recta pp está definida por dois pontos (AA e BB).
Em seguida, teve-se em conta que uma recta de topo é um caso particular das rectas horizontais (de nível). Assim, começou-se por transfor-
mar pp numa recta horizontal (de nível) com 3 cm de cota. Nesse sentido, substituiu-se o Plano Horizontal de Projecção (o ppllaannoo 11) por um
novo plano de projecção (o ppllaannoo 44), paralelo a pp e a 3 cm desta. O novo eixo XX (o eixo XX’’) é a recta de intersecção do Plano Frontal de Pro-
jecção (ppllaannoo 22 – o plano de projecção que se mantém) com o ppllaannoo 44 e é paralelo a pp22. Mantêm-se as projecções frontais e os afastamen-
tos. AA44 e BB44 determinaram-se em função dos seus afastamentos, que se mantêm – pp44 fica definida por AA44 e BB44. No novo diedro de
projecção, a recta pp é uma recta horizontal (de nível). Uma recta de topo é ortogonal ao Plano Frontal de Projecção. Assim, em seguida
substituiu-se o Plano Frontal de Projecção (o ppllaannoo 22) por um novo plano de projecção (o ppllaannoo 55), ortogonal a pp. O novo eixo XX (o eixo XX’’’’)
é a recta de intersecção do ppllaannoo 44 com o ppllaannoo 55 e é perpendicular a pp44. Mantêm-se as projecções no ppllaannoo 44 e as cotas (agora referen-
ciadas ao ppllaannoo 44) – note que, agora, todos os pontos da recta já têm a mesma cota, que é 3 cm. AA55 e BB55 determinaram-se em função das
suas cotas (e estão coincidentes) – pp55, a projecção da recta pp no ppllaannoo 55, é um ponto, pois no diedro de projecção formado pelo ppllaannoo 44 e
pelo ppllaannoo 55 a recta pp é de topo (projectante frontal).

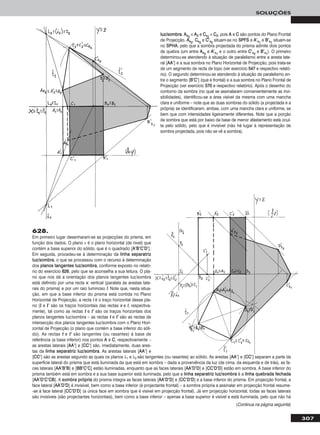
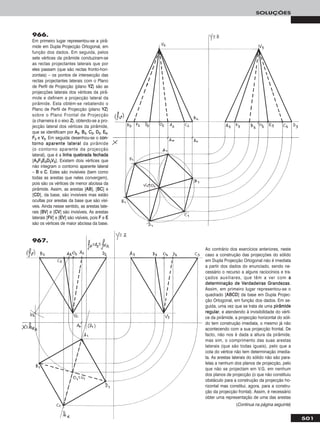
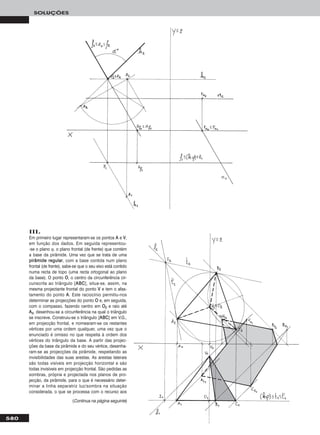
40. Em primeiro lugar representou-se o plano α, pelos seus traços, e dese-
nharam-se as projecções do triângulo [AABBCC], contido no plano, em
função dos dados. AA e BB e CC pertencem ao plano α, pois pertencem a
rectas do plano – AA pertence a ffα (que é uma recta frontal do plano
com afastamento nulo) e BB e CC pertencem a uma recta frontal (de frente)
do plano com 4 cm de afastamento. Para transformar o plano α num
plano horizontal (de nível), há que ter em conta que um plano horizontal
(de nível) é um caso particular dos planos projectantes frontais. Assim,
em primeiro lugar há que transformar o plano α num plano projectante
frontal, para o que se substituiu o Plano Frontal de Projecção (ppllaannoo 22)
pelo ppllaannoo 44, ortogonal a α. Manteve-se o Plano Horizontal de Pro-
jecção (o ppllaannoo 11), pelo que se mantiveram as projecções horizontais
e as cotas dos pontos. O novo eixo XX (o eixo XX’’) é a recta de intersec-
ção do Plano Horizontal de Projecção (o ppllaannoo 11 – o plano de projec-
ção que se manteve) com o ppllaannoo 44 e é perpendicular a hhα. Note que
se manteve, também, o traço horizontal do plano (hhα), pois situa-se no
plano de projecção que se manteve. Tenha em conta que se conduziu o
novo eixo XX (o eixo XX’’) por AA11, o que significa que, no novo diedro de
projecção, AA tem afastamento nulo – no entanto, o exposto não é uma
condição essencial. As projecções de AA, BB e CC no ppllaannoo 44 (AA44, BB44 e CC44)
determinaram-se em função das suas cotas, que se mantiveram. O traço do plano α no ppllaannoo 44, ff44α, passa por AA44, BB44 e CC44 e é concorrente com
hhα no eixo XX’’ – no novo diedro de projecção, o plano α é, agora, um plano pprroojjeeccttaannttee ffrroonnttaall. Nesse sentido, note que bastaria determinar BB44,
por exemplo, e, em seguida, conduzir ff44α por BB44 e concorrente com hhα no eixo XX’’ – as projecções de AA e CC no ppllaannoo 44 situar-se-iam
necessariamente sobre ff44α, nas respectivas linhas de chamada (perpendiculares ao eixo XX’’). No novo diedro de projecção, o plano α já é um
plano de topo (projectante frontal). Um plano horizontal (de nível) é um plano projectante frontal que é paralelo ao Plano Horizontal de Projecção.
Assim, em seguida substituiu-se o Plano Horizontal de Projecção (ppllaannoo 11) por um novo plano de projecção (o ppllaannoo 55), paralelo a α e situado
a 2 cm deste (a cota pretendida). O novo eixo XX (o eixo XX’’’’) é a recta de intersecção do ppllaannoo 44 com o ppllaannoo 55 e é paralelo a ff44α. Mantiveram-se
as projecções no ppllaannoo 44 e os afastamentos, agora referenciados ao ppllaannoo 44. As projecções de AA, BB e CC no ppllaannoo 55 (AA55, BB55 e CC55) determina-
ram-se em função dos seus afastamentos, que se mantiveram. No diedro de projecção formado entre o ppllaannoo 44 e o ppllaannoo 55, o plano α é hori-
zontal (de nível) com 2 cm de cota e não tem traço horizontal. A V.G. do triângulo [AABBCC] está no triângulo [AA55BB55CC55].
40
SOLUÇÕES
138.
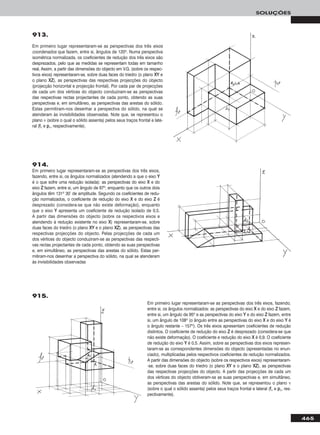
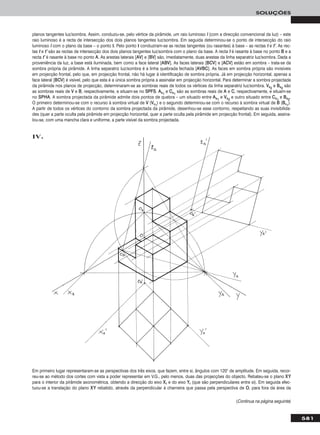
Em primeiro lugar representou-se a recta pp, pelas suas projec-
ções, em função dos dados – a recta pp está definida por dois
pontos (AA e BB). Uma recta fronto-horizontal é simultaneamente
um caso particular das rectas frontais (de frente) e das rectas
horizontais (de nível), pelo que, em primeiro lugar, há que
transformar a recta pp numa recta frontal (de frente) ou numa
recta horizontal (de nível). Optou-se pela primeira hipótese.
Assim, começou-se por transformar pp numa recta frontal
(de frente) com 4 cm de afastamento. Nesse sentido, substi-
tuiu-se o Plano Frontal de Projecção (o ppllaannoo 22) por um novo
plano de projecção (o ppllaannoo 44), paralelo a pp e a 4 cm desta.
O novo eixo XX (o eixo XX’’) é a recta de intersecção do Plano Ho-
rizontal de Projecção (ppllaannoo 11 – o plano de projecção que se
mantém) com o ppllaannoo 44 e é paralelo a pp11. Mantêm-se as pro-
jecções horizontais e as cotas. AA44 e BB44 determinaram-se em
função das suas cotas, que se mantêm – pp44 fica definida por
AA44 e BB44. No novo diedro de projecção, a recta pp é uma recta
frontal (de frente). Uma recta fronto-horizontal é paralela ao
Plano Horizontal de Projecção. Assim, em seguida substituiu-
-se o Plano Horizontal de Projecção (o ppllaannoo 11) por um novo
plano de projecção (o ppllaannoo 55), paralelo a pp. O novo eixo XX
(o eixo XX’’’’) é a recta de intersecção do ppllaannoo 44 com o ppllaannoo 55
e é paralelo a pp44. Mantêm-se as projecções no ppllaannoo 44 e os
afastamentos (agora referenciados ao ppllaannoo 44) – note que,
agora, todos os pontos da recta já têm o mesmo afastamento, que é 4 cm. AA55 e BB55 determinaram-se em função dos seus afastamentos – pp55, a
projecção da recta pp no ppllaannoo 55, está definida por AA55 e BB55 e é paralela ao eixo XX’’’’. No diedro de projecção formado pelo ppllaannoo 44 e pelo ppllaannoo 55
a recta pp é fronto-horizontal. Note que se localizou o ppllaannoo 55 de forma a evitar a sobreposição dos traçados. Note ainda que se poderia ter
começado por transformar a recta pp numa recta horizontal (à semelhança do efectuado no exercício anterior) e, em seguida, transformá-la
numa recta fronto-horizontal.
139.

41. 41
SOLUÇÕES
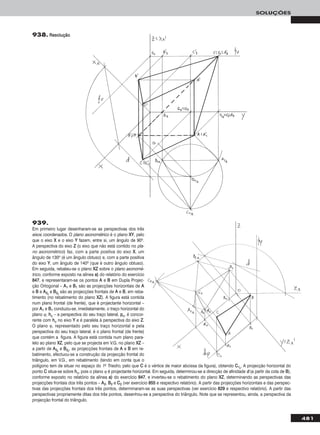
140.
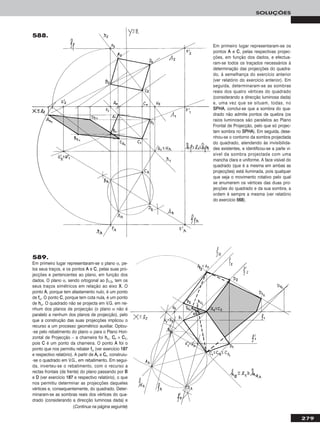
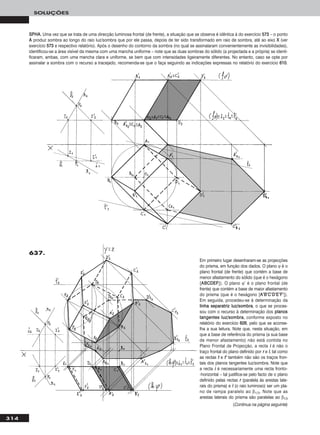
Em primeiro lugar representou-se o plano α, pelos seus traços, e desenharam-se as projecções do triângulo [AABBCC], em função dos dados
(ver relatório do exercício anterior). Para transformar o plano α num plano frontal (de frente), há que ter em conta que um plano frontal
(de frente) é um caso particular dos planos projectantes horizontais. Assim, em primeiro lugar há que transformar o plano α num plano pro-
jectante horizontal, para o que se substituiu o Plano Horizontal de Projecção (ppllaannoo 11) pelo ppllaannoo 44, ortogonal a α. Manteve-se o Plano
Frontal de Projecção (o ppllaannoo 22), pelo que se mantiveram as projecções frontais e os afastamentos dos pontos. O novo eixo XX (o eixo XX’’) é
a recta de intersecção do Plano Frontal de Projecção (o ppllaannoo 22 – o plano de projecção que se manteve) com o ppllaannoo 44 e é perpendicular a ffα.
Note que se manteve, também, o traço frontal do plano (ffα), pois situa-se no plano de projecção que se manteve. As projecções de AA, BB e CC no
ppllaannoo 44 (AA44, BB44 e CC44) determinaram-se em função dos seus afastamentos, que se mantiveram. O traço do plano α no ppllaannoo 44, hh44α, passa
por AA44, BB44 e CC44 e é concorrente com ffα no eixo XX’’ – no novo diedro de projecção, o plano α é, agora, um plano pprroojjeeccttaannttee hhoorriizzoonnttaall. Nesse
sentido, note que bastaria determinar BB44, por exemplo, e, em seguida, conduzir hh44α por BB44 e concorrente com ffα no eixo XX’’ – as projecções
de AA e CC no ppllaannoo 44 situar-se-iam necessariamente sobre hh44α, nas respectivas linhas de chamada (perpendiculares ao eixo XX’’). No novo diedro
de projecção, o plano α já é um plano vertical (projectante horizontal). Um plano frontal (de frente) é um plano projectante horizontal que é
paralelo ao Plano Frontal de Projecção. Assim, em seguida substituiu-se o Plano Frontal de Projecção (ppllaannoo 22) por um novo plano de pro-
jecção (o ppllaannoo 55), paralelo a α (note que não é pretendido nenhum afastamento em particular). O novo eixo XX (o eixo XX’’’’) é a recta de inter-
secção do ppllaannoo 44 com o ppllaannoo 55 e é paralelo a hh44α. Mantiveram-se as projecções no ppllaannoo 44 e as cotas, agora referenciadas ao ppllaannoo 44.
As projecções de AA, BB e CC no ppllaannoo 55 (AA55, BB55 e CC55) determinaram-se em função das suas cotas, que se mantiveram. No diedro de projec-
ção formado entre o ppllaannoo 44 e o ppllaannoo 55, o plano α é frontal (de frente) e não tem traço frontal. A V.G. do triângulo [AABBCC] está no triângulo
[AA55BB55CC55].
141.
Em primeiro lugar representou-se o plano γ, pelos seus traços, e desenha-
ram-se as projecções do triângulo [AABBCC], em função dos dados. O plano γ
tem os seus traços coincidentes, pois é ortogonal ao β2/4. AA e BB e CC per-
tencem ao plano γ, pois pertencem a rectas do plano – AA pertence a hhγ
(que é uma recta horizontal do plano com cota nula), BB pertence a ffγ (que
é uma recta frontal do plano com afastamento nulo) e CC pertence a uma
recta horizontal (de nível) do plano com 4 cm de cota. Para transformar o
plano γ num plano frontal (de frente), há que ter em conta que um plano
frontal (de frente) é um caso particular dos planos projectantes horizontais,
o que consiste nos procedimentos efectuados no exercício anterior, pelo
que se aconselha a leitura do respectivo relatório. Note que o facto de o
plano γ ter os seus traços coincidentes não altera em nada os procedimen-
tos expostos naquele relatório. Note ainda que, uma vez que se pretende
que o plano γ seja transformado num plano frontal (de frente) com 3 cm de
afastamento, o ppllaannoo 55 situa-se a 3 cm (o afastamento pretendido) de hh44γ
(o eixo XX’’’’ situa-se a 3 cm de hh44γ).

42. 42
SOLUÇÕES
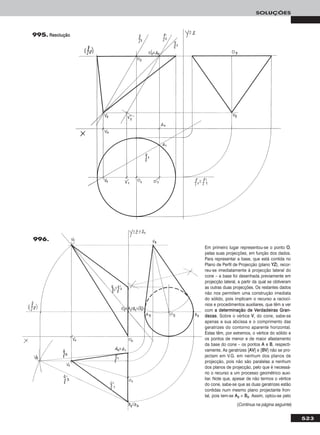
143.
Em primeiro lugar representaram-se os pontos PP e QQ, pelas respectivas projecções, determinaram-se os traços do plano ρ e desenharam-
-se as projecções do triângulo [PPQQRR] (ver relatório do exercício anterior). Para transformar o plano ρ num plano horizontal (de nível), há que
ter em conta que um plano horizontal (de nível) é um caso particular dos planos projectantes frontais, o que consiste nos procedimentos
efectuados no exercício 113399, pelo que se aconselha a leitura do respectivo relatório. Note que o facto de se tratar de um plano de rampa
não altera em nada os procedimentos expostos naquele relatório. Note ainda que, uma vez que se pretende que o plano ρ seja transformado
num plano horizontal (de nível) com 1 cm de cota, o ppllaannoo 55 situa-se a 1 cm (a cota pretendida) de ff44ρ (o eixo XX’’’’ situa-se a 1 cm de ff44ρ).
144.
Em primeiro lugar representou-se o plano ρ (cujos traços estão coincidentes no eixo XX), que está definido pelo eixo XX e pelas projecções do
ponto AA. Os dados do enunciado permitem-nos, ainda, determinar BB22, a projecção frontal de BB, e CC11 a projecção horizontal de CC. Em seguida,
recorreu-se a uma recta rr, passante, tal que rr22 passa por AA22 e BB22 – após determinar rr11 (definida pelo seu ponto de concorrência com o eixo XX
e por AA11), determinou-se BB11, sobre rr11. A recta ss é a recta a que se recorreu para determinar a projecção frontal de CC (CC22) e determinou-se a
partir da sua projecção horizontal, ss11, por raciocínios semelhantes aos expostos para a recta rr. A partir das projecções dos três pontos,
(Continua na página seguinte)
142.
Em primeiro lugar representaram-se os pontos PP e QQ, pelas respectivas
projecções. Em seguida, desenharam-se as projecções da recta rr, a
recta que passa por PP e QQ, e determinaram-se os seus traços – PP é,
imediatamente, o traço frontal de rr. Pelos traços de rr conduziram-se os
traços homónimos do plano ρ. Os dados do exercício permitiram-nos,
ainda, determinar a projecção frontal de RR. Por RR conduziu-se uma
recta ss, paralela a rr e pertencente ao plano ρ, o que nos permitiu
determinar a projecção horizontal de RR e, em seguida, desenhar as
projecções do triângulo [PPQQRR]. Para transformar o plano ρ num plano
frontal (de frente), há que ter em conta que um plano frontal (de frente)
é um caso particular dos planos projectantes horizontais, o que con-
siste nos procedimentos efectuados no exercício 114400, pelo que se
aconselha a leitura do respectivo relatório. Note que o facto de se tratar
de um plano de rampa não altera em nada os procedimentos expostos
naquele relatório. Note ainda que, uma vez que se pretende que o
plano ρ seja transformado num plano frontal (de frente) com 2 cm de
afastamento, o ppllaannoo 55 situa-se a 2 cm (o afastamento pretendido)
de hh44ρ (o eixo XX’’’’ situa-se a 2 cm de hh44ρ).

43. 43
SOLUÇÕES
desenharam-se as projecções do triân-
gulo [AABBCC]. Para transformar o plano ρ
num plano frontal (de frente), há que
ter em conta que um plano frontal (de
frente) é um caso particular dos planos
projectantes horizontais, o que consiste
nos procedimentos efectuados no
exercício 114400, pelo que se aconselha a
leitura do respectivo relatório. Note que
o facto de se tratar de um plano de
rampa passante não altera em nada os
procedimentos expostos naquele rela-
tório. Note ainda que, uma vez que se
pretende que o plano ρ seja transfor-
mado num plano frontal (de frente)
com 3 cm de afastamento, o ppllaannoo 55
situa-se a 3 cm (o afastamento preten-
dido) de hh44ρ (o eixo XX’’’’ situa-se a 3 cm
de hh44ρ). Note ainda que se localizou o
ppllaannoo 55 de forma a evitar a sobreposi-
ção de traçados.
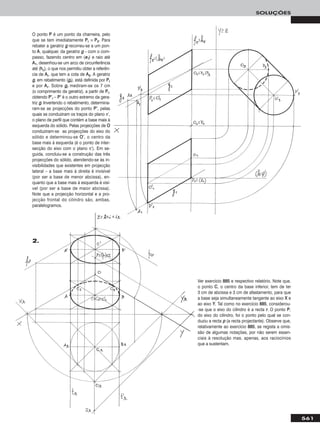
a) Em primeiro lugar representaram-se os pontos AA, MM e NN, pelas respectivas projecções. Em seguida conduziu-se, por MM, uma recta verti-
cal – a recta ee, que é o eixo da rotação pretendida. Uma vez que se pretende rodar o ponto AA em torno de um eixo vertical (projectante
horizontal), o arco da rotação de AA existe num plano ortogonal à recta ee – um plano horizontal (de nível). O plano ν, horizontal (de nível),
é, assim, o plano que contém o ponto AA e que contém o arco da rotação a efectuar. O ponto OO é o ponto de intersecção do plano ν com
o eixo ee e é o centro do arco da rotação de AA – OOෆAAෆ é o raio do arco da rotação de AA.
Com o compasso, fazendo centro em OO11 e raio até AA11, desenhou-se um arco com
80° de amplitude, no sentido contrário ao dos ponteiros do relógio (que é a projec-
ção horizontal do arco
២២
AAAA’’), obtendo AA’’11 no seu extremo (sendo AA’’ o ponto AA roda-
do). Uma vez que o arco da rotação de AA está contido no plano ν, o ponto AA
mantém a sua cota na rotação, pelo que AA’’22 se situa sobre (ffν), na linha de chamada
de AA’’11. O ponto AA’’, definido pelas suas projecções, é o ponto AA após a rotação pre-
tendida.
b) Pelo ponto NN conduziu-se uma recta de topo – a recta ee’’, que é o eixo da rotação
pretendida. Uma vez que se pretende rodar o ponto AA’’ em torno de um eixo de topo
(projectante frontal), o arco da rotação de AA’’ existe num plano ortogonal à recta ee’’ –
um plano frontal (de frente). O plano ϕ, frontal (de frente), é, assim, o plano que con-
tém o ponto AA’’ e que contém o arco da rotação a efectuar. O ponto QQ é o ponto de
intersecção do plano ϕ com o eixo ee’’ e é o centro do arco da rotação de AA’’ – QQෆAAෆ’’ෆ é
o raio do arco da rotação de AA’’. Com o compasso, fazendo centro em QQ22 e raio até
AA’’22, desenhou-se um arco com 120o de amplitude, no sentido dos ponteiros do reló-
gio (que é a projecção frontal do arco
២២
AA’’AA’’’’), obtendo AA’’’’22 no seu extremo (sendo AA’’’’
o ponto AA’’ rodado). Uma vez que o arco da rotação de AA’’ está contido no plano ϕ, o
ponto AA’’ mantém o seu afastamento na rotação, pelo que AA’’’’11 se situa sobre (hhϕ), na
linha de chamada de AA’’’’22. O ponto AA’’’’, definido pelas suas projecções, é o ponto AA’’
após a rotação pretendida.
147.
145.
O processo da rroottaaççããoo consiste em, mantendo o diedro de projecção inicial, mmuuddaarr aa ppoossiiççããoo ddoo oobbjjeeccttoo projectado, rodando-o em torno
de uma recta (eixo de rotação), de forma a obter uma posição mais favorável do objecto para o estudo em curso, no diedro de projecção
em que se situa. Nesse sentido, o objecto é rodado em torno de uma recta (um eixo), que tem de ser ortogonal a um dos planos de projec-
ção (tem de ser projectante), até atingir a posição pretendida, mas mantendo fixa a sua posição em relação ao eixo.
146.
Em primeiro lugar há que ter em conta que os arcos das rotações existem em planos oorrttooggoonnaaiiss aos respectivos eixos de rotação. Para
efectuar uma rotação, há que desenhar os arcos de rotação dos pontos rodados, o que apenas se pode efectuar se aqueles se projectarem
em verdadeira grandeza. Ora, para que os arcos de rotação se projectem em verdadeira grandeza, têm de estar contidos em plano parale-
los aos planos de projecção – planos horizontais (de nível) ou planos frontais (de frente). Se os arcos estão contidos em planos frontais (de
frente), e uma vez que os planos que contêm os arcos de rotação são ortogonais ao eixo de rotação, o eixo da rotação tem de ser uma rec-
ta de topo (projectante frontal). Se, por outro lado, os arcos estão contidos em planos horizontais (de nível), e atendendo mais uma vez que
os planos que contêm os arcos de rotação são ortogonais ao eixo de rotação, o eixo da rotação tem de ser uma recta vertical (projectante
horizontal). Assim, só se estudam as rotações em que os respectivos eixos de rotação são rectas projectantes.

44. 44
SOLUÇÕES
149.
Em primeiro lugar desenharam-se as projecções do segmento [MMNN], em função dos da-
dos. A recta rr é a recta suporte do segmento – rr é paralela ao β2/4, pelo que as suas projec-
ções são paralelas entre si. O ponto NN é o ponto da recta rr que tem 6 cm de afastamento.
Em seguida, teve-se em conta que uma recta fronto-horizontal é simultaneamente um caso
particular das rectas frontais (de frente) e um caso particular das rectas horizontais (de ní-
vel). Assim, em primeiro lugar há que transformar o segmento [MMNN] num segmento de rec-
ta frontal (de frente) ou num segmento de recta horizontal (de nível). Optou-se pela primeira
hipótese. Assim, começou-se por transformar [MMNN] num segmento frontal (de frente). São
os afastamentos que se alteram (de forma a ficarem todos iguais), pelo que a rotação se
processa em planos horizontais (de nível), pois mantêm-se as cotas – o eixo é uma recta
vertical, qualquer, cujas projecções se desenharam imediatamente (recta ee). Note que se
localizou o eixo ee, de forma a que NN seja o ponto a rodar. Note que se omitiu a representa-
ção do centro da rotação de NN (o ponto OO, o ponto de intersecção de ee com o plano hori-
zontal que contém NN), bem como a representação do plano horizontal (de nível) no qual
existe o arco da rotação de NN – o segmento [OONN] (recorde que se omitiu a identificação do
ponto OO) é simultaneamente perpendicular a [MMNN] e a ee. O ponto NN rodou até a recta
suporte de [MM11NN11] ficar paralela ao eixo XX (o ponto NN’’ é o ponto NN rodado e [OO11NN’’11] é per-
pendicular ao eixo XX). O ponto NN manteve a sua cota, tal como MM. Note que se omitiu a
representação dos planos horizontais (de nível) que contêm os arcos da rotação de MM e NN,
apesar de ser ter recorrido a eles (através das paralelas ao eixo XX que passam por MM22 e
NN22). MM11 rodou até encontrar a recta suporte de [MM’’11NN’’11] (que é paralela ao eixo XX e passa
por NN’’11). [MM’’NN’’] é o segmento [MMNN] rodado e é frontal (de frente). Uma recta fronto-horizontal é uma recta frontal (de frente) que é paralela ao
Plano Horizontal de Projecção – assim, para transformar [MM’’NN’’] num segmento de recta fronto-horizontal, são as cotas que se alteram – a rota-
ção do segmento processa-se num plano frontal (de frente), pelo que na rotação seguinte o eixo é de topo (o eixo ee’’ escolheu-se criteriosa-
mente, de forma a ser MM’’ o ponto a rodar). O centro da rotação de MM’’ é QQ (cuja representação se omitiu) – [QQMM’’] é simultaneamente
perpendicular a [MM’’NN’’] e a ee’’. O ponto MM’’ rodou até a recta suporte de [MM’’22NN’’22] ficar paralela ao eixo XX (o ponto MM’’’’ é o ponto MM’’ rodado e
[QQ22MM’’’’22] é perpendicular ao eixo XX – recorde que se omitiu a identificação do ponto QQ). O ponto MM’’ manteve o seu afastamento, tal como NN’’
(note que o plano frontal que contém o arco da rotação de MM’’ é o mesmo que contém o arco da rotação de NN’’ – é o plano frontal que contém o
segmento [MM’’NN’’]). NN’’22 rodou até encontrar a recta suporte de [MM’’’’22NN’’’’22] (que é paralela ao eixo XX e passa por NN’’’’22). [MM’’’’NN’’’’] é [MM’’NN’’] rodado. Na
sua nova posição, [MMNN] é fronto-horizontal e a sua V.G. é MMෆ’’ෆ’’ෆ22ෆNNෆ’’ෆ22ෆ = MMෆ’’ෆ’’ෆ11ෆNNෆ’’ෆ11ෆ.
148.
Em primeiro lugar desenharam-se as projecções do segmento [AABB], em função dos da-
dos. Em seguida, teve-se em conta que uma recta vertical é um caso particular das rectas
frontais (de frente). Assim, começou-se por transformar [AABB] num segmento frontal (de
frente). São os afastamentos que se alteram (de forma a ficarem todos iguais), pelo que a
rotação se processa em planos horizontais (de nível), pois mantêm-se as cotas – o eixo é
uma recta vertical, qualquer, cujas projecções se desenharam imediatamente (recta ee).
Note que se localizou o eixo ee, de forma a que BB seja o ponto a rodar, mas o eixo poderia
ter outra localização qualquer (seria necessário, nesse caso, determinar o ponto que per-
mitiria rodar o segmento). Note que se omitiu a representação do centro da rotação de BB
(o ponto OO, o ponto de intersecção de ee com o plano horizontal que contém BB), bem
como a representação do plano horizontal (de nível) no qual existe o arco da rotação de BB
– o segmento [OOBB] (recorde que se omitiu a identificação do ponto OO) é simultaneamente
perpendicular a [AABB] e a ee. O ponto BB rodou até a recta suporte de [AA11BB11] ficar paralela ao
eixo XX (o ponto BB’’ é o ponto BB rodado e [OO11BB’’11] é perpendicular ao eixo XX). O ponto BB
manteve a sua cota, tal como AA. Note que se omitiu a representação dos planos horizon-
tais (de nível) que contêm os arcos da rotação de AA e BB, apesar de se ter recorrido a eles
(através das paralelas ao eixo XX que passam por AA22 e BB22). AA11 rodou até encontrar a recta
suporte de [AA’’11BB’’11] (que é paralela ao eixo XX e passa por BB’’11). [AA’’BB’’] é o segmento [AABB]
rodado e é frontal (de frente). Uma recta vertical é uma recta frontal (de frente) que é orto-
gonal ao Plano Horizontal de Projecção. Assim, para transformar [AA’’BB’’] num segmento de
recta vertical, são as cotas que se alteram – a rotação do segmento processa-se num plano frontal (de frente), pelo que na rotação seguinte o
eixo é de topo (o eixo ee’’ escolheu-se criteriosamente, de forma a ser AA’’ o ponto a rodar). O centro da rotação de AA’’ é QQ (cuja representação se
omitiu) – [QQAA’’] é simultaneamente perpendicular a [AA’’BB’’] e a ee’’. O ponto AA’’ rodou até a recta suporte de [AA’’22BB’’22] ficar perpendicular ao eixo XX
(o ponto AA’’’’ é o ponto AA’’ rodado e [QQ22AA’’’’22] é paralelo ao eixo XX – recorde que se omitiu a identificação do ponto QQ). O ponto AA’’ manteve o seu
afastamento, tal como BB’’ (note que o plano frontal que contém o arco da rotação de AA’’ é o mesmo que contém o arco da rotação de BB’’ – é
o plano frontal que contém o segmento [AA’’BB’’]). BB’’22 rodou até encontrar a recta suporte de [AA’’’’22BB’’’’22] (que é perpendicular ao eixo XX e passa por
AA’’’’22). [AA’’’’BB’’’’] é [AA’’BB’’] rodado. Na sua nova posição, [AABB] é vertical e a sua V.G. é AAෆ’’ෆ’’ෆ22ෆBBෆ’’ෆ’’ෆ22ෆ.

45. 150.
Em primeiro lugar desenharam-se as projecções da recta rr, em função dos dados – a
recta rr é paralela ao β1/3, pelo que as suas projecções fazem, com o eixo XX, ângulos
iguais e com o mesmo sentido de abertura. Em seguida, teve-se em conta que uma
recta de topo é um caso particular das rectas horizontais (de nível). Assim, começou-se
por transformar a recta rr numa recta horizontal (de nível). São as cotas que se alteram
(de forma a ficarem todas iguais), pelo que a rotação se processa em planos frontais
(de frente), pois mantêm-se os afastamentos – o eixo é uma recta de topo, qualquer,
cujas projecções se desenharam imediatamente (recta ee). Note que se localizou o eixo
ee de forma a que AA seja o ponto a rodar. Note que se omitiu a representação do centro
da rotação de AA (o ponto OO, o ponto de intersecção de ee com o plano frontal que con-
tém AA), bem como a representação do plano frontal (de frente) no qual existe o arco da
rotação de AA – o segmento [OOAA] (recorde que se omitiu a identificação do ponto OO) é
simultaneamente perpendicular à recta rr e ao eixo ee. O ponto AA rodou até rr22 ficar para-
lela ao eixo XX (o ponto AA’’ é o ponto AA rodado e [OO22AA’’22] é perpendicular ao eixo XX).
O ponto AA manteve o seu afastamento (tal como todos os pontos da recta rr). Note que
apesar de se ter omitido a representação do plano frontal (de frente) que contém o arco da rotação de AA, se recorreu a ele (através da para-
lela ao eixo XX que passa por AA11). Já temos a projecção frontal da recta rr rodada – rr’’22 (rr’’ é a recta rr rodada). Para definirmos uma recta ne-
cessitamos de dois pontos ou de um ponto e uma direcção. Assim, é necessário o recurso a um outro ponto da recta rr, para definirmos rr’’11.
O ponto escolhido foi o seu traço frontal – FF. FF22 rodou até encontrar rr’’22, mantendo-se o afastamento de FF (que é nulo) – rr’’11 fica definida por
AA’’11 e FF’’11. A recta rr’’ é a recta rr rodada e é horizontal (de nível), na sua nova posição. Uma recta de topo é uma recta horizontal (de nível) que
é ortogonal ao Plano Frontal de Projecção – assim, para transformar rr’’ numa recta de topo são os afastamentos que se alteram, mantendo-
-se as cotas. A rotação seguinte processa-se, assim, num plano horizontal (de nível) e o eixo é a recta ee’’, que é vertical (note que se esco-
lheu ee’’ criteriosamente, de forma a AA’’ ser o ponto a rodar). O centro da rotação de AA’’ é QQ (cuja representação se omitiu) – [QQAA’’] é
simultaneamente perpendicular a rr’’ e a ee’’. O ponto AA’’ rodou até a recta rr’’11 ficar perpendicular ao eixo XX – o ponto AA’’’’ é o ponto AA’’ rodado e
[QQ11AA’’’’11] é paralelo ao eixo XX. AA’’ manteve a sua cota na rotação efectuada. A recta rr’’’’ é de topo e passa por AA’’’’, não tendo sido necessária a
rotação de FF’’ para a determinação das projecções da recta na sua nova posição. A projecção frontal da recta é, agora, um ponto – a recta rr’’’’
é a recta rr’’ rodada e é de topo (está definida por um ponto – AA’’’’ – e uma direcção – é de topo).
45
SOLUÇÕES
151.
Em primeiro lugar desenharam-se as projecções da recta ss em função dos dados – a recta ss é para-
lela ao β2/4, pelo que as suas projecções são paralelas entre si. Em seguida, teve-se em conta que
uma recta fronto-horizontal é simultaneamente um caso particular das rectas frontais (de frente) e um
caso particular das rectas horizontais (de nível). Assim, em primeiro lugar há que transformar a recta
ss numa recta frontal (de frente) ou numa recta horizontal (de nível). Optou-se pela primeira hipótese.
Assim, começou-se por transformar a recta ss numa recta frontal (de frente). São os afastamentos
que se alteram (de forma a ficarem todos iguais), pelo que a rotação se processa em planos horizon-
tais (de nível), pois mantêm-se as cotas – o eixo é uma recta vertical, qualquer, cujas projecções se
desenharam imediatamente (recta ee). Note que se localizou o eixo ee de forma a que AA seja o ponto a
rodar. Note que se omitiu a representação do centro da rotação de AA (o ponto OO, o ponto de inter-
secção de ee com o plano horizontal que contém AA), bem como a representação do plano horizontal
(de nível) no qual existe o arco da rotação de AA – o segmento [OOAA] (recorde que se omitiu a identifi-
cação do ponto OO) é simultaneamente perpendicular à recta ss e ao eixo ee. O ponto AA rodou até ss11
ficar paralela ao eixo XX (o ponto AA’’ é o ponto AA rodado e [OO11AA’’11] é perpendicular ao eixo XX). O ponto
AA manteve a sua cota (tal como todos os pontos da recta ss). Note que apesar de se ter omitido a
representação do plano horizontal (de nível) que contém o arco da rotação de AA, se recorreu a ele (através da paralela ao eixo XX que passa
por AA22). Já temos a projecção horizontal da recta ss rodada – ss’’11 (ss’’ é a recta ss rodada). Para definirmos uma recta necessitamos de dois pontos
ou de um ponto e uma direcção. Assim, é necessário o recurso a um outro ponto da recta ss, para definirmos ss’’22. O ponto escolhido foi um
ponto BB, qualquer. BB11 rodou até encontrar ss’’11, mantendo-se a cota de BB – ss’’22 fica definida por AA’’22 e BB’’22. A recta ss’’ é a recta ss rodada e é frontal
(de frente), na sua nova posição. Uma recta vertical é uma recta frontal (de frente) que é ortogonal ao Plano Horizontal de Projecção – assim,
para transformar ss’’ numa recta vertical são as cotas que se alteram, mantendo-se os afastamentos. A rotação seguinte processa-se, assim, num
plano frontal (de frente) e o eixo é a recta ee’’, que é de topo (note que se escolheu ee’’ criteriosamente, de forma a AA’’ ser o ponto a rodar). O centro
da rotação de AA’’ é QQ (cuja representação se omitiu) – [QQAA’’] é simultaneamente perpendicular a ss’’ e a ee’’. O ponto AA’’ rodou até a recta ss’’22 ficar
paralela ao eixo XX – o ponto AA’’’’ é o ponto AA’’ rodado e [QQ22AA’’’’22] é perpendicular ao eixo XX. AA’’ manteve o seu afastamento na rotação efectuada.
A recta ss’’’’ é fronto-horizontal e passa por AA’’’’, não tendo sido necessária a rotação de BB’’ para a determinação das projecções da recta na sua
nova posição. A projecção horizontal da recta ss’’’’ está coincidente com ss’’11, pois a rotação processou-se no plano frontal (de frente) que contém a
recta ss’’ – a recta ss’’’’ está definida por um ponto (AA’’’’) e por uma direcção (é fronto-horizontal).
152.
Em primeiro lugar representou-se a recta vv, pelas suas projecções, em função dos dados. Em seguida, para transformar a recta vv numa recta oblí-
qua, há que efectuar os raciocínios expostos no relatório do exercício 114488 por ordem inversa. Assim, uma vez que uma recta vertical é um caso
particular das rectas frontais (de frente), em primeiro lugar há que transformar a recta vv numa recta frontal (de frente) – uma recta frontal (de frente)
é paralela ao Plano Frontal de Projecção e oblíqua ao Plano Horizontal de Projecção. Assim, começou-se por transformar a recta vv numa recta
frontal (de frente). São as cotas que se alteram – note que para transformar uma recta vertical numa recta frontal (de frente), os afastamentos
(Continua na página seguinte)

46. 46
SOLUÇÕES
153.
Em primeiro lugar representou-se a recta pp, pelas suas projecções, em função dos dados –
a recta pp está definida por dois pontos (AA e BB). Em seguida, teve-se em conta que uma rec-
ta de topo é um caso particular das rectas horizontais (de nível). Assim, começou-se por
transformar a recta pp numa recta horizontal (de nível). São as cotas que se alteram (de for-
ma a ficarem todas iguais), pelo que a rotação se processa em planos frontais (de frente),
pois mantêm-se os afastamentos – o eixo é uma recta de topo, qualquer, cujas projecções
se desenharam imediatamente (recta ee). Note que se localizou o eixo ee de forma a que o
ponto AA seja o ponto a rodar. Note que se omitiu a representação do centro da rotação de
AA (o ponto OO, o ponto de intersecção de ee com o plano frontal que contém AA), bem como a
representação do plano frontal (de frente) no qual existe o arco da rotação de AA – o seg-
mento [OOAA] (recorde que se omitiu a identificação do ponto OO) é simultaneamente per-
pendicular à recta pp e ao eixo ee. O ponto AA rodou até pp22 ficar paralela ao eixo XX (o ponto AA’’
é o ponto AA rodado e [OO22AA’’22] é perpendicular ao eixo XX). O ponto AA manteve o seu afasta-
mento (tal como todos os pontos da recta pp). Note que apesar de se ter omitido a repre-
sentação do plano frontal (de frente) que contém o arco da rotação de AA, se recorreu a ele
(através da paralela ao eixo XX que passa por AA11). Já temos a projecção frontal da recta pp
rodada – pp’’22 (pp’’ é a recta pp rodada). Para definirmos uma recta necessitamos de dois pon-
tos ou de um ponto e uma direcção. Assim, é necessário o recurso a um outro ponto da
recta pp, para definirmos pp’’11 – o ponto BB. BB22 rodou até encontrar pp’’22, mantendo-se o afasta-
mento de BB – pp’’11 fica definida por AA’’11 e BB’’11. A recta pp’’ é a recta pp rodada e é horizontal (de
nível), na sua nova posição. Uma recta de topo é uma recta horizontal (de nível) que é orto-
gonal ao Plano Frontal de Projecção – assim, para transformar pp’’ numa recta de topo são
os afastamentos que se alteram, mantendo-se as cotas. A rotação seguinte processa-se,
assim, num plano horizontal (de nível) e o eixo é a recta ee’’, que é vertical (note que se loca-
lizou ee’’ criteriosamente, de forma a que o ponto BB’’ seja o ponto a rodar). O centro da rotação de BB’’ é QQ (cuja representação se omitiu) –
[QQBB’’] é simultaneamente perpendicular a pp’’ e a ee’’. O ponto BB’’ rodou até a recta pp’’11 ficar perpendicular ao eixo XX – o ponto BB’’’’ é o ponto BB’’
rodado e [QQ11BB’’’’11] é paralelo ao eixo XX. BB’’ manteve a sua cota na rotação efectuada. A recta pp’’’’ é de topo e passa por BB’’’’, não sendo neces-
sária a rotação de AA’’ para a determinação das projecções da recta na sua nova posição. No entanto, optou-se por efectuar a rotação de AA’’ –
AA’’11 rodou até encontrar pp’’’’11, sendo que manteve a sua cota, pelo que se tem AA’’’’11 ≡ BB’’’’11. A projecção frontal da recta é, agora, um ponto – a
recta pp’’’’ é a recta pp’’ rodada e é de topo.
mantêm-se, pois ambas as rectas são paralelas ao Plano Frontal de Projecção. A rotação processa-
-se, assim, em planos frontais (de frente) – a rotação processa-se no plano frontal (de frente) que con-
tém a recta e o eixo é uma recta vertical qualquer, cujas projecções se desenharam imediatamente
(recta ee). O ponto AA é o ponto que nos permite rodar a recta – o ponto AA é o ponto da recta tal que o
segmento [OOAA] (sendo OO o centro do arco da rotação de AA) é simultaneamente perpendicular à recta
vv e ao eixo ee. Note que se omitiu a representação do ponto OO (que é o ponto de intersecção de ee com
o plano horizontal que contém AA), bem como a representação do próprio plano horizontal (de nível)
no qual existe o arco da rotação de AA. O ponto AA rodou até vv22 ficar oblíqua ao eixo XX (o ponto AA’’ é o
ponto AA rodado e [OO11AA’’11] é oblíquo ao eixo XX). Note que a obliquidade da recta vv’’22 em relação ao eixo
XX pode ser uma qualquer. Ao longo da rotação, o ponto AA manteve o seu afastamento (tal como todos
os pontos da recta vv). Note que apesar de se ter omitido a representação do plano horizontal (de ní-
vel) que contém o arco da rotação de AA, se recorreu a ele (através da paralela ao eixo XX que passa
por AA22). Já temos a projecção frontal da recta vv rodada – vv’’22 (vv’’ é a recta vv rodada). Por outro lado,
uma vez que a recta vv’’, após a rotação, é uma recta frontal (de frente), não é necessário qualquer ou-
tro ponto da recta, pois é possível desenhar imediatamente vv’’11 (vv’’11 passa por AA’’11 e é paralela ao eixo
XX, pois a recta vv’’ é paralela ao Plano Frontal de Projecção). No entanto, com vista à determinação das
projecções da recta após a segunda rotação, optou-se por rodar um outro ponto da recta – o ponto BB.
BB22 rodou até encontrar vv’’22, mantendo-se o afastamento de BB – BB’’11 situa-se sobre vv’’11. A recta vv’’ é a rec-
ta vv rodada e é frontal (de frente), na sua nova posição. Em seguida, para transfomar a recta vv’’ numa
recta oblíqua (que é oblíqua ao Plano Frontal de Projecção), as alterações processam-se ao nível dos
afastamentos (mantendo--se as cotas) – a rotação processa-se, assim, em planos horizontais (de ní-
vel), pelo que o segundo eixo de rotação terá de ser uma recta vertical. Desenharam-se as projecções
de um eixo vertical ee’’, qualquer – note que se localizou criteriosamente o eixo ee’’ de forma a que o
ponto BB’’ seja o ponto a rodar. O centro da rotação de BB’’ é QQ (cuja representação se omitiu) – [QQBB’’] é
simultaneamente perpendicular a vv’’ e a ee’’. O ponto BB’’ rodou até a recta vv’’11 fazer, com o eixo XX, um ângulo de 45o (a.d.) – o ângulo pretendido.
Note que, para que tal se verifique, o segmento [QQBB’’] tem de fazer um ângulo de 45o (a.e.) com o eixo XX em projecção horizontal – o ponto BB’’’’ é o
ponto BB’’ rodado e [QQ11BB’’’’11] faz, com o eixo XX, um ângulo de 45o (a.e.). A projecção horizontal da recta vv’’’’ (a recta vv’’ rodada) passa por BB’’’’11 e é per-
pendicular a [QQ11BB’’’’11], pelo que faz, com o eixo XX, um ângulo de 45o (a.d.) – o ângulo pretendido. BB’’ manteve a sua cota na rotação efectuada. A
recta vv’’’’ é oblíqua e passa por BB’’’’, mas para definir uma recta são necessários dois pontos ou um ponto e uma direcção. É necessário, então, ro-
dar um outro ponto da recta – o ponto AA’’. AA’’ rodou em torno de ee’’ até AA’’11 se situar sobre vv’’’’11, onde se situa AA’’’’11. O ponto AA, ao longo da sua rota-
ção, manteve a sua cota, o que nos permitiu determinar AA’’’’22 (AA’’’’ é o ponto AA rodado). A projecção frontal da recta vv’’ na sua nova posição (vv’’’’22) está
definida por AA’’’’22 e BB’’’’22 – a recta vv é, agora, uma recta oblíqua cuja projecção horizontal faz um ângulo de 45o (a.d.) com o eixo XX.

47. 47
SOLUÇÕES
Em primeiro lugar representou-se a recta pp, pelas suas projecções, em função
dos dados – a recta pp está definida por dois pontos (AA e BB). Uma recta fronto-hori-
zontal é simultaneamente um caso particular das rectas frontais (de frente) e das
rectas horizontais (de nível), pelo que, em primeiro lugar, há que transformar a
recta pp numa recta frontal (de frente) ou numa recta horizontal (de nível). Optou-se
pela primeira hipótese. Assim, começou-se por transformar a recta pp numa recta
frontal (de frente). São os afastamentos que se alteram (de forma a ficarem todos
iguais), pelo que a rotação se processa em planos horizontais (de nível), pois
mantêm-se as cotas – o eixo é uma recta vertical, qualquer, cujas projecções se
desenharam imediatamente (recta ee). Note que se localizou o eixo ee de forma a
que o ponto BB seja o ponto a rodar. Note que se omitiu a representação do centro
da rotação de BB (o ponto OO, o ponto de intersecção de ee com o plano horizontal
que contém AA), bem como a representação do plano horizontal (de nível) no qual
existe o arco da rotação de BB – o segmento [OOBB] (recorde que se omitiu a identifi-
cação do ponto OO) é simultaneamente perpendicular à recta pp e ao eixo ee. O pon-
to BB rodou até pp11 ficar paralela ao eixo XX (o ponto BB’’ é o ponto BB rodado e [OO11BB’’11]
é perpendicular ao eixo XX). O ponto BB manteve a sua cota (tal como todos os
pontos da recta pp). Note que apesar de se ter omitido a representação do plano
horizontal (de nível) que contém o arco da rotação de BB, se recorreu a ele (através
da paralela ao eixo XX que passa por BB22). Já temos a projecção horizontal da recta
pp rodada – pp’’11 (pp’’ é a recta pp rodada). Para definirmos uma recta necessitamos de
dois pontos ou de um ponto e uma direcção. Assim, é necessário o recurso a um outro ponto da recta pp, para definirmos pp’’22 – o ponto AA. AA11 ro-
dou até encontrar pp’’11, mantendo-se a cota de AA – pp’’22 fica definida por AA’’22 e BB’’22. A recta pp’’ é a recta pp rodada e é frontal (de frente), na sua nova
posição. Uma recta fronto-horizontal é uma recta frontal (de frente) que é paralela ao Plano Horizontal de Projecção – assim, para transformar pp’’
numa recta fronto-horizontal são as cotas que se alteram, mantendo-se os afastamentos. A rotação seguinte processa-se, assim, num plano frontal
(de frente) e o eixo é a recta ee’’, que é de topo (note que se escolheu ee’’ criteriosamente, de forma a que o ponto BB’’ seja o ponto a rodar). O cen-
tro da rotação de BB’’ é QQ (cuja representação se omitiu) – [QQBB’’] é simultaneamente perpendicular a pp’’ e a ee’’. O ponto BB’’ rodou até a recta pp’’22 ficar
paralela ao eixo XX – o ponto BB’’’’ é o ponto BB’’ rodado e [QQ22BB’’’’22] é perpendicular ao eixo XX. BB’’ manteve o seu afastamento na rotação efectuada.
A recta pp’’’’ é fronto-horizontal e passa por BB’’’’, não sendo necessária a rotação de AA’’ para a determinação das projecções da recta na sua nova
posição. No entanto, optou-se por efectuar a rotação de AA’’ – AA’’22 rodou até encontrar pp’’’’22, sendo que manteve o seu afastamento. A projecção
horizontal da recta pp’’’’ está coincidente com pp’’11, pois a rotação processou-se no plano frontal (de frente) que contém a recta pp’’ – a recta pp’’’’ é
fronto-horizontal.
155.
Em primeiro lugar representaram-se os pontos AA, BB e CC, pelas
respectivas projecções, e desenharam-se as projecções do
triângulo [AABBCC]. Para determinar os traços do plano definido
pelos três pontos conduziu-se, por AA e CC, uma recta frontal (de
frente), que não se identificou (para evitar a complexidade da
resolução gráfica final), e determinou-se o seu traço horizontal.
Em seguida, por AA e BB conduziu-se uma recta horizontal (de
nível), que pelos mesmos motivos também não se identificou,
e determinou-se o seu traço frontal. O traço frontal do plano, ffα,
passa pelo traço frontal da recta AABB e é paralelo à recta AACC. O
traço horizontal do plano, hhα, passa pelo traço horizontal da
recta AACC, é concorrente com ffα no eixo XX e é paralelo à recta
AABB. Em seguida, para transformar o plano α num plano frontal
(de frente), teve-se em conta que um plano frontal (de frente) é
um caso particular dos planos projectantes horizontais. Nesse
sentido, começou-se por transformar o plano α num plano pro-
jectante horizontal (vertical) – as rectas frontais (de frente) de
um plano vertical são verticais, pelo que ffα tem de ficar perpen-
dicular ao eixo XX (vertical). Os afastamentos mantêm-se, pelo
que a rotação se processa em planos frontais (de frente) – o
eixo da rotação, ee, é uma recta de topo qualquer (por econo-
mia de traçados optou-se por conduzir o eixo de rotação ee
pelo ponto AA). O ponto PP é o ponto de ffα que nos permite ro-
dar o plano. O segmento [OOPP] é simultaneamente perpendicu-
lar a ffα e a ee – OO é o ponto de intersecção de ee com o plano
frontal (de frente) que contém o arco da rotação de PP (o próprio Plano Frontal de Projecção) e é o centro da rotação de PP, que não se identificou.
O ponto PP rodou até [OOPP] (recorde que não se identificou o ponto OO, que é o traço frontal de ee) ficar paralelo ao eixo XX – ff’’α que é perpendicular
a [OOPP], fica perpendicular ao eixo XX e passa por PP’’ (PP’’ é o ponto PP rodado). Note que não se determinaram PP11 e PP’’11, as projecções horizontais
de PP e PP’’ que se situam no eixo XX, por não serem necessárias. AA’’ ≡ AA, pois AA é um ponto do eixo da rotação (roda sobre si próprio, pois é fixo). O
novo traço horizontal de α, hh’’α, é concorrente com ff’’α no eixo XX e contém AA’’11, pois α, após a rotação, é projectante horizontal (é vertical).
(Continua na página seguinte)
154.

48. 48
SOLUÇÕES
157.
a) Em primeiro lugar representaram-se os pontos PP e QQ, pelas respectivas projecções. Em seguida, desenharam-se as projecções de uma
recta rr, a recta que passa por PP e QQ (que não se identificou) e determinaram-se os seus traços – PP é, imediatamente, o traço frontal da
recta (note que não se identificou o traço horizontal da recta). Pelos traços da recta PPQQ conduziram-se os traços homónimos do plano ρ.
Os dados do exercício permitiram-nos, ainda, determinar a projecção frontal de RR. Por RR conduziu-se uma recta ss (que também não se
identificou), paralela à recta PPQQ e pertencente ao plano ρ, o que nos permitiu determinar a projecção horizontal de RR e, em seguida, de-
senhar as projecções do triângulo [PPQQRR].
b) Para transformar o plano ρ num plano frontal (de frente), há que ter em conta que um plano frontal (de frente) é um caso particular dos
planos projectantes horizontais, o que consiste nos procedimentos efectuados no exercício 115555, pelo que se aconselha a leitura do
Os pontos BB e CC mantêm os afastamentos na sua rotação, o que nos permite determinar BB’’11 e CC’’11 sobre hh’’α, pela respectiva translação ao longo
dos planos frontais (de frente) que contêm os respectivos arcos de rotação. BB22 e CC22 rodaram até às respectivas linhas de chamada (a amplitude
da rotação de BB22 e CC22 é igual à da rotação de PP22). Um plano frontal (de frente) é um plano projectante horizontal que é paralelo ao Plano Frontal
de Projecção. Assim, na rotação seguinte, com vista a transformar o plano α num plano paralelo ao Plano Frontal de Projecção, as alterações
processam-se ao nível dos afastamentos – a rotação processa-se, pois, em planos horizontais (de nível), pelo que o eixo é vertical. O segundo
eixo de rotação, ee’’, escolheu-se por forma a ser AA’’ o ponto a rodar – [QQAA’’] é perpendicular a α e a ee’’ (QQ é o centro da rotação de AA’’ e não se
identificou – QQ é o ponto de intersecção do eixo ee’’ com o plano horizontal que contém o arco da rotação de AA’’). AA’’ rodou até [QQAA’’’’] ficar perpen-
dicular ao eixo XX – hh’’α, na sua nova posição (hh’’’’α) ficou paralelo ao eixo XX. O plano α é, agora, frontal (de frente) e não tem traço frontal. BB’’11 e CC’’11
rodaram até (hh’’’’α), obtendo-se BB’’’’11 e CC’’’’11. BB’’22 e CC’’22 mantiveram as suas cotas, o que nos permitiu determinar BB’’’’22 e CC’’’’22 nas linhas de chamada
de BB’’’’11 e CC’’’’11, respectivamente. O plano α, na sua nova posição, é um plano frontal (de frente), pelo que a V.G. do triângulo [AABBCC] está no triân-
gulo [AA’’’’22BB’’’’22CC’’’’22].
156.
Em primeiro lugar representaram-se os pontos AA, BB e
CC, pelas respectivas projecções, e desenharam-se as
projecções do triângulo [AABBCC]. Os traços do plano
determinaram-se conforme exposto no relatório do
exercício anterior. Em seguida, para transformar o
plano α num plano horizontal (de nível), teve-se em
conta que um plano horizontal (de nível) é um caso
particular dos planos projectantes frontais. Nesse
sentido, começou-se por transformar o plano α num
plano projectante frontal (de topo) – as rectas hori-
zontais (de nível) de um plano de topo são de topo,
pelo que hhα tem de ficar perpendicular ao eixo XX (de
topo). As cotas mantêm-se, pelo que a rotação se
processa em planos horizontais (de nível) – o eixo da
rotação, ee, é uma recta vertical qualquer (por econo-
mia de traçados optou-se por conduzir o eixo de ro-
tação ee pelo ponto AA). O ponto PP é o ponto de hhα
que nos permite rodar o plano. O segmento [OOPP] é
simultaneamente perpendicular a hhα e a ee – OO é o
ponto de intersecção de ee com o plano horizontal (de
nível) que contém o arco da rotação de PP (o próprio
Plano Horizontal de Projecção) e é o centro da rotação
de PP, que não se identificou. O ponto PP rodou até
[OOPP] (recorde que não se identificou o ponto OO, que é
o traço horizontal de ee) ficar paralelo ao eixo XX – hh’’α,
que é perpendicular a [OOPP], fica perpendicular ao eixo
XX e passa por PP’’ (PP’’ é o ponto PP rodado). Note que
não se determinaram PP22 e PP’’22, as projecções frontais de PP e PP’’ que se situam no eixo XX, por não serem necessárias. AA ’’≡ AA, pois AA é um ponto
do eixo da rotação (roda sobre si próprio, pois é fixo). O novo traço frontal de α, ff’’α, é concorrente com hh’’α no eixo XX e contém AA’’22, pois α,
após a rotação, é projectante frontal (é de topo). Os pontos BB e CC mantêm as cotas na sua rotação, o que nos permite determinar BB’’22 e CC’’22
sobre ff’’α, pela respectiva translação ao longo dos planos horizontais (de nível) que contêm os respectivos arcos de rotação. BB11 e CC11 roda-
ram até às respectivas linhas de chamada (a amplitude da rotação de BB11 e CC11 é igual à da rotação de PP11). Um plano horizontal (de nível) é
um plano projectante frontal que é paralelo ao Plano Horizontal de Projecção. Assim, na rotação seguinte, com vista a transformar o plano α
num plano paralelo ao Plano Horizontal de Projecção, as alterações processam-se ao nível das cotas – a rotação processa-se, pois, em pla-
nos frontais (de frente), pelo que o eixo é de topo. O segundo eixo de rotação, ee’’, escolheu-se por forma a ser CC’’ o ponto a rodar – [QQCC’’] é
perpendicular a α e a ee’’ (QQ é o centro da rotação de CC’’ e não se identificou – QQ é o ponto de intersecção do eixo ee’’ com o plano frontal que
contém o arco da rotação de CC’’). CC’’ rodou até [QQCC’’’’] ficar perpendicular ao eixo XX – ff’’α, na sua nova posição (ff’’’’α) ficou paralelo ao eixo XX.
O plano α é, agora, horizontal (de nível) e não tem traço horizontal. AA’’22 e BB’’22 rodaram até (ff’’’’α), obtendo-se AA’’’’22 e BB’’’’22. AA’’22 e BB’’22 mantiveram
os seus afastamentos, o que nos permitiu determinar AA’’’’11 e BB’’’’11 nas linhas de chamada de AA’’’’22 e BB’’’’22, respectivamente. O plano α, na sua
nova posição, é um plano horizontal (de nível), pelo que a V.G. do triângulo [AABBCC] está no triângulo [AA’’’’11BB’’’’11CC’’’’11].
(Continua na página seguinte)

49. 49
SOLUÇÕES
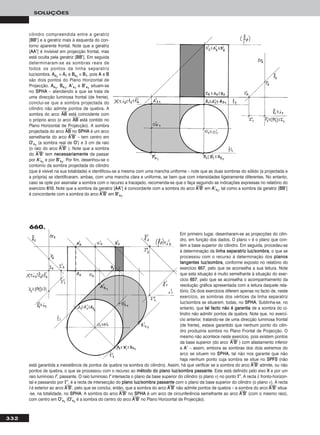
Em primeiro lugar representaram-se os pontos PP e QQ,
pelas respectivas projecções. Em seguida, determi-
naram-se os traços do plano ρ e as projecções do
ponto RR e do triângulo (ver alínea aa)) do relatório do
exercício anterior). Em seguida, para transformar o
plano ρ num plano horizontal (de nível), há que ter em
conta que um plano horizontal (de nível) é um caso
particular dos planos projectantes frontais, o que con-
siste nos procedimentos efectuados no exercício 115566,
pelo que se aconselha a leitura do respectivo relató-
rio. Note que o facto de se tratar de um plano de ram-
pa não altera em nada os procedimentos expostos
naquele relatório. O primeiro eixo de rotação é a recta
vertical ee, que contém o ponto PP (por uma questão
de economia de traçados) – PP’’ ≡ PP, pois PP situa-se no
eixo de rotação (roda sobre si próprio). O ponto AA é o ponto de hhρ que nos permite rodar hhρ. O segundo eixo de rotação é a recta de topo ee’’, que
se localizou de forma a ser o ponto QQ’’ o ponto a rodar. Após a segunda rotação, o plano ρ é um plano horizontal (de nível), pelo que a V.G. do
triângulo [PPQQRR] está do triângulo [PP’’’’11QQ’’’’11RR’’’’11].
158.
159.
Em primeiro lugar representou-se o plano ρ (cujos traços
estão coincidentes no eixo XX), que está definido pelo eixo XX e
pelas projecções do ponto PP. Os dados do enunciado permi-
tem-nos, ainda, determinar QQ11, a projecção horizontal de QQ, e
RR22 a projecção frontal de RR. Em seguida recorreu-se a uma
recta rr, passante, tal que rr11 passa por PP11 e QQ11 – após determi-
nar rr22 (definida pelo seu ponto de concorrência com o eixo XX e
por PP22), determinou-se QQ22, sobre rr22. A recta ss é a recta a que
se recorreu para determinar a projecção horizontal de RR (RR11) e
determinou-se a partir da sua projecção frontal, ss22, por raciocí-
nios semelhantes aos expostos para a recta rr. A partir das pro-
jecções dos três pontos, desenharam-se as projecções do
triângulo [PPQQRR]. Para transformar o plano ρ num plano frontal
(de frente), há que ter em conta que um plano frontal (de frente)
é um caso particular dos planos projectantes horizontais, o que
consiste nos procedimentos efectuados no exercício 115555, pelo
que se aconselha a leitura do respectivo relatório. Note que o
facto de se tratar de um plano passante não altera em nada os
procedimentos expostos naquele relatório. O primeiro eixo de
rotação é a recta de topo ee, que contém o ponto RR (por uma
questão de economia de traçados) – RR’’ ≡ RR, pois RR situa-se no eixo de rotação (roda sobre si próprio). O ponto AA, do eixo XX, é o ponto de ffρ que
nos permite rodar ffρ. O segundo eixo de rotação é a recta vertical ee’’, que se localizou de forma a ser o ponto RR’’ o ponto a rodar. Após a segunda
rotação, o plano ρ é um plano frontal (de frente), pelo que a V.G. do triângulo [PPQQRR] está do triângulo [PP’’’’22QQ’’’’22RR’’’’22].
respectivo relatório. Note que o facto de se tratar de um plano de rampa
não altera em nada os procedimentos expostos naquele relatório. O pri-
meiro eixo de rotação é a recta de topo ee, que contém o ponto QQ (por
uma questão de economia de traçados) – QQ’’ ≡ QQ, pois QQ situa-se no
eixo de rotação (roda sobre si próprio). O ponto AA é o ponto de ffρ que
nos permite rodar ffρ. O segundo eixo de rotação é a recta vertical ee’’,
que se localizou de forma a ser o ponto RR’’ o ponto a rodar. Após a se-
gunda rotação, o plano ρ é um plano frontal (de frente), pelo que a V.G.
do triângulo [PPQQRR] está do triângulo [PP’’’’22QQ’’’’22RR’’’’22].

50. 50
SOLUÇÕES
160.
A afirmação é vveerrddaaddeeiirraa. Um rebatimento consiste efectivamente na rroottaaççããoo de um plano em torno de uma das suas rectas – o eixo da
rotação, no caso dos rebatimentos, é complanar com o plano a rodar e chama-se charneira (ou eixo) do rebatimento.
161.
a) Rebatendo o plano para o Plano Horizontal de Projecção, a charneira do rebatimento é o traço horizontal do plano – o arco do rebatimento
existe num plano ortogonal à charneira do rebatimento. Uma vez que o traço horizontal do plano é uma recta horizontal (de nível) do plano,
o aarrccoo ddoo rreebbaattiimmeennttoo desse ponto está, assim, contido num plano vertical que é ortogonal ao traço horizontal do plano e que contém o
ponto. O cceennttrroo ddoo aarrccoo ddoo rreebbaattiimmeennttoo desse ponto, por sua vez, situa-se necessariamente na charneira do rebatimento – uma vez que o
arco do rebatimento existe num plano que contém o ponto e é ortogonal à charneira do rebatimento, o centro do arco do rebatimento é, en-
tão, o ponto de intersecção da charneira do rebatimento com o plano ortogonal à charneira que contém o arco do rebatimento desse ponto.
b) A distância que nos permite rebater o ponto é o rraaiioo ddoo aarrccoo ddoo rreebbaattiimmeennttoo e é a distância do ponto (a rebater) ao centro do arco do seu
rebatimento.
162.
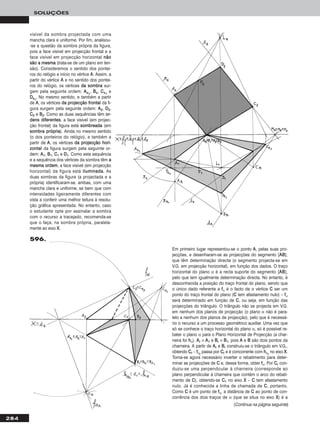
Em primeiro lugar representou-se o plano α, pelos seus traços, e desenharam-se
as projecções do triângulo [AABBCC], contido no plano, em função dos dados. AA e BB
e CC pertencem ao plano α, pois pertencem a rectas do plano – AA pertence a ffα
(que é uma recta frontal do plano com afastamento nulo) e BB e CC pertencem a
uma recta frontal (de frente) do plano com 4 cm de afastamento. Em seguida,
para determinar a V.G. do triângulo, rebateu-se o plano α para o Plano Frontal de
Projecção (a charneira é ffα, que se identificou imediatamente – ffα ≡ ee22 ≡ ffαrr
), con-
forme é expressamente pedido no enunciado. Note que AA é um ponto de ffα, que
é a charneira, pelo que se tem imediatamente AArr ≡ AA22. Rebateu-se hhα rebatendo HH
(o traço horizontal da recta ff, a recta frontal (de frente) a que se recorreu para deter-
minar as projecções dos pontos BB e CC) ao longo de θ, o plano ortogonal a ffα que
contém o arco do rebatimento de HH (o plano θ, o plano ortogonal a ffα que contém
o arco do rebatimento de HH, é um plano de topo que se representou apenas pelo
seu traço frontal, razão pela qual este se assinalou entre parêntesis). O ponto MM é o
ponto de concorrência dos dois traços do plano e é fixo, pois pertence à charneira.
Com centro em MM, transportou-se MMෆ11ෆHHෆ11ෆ para (ffθ), obtendo HHrr – hhαrr
está definido
por HHrr e MMrr. Por HHrr conduziu-se ffrr, paralela a ffαrr
(rectas frontais de um plano são
paralelas entre si e paralelas ao traços frontal do plano, o que se verifica no espa-
ço, em projecções e em rebatimento) – BBrr e CCrr estão sobre ffrr, nas respectivas
perpendiculares a ffαrr
que passam por BB22 e CC22. Note que as perpendiculares a ffα
que passam por BB22 e CC22 correspondem aos traços frontais dos planos ortogonais a ffα (planos de topo) que contêm os arcos do rebatimento de
BB e CC, mas que não se identificaram. Tenha em conta que BB e CC são dois pontos da recta ff pelo que, em rebatimento, BBrr e CCrr são também dois
pontos da recta ffrr (que é a recta ff rebatida). A partir de AArr, BBrr e CCrr, desenhou-se o triângulo [AArrBBrrCCrr], que é a V.G. do triângulo [AABBCC].
163.
Em primeiro lugar representou-se o plano α, pelos seus traços, e desenha-
ram-se as projecções do triângulo [AABBCC], contido no plano, em função dos
dados (ver relatório do exercício anterior). Em seguida, para determinar a
V.G. do triângulo, rebateu-se o plano α para o Plano Horizontal de Projecção
(a charneira é hhα, que se identificou imediatamente – hhα ≡ ee11 ≡ hhαrr
), conforme
é expressamente pedido no enunciado. Rebateu-se ffα rebatendo AA (que é
um ponto de ffα) ao longo do plano ortogonal a hhα que contém o arco do re-
batimento de AA (note que não se identificou o plano que contém o arco do
rebatimento do ponto AA, que é um plano vertical). O ponto MM é o ponto de
concorrência dos dois traços do plano e é fixo, pois pertence à charneira.
Com centro em MM, transportou-se MMෆ22ෆAAෆ22ෆ para a perpendicular à charneira que
passa por AA11 (e que corresponde ao plano ortogonal à charneira que contém
o arco do rebatimento de AA), obtendo AArr – ffαrr
está definido por AArr e MMrr. HH, o
traço horizontal da recta ff (a recta que nos permitiu determinar as projecções
de BB e CC) é um ponto da charneira, pelo que é fixo (roda sobre si próprio) –
tem-se, imediatamente, HH11 ≡ HHrr. Por HHrr conduziu-se ffrr, paralela a ffαrr
(rectas
frontais de um plano são paralelas entre si e paralelas ao traços frontal do
plano, o que se verifica no espaço, em projecções e em rebatimento) – BBrr e
CCrr estão sobre ffrr, nas respectivas perpendiculares a hhαrr
que passam por BB11 e
CC11. Note que as perpendiculares a hhα que passam por BB11 e CC11 correspon-
dem aos traços horizontais dos planos ortogonais a hhα (planos verticais) que
contêm os arcos do rebatimento de BB e CC, mas que não se identificaram.
Tenha em conta que BB e CC são dois pontos da recta ff pelo que, em rebatimento, BBrr e CCrr são também dois pontos da recta ffrr (que é a recta ff
rebatida). A partir de AArr, BBrr e CCrr, desenhou-se o triângulo [AArrBBrrCCrr], que é a V.G. do triângulo [AABBCC].

51. 51
SOLUÇÕES
164.
Em primeiro lugar representou-se o plano α, pelos seus traços, e desenha-
ram-se as projecções do triângulo [AABBCC], contido no plano, em função dos
dados (ver relatório do exercício 116622). Rebateu-se o plano α para o Plano
Horizontal de Projecção (a charneira é hhα, que se identificou imediatamente
– hhα ≡ ee11 ≡ hhαrr
), conforme é expressamente pedido no enunciado. Rebateu-
-se o ponto AA conduzindo, por AA11, uma perpendicular a hhα (que é o traço
horizontal do plano ortogonal à charneira que contém o arco do rebati-
mento de AA – o plano θ, representado apenas pelo seu traço horizontal,
razão pela qual se assinalou entre parêntesis). O centro do arco do rebati-
mento de AA é OO, que é o ponto de intersecção de hhα com θ. O triângulo do
rebatimento de AA (no espaço) é o triângulo [AAAA11OO], que está contido em θ
e a sua hipotenusa é [OOAA], que é o raio do arco do rebatimento. O raio do
arco do rebatimento não se projecta em V.G., pelo que é necessário efec-
tuar um rebatimento do plano θ – sobre uma paralela à charneira passando
por AA11, representou-se a cota de AA, obtendo-se AArr11
. O triângulo do rebati-
mento de AA, em V.G., é [OOAArr11
AA11] e a V.G. do raio do arco do rebatimento de
AA é OOෆAAෆrrෆ11
ෆ. Com o compasso, fazendo centro em OO e raio até AArr11
, transpor-
tou-se OOෆAAෆrrෆ11
ෆ para (hhθ), obtendo-se AArr. O procedimento foi idêntico para BB.
O arco do rebatimento de BB está contido num outro plano ortogonal a hhα
(que não se identificou) e o seu centro é QQ. O triângulo do rebatimento de BB,
em V.G., é [QQBBrr11
BB11] e o raio do arco do rebatimento de BB, em V.G., é QQෆBBෆrrෆ11
ෆ.
Note que as hipotenusas dos triângulos do rebatimento de AA e BB são para-
lelas entre si. O procedimento foi idêntico para o ponto CC, o que nos permi-
tiu determinar CCrr (e constata-se que as hipotenusas dos três triângulos do
rebatimento são paralelas entre si). A V.G. do triângulo [AABBCC] está no triân-
gulo [AArrBBrrCCrr].
165.
a) Em primeiro lugar representou-se o plano γ, pelos seus traços, e
o triângulo [AABBCC], contido em γ, pelas suas projecções, em fun-
ção dos dados. O plano γ é ortogonal ao β2/4, pelo que tem os
seus traços coincidentes. O ponto AA pertence a hhγ, que é uma
recta horizontal do plano com cota nula. A recta hh, horizontal (de
nível), com 3 cm de cota, foi a recta do plano a que se recorreu
para determinar as projecções de BB. A recta hh’’, horizontal (de ní-
vel), com 5 cm de cota, foi a recta do plano a que se recorreu
para determinar as projecções de CC. Em seguida, para determi-
nar a V.G. do triângulo, rebateu-se o plano γ para o Plano Hori-
zontal de Projecção (a charneira é hhγ, que se identificou
imediatamente – hhγ ≡ ee11 ≡ hhγrr
), conforme é expressamente pedido
no enunciado. Note que se trata de uma situação idêntica à do
exercício 116633, pelo que se aconselha a leitura do respectivo rela-
tório. De facto, a diferença entre as duas situações reside, ape-
nas, no facto de o plano γ ter os seus traços coincidentes, mas tal
não deverá ser factor de diferença entre os dois exercícios, uma
vez que se mantêm todos os raciocínios expostos naquele relató-
rio (os traços do plano γ são dduuaass rreeccttaass, à semelhança da situa-
ção do exercício 116633). O ponto que nos permitiu rebater ffγ foi FF’’,
o traço frontal da recta hh’’ – ffγrr
está definido por FF’’rr e pelo ponto
de concorrência dos dois traços do plano, que é fixo. A recta hh’’rr
(a recta hh’’ rebatida) passa por FF’’rr e é paralela a hhγrr
(rectas hori-
zontais de um plano são paralelas entre si e paralelas ao traço horizontal do plano, o que se verifica no espaço, em projecções e em rebati-
mento). O ponto CCrr situa-se sobre hh’’rr, na perpendicular à charneira que passa por CC11 (é o ponto de intersecção de hh’’rr com a perpendicular
à charneira que passa por CC11). Note que a perpendicular à charneira que passa por CC11 corresponde ao traço horizontal do plano ortogonal à
charneira (um plano vertical) que contém o arco do rebatimento de CC. Por FF11 (FF é o traço frontal da recta hh) conduziu-se uma perpendicular
à charneira – o ponto de intersecção desta com ffγrr
é FFrr (a perpendicular à charneira que passa por FF11 corresponde ao plano ortogonal à
charneira que contém o arco do rebatimento de FF). Por FFrr conduziu-se hhrr, paralela a hhγrr
(e a hh’’rr). BBrr situa-se sobre hhrr (BB é um ponto da recta hh)
na perpendicular à charneira que passa por BB11 (e que corresponde ao plano ortogonal à charneira que contém o arco do rebatimento de BB).
Note que, uma vez que o ponto AA se situa na charneira do rebatimento (é um ponto de hhγ), se tem imediatamente AArr ≡ AA11 (o ponto AA roda
sobre si próprio).
b) As vantagens do rebatimento efectuado em relação ao rebatimento do plano γ para o Plano Frontal de Projecção têm a ver com economia
de traçados, pois sendo o ponto AA um ponto da charneira, que fica imediatamente rebatido (roda sobre si próprio), para rebater o plano é
necessário rebater, apenas, dois dos seus pontos – os pontos BB e CC. De facto, caso se tivesse efectuado o rebatimento do plano γ para o
Plano Frontal de Projecção, seria necessário rebater os três pontos – AA, BB e CC.

52. 52
SOLUÇÕES
166.
a) Em primeiro lugar representou-se o plano θ, pelos seus traços, e o triân-
gulo [PPQQRR], contido em θ, pelas suas projecções, em função dos dados.
O plano θ é ortogonal ao β1/3, pelo que os seus traços são simétricos em
relação ao eixo XX. A recta ff, frontal (de frente), com 3 cm de afastamento,
foi a recta do plano a que se recorreu para determinar as projecções do
ponto PP. A recta hh, horizontal (de nível), com 2 cm de cota, foi a recta do
plano a que se recorreu para determinar as projecções do ponto QQ – a rec-
ta hh é também a recta suporte do lado [QQRR] do triângulo, que se projecta
em V.G. no Plano Horizontal de Projecção. Assim, a partir de QQ11, sobre hh11,
mediram-se os 5 cm (o comprimento do lado [QQRR]) e determinaram-se as
projecções de RR, sobre as projecções homónimas da recta hh. Em seguida,
desenharam-se as projecções do triângulo [PPQQRR]. O plano ϕ é o plano
frontal (de frente) que contém o ponto QQ – ϕ é o plano para o qual se pre-
tende rebater o plano θ. Rebatendo o plano θ para um plano frontal (de fren-
te), que é paralelo ao Plano Frontal de Projecção, a figura rebatida
projecta-se em V.G. no Plano Frontal de Projecção. A charneira do rebati-
mento é a recta de intersecção dos dois planos (a charneira do rebatimento
é a recta de intersecção do plano a rebater com o plano para o qual se pro-
cessa o rebatimento) – a recta ee é a charneira do rebatimento e é uma rec-
ta frontal (de frente) do plano θ (está definida por um ponto – QQ – e por
uma direcção – é paralela às rectas frontais do plano θ). QQ é um ponto da
charneira, pelo que roda sobre si próprio – tem-se imediatamente QQrr ≡ QQ22.
O ponto RR rebateu-se pelo triângulo do rebatimento – este construiu-se
com base na distância aa, que é a distância de RR ao plano ϕ (é o afastamento do ponto RR em relação ao plano ϕ). O centro do arco do re-
batimento de RR é o ponto de intersecção da charneira (recta ee) com a perpendicular à charneira que passa por RR22 (e que corresponde ao
plano ortogonal à charneira que contém o arco do rebatimento de RR – um plano de topo). O ponto PP rebateu-se igualmente pelo triângu-
lo do rebatimento – este construiu-se com base na distância bb, que é a distância de PP ao plano ϕ (é o afastamento do ponto PP em rela-
ção ao plano ϕ). O centro do arco do rebatimento de PP é o ponto de intersecção da charneira (recta ee) com a perpendicular à charneira
que passa por PP22 (e que corresponde ao plano ortogonal à charneira que contém o arco do rebatimento de PP – outro plano de topo). A
V.G. do triângulo [PPQQRR] está no triângulo [PPrrQQrrRRrr].
b) As vantagens do rebatimento proposto em relação ao rebatimento do plano θ para qualquer dos planos de projecção tem a ver com eco-
nomia de traçados – de facto, no rebatimento efectuado foi necessário, apenas, rebater dois pontos (o ponto QQ é um ponto da charneira,
pelo que é fixo), enquanto que, ao rebater o plano θ para qualquer dos planos de projecção, seria necessário rebater os três pontos.
a) Em primeiro lugar representou-se o plano θ, pelos seus traços, e o triângulo
[PPQQRR], contido em θ, pelas suas projecções, em função dos dados (ver alí-
nea aa)) do relatório do exercício anterior). O plano ν é o plano horizontal (de
nível) que contém o lado [QQRR] do triângulo – ν é o plano para o qual se pre-
tende rebater o plano θ. Rebatendo o plano θ para um plano horizontal (de
nível), que é paralelo ao Plano Horizontal de Projecção, a figura rebatida pro-
jecta-se em V.G. no Plano Horizontal de Projecção. A charneira do rebati-
mento é a recta de intersecção dos dois planos – a recta ee é a própria recta
hh (a recta suporte do lado [QQRR]). QQ e RR são dois pontos da charneira, pelo
que rodam sobre si próprios – tem-se imediatamente QQrr ≡ QQ11 e RRrr ≡ RR11. O
ponto PP rebateu-se pelo triângulo do rebatimento – este construiu-se com
base na distância dd, que é a distância de PP ao plano ν (é a cota do ponto PP
em relação ao plano ν). O centro do arco do rebatimento de PP é o ponto de
intersecção da charneira (recta ee) com a perpendicular à charneira que pas-
sa por PP11 (e que corresponde ao plano ortogonal à charneira que contém o
arco do rebatimento de PP – um plano vertical). A V.G. do triângulo [PPQQRR]
está no triângulo [PPrrQQrrRRrr].
b) As vantagens do rebatimento proposto em relação a qualquer outro rebati-
mento do plano θ (incluindo o do exercício anterior) tem a ver com economia
de traçados – no rebatimento efectuado foi necessário, apenas, rebater um
ponto (os pontos QQ e RR são dois pontos da charneira, pelo que são fixos).
De facto, ao rebater o plano θ para qualquer dos planos de projecção, seria
necessário rebater os três pontos e no rebatimento anterior foi necessário
rebater dois pontos.
167.

53. 53
SOLUÇÕES
168.
Em primeiro lugar representaram-se os pontos AA e BB, pelas suas projecções, e
determinaram-se os traços do plano ρ. Para tal conduziu-se, por AA e BB, uma
recta rr. Determinaram-se os traços da recta rr e por estes conduziram-se os tra-
ços homónimos de ρ. Os dados do exercício permitiram-nos, ainda, determinar
CC22, a projecção frontal de CC. A recta ss, paralela à recta rr e passando por CC (ss22
passa por CC22), foi a recta do plano a que se recorreu para determinar CC11, a pro-
jecção horizontal do ponto CC. A partir das projecções dos três pontos, desenha-
ram-se as projecções do triângulo [AABBCC]. Para determinar a V.G. do triângulo
rebateu-se o plano ρ para o Plano Frontal de Projecção (conforme é expressa-
mente pedido no enunciado). A charneira é ffρ, pelo que se tem imediatamente
ffρ ≡ ee22 ≡ ffρrr
. Rebateu-se o ponto AA conduzindo, por AA22, uma perpendicular a ffρ
(essa perpendicular é o plano π, que é o plano ortogonal à charneira que con-
tém o arco do rebatimento de AA – é um plano de perfil). O centro do arco do
rebatimento de AA é OO, que é o ponto de intersecção de ffρ (a charneira) com o
plano π (o plano que contém o arco do rebatimento de AA). O triângulo do rebati-
mento de AA (no espaço) é o triângulo [AAAA22OO], que está contido em π e a sua hi-
potenusa é [OOAA], que é o raio do arco do rebatimento. O raio do arco do
rebatimento não se projecta em V.G., pelo que é necessário efectuar um rebati-
mento do plano π – sobre uma paralela à charneira passando por AA22, represen-
tou-se o afastamento de AA, obtendo-se AArr11
. O triângulo do rebatimento de AA,
em V.G., é [OOAArr11
AA22] e a V.G. do raio do arco do rebatimento de AA é OOෆAAෆrrෆ11
ෆ. Com o
compasso, fazendo centro em OO e raio até AArr11
, transportou-se OOෆAAෆrrෆ11
ෆ para ffπ, ob-
tendo-se AArr. O procedimento foi idêntico para CC. O arco do rebatimento de CC
está contido num outro plano ortogonal a ffρ (que não se identificou) e o seu
centro é QQ. O triângulo do rebatimento de CC, em V.G., é [QQCCrr11
CC11] e o raio do
arco do rebatimento de CC, em V.G., é QQෆCCෆrrෆ11
ෆ. Note que as hipotenusas dos triân-
gulos do rebatimento de AA e CC são paralelas entre si. O procedimento foi idêntico para o ponto BB, o que nos permitiu determinar BBrr (e cons-
tata-se que as hipotenusas dos três triângulos do rebatimento são paralelas entre si). A V.G. do triângulo [AABBCC] está no triângulo [AArrBBrrCCrr].
169.
a) Em primeiro lugar representaram-se os pontos PP e QQ, pelas suas projecções, e
determinaram-se os traços do plano ρ. Para tal conduziu-se, por PP e QQ, uma
recta rr. Determinaram-se os traços da recta rr (QQ é, imediatamente, o traço hori-
zontal da recta rr) e por estes conduziram-se os traços homónimos do plano ρ.
Os dados do exercício permitiram-nos, ainda, determinar RR11, a projecção hori-
zontal de RR. A recta ss, paralela à recta rr e passando por RR (ss11 passa por RR11), foi
a recta do plano a que se recorreu para determinar RR22, a projecção frontal do
ponto RR. A partir das projecções dos três pontos, desenharam-se as projec-
ções do triângulo [PPQQRR]. Para determinar a V.G. do triângulo rebateu-se o plano
ρ para o Plano Horizontal de Projecção (conforme é expressamente pedido no
enunciado). A charneira é hhρ, pelo que se tem imediatamente hhρ ≡ ee11 ≡ hhρrr
. Re-
bateu-se o ponto PP conduzindo, por PP11, uma perpendicular a hhρ (que corres-
ponde ao plano ortogonal à charneira que contém o arco do rebatimento de PP
– um plano de perfil). Note que se omitiu a identificação do plano de perfil (o
plano ortogonal à charneira que contém o arco do rebatimento de PP). O centro
do arco do rebatimento de PP é OO, que é o ponto de intersecção de hhρ (a char-
neira) com o plano ortogonal à charneira que contém o arco do rebatimento de PP.
O triângulo do rebatimento de PP (no espaço) é o triângulo [PPPP11OO] e a sua hipo-
tenusa é [OOPP], que é o raio do arco do rebatimento de PP. Para determinar a
V.G. do raio do arco do rebatimento representou-se a cota de PP sobre uma pa-
ralela à charneira que passa por PP11, obtendo-se PPrr11
. O triângulo do rebatimento
de PP, em V.G., é [OOPPrr11
PP11] e a V.G. do raio do arco do rebatimento de PP é OOෆPPෆrrෆ11
ෆ.
Com o compasso, fazendo centro em OO e raio até PPrr11
, transportou-se OOෆPPෆrrෆ11
ෆ para
a perpendicular à charneira, obtendo-se PPrr. O ponto RR rebateu-se a partir de procedimentos idênticos aos expostos para o ponto PP (note
que se omitiu a identificação do plano ortogonal à charneira que contém o arco do rebatimento de RR, bem como do centro do respectivo
arco do rebatimento). QQ é um ponto da charneira, pelo que é fixo (roda sobre si próprio) – tem-se imediatamente QQrr ≡ QQ11. A V.G. do triân-
gulo [PPQQRR] está no triângulo [PPrrQQrrRRrr].
b) As vantagens do rebatimento efectuado em relação ao rebatimento do plano ρ para o Plano Frontal de Projecção têm a ver com econo-
mia de traçados, pois sendo o ponto QQ um ponto da charneira, que fica imediatamente rebatido (roda sobre si próprio), para rebater o
plano é necessário rebater, apenas, dois dos seus pontos – os pontos PP e RR. De facto, caso se tivesse efectuado o rebatimento do plano
ρ para o Plano Frontal de Projecção, seria necessário rebater os três pontos – PP, QQ e RR.

54. 54
SOLUÇÕES
170.
Em primeiro lugar representaram-se os pontos PP e QQ, pelas suas projecções,
determinaram-se os traços do plano ρ e desenharam-se as projecções do
triângulo [PPQQRR] (ver alínea aa)) do relatório do exercício anterior). Para determi-
nar a V.G. do triângulo rebateu-se o plano ρ para o Plano Frontal de Projec-
ção (conforme é expressamente pedido no enunciado) – a charneira é ffρ,
pelo que se tem imediatamente ffρ ≡ ee22 ≡ ffρrr
,. Rebateu-se hhρ rebatendo um
dos seus pontos – QQ, que é o traço horizontal da recta rr e, simultaneamente,
um dos vértices do triângulo. Rebateu-se QQ ao longo de um plano de perfil
(o plano ortogonal à charneira que contém o arco do rebatimento de QQ e que
não se identificou) – OO é o centro do arco do rebatimento de QQ (OO é o ponto
de intersecção de ffρ com o plano de perfil que contém o arco do rebatimento
de QQ). Construiu-se o triângulo do rebatimento de QQ em V.G. – numa paralela
à charneira que passa por QQ22 (ou seja, no próprio eixo XX) representou-se o
afastamento de QQ, obtendo QQrr11
(note que correspondeu ao transporte do
afastamento de QQ para o eixo XX, com o compasso e fazendo centro em QQ22).
O triângulo do rebatimento de QQ em V.G. é [OOQQrr11
QQ22]. Com centro em OO trans-
portou-se OOෆQQෆrrෆ11
ෆ para a perpendicular à charneira que passa por QQ22, obtendo
QQrr – hhρrr
passa por QQrr e é paralelo ao eixo XX. FFrr ≡ FF22, pois FF é fixo (roda sobre
si próprio, pois é um ponto da charneira). A recta rrrr fica definida por FFrr e por
QQrr. Por PP22 conduziu-se uma perpendicular à charneira (que corresponde ao
plano ortogonal à charneira que contém o arco do rebatimento de PP) e obte-
ve-se PPrr sobre rrrr (PP e um ponto da recta rr, pelo que PPrr tem de se situar sobre
rrrr). Para rebater o ponto RR foi necessário rebater a recta ss (uma recta do plano
à qual o ponto pertence). FF’’ é o traço frontal da recta ss, que é um ponto da
charneira, pelo que é fixo – FF’’rr ≡ FF’’22. A recta ssrr está já definida – está definida
por um ponto (FF’’rr) e por uma direcção (é paralela à recta rrrr, pois rr e ss são
rectas paralelas e o paralelismo verifica-se no espaço, em projecções e em
rebatimento). No entanto, optou-se por determinar o traço horizontal da recta ss em rebatimento, o que se efectuou conduzindo, por HH’’22 (HH’’ é o
traço horizontal da recta ss), uma perpendicular à charneira – o ponto de intersecção da perpendicular à charneira com hhρrr
é HH’’rr. A recta ssrr fica
definida por FF’’rr e por HH’’rr (note que ssrr é paralela a rrrr). O ponto RR é um ponto da recta ss, pelo que RRrr tem de se situar sobre ssrr – conduzindo uma
perpendicular à charneira por RR22, determinou-se RRrr no ponto de intersecção daquela com ssrr. A V.G. do triângulo [PPQQRR] está no triângulo
[PPrrQQrrRRrr].
171.
Em primeiro lugar representou-se o plano ρ, pelos seus traços, em função dos dados.
Os dados do exercício permitem-nos, ainda, determinar AA22 e BB22, as projecções fron-
tais de AA e BB, respectivamente. A recta rr, passando por AA e BB (rr22 passa por AA22 e por
BB22) foi a recta do plano a que se recorreu para determinar as projecções horizontais
de AA e BB. Em seguida, pelas projecções de BB conduziram-se as projecções homóni-
mas de uma recta gg, fronto-horizontal (a recta suporte do lado [BBCC] do triângulo) –
uma vez que gg é paralela a ambos os planos de projecção, o lado [BBCC] projecta-se em
V.G. em ambos os planos de projecção, o que nos permitiu determinar as projecções
de CC sobre as projecções homónimas da recta gg e, em seguida, desenhar as projec-
ções do triângulo [AABBCC]. Para determinar a V.G. do triângulo rebateu-se o plano ρ para
o Plano Horizontal de Projecção (conforme é expressamente pedido no enunciado) –
a charneira é hhρ, pelo que se tem imediatamente hhρ ≡ ee11 ≡ hhρrr
. Rebateu-se ffρ, rebaten-
do um dos seus pontos – FF, que é o traço frontal da recta rr. Rebateu-se FF ao longo de
um plano de perfil (o plano ortogonal à charneira que contém o arco do rebatimento
de FF e que não se identificou). Com o compasso, fazendo centro em FF11, transportou-
-se a cota de FF para o eixo XX (que é a paralela à charneira que passa por FF11) e dese-
nhou-se o triângulo do rebatimento de FF em V.G. – com centro na charneira e raio
igual à hipotenusa do triângulo de rebatimento de FF transportou-se o raio do arco do
rebatimento para a perpendicular à charneira que passa por FF11, obtendo-se FFrr. Por FFrr
conduziu-se ffρrr
, paralelo a hhρrr
. HH, o traço horizontal da recta rr, é um ponto da charnei-
ra, pelo que é fixo – HHrr ≡ HH11. A recta rr, em rebatimento (a recta rrrr), está definida por FFrr
e HHrr. Os pontos AA e BB são dois pontos da recta rr, pelo que AArr e BBrr se situam necessa-
riamente sobre rrrr – conduzindo, por AA11 e BB11, as respectivas perpendiculares à char-
neira (que correspondem aos planos ortogonais à charneira que contêm os arcos do
rebatimento de AA e BB) determinaram-se AArr e BBrr sobre rrrr. A recta gg, em rebatimento, passa por BB e é paralela aos traços do plano em rebatimento
– este raciocínio permitiu-nos determinar ggrr imediatamente. O ponto CC é um ponto da recta gg, pelo que CCrr tem de se situar sobre ggrr – con-
duzindo, por CC11, uma perpendicular à charneira (que corresponde ao plano ortogonal à charneira que contém o arco do rebatimento de CC),
determinou-se CCrr sobre ggrr. Note que o rebatimento de um plano de rampa pelo rebatimento dos seus traços consiste, afinal, em rebater rectas
do plano às quais os pontos pertençam e, em seguida, determinar os pontos rebatidos sobre as respectivas rectas rebatidas. A V.G. do triângulo
[AABBCC] está no triângulo [AArrBBrrCCrr].

55. 55
SOLUÇÕES
172.
173.
Em primeiro lugar representaram-se os traços do plano ρ, coincidentes com o eixo XX, e o ponto AA, pelas suas projecções. Em seguida
representaram-se, ainda, a projecção frontal de BB e a projecção horizontal de CC, que os dados do exercício nos permitem representar. Para
determinar as projecções do ponto BB conduziu-se, por AA22 e BB22, a projecção frontal de uma recta rr (rr22), do plano – é uma recta passante
(concorrente com o eixo XX num ponto MM) que contém AA e BB. A projecção horizontal da recta, rr11, está definida por MM11 e por AA11 e permite-nos
determinar BB11. Em seguida, recorreu-se a uma recta ss, do plano, passando
por CC e paralela à recta rr – ss11 passa por CC11. A projecção frontal da recta ss,
ss22, fica definida pelo ponto de concorrência com o eixo XX (o ponto NN) e
pela direcção de rr22 e permite-nos determinar CC22. A partir das projecções
dos três pontos, desenharam-se as projecções do triângulo [AABBCC]. Para
determinar a V.G. do triângulo rebateu-se o plano ρ para o Plano Horizontal
de Projecção, conforme é expressamente pedido no enunciado – a charneira
é o próprio eixo XX. Rebateu-se AA ao longo do plano ortogonal à charneira (ao
eixo XX) que contém o arco do rebatimento de AA (que é um plano de perfil) – o
centro do arco do rebatimento de AA é AAoo (o ponto de intersecção do eixo XX
com o plano de perfil que passa por AA). Numa paralela à charneira represen-
tou-se a cota de AA, obtendo AArr11
. O triângulo do rebatimento de AA em V.G.,
pelo rebatimento do plano de perfil que o contém, é [AAooAArr11
AA11]. AAෆooෆAAෆrrෆ11
ෆ
é o raio do arco do rebatimento de AA. Com centro em AAoo transportou-se
AAෆooෆAAෆrrෆ11
ෆ para a perpendicular à charneira que passa por AA (e que corresponde
ao plano de perfil que contém o arco do rebatimento de AA), obtendo AArr.
O procedimento foi idêntico para BB e CC. O triângulo do rebatimento de BB em
V.G., pelo rebatimento do plano de perfil que o contém (o plano ortogonal à
charneira que contém o arco do rebatimento de BB), é [BBooBBrr11
BB11]. BBෆooෆBBෆrrෆ11
ෆ é o
raio do arco do rebatimento de BB, em V.G. O triângulo do rebatimento de CC
em V.G., pelo rebatimento do plano de perfil que o contém (o plano ortogo-
nal à charneira que contém o arco do rebatimento de CC), é [CCooCCrr11
CC11].
CCෆooෆCCෆrrෆ11
ෆ é o raio do arco do rebatimento de CC, em V.G. A V.G. do triângulo
[AABBCC] está no triângulo [AArrBBrrCCrr].
a) Em primeiro lugar representou-se o plano ρ, pelos seus traços, e o triângulo
[AABBCC], contido em ρ, pelas suas projecções, em função dos dados (ver alínea
aa)) do relatório do exercício anterior). O plano ϕ é o plano frontal (de frente)
que contém o lado [BBCC] do triângulo – ϕ é o plano para o qual se pretende
rebater o plano ρ. Rebatendo o plano ρ para um plano frontal (de frente), que
é paralelo ao Plano Frontal de Projecção, a figura rebatida projecta-se em V.G.
no Plano Frontal de Projecção. A charneira do rebatimento é a recta de inter-
secção dos dois planos – a recta ee é a própria recta gg (a recta suporte do lado
[BBCC]). BB e CC são dois pontos da charneira, pelo que rodam sobre si próprios
– tem-se imediatamente BBrr ≡ BB22 e CCrr ≡ CC22. O ponto AA rebateu-se pelo triângulo
do rebatimento – este construiu-se com base na distância dd, que é a distância
de AA ao plano ϕ (é o afastamento do ponto AA em relação ao plano ϕ). O cen-
tro do arco do rebatimento de AA é o ponto de intersecção da charneira (recta
ee) com a perpendicular à charneira que passa por AA22 (e que corresponde
ao plano ortogonal à charneira que contém o arco do rebatimento de AA – um
plano de perfil). A V.G. do triângulo [AABBCC] está no triângulo [AArrBBrrCCrr].
b) As vantagens do rebatimento proposto em relação a qualquer outro rebati-
mento do plano ρ tem a ver com economia de traçados – no rebatimento efec-
tuado foi necessário, apenas, rebater um ponto (os pontos BB e CC são dois
pontos da charneira, pelo que são fixos).

56. 56
SOLUÇÕES
174.
Em primeiro lugar representaram-se os traços do plano ρ, coincidentes
com o eixo XX, e o ponto AA, pelas suas projecções. Em seguida, desenha-
ram-se as projecções do triângulo [AABBCC] (ver relatório do exercício ante-
rior). Para determinar a V.G. do triângulo rebateu-se o plano ρ para o Plano
Horizontal de Projecção, conforme é expressamente pedido no enunciado
– a charneira é o próprio eixo XX. O rebatimento do ponto AA efectuou-se com
o recurso ao seu triângulo do rebatimento, conforme exposto no relatório
do exercício anterior. Em seguida, desenhou-se a recta rr em rebatimento –
o ponto MM, o ponto de concorrência da recta rr com o eixo XX, é fixo (é um
ponto da charneira), pelo que se tem imediatamente MM11 ≡ MM22 ≡ MMrr. A recta
rrrr fica definida por AArr e por MMrr. O ponto BB é um ponto da recta rr, pelo que
BBrr tem de se situar sobre rrrr – conduziu-se, por BB11, uma perpendicular à
charneira (que corresponde ao plano ortogonal à charneira que contém o
arco do rebatimento de BB) e determinou-se BBrr sobre rrrr. Em seguida, reba-
teu-se a recta ss – a recta ss é paralela à recta rr, pelo que ssrr é necessaria-
mente paralela a rrrr. O ponto de concorrência da recta ss com o eixo XX é fixo,
pois situa-se na charneira (NN11 ≡ NN22 ≡ NNrr) e ssrr fica definida por um ponto (NNrr)
e por uma direcção (é paralela a rrrr). O ponto CC é um ponto da recta ss, pelo
que CCrr tem de se situar sobre ssrr – por CC11 conduziu-se uma perpendicular à
charneira (que corresponde ao plano ortogonal à charneira que contém o
arco do rebatimento de CC) e determinou-se CCrr sobre ssrr. A V.G. do triângulo
[AABBCC] está no triângulo [AArrBBrrCCrr].
Em primeiro lugar representou-se o plano ρ (cujos
traços estão coincidentes no eixo XX), que está defi-
nido pelo eixo XX e pelas projecções do ponto AA. Os
dados do enunciado permitem-nos, ainda, determi-
nar as projecções horizontais de BB e CC. Em segui-
da, recorreu-se a uma recta rr, passante (do plano),
tal que rr11 passa por AA11 e BB11 – após determinar rr22
(definida pelo seu ponto de concorrência com o
eixo XX e por AA22), determinou-se BB22, sobre rr22. A recta
ss é a recta paralela à recta rr a que se recorreu para
determinar a projecção frontal de CC (CC22) – as projec-
ções da recta ss determinaram-se a partir da sua pro-
jecção horizontal, ss11, que passa por CC11 e é paralela
a rr11. A recta ss, porque pertence ao plano ρ, é tam-
bém uma recta passante – a projecção frontal da
recta ss está definida por um ponto (o ponto de con-
corrência da recta ss com o eixo XX) e pela sua direc-
ção (é paralela a rr22). CC22 situa-se sobre ss22. A partir
das projecções dos três pontos, desenharam-se as
projecções do triângulo [AABBCC]. Para transformar o
plano ρ num plano horizontal (de nível), há que ter
em conta que um plano horizontal (de nível) é um caso particular dos planos projectantes frontais, o que consiste nos procedimentos efectua-
dos no exercício 113399, pelo que se aconselha a leitura do respectivo relatório. Note que o facto de se tratar de um plano de rampa passante não
altera em nada os procedimentos expostos naquele relatório. Note ainda que, uma vez que se pretende que o plano ρ seja transformado num
plano horizontal (de nível) com 1 cm de cota, o ppllaannoo 55 situa-se a 1 cm (a cota pretendida) de ff44ρ
(o eixo XX’’’’ situa-se a 1 cm de hh44ρ
). Note ainda
que se localizou o ppllaannoo 55 de forma a evitar a sobreposição de traçados.
175.

57. 57
SOLUÇÕES
176.
Em primeiro lugar representou-se o plano ρ (cujos tra-
ços estão coincidentes no eixo XX), que está definido
pelo eixo XX e pelas projecções do ponto AA. Em seguida,
desenharam-se as projecções do triângulo [AABBCC] (ver
relatório do exercício anterior). Para transformar o plano
ρ num plano horizontal (de nível), há que ter em conta
que um plano horizontal (de nível) é um caso particular
dos planos projectantes frontais, o que consiste nos pro-
cedimentos efectuados no exercício 115566, pelo que se
aconselha a leitura do respectivo relatório. Note que o
facto de se tratar de um plano passante não altera em
nada os procedimentos expostos naquele relatório. O
primeiro eixo de rotação é a recta vertical ee, que contém
o ponto AA (por uma questão de economia de traçados)
– AA’’ ≡ AA, pois AA situa-se no eixo de rotação (roda sobre
si próprio). O ponto PP, do eixo XX, é o ponto de hhρ que
nos permite rodar hhρ. O segundo eixo de rotação é a
recta de topo ee’’, que se localizou de forma a ser o ponto
CC’’ o ponto a rodar. Após a segunda rotação, o plano ρ é
um plano horizontal (de nível), pelo que a V.G. do triân-
gulo [PPQQRR] está no triângulo [PP’’’’11QQ’’’’11RR’’’’11].
177.
Em primeiro lugar representaram-se os pontos AA, BB e CC, pelas respec-
tivas projecções – os pontos situam-se no β1/3, pelo que têm coordena-
das iguais e projecções simétricas em relação ao eixo XX. A partir das
projecções dos três pontos, desenharam-se as projecções do triângu-
lo. Em seguida, desenharam-se as projecções das rectas rr e ss – a rec-
ta rr é a recta suporte do lado [AABB] do triângulo e a recta ss é a recta
paralela à recta rr que passa por CC. Para determinar a V.G. do triângulo,
optou-se por rebater o β1/3 para o Plano Horizontal de Projecção. O β1/3
é um plano passante, pelo que o rebatimento do β1/3 para o Plano Ho-
rizontal de Projecção é idêntico ao rebatimento do plano passante ex-
posto no relatório do exercício 117744, pelo que se aconselha a leitura do
respectivo relatório.

58. 58
SOLUÇÕES
178.
Em primeiro lugar representaram-se os pontos PP, QQ e RR, pelas respectivas projecções,
em função dos dados. A recta ff é a recta do plano que está definida pelos pontos PP e QQ
(trata-se de uma recta frontal). A recta hh é a recta do plano que está definida pelos pon-
tos PP e RR. O plano α está definido por duas rectas concorrentes (as rectas ff e hh são con-
correntes no ponto PP). Uma vez que se pretende rebater o plano α para o plano frontal
(de frente) que contém os vértices PP e QQ, não é necessária a determinação dos traços
do plano. De facto, apenas é fundamental a determinação da charneira do rebatimento,
que é a recta de intersecção do plano a rebater (o plano α) com o plano para o qual se
processa o rebatimento – o plano ϕ, frontal (de frente) que contém os pontos PP e QQ (e
que contém a recta ff). A recta de intersecção dos dois planos é a própria recta ff (pois
pertence simultaneamente aos dois planos), que é, assim, a charneira, pelo que se tem
ee ≡ ff. Rebatendo o plano α para um plano frontal (de frente), que é paralelo ao Plano
Frontal de Projecção, a figura em rebatimento projecta-se em V.G. no Plano Frontal de
Projecção. PP e QQ são dois pontos da charneira, pelo que rodam sobre si próprios (são
fixos) – PPrr ≡ PP22 e QQrr ≡ QQ22. Para rebater o ponto RR (o único ponto que não se situa na
charneira do rebatimento) recorreu-se ao seu triângulo do rebatimento – este construiu-
-se com base na distância dd, que é a distância de RR ao plano ϕ (é o afastamento do
ponto RR em relação ao plano ϕ). O centro do arco do rebatimento de RR é o ponto de
intersecção da charneira (recta ee) com a perpendicular à charneira que passa por RR22
(e que corresponde ao plano ortogonal à charneira que contém o arco do rebatimento
de RR – um plano de topo). A V.G. do triângulo [PPQQRR] está no triângulo [PPrrQQrrRRrr]. As vvaann--
ttaaggeennss ddoo rreebbaattiimmeennttoo eeffeeccttuuaaddoo em relação ao rebatimento do plano α para qualquer dos planos de projecção tem a ver com uma enorme
economia de traçados e de tempo de execução – de facto, no rebatimento efectuado não foi necessária a determinação de qualquer dos
traços do plano e foi suficiente rebater, apenas, um único ponto (os pontos PP e QQ são dois pontos da charneira, pelo que são fixos). Pelo
contrário, ao rebater o plano α para qualquer dos planos de projecção, seria necessário determinar os traços do plano (ou, pelo menos, um
deles) e, além disso, rebater os três pontos.
Em primeiro lugar representaram-se os pontos AA e BB, pelas suas projecções,
e determinou-se o traço horizontal do plano ρ. Para tal conduziu-se, por AA e BB,
uma recta rr e determinou-se o seu traço horizontal, HH, pelo qual se conduziu
hhρ – neste exercício, como em seguida se observará, não é necessária a
determinação do traço frontal do plano. Os dados do enunciado permitem-nos,
ainda, determinar CC11, a projecção horizontal do ponto CC. Para determinar CC22
conduziu-se, por CC, uma recta ss, paralela à recta rr – ss11 passa por CC11 e é para-
lela a rr11. HH’’ é o traço horizontal da recta ss e esta fica definida por um ponto (HH’’)
e por uma direcção (é paralela à recta rr). CC22 situa-se sobre rr22. O plano ν é o
plano horizontal (de nível) que contém o vértice AA do triângulo – ν é o plano
para o qual se pretende rebater o plano ρ. Rebatendo o plano ρ para um plano
horizontal (de nível), que é paralelo ao Plano Horizontal de Projecção, a figura
rebatida projecta-se em V.G. no Plano Horizontal de Projecção. A charneira do
rebatimento é a recta de intersecção dos dois planos – a recta ee é uma recta
fronto-horizontal, que está definida por um ponto (o ponto AA, que pertence
simultaneamente aos dois planos) e por uma direcção (é fronto-horizontal,
pois as rectas fronto-horizontais são a única «família» de rectas comum aos
dois planos). AA é um ponto da charneira, pelo que roda sobre si próprio –
tem-se imediatamente AArr ≡ AA11. O ponto BB rebateu-se pelo triângulo do rebati-
mento – este construiu-se com base na distância dd, que é a distância de BB ao
plano ν (é a cota do ponto BB em relação ao plano ν). O centro do arco do
rebatimento de BB (ponto OO) é o ponto de intersecção da charneira (recta ee) com a perpendicular à charneira que passa por BB11 (e que corres-
ponde ao plano ortogonal à charneira que contém o arco do rebatimento de BB – um plano de perfil). O ponto CC rebateu-se pelo triângulo do
rebatimento – este construiu-se com base na distância dd11, que é a distância de CC ao plano ν (é a cota do ponto CC em relação ao plano ν).
O centro do arco do rebatimento de CC (ponto QQ) é o ponto de intersecção da charneira (recta ee) com a perpendicular à charneira que passa
por CC11 (e que corresponde ao plano ortogonal à charneira que contém o arco do rebatimento de CC – um plano de perfil). A V.G. do triângulo
[AABBCC] está no triângulo [AArrBBrrCCrr]. As vvaannttaaggeennss ddoo rreebbaattiimmeennttoo eeffeeccttuuaaddoo em relação a qualquer outro rebatimento do plano ρ tem a ver
com economia de traçados – no rebatimento efectuado, por um lado não foi necessário determinar sequer o traço frontal do plano e, por
outro lado, foi suficiente rebater, apenas, dois pontos (o ponto AA é um ponto da charneira, pelo que é fixo).
179.

59. 59
SOLUÇÕES
180.
Em primeiro lugar representou-se o plano α, pelos seus traços, e os pontos AA e BB, pelas
suas projecções, em função dos dados – o plano α é ortogonal ao β1/3, pelo que os
seus traços são simétricos em relação ao eixo XX. O ponto AA é um ponto de hhα, que é
uma recta horizontal (de nível) do plano com cota nula. A recta hh, horizontal (de nível),
com 3 cm de cota e pertencente ao plano, foi a recta a que se recorreu para determinar
as projecções do ponto BB. O plano α não é paralelo a nenhum dos planos de projecção,
pelo que o triângulo [AABBCC] não se projecta em V.G. em nenhum dos planos de projec-
ção – é necessário o recurso a um processo geométrico auxiliar. Uma vez que o ponto AA
é um ponto do Plano Horizontal de Projecção, no sentido de uma maior economia de
traçados optou-se por rebater o plano α para o Plano Horizontal de Projecção (a char-
neira é hhα – hhα ≡ ee11 ≡ hhαrr
), pelo que se tem imediatamente AArr ≡ AA11, pois AA é um ponto da
charneira. Para rebater o plano α há que rebater o seu traço frontal, o que se processa
rebatendo um dos seus pontos – o ponto FF (traço frontal da recta hh), por exemplo. Para
tal conduziu-se, por FF, o plano ortogonal à charneira que contém o arco do seu rebati-
mento (note que se omitiu a representação do plano mas que este corresponde à per-
pendicular à charneira que passa por FF11). Os traços do plano α são concorrentes num
ponto fixo (um ponto do eixo XX, que é um ponto da charneira) – com o recurso ao com-
passo, fazendo centro nesse ponto e raio até FF22, transportou-se essa distância até à per-
pendicular à charneira que passa por FF11 e obteve-se FFrr. O traço frontal do plano α em
rebatimento (ffαrr
) passa por FFrr e é concorrente com hhαrr
no eixo XX (ffαrr
está definido por
dois pontos). A recta hhrr passa por FFrr e é paralela a hhαrr
(rectas horizontais de um plano
são paralelas entre si e paralelas ao traço horizontal do plano, o que se verifica no espaço, em projecções e em rebatimento) – hhrr está definida
por um ponto e uma direcção. Por BB11 conduziu-se uma perpendicular à charneira (que corresponde ao plano ortogonal à charneira que contém
o arco do rebatimento de BB) e determinou-se BBrr sobre hhrr (BB é um ponto de hh, pelo que BBrr tem de se situar sobre hhrr). A partir de AArr e BBrr, cons-
truiu-se o triângulo [AABBCC] em V.G., em rebatimento, determinando-se CCrr. Para determinar as projecções do triângulo, inverteu-se o rebatimento
do plano α, invertendo o rebatimento de CC. Para tal conduziu-se, em rebatimento, uma recta pelo ponto CC – a recta ff, frontal (de frente). A recta ffrr
passa por CCrr e é paralela a ffαrr
(rectas frontais de um plano são paralelas entre si e paralelas ao traço frontal do plano, o que se verifica no espa-
ço, em projecções e em rebatimento). A recta ffrr é concorrente com hhαrr
em HHrr – HH é o traço horizontal de ff e é um ponto da charneira, pelo que se
determinaram imediatamente as projecções de HH (HH11 ≡ HHrr e HH22 está no eixo XX). Pelas projecções de HH conduziram-se as projecções homónimas
de ff (que é paralela a ffα). Em seguida conduziu-se, por CCrr, uma perpendicular à charneira (que corresponde ao plano ortogonal à charneira que
contém o arco do rebatimento de CC) – o ponto em que esta intersecta ff11 é CC11. CC22 situa-se sobre ff22, na linha de chamada de CC11. A partir das pro-
jecções de CC, construíram-se as projecções do triângulo [AABBCC].
181.
Em primeiro lugar representou-se o plano ψ, pelos seus traços, e os
pontos AA e OO, pelas suas projecções, em função dos dados. O pon-
to AA é um ponto de ffψ, que é uma recta frontal (de frente) do plano
com afastamento nulo. A recta ff, frontal (de frente), com 3 cm de
afastamento e pertencente ao plano, foi a recta a que se recorreu
para determinar as projecções do ponto OO. O plano ψ não é paralelo
a nenhum dos planos de projecção, pelo que o quadrado [AABBCCDD]
não se projecta em V.G. em nenhum dos planos de projecção – é
necessário o recurso a um processo geométrico auxiliar. Uma vez
que o ponto AA é um ponto do Plano Frontal de Projecção, no sentido
de uma maior economia de traçados optou-se por rebater o plano ψ
para o Plano Frontal de Projecção (a charneira é ffψ – ffψ ≡ ee22 ≡ ffψrr
),
pelo que se tem imediatamente AArr ≡ AA22, pois AA é um ponto da char-
neira. Para rebater o plano ψ há que rebater o seu traço horizontal,
o que se processa rebatendo um dos seus pontos – o ponto HH
(traço horizontal da recta ff), por exemplo. Para tal conduziu-se, por HH,
o plano ortogonal à charneira que contém o arco do seu rebatimento
(note que se omitiu a representação do plano mas que este corres-
ponde à perpendicular à charneira que passa por HH22). Os traços do
plano ψ são concorrentes num ponto fixo (um ponto do eixo XX, que
é um ponto da charneira) – com o recurso ao compasso, fazendo
centro nesse ponto e raio até HH11, transportou-se essa distância até à
perpendicular à charneira que passa por HH22 e obteve-se HHrr. O traço
horizontal do plano ψ em rebatimento (hhψrr
) passa por HHrr e é
REPRESENTAÇÃO DE FIGURAS PLANAS III
16
(Continua na página seguinte)

60. 60
SOLUÇÕES
concorrente com ffψrr
no eixo XX (hhψrr
está definido por dois pontos). A recta ffrr passa por HHrr e é paralela a ffψrr
(rectas frontais de um plano são
paralelas entre si e paralelas ao traço frontal do plano, o que se verifica no espaço, em projecções e em rebatimento) – ffrr está definida por um
ponto e uma direcção. Por OO22 conduziu-se uma perpendicular à charneira (que corresponde ao plano ortogonal à charneira que contém o
arco do rebatimento de OO) e determinou-se OOrr sobre ffrr (OO é um ponto de ff, pelo que OOrr tem de se situar sobre ffrr). Com centro em OOrr e raio até
AArr desenhou-se a circunferência circunscrita ao quadrado e construiu-se o quadrado em V.G., em rebatimento. Para determinar as projecções
do quadrado, inverteu-se o rebatimento do plano ψ, invertendo o rebatimento de BB, CC e DD. Para inverter o rebatimento de CC conduziu-se, em
rebatimento, uma recta por CC – a recta hh, horizontal (de nível). A recta hhrr passa por CCrr e é paralela a hhψrr
(rectas horizontais de um plano são
paralelas entre si e paralelas ao traço horizontal do plano, o que se verifica no espaço, em projecções e em rebatimento). A recta hhrr é con-
corrente com ffψrr
em FFrr – FF é o traço frontal de hh e é um ponto da charneira, pelo que se determinaram imediatamente as projecções de FF
(FF22 ≡ FFrr e FF11 está no eixo XX). Pelas projecções de FF conduziram-se as projecções homónimas de hh (que é paralela a hhψ). Em seguida condu-
ziu-se, por CCrr, uma perpendicular à charneira (que corresponde ao plano ortogonal à charneira que contém o arco do rebatimento de CC) – o
ponto em que esta intersecta hh22 é CC22. CC11 situa-se sobre hh11, na linha de chamada de CC22. Para inverter o rebatimento de BB e DD conduziu-se, em
rebatimento, uma recta pelos dois pontos – a recta rr. A recta rrrr passa por BBrr e DDrr e é concorrente com hhψrr
em HH’’rr (HH’’ é o traço horizontal de rr)
e é concorrente com ffψrr
em FF’’rr (FF’’ é o traço frontal de rr e é um ponto da charneira, pelo que as suas projecções se determinaram imediata-
mente – FF’’22 ≡ FF’’rr e FF’’11 está no eixo XX). Por HH’’rr conduziu-se uma perpendicular à charneira (que corresponde ao plano ortogonal à charneira
que contém o arco do seu rebatimento) e determinou-se HH’’22 no eixo XX – HH’’11 situa-se sobre hhψ. Pelas projecções de FF’’ e HH’’ conduziram-se as
projecções homónimas da recta rr. Por BBrr e DDrr conduziram-se perpendiculares à charneira (que correspondem aos planos ortogonais à char-
neira que contêm os respectivos arcos do rebatimento) e determinaram-se as projecções de BB e DD, sobre as projecções homónimas da recta
rr. A partir das projecções de BB, CC e DD, construíram-se as projecções do quadrado [AABBCCDD]. Note que a inversão do rebatimento de BB e DD se
poderia ter processado, por exemplo, com o recurso a rectas horizontais (de nível) do plano, à semelhança do efectuado para inverter o reba-
timento do vértice CC. Tal possibilidade resultaria, no entanto, na necessidade de se ter de recorrer a duas rectas para inverter o rebatimento
(uma recta por ponto) o que, na situação apresentada, se evitou, pois a recta rr contém os dois pontos.
182.
Em primeiro lugar representou-se o plano μ, pelos seus traços, e o ponto
OO, pelas suas projecções, em função dos dados. A recta hh, horizontal
(de nível), com 3 cm de cota e pertencente ao plano, foi a recta a que se
recorreu para determinar as projecções do ponto OO. O plano μ não é para-
lelo a nenhum dos planos de projecção, pelo que o pentágono não se
projecta em V.G. em nenhum dos planos de projecção – é necessário o
recurso a um processo geométrico auxiliar. Optou-se por rebater o plano μ
para o Plano Horizontal de Projecção (a charneira é hhμ – hhμ ≡ ee11 ≡ hhμrr
).
Para rebater o plano μ há que rebater o seu traço frontal, o que se processa
rebatendo um dos seus pontos – o ponto FF (traço frontal da recta hh), por
exemplo. Para tal conduziu-se, por FF, o plano ortogonal à charneira que
contém o arco do seu rebatimento (note que se omitiu a representação do
plano mas que este corresponde à perpendicular à charneira que passa
por FF11). Os traços do plano μ são concorrentes num ponto fixo (um ponto
do eixo XX, que é um ponto da charneira) – com o recurso ao compasso,
fazendo centro nesse ponto e raio até FF22, transportou-se essa distância até
à perpendicular à charneira que passa por FF11 e obteve-se FFrr. O traço frontal
do plano μ em rebatimento (ffμrr
) passa por FFrr e é concorrente com hhμrr
no
eixo XX (ffμrr
está definido por dois pontos). A recta hhrr passa por FFrr e é para-
lela a hhμrr
(rectas horizontais de um plano são paralelas entre si e paralelas
ao traço horizontal do plano, no espaço, em projecções e em rebatimento)
– hhrr está definida por um ponto e uma direcção. Por OO11 conduziu-se uma
perpendicular à charneira (que corresponde ao plano ortogonal à charneira
que contém o arco do rebatimento de OO) e determinou-se OOrr sobre hhrr (OO é
um ponto de hh, pelo que OOrr tem de se situar sobre hhrr). Uma vez que um
dos vértices do polígono tem cota nula (situa-se sobre hhμ) e o seu lado de maior cota é horizontal (paralelo a hhμ), infere-se que a circunferência
circunscrita ao pentágono é tangente a hhμ. Assim, com centro em OOrr desenhou-se uma circunferência tangente a hhμrr
– um dos vértices do polí-
gono (o vértice AA, por exemplo) é o ponto de tangência da circunferência com hhμrr
. Em seguida, construiu-se o pentágono em V.G., em rebati-
mento. Para determinar as projecções do pentágono inverteu-se o rebatimento. AA é um ponto da charneira, pelo que se tem imediatamente
AArr ≡ AA11 – AA22 situa-se no eixo XX. Para inverter o rebatimento de CC e DD conduziu-se, em rebatimento, uma recta pelos dois pontos – a recta hh’’,
horizontal (de nível). A recta hh’’rr passa por CCrr e DDrr e é paralela a hhμrr
e a hhrr (rectas horizontais de um plano são paralelas entre si e paralelas ao
traço horizontal do plano, no espaço, em projecções e em rebatimento). A recta hh’’rr é concorrente com ffμrr
em FF’’rr – FF’’ é o traço frontal de hh’’. Por
FF’’rr conduziu-se uma perpendicular à charneira (que corresponde ao plano ortogonal à charneira que contém o arco do seu rebatimento) e
determinou-se FF’’11 no eixo XX – FF’’22 situa-se sobre ffμ. Pelas projecções de FF’’ conduziram-se as projecções homónimas de hh’’ (que é paralela a hhμ
e a hh). Em seguida, por CCrr e DDrr conduziram-se perpendiculares à charneira (que correspondem aos planos ortogonais à charneira que contêm
os respectivos arcos do rebatimento) e determinaram-se as projecções de CC e DD, sobre as projecções homónimas da recta hh’’. O processo
repetiu-se para os pontos BB e EE. A recta hh’’’’ é a recta horizontal (de nível) a que se recorreu para inverter o rebatimento dos dois pontos, e FF’’’’ é
o seu traço frontal. A partir das projecções dos cinco pontos desenharam-se as projecções da figura. Note que a inversão do rebatimento de BB,
CC, DD e EE se poderia ter processado, por exemplo, com o recurso a rectas frontais (de frente) do plano, conforme exposto no relatório do exercí-
cio 118800. Tal possibilidade resultaria, no entanto, na necessidade de se ter de recorrer a quatro rectas para inverter o rebatimento (uma recta por
ponto) o que, na situação apresentada, se evitou, pois cada recta contém dois pontos.

61. 61
SOLUÇÕES
Em primeiro lugar representou-se o plano α, pelos seus traços, e os
pontos AA e CC, pelas suas projecções, em função dos dados – o plano α
é ortogonal ao β1/3, pelo que os seus traços são simétricos em relação ao
eixo XX. A recta ff, frontal (de frente), com 2 cm de afastamento e pertencente
ao plano, foi a recta a que se recorreu para determinar as projecções do
ponto AA. A recta ff’’, frontal (de frente), com 5 cm de afastamento e perten-
cente ao plano, foi a recta a que se recorreu para determinar as projec-
ções do ponto CC. O plano α não é paralelo a nenhum dos planos de
projecção, pelo que o quadrado [AABBCCDD] não se projecta em V.G. em ne-
nhum dos planos de projecção – é necessário o recurso a um processo
geométrico auxiliar. Optou-se por rebater o plano α para o Plano Horizontal
de Projecção (a charneira é hhα – hhα ≡ ee11 ≡ hhαrr
). Para rebater o plano α há
que rebater o seu traço frontal, o que se processa rebatendo um dos seus
pontos – o ponto PP (PP é um ponto qualquer de ffα, escolhido aleatoriamente,
para rebater ffα). Para tal conduziu-se, por PP11, uma perpendicular à char-
neira (que corresponde ao plano ortogonal à charneira que contém o arco
do seu rebatimento). Os traços do plano α são concorrentes no ponto MM,
que é fixo (é um ponto da charneira) – com o recurso ao compasso, fazen-
do centro em MM e raio até PP22, transportou-se MMෆ22ෆPPෆ22ෆ para a perpendicular à
charneira que passa por PP11 e obteve-se PPrr. O traço frontal do plano α em
rebatimento (ffαrr
) passa por PPrr e é concorrente com hhαrr
no ponto MMrr
(ffαrr
está definido por dois pontos). Para rebater o ponto AA, é necessário re-
bater uma recta a que o ponto pertença – a recta ff, por exemplo. HH, o tra-
ço horizontal de ff é um ponto da charneira, pelo que é fixo – HHrr ≡ HH11.
A recta ff em rebatimento, ffrr, passa por HHrr e é paralela a ffαrr
(rectas frontais
de um plano são paralelas entre si e paralelas ao traço frontal do plano, no
espaço, em projecções e em rebatimento) – ffrr está definida por um ponto
e uma direcção. Por AA11 conduziu-se uma perpendicular à charneira (que corresponde ao plano ortogonal à charneira que contém o arco do
rebatimento de AA) e determinou-se AArr sobre ffrr (AA é um ponto de ff, pelo que AArr tem de se situar sobre ffrr). O processo repetiu-se em relação à
recta ff’’ (a recta que contém o ponto CC), obtendo-se CCrr sobre ff’’rr (HH’’ é o traço horizontal da recta ff’’). A partir de AArr e CCrr construiu-se o quadrado
183.
Em primeiro lugar representou-se o plano α, pelos seus traços, e o
pontos PP, pelas suas projecções, em função dos dados. O ponto PP é
um ponto de hhα, que é uma recta horizontal (de nível) do plano com
cota nula. Note que o ângulo dado (o ângulo que o lado [PPQQ] do qua-
drado faz com o traço horizontal do plano) é um âânngguulloo rreeaall e não um
ângulo em projecções – esse ângulo existe nnoo eessppaaççoo ou, mais preci-
samente, está contido nnoo ppllaannoo α e não é possível representá-lo direc-
tamente em projecções. O plano α não é paralelo a nenhum dos
planos de projecção, pelo que é necessário o recurso a um processo
geométrico auxiliar. Uma vez que o ponto PP é um ponto do Plano Hori-
zontal de Projecção, no sentido de uma maior economia de traçados
optou-se por rebater o plano α para o Plano Horizontal de Projecção (a
charneira é hhα – hhα ≡ ee11 ≡ hhαrr
), pelo que se tem imediatamente PPrr ≡ PP11,
pois PP é um ponto da charneira. Para rebater o plano α há que rebater
o seu traço frontal, o que se processa rebatendo um dos seus pontos –
o ponto AA (AA é um ponto qualquer de ffα, escolhido aleatoriamente,
para rebater ffα). Para tal conduziu-se, por AA11, uma perpendicular à
charneira (que corresponde ao plano ortogonal à charneira que contém
o arco do seu rebatimento). Os traços do plano α são concorrentes
num ponto fixo (um ponto do eixo XX, que é um ponto da charneira) –
com o recurso ao compasso, fazendo centro nesse ponto e raio até AA22, transportou-se essa distância até à perpendicular à charneira que
passa por AA11 e obteve-se AArr. O traço frontal do plano α em rebatimento (ffαrr
) passa por AArr e é concorrente com hhαrr
no eixo XX (ffαrr
está definido
por dois pontos). EEmm rreebbaattiimmeennttoo, a partir de PPrr, mediu-se o ângulo dado (o ângulo que o lado [PPQQ] faz com hhα – 30°) e determinou-se QQrr
sobre ffαrr
(o ponto QQ tem afastamento nulo, pelo que é um ponto de ffα). A partir de PPrr e QQrr construiu-se o quadrado em VG., em rebatimento,
obtendo RRrr e SSrr. Para inverter o rebatimento de SS conduziu-se, em rebatimento, uma recta por SSrr – a recta ff, frontal (de frente). A recta ffrr pas-
sa por SSrr e é paralela a ffαrr
(rectas frontais de um plano são paralelas entre si e paralelas ao traço frontal do plano, no espaço, em projecções
e em rebatimento). A recta ffrr é concorrente com hhαrr
em HHrr – HH é o traço horizontal de ff. HH é um ponto da charneira, pelo que as suas projec-
ções se determinam imediatamente – HH11 ≡ HHrr e HH22 situa-se no eixo XX. Pelas projecções de HH conduziram-se as projecções homónimas de ff
(que é paralela a ffα). Em seguida, por SSrr conduziu-se uma perpendicular à charneira (que corresponde ao plano ortogonal à charneira que
contém os arcos do seu rebatimento) e determinaram-se as projecções de SS sobre as projecções homónimas da recta ff O processo repetiu-
-se para o ponto RR. A recta ff é a recta frontal (de frente) a que se recorreu para inverter o rebatimento de RR e HH’’ é o seu traço horizontal.
A partir das projecções dos quatro pontos, desenharam-se as projecções do quadrado.
(Continua na página seguinte)
184.

62. 62
SOLUÇÕES
em VG., em rebatimento, obtendo BBrr e DDrr. Para inverter o rebatimento de DD conduziu-se, em rebatimento, uma recta por DDrr – a recta rr (note que
a recta rr é a recta suporte do lado [CCDD] do quadrado). A recta rrrr passa por CCrr e DDrr e é concorrente com ffαrr
em FFrr (FF é o traço frontal de rr) e é
concorrente com hhαrr
em HH’’’’rr (HH’’’’ é o traço horizontal de rr e é um ponto da charneira, pelo que as suas projecções se determinaram imediata-
mente – HH’’’’11 ≡ HH’’’’rr e HH’’’’22 está no eixo XX). Por FFrr conduziu-se uma perpendicular à charneira (que corresponde ao plano ortogonal à charneira
que contém o arco do seu rebatimento) e determinou-se FF11 no eixo XX – FF22 situa-se sobre ffα. Pelas projecções de FF e HH’’’’ conduziram-se as pro-
jecções homónimas da recta rr (note que as projecções de rr têm nneecceessssaarriiaammeennttee de passar pelas projecções homónimas do ponto CC, pois CC
é um ponto da recta rr). Por DDrr conduziu-se uma perpendicular à charneira (que corresponde ao plano ortogonal à charneira que contém o arco
do seu rebatimento) e determinaram-se as projecções de DD, sobre as projecções homónimas da recta rr. Para inverter o rebatimento de BB con-
duziu-se, em rebatimento, uma recta por BBrr – a recta ss (note que a recta ss é a recta suporte do lado [AABB] do quadrado e é paralela à recta rr). A
recta rrrr passa por AArr e BBrr e é paralela à recta rrrr (o paralelismo verifica-se no espaço, em projecções e em rebatimento). As projecções da recta
ss determinam-se imediatamente – passam pelas projecções homónimas do ponto AA (que é um ponto da recta ss) e são paralelas às projecções
homónimas da recta rr (as duas rectas são paralelas). Por BBrr conduziu-se uma perpendicular à charneira (que corresponde ao plano ortogonal
à charneira que contém o arco do seu rebatimento) e determinaram-se as projecções de BB, sobre as projecções homónimas da recta ss. A partir
das projecções dos quatro vértices do polígono, desenharam-se as suas projecções. Note que a inversão do rebatimento de BB e DD se poderia
ter processado, por exemplo, com o recurso a rectas horizontais (de nível) do plano, conforme exposto no relatório do exercício 118822.
186.
Em primeiro lugar representaram-se os planos δ e ρ, pelos respectivos
traços, e os pontos AA e BB, pertencentes ao plano δ, pelas suas projec-
ções, em função dos dados. O plano δ é ortogonal ao β1/3, pelo que os
seus traços são simétricos em relação ao eixo XX. O ponto AA é um ponto
de ffδ, que é uma recta frontal (de frente) do plano com cota nula. O
ponto BB é um ponto de hhδ, que é uma recta horizontal (de nível) do pla-
no com cota nula. O plano δ não é paralelo a nenhum dos planos de
projecção, pelo que é necessário o recurso a um processo geométrico
auxiliar. Uma vez que o ponto AA é um ponto do Plano Frontal de Projec-
ção e que o ponto BB é um ponto do Plano Horizontal de Projecção, ao
nível da economia de traçados é indistinto efectuar o rebatimento do
plano δ para o Plano Horizontal de Projecção ou para o Plano Frontal de
Projecção. Optou-se por rebater o plano δ para o Plano Horizontal de
Projecção (a charneira é hhδ – hhδ ≡ ee11 ≡ hhδrr
), pelo que se tem imediata-
mente BBrr ≡ BB11, pois BB é um ponto da charneira. Para rebater o plano δ
há que rebater o seu traço frontal, o que se processa rebatendo um dos
seus pontos – o ponto AA, que é um ponto de ffδ (ver relatório do exer-
cício 117755). A partir de AArr e de BBrr construiu-se o quadrado em V.G., em
Em primeiro lugar representou-se o plano δ, pelos seus traços, e o ponto QQ,
pelas suas projecções, em função dos dados. O plano δ é ortogonal ao β2/4,
pelo que tem os seus traços coincidentes. A recta hh, horizontal (de nível), com
5 cm de cota e pertencente ao plano, foi a recta a que se recorreu para deter-
minar as projecções do ponto QQ. O plano δ não é paralelo a nenhum dos pla-
nos de projecção, pelo que o hexágono não se projecta em V.G. em nenhum
dos planos de projecção – é necessário o recurso a um processo geométrico
auxiliar. Optou-se por rebater o plano δ para o Plano Horizontal de Projecção (a
charneira é hhδ – hhδ ≡ ee11 ≡ hhδrr
). Para rebater o plano δ há que rebater o seu traço
frontal, o que se processa rebatendo um dos seus pontos – o ponto FF (traço
frontal da recta hh), por exemplo. Sobre o rebatimento de FF, de ffδ e de QQ, ver
relatório do exercício 118822, uma vez que os dois exercícios são semelhantes.
Com o compasso, fazendo centro em QQrr e com 4 cm de raio (o raio da cir-
cunferência circunscrita ao hexágono é igual ao comprimento do lado do
hexágono) desenhou-se a circunferência circunscrita ao polígono e cons-
truiu-se o hexágono em V.G., em rebatimento. Dois dos lados do hexágono
são horizontais (de nível), pelo que são paralelos ao traço horizontal do plano
(ou seja, em rebatimento são paralelos a hhδrr
, pois rectas horizontais de um
plano são paralelas entre si e paralelas ao traço horizontal do plano, no
espaço, em projecções e em rebatimento). Para inverter o rebatimento recor-
reu-se a rectas horizontais (de nível) do plano (as rectas suporte dos lados
horizontais do hexágono) – ver exercício 118822. A partir das projecções de
todos os vértices do hexágono, desenharam-se as suas projecções.
(Continua na página seguinte)
185.

63. 63
SOLUÇÕES
rebatimento, obtendo CCrr e DDrr. Para inverter o rebatimento recorreu-se às rectas suporte de dois lados do quadrado – o lado [AABB] e o lado
[CCDD]. A recta rrrr é a recta suporte do lado [AABB], em rebatimento – as projecções de rr determinaram-se imediatamente, a partir das projec-
ções homónimas de AA e BB. Por CCrr e DDrr conduziu-se uma recta ssrr, que é a recta suporte do lado [CCDD] em rebatimento – ssrr é paralela a rrrr,
pois os dois lados em questão são paralelos. HHrr é o ponto de concorrência de ssrr com hhδrr
– HH é o traço horizontal da recta ss e é um ponto da
charneira, pelo que é fixo (HH11 ≡ HHrr e HH22 situa-se no eixo XX). Uma vez que as rectas rr e ss são paralelas, as suas projecções homónimas são
também paralelas entre si – as projecções da recta ss determinaram-se imediatamente, paralelas às projecções homónimas da recta rr e pas-
sando pelas projecções homónimas de HH, o seu traço horizontal (a recta ss está definida por um ponto e uma direcção). Conduzindo, por CCrr
e DDrr, as perpendiculares à charneira que por eles passam (e que correspondem aos planos ortogonais à charneira que contêm os respectivos
arcos do rebatimento), determinaram-se CC11 e DD11 sobre ss11 – CC22 e DD22 situam-se sobre ss22, nas respectivas linhas de chamada. A partir das pro-
jecções dos quatro vértices do quadrado, desenharam-se as suas projecções. Note que a inversão do rebatimento se poderia ter processado
com o recurso a rectas horizontais (de nível) do plano (à semelhança do efectuado no exercício 118822) ou com o recurso a recta frontais (de
frente) do plano (à semelhança do efectuado no exercício 118800), mas tal implicaria o recurso a duas rectas para inverter o rebatimento, o que
se processou com o recurso a, apenas, uma única recta, o que se traduziu em maior economia de traçados. Para determinar as projecções
do segmento [RRSS], o segmento resultante da intersecção do plano ρ com o quadrado [AABBCCDD] (que está contido no plano δ), é necessário
determinar a recta de intersecção dos dois planos – a recta ii. A recta ii determinou-se a partir dos seus traços (trata-se do caso geral da
intersecção entre planos). FF é o traço frontal da recta ii e HH’’ é o seu traço horizontal. A recta ii intersecta o lado [AADD] do quadrado no ponto RR
e intersecta o lado [CCDD] do quadrado no ponto SS – o segmento [RRSS] é, assim, o segmento da recta ii que se situa no quadrado [AABBCCDD].
Em primeiro lugar representaram-se os pontos AA e BB, pelas suas
projecções, em função dos dados. Em seguida, pelas projecções
de AA e BB conduziram-se as projecções homónimas da recta rr, a
recta que passa por AA e BB, e determinaram-se os seus traços nos
planos de projecção – FF e HH. Uma vez que, de acordo com o
enunciado, a recta rr é uma recta de maior inclinação do plano α,
por FF (o traço frontal da recta rr) conduziu-se ffα, perpendicular a rr22
– hhα é concorrente com ffα no eixo XX e passa por HH, o traço hori-
zontal da recta rr. O plano α não é paralelo a nenhum dos planos
de projecção, pelo que é necessário o recurso a um processo
geométrico auxiliar. Uma vez que FF é um ponto do Plano Frontal
de Projecção e que HH é um ponto do Plano Horizontal de Projec-
ção, ao nível da economia de traçados é indistinto efectuar o reba-
timento do plano α para o Plano Horizontal de Projecção ou para
o Plano Frontal de Projecção. Optou-se por rebater o plano α para
o Plano Horizontal de Projecção (a charneira é hhα – hhα ≡ ee11 ≡ hhαrr
),
pelo que se tem imediatamente HHrr ≡ HH11, pois HH é um ponto da
charneira. Para rebater o plano α há que rebater o seu traço fron-
tal, o que se processa rebatendo um dos seus pontos – o ponto
FF, que é um ponto de ffα (ver relatório do exercício 117755). A recta rrrr
(a recta rr em rebatimento) fica definida por HHrr e FFrr e o traço fron-
tal do plano, em rebatimento (ffαrr
) é concorrente com hhαrr
no eixo
XX e passa por FFrr (note que ffαrr
é perpendicular a rrrr, pois rr é uma
recta de maior inclinação do plano). Conduzindo, por AA11 e por
BB11, as perpendiculares à charneira que por eles passam (e que
correspondem aos planos ortogonais à charneira que contêm os
respectivos arcos do rebatimento), determinaram-se AArr e BBrr so-
bre rrrr. A partir de AArr e BBrr construiu-se o quadrado em V.G., em re-
batimento, obtendo CCrr e DDrr. Após a construção do quadrado em
rebatimento, constata-se que dois dos lados do quadrado são
paralelos a ffαrr
– este facto tem uma justificação científica, que em
seguida se apresenta. Recorde que rectas de maior inclinação de
um plano são perpendiculares ao traço frontal do plano (e a to-
das as rectas frontais do plano) – o lado [AABB] do quadrado está contido numa recta de maior inclinação do plano (bem como o lado [CCDD], que é
paralelo a [AABB]). Uma vez que os lados [BBCC] e [AADD] do quadrado são perpendiculares aos outros dois lados (que estão contidos em rectas de
maior inclinação do plano), então os lados [BBCC] e [AADD] estão nneecceessssaarriiaammeennttee contidos em rectas frontais (de frente) do plano e, por isso, são
paralelos a ffαrr
(rectas frontais de um plano são paralelas entre si e paralelas ao traço frontal do plano, no espaço, em projecção e em rebatimen-
to). Assim, por AArr e DDrr conduziu-se uma recta ffrr, que é paralela a ffαrr
– ff é uma recta frontal (de frente) do plano e é a recta suporte do lado [AADD]. A
recta ffrr é concorrente com hhαrr
em HH’’rr – HH’’ é o traço horizontal da recta ff e é um ponto da charneira, pelo que é fixo (HH’’11 ≡ HH’’rr e HH’’22 situa-se no
eixo XX). As projecções da recta ff determinaram-se imediatamente, pois ff é paralela a ffα (a recta ff está definida por um ponto e uma direcção).
Note que as projecções da recta ff passam pelas projecções homónimas de AA, que é um ponto da recta ff. Conduzindo, por DDrr, uma perpendicu-
lar à charneira (que corresponde ao plano ortogonal à charneira que contém o arco do seu rebatimento), determinou-se DD11 sobre ff11 – DD22 situa-se
sobre ff22, na respectiva linha de chamada. O processo repetiu-se para o ponto CC – ff’’ é a recta frontal (de frente) que é a recta suporte do lado
[BBCC] e HH’’’’ é o seu traço horizontal. As projecções da recta ff’’ passam pelas projecções homónimas de BB, que é um ponto da recta ff’’. A partir das
projecções dos quatro vértices do quadrado, desenharam-se as projecções do polígono. Note que a projecção frontal do lado [CCDD] do quadrado
é perpendicular a ffα (pois é o outro lado do quadrado que também está contido numa recta de maior inclinação do plano α).
187.

64. 64
SOLUÇÕES
188.
Em primeiro lugar representaram-se os pontos AA e BB, pelas suas projecções, em fun-
ção dos dados. Uma vez que AA tem afastamento nulo e BB tem cota nula, sabe-se imedia-
tamente que AA é um ponto do traço frontal do plano e que BB é um ponto do traço
horizontal do plano, o que nos permitiu desenhar ffρ e hhρ. O triângulo não se projecta
em V.G. em nenhum dos planos de projecção, pois o plano ρ não é paralelo a nenhum
dos planos de projecção, pelo que é necessário o recurso a um processo geométrico
auxiliar. Optou-se pelo rebatimento do plano. Uma vez que o ponto AA é um ponto do
Plano Frontal de Projecção e que BB é um ponto do Plano Horizontal de Projecção, no
sentido de uma maior economia de traçados é indistinto rebater o plano ρ para o Plano
Frontal de Projecção ou para o Plano Horizontal de Projecção. Optou-se, no entanto,
por rebater o plano ρ para o Plano Frontal de Projecção (a charneira é ffρ), pelo que se
tem imediatamente AArr ≡ AA22, pois AA é um ponto da charneira. Para rebater o plano ρ há
que rebater o seu traço horizontal, o que se processa rebatendo um dos seus pontos –
o ponto BB (que é um ponto de hhρ). Para tal conduziu-se, por BB, o plano ortogonal à
charneira que contém o arco do seu rebatimento (que é um plano de perfil e, na pre-
sente situação, é o próprio plano YYZZ). O ponto BB rebateu-se através do seu triângulo do
rebatimento. OO é o ponto de intersecção do plano YYZZ com a charneira (note que não se
identificou o ponto OO) e é o centro do arco do rebatimento de BB. O triângulo do rebati-
mento de BB é [OOBBBB22], que é rectângulo em BB22, e o comprimento da sua hipotenusa
([OOBB]) é a distância que nos permite rebater BB. Construiu-se o triângulo do rebatimento
de BB em V.G. (pelo rebatimento do plano YYZZ) – numa paralela à charneira (ou seja, no
próprio eixo XX) representou-se o afastamento de BB, obtendo BBrr11
. O triângulo do rebati-
mento de BB em V.G. é [OOBBrr11
BB22] (recorde que não se identificou o ponto OO, apesar de
se lhe fazer referência). Com centro em OO transportou-se OOෆBBෆrrෆ11
ෆ para a perpendicular à
charneira que passa por BB22 (que é YY ≡ ZZ), obtendo BBrr – hhρrr
passa por BBrr e é paralelo ao
eixo XX (e a ffρrr
). A partir de AArr e BBrr construiu-se o triângulo em V.G., em rebatimento, de-
terminando CCrr. Para determinar as projecções do triângulo inverteu-se o rebatimento do plano ρ, invertendo o rebatimento de CC. Para tal con-
duziu-se, em rebatimento, uma recta rr, do plano, passando por CC – por economia de traçados optou-se por fazer com que a recta rr seja a recta
suporte do lado [BBCC] do triângulo. Assim, a recta rr, em rebatimento (rrrr), passa por CCrr e BBrr. A recta rrrr é concorrente com ffρrr
no ponto FFrr – FF é o
traço frontal da recta rr. FF é um ponto da charneira (é fixo – roda sobre si próprio), pelo que se tem imediatamente FFrr ≡ FF22 – FF11 situa-se no eixo XX.
O ponto BB é o próprio traço horizontal da recta rr – as projecções da recta rr desenharam-se imediatamente, passando pelas projecções homó-
nimas de FF e BB (a recta rr está definida por dois pontos). Conduzindo, por CCrr, uma perpendicular à charneira (que corresponde ao plano ortogo-
nal à charneira que contém o arco do seu rebatimento), determinaram-se as projecções de CC sobre as projecções homónimas da recta rr.
A partir das projecções dos três vértices do triângulo, desenharam-se as suas projecções.
189.
Em primeiro lugar representaram-se os pontos OO e AA, pelas suas projecções,
em função dos dados. Uma vez que AA tem cota nula, sabe-se imediatamente
que AA é um ponto do traço horizontal do plano, o que nos permitiu desenhar hhρ.
Por OO e AA conduziu-se uma recta rr e determinou-se o seu traço frontal – FF.
Por FF conduziu-se ffρ, o traço frontal do plano. Note que AA é, imediatamente, o
traço horizontal da recta rr. O quadrado não se projecta em V.G. em nenhum
dos planos de projecção, pois o plano ρ não é paralelo a nenhum dos planos
de projecção, pelo que é necessário o recurso a um processo geométrico
auxiliar. Optou-se pelo rebatimento do plano. Uma vez que o ponto AA é um
ponto do Plano Horizontal de Projecção, no sentido de uma maior economia
de traçados optou-se por rebater o plano ρ para o Plano Horizontal de Pro-
jecção (a charneira é hhρ), pelo que se tem imediatamente AArr ≡ AA11, pois AA é
um ponto da charneira. Para rebater o plano ρ há que rebater o seu traço
frontal, o que se processa rebatendo um dos seus pontos – o ponto FF (que é
um ponto de ffρ). Para tal conduziu-se, por FF, o plano ortogonal à charneira
que contém o arco do seu rebatimento (que é um plano de perfil). O ponto FF
rebateu-se através do seu triângulo do rebatimento. MM é o ponto de intersec-
ção da charneira com o plano ortogonal à charneira que contém o arco do
rebatimento de FF (note que não se identificou o ponto MM no desenho) – MM é o
centro do arco do rebatimento de FF. O triângulo do rebatimento de FF é
[MMFFFF11], que é rectângulo em FF11, e o comprimento da sua hipotenusa ([MMFF])
é a distância que nos permite rebater FF. Construiu-se o triângulo do rebati-
mento de FF em V.G. (pelo rebatimento do plano de perfil que contém o arco
do rebatimento de FF) – numa paralela à charneira (ou seja, no próprio eixo XX)
representou-se a cota de FF, obtendo FFrr11
. O triângulo do rebatimento de FF em
V.G. é [MMFFrr11
FF11] (recorde que não se identificou o ponto MM, apesar de se lhe
(Continua na página seguinte)

65. 65
SOLUÇÕES
fazer referência). Note que, devido a se ter efectuado o rebatimento do plano de perfil para a direita, FFrr11
ficou coincidente com AA22, mas que
tal não se verificaria caso se tivesse rebatido o plano de perfil para a esquerda. Com centro em MM transportou-se MMෆFFෆrrෆ11
ෆ para a perpendicular
à charneira que passa por FF11 (que é o plano ortogonal à charneira que contém o arco do rebatimento de FF), obtendo FFrr – ffρrr
passa por FFrr e
é paralelo ao eixo XX (e a hhρrr
). Por FFrr e AArr conduziu-se uma recta, que é rrrr – a recta rr em rebatimento. Por OO11 conduziu-se uma perpendicular
à charneira (que corresponde ao plano ortogonal à charneira que contém o arco do rebatimento de OO) e determinou-se OOrr sobre rrrr (OO é um
ponto de rr, pelo que OOrr se situa sobre rrrr). Com o compasso, fazendo centro em OOrr e raio até AArr, desenhou-se a circunferência circunscrita
ao quadrado em V.G., em rebatimento, e construiu-se o polígono, inscrito na circunferência, em rebatimento. Note que o vértice CCrr, do qua-
drado em rebatimento, se situa sobre a recta rrrr (a recta rr é a recta suporte de uma diagonal do quadrado). Para inverter o rebatimento de CC
conduziu-se, por CCrr, uma perpendicular à charneira (que corresponde ao plano ortogonal à charneira que contém o arco do seu rebatimento)
– o ponto em que esta intersecta rr11 é a projecção horizontal de CC (CC11), o que nos permitiu determinar CC22, em seguida, sobre rr22. Para inverter
o rebatimento de BB e DD conduziu-se, em rebatimento, uma recta ss, do plano, passando pelos dois pontos – a recta ss é a recta suporte da
diagonal [BBDD] do quadrado. Assim, a recta ss, em rebatimento (ssrr), passa por BBrr e DDrr – uma vez que ss é a recta suporte da diagonal [BBDD], ve-
rifica-se que ssrr passa por OOrr. A recta ssrr é concorrente com hhρrr
no ponto HH’’rr – HH’’ é o traço horizontal da recta ss. HH’’ é um ponto da charneira
(é fixo – roda sobre si próprio), pelo que se tem imediatamente HH’’rr ≡ HH’’11 – HH’’22 situa-se no eixo XX. A recta ssrr é concorrente com ffρrr
no ponto
FF’’rr – FF’’ é o traço frontal da recta ss. Para determinar as projecções de FF’’ conduziu-se, por FF’’rr, uma perpendicular à charneira (que corresponde
ao plano ortogonal à charneira que contém o arco do seu rebatimento) e determinou-se FF’’11 sobre o eixo XX – FF’’22 determinou-se em seguida,
sobre ffρ (FF’’ é um ponto de ffρ). A partir das projecções de HH’’ e de FF’’ desenharam-se as projecções da recta ss (note que as projecções da
recta ss passam nneecceessssaarriiaammeennttee pelas projecções homónimas de OO). Conduzindo, por BBrr e DDrr, as perpendiculares à charneira que por
eles passam (que correspondem aos planos ortogonais à charneira que contêm os respectivos arcos do rebatimento) determinaram-se as
projecções de BB e DD sobre as projecções homónimas da recta ss. A partir das projecções dos quatro vértices do quadrado, desenharam-se
as suas projecções.
190.
Em primeiro lugar representou-se o plano ρ, pelos seus traços, e o pon-
to PP, pelas suas projecções, em função dos dados. O ponto PP é um
ponto de hhρ, que é uma recta horizontal (fronto-horizontal) do plano com
cota nula. Note que o ângulo dado (o ângulo que o lado [PPQQ] do qua-
drado faz com o traço horizontal do plano) é um âânngguulloo rreeaall e não um
ângulo em projecções – esse ângulo existe nnoo eessppaaççoo ou, mais precisa-
mente, está contido nnoo ppllaannoo ρ e não é possível representá-lo directa-
mente em projecções. O plano ρ não é paralelo a nenhum dos planos
de projecção, pelo que é necessário o recurso a um processo geométrico
auxiliar. Uma vez que o ponto PP é um ponto do Plano Horizontal de Pro-
jecção, no sentido de uma maior economia de traçados optou-se por
rebater o plano ρ para o Plano Horizontal de Projecção (a charneira é hhρ
– hhρ ≡ ee11 ≡ hhρrr
), pelo que se tem imediatamente PPrr ≡ PP11, pois PP é um
ponto da charneira. Para rebater o plano ρ há que rebater o seu traço
frontal, o que se processa rebatendo um dos seus pontos – o ponto AA
(AA é um ponto qualquer de ffρ, escolhido aleatoriamente, para rebater ffρ).
O ponto AA rebateu-se conforme exposto no relatório do exercício anterior
para o rebatimento de FF. Por AArr conduziu-se ffρrr
, paralelo a hhρrr
(e ao eixo
XX). EEmm rreebbaattiimmeennttoo, a partir de PPrr, mediu-se o ângulo dado (o ângulo
que o lado [PPQQ] faz com hhρ – 30°) e determinou-se QQrr, a 4 cm de PPrr. A
partir de PPrr e QQrr construiu-se o quadrado em VG., em rebatimento, ob-
tendo RRrr e SSrr. Para inverter o rebatimento, recorreu-se a duas rectas do
plano – as rectas rr e ss, que são as rectas suporte de dois lados do qua-
drado. A recta rrrr é, em rebatimento, a recta suporte do lado [PPSS] – FFrr é o
ponto de concorrência entre rrrr e ffρrr
(FF é o traço frontal da recta rr). As
projecções de FF determinaram-se conduzindo, por FFrr, uma perpen-
dicular à charneira (que corresponde ao plano ortogonal à charneira
que contém o arco do seu rebatimento) – FF11 situa-se no eixo XX e FF22 situa-se sobre ffρ. As projecções da recta rr determinam-se imediatamente,
a partir das projecções homónimas de FF e de PP (PP é o traço horizontal da recta rr). Para determinar as projecções do ponto SS conduziu-se,
por SSrr, uma perpendicular à charneira (que corresponde ao plano ortogonal à charneira que contém o arco do seu rebatimento) – as projec-
ções de SS estão sobre as projecções homónimas da recta rr (o ponto SS é um ponto da recta rr). A recta ssrr é, em rebatimento, a recta suporte
do lado [QQRR] – as rectas rrrr e ssrr são paralelas entre si. HH’’rr é o ponto de concorrência da recta ssrr com hhρrr
– HH’’ é o traço horizontal da recta ss e
é um ponto da charneira, pelo que é fixo (roda sobre si próprio), pelo que se tem imediatamente HH’’11 ≡ HH’’rr e HH’’22 situa-se no eixo XX. FF’’rr é o
ponto de concorrência entre ssrr e ffρrr
(FF’’ é o traço frontal da recta ss). As projecções de FF’’ determinaram-se de forma semelhante à exposta
para o ponto FF. As projecções da recta ss determinam-se imediatamente, a partir das projecções homónimas de FF’’ e de HH’’. Para determinar
as projecções dos pontos QQ e RR conduziram-se, por QQrr e por RRrr, as perpendiculares à charneira que por eles passam (e que correspondem
aos planos ortogonais à charneira que contêm os respectivos arcos do rebatimento) – as projecções de QQ e RR estão sobre as projecções
homónimas da recta ss (QQ e RR são dois pontos da recta ss). A partir das projecções dos quatro vértices do quadrado, desenharam-se as suas
projecções. Note que o ponto FF’’ não é fundamental para a determinação das projecções da recta ss, pois esta poderia estar definida por um
ponto (HH’’ o seu traço horizontal) e por uma direcção (a direcção da recta rr, pois as duas rectas são paralelas).

66. 66
SOLUÇÕES
Um plano de rampa paralelo ao β2/4 é nneecceessssaarriiaammeennttee ortogonal ao β1/3,
pelo que o plano ρ tem os seus traços simétricos em relação ao eixo XX. Com
base no raciocínio acima apresentado, em primeiro lugar representou-se o pla-
no ρ, pelos seus traços, em função dos dados. Em seguida constatou-se que
não é dada a medida do lado da figura. No entanto, sendo dado que o lado
[AABB] pertence ao Plano Frontal de Projecção, sabe-se imediatamente que
[AABB] tem afastamento nulo, pelo que AA e BB são dois pontos de ffρ. Por outro
lado, uma vez que o lado [DDEE] pertence ao Plano Horizontal de Projecção,
sabe-se imediatamente que [DDEE] tem cota nula, pelo que DD e EE são dois pon-
tos de hhρ. Por outro lado, ainda, sabendo que as diagonais [AAEE] e [BBDD] são de
perfil, é possível, de forma imediata, representar os pontos AA e EE pelas respec-
tivas projec-ções, pois os dois pontos têm a mesma abcissa – não é possível
representar os pontos BB e DD, pois não é conhecida a medida do lado do hexá-
gono. O plano ρ não é paralelo a nenhum dos planos de projecção, pelo que é
necessário o recurso a um processo geométrico auxiliar. Uma vez que o ponto
AA é um ponto do Plano Frontal de Projecção e o ponto EE é um ponto do Plano
Horizontal de Projecção, no sentido de uma maior economia de traçados é in-
distinto rebater o plano ρ para o Plano Frontal de Projecção ou para o Plano
Horizontal de Projecção. Optou-se por rebater o plano ρ para o Plano Horizon-
tal de Projecção (a charneira é hhρ – hhρ ≡ ee11 ≡ hhρrr
), pelo que se tem imediata-
mente EErr ≡ EE11, pois EE é um ponto da charneira. Para rebater o plano ρ há que
rebater o seu traço frontal, o que se processa rebatendo um dos seus pontos –
o ponto AA (AA é um ponto de ffρ). O ponto AA rebateu-se conforme exposto no
relatório do exercício 118899 para o rebatimento de FF. Por AArr conduziu-se ffρrr
, pa-
ralelo a hhρrr
(e ao eixo XX). Em rebatimento, já temos dois pontos do hexágono
em V.G. – AArr e EErr são dois extremos de uma das diagonais menores do hexá-
gono, pelo que a construção do hexágono requer um raciocínio particular. Esse raciocínio é que a diagonal [AAEE] do hexágono faz, com a diago-
nal [AADD], um ângulo de 30o (a diagonal [AADD] contém dois vértices diametralmente opostos do hexágono e, por isso mesmo, contém o centro da
figura). Por outro lado, sabe-se que DD é um ponto de hhρ. Assim, a partir de AArr mediram-se 30o em V.G. e obteve-se DDrr sobre hhρrr
– uma vez que a
diagonal [BBDD] é de perfil e BB é um ponto de ffρ, a determinação de BBrr, sobre ffρrr
é imediata. As diagonais [AADD] e [BBEE] bissectam-se no centro do
hexágono (que é o centro da circunferência circunscrita ao hexágono), o que nos permitiu determinar OOrr (OO é o centro da figura). Com o
compasso, fazendo centro em OOrr e raio até AArr (ou até BBrr ou até DDrr ou até EErr, pois todos estes pontos estão equidistantes de OOrr), desenhou-se a
circunferência circunscrita ao hexágono (a circunferência passa pelos quatro pontos). Em seguida, construiu-se o hexágono em V.G., em rebati-
mento, obtendo CCrr e FFrr. Para determinar as projecções da figura, há que inverter o rebatimento, o que se processa invertendo o rebatimento de
cada um dos pontos. A inversão do rebatimento dos pontos DD e BB é imediata, com o recurso a uma perpendicular à charneira que contém os
dois pontos (que corresponde ao plano ortogonal à charneira que contém os respectivos arcos do rebatimento, que é o mesmo plano). DD11 ≡ DDrr,
pois DD é um ponto da charneira e DD22 situa-se no eixo XX. BB11 situa-se no eixo XX, pois BB é um ponto de ffρ (tem afastamento nulo) e BB22 situa-se
sobre ffρ. Os pontos CC e FF situam-se numa recta fronto-horizontal do plano ρ – essa recta é a recta gg, que passa pelo centro da figura – (OO).
Assim, determinaram-se as projecções da diagonal [BBEE] (poderia ter-se recorrido à diagonal [AADD]) e por OO conduziu-se uma perpendicular à
charneira (que corresponde ao plano ortogonal à charneira que contém o arco do seu rebatimento), o que nos permitiu determinar as projec-
ções de OO sobre as projecções da diagonal [BBEE]. Pelas projecções de OO conduziram-se as projecções homónimas da recta gg – gg está defini-
da por um ponto (o ponto OO) e uma direcção (é fronto-horizontal). Por CCrr e FFrr conduziram-se as perpendiculares à charneira que por eles passam
(que correspondem aos planos ortogonais à charneira que contêm os respectivos arcos do rebatimento) e determinaram-se as projecções de CC e
FF sobre as projecções homónimas da recta gg (recorde que CC e FF são dois pontos da recta gg). A partir das projecções dos seis vértices da figura,
desenharam-se as suas projecções.
192.
Em primeiro lugar representou-se o plano ρ pelos seus traços, em função dos da-
dos. Note que não é possível, de forma imediata, determinar as projecções do ponto
OO, o centro da circunferência, pois apenas se sabe que a figura é tangente ao dois
planos de projecção – OO está necessariamente equidistante dos dois traços do pla-
no. Este raciocínio permitir-nos-ia determinar as projecções de OO com alguns traça-
dos auxiliares, mas optou-se por determinar o ponto OO previamente em
rebatimento. O plano ρ não é paralelo a nenhum dos planos de projecção, pelo que
é necessário o recurso a um processo geométrico auxiliar – optou-se pelo rebati-
mento do plano para o Plano Horizontal de Projecção (ao nível da economia de tra-
çados, é indistinto rebater o plano ρ para o Plano Horizontal de Projecção ou para o
Plano Frontal de Projecção), pelo que a charneira é hhρ – hhρ ≡ ee11 ≡ hhρrr
. Para rebater o
plano ρ há que rebater o seu traço frontal, o que se processa rebatendo um dos
seus pontos – o ponto AA (AA é um ponto qualquer de ffρ, escolhido aleatoriamente,
para rebater ffρ). O ponto AA rebateu-se conforme exposto no relatório do exercício
118899 para o rebatimento de FF. Por AArr conduziu-se ffρrr
, paralelo a hhρrr
(e ao eixo XX). Em
rebatimento, determinou-se OOrr, equidistante de ffρrr
e de hhρrr
(optou-se por localizar
OOrr no plano de perfil que contém AA, mas tal não é essencial – tem vantagens ape-
nas ao nível da economia de traçados). Com centro em OOrr, desenhou-se a circunfe-
rência em V.G., em rebatimento, tangente a ffρrr
e a hhρrr
(note que a circunferência é
(Continua na página seguinte)
191.

67. 67
SOLUÇÕES
tangente a ffρrr
em AArr. As dduuaass pprroojjeeccççõõeess da circunferência serão eelliippsseess, cujo desenho requer, no mínimo, oito dos seus pontos, para além
do paralelogramo envolvente e, de preferência, os seus dois eixos. Note que o diâmetro que não sofre deformação em projecção frontal é o
mesmo que também não sofre deformação em projecção horizontal (é o diâmetro fronto-horizontal da circunferência) – esse diâmetro é aque-
le que nos dará os eixos maiores das duas elipses. Por outro lado, o diâmetro da circunferência que sofre a deformação máxima em projec-
ção frontal é o mesmo que também sofre a deformação máxima em projecção horizontal (é o diâmetro de perfil da circunferência) – esse
diâmetro é aquele que nos dará os eixos menores das duas elipses. O eixo de homologia é a charneira, que é hhρ. Assim, inscreveu-se a cir-
cunferência num quadrado de lados paralelos a hhρ (o quadrado [PPQQRRSS]) e desenharam-se as suas medianas e as suas diagonais (que se
bissectam duas a duas em OOrr). Os pontos em que as medianas se apoiam nos lados do quadrado dão-nos, imediatamente, os extremos dos
dois eixos das elipses – a mediana fronto-horizontal é o diâmetro cujas projecções são os eixos maiores das duas elipses, enquanto que a
mediana de perfil é o diâmetro cujas projecções são os eixos menores das duas elipses. Em seguida, inverteu-se o rebatimento dos vértices
do quadrado e determinaram-se as duas projecções da figura (o quadrado), a partir dos seus vértices – um dos lados do quadrado está con-
tido em hhρ e outro lado está contido em ffρ. Note que as duas projecções do quadrado são rectângulos. Em seguida, desenharam-se, em pro-
jecções, as medianas e das diagonais do quadrado (as diagonais e as medianas dos dois rectângulos). Os pontos em que as medianas do
quadrado se apoiam nos seus lados (em projecções) são, imediatamente, quatro pontos de cada uma das elipses e são, também, os pontos
de tangência das elipses aos lados do quadrado (dos rectângulos que são as projecções do quadrado). Já temos quatro pontos para o dese-
nho de cada uma das elipses. Os outros quatro pontos são os pontos de intersecção da circunferência com as diagonais do quadrado – es-
tes transportaram-se para as projecções das diagonais através das perpendiculares à charneira que por eles passam (que correspondem aos
planos ortogonais à charneira que contêm os respectivos arcos do rebatimento). A partir dos oito pontos assim determinados, desenharam-
-se as duas elipses que são as projecções da circunferência pedida, atendendo às situações de tangência atrás referidas.
Em primeiro lugar representou-se o plano ρ, pelo seu traço hori-
zontal (o único que é dado, uma vez que o plano ρ está definido
pela sua orientação), bem como o ponto AA, pelas suas projec-
ções, em função dos dados – AA é um ponto de hhρ, que é uma
recta horizontal (fronto-horizontal) do plano com cota nula. O pla-
no ρ não é paralelo a nenhum dos planos de projecção, pelo que
é necessário o recurso a um processo geométrico auxiliar. Uma
vez que o ponto AA é um ponto do Plano Horizontal de Projecção,
no sentido de uma maior economia de traçados optou-se por
rebater o plano ρ para o Plano Horizontal de Projecção (a char-
neira é hhρ – hhρ ≡ ee11 ≡ hhρrr
), pelo que se tem imediatamente AArr ≡ AA11,
pois AA é um ponto da charneira. Note ainda que não seria possí-
vel rebater o plano ρ para o Plano Frontal de Projecção, pois não
é conhecido o seu traço frontal (que seria, nessa situação, a
charneira). Para rebater o plano ρ há que rebater o seu traço
frontal, mesmo sem este ser conhecido. Para rebater ffρ é neces-
sário rebater um dos seus pontos – considerou-se um ponto PP,
qualquer, pertencente a ffρ. Uma vez que PP será um ponto com
afastamento nulo, sabe-se imediatamente que PP11 se situa no eixo
XX. No sentido de uma maior economia de traçados, optou-se por
se situar o ponto PP no plano de perfil que contém AA, pelo que
se tem PP11 ≡ AA22. O plano de perfil que contém os dois pontos é o
plano ortogonal à charneira que contém o arco do rebatimento
de PP e, por conseguinte, também contém o triângulo do rebati-
mento de PP. O triângulo do rebatimento de PP, nnoo eessppaaççoo, é o
triângulo [AAPPPP11] (note que AA é o ponto de intersecção da char-
neira com o plano de perfil que contém o triângulo, pelo que AA é
o centro do arco do rebatimento de PP). O triângulo [AAPPPP11] é rec-
tângulo em PP11 e a hipotenusa [AAPP] está contida numa recta de
perfil (que é a recta de intersecção do plano ρ com o plano de
perfil que contém o triângulo). Sabe-se que o diedro que um plano de rampa faz com o Plano Horizontal de Projecção tem a mesma amplitude
que o ângulo que as rectas de perfil do plano fazem com o Plano Horizontal de Projecção – assim, sabe-se imediatamente que a hipotenusa
[AAPP] faz, com o Plano Horizontal de Projecção, um ângulo de 60o, sendo que PP se situa no SSPPFFSS. Assim, desenhou-se o triângulo do rebatimento
de PP directamente em V.G., pelo rebatimento do plano de perfil – com vértice em AArr mediu-se o ângulo de 60o com hhffrr
, obtendo PPrr11
no eixo XX. PPrr11
é o ponto PP rebatido pelo rebatimento do plano de perfil e o triângulo [AArrPP11PPrr11
] é o triângulo do rebatimento de PP em V.G. – com o compasso,
fazendo centro em PP11 e raio até PPrr11
(o raio corresponde à cota de PP) inverteu-se o rebatimento do plano de perfil, obtendo PP22, pelo qual se con-
duziu ffρ. Para rebater o ponto PP, pelo rebatimento do plano ρ, com o recurso ao compasso, com centro em AArr (que é o centro do arco do rebati-
mento de PP, no rebatimento do plano ρ) e raio até PPrr11
(a medida da hipotenusa do triângulo do rebatimento de PP, em V.G.), desenhou-se um
arco até à perpendicular à charneira que passa por PP11 (que corresponde ao plano ortogonal à charneira que contém o arco do seu rebatimento),
obtendo PPrr. Por PPrr conduziu-se ffρrr
. A partir de todos os procedimentos efectuados, que consistiram em rebater o plano ρ que estava definido por
uma recta e pela sua orientação, passou-se à realização dos traçados necessários à determinação das projecções do quadrado [AABBCCDD]. Note
que o ângulo dado (o ângulo que o lado [AABB] do quadrado faz com o traço horizontal do plano) é um âânngguulloo rreeaall e não um ângulo em projec-
ções – esse ângulo existe nnoo eessppaaççoo ou, mais precisamente, está contido nnoo ppllaannoo ρ e não é possível representá-lo directamente em projecções.
Esta situação é semelhante à do exercício 119900, pelo que se aconselha o acompanhamento da restante resolução com a leitura daquele relatório.
193.

68. 195.
Em primeiro lugar representou-se o plano ρ, pelos seus traços (que estão coincidentes com o eixo XX) e pelas projecções do ponto PP. Para
determinar as projecções do quadrado, há que rebater previamente o plano ρ e construir o quadrado em V.G., em rebatimento, pois o polígono
não se projecta em V.G. em nenhum dos planos de projecção (o plano ρ não é paralelo a nenhum dos planos de projecção). Na presente situa-
ção, não há qualquer diferença quanto ao plano de projecção para o qual se deverá rebater o plano ρ, no sentido de uma maior economia de
traçados. Optou-se por rebater o plano ρ para o Plano Horizontal de Projecção (a charneira é hhρ, que é o próprio eixo XX). Para rebater o ponto PP
recorreu-se ao seu triângulo do rebatimento. Assim, por PP conduziu-se uma perpendicular à charneira (que corresponde ao plano ortogonal à
charneira que contém o arco do seu rebatimento) – OO é o centro do arco do rebatimento de PP (note que não se identificou o ponto OO, que é o
ponto de intersecção da charneira com o plano ortogonal à charneira que contém o arco do rebatimento de PP). O triângulo do rebatimento de
PP é [OOPPPP11], que é rectângulo em PP11, e o comprimento da sua hipotenusa ([OOPP]) é a distância que nos permite rebater PP. Construiu-se o triân-
gulo do rebatimento de PP em V.G. (pelo rebatimento do plano de perfil que contém PP, que é o plano ortogonal à charneira que contém o arco
68
SOLUÇÕES
194.
Em primeiro lugar representou-se o plano ρ, pelo seu traço
horizontal (o único dado concreto, uma vez que é referido
que os traços do plano distam, entre si, 9 cm, e essa medida
não se projecta em V.G. em nenhum dos planos de projec-
ção), bem como o ponto AA, pelas suas projecções, em fun-
ção dos dados – AA é um ponto de hhρ, que é uma recta
horizontal (fronto-horizontal) do plano com cota nula. O pla-
no ρ não é paralelo a nenhum dos planos de projecção, pelo
que é necessário o recurso a um processo geométrico auxi-
liar. O ponto AA é um ponto do Plano Horizontal de Projecção,
pelo que se rebateu o plano ρ para o Plano Horizontal de
Projecção (a charneira é hhρ – hhρ ≡ ee11 ≡ hhρrr
) – tem-se imedia-
tamente AArr ≡ AA11, pois AA é um ponto da charneira. Note que
não seria possível rebater o plano ρ para o Plano Frontal de
Projecção, pois não é conhecido o seu traço frontal (que se-
ria, nessa situação, a charneira). Para rebater o plano ρ há
que rebater o seu traço frontal, mesmo sem este ser conheci-
do. Para rebater ffρ é necessário rebater um dos seus pontos
– considerou-se um ponto PP, qualquer, pertencente a ffρ. Uma
vez que PP será um ponto com afastamento nulo, sabe-se
imediatamente que PP11 se situa no eixo XX. No sentido de uma
maior economia de traçados, optou-se por se situar o ponto
PP no plano de perfil que contém AA, pelo que se tem PP11 ≡ AA22.
O plano de perfil que contém os dois pontos é o plano orto-
gonal à charneira que contém o arco do rebatimento de PP e,
por conseguinte, também contém o triângulo do rebatimento
de PP. O triângulo do rebatimento de PP, nnoo eessppaaççoo, é o triân-
gulo [AAPPPP11] (note que AA é o ponto de intersecção da char-
neira com o plano de perfil que contém o triângulo, pelo que
AA é o centro do arco do rebatimento de PP). O triângulo [AAPPPP11] é rectângulo em PP11 e a hipotenusa [AAPP] está contida numa recta de perfil (que é a
recta de intersecção do plano ρ com o plano de perfil que contém o triângulo) – [AAPP] mede 9 cm, que é a distância entre os dois traços do plano.
Assim, desenhou-se o triângulo do rebatimento de PP directamente em V.G., pelo rebatimento do plano de perfil – com o recurso ao compasso,
fazendo centro em AArr e com 9 cm de raio (a distância entre os dois traços do plano) determinou-se PPrr11
no eixo XX (PPrr11
está a 9 cm de AArr). PPrr11
é o
ponto PP rebatido pelo rebatimento do plano de perfil e o triângulo [AArrPP11PPrr11
] é o triângulo do rebatimento de PP em V.G. – com o compasso, fazen-
do centro em PP11 e raio até PPrr11
(o raio corresponde à cota de PP) inverteu-se o rebatimento do plano de perfil, obtendo PP22, pelo qual se conduziu
ffρ. Para rebater o ponto PP, pelo rebatimento do plano ρ, com o recurso ao compasso, com centro em AArr (que é o centro do arco do rebatimento
de PP, no rebatimento do plano ρ) e raio até PPrr11
(o raio é 9 cm, que é a medida da hipotenusa do triângulo do rebatimento de PP), desenhou-se um
arco até à perpendicular à charneira que passa por PP11 (que corresponde ao plano ortogonal à charneira que contém o arco do seu rebatimento),
obtendo PPrr. Por PPrr conduziu-se ffρrr
. Note que o ângulo dado (o ângulo que o lado [AABB] do triângulo faz com o traço horizontal do plano) é um âânn--
gguulloo rreeaall e não um ângulo em projecções – esse ângulo existe nnoo eessppaaççoo ou, mais precisamente, está contido nnoo ppllaannoo ρ e não é possível
representá-lo directamente em projecções. Esta situação é semelhante à do exercício 119900, pelo que se aconselha o acompanhamento da restan-
te resolução com a leitura daquele relatório. Após a construção do triângulo [AABBCC] em V.G., em rebatimento, para determinar as projecções da
figura é necessário inverter o rebatimento, invertendo o rebatimento dos pontos BB e CC. Para tal recorreu-se a uma recta rr, que contém os dois
pontos – a recta rr é a recta suporte do lado [BBCC] do triângulo. A recta rrrr é, em rebatimento, a recta suporte do lado [BBCC]. HHrr é o ponto de concor-
rência da recta rrrr com hhρrr
– HH é o traço horizontal da recta rr e é um ponto da charneira, pelo que é fixo (roda sobre si próprio), pelo que se tem
imediatamente HH11 ≡ HHrr e HH22 situa-se no eixo XX. FFrr é o ponto de concorrência entre rrrr e ffρrr
(FF é o traço frontal da recta rr). As projecções de FF
determinaram-se de forma semelhante à exposta para o ponto FF no relatório do exercício 118899. As projecções da recta rr determinam-se imediata-
mente, a partir das projecções homónimas de FF e de HH. Para determinar as projecções dos pontos BB e CC conduziram-se, por BBrr e por CCrr, as
perpendiculares à charneira que por eles passam (e que correspondem aos planos ortogonais à charneira que contêm os respectivos arcos do
rebatimento) – as projecções de BB e CC estão sobre as projecções homónimas da recta rr (BB e CC são dois pontos da recta rr). A partir das projec-
ções dos três vértices do triângulo, desenharam-se as suas projecções.
(Continua na página seguinte)

69. 69
SOLUÇÕES
do seu rebatimento) – numa paralela à charneira que passa por PP11
representou-se a cota de PP, obtendo PPrr11
. O triângulo do rebatimento
de PP em V.G. é [OOPPrr11
PP11]. Com centro em OO transportou-se OOෆPPෆrrෆ11
ෆ para
a perpendicular à charneira que passa por PP11, obtendo PPrr. A partir de
PPrr, construiu-se o quadrado em V.G., em rebatimento, de acordo com
os dados – QQrr está no eixo XX (QQ é um ponto do eixo XX), à direita de PP,
tal que PPෆrrෆQQෆrrෆ = 6 cm (que é a medida do lado do polígono). A constru-
ção do quadrado em rebatimento permitiu-nos determinar também RRrr
e SSrr. Para determinar as projecções do quadrado, há que inverter o
rebatimento e determinar as projecções de QQ, RR e SS. QQ é um ponto
da charneira (roda sobre si próprio, pelo que é fixo), pelo que as suas
projecções se determinam imediatamente. Para inverter o rebatimento
de SS recorreu-se a uma recta do plano – a recta rr, que é a recta su-
porte do lado [PPSS] do quadrado. A recta rrrr é a recta rr em rebatimento
e passa por PPrr e por SSrr. A recta rrrr é concorrente com o eixo XX (que é a
charneira) num ponto, que é fixo (roda sobre si próprio) – as projec-
ções da recta rr determinaram-se imediatamente, a partir do seu ponto
de concorrência com o eixo XX e das projecções do ponto PP. Condu-
zindo, por SSrr, uma perpendicular à charneira (que corresponde ao
plano ortogonal à charneira que contém o arco do seu rebatimento),
determinaram-se as projecções de SS sobre as projecções homónimas
da recta rr. Para inverter o rebatimento do ponto RR recorreu-se a outra
recta do plano – a recta ss, que é a recta suporte do lado [QQRR] do quadrado. A recta ss é paralela à recta rr. A recta ssrr passa por QQrr e por RRrr e é
paralela a rrrr. QQ é o ponto de concorrência da recta ss com o eixo XX, e é fixo – as projecções da recta ss desenharam-se imediatamente, pois a
recta está definida por um ponto (o ponto QQ) e por uma direcção (é paralela à recta rr). Conduzindo, por RRrr, uma perpendicular à charneira (que
corresponde ao plano ortogonal à charneira que contém o arco do seu rebatimento), determinaram-se as projecções de RR sobre as projecções
homónimas da recta ss. A partir das projecções dos quatro vértices do quadrado, desenharam-se as suas projecções.
Em primeiro lugar representou-se o plano ρ, pelos seus traços (que
estão coincidentes com o eixo XX) e pelas projecções do ponto AA. Para
determinar as projecções do triângulo, há que rebater previamente o
plano ρ e construir o triângulo em V.G., em rebatimento, pois o polígono
não se projecta em V.G. em nenhum dos planos de projecção (o plano
ρ não é paralelo a nenhum dos planos de projecção). Nesta situação
não há qualquer diferença quanto ao plano de projecção para o qual
se deverá rebater o plano ρ, no sentido de uma maior economia de
traçados. Optou-se por rebater o plano ρ para o Plano Horizontal de
Projecção (a charneira é hhρ, que é o próprio eixo XX). Para rebater o
ponto AA recorreu-se ao seu triângulo do rebatimento, o que consiste
no processo exposto no relatório do exercício anterior para o rebati-
mento do ponto PP, pelo que se aconselha a leitura do respectivo rela-
tório. A partir de AArr, construiu-se o triângulo em V.G., em rebatimento,
de acordo com os dados – BBrr está no eixo XX (BB é um ponto do eixo XX),
à direita de AA, tal que AAෆrrෆBBෆrrෆ = 7 cm (que é a medida do lado do polígo-
no). A partir de AArr e de BBrr construiu-se o triângulo em V.G., em rebati-
mento, e determinou-se CCrr. Para determinar as projecções do
triângulo, há que inverter o rebatimento e determinar as projecções de BB e CC. BB é um ponto da charneira (roda sobre si próprio, pelo que é
fixo), pelo que as suas projecções se determinam imediatamente. Para inverter o rebatimento de CC recorreu-se a uma recta do plano – a
recta ss. A recta ss é uma recta do plano ρ, paralela a uma outra recta do plano ρ – a recta rr, que é a recta suporte do lado [AABB] do triângulo.
A recta rrrr é a recta rr em rebatimento e passa por AArr e por BBrr. As projecções da recta rr determinam-se imediatamente, a partir das projecções
homónimas de AA e BB (note que a recta rr é apenas uma recta auxiliar, essencial à determinação das projecções da recta ss). A recta ssrr passa
por CCrr e é paralela a rrrr. A recta ssrr é concorrente com o eixo XX num ponto que é fixo – as projecções da recta ss determinam-se imediatamente,
a partir do seu ponto de concorrência com o eixo XX, sendo paralelas às projecções homónimas da recta rr (as duas rectas são paralelas e
a recta ss está definida por um ponto e uma direcção). Conduzindo, por CCrr, uma perpendicular à charneira (que corresponde ao plano orto-
gonal à charneira que contém o arco do seu rebatimento), determinaram-se as projecções de CC sobre as projecções homónimas da recta ss.
A partir das projecções dos três vértices do triângulo, desenharam-se as suas projecções.
196.

70. 70
SOLUÇÕES
197.
Em primeiro lugar representou-se o plano ρ, pelos seus traços (que estão
coincidentes com o eixo XX) e pelas projecções do ponto PP. Os dados do
enunciado permitiram-nos, ainda, determinar a projecção frontal do ponto
AA. Para determinar a projecção horizontal de AA recorreu-se a uma recta rr,
do plano, passando por PP e por AA – as projecções da recta rr (que é uma
recta passante) desenharam-se a partir da sua projecção frontal, que pas-
sa por PP22 e por AA22. AA11 situa-se sobre rr11, na linha de chamada de AA22. Para
determinar as projecções do quadrado, há que rebater previamente o pla-
no ρ e construir o quadrado em V.G., em rebatimento, pois o polígono não
se projecta em V.G. em nenhum dos planos de projecção (o plano ρ não é
paralelo a nenhum dos planos de projecção). Mais uma vez não há qual-
quer diferença quanto ao plano de projecção para o qual se deverá reba-
ter o plano ρ, no sentido de uma maior economia de traçados. Optou-se
por rebater o plano ρ para o Plano Frontal de Projecção (a charneira é ffρ,
que é o próprio eixo XX). Assim, por PP conduziu-se uma perpendicular à
charneira (que corresponde ao plano ortogonal à charneira que contém o
arco do seu rebatimento) – OO é o centro do arco do rebatimento de PP
(note que não se identificou o ponto OO, que é o ponto de intersecção da
charneira com o plano ortogonal à charneira que contém o arco do rebati-
mento de PP). O triângulo do rebatimento de PP é [OOPPPP22], que é rectângulo
em PP22, e o comprimento da sua hipotenusa ([OOPP]) é a distância que nos
permite rebater PP. Construiu-se o triângulo do rebatimento de PP em V.G.
(pelo rebatimento do plano de perfil que contém PP, que é o plano ortogo-
nal à charneira que contém o arco do seu rebatimento) – numa paralela à
charneira que passa por PP22 representou-se o afastamento de PP, obtendo PPrr11
. O triângulo do rebatimento de PP em V.G. é [OOPPrr11
PP22]. Com centro
em OO transportou-se OOෆPPෆrrෆ11
ෆ para a perpendicular à charneira que passa por PP22, obtendo PPrr. A partir de PPrr rebateu-se a recta rr – rrrr fica definida por
PPrr e pelo seu ponto de concorrência com o eixo XX, que é fixo. Conduzindo, por AA22, uma perpendicular à charneira (que corresponde ao plano or-
togonal à charneira que contém o arco do seu rebatimento) determinou-se AArr sobre rrrr (AA é um ponto da recta rr). Note que o ângulo dado (o ân-
gulo que o lado [AABB] do triângulo faz com o eixo XX) é um âânngguulloo rreeaall e não um ângulo em projecções – esse ângulo existe nnoo eessppaaççoo ou, mais
precisamente, está contido nnoo ppllaannoo ρ e não é possível representá-lo directamente em projecções. Assim, eemm rreebbaattiimmeennttoo, a partir de AArr,
mediu-se o ângulo dado (o ângulo que o lado [AABB] faz com o eixo XX – 60o) e determinou-se BBrr, a 5 cm (a medida do lado do quadrado) de AArr.
A partir de AArr e BBrr construiu-se o quadrado em VG., em rebatimento, obtendo CCrr e DDrr. Para inverter o rebatimento, recorreu-se a duas rectas do
plano – as rectas aa e bb, que são as rectas suporte de dois lados do quadrado. A situação exposta é, assim, semelhante à utilizada para inverter o
rebatimento do plano ρ no exercício 119955, pelo que se aconselha o acompanhamento da resolução sequente com a leitura daquele relatório.
198.
Em primeiro lugar representou-se o plano ρ, pelos seus traços
(que estão coincidentes com o eixo XX). Uma vez que é dada a
orientação do plano ρ, não nos é possível determinar as pro-
jecções do ponto AA – os dados do enunciado permitiram-nos,
apenas, determinar a projecção horizontal do ponto AA. Para
determinar as projecções do triângulo, há que rebater previa-
mente o plano ρ e construir o triângulo em V.G., em rebati-
mento, pois o polígono não se projecta em V.G. em nenhum
dos planos de projecção (o plano ρ não é paralelo a nenhum
dos planos de projecção). Mais uma vez não há qualquer dife-
rença quanto ao plano de projecção para o qual se deverá
rebater o plano ρ, no sentido de uma maior economia de traça-
dos. Optou-se por rebater o plano ρ para o Plano Horizontal de
Projecção (a charneira é hhρ, que é o próprio eixo XX). Para reba-
ter o plano ρ é necessário rebater o ponto AA, para o que é
necessário o recurso ao seu triângulo do rebatimento. O triân-
gulo do rebatimento de AA, nnoo eessppaaççoo, é o triângulo [OOAAAA11] – OO
é o centro do arco do rebatimento de AA e é o ponto de inter-
secção da charneira com o plano de ortogonal à charneira
que contém o triângulo do rebatimento de AA. O triângulo
[OOAAAA11] é rectângulo em AA11 e a hipotenusa [OOAA] está contida numa recta de perfil (que é a recta de intersecção do plano ρ com o plano de
perfil que contém o triângulo do rebatimento de AA). Sabe-se que o diedro que um plano de rampa (um plano passante é um plano de rampa)
faz com o Plano Frontal de Projecção tem a mesma amplitude que o ângulo que as rectas de perfil do plano fazem com o Plano Frontal de
(Continua na página seguinte)

71. 71
SOLUÇÕES
Em primeiro lugar representaram-se os pontos RR e SS, pelas respectivas
projecções, em função dos dados – os dois pontos pertencem ao β1/3,
pelo que as suas projecções são simétricas em relação ao eixo XX (os dois
pontos têm cota igual ao afastamento, pois pontos do β1/3 têm coordenadas
iguais). Note que não é necessário representar os traços do β1/3 (que
estão coincidentes no eixo XX, pois trata-se de um plano passante). Note
ainda que se trata de uma situação semelhante à do exercício anterior, se
bem que com alguns contornos diferentes – o β1/3 está igualmente definido
por uma recta (o eixo XX) e pela sua orientação (faz diedros de 45o com os
dois planos de projecção). No entanto, ao contrário da situação anterior, foi
possível determinar, imediatamente, as dduuaass pprroojjeeccççõõeess dos pontos
dados. Para determinar as projecções do triângulo, há que rebater previa-
mente o β1/3 e construir o triângulo em V.G., em rebatimento, pois o polí-
gono não se projecta em V.G. em nenhum dos planos de projecção (o β1/3
não é paralelo a nenhum dos planos de projecção). Não há qualquer dife-
rença quanto ao plano de projecção para o qual se deverá rebater o β1/3,
no sentido de uma maior economia de traçados. Optou-se por rebater o
β1/3 para o Plano Horizontal de Projecção (a charneira é o próprio eixo XX).
Assim, por SS conduziu-se uma perpendicular à charneira (que correspon-
de ao plano ortogonal à charneira que contém o arco do seu rebatimento)
– SSoo é o centro do arco do rebatimento de SS (SSoo é o ponto de intersecção
da charneira com o plano ortogonal à charneira que contém o arco do
rebatimento de SS). O triângulo do rebatimento de SS é [SSooSSSS11], que é rec-
tângulo em SS11, e o comprimento da sua hipotenusa ([SSooSS]) é a distância
que nos permite rebater SS. Construiu-se o triângulo do rebatimento de SS em V.G. (pelo rebatimento do plano de perfil que contém SS, que é o
plano ortogonal à charneira que contém o arco do seu rebatimento e, nesta siuação, é o próprio plano YYZZ) – numa paralela à charneira que
passa por SS11 representou-se a cota de SS, obtendo SSrr11
. O triângulo do rebatimento de SS em V.G. é [SSooSSrr11
SS11]. Note que [SSooSSrr11
] é a hipotenusa
do triângulo do rebatimento de SS e o seu comprimento é o raio do arco do rebatimento de SS – [SSooSS] está contido numa recta de perfil do
β1/3, pelo que [SSooSSrr11
] faz um ângulo de 45o com o eixo XX e um ângulo de 45o com [SSooSS11]). Com centro em SSoo transportou-se SSෆooෆSSෆrrෆ11
ෆ para a
perpendicular à charneira que passa por SS11, obtendo SSrr. Para determinar RRrr, e para evitar a construção de novo triângulo do rebatimento,
recorreu-se a uma recta rr, do β1/3 – a recta que passa por RR e SS (é uma recta passante, concorrente com o eixo XX num ponto fixo). A recta rrrr
(a recta rr em rebatimento) fica definida pelo seu ponto de concorrência com o eixo XX e por SSrr. Conduzindo, por RR11, uma perpendicular à
charneira (que corresponde ao plano ortogonal à charneira que contém o arco do seu rebatimento) determinou-se RRrr sobre rrrr (RR é um ponto
da recta rr). A partir de RRrr e SSrr construiu-se o triângulo em V.G., em rebatimento, obtendo TTrr. Para inverter o rebatimento de TT recorreu-se a
uma recta do plano – a recta ss. A recta ss é uma recta do β1/3 paralela à recta rr. A recta ssrr passa por TTrr e é paralela a rrrr. A recta ssrr é concor-
rente com o eixo XX num ponto que é fixo – as projecções da recta ss determinam-se imediatamente, a partir do seu ponto de concorrência
com o eixo XX, sendo paralelas às projecções homónimas da recta rr (as duas rectas são paralelas e a recta ss está definida por um ponto e
uma direcção). Conduzindo, por TTrr, uma perpendicular à charneira (que corresponde ao plano ortogonal à charneira que contém o arco do
seu rebatimento), determinaram-se as projecções de TT sobre as projecções homónimas da recta ss. A partir das projecções dos três vértices
do triângulo, desenharam-se as suas projecções.
Projecção – assim, sabe-se imediatamente que a hipotenusa [OOAA] faz, com o Plano Frontal de Projecção, um ângulo de 60°. Esse ângulo
estará em V.G. no ângulo que a hipotenusa do triângulo fará com o eixo XX (sugere-se que tente visualizar a situação no espaço, para uma
melhor compreensão do exposto). Assim, desenhou-se o triângulo do rebatimento de AA directamente em V.G., pelo rebatimento do plano de
perfil – com vértice em OO mediu-se o ângulo de 60o, o que nos permitiu determinar AArr com o eixo XX (que corresponde a um ângulo de 30o
com o lado [OOAA11] do triângulo), obtendo AArr11
na paralela ao eixo XX que passa por AA11 (note que o segmento [AArr11
AA11] corresponde à cota de AA,
que era desconhecida. AArr11
é o ponto AA rebatido pelo rebatimento do plano de perfil e o triângulo [OOAA11AArr11
] é o triângulo do rebatimento de AA
em V.G. – com o compasso, fazendo centro em OO e raio até AArr11
(a hipotenusa do triângulo do rebatimento de AA, que é o raio do arco do
rebatimento de AA), desenhou-se um arco até à perpendicular à charneira que passa por AA11 (que corresponde ao plano ortogonal à charneira
que contém o arco do seu rebatimento), obtendo AArr. Note que todos os procedimentos atrás explicitados consistiram em rebater o plano ρ,
que estava definido por uma recta e pela sua orientação. Em seguida passou-se à realização dos traçados necessários à determinação das
projecções do triângulo [AABBCC], que se trata de uma situação semelhante à do exercício 119966, pelo que se aconselha o acompanhamento da
resolução sequente com a leitura daquele relatório.
199.

72. 72
SOLUÇÕES
200.
Em primeiro lugar representou-se o plano α, pelos seus traços,
e os pontos AA e BB, pertencentes ao plano α, pelas suas pro-
jecções, em função dos dados. O plano α é ortogonal ao β2/4,
pelo que tem os seus traços coincidentes. O ponto AA é um
ponto de hhα, que é uma recta horizontal (de nível) do plano
com afastamento nulo. O ponto BB é um ponto de ffα, que é
uma recta frontal (de frente) do plano com afastamento nulo.
O plano α não é paralelo a nenhum dos planos de projecção,
pelo que é necessário o recurso a um processo geométrico
auxiliar. Uma vez que o ponto AA é um ponto do Plano Horizon-
tal de Projecção e que o ponto BB é um ponto do Plano Frontal
de Projecção, ao nível da economia de traçados é indistinto
efectuar o rebatimento do plano α para o Plano Frontal de Pro-
jecção ou para o Plano Horizontal de Projecção. Optou-se por
rebater o plano α para o Plano Horizontal de Projecção (a
charneira é hhα – hhα ≡ ee11 ≡ hhαrr
), pelo que se tem imediatamente
AArr ≡ AA11, pois AA é um ponto da charneira. Para rebater o plano
α há que rebater o seu traço frontal, o que se processa reba-
tendo um dos seus pontos – o ponto BB, que é um ponto de ffα
(ver relatório do exercício 117755). A partir de AArr e de BBrr cons-
truiu-se o rectângulo em V.G., em rebatimento, obtendo CCrr e
DDrr. Para inverter o rebatimento recorreu-se à recta suporte
do lado [CCDD] do rectângulo – a recta rr. A recta rrrr é a recta rr em
rebatimento e passa por CCrr e por DDrr. HHrr é o ponto de concor-
rência de rrrr com hhαrr
– HH é o traço horizontal da recta rr e é um
ponto da charneira, pelo que é fixo (HH11 ≡ HHrr e HH22 situa-se no
eixo XX). FFrr é o ponto de concorrência de rrrr com ffαrr
– FF é o tra-
ço frontal da recta rr (é um ponto com afastamento nulo). Para
inverter o rebatimento de FF conduziu-se, por FF11, uma perpen-
dicular à charneira (que corresponde ao plano ortogonal à charneira que contém o arco do seu rebatimento) e determinou-se FF11 sobre o eixo XX –
FF22 situa-se sobre ffα, pois FF é um ponto de ffα. As projecções da recta rr estão definidas pelas projecções homónimas de FF e HH. Conduzindo, por
CCrr e DDrr, as perpendiculares à charneira que por eles passam (e que correspondem aos planos ortogonais à charneira que contêm os respectivos
arcos do rebatimento), determinaram-se CC11 e DD11 sobre rr11 – CC22 e DD22 situam-se sobre rr22, nas respectivas linhas de chamada. A partir das projec-
ções dos quatro vértices do rectângulo, desenharam-se as suas projecções. Note que a inversão do rebatimento se poderia ter processado com
o recurso a rectas horizontais (de nível) do plano (à semelhança do efectuado no exercício 118822) ou com o recurso a recta frontais (de frente) do
plano (à semelhança do efectuado no exercício 118800), mas tal implicaria o recurso a duas rectas para inverter o rebatimento, o que se processou
com o recurso a, apenas, uma única recta, o que se traduziu em maior economia de traçados.
201.
Em primeiro lugar representou-se o plano θ, pelos seus
traços, e determinaram-se as projecções do ponto OO,
pertencente ao plano, em função dos dados. O plano θ é
ortogonal ao β2/4, pelo que tem os seus traços coinciden-
tes. A recta hh é a recta horizontal (de nível) do plano, com
4 cm de cota, a que se recorreu para determinar as pro-
jecções do ponto OO. Para determinar as projecções da
circunferência, há que rebater o plano θ e construir a cir-
cunferência em V.G., em rebatimento, pois a figura não
se projecta em V.G. em nenhum dos planos de projecção
(o plano θ não é paralelo a nenhum dos planos de pro-
jecção). Na presente situação, não há qualquer diferença
quanto ao plano de projecção para o qual se deverá
rebater o plano θ, no sentido de uma maior economia de
traçados. Optou-se por rebater o plano θ para o Plano
Horizontal de Projecção (a charneira foi hhθ). Para rebater
o plano θ há que rebater o seu traço frontal, o que se pro-
cessa rebatendo um dos seus pontos – o ponto FF
(o traço frontal da recta hh), por exemplo. O rebatimento
de FF e de ffθ processou-se conforme exposto no relatório
do exercício 117755. A recta hhrr é a recta hh em rebatimento –
está definida por um ponto (FFrr) e por uma direcção (é pa-
ralela a hhθrr
, pois rectas horizontais de um plano são para-
lelas entre si e ao traço horizontal do plano, no espaço,
(Continua na página seguinte)

73. 73
SOLUÇÕES
em projecções e em rebatimento). Conduzindo, por OO11, uma perpendicular à charneira (que corresponde ao plano ortogonal à charneira que
contém o arco do seu rebatimento), determinou-se OOrr sobre hhrr. Em seguida, com o compasso, fazendo centro em OOrr e com 3,5 cm de raio,
desenhou-se a circunferência em V.G., em rebatimento. Note que as dduuaass pprroojjeeccççõõeess da circunferência serão eelliippsseess. Assim, tratando-se de
dduuaass eelliippsseess, é necessário ter em conta que o desenho de cada uma requer alguns cuidados particulares, nomeadamente uumm mmíínniimmoo de oito
pontos e, se possível, os dois eixos (de cada uma) e um paralelogramo envolvente. A relação mais directa é a que existe entre a circunferência
em V.G. e a elipse que é a sua projecção horizontal, sendo uma relação homológica cujo eixo de homologia é hhθ (a charneira do rebatimento).
Tratemos, então, da eelliippssee que é a pprroojjeeccççããoo hhoorriizzoonnttaall ddaa cciirrccuunnffeerrêênncciiaa. Assim, inscreveu-se a circunferência num quadrado (o quadrado
[AABBCCDD]) de lados paralelos ao eixo de homologia (que é hhθ) e desenharam-se as suas medianas e as suas diagonais. Os extremos das media-
nas do quadrado são os pontos em que a circunferência é tangente aos quatro lados do quadrado e dão-nos, imediatamente, os extremos dos
dois eixos da elipse que é a projecção horizontal da circunferência. Assim, a projecção horizontal do diâmetro da circunferência que é paralelo a
hhθrr
corresponderá ao eixo maior da referida elipse (por ser paralelo ao eixo de homologia e, assim, não sofrer qualquer deformação), enquanto
que a projecção horizontal do diâmetro que é perpendicular a hhθrr
corresponderá ao eixo menor da elipse (por ser aquele que é perpendicular ao
eixo de homologia e, assim, sofrer a maior redução). As projecções horizontais dos extremos dos dois diâmetros referidos serão, imediatamente,
quatro pontos da elipse – os outros quatro pontos serão os pontos de intersecção da circunferência com as diagonais do quadrado em que
aquela se inscreve. Para determinar as projecções da circunferência começou-se, então, por inverter o rebatimento e construir as projecções do
quadrado [AABBCCDD]. A recta hh’’ é a recta horizontal (de nível) do plano a que se recorreu para inverter o rebatimento dos pontos AA e BB – a recta hh’’ é
a recta suporte do lado [AABB] do quadrado (ver exercício 118822 e respectivo relatório). A recta hh’’’’ é a recta horizontal (de nível) do plano a que se
recorreu para inverter o rebatimento dos pontos CC e DD – a recta hh’’’’ é a recta suporte do lado [CCDD] do quadrado (ver exercício 118822 e respectivo
relatório). A partir das projecções de AA, BB, CC e DD desenharam-se as duas projecções do quadrado envolvente da circunferência – a projecção
horizontal do quadrado é um rectângulo e a sua projecção frontal é um paralelogramo. Em projecções, desenharam-se as projecções das me-
dianas e das diagonais do quadrado, que se bissectam duas a duas sobre as projecções homónimas do ponto OO. Os pontos em que as media-
nas do rectângulo (que é a projecção horizontal do quadrado) se apoiam nos lados do polígono são, imediatamente, quatro pontos da elipse
que é aa pprroojjeeccççããoo hhoorriizzoonnttaall ddaa cciirrccuunnffeerrêênncciiaa e são, também, os extremos dos dois eixos da figura. Os pontos em que as medianas do para-
lelogramo (que é a projecção frontal do quadrado) se apoiam nos lados do polígono são, imediatamente, quatro pontos da elipse que é aa
pprroojjeeccççããoo ffrroonnttaall ddaa cciirrccuunnffeerrêênncciiaa – ao contrário da projecção horizontal, no entanto, estes quatro pontos nnããoo ssããoo os extremos dos dois
eixos da elipse. Já temos quatro pontos de cada uma das elipses. Conduzindo, pelos pontos em que a circunferência (em rebatimento) corta as
diagonais do quadrado [AABBCCDD], as perpendiculares à charneira que por eles passam (e que correspondem aos planos ortogonais à charneira
que contêm os respectivos arcos do rebatimento), determinaram-se as projecções horizontais daqueles pontos – a partir das projecções horizon-
tais desses quatro pontos, determinaram-se as suas projecções frontais sobre as projecções frontais das diagonais do quadrado. Já temos oito
pontos para desenhar cada uma das duas curvas. No que respeita à eelliippssee que é a pprroojjeeccççããoo hhoorriizzoonnttaall ddaa cciirrccuunnffeerrêênncciiaa, esta foi desenha-
da a partir dos seus dois eixos e atendendo às situações de tangência da curva em relação aos lados do rectângulo em que se inscreve. Já no
que respeita à eelliippssee que é a pprroojjeeccççããoo hhoorriizzoonnttaall ddaa cciirrccuunnffeerrêênncciiaa, optou-se por desenhá-la imediatamente, a partir dos oito pontos determi-
nados e dos seus pontos de tangência ao paralelogramo envolvente. No entanto, este desenho carece do rigor da outra elipse, uma vez que não
foram determinados os seus dois eixos. Para tal bastaria, em rebatimento, determinar o diâmetro da circunferência que é paralelo a ffθrr
e o outro
que lhe é perpendicular – a projecção frontal do primeiro seria o eixo maior dessa elipse e a projecção frontal do segundo seria o eixo menor
dessa mesma elipse. Esse procedimento dar-nos-ia mais quatro pontos da curva em cada uma das projecções, o que permitiria um desenho
ainda mais preciso das duas elipses (com um total de doze pontos). No entanto, optou-se por não efectuar esses procedimentos na solução
apresentada, uma vez que a quantidade de informação gráfica que tal iria provocar dificultaria, em muito, a leitura da resolução gráfica proposta.
(Continua na página seguinte)
Em primeiro lugar representou-se o plano ρ, pelo seu traço horizontal
(o único que é conhecido), bem como os pontos AA e BB, pelas suas projec-
ções, em função dos dados. Note que o lado [AABB] do hexágono, porque
tem cota nula, se situa em hhρ (que é uma recta horizontal do plano com
cota nula) e, atendendo a que hhρ é uma recta fronto-horizontal, o segmento
[AABB] projecta-se em V.G. em ambas as projecções. Os dados do enuncia-
do não nos permitem desenhar ffρ, mas é possível prosseguir com o exercí-
cio. O plano ρ não é paralelo a nenhum dos planos de projecção, pelo que
é necessário o recurso a um processo geométrico auxiliar. Optou-se pelo
processo do rebatimento, o que nos obriga a rebater o plano ρ para o Pla-
no Horizontal de Projecção, pois não se conhece o seu traço frontal (que
seria a charneira, caso se efectuasse o rebatimento do plano ρ para o Pla-
no Frontal de Projecção). Assim, a charneira foi hhρ, pelo que se tem imedia-
tamente hhρ ≡ ee11 ≡ hhρrr
– AArr ≡ AA11 e BBrr ≡ BB11, pois AA e BB são dois pontos da
charneira. A partir de AArr e BBrr efectuaram-se os traçados necessários à de-
terminação do centro da figura em rebatimento (o ponto OOrr) e à construção
do hexágono em V.G., em rebatimento. Sabe-se que os vértices DD e EE têm
afastamento nulo, pelo que é possível conduzir ffρrr
directamente por DDrr e
por EErr – DD e EE são dois pontos de ffρ. Tenha em conta que, sabendo que DD
e EE são dois pontos de ffρ é possível, de forma imediata, determinar as suas
projecções horizontais, que se situam no eixo XX – conduzindo, por DDrr e EErr
as perpendiculares à charneira que por eles passam (e que correspondem
aos planos ortogonais à charneira que contêm os respectivos arcos do
202.

74. 74
SOLUÇÕES
rebatimento), é possível determinar DD11 e EE11 no eixo XX (DD11 ≡ BB22 e EE11 ≡ AA22). Para inverter o rebatimento, é necessário determinar ffρ em primeiro
lugar, o que se processa invertendo o rebatimento de um dos seus pontos – o ponto DD, por exemplo. Consideremos, então, o ponto DD – o
triângulo do rebatimento de DD está contido num plano ortogonal à charneira (que é o plano de perfil que contém a diagonal [BBDD] do hexá-
gono), plano esse que corta a charneira no ponto BB. O ponto BB é, assim, um dos vértices do triângulo do rebatimento de DD e é o centro do
arco do rebatimento de DD (o triângulo do rebatimento de DD é o triângulo [BBDDDD11], que é rectângulo em DD11). Com o compasso, fazendo cen-
tro em BBrr e com raio até DDrr (a hipotenusa do triângulo em rebatimento é [BBrrDDrr], e o seu comprimento está em V.G. e é o raio do arco do
rebatimento de DD) desenhou-se um arco de circunferência até ao eixo XX, onde se situa DDrr11
. DDrr11
é o ponto DD rebatido pelo rebatimento do
plano de perfil e o triângulo [BBrrDD11DDrr11
] é o triângulo do rebatimento de DD em V.G. – com o compasso, fazendo centro em DD11 e raio até DDrr11
(o
raio corresponde à cota de DD) inverteu-se o rebatimento do plano de perfil, obtendo DD22, pelo qual se conduziu ffρ. Sobre a inversão do rebati-
mento dos restantes vértices do hexágono, a atendendo a que doravante esta situação é semelhante à situação do exercício 119911, sugere-se
o acompanhamento da resolução sequente com a leitura daquele relatório. A recta rr é a recta suporte da diagonal [AADD] do hexágono. A recta
mm é a recta fronto-horizontal que contém os vértices CC e FF do hexágono – é a recta suporte da diagonal [CCFF] do hexágono e é concorrente
com a recta rr no ponto OO.
204.
Em primeiro lugar representou-se o ponto OO, pelas suas projecções, em função dos dados – OO pertence ao β1/3, pelo que as suas projecções
são simétricas em relação ao eixo XX (o ponto tem coordenadas iguais, pois pertence ao β1/3). Note que não é necessário representar os
traços do β1/3 (que estão coincidentes no eixo XX, pois trata-se de um plano passante) – ver relatório do exercício 119999. Para determinar as
projecções do pentágono, há que rebater previamente o β1/3 e construir o polígono em V.G., em rebatimento, pois o pentágono não se pro-
jecta em V.G. em nenhum dos planos de projecção (o β1/3 não é paralelo a nenhum dos planos de projecção). Não há qualquer diferença
quanto ao plano de projecção para o qual se deverá rebater o β1/3, no sentido de uma maior economia de traçados. Optou-se por rebater o
β1/3 para o Plano Horizontal de Projecção (a charneira é o próprio eixo XX) – o ponto OO rebateu-se com o recurso ao seu triângulo do rebati-
mento, de forma semelhante à exposta para o rebatimento de SS no relatório do exercício 119999, pelo que se aconselha a leitura do respectivo
relatório. Com o compasso, fazendo centro em OOrr e com 3,5 cm de raio, desenhou-se a circunferência circunscrita ao pentágono e cons-
truiu-se a figura, inscrita na circunferência, de acordo com os dados. Para determinar as projecções do pentágono, há que inverter o rebati-
mento, o que se processou com o recurso a rectas do plano, para evitar o recurso a cinco triângulos do rebatimento. Assim, começou-se
por desenhar, em rebatimento, três rectas do plano – a recta aa (a recta suporte do lado [AABB] do pentágono), a recta bb (a recta suporte da
diagonal [CCEE] do pentágono, que é paralela à recta aa) e a recta cc (que é a recta paralela às rectas aa e bb e contém o vértice DD do pentágono).
203.
Em primeiro lugar representou-se o plano α, pelo seu traço horizontal
(o único que é conhecido), bem como o ponto AA, pelas suas projecções, em
função dos dados – AA é um ponto de hhα, que é uma recta horizontal (de ní-
vel) do plano com cota nula. Os dados do enunciado não nos permitem de-
senhar ffα – note que o ângulo dado (o ângulo entre os dois traços do plano)
é o âânngguulloo rreeaall, que existe nnoo eessppaaççoo (ou, mais correctamente, que está
contido no plano α) e não tem correspondência directa em projecções, pois
o plano α não é paralelo a nenhum dos planos de projecção. No entanto, é
possível prosseguir com o exercício. O plano α não é paralelo a nenhum dos
planos de projecção, pelo que é necessário o recurso a um processo geo-
métrico auxiliar. Optou-se pelo processo do rebatimento, o que nos obriga a
rebater o plano α para o Plano Horizontal de Projecção, pois não se conhe-
ce o seu traço frontal (que seria a charneira, caso se efectuasse o rebatimen-
to do plano α para o Plano Frontal de Projecção). Assim, a charneira foi hhα,
pelo que se tem imediatamente hhα ≡ ee11 ≡ hhαrr
– AArr ≡ AA11, pois AA é um ponto da
charneira. Em rebatimento, com vértice no ponto de concorrência dos dois
traços do plano (que é um ponto fixo, pois é um ponto da charneira) e a
partir de hhαrr
, mediram-se os 70° (o ângulo entre os dois traços do plano)
em V.G., em rebatimento, o que nos permitiu desenhar ffαrr
. O vértice BB, do
quadrado, tem afastamento nulo, pelo que BB é um ponto de ffα – BBrr tem de
se situar sobre ffαrr
. Com o compasso, fazendo centro em AArr e com 5 cm de
raio (a medida do lado do quadrado), determinou-se BBrr sobre ffαrr
. A partir
de AArr e BBrr construiu-se o quadrado em V.G., em rebatimento, obtendo CCrr e
DDrr. Para inverter o rebatimento, é necessário determinar ffα, o que se pro-
cessa determinando as projecções de um dos seus pontos – o ponto BB, neste caso, que é o único ponto conhecido de ffα (note que se
poderia, de qualquer forma, representar um outro ponto qualquer sobre ffαrr
). Por BBrr conduziu-se uma perpendicular à charneira (que corres-
ponde ao plano ortogonal à charneira que contém o arco do seu rebatimento) e determinou-se BB11 no eixo XX (BB é um ponto com afastamento
nulo). Com o compasso, fazendo centro no ponto de concorrência dos dois traços do plano (que é fixo) e raio até BBrr, desenhou-se um arco
de circunferência até à linha de chamada de BB11, onde se situa BB22 – ffα passa por BB22 e é concorrente com hhα no eixo XX. A inversão do rebati-
mento dos pontos CCrr e DDrr processou-se com o recurso a rectas frontais (de frente) do plano α, à semelhança do exercício 118800, pelo que se
aconselha a leitura do respectivo relatório. A partir das projecções dos quatro vértices do quadrado, desenharam-se as suas projecções.
(Continua na página seguinte)

75. Para determinar as projecções destas três rectas recorreu-se a
uma outra recta, paralela às rectas aa, bb e cc, que contenha um
ponto conhecido do plano – a recta rr, que contém o ponto OO. A
recta rrrr é paralela a aarr, a bbrr e a ccrr e passa por OOrr – as projecções
da recta rr determinam-se imediatamente, pois a recta rr é uma
recta passante (é concorrente com o eixo XX num ponto fixo) e as
suas projecções passam pelas projecções homónimas do ponto
OO. Em seguida, determinaram-se as projecções da recta aa – estas
são paralelas às projecções homónimas da recta rr e são concor-
rentes entre si num ponto do eixo XX, que é o ponto fixo da recta
(o seu ponto de concorrência com o eixo XX, que é a charneira).
Conduzindo, por AArr e por BBrr, as perpendiculares à charneira que
por eles passam (e que correspondem aos planos ortogonais à
charneira que contêm os respectivos arcos do rebatimento),
determinaram-se as projecções de AA e BB sobre as projecções
homónimas da recta aa. O processo descrito repetiu-se em relação
à recta bb e aos pontos CC e EE, bem como em relação à recta cc e
ao ponto DD, o que nos permitiu determinar as projecções dos cinco
vértices do polígono e, em seguida, desenhar as projecções do
pentágono.
75
SOLUÇÕES
205.
Em primeiro lugar representou-se o plano α, pelos seus traços,
e o ponto AA, pertencente ao plano, pelas suas projecções, em
função dos dados. O plano θ é ortogonal ao β2/4, pelo que tem
os seus traços coincidentes. O ponto AA é um ponto de ffα, que
é uma recta frontal (de frente) do plano com afastamento nulo.
Em seguida, há que determinar as projecções do ponto BB.
Uma vez que o lado [AABB] tem as suas projecções paralelas
entre si, para que tal se verifique BB tem de ter afastamento
igual à cota de AA (o lado [AABB] está contido numa recta paralela
ao β2/4). Um outro processo para determinar as projecções de
BB seria determinar, em primeiro lugar, a recta de intersecção do
plano α com o β2/4 (a recta ii) – a recta suporte do lado [AABB],
por ser paralela ao β2/4, seria paralela à recta ii. Assim, pelas
projecções de AA conduzir-se-iam as projecções homónimas de
uma recta paralela à recta ii e BB seria o traço horizontal dessa
recta. O plano α não é paralelo a nenhum dos planos de
projecção, pelo que o triângulo não se projecta em V.G. em
nenhum dos planos de projecção – é necessário o recurso a
um processo geométrico auxiliar. Uma vez que o ponto AA é um
ponto do Plano Frontal de Projecção e BB é um ponto do Plano
Horizontal de Projecção, ao nível da economia de traçados é
indistinto rebater o plano α para o Plano Frontal de Projecção
ou para o Plano Horizontal de Projecção. Optou-se por rebater
o plano α para o Plano Horizontal de Projecção (a charneira é
hhα – hhα ≡ ee11 ≡ hhαrr
). BB é um ponto da charneira, pelo que se tem
imediatamente BBrr ≡ BB11. Para rebater o plano α há que rebater o
seu traço frontal, o que se processa rebatendo um dos seus
pontos – o ponto AA. Sobre o rebatimento de AA e de ffα, ver relató-
rio do exercício 118822. A partir de AArr e BBrr construiu-se o triângulo
[AABBCC] em V.G., em rebatimento. Para inverter o rebatimento
recorreu-se a uma recta horizontal (de nível) do plano – a recta
hh, que contém o ponto CC – ver exercício 118822. A partir das pro-
jecções de todos os vértices do triângulo, desenharam-se as
suas projecções.
(Continua na página seguinte)
206.
Em primeiro lugar representou-se o ponto OO, pelas suas projecções, em função dos dados – OO pertence ao β1/3, pelo que as suas projecções são
simétricas em relação ao eixo XX (o ponto tem 4 cm de cota e 4 cm de afastamento, pois pontos do β1/3 têm coordenadas iguais). Note que não é
necessário representar os traços do β1/3 (que estão coincidentes no eixo XX, pois trata-se de um plano passante) – ver relatório do exercício 119999.
Para determinar as projecções do pentágono, há que rebater previamente o β1/3 e construir o polígono em V.G., em rebatimento, pois o pentágono

76. Em primeiro lugar representou-se o plano α, pelo seu traço horizontal
(o único que é conhecido), bem como o ponto AA, pelas suas projecções,
em função dos dados – AA é um ponto de hhα, que é uma recta horizontal (de
nível) do plano com cota nula. Os dados do enunciado não nos permitem
desenhar ffα – note que o ângulo dado (o ângulo entre os dois traços do
plano) é o âânngguulloo rreeaall, que existe nnoo eessppaaççoo (ou, mais correctamente, que
está contido no plano α) e não tem correspondência directa em projec-
ções, pois o plano α não é paralelo a nenhum dos planos de projecção.
Trata-se, portanto, de uma situação semelhante à do exercício 220033, pelo
que se aconselha a leitura do respectivo relatório. O plano α não é paralelo
a nenhum dos planos de projecção, pelo que é necessário o recurso a um
processo geométrico auxiliar. Rebateu-se o plano α para o Plano Horizontal
de Projecção, pois não se conhece o seu traço frontal (que seria a charnei-
ra, caso se efectuasse o rebatimento do plano α para o Plano Frontal de
Projecção). Assim, a charneira foi hhα, pelo que se tem imediatamente
hhα ≡ ee11 ≡ hhαrr
– AArr ≡ AA11, pois AA é um ponto da charneira. Em rebatimento,
com vértice no ponto de concorrência dos dois traços do plano (que é um
ponto fixo, pois é um ponto da charneira) e a partir de hhαrr
, mediram-se os
60o (o ângulo entre os dois traços do plano) em V.G., em rebatimento, o
que nos permitiu desenhar ffαrr
. O vértice BB, do triângulo, tem afastamento
nulo, pelo que BB é um ponto de ffα – BBrr tem de se situar sobre ffαrr
. Por outro
lado, o ângulo que o lado [AABB] faz com hhα é, também, um âânngguulloo rreeaall que
está contido no próprio plano α (e que também não tem correspondência
76
SOLUÇÕES
não se projecta em V.G. em nenhum dos planos de projecção (o β1/3
não é paralelo a nenhum dos planos de projecção). Não há qualquer
diferença quanto ao plano de projecção para o qual se deverá reba-
ter o β1/3, no sentido de uma maior economia de traçados. Optou-se
por rebater o β1/3 para o Plano Horizontal de Projecção (a charneira é
o próprio eixo XX) – o ponto OO rebateu-se com o recurso ao seu triân-
gulo do rebatimento, de forma semelhante à exposta para o rebati-
mento de SS no relatório do exercício 119999, pelo que se aconselha a
leitura do respectivo relatório. Com o compasso, fazendo centro em
OOrr, desenhou-se a circunferência circunscrita ao pentágono (que é
tangente ao eixo XX) e construiu-se a figura, inscrita na circunferência,
de acordo com os dados (AA tem cota nula, pelo que é um ponto do
eixo XX –os pontos do β1/3 que têm cota nula situam-se todos no eixo
XX, pelo que AA é o ponto em que a circunferência é tangente ao eixo
XX). Para determinar as projecções do pentágono, há que inverter o
rebatimento, o que se processou com o recurso a rectas do plano,
para evitar o recurso a quatro triângulos do rebatimento. Assim,
começou-se por desenhar, em rebatimento, a recta rr – a recta rr é
uma recta que contém o ponto OO e que contém um vértice do pentá-
gono (o vértice CC). A recta rrrr passa por OOrr e CCrr – as projecções da
recta rr determinam-se imediatamente, pois trata-se de uma recta
passante (é concorrente com o eixo XX num ponto fixo) e as suas pro-
jecções passam pelas projecções homónimas do ponto OO. Condu-
zindo, por CCrr, uma perpendicular à charneira (que corresponde ao
plano ortogonal à charneira que contém o arco do seu rebatimento),
determinaram-se as projecções de CC sobre as projecções homóni-
mas da recta rr. A recta aa é a recta suporte da diagonal [BBEE] do pen-
tágono – é uma recta fronto-horizontal. A recta aarr passa por BBrr e EErr e
é concorrente com rrrr no ponto PPrr. As projecções de PP determinaram-se imediatamente, sobre as projecções homónimas da recta rr, recorrendo ao
plano ortogonal à charneira que contém o arco do seu rebatimento. Pelas projecções de PP conduziram-se as projecções homónimas da recta aa –
a recta aa está definida por um ponto (o ponto PP) e por uma direcção (é fronto-horizontal). Conduzindo, por BBrr e por EErr, as perpendiculares à char-
neira que por eles passam (e que correspondem aos planos ortogonais à charneira que contêm os respectivos arcos do rebatimento), determina-
ram-se as projecções de BB e EE sobre as projecções homónimas da recta aa. A recta bb é a recta suporte do lado [CCDD] do pentágono – é outra recta
fronto-horizontal. A recta bbrr passa por CCrr e DDrr e é concorrente com rrrr em CCrr. As projecções de CC já são conhecidas. Pelas projecções de CC
conduziram-se as projecções homónimas da recta bb – a recta bb está definida por um ponto (o ponto CC) e por uma direcção (é fronto-horizontal).
Conduzindo, por DDrr, uma perpendicular à charneira (que corresponde ao plano ortogonal à charneira que contém o arco do seu rebatimento),
determinaram-se as projecções de DD sobre as projecções homónimas da recta bb. AA é um ponto de charneira, que é o eixo XX pelo que se tem ime-
diatamente AArr ≡ AA11 ≡ AA22. A partir das projecções dos cinco vértices do polígono, desenharam-se as projecções do pentágono.
207.
(Continua na página seguinte)

77. 77
SOLUÇÕES
directa em projecções). Uma vez que o plano α já está rebatido, esse ângulo já pode ser medido em V.G. (em rebatimento). Assim, com
vértice em AArr e a partir de hhαrr
, mediram-se os 60°, havendo duas hipóteses de o fazer – numa delas, o outro lado do ângulo fica paralelo a
ffαrr
, pelo que o ponto BB se situaria no infinito. Assim, das duas hipóteses para medir os 60°, apenas a apresentada é a solução pretendida –
o ponto BBrr situa-se sobre ffαrr
. A partir de AArr e de BBrr construiu-se o triângulo [AABBCC] em V.G., em rebatimento – note que, em função dos ângu-
los dados, o lado [BBrrCCrr] é nneecceessssaarriiaammeennttee paralelo a hhαrr
(está contido numa recta horizontal do plano) e o lado [AArrCCrr] é nneecceessssaarriiaammeennttee
paralelo a ffαrr
(está contido numa recta frontal do plano). Para inverter o rebatimento, é necessário determinar ffα, o que se processa determi-
nando as projecções de um dos seus pontos – o ponto BB, neste caso, que é o único ponto conhecido de ffα (note que se poderia, de qual-
quer forma, representar um outro ponto qualquer sobre ffαrr
). Por BBrr conduziu-se uma perpendicular à charneira (que corresponde ao plano
ortogonal à charneira que contém o arco do seu rebatimento) e determinou-se BB11 no eixo XX (BB é um ponto com afastamento nulo). Com o
compasso, fazendo centro no ponto de concorrência dos dois traços do plano (que é fixo) e raio até BBrr, desenhou-se um arco de circunfe-
rência até à linha de chamada de BB11, onde se situa BB22 – ffα passa por BB22 e é concorrente com hhα no eixo XX. A inversão do rebatimento do
ponto CCrr processou-se com o recurso a uma recta horizontal (de nível) do plano α (a recta hh, que é a recta suporte do lado [BBCC] do triân-
gulo), à semelhança do exercício 118822, pelo que se aconselha a leitura do respectivo relatório. Note que o ponto BB é o traço frontal da recta
hh. A partir das projecções dos três vértices do triângulo, desenharam-se as suas projecções.
208.
Em primeiro lugar representou-se o plano ρ, pelo seu traço hori-
zontal (o único dado concreto, uma vez que o enunciado é omisso
em relação ao traço frontal do plano), bem como o ponto CC, pelas
suas projecções, em função dos dados – CC é um ponto de hhρ, que
é uma recta horizontal (fronto-horizontal) do plano com cota nula.
O plano ρ não é paralelo a nenhum dos planos de projecção, pelo
que é necessário o recurso a um processo geométrico auxiliar. O
ponto CC é um ponto do Plano Horizontal de Projecção, pelo que se
rebateu o plano ρ para o Plano Horizontal de Projecção (a charneira
é hhρ – hhρ ≡ ee11 ≡ hhρrr
) – tem-se imediatamente CCrr ≡ CC11, pois CC é um
ponto da charneira. Note que não seria possível rebater o plano ρ
para o Plano Frontal de Projecção, pois não é conhecido o seu tra-
ço frontal (que seria, nessa situação, a charneira). Não é possível
rebater o traço frontal do plano, pois aquele não é conhecido, mas
é possível prosseguir com o exercício. Consideremos, então, plano
ρ já rebatido e efectuemos os traçados necessários à construção
do quadrado em rebatimento. O ângulo dado entre a diagonal
[AACC] e o traço horizontal do plano é um âânngguulloo rreeaall, que existe nnoo
eessppaaççoo e não em projecções (esse ângulo eessttáá ccoonnttiiddoo nnoo ppllaannoo
ρ) – ver exercício 119900 e respectivo relatório. Assim, uma vez que o
plano está rebatido, esse ângulo está em V.G. – com vértice em CCrr,
e a partir de hhρrr
, mediram-se os 60° (o ângulo dado), garantindo
que AA se situa à esquerda de CC, e obtendo uma recta rrrr (a recta rr é
a recta suporte da diagonal [AACC] do quadrado). Sobre rrrr mediram-
-se os 8 cm (o comprimento da diagonal) e determinou-se AArr (note
que AArr se situa à esquerda de CCrr – caso o ângulo se tivesse medido
para a direita, AArr situar-se-ia à direita de CCrr). Por AArr conduziu-se ffαrr
, paralelo a hhρrr
(e ao eixo XX) – note que é dado, no enunciado, que AA tem afas-
tamento nulo, pelo que AA é um ponto de ffρ. A partir de AArr e CCrr, construiu-se o quadrado [AABBCCDD] em V.G., em rebatimento. Para determinar as
projecções do polígono, há que inverter o rebatimento. Comecemos por determinar ffρ – para tal é necessário inverter o rebatimento de um ponto
de ffρ, que é o ponto AA. Por AArr conduziu-se uma perpendicular à charneira, que corresponde ao plano ortogonal à charneira que contém o arco
do seu rebatimento (que é um plano de perfil, que também contém o triângulo do rebatimento de AA) e determinou-se AA11 no eixo XX (AA tem afasta-
mento nulo). O triângulo do rebatimento de AA, nnoo eessppaaççoo, é o triângulo [OOAAAA11] – note que OO é o ponto de intersecção da charneira com o plano
de perfil que contém o triângulo, pelo que OO é o centro do arco do rebatimento de AA (OO é um ponto fixo do qual não se assinalaram as projec-
ções, por questões de simplificação da leitura da resolução gráfica apresentada). O triângulo [OOAAAA11] é rectângulo em AA11 e a hipotenusa [OOAA]
está contida numa recta de perfil (que é a recta de intersecção do plano ρ com o plano de perfil que contém o triângulo). Com o compasso,
fazendo centro em OO e raio até AArr ([OOAA] é a hipotenusa do triângulo do rebatimento de AA e está em V.G. no rebatimento do plano ρ) desenhou-
-se um arco de circunferência até ao eixo XX, onde se situa AArr11
– o triângulo do rebatimento de AA está em V.G. (pelo rebatimento do plano de perfil
que o contém) no triângulo [OOAA11AArr11
]. Note que AAෆ11ෆAAෆrrෆ11
ෆ é a cota de AA – com o compasso, fazendo centro em AA11 e raio até AArr11
, desenhou-se um
arco de circunferência até à perpendicular à charneira que passa por AArr (e que corresponde ao plano ortogonal à charneira que contém o arco
do seu rebatimento bem como o seu triângulo do rebatimento) e determinou-se AA22. O traço frontal do plano ρ, ffρ, passa por AA22 e é paralelo ao
eixo XX. Para inverter o rebatimento dos pontos BB e DD recorreu-se a duas rectas do plano, paralelas à recta rr – a recta aa e a recta bb. A recta aarr
passa por BBrr e é paralela a rrrr – HHrr é o ponto de concorrência de aarr com hhρrr
e é um ponto da charneira (é fixo), pelo que se tem imediatamente
HH11 ≡ HHrr (HH22 situa-se no eixo XX). As projecções da recta aa determinaram-se imediatamente, passando pelas projecções homónimas de HH e parale-
las às projecções homónimas da recta rr – a recta aa está definida por um ponto (HH) e por uma direcção (é paralela à recta rr). Note que as projec-
ções da recta aa se poderiam ter determinado a partir dos seus dois traços, à semelhança da situação do exercício 119900. Conduzindo, por BBrr, uma
perpendicular à charneira (que corresponde ao plano ortogonal à charneira que contém o arco do seu rebatimento), determinaram-se as projec-
ções de BB sobre as projecções homónimas da recta aa. O processo exposto repetiu-se para o vértice DD – a recta bb é a recta paralela à recta rr que
contém DD e HH’’ é o seu traço horizontal. A partir das projecções dos quatro vértices do quadrado, desenharam-se as suas projecções.

78. 212.
Em primeiro lugar representaram-se os pontos AA e BB pelas suas projecções, em
função dos dados. A V.G. da distância entre os pontos AA e BB é o comprimento do
segmento de recta que tem extremos nesses dois pontos. Como o segmento
[AABB] é oblíquo a ambos os planos de projecção, não se projecta em V.G. em
nenhum dos planos de projecção, pelo que a determinação da V.G. do seu com-
primento passa, necessariamente, pelo recurso a um dos processos geométricos
auxiliares. Recorreu-se a uma mudança do diedro de projecção, conforme se
pede expressamente no enunciado. Na presente situação optou-se por transfor-
mar o segmento [AABB] num segmento de recta horizontal (de nível) – manteve-se
o Plano Frontal de Projecção (ppllaannoo 22), substituindo o Plano Horizontal de Pro-
jecção (ppllaannoo 11) por um outro plano (ppllaannoo 44), paralelo ao segmento. Dessa for-
ma, mantêm-se as projecções frontais e alteram-se as projecções horizontais. Já em relação às coordenadas, mantêm-se os afastamentos
(a relação entre os pontos e o Plano Frontal de Projecção manteve-se) e alteram-se as cotas (mudou a relação entre os pontos e o Plano
Horizontal de Projecção). O novo eixo XX (eixo XX’’) é a recta de intersecção do ppllaannoo 22 com o ppllaannoo 44 e é paralelo à projecção frontal do seg-
mento (a uma distância qualquer desta). As novas projecções de AA e BB (AA44 e BB44) determinaram-se em função dos seus afastamentos (que
se mantiveram) nas novas linhas de chamada dos pontos (perpendiculares ao eixo XX’’). A V.G. da distância de AA a BB é o comprimento do
segmento [AA44BB44]. Note que a resolução poderia passar pela transformação do segmento [AABB] num segmento frontal (de frente).
78
SOLUÇÕES
209.
Por pprroobblleemmaass mmééttrriiccooss entende-se o conjunto dos problemas e exercícios que envolvem a determinação da real dimensão (verdadeira
grandeza) de algumas grandezas mensuráveis, nomeadamente ddiissttâânncciiaass (entre pontos, entre pontos e planos, entre pontos e rectas e entre
planos paralelos) e âânngguullooss (entre rectas, entre rectas e planos e entre planos).
210.
Em primeiro lugar representaram-se os pontos AA e BB pelas suas projecções, em
função dos dados. A V.G. da distância entre os pontos AA e BB é o comprimento do
segmento de recta que tem extremos nesses dois pontos. Como o segmento
[AABB] é oblíquo a ambos os planos de projecção, não se projecta em V.G. em ne-
nhum dos planos de projecção, pelo que a determinação da V.G. do seu compri-
mento passa, necessariamente, pelo recurso a um dos processos geométricos
auxiliares. Recorreu-se ao rebatimento do plano projectante frontal do segmento
(o plano α) para o Plano Horizontal de Projecção, conforme se pede expressa-
mente no enunciado. A charneira do rebatimento é a recta de intersecção do pla-
no com o Plano Horizontal de Projecção – é o seu traço horizontal (que é uma
recta de topo do plano com cota nula). Os arcos do rebatimento estão contidos
em planos frontais (planos ortogonais à charneira), pelo que se projectam em
V.G. no Plano Frontal de Projecção. Os pontos mantêm, assim, o seu afastamento.
A V.G. da distância entre AA e BB é o comprimento do segmento [AArrBBrr].
Em primeiro lugar representaram-se os pontos AA e BB pelas suas projecções, em
função dos dados. A V.G. da distância entre os pontos AA e BB é o comprimento do
segmento de recta que tem extremos nesses dois pontos. Como o segmento [AABB]
é oblíquo a ambos os planos de projecção, não se projecta em V.G. em nenhum
dos planos de projecção, pelo que a determinação da V.G. do seu comprimento
passa, necessariamente, pelo recurso a um dos processos geométricos auxiliares.
Recorreu-se ao rebatimento do plano projectante frontal do segmento (o plano α)
para o Plano Frontal de Projecção, conforme se pede expressamente no enunciado.
Na presente situação, a charneira do rebatimento é o traço frontal do plano (que
é uma recta frontal do plano com afastamento nulo) – a recta de intersecção do
plano com o Plano Frontal de Projecção. O rebatimento dos pontos processa-se
em planos ortogonais à charneira – planos de topo ortogonais a ffα. Assim, por AA22
conduziu-se uma perpendicular à charneira (que corresponde ao plano ortogonal à
charneira que contém o arco do seu rebatimento) e, sobre esta, representou-se em
V.G. o afastamento de AA, que é o raio do seu arco do rebatimento, obtendo AArr. O
processo repetiu-se para BB, obtendo BBrr. A V.G. da distância entre AA e BB é o compri-
mento do segmento [AArrBBrr].
PROBLEMAS MÉTRICOS
17
211.

79. 79
SOLUÇÕES
213.
Em primeiro lugar representaram-se os pontos AA e BB pelas suas projecções, em função
dos dados. A V.G. da distância entre os pontos AA e BB é o comprimento do segmento de
recta que tem extremos nesses dois pontos. Como o segmento [AABB] é oblíquo a ambos
os planos de projecção, não se projecta em V.G. em nenhum dos planos de projecção,
pelo que a determinação da V.G. do seu comprimento passa, necessariamente, pelo
recurso a um dos processos geométricos auxiliares. Recorreu-se ao rebatimento do plano
projectante horizontal do segmento (o plano γ) para o plano frontal (de frente) que con-
tém o ponto AA (o plano ϕ, representado pelo seu traço horizontal), conforme se pede
expressamente no enunciado. A charneira do rebatimento é a recta de intersecção do
plano γ (o plano projectante horizontal de [AABB]) com o plano ϕ (o plano frontal que passa
por AA) – é a recta vertical (ee) que passa por AA, pois AA é um ponto dos dois planos. O plano
projectante horizontal do segmento (plano γ) está definido pelo segmento e pela charneira.
O segmento rebatido sobre o plano frontal ϕ projecta-se em V.G. no Plano Frontal de Pro-
jecção, pois ϕ é paralelo àquele. AA22 ≡ AArr, pois AA é um ponto da charneira. O rebatimento
de BB processa-se num plano ortogonal à charneira – um plano horizontal (de nível). Dessa
forma, o arco do rebatimento de BB projecta-se em V.G. no Plano Horizontal de Projecção e o seu centro é o ponto de intersecção da charneira
com o plano horizontal (de nível) que contém o arco do rebatimento de BB. Note que não se identificou nem o plano horizontal (de nível) nem o
centro do arco do rebatimento de BB. O ponto BB, no seu rebatimento, mantém a sua cota, pelo que BBrr tem a cota de BB22. A V.G. da distância
de AA a BB é o comprimento do segmento [AArrBBrr], que está em V.G. no Plano Frontal de Projecção.
Em primeiro lugar representaram-se os pontos AA e BB pelas suas projecções, em
função dos dados. A V.G. da distância entre os pontos AA e BB é o comprimento do
segmento de recta que tem extremos nesses dois pontos. Como o segmento [AABB]
é oblíquo a ambos os planos de projecção, não se projecta em V.G. em nenhum
dos planos de projecção, pelo que a determinação da V.G. do seu comprimento
passa, necessariamente, pelo recurso a um dos processos geométricos auxiliares.
Recorreu-se ao rebatimento do plano projectante horizontal do segmento (o plano γ)
para o plano horizontal (de nível) que contém o ponto AA (o plano ν, representado
pelo seu traço frontal), conforme se pede expressamente no enunciado. A charneira
do rebatimento é a recta de intersecção do plano projectante horizontal de [AABB] (o
plano γ) com o plano horizontal (de nível) que passa por AA – é uma recta horizontal
(ee) que passa por AA, pois AA é um ponto dos dois planos. O plano projectante hori-
zontal do segmento (plano γ) está definido pelo segmento e pela charneira. O seg-
mento rebatido sobre o plano horizontal (de nível) ν projecta-se em V.G. no Plano
Horizontal de Projecção, pois ν é paralelo àquele. AA11 ≡ AArr, pois AA é um ponto da
charneira. O rebatimento de BB processa-se num plano ortogonal à charneira – um
plano vertical ortogonal à charneira. Assim, por BB11 conduziu-se uma perpendicular
à charneira (que corresponde ao plano ortogonal à charneira que contém o arco
do seu rebatimento) e, sobre esta, representou-se em V.G. a cota de BB em relação
ao plano ν (a distância de BB a ν), que é o raio do seu arco do rebatimento, obtendo BBrr. A V.G. da distância entre AA e BB é o comprimento do
segmento [AArrBBrr], que está em V.G. no Plano Horizontal de Projecção.
214.
215.
Em primeiro lugar representaram-se os pontos RR e SS pelas suas projecções, em função
dos dados, bem como o plano de perfil (o plano π) que os contém, pelos seus traços.
A V.G. da distância entre os pontos RR e SS é o comprimento do segmento de recta que tem
extremos nesses dois pontos. Como o segmento [RRSS] é oblíquo a ambos os planos de
projecção, não se projecta em V.G. em nenhum dos planos de projecção, pelo que a deter-
minação da V.G. do seu comprimento passa, necessariamente, pelo recurso a um dos pro-
cessos geométricos auxiliares. Recorreu-se ao rebatimento do plano π para o Plano Frontal
de Projecção, conforme se pede expressamente no enunciado. Na presente situação, a
charneira do rebatimento é o traço frontal do plano (que é uma recta vertical do plano com
afastamento nulo) – a recta de intersecção do plano com o Plano Frontal de Projecção. O
rebatimento dos pontos processa-se em planos ortogonais à charneira – planos horizontais
(de nível). Os arcos do rebatimento projectam-se em V.G. no Plano Horizontal de Projecção
e os pontos, ao longo do seu rebatimento, mantêm as respectivas cotas. A V.G. da distân-
cia de RR a SS é o comprimento do segmento [RRrrSSrr].

80. 80
SOLUÇÕES
216.
Em primeiro lugar representaram-se os pontos RR e SS pelas suas projecções, em função
dos dados, bem como o plano de perfil (o plano π) que os contém, pelos seus traços.
A V.G. da distância entre os pontos RR e SS é o comprimento do segmento de recta que tem
extremos nesses dois pontos. Como o segmento [RRSS] é oblíquo a ambos os planos de
projecção, não se projecta em V.G. em nenhum dos planos de projecção, pelo que a
determinação da V.G. do seu comprimento passa, necessariamente, pelo recurso a um dos
processos geométricos auxiliares. Recorreu-se a uma mudança do diedro de projecção,
conforme se pede expressamente no enunciado. Na presente situação optou-se por trans-
formar o segmento [RRSS] num segmento de recta frontal (de frente) – manteve-se o Plano
Horizontal de Projecção (ppllaannoo 11), substituindo o Plano Frontal de Projecção (ppllaannoo 22)
por um outro plano (ppllaannoo 44), paralelo ao segmento. Dessa forma, mantêm-se as projec-
ções horizontais e alteram-se as projecções frontais. Já em relação às coordenadas, man-
têm-se as cotas (a relação entre os pontos e o Plano Horizontal de Projecção manteve-se)
e alteram-se os afastamentos (mudou a relação entre os pontos e o Plano Frontal de Pro-
jecção). O novo eixo XX (eixo XX’’) é a recta de intersecção do ppllaannoo 11 com o ppllaannoo 44 e é pa-
ralelo à projecção horizontal do segmento (a uma distância qualquer desta). As novas
projecções de RR e SS (RR44 e SS44) determinaram-se em função das suas cotas (que se manti-
veram) nas novas linhas de chamada dos pontos (perpendiculares ao eixo XX’’). A V.G. da
distância de RR a SS é o comprimento do segmento [RR44SS44]. Note que a resolução poderia
passar pela transformação do segmento [RRSS] num segmento horizontal (de nível).
Em primeiro lugar representaram-se os pontos MM e NN pelas suas projecções, em fun-
ção dos dados. A V.G. da distância entre os pontos MM e NN é o comprimento do seg-
mento de recta que tem extremos nesses dois pontos. Como o segmento [MMNN] é
oblíquo a ambos os planos de projecção, não se projecta em V.G. em nenhum dos
planos de projecção, pelo que a determinação da V.G. do seu comprimento passa,
necessariamente, pelo recurso a um dos processos geométricos auxiliares. Recor-
reu-se a uma mudança do diedro de projecção, optando-se por transformar o seg-
mento [MMNN] num segmento de recta frontal (de frente), o que resulta na situação do
exercício anterior, pelo que se aconselha a leitura do respectivo relatório. A V.G. da
distância de MM a NN é o comprimento do segmento [MM44NN44]. Note que a resolução
poderia passar pela transformação do segmento [MMNN] num segmento horizontal (de
nível) ou, ainda, pelo rebatimento de um plano projectante do segmento (o plano
projectante frontal do segmento ou o seu plano projectante horizontal), uma vez que
o enunciado é omisso em relação ao processo geométrico auxiliar a utilizar.
218.
Em primeiro lugar representaram-se os pontos MM e NN pelas suas projecções, em
função dos dados. A V.G. da distância entre os pontos MM e NN é o comprimento do
segmento de recta que tem extremos nesses dois pontos. Como o segmento
[MMNN] é oblíquo a ambos os planos de projecção, não se projecta em V.G. em
nenhum dos planos de projecção, pelo que a determinação da V.G. do seu com-
primento passa, necessariamente, pelo recurso a um dos processos geométricos
auxiliares. Recorreu-se a uma mudança do diedro de projecção, optando-se por
transformar o segmento [MMNN] num segmento de recta frontal (de frente), o que
resulta na situação do exercício 221166, pelo que se aconselha a leitura do respectivo
relatório. Note que NN44, a projecção no ponto NN no ppllaannoo 44, se determinou em fun-
ção da sua cota, que se manteve e é negativa. A V.G. da distância de MM a NN é o
comprimento do segmento [MM44NN44]. Note mais uma vez que a resolução poderia
passar pela transformação do segmento [MMNN] num segmento horizontal (de nível)
ou, ainda, pelo rebatimento de um plano projectante do segmento (o plano pro-
jectante frontal do segmento ou o seu plano projectante horizontal), uma vez que
o enunciado é omisso em relação ao processo geométrico auxiliar a utilizar.
217.

81. 219.
Por ddiissttâânncciiaa ddee uumm ppoonnttoo aa uumm ppllaannoo entende-se o comprimento do segmento de recta ortogonal ao plano que tem um extremo no ponto
e o outro extremo no plano (no ponto de intersecção do plano com a recta suporte do segmento).
220.
O mmééttooddoo ggeerraall ppaarraa aa ddeetteerrmmiinnaaççããoo ddaa ddiissttâânncciiaa ddee uumm ppoonnttoo aa uumm ppllaannoo consiste em: 11.. conduzir, pelo ponto, uma recta ortogonal ao
plano; 22.. determinar o ponto de intersecção dessa recta com o plano; 33.. a distância do ponto ao plano é o comprimento do segmento de
recta que tem extremos nos dois pontos – o ponto dado e o ponto de intersecção da recta com o plano.
221.
Em primeiro lugar representaram-se o plano ν, pelo seu traço frontal, e o ponto AA, pelas suas
projecções, em função dos dados. Para determinar a distância do ponto AA ao plano ν recorreu-
-se ao mmééttooddoo ggeerraall ppaarraa aa ddeetteerrmmiinnaaççããoo ddaa ddiissttâânncciiaa ddee uumm ppoonnttoo aa uumm ppllaannoo, conforme
se expõe em seguida. 11.. Pelo ponto AA conduziu-se uma recta pp, ortogonal ao plano (a recta pp é
uma recta vertical). 22.. Determinou-se o ponto II, o ponto de intersecção da recta pp com o plano
ν – o ponto II teve determinação directa, pois tanto a recta como o plano são projectantes. 33.. A
distância do ponto AA ao plano ν é o comprimento do segmento de recta [AAII]. O segmento [AAII]
é vertical, pelo que se projecta em V.G. no Plano Frontal de Projecção – a V.G. da distância de
AA a ν é AAෆ22ෆIIෆ22ෆ.
81
SOLUÇÕES
223.
Em primeiro lugar representaram-se o plano π, pelos seus traços, e o ponto AA, pelas suas
projecções, em função dos dados. Para determinar a distância do ponto AA ao plano π recor-
reu-se ao mmééttooddoo ggeerraall ppaarraa aa ddeetteerrmmiinnaaççããoo ddaa ddiissttâânncciiaa ddee uumm ppoonnttoo aa uumm ppllaannoo, à se-
melhança do exercício anterior, pelo que se aconselha a leitura do respectivo relatório. A
recta pp (a recta ortogonal ao plano π que passa por AA) é fronto-horizontal. O plano π é um
plano duplamente projectante (a determinação do ponto II é directa, a partir das suas duas
projecções). O segmento [AAII] é fronto-horizontal, pelo que se projecta em V.G. em ambas as
projecções – a V.G. da distância de AA a π é AAෆ22ෆIIෆ22ෆ = AAෆ11ෆIIෆ11ෆ.
Em primeiro lugar representaram-se o plano γ, pelos seus traços, e o ponto PP, pelas
suas projecções, em função dos dados. Para determinar a distância do ponto PP ao pla-
no γ recorreu-se ao mmééttooddoo ggeerraall ppaarraa aa ddeetteerrmmiinnaaççããoo ddaa ddiissttâânncciiaa ddee uumm ppoonnttoo aa
uumm ppllaannoo, conforme se expõe em seguida. 11.. Pelo ponto PP conduziu-se uma recta pp,
ortogonal ao plano (a recta pp é uma recta horizontal). 22.. Determinou-se o ponto II, o
ponto de intersecção da recta pp com o plano γ – o ponto II teve determinação directa a
partir da sua projecção horizontal, pois o plano é projectante horizontal. 33.. A distância
do ponto PP ao plano γ é o comprimento do segmento de recta [PPII]. O segmento [PPII] é
horizontal (de nível), pelo que se projecta em V.G. no Plano Horizontal de Projecção – a
V.G. da distância de PP a γ é PPෆ11ෆIIෆ11ෆ.
222.

82. 82
SOLUÇÕES
225.
Em primeiro lugar representaram-se o plano α, pelos seus traços, e o
ponto PP, pelas suas projecções, em função dos dados. Para determinar a
distância do ponto PP ao plano α recorreu-se ao mmééttooddoo ggeerraall ppaarraa aa
ddeetteerrmmiinnaaççããoo ddaa ddiissttâânncciiaa ddee uumm ppoonnttoo aa uumm ppllaannoo – uma vez que o
plano α é um plano oblíquo, a presente situação é semelhante à situação
do exercício anterior, pelo que se aconselha a leitura do respectivo relatório.
A determinação da V.G. do comprimento do segmento [PPII] processou-se
através do rebatimento do plano γ (o plano projectante horizontal da
distância) para o Plano Frontal de Projecção – o ponto PP é um ponto da
charneira, pelo que se tem imediatamente PPrr ≡ PP22. A V.G. da distância de
PP a α é PPෆrrෆIIෆrrෆ.
224.
Em primeiro lugar representaram-se o plano α, pelos seus traços, e o ponto PP, pelas
suas projecções, em função dos dados. O plano α tem os seus traços simétricos em
relação ao eixo XX, pois é ortogonal ao β1/3. O ponto PP tem as suas projecções simétricas
em relação ao eixo XX, pois é um ponto do β1/3 (pontos do β1/3 têm coordenadas iguais e
projecções simétricas em relação ao eixo XX). Para determinar a distância do ponto PP ao
plano α recorreu-se ao mmééttooddoo ggeerraall ppaarraa aa ddeetteerrmmiinnaaççããoo ddaa ddiissttâânncciiaa ddee uumm ppoonnttoo aa
uumm ppllaannoo, conforme se expõe em seguida. 11.. Pelo ponto PP conduziu-se uma recta pp,
ortogonal ao plano (a recta pp é uma recta oblíqua, cujas projecções são perpendiculares
aos traços homónimos do plano). 22.. Determinou-se o ponto II, o ponto de intersecção da
recta pp com o plano α – a determinação do ponto II processou-se com o recurso ao
mmééttooddoo ggeerraall ddaa iinntteerrsseeccççããoo ddee rreeccttaass ccoomm ppllaannooss, pois nem a recta nem o plano são
projectantes. O plano γ é o plano auxiliar a que se recorreu (é o plano projectante hori-
zontal da recta pp). A recta ii é a recta de intersecção dos dois planos (o plano α e o plano γ)
e determinou-se a partir do caso geral da intersecção entre planos. O ponto II é o ponto
de concorrência das rectas pp e ii. 33.. A distância do ponto PP ao plano α é o comprimento
do segmento de recta [PPII]. O segmento [PPII] é oblíquo, pelo que não se projecta em V.G.
em nenhuma das suas projecções. A determinação da V.G. da distância obriga, assim,
ao recurso a um processo geométrico auxiliar. Optou-se por rebater o plano projectante
horizontal da distância para o plano horizontal (de nível) que contém o ponto II (ver exer-
cício 221144 e respectivo relatório). O ponto PP rebateu-se em função da sua cota em relação
ao plano ν (a distância do ponto PP ao plano ν). A V.G. da distância de PP a α é PPෆrrෆIIෆrrෆ.
226.
Em primeiro lugar representaram-se o plano δ, pelos seus traços, e o ponto PP,
pelas suas projecções, em função dos dados. O plano δ tem os seus traços
coincidentes, pois é ortogonal ao β2/4. Para determinar a distância do ponto PP ao
plano δ recorreu-se ao mmééttooddoo ggeerraall ppaarraa aa ddeetteerrmmiinnaaççããoo ddaa ddiissttâânncciiaa ddee uumm
ppoonnttoo aa uumm ppllaannoo – uma vez que o plano δ é um plano oblíquo, a presente
situação é semelhante à situação do exercício 222244, pelo que se aconselha a lei-
tura do respectivo relatório. A recta pp (a recta ortogonal ao plano δ que passa
por PP) tem as suas projecções paralelas entre si. A determinação da V.G. do
comprimento do segmento [PPII] processou-se com o recurso a uma mudança
do diedro de projecção, transformando o segmento (que é oblíquo) num seg-
mento horizontal (de nível). Para tal, manteve-se o Plano Frontal de Projecção
(ppllaannoo 22), substituindo o Plano Horizontal de Projecção (ppllaannoo 11) por um outro
plano (ppllaannoo 44), paralelo ao segmento. Dessa forma, mantêm-se as projecções
frontais e alteram-se as projecções horizontais. Já em relação às coordenadas,
mantêm-se os afastamentos (a relação entre os pontos e o Plano Frontal de Pro-
jecção manteve-se) e alteram-se as cotas (mudou a relação entre os pontos e o Plano Horizontal de Projecção). O novo eixo XX (eixo XX’’) é a
recta de intersecção do ppllaannoo 22 com o ppllaannoo 44 e é paralelo à projecção frontal do segmento (a uma distância qualquer desta). As novas
projecções de PP e II (PP44 e II44) determinaram-se em função dos seus afastamentos (que se mantiveram) nas novas linhas de chamada dos
pontos (perpendiculares ao eixo XX’’). A V.G. da distância de PP a II é o comprimento do segmento [PP44II44].

83. 83
SOLUÇÕES
227.
Em primeiro lugar representaram-se a recta rr e o ponto PP, pelas suas projecções,
em função dos dados. As projecções da recta rr determinaram-se em função das
projecções de AA e BB. Em seguida, determinaram-se os traços da recta rr nos planos
de projecção. A recta rr é uma recta de maior declive do plano λ, pelo que hhλ passa
por HH11 e é perpendicular a rr11. O traço frontal de λ, ffλ, é concorrente com hhλ no eixo
XX e passa por FF22. A determinação dos traços de λ foi essencial para conduzir, por PP,
uma recta ortogonal a λ. Para determinar a distância do ponto PP ao plano δ recor-
reu-se ao mmééttooddoo ggeerraall ppaarraa aa ddeetteerrmmiinnaaççããoo ddaa ddiissttâânncciiaa ddee uumm ppoonnttoo aa uumm ppllaa--
nnoo – uma vez que o plano δ é um plano oblíquo, a presente situação é semelhante à
situação do exercício 222244, pelo que se aconselha a leitura do respectivo relatório. A
determinação da V.G. do comprimento do segmento [PPII] processou-se rebatendo o
plano α (o plano projectante horizontal da distância) para o plano horizontal (de ní-
vel) que passa por PP (ver exercício 221144 e respectivo relatório). PP é um ponto da
charneira (é fixo) e o ponto II rebateu-se em função da sua cota em relação ao plano
ν (a distância de II a ν). A V.G. da distância de PP a λ é PPෆrrෆIIෆrrෆ.
Em primeiro lugar representaram-se as rectas ff e hh, bem como o ponto PP, pelas res-
pectivas projecções, em função dos dados. O ponto de concorrência das rectas ff e hh
(o ponto AA) tem 3 cm de afastamento (o afastamento da recta frontal) e 4 cm de cota
(a cota da recta horizontal). Para determinar a distância do ponto PP ao plano α recor-
reu-se ao mmééttooddoo ggeerraall ppaarraa aa ddeetteerrmmiinnaaççããoo ddaa ddiissttâânncciiaa ddee uumm ppoonnttoo aa uumm ppllaa--
nnoo, conforme se expõe em seguida. 11.. Pelo ponto PP conduziu-se uma recta pp,
ortogonal ao plano. A recta ortogonal ao plano α que passa por PP tem de ser ortogo-
nal a duas rectas concorrentes do plano α – a recta pp é ortogonal à recta ff (pp22 é per-
pendicular a ff22) e é ortogonal à recta hh (pp11 é perpendicular a hh11), pelo que a recta pp é
ortogonal ao plano α (é ortogonal a duas rectas concorrentes do plano α – as rectas ff
e hh). 22.. Determinou-se o ponto II, o ponto de intersecção da recta pp com o plano α – a
determinação do ponto II processou-se com o recurso ao mmééttooddoo ggeerraall ddaa iinntteerrsseecc--
ççããoo ddee rreeccttaass ccoomm ppllaannooss, pois nem a recta nem o plano são projectantes. O plano
θ é o plano auxiliar a que se recorreu (é o plano projectante frontal da recta pp e está
representado apenas pelo seu traço frontal, razão pela qual aquele se assinalou entre
parêntesis). A recta ii é a recta de intersecção dos dois planos (o plano α e o plano θ)
e está definida por dois pontos – o ponto MM (o ponto em que o plano θ corta a recta hh)
e o ponto NN (o ponto em que o plano θ corta a recta ff). Os pontos MM e NN foram
determinados a partir das respectivas projecções frontais, pois o plano θ é projectante frontal. O ponto II é o ponto de concorrência das rec-
tas pp e ii. 33.. A distância do ponto PP ao plano α é o comprimento do segmento de recta [PPII]. O segmento [PPII] é oblíquo, pelo que não se pro-
jecta em V.G. em nenhuma das suas projecções. A determinação da V.G. da distância obriga, assim, ao recurso a um processo geométrico
auxiliar. Optou-se por rebater o plano projectante horizontal da distância para o plano horizontal (de nível) que contém o ponto PP (ver exercí-
cio 221144 e respectivo relatório). PP é um ponto da charneira (é fixo) e o ponto II rebateu-se em função da sua cota em relação ao plano ν (a
distância de II a ν). A V.G. da distância de PP a α é PPෆrrෆIIෆrrෆ. Note que para a resolução do exercício (e tal como o enunciado expressamente refere)
não foi necessária a determinação dos traços do plano. No entanto, caso o enunciado fosse omisso a esse respeito, a resolução do exercí-
cio poderia passar pela determinação dos traços do plano, apesar desses traçados serem desnecessários (a resolução efectuada apresenta
maior economia de traçados).
229.
Em primeiro lugar representaram-se os pontos AA, BB, CC e PP, pelas respectivas projec-
ções, em função dos dados. Para determinar a distância do ponto PP ao plano δ recor-
reu-se ao mmééttooddoo ggeerraall ppaarraa aa ddeetteerrmmiinnaaççããoo ddaa ddiissttâânncciiaa ddee uumm ppoonnttoo aa uumm
ppllaannoo, conforme se expõe em seguida. 11.. Pelo ponto PP conduziu-se uma recta pp,
ortogonal ao plano. A recta ortogonal ao plano δ que passa por PP tem de ser ortogonal
a duas rectas concorrentes do plano δ. Assim, atendendo a que os pontos AA e CC
(dois dos pontos que definem o plano) têm a mesma cota, pelos dois pontos condu-
ziu-se uma recta do plano, que é uma recta horizontal (de nível) – a recta hh. Por outro
lado, atendendo a que os pontos BB e CC (dois dos pontos que definem o plano) têm o
mesmo afastamento, pelos dois pontos conduziu-se uma recta do plano, que é uma
recta frontal (de frente) – a recta ff. As rectas hh e ff são duas rectas do plano que são
concorrentes no ponto CC. Esta situação redunda, assim, na situação do exercício
anterior, pelo que se aconselha o acompanhamento da resolução gráfica apresentada
com a leitura do relatório do exercício anterior.
228.

84. 84
SOLUÇÕES
231.
Em primeiro lugar representaram-se o plano ρ, pelos seus traços, e o ponto PP, pelas suas
projecções, em função dos dados. Em seguida, procedeu-se à execução sequencial das
etapas do mmééttooddoo ggeerraall ppaarraa aa ddeetteerrmmiinnaaççããoo ddaa ddiissttâânncciiaa ddee uumm ppoonnttoo aa uumm ppllaannoo,
conforme exposto no relatório do exercício 222244. 11.. Por PP conduziu-se uma recta pp, orto-
gonal ao plano ρ – a recta pp é uma recta de perfil. 22.. Determinou-se o ponto II, o ponto de
intersecção da recta pp com o plano ρ. Para resolver esta etapa recorreu-se a uma mudança
do diedro de projecção, conforme é expressamente pedido no enunciado. Assim, optou-se
por transformar o plano ρ num plano de topo, para o que se substituiu o Plano Frontal de
Projecção (ppllaannoo 22) por um outro plano de projecção (ppllaannoo 44), ortogonal ao plano ρ. Man-
teve-se o Plano Horizontal de Projecção, pelo que se mantiveram as projecções horizontais,
o traço horizontal do plano ρ e as cotas. O novo eixo XX (o eixo XX’’) é a recta de intersecção
do ppllaannoo 11 com o ppllaannoo 44 e é perpendicular a hhρ. Para determinar o traço do plano ρ no
ppllaannoo 44 recorreu-se a um ponto qualquer do plano – o ponto AA, que é um ponto de ffρ. AA44 é
a projecção de AA no ppllaannoo 44 e determinou-se em função da sua cota, que se manteve. O
traço do plano ρ no ppllaannoo 44 (ff44ρ) passa por AA44 (no novo diedro de projecção, o plano ρ é
projectante frontal) e é concorrente com hhρ no eixo XX’’. PP44 é a projecção de PP no ppllaannoo 44 e
determinou-se, tal como AA44, em função da sua cota, que se manteve. No novo diedro de
projecção (formado pelo ppllaannoo 11 e pelo ppllaannoo 44), o plano ρ é um plano de topo e a recta
pp (a recta ortogonal ao plano ρ que passa por PP) é uma recta frontal (note que o eixo XX é paralelo a pp11). Assim, por PP44 conduziu-se pp44, perpendi-
cular a ff44ρ – pp44 é a projecção da recta pp no ppllaannoo 44. O ponto II (o ponto de intersecção da recta pp com o plano ρ) teve determinação directa, no
novo diedro de projecção, a partir da sua projecção no ppllaannoo 44 – II44 é a projecção de II no ppllaannoo 44 e II 11 determinou-se directamente. Note que o
exposto se refere apenas à segunda etapa da determinação da distância do ponto PP ao plano ρ. 33.. A distância de PP ao plano ρ é o comprimento
do segmento de recta [PPII] – no diedro de projecção formado entre o ppllaannoo 11 e o ppllaannoo 44, o segmento [PPII] é frontal (de frente), pelo que a V.G.
da distância é PPෆ44ෆIIෆ44ෆ. A projecção frontal de II (no diedro de projecção inicial) determinou-se em função da sua cota, o que nos permitiu determinar
as projecções do segmento [PPII] no diedro de projecção inicial – [PPII] é o segmento representativo da distância de PP ao plano ρ.
230.
Em primeiro lugar representaram-se o plano ρ, pelos seus traços, e o ponto PP, pelas
suas projecções, em função dos dados. Em seguida, procedeu-se à execução
sequencial das etapas do mmééttooddoo ggeerraall ppaarraa aa ddeetteerrmmiinnaaççããoo ddaa ddiissttâânncciiaa ddee uumm
ppoonnttoo aa uumm ppllaannoo, conforme exposto no relatório do exercício 222244. 11.. Por PP conduziu-
-se uma recta pp, ortogonal ao plano ρ – a recta pp é uma recta de perfil. 22.. Determinou-se
o ponto II, o ponto de intersecção da recta pp com o plano ρ – a determinação do ponto II
processou-se com o recurso ao mmééttooddoo ggeerraall ddaa iinntteerrsseeccççããoo ddee rreeccttaass ccoomm ppllaannooss,
pois nem a recta nem o plano são projectantes. O plano π é o plano auxiliar a que se
recorreu (é o plano projectante da recta pp). A recta ii é a recta de intersecção dos dois
planos (é uma recta de perfil) e determinou-se a partir do caso geral da intersecção
entre planos – a recta ii está definida pelos seus traços nos planos de projecção. A de-
terminação do ponto de concorrência das duas rectas processou-se com o recurso
ao rebatimento do plano π (para o Plano Frontal de Projecção – a charneira foi ffπ).
A recta iirr está definida por FFrr e HHrr. A recta pp, em rebatimento (a recta pprr) contém PPrr e
é perpendicular a iirr. As rectas pprr e iirr são concorrentes em IIrr – II é o ponto de intersec-
ção da recta pp com o plano ρ. 33.. A distância do ponto PP ao plano ρ é o comprimento
do segmento de recta [PPII], que está em V.G. em rebatimento – PPෆrrෆIIෆrrෆ é a V.G. da distân-
cia de PP a ρ. Em seguida, inverteu-se o rebatimento do plano π, determinando as projecções do ponto II, o que nos permitiu desenhar as
projecções do segmento [PPII], que é o segmento representativo da distância de PP a ρ. Tenha em conta que o exercício se poderia ter resolvido
com o recurso a uma mudança do diedro de projecção (que corresponde à situação do exercício seguinte), mas o enunciado refere expres-
samente o recurso ao rebatimento.
Em primeiro lugar representaram-se o plano ρ, pelos seus traços, e o ponto PP, pelas
suas projecções, em função dos dados. Em seguida, procedeu-se à execução
sequencial das etapas do mmééttooddoo ggeerraall ppaarraa aa ddeetteerrmmiinnaaççããoo ddaa ddiissttâânncciiaa ddee uumm
ppoonnttoo aa uumm ppllaannoo. Uma vez que se optou por recorrer a uma mudança do diedro de
projecção, a situação deste exercício redunda na situação do exercício anterior, pelo
que se sugere o acompanhamento da resolução gráfica apresentada com a leitura do
relatório do exercício anterior. Note que o exercício se poderia resolver com o recurso
a um plano de perfil e ao seu rebatimento, redundando, nesse caso, na situação apre-
sentada no exercício 223300.
232.

85. 233.
Em primeiro lugar representaram-se o plano ρ, pelos seus traços, e o ponto AA, pelas
suas projecções, em função dos dados. Em seguida, procedeu-se à execução
sequencial das etapas do mmééttooddoo ggeerraall ppaarraa aa ddeetteerrmmiinnaaççããoo ddaa ddiissttâânncciiaa ddee
uumm ppoonnttoo aa uumm ppllaannoo. Tenha em conta que a situação deste exercício e a do
exercício 223311 são muito semelhantes, diferindo, apenas, no facto de as projecções
do ponto AA se situarem sobre os traços homónimos do plano ρ, o que pode pro-
vocar alguma confusão, nomeadamente no facto de induzir na falsidade de o ponto
pertencer ao plano – tal não é verdade, pois o ponto AA não pertence a nenhuma
recta do plano (condição para que um ponto pertença a um plano). Assim, e uma
vez que se optou igualmente por recorrer a uma mudança do diedro de projecção,
a situação deste exercício redunda na situação do exercício 223311, pelo que se
sugere o acompanhamento da resolução gráfica apresentada com a leitura do
relatório daquele exercício. O ponto PP é o ponto do plano ρ (pertencente a ffρ) a
que se recorreu para determinar o traço do plano ρ no ppllaannoo 44. Sublinha-se que o
exercício se poderia resolver com o recurso a um plano de perfil e ao seu rebati-
mento, redundando, nesse caso, na situação apresentada no exercício 223300.
85
SOLUÇÕES
235.
Em primeiro lugar representou-se o plano ρ, indicando os seus traços (que estão
coincidentes com o eixo XX) e determinando as projecções do ponto AA, e o ponto
PP, pelas suas projecções. Em seguida, procedeu-se à execução sequencial das
etapas do mmééttooddoo ggeerraall ppaarraa aa ddeetteerrmmiinnaaççããoo ddaa ddiissttâânncciiaa ddee uumm ppoonnttoo aa uumm
ppllaannoo, conforme exposto no relatório do exercício 223300. 11.. Por PP conduziu-se uma
recta pp, ortogonal ao plano ρ – a recta pp é uma recta de perfil. 22.. Determinou-se o
ponto II, o ponto de intersecção da recta pp com o plano ρ – a determinação do
ponto II processou-se com o recurso ao mmééttooddoo ggeerraall ddaa iinntteerrsseeccççããoo ddee rreeccttaass
ccoomm ppllaannooss, pois nem a recta nem o plano são projectantes. O plano π é o plano
auxiliar a que se recorreu (é o plano projectante da recta pp). A recta ii é a recta de
intersecção dos dois planos (é uma recta de perfil ppaassssaannttee). Para definir a recta
ii, da qual já temos um ponto (o seu ponto de concorrência com o eixo XX) recor-
reu-se a uma recta auxiliar do plano ρ – a recta gg, fronto-horizontal, que passa por
AA. O ponto AA’’ é o ponto de intersecção de gg com o plano π e é outro ponto da
recta ii – a recta ii está definida pelo seu ponto de concorrência com o eixo XX e por
AA’’. A determinação do ponto de concorrência das duas rectas processou-se com
o recurso ao rebatimento do plano π (para o Plano Frontal de Projecção – a charneira foi ffπ). A recta iirr está definida por AA’’rr e pelo seu ponto
de concorrência com o eixo XX (que é fixo, pois é um ponto da charneira). A recta pp, em rebatimento (a recta pprr) contém PPrr e é perpendicular
Em primeiro lugar representaram-se o plano ρ, pelo seu traço frontal (o plano está de-
finido pelo seu traço frontal e pela sua orientação), e o ponto AA, pelas suas projec-
ções, em função dos dados. Em seguida, procedeu-se à execução sequencial das
etapas do mmééttooddoo ggeerraall ppaarraa aa ddeetteerrmmiinnaaççããoo ddaa ddiissttâânncciiaa ddee uumm ppoonnttoo aa uumm
ppllaannoo, conforme exposto no relatório do exercício 223300. 11.. Por AA conduziu-se uma rec-
ta pp, ortogonal ao plano ρ – a recta pp é uma recta de perfil. 22.. Determinou-se o ponto II,
o ponto de intersecção da recta pp com o plano ρ – a determinação do ponto II proces-
sou-se com o recurso ao mmééttooddoo ggeerraall ddaa iinntteerrsseeccççããoo ddee rreeccttaass ccoomm ppllaannooss, pois
nem a recta nem o plano são projectantes. O plano π é o plano auxiliar a que se
recorreu (é o plano projectante da recta pp). A recta ii é a recta de intersecção dos dois
planos (é uma recta de perfil) – a recta ii está definida por um ponto (o seu traço fron-
tal) e por uma direcção (faz um ângulo de 60o com o Plano Frontal de Projecção).
Note que a amplitude do diedro formado entre um plano de rampa e o Plano Frontal
de Projecção é igual à amplitude do ângulo que qualquer recta de perfil do plano de
rampa faz com o Plano Frontal de Projecção. A determinação do ponto de concorrên-
cia das duas rectas processou-se com o recurso ao rebatimento do plano π (para o
Plano Frontal de Projecção – a charneira foi ffπ). A recta iirr passa por FFrr e faz um ângulo
de 60o com ffπrr
(tendo-se garantido que o traço horizontal da recta tem afastamento
positivo, pois o enunciado refere expressamente que o traço horizontal do plano ρ se
situa no SSPPHHAA). A recta pp, em rebatimento (a recta pprr) contém AArr e é perpendicular a iirr.
As rectas pprr e iirr são concorrentes em IIrr – II é o ponto de intersecção da recta pp com o
plano ρ. 33.. A distância do ponto AA ao plano ρ é o comprimento do segmento de recta [AAII], que está em V.G. em rebatimento – AAෆrrෆIIෆrrෆ é a V.G. da
distância de AA a ρ. Em seguida, inverteu-se o rebatimento do plano π, determinando as projecções do ponto II, o que nos permitiu desenhar
as projecções do segmento [AAII], que é o segmento representativo da distância de AA a ρ.
234.
(Continua na página seguinte)

86. 86
SOLUÇÕES
237.
Em primeiro lugar representou-se o ponto PP, pelas suas projecções, em função dos dados
– o β1/3 não carece de representação, mas trata-se de um plano passante definido por uma
recta (o eixo XX) e pela sua orientação (faz diedros de 45° com os planos de projecção). Em
seguida, procedeu-se à execução sequencial das etapas do mmééttooddoo ggeerraall ppaarraa aa ddeetteerr--
mmiinnaaççããoo ddaa ddiissttâânncciiaa ddee uumm ppoonnttoo aa uumm ppllaannoo, conforme exposto no relatório do exercí-
cio 223300. 11.. Por PP conduziu-se uma recta pp, ortogonal ao β1/3 – a recta pp é uma recta de
perfil. 22.. Determinou-se o ponto II, o ponto de intersecção da recta pp com o β1/3 – a deter-
minação do ponto II processou-se com o recurso ao mmééttooddoo ggeerraall ddaa iinntteerrsseeccççããoo ddee rreecc--
ttaass ccoomm ppllaannooss, pois nem a recta nem o β1/3 são projectantes. O plano π é o plano auxiliar
a que se recorreu (é o plano projectante da recta pp). A recta ii é a recta de intersecção dos
dois planos – é uma recta de perfil ppaassssaannttee que faz ângulos de 45o com os planos de
projecção e que atravessa os 1o e 3o Diedros. A recta ii está definida por um ponto e uma
direcção. A determinação do ponto de concorrência das duas rectas processou-se com o
recurso ao rebatimento do plano π (para o Plano Frontal de Projecção – a charneira foi ffπ).
A recta iirr está definida pelo seu ponto de concorrência com o eixo XX (que é fixo, pois situa-
-se na charneira) e atravessa o quadrante em que se situa PPrr (note que PP é um ponto do
1o Diedro e que a recta ii atravessa o 1o Diedro). A recta pp, em rebatimento (a recta pprr) con-
tém PPrr e é perpendicular a iirr. As rectas pprr e iirr são concorrentes em IIrr – II é o ponto de inter-
secção da recta pp com o β1/3. 33.. A distância do ponto PP ao β1/3 é o comprimento do
segmento de recta [PPII], que está em V.G. em rebatimento – PPෆrrෆIIෆrrෆ é a V.G. da distância de PP
ao β1/3. Em seguida, inverteu-se o rebatimento do plano π, determinando as projecções do ponto II, o que nos permitiu desenhar as projec-
ções do segmento [PPII], que é o segmento representativo da distância de PP ao β1/3. Tenha em conta que o exercício se poderia ter resolvido
com o recurso a uma mudança do diedro de projecção (o que resulta na situação do exercício seguinte), mas o enunciado refere expressa-
mente o recurso ao rebatimento.
Em primeiro lugar representou-se o plano ρ, indicando os seus traços (que
estão coincidentes com o eixo XX) e determinando as projecções do ponto
AA, e o ponto PP, pelas suas projecções. Em seguida, procedeu-se à execu-
ção sequencial das etapas do mmééttooddoo ggeerraall ppaarraa aa ddeetteerrmmiinnaaççããoo ddaa ddiiss--
ttâânncciiaa ddee uumm ppoonnttoo aa uumm ppllaannoo. 11.. Por PP conduziu-se uma recta pp,
ortogonal ao plano ρ – a recta pp é uma recta de perfil. 22.. Determinou-se o
ponto II, o ponto de intersecção da recta pp com o plano ρ. Para resolver
esta etapa recorreu-se a uma mudança do diedro de projecção, conforme
é expressamente pedido no enunciado. Assim, optou-se por transformar o
plano ρ num plano de topo, para o que se substituiu o Plano Frontal de
Projecção (ppllaannoo 22) por um outro plano de projecção (ppllaannoo 44), ortogonal
ao plano ρ. Manteve-se o Plano Horizontal de Projecção, pelo que se man-
tiveram as projecções horizontais, o traço horizontal do plano ρ e as cotas.
O novo eixo XX (o eixo XX’’) é a recta de intersecção do ppllaannoo 11 com o ppllaannoo
44 e é perpendicular a hhρ. Para determinar o traço do plano ρ no ppllaannoo 44
recorreu-se ao ponto AA, que é o ponto que define o plano. AA44 é a projecção
de AA no ppllaannoo 44 e determinou-se em função da sua cota, que se manteve.
O traço do plano ρ no ppllaannoo 44 (ff44ρ) passa por AA44 (no novo diedro de projec-
ção, o plano ρ é projectante frontal) e é concorrente com hhρ no eixo XX’’. PP44 é
a projecção de PP no ppllaannoo 44 e determinou-se, tal como AA44, em função da
sua cota, que se manteve. No novo diedro de projecção (formado pelo ppllaannoo 11 e pelo ppllaannoo 44), o plano ρ é um plano de topo e a recta pp
(a recta ortogonal ao plano ρ que passa por PP) é uma recta frontal (note que o eixo XX é paralelo a pp11). Assim, por PP44 conduziu-se pp44, perpen-
dicular a ff44ρ – pp44 é a projecção da recta pp no ppllaannoo 44. O ponto II (o ponto de intersecção da recta pp com o plano ρ) teve determinação direc-
ta, no novo diedro de projecção, a partir da sua projecção no ppllaannoo 44 – II44 é a projecção de II no ppllaannoo 44 e II11 determinou-se directamente.
Note que o exposto se refere apenas à segunda etapa da determinação da distância do ponto PP ao plano ρ. 33.. A distância de PP ao plano ρ é
o comprimento do segmento de recta [PPII] – no diedro de projecção formado entre o ppllaannoo 11 e o ppllaannoo 44, o segmento [PPII] é frontal (de frente),
pelo que a V.G. da distância é PPෆ44ෆIIෆ44ෆ. A projecção frontal de II (no diedro de projecção inicial) determinou-se em função da sua cota, o que nos
permitiu determinar as projecções do segmento [PPII] no diedro de projecção inicial – [PPII] é o segmento representativo da distância de PP ao
plano ρ. VVaannttaaggeennss ddeessttee pprroocceessssoo ddee rreessoolluuççããoo eemm rreellaaççããoo aaoo uuttiilliizzaaddoo nnoo eexxeerrccíícciioo aanntteerriioorr: têm a ver com a possibilidade de resol-
ver directamente o problema da intersecção da recta pp com o plano ρ, no novo diedro de projecção, evitando os raciocínios necessários à
determinação da recta de intersecção do plano π com um plano passante (o plano ρ).
236.
a iirr. As rectas pprr e iirr são concorrentes em IIrr – II é o ponto de intersecção da recta pp com o plano ρ. 33.. A distância do ponto PP ao plano ρ é o
comprimento do segmento de recta [PPII], que está em V.G. em rebatimento – PPෆrrෆIIෆrrෆ é a V.G. da distância de PP a ρ. Em seguida, inverteu-se o
rebatimento do plano π, determinando as projecções do ponto II, o que nos permitiu desenhar as projecções do segmento [PPII], que é o
segmento representativo da distância de PP a ρ. Tenha em conta que o exercício se poderia ter resolvido com o recurso a uma mudança do
diedro de projecção (que corresponde à situação do exercício seguinte, mas o enunciado refere expressamente o recurso ao rebatimento).

87. 87
SOLUÇÕES
Em primeiro lugar representou-se o ponto PP, pelas suas projecções, em função dos da-
dos – o β1/3 não carece de representação. No entanto, em função do processo de reso-
lução pedido (o recurso a uma mudança do diedro de projecção), optou-se por
representar os traços do plano (que se denominou apenas por β), que estão coinciden-
tes no eixo XX. Em seguida, procedeu-se à execução sequencial das etapas do mmééttooddoo
ggeerraall ppaarraa aa ddeetteerrmmiinnaaççããoo ddaa ddiissttâânncciiaa ddee uumm ppoonnttoo aa uumm ppllaannoo. 11.. Por PP conduziu-
-se uma recta pp, ortogonal ao β1/3 – a recta pp é uma recta de perfil. 22.. Determinou-se o
ponto II, o ponto de intersecção da recta pp com o β1/3. Para resolver esta etapa recorreu-
-se a uma mudança do diedro de projecção, conforme é expressamente pedido no
enunciado. Assim, optou-se por transformar o β1/3 num plano vertical, para o que se
substituiu o Plano Horizontal de Projecção (ppllaannoo 11) por um outro plano de projecção
(ppllaannoo 44), ortogonal ao β1/3. Manteve-se o Plano Frontal de Projecção, pelo que se man-
tiveram as projecções frontais, o traço frontal do β1/3 e os afastamentos. O novo eixo XX (o
eixo XX’’) é a recta de intersecção do ppllaannoo 11 com o ppllaannoo 44 e é perpendicular a ffβ. Para
determinar o traço do β1/3 no ppllaannoo 44 recorreu-se a um ponto qualquer do plano – o
ponto AA (que é um ponto com projecções simétricas em relação ao eixo XX). AA44 é a
projecção de AA no ppllaannoo 44 e determinou-se em função do seu afastamento, que se
manteve. O traço do β1/3 no ppllaannoo 44 (hh44β
) passa por AA44 (no novo diedro de projecção, o
β1/3 é projectante horizontal) e é concorrente com ffβ no eixo XX’’. PP44 é a projecção de PP no
ppllaannoo 44 e determinou-se, tal como AA44, em função do seu afastamento, que se manteve. No novo diedro de projecção (formado pelo ppllaannoo 11
e pelo ppllaannoo 44), o β1/3 é um plano vertical e a recta pp (a recta ortogonal ao β1/3 que passa por PP) é uma recta horizontal (note que o eixo XX é
paralelo a pp22). Assim, por PP44 conduziu-se pp44, perpendicular a hh44β – pp44 é a projecção da recta pp no ppllaannoo 44. O ponto II (o ponto de intersec-
ção da recta pp com o β1/3) teve determinação directa, no novo diedro de projecção, a partir da sua projecção no ppllaannoo 44 – II44 é a projecção
de II no ppllaannoo 44 e II11 determinou-se directamente. Note que o exposto se refere apenas à segunda etapa da determinação da distância do
ponto PP ao β1/3. 33.. A distância de PP ao β1/3 é o comprimento do segmento de recta [PPII] – no diedro de projecção formado entre o ppllaannoo 11 e
o ppllaannoo 44, o segmento [PPII] é horizontal (de nível), pelo que a V.G. da distância é PPෆ44ෆIIෆ44ෆ. A projecção horizontal de II (no diedro de projecção
inicial) determinou-se em função do seu afastamento, o que nos permitiu determinar as projecções do segmento [PPII] no diedro de projec-
ção inicial – [PPII] é o segmento representativo da distância de PP ao β1/3.
239.
Em primeiro lugar representou-se o plano ρ, indicando os seus traços (que estão coin-
cidentes com o eixo XX), e o ponto PP, pelas suas projecções, em função dos dados.
O plano ρ está definido pelo por uma recta (o eixo XX) e pela sua orientação. Em segui-
da, procedeu-se à execução sequencial das etapas do mmééttooddoo ggeerraall ppaarraa aa ddeetteerrmmii--
nnaaççããoo ddaa ddiissttâânncciiaa ddee uumm ppoonnttoo aa uumm ppllaannoo. 11.. Por PP conduziu-se uma recta pp,
ortogonal ao plano ρ – a recta pp é uma recta de perfil. 22.. Determinou-se o ponto II, o
ponto de intersecção da recta pp com o plano ρ – a determinação do ponto II proces-
sou-se com o recurso ao mmééttooddoo ggeerraall ddaa iinntteerrsseeccççããoo ddee rreeccttaass ccoomm ppllaannooss, pois
nem a recta nem o plano ρ são projectantes. O plano π é o plano auxiliar a que se
recorreu (é o plano projectante da recta pp). A recta ii é a recta de intersecção dos dois
planos – é uma recta de perfil ppaassssaannttee que faz um ângulo de 30° com o Plano Hori-
zontal de Projecção. Note que a amplitude do diedro formado entre um plano de rampa
(um plano passante é um plano de rampa) e o Plano Horizontal de Projecção é igual à
amplitude do ângulo que qualquer recta de perfil do plano de rampa faz com o Plano
Horizontal de Projecção. Por outro lado, é necessário ter em conta que o plano ρ atra-
vessa os 1o e 3o Diedros. A recta ii está definida por um ponto e uma direcção. A deter-
minação do ponto de concorrência das duas rectas processou-se com o recurso ao
rebatimento do plano π (para o Plano Frontal de Projecção – a charneira foi ffπ). A recta iirr
está definida pelo seu ponto de concorrência com o eixo XX (que é fixo, pois situa-se na
charneira), faz um ângulo de 30o com hhππrr e atravessa o quadrante em que se situa PPrr
(note que PP é um ponto do 1o Diedro e que a recta ii atravessa o 1o Diedro). A recta pp,
em rebatimento (a recta pprr) contém PPrr e é perpendicular a iirr. As rectas pprr e iirr são con-
correntes em IIrr – II é o ponto de intersecção da recta pp com o plano ρ. 33.. A distância do ponto PP ao plano ρ é o comprimento do segmento
de recta [PPII], que está em V.G. em rebatimento – PPෆrrෆIIෆrrෆ é a V.G. da distância de PP ao plano ρ. Em seguida, inverteu-se o rebatimento do plano π,
determinando as projecções do ponto II, o que nos permitiu desenhar as projecções do segmento [PPII], que é o segmento representativo da
distância de PP ao plano ρ. Tenha em conta que o exercício se poderia ter resolvido com o recurso a uma mudança do diedro de projecção,
mas o enunciado refere expressamente o recurso ao rebatimento.
238.

88. 88
SOLUÇÕES
Em primeiro lugar representaram-se as rectas rr e ss, pelas respectivas
projecções, em função dos dados. O plano β é paralelo à recta rr, que
é uma recta fronto-horizontal, pelo que o plano β contém rectas fronto-
-horizontais – é nneecceessssaarriiaammeennttee um plano de rampa. Pelos traços da
recta ss conduziram-se os traços homónimos do plano β. A distância
entre uma recta e um plano paralelo à recta redunda na situação da
ddiissttâânncciiaa ddee uumm ppoonnttoo aa uumm ppllaannoo, pois todos os pontos da recta
(que é paralela ao plano) estão equidistantes do plano. Assim, repre-
sentou-se um ponto AA, qualquer, sobre a recta rr, e efectuaram-se os
traçados necessários à determinação da distância do ponto AA ao pla-
no β – tendo em conta que se optou por recorrer a uma mudança do
diedro de projecção, este exercício é semelhante à situação do exercí-
cio 223311, pelo que se sugere o acompanhamento da resolução gráfica
apresentada com a leitura do relatório daquele exercício.
Em primeiro lugar representaram-se os planos ϕ e ϕ1, pelos seus traços horizontais, em função dos
dados. Em seguida, procedeu-se à execução sequencial das etapas do mmééttooddoo ggeerraall ppaarraa aa ddeetteerr--
mmiinnaaççããoo ddaa ddiissttâânncciiaa eennttrree ddooiiss ppllaannooss. 11.. Conduziu-se uma recta pp, qualquer, ortogonal aos dois
planos – a recta pp é uma recta de topo. 22.. Determinaram-se os pontos II e II’’, os pontos de intersec-
ção da recta pp com os planos ϕ e ϕ1, respectivamente (os pontos II e II’’ determinaram-se directa-
mente a partir das suas projecções horizontais, pois os planos são projectantes horizontais). 33.. A
distância entre os pontos II e II’’ é a distância entre os dois planos – o segmento [IIII’’] é um segmento
representativo da distância entre os dois planos. O segmento [IIII’’] projecta-se em V.G. no Plano Ho-
rizontal de Projecção, pois é paralelo a este – IIෆ11ෆIIෆ’’ෆ11ෆ é a V.G. da distância entre os dois planos.
244.
240.
Em primeiro lugar representou-se o ponto AA, pelas suas projecções, em função dos da-
dos – o β2/4 não carece de representação, mas trata-se de um plano passante definido
por uma recta (o eixo XX) e pela sua orientação (faz diedros de 45o com os planos de
projecção). Em seguida, procedeu-se à execução sequencial das etapas do mmééttooddoo
ggeerraall ppaarraa aa ddeetteerrmmiinnaaççããoo ddaa ddiissttâânncciiaa ddee uumm ppoonnttoo aa uumm ppllaannoo. 11.. Por AA conduziu-
-se uma recta pp, ortogonal ao β2/4 – a recta pp é uma recta de perfil. 22.. Determinou-se o
ponto II, o ponto de intersecção da recta pp com o β2/4 – a determinação do ponto II
processou-se com o recurso ao mmééttooddoo ggeerraall ddaa iinntteerrsseeccççããoo ddee rreeccttaass ccoomm ppllaannooss,
pois nem a recta nem o β2/4 são projectantes. O plano π é o plano auxiliar a que se
recorreu (é o plano projectante da recta pp). A recta ii é a recta de intersecção dos dois
planos – é uma recta de perfil ppaassssaannttee que faz ângulos de 45o com os planos de pro-
jecção e que atravessa os 2o e 4o Diedros. A recta ii está definida por um ponto e uma
direcção. A determinação do ponto de concorrência das duas rectas processou-se com o recurso ao rebatimento do plano π (para o Plano
Frontal de Projecção – a charneira foi ffπ). A recta iirr está definida pelo seu ponto de concorrência com o eixo XX (que é fixo, pois situa-se na
charneira) e nnããoo aattrraavveessssaa o quadrante em que se situa AArr (note que AA é um ponto do 1o Diedro e que a recta ii não atravessa o 1o Diedro).
A recta pp, em rebatimento (a recta pprr) contém AArr e é perpendicular a iirr. As rectas pprr e iirr são concorrentes em IIrr – II é o ponto de intersecção
da recta pp com o β2/4. 33.. A distância do ponto AA ao β2/4 é o comprimento do segmento de recta [AAII], que está em V.G. em rebatimento – AAෆrrෆIIෆrrෆ
é a V.G. da distância de AA ao β2/4. Em seguida, inverteu-se o rebatimento do plano π, determinando as projecções do ponto II, o que nos
permitiu desenhar as projecções do segmento [AAII], que é o segmento representativo da distância de AA ao β2/4. Tenha em conta que o exer-
cício se poderia ter resolvido com o recurso a uma mudança do diedro de projecção, à semelhança do exercício anterior.
242.
Por ddiissttâânncciiaa eennttrree ddooiiss ppllaannooss ppaarraalleellooss entende-se a distância entre dois pontos quaisquer dos planos (um ponto de cada plano) conti-
dos na mesma recta ortogonal aos planos, ou seja, é o comprimento de um segmento de recta ortogonal aos dois planos que tem um extre-
mo em cada um dos planos.
243.
O mmééttooddoo ggeerraall ppaarraa aa ddeetteerrmmiinnaaççããoo ddaa ddiissttâânncciiaa eennttrree ddooiiss ppllaannooss ppaarraalleellooss consiste em: 11.. conduzir uma recta qualquer, ortogonal
aos dois planos; 22.. determinar os pontos de intersecção dessa recta com ambos os planos; 33.. a distância entre os dois pontos de intersec-
ção é a distância entre os dois planos (é o comprimento do segmento de recta que tem extremos nos dois pontos).
241.

89. 89
SOLUÇÕES
Em primeiro lugar representaram-se os planos π e π1, pelos seus traços, em função dos da-
dos. Em seguida, procedeu-se à execução sequencial das etapas do mmééttooddoo ggeerraall ppaarraa aa
ddeetteerrmmiinnaaççããoo ddaa ddiissttâânncciiaa eennttrree ddooiiss ppllaannooss. 11.. Conduziu-se uma recta pp, qualquer, ortogo-
nal aos dois planos – a recta pp é uma recta fronto-horizontal. 22.. Determinaram-se os pontos II
e II’’, os pontos de intersecção da recta pp com os planos π e π1, respectivamente (os pontos II e
II’’ têm determinação directa, pois os planos são duplamente projectantes – são projectantes
frontais e projectantes horizontais). 33.. A distância entre os pontos II e II’’ é a distância entre os
dois planos – o segmento [IIII’’] é um segmento representativo da distância entre os dois pla-
nos. O segmento [IIII’’] projecta-se em V.G. nos dois planos de projecção, pois é paralelo a am-
bos – IIෆ11ෆIIෆ’’ෆ11ෆ = IIෆ22ෆIIෆ’’ෆ22ෆ é a V.G. da distância entre os dois planos.
246.
245.
Em primeiro lugar representaram-se os planos δ e θ, pelos seus traços, em função dos
dados. Em seguida, procedeu-se à execução sequencial das etapas do mmééttooddoo ggeerraall
ppaarraa aa ddeetteerrmmiinnaaççããoo ddaa ddiissttâânncciiaa eennttrree ddooiiss ppllaannooss. 11.. Conduziu-se uma recta pp,
qualquer, ortogonal aos dois planos – a recta pp é uma recta frontal (de frente). 22.. Deter-
minaram-se os pontos II e II’’, os pontos de intersecção da recta pp com os planos δ e θ,
respectivamente (os pontos II e II’’ determinaram-se directamente a partir das suas pro-
jecções frontais, pois os planos são projectantes frontais). 33.. A distância entre os pon-
tos II e II’’ é a distância entre os dois planos – o segmento [IIII’’] é um segmento
representativo da distância entre os dois planos. O segmento [IIII’’] projecta-se em V.G.
no Plano Frontal de Projecção, pois é paralelo a este – IIෆ22ෆIIෆ’’ෆ22ෆ é a V.G. da distância entre
os dois planos.
247.
Em primeiro lugar representaram-se os planos α e δ, pelos seus traços, em
função dos dados – os dois planos, porque são paralelos, têm os traços ho-
mónimos paralelos entre si. Em seguida, procedeu-se à execução sequencial
das etapas do mmééttooddoo ggeerraall ppaarraa aa ddeetteerrmmiinnaaççããoo ddaa ddiissttâânncciiaa eennttrree ddooiiss
ppllaannooss. 11.. Conduziu-se uma recta pp, qualquer, ortogonal aos dois planos – a
recta pp é uma recta oblíqua, cujas projecções são perpendiculares aos tra-
ços homónimos dos dois planos. 22.. Determinaram-se os pontos II e II’’, os
pontos de intersecção da recta pp com os planos α e δ, respectivamente.
Uma vez que nem a recta pp nem os planos são projectantes, a determinação
dos pontos II e II’’ processou-se com o recurso ao mmééttooddoo ggeerraall ddaa iinntteerrsseecc--
ççããoo eennttrree rreeccttaass ee ppllaannooss. O plano γ é o plano auxiliar a que se recorreu (é
o plano projectante horizontal da recta pp). A recta aa é a recta de intersecção
do plano γ com o plano α (está definida por dois pontos, que são os seus tra-
ços) – a recta aa é concorrente com a recta pp no ponto II, que é o ponto de
intersecção da recta pp com o plano α. A recta bb é a recta de intersecção do
plano γ com o plano δ (está definida por dois pontos, que são os seus tra-
ços) – a recta bb é concorrente com a recta pp no ponto II’’, que é o ponto de
intersecção da recta pp com o plano δ. Note que as rectas aa e bb são paralelas
entre si, pois qualquer plano corta dois planos paralelos segundo duas rec-
tas paralelas. 33.. A distância entre os pontos II e II’’ é a distância entre os dois
planos – o segmento [IIII’’] é um segmento representativo da distância entre os dois planos. O segmento [IIII’’] é oblíquo aos dois planos de
projecção, pelo que não se projecta em V.G. em nenhum dos planos de projecção – é necessário o recurso a um processo geométrico auxi-
liar. Optou-se pelo rebatimento do plano γ (o plano projectante horizontal do segmento) para o Plano Horizontal de Projecção. A V.G. da dis-
tância dos dois planos é IIෆrrෆIIෆ’’ෆrrෆ. Tenha em conta que se poderia ter recorrido a uma mudança do diedro de projecção, por exemplo, para
determinar a V.G. do comprimento do segmento [IIII’’].

90. 90
SOLUÇÕES
248.
Em primeiro lugar representaram-se os planos α e δ, pelos seus traços, em
função dos dados – os dois planos, porque são paralelos, têm os traços homó-
nimos paralelos entre si. Em seguida, procedeu-se à execução sequencial
das etapas do mmééttooddoo ggeerraall ppaarraa aa ddeetteerrmmiinnaaççããoo ddaa ddiissttâânncciiaa eennttrree ddooiiss
ppllaannooss, à semelhança do exercício anterior, pelo que se aconselha o acom-
panhamento da resolução gráfica apresentada com a leitura do relatório do
exercício anterior. Note que a recta bb (a recta de intersecção do plano auxiliar
γ com o plano δ) está definida por um ponto – o seu traço horizontal – e por
uma direcção – é paralela à recta aa, pois qualquer plano corta dois planos
paralelos segundo duas rectas paralelas. A V.G. da distância (a V.G. do com-
primento do segmento [IIII’’]) determinou-se com o recurso a uma mudança
do diedro de projecção – transformou-se o segmento [IIII’’] num segmento
frontal (de frente). Tenha em conta que se poderia ter recorrido a um rebati-
mento, por exemplo, para determinar a V.G. do comprimento do segmento
[IIII’’] (à semelhança do efectuado no exercício anterior).
250.
Em primeiro lugar representaram-se os planos α e μ, em função dos
dados – o plano α está definido pelas projecções das rectas hh e ff e o
plano μ está definido pelas projecções do ponto NN e pela sua orienta-
ção (é paralelo ao plano α). Note que, tal como em seguida se expõe,
não é necessária a determinação dos traços de nenhum dos dois pla-
nos, o que se traduz numa maior economia de traçados. Assim, proce-
deu-se à execução sequencial das etapas do mmééttooddoo ggeerraall ppaarraa aa
ddeetteerrmmiinnaaççããoo ddaa ddiissttâânncciiaa eennttrree ddooiiss ppllaannooss. 11.. Conduziu-se uma
recta pp, qualquer, ortogonal aos dois planos. Com vista a uma maior
economia de traçados, e uma vez que o único dado conhecido do pla-
no μ é o ponto NN, optou-se por conduzir a recta pp pelo ponto NN. A pro-
jecção frontal da recta pp é perpendicular a ff22, o que garante a
ortogonalidade entre a recta pp22 e uma recta frontal do plano α. A pro-
jecção horizontal da recta pp (pp11) é perpendicular a hh11, o que garante a
ortogonalidade entre a recta pp e uma recta horizontal do plano α. As
rectas ff e hh são duas rectas concorrentes do plano α, pelo que a recta
pp é, então, ortogonal ao plano α, pois é ortogonal a duas rectas concor-
rentes do plano. Uma vez que os planos α e μ são paralelos entre si, a
recta pp é também ortogonal ao plano μ. Como se pôde constatar, foi
possível determinar a recta pp sem o recurso aos traços dos planos, mas
Em primeiro lugar representaram-se os planos θ e γ, pelos seus traços, em
função dos dados. O plano θ, porque é ortogonal ao β2/4, tem os seus tra-
ços coincidentes. Os dois planos, porque são paralelos, têm os traços ho-
mónimos paralelos entre si – o plano γ também tem os seus traços
coincidentes. Em seguida, procedeu-se à execução sequencial das etapas
do mmééttooddoo ggeerraall ppaarraa aa ddeetteerrmmiinnaaççããoo ddaa ddiissttâânncciiaa eennttrree ddooiiss ppllaannooss, à
semelhança do exercício 224477, pelo que se aconselha o acompanhamento
da resolução gráfica apresentada com a leitura do relatório daquele exercí-
cio. A recta pp (a recta ortogonal aos dois planos) tem necessariamente as
suas projecções paralelas entre si. O plano α foi o plano auxiliar (o plano
projectante horizontal da recta pp) a que se recorreu para a determinação
dos pontos de intersecção da recta pp com os planos θ e γ. A recta bb (a recta
de intersecção do plano auxiliar α com o plano γ) está definida por um pon-
to – o seu traço horizontal – e por uma direcção – é paralela à recta aa (a recta
de intersecção do plano α com o plano θ), pois qualquer plano corta dois
planos paralelos segundo duas rectas paralelas. A V.G. da distância (a V.G.
do comprimento do segmento [IIII’’]) determinou-se com o recurso ao re-
batimento do plano α (o plano projectante horizontal do segmento) para o
Plano Horizontal de Projecção, mas poder-se-ia ter recorrido a uma mu-
dança do diedro de projecção para o efeito.
(Continua na página seguinte)
249.

91. 91
SOLUÇÕES
251.
Em primeiro lugar representou-se o plano α,
pelos seus traços, em função dos dados – o
plano α, porque é ortogonal ao β1/3, tem os
seus traços simétricos em relação ao eixo XX.
Tenha em conta que o problema proposto
consiste numa variação dos problemas de
distâncias entre planos – o plano δ (o plano
pretendido) será determinado em função da
sua distância ao plano α. Assim, a resolução
do exercício passa necessariamente pela
execução sequencial das etapas do mmééttooddoo
ggeerraall ppaarraa aa ddeetteerrmmiinnaaççããoo ddaa ddiissttâânncciiaa eenn--
ttrree ddooiiss ppllaannooss, como em seguida se expõe.
11.. Conduziu-se uma recta pp, qualquer, orto-
gonal aos dois planos – com vista a uma maior
economia de traçados, optou-se por fazer
com que a recta pp seja uma recta passante.
22.. Determinou-se o ponto AA, o ponto de inter-
secção da recta pp com o plano α – note que
não é possível determinar o ponto de inter-
secção da recta pp com o plano δ, pois este é
o que é pedido no enunciado (não é conheci-
do). De qualquer forma, o ponto de intersec-
ção da recta pp com o plano δ é um ponto que
se situa na recta pp a 3 cm (a distância entre os dois planos) do ponto AA. Note que, atendendo a que nem a recta pp nem o plano α são pro-
jectantes, a determinação do ponto AA se processou com o recurso ao mmééttooddoo ggeerraall ddaa iinntteerrsseeccççããoo eennttrree rreeccttaass ee ppllaannooss. O plano θ é o
plano auxiliar a que se recorreu (é o plano projectante frontal da recta pp). A recta ii é a recta de intersecção do plano θ com o plano α (está
definida por dois pontos, que são os seus traços) – a recta ii é concorrente com a recta pp no ponto AA, que é o ponto de intersecção da recta
pp com o plano α. 33.. A distância entre os dois planos tem de ser medida sobre a recta pp, a partir de AA. Uma vez que a recta pp é oblíqua aos
dois planos de projecção, é necessário o recurso a um processo geométrico auxiliar para se medir a distância em V.G. – optou-se pelo reba-
timento do plano θ (o plano projectante frontal da recta pp) para o Plano Horizontal de Projecção. A charneira foi hhθ e o ponto de concor-
rência da recta pp com o eixo XX (a recta pp é passante) é fixo – pprr fica definida por dois pontos (o seu ponto de concorrência com o eixo XX e
AArr). 33.. Sobre pprr, a partir de AArr, mediram-se os 3 cm (a distância entre os dois planos), obtendo um ponto BBrr – BB será o ponto de intersecção
da recta pp com o plano δ. O ponto BBrr situou-se sobre pprr de forma a garantir que o plano δ (que contém o ponto BB) corte o eixo XX num ponto
com abcissa positiva (como é pedido no enunciado). Invertendo o rebatimento, determinaram-se as projecções do ponto BB, sobre as pro-
jecções homónimas da recta pp. A conclusão do exercício passa, agora, por determinar os traços do plano δ, paralelos aos traços homóni-
mos do plano α, fazendo com que o plano δ contenha o ponto BB. Para tal, recorreu-se a uma recta do plano δ que passe por BB – a recta ff,
que é uma recta frontal (de frente) do plano δ, que é paralela a ffα (para que um ponto pertença a um plano, tem de pertencer a uma recta do
plano). HH’’ é o traço horizontal da recta ff – hhδ passa por HH’’ e é paralelo a hhα e ffδ é concorrente com hhδ no eixo XX e é paralelo a ff22 (e a ffα).
apenas porque as rectas que definem o plano α são uma recta frontal (de frente) e uma recta horizontal (de nível) – caso fossem duas rectas
oblíquas, por exemplo, seria necessário determinar os traços do plano ou determinar uma recta horizontal (de nível) e uma recta frontal (de
frente) do plano. 22.. Determinaram-se os pontos de intersecção da recta pp com os planos α e μ. Uma vez que a recta pp passa pelo ponto NN,
que é um ponto do plano μ, o ponto NN é, imediatamente, o ponto de intersecção da recta pp com o plano μ. A determinação do ponto de
intersecção da recta pp com o plano α (ponto II) processou-se com o recurso ao mmééttooddoo ggeerraall ddaa iinntteerrsseeccççããoo eennttrree rreeccttaass ee ppllaannooss (nem a
recta nem o plano são projectantes). O plano γ (que está definido apenas pelo seu traço horizontal, razão pela qual este se assinalou entre
parêntesis) é o plano auxiliar a que se recorreu (é o plano projectante horizontal da recta pp). A recta ii é a recta de intersecção do plano γ
com o plano α e está definida por dois pontos – os pontos AA e BB (que são os pontos em que o plano γ corta as rectas ff e hh, respectivamente).
A recta ii é concorrente com a recta pp no ponto II, que é o ponto de intersecção da recta pp com o plano α. 33.. A distância entre os pontos II e NN
é a distância entre os dois planos – o segmento [IINN] é um segmento representativo da distância entre os dois planos. O segmento [IINN] é
oblíquo aos dois planos de projecção, pelo que não se projecta em V.G. em nenhum dos planos de projecção – é necessário o recurso a
um processo geométrico auxiliar. Optou-se pelo recurso a uma mudança do diedro de projecção – transformou-se o segmento [IINN] num
segmento horizontal (de nível). Note que, em função dos limites do desenho, se transformou o segmento [IINN] num segmento horizontal (de
nível) com cota negativa, mas que tal não é estritamente necessário nem deve fazer confusão. Tenha em conta que também se poderia ter
recorrido a um rebatimento, por exemplo, para determinar a V.G. da distância.

92. 92
SOLUÇÕES
Em primeiro lugar representaram-se os dois planos, em função dos dados – o pla-
no ρ está definido pelos seus traços e o plano σ está definido pelo seu traço frontal
e pela sua orientação (é paralelo a ρ). Em seguida, procedeu-se à execução se-
quencial das etapas do mmééttooddoo ggeerraall ddaa ddiissttâânncciiaa eennttrree ddooiiss ppllaannooss. 11.. Condu-
ziu-se uma recta pp, qualquer, ortogonal aos dois planos – a recta pp é uma recta de
perfil. 22.. Determinaram-se os pontos II e II’’, os pontos de intersecção da recta pp com
os planos ρ e σ, respectivamente. Como nem a recta pp nem os planos ρ e σ são
projectantes, recorreu-se ao mmééttooddoo ggeerraall ddaa iinntteerrsseeccççããoo eennttrree rreeccttaass ee ppllaannooss.
Assim, conduziu-se, pela recta pp, um plano π, auxiliar (π é um plano de perfil). Em
seguida determinou-se a recta ii, a recta de intersecção dos planos π e ρ (que está
definida por FF e HH, os seus traços). Não é possível determinar directamente o ponto
de concorrência das rectas pp e ii. Em seguida determinou-se a recta ii’’, a recta de in-
tersecção dos planos π e σ (que está definida por FF’’ e pela sua direcção – é parale-
la à recta ii, pois qualquer plano corta dois planos paralelos segundo duas rectas
paralelas). Também não é possível determinar directamente o ponto de concorrên-
cia das rectas ii’’ e pp. Há que resolver o exercício com o recurso a um processo geo-
métrico auxiliar – o do rebatimento, segundo é expressamente pedido no
enunciado. Rebateu-se o plano π para o Plano Frontal de Projecção – a charneira
foi ffπ. A recta iirr está definida por FFrr e HHrr e a recta ii’’rr está definida por FF’’rr e pela sua
direcção (é paralela a iirr). Em rebatimento, desenhou-se pprr, qualquer, perpendicular a iirr e ii’’rr e determinaram-se os pontos de concorrência
de pprr com aquelas – IIrr e II’’rr, respectivamente. II é o ponto de intersecção de pp com ρ e II’’ é o ponto de intersecção de pp com σ. 33.. A distância
entre os dois pontos é a distância entre os dois planos. IIෆrrෆIIෆ’’ෆrrෆ é, assim, a V.G. da distância entre os dois pontos (e da distância entre os dois
planos). Inverteu-se o rebatimento, obtendo as projecções de II e II’’. As projecções do segmento [IIII’’] são as projecções de um segmento
representativo da distância entre os dois planos.
252.
253.
Em primeiro lugar representaram-se os dois planos, em função dos dados – o plano
ρ está definido pelos seus traços e o plano σ está definido pelo seu traço frontal e
pela sua orientação (é paralelo a ρ). Em seguida, procedeu-se à execução sequen-
cial das etapas do mmééttooddoo ggeerraall ddaa ddiissttâânncciiaa eennttrree ddooiiss ppllaannooss. 11.. Conduziu-se
uma recta pp, qualquer, ortogonal aos dois planos – a recta pp é uma recta de perfil.
22.. Determinaram-se os pontos II e II’’, os pontos de intersecção da recta pp com os
planos ρ e σ, respectivamente. O recurso à mudança do diedro de projecção (que é
expressamente pedido no enunciado) simplifica bastante o exercício, tanto ao nível
dos raciocínios como dos traçados. Como não é dado o traço horizontal de σ, op-
tou-se por substituir o Plano Horizontal de Projecção (ppllaannoo 11) por um outro plano
(ppllaannoo 44), obtendo um diedro de projecção no qual os dois planos são planos verti-
cais (que mantêm o paralelismo). O novo eixo XX (o eixo XX’’) é perpendicular a ffρ e a
ffσ. Mantiveram-se os traços frontais dos dois planos (manteve-se o Plano Frontal de
Projecção) e determinou-se o traço de ρ no ppllaannoo 44 com o recurso a um ponto
qualquer de hhρ – o ponto AA. A projecção do ponto AA no ppllaannoo 44 (AA44) determinou-se
em função do seu afastamento, que se manteve. O traço de ρ no ppllaannoo 44, hh44ρ, pas-
sa por AA44 (no novo diedro de projecção, o plano ρ é projectante horizontal) e é con-
corrente com ffρ no eixo XX’’. O traço de σ no ppllaannoo 44 é paralelo a hh44ρ, sendo
concorrente com ffσ no eixo XX’’. No novo diedro de projecção, os dois planos são
verticais e a recta pp é uma recta horizontal (de nível) – pp44 é, assim, perpendicular
aos traços dos dois planos no ppllaannoo 44 e os pontos de intersecção de pp com os dois planos têm determinação imediata, a partir das suas
projecções no ppllaannoo 44 (no novo diedro de projecção os planos são projectantes horizontais). Este raciocínio permitiu-nos determinar II44 e
II’’44. 33.. A distância entre os pontos II e II’’ é a distância entre os dois planos. Como a recta pp é horizontal (no diedro de projecção formado pelo
ppllaannoo 22 e pelo ppllaannoo 44), o segmento [IIII’’] é horizontal (é paralelo ao ppllaannoo 44) e projecta-se em V.G. no ppllaannoo 44. IIෆ44ෆIIෆ’’ෆ44ෆ é, assim, a V.G. da dis-
tância entre os dois planos. As projecções frontais de II e II’’ determinam-se directamente e as suas projecções horizontais, no diedro de pro-
jecção inicial (o diedro de projecção formado entre o ppllaannoo 11 e o ppllaannoo 22), determinam-se em função dos seus afastamentos, que se
mantêm, obtendo-se assim as projecções do segmento [IIII’’], que é um segmento representativo da distância entre os dois planos.

93. 93
SOLUÇÕES
254.
Em primeiro lugar representaram-se os dois planos, em função dos dados – o plano ρ
está definido pelos seus traços e o plano σ está definido pelo seu traço horizontal e pela
sua orientação (é paralelo a ρ). Em seguida, procedeu-se à execução sequencial das
etapas do mmééttooddoo ggeerraall ddaa ddiissttâânncciiaa eennttrree ddooiiss ppllaannooss. 11.. Conduziu-se uma recta pp,
qualquer, ortogonal aos dois planos – a recta pp é uma recta de perfil. 22.. Determinaram-
-se os pontos II e II’’, os pontos de intersecção da recta pp com os planos ρ e σ, respecti-
vamente. Para tal, recorreu-se a uma mudança do diedro de projecção, à semelhança
do exercício anterior. Como não é dado o traço frontal de σ, optou-se por substituir o
Plano Frontal de Projecção (ppllaannoo 22) por um outro plano (ppllaannoo 44), obtendo um diedro
de projecção no qual os dois planos são planos de topo (que mantêm o paralelismo). O
novo eixo XX (o eixo XX’’) é perpendicular a hhρ e a hhσ. Mantiveram-se os traços horizontais
dos dois planos (manteve-se o Plano Horizontal de Projecção) e determinou-se o traço
de ρ no ppllaannoo 44 com o recurso a um ponto qualquer de ffρ – o ponto AA. A projecção do
ponto AA no ppllaannoo 44 (AA44) determinou-se em função da sua cota, que se manteve. O traço
de ρ no ppllaannoo 44, ff44ρ, passa por AA44 (no novo diedro de projecção, o plano ρ é projectante
frontal) e é concorrente com hhρ no eixo XX’’. O traço de σ no ppllaannoo 44 é paralelo a ff44ρ, sendo
concorrente com hhσ no eixo XX’’. No novo diedro de projecção, os dois planos são de
topo e a recta pp é uma recta frontal (de frente) – pp44 é, assim, perpendicular aos traços
dos dois planos no ppllaannoo 44 e os pontos de intersecção de pp com os dois planos têm
determinação imediata, a partir das suas projecções no ppllaannoo 44 (no novo diedro de pro-
jecção os planos são projectantes frontais). Este raciocínio permitiu-nos determinar II44 e II’’44. 33.. A distância entre os pontos II e II’’ é a distância
entre os dois planos. Como a recta pp é frontal (no diedro de projecção formado pelo ppllaannoo 11 e pelo ppllaannoo 44), o segmento [IIII’’] é frontal (é
paralelo ao ppllaannoo 44) e projecta-se em V.G. no ppllaannoo 44. IIෆ44ෆIIෆ’’ෆ44ෆ é, assim, a V.G. da distância entre os dois planos. As projecções horizontais de II e II’’
determinam-se directamente e as suas projecções frontais, no diedro de projecção inicial (o diedro de projecção formado entre o ppllaannoo 11 e o
ppllaannoo 22), determinam-se em função das suas cotas, que se mantêm, obtendo-se assim as projecções do segmento [IIII’’], que é um segmento
representativo da distância entre os dois planos.
255.
Em primeiro lugar representaram-se os dois planos, em função dos dados – o pla-
no ρ está definido pelo seu traço frontal e pela sua orientação (faz um diedro de
60° com o Plano Horizontal de Projecção e o seu traço horizontal situa-se no
SSPPHHAA) e o plano σ está definido pelo seu traço horizontal e pela sua orientação
(é paralelo a ρ, pelo que faz igualmente um diedro de 60o com o Plano Horizontal
de Projecção). Em seguida, procedeu-se à execução sequencial das etapas do
mmééttooddoo ggeerraall ddaa ddiissttâânncciiaa eennttrree ddooiiss ppllaannooss. 11.. Conduziu-se uma recta pp, qual-
quer, ortogonal aos dois planos – a recta pp é uma recta de perfil. 22.. Determinaram-
se os pontos II e II’’, os pontos de intersecção da recta pp com os planos ρ e σ,
respectivamente. Como nem a recta pp nem os planos ρ e σ são projectantes, re-
correu-se ao mmééttooddoo ggeerraall ddaa iinntteerrsseeccççããoo eennttrree rreeccttaass ee ppllaannooss. Assim, condu-
ziu-se, pela recta pp, um plano π, auxiliar (π é um plano de perfil). Em seguida,
determinou-se a recta ii, a recta de intersecção dos planos π e ρ. A recta ii está defini-
da por um ponto (o seu traço frontal, FF) e por uma direcção (faz um ângulo de 60o
com o Plano Horizontal de Projecção). Note que a amplitude do diedro formado en-
tre um plano de rampa e o Plano Horizontal de Projecção é igual à amplitude do ân-
gulo que qualquer recta de perfil do plano de rampa faz com o Plano Horizontal de
Projecção. Não é possível determinar directamente o ponto de concorrência das
rectas pp e ii. Em seguida, determinou-se a recta ii’’, a recta de intersecção dos pla-
nos π e σ (que está definida por HH, o seu traço horizontal, e pela sua direcção – é
paralela à recta ii, pois qualquer plano corta dois planos paralelos segundo duas
rectas paralelas). Também não é possível determinar directamente o ponto de
concorrência das rectas ii’’ e pp. Há que resolver o exercício com o recurso a um
processo geométrico auxiliar – o do rebatimento, por exemplo. Rebateu-se o plano π para o Plano Frontal de Projecção – a charneira foi ffπ.
A recta iirr passa por FFrr e faz um ângulo de 60o com hhπrr
. Note que, apesar de não se ter assinalado o traço horizontal da recta iirr em rebati-
mento, se garantiu que este se situa no SSPPHHAA. A recta ii’’rr passa por HHrr e é paralela a iirr. Em rebatimento, desenhou-se pprr, qualquer, perpen-
dicular a iirr e ii’’rr e determinaram-se os pontos de concorrência de pprr com aquelas – IIrr e II’’rr, respectivamente. II é o ponto de intersecção de pp
com ρ e II’’ é o ponto de intersecção de pp com σ. 33.. A distância entre os dois pontos é a distância entre os dois planos. IIෆrrෆIIෆ’’ෆrrෆ é, assim, a V.G.
da distância entre os dois pontos (e da distância entre os dois planos). Inverteu-se o rebatimento, obtendo as projecções de II e II’’. As pro-
jecções do segmento [IIII’’] são as projecções de um segmento representativo da distância entre os dois planos.

94. 94
SOLUÇÕES
256.
Em primeiro lugar representaram-se os dois planos, em função dos dados
– ambos os planos estão definidos pelos seus traços. O plano σ, no en-
tanto, porque os seus traços são uma única recta (o eixo XX) está definido
por uma recta (o eixo XX) e pela sua orientação (é paralelo a ρ). Em segui-
da, procedeu-se à execução sequencial das etapas do mmééttooddoo ggeerraall ddaa
ddiissttâânncciiaa eennttrree ddooiiss ppllaannooss. 11.. Conduziu-se uma recta pp, qualquer,
ortogonal aos dois planos – a recta pp é uma recta de perfil. 22.. Determina-
ram-se os pontos II e II’’, os pontos de intersecção da recta pp com os pla-
nos ρ e σ, respectivamente. Optou-se pelo recurso a uma mudança do
diedro de projecção – substituiu-se o Plano Horizontal de Projecção (ppllaa--
nnoo 11) por um outro plano (ppllaannoo 44), obtendo um diedro de projecção no
qual os dois planos são planos verticais (que mantêm o paralelismo). O
exercício é, assim, semelhante ao exercício 225533, mantendo-se os traça-
dos naquele efectuados, bem como os raciocínios que os justificam, pelo
que se aconselha o acompanhamento da resolução gráfica apresentada
com a leitura do relatório daquele exercício.
258.
Em primeiro lugar representou-se o plano ρ, pelos seus traços, em função dos
dados. Tenha em conta que o problema proposto consiste numa variação dos pro-
blemas de distâncias entre planos – o plano σ (o plano pretendido) será determi-
nado em função da sua distância ao plano ρ. Assim, a resolução do exercício
passa necessariamente pela execução sequencial das etapas do mmééttooddoo ggeerraall
ppaarraa aa ddeetteerrmmiinnaaççããoo ddaa ddiissttâânncciiaa eennttrree ddooiiss ppllaannooss, como em seguida se
expõe. 11.. Conduziu-se uma recta pp, qualquer, ortogonal aos dois planos – a recta pp
é uma recta de perfil. 22.. Determinou-se o ponto II, o ponto de intersecção da recta pp
com o plano ρ, conforme exposto no relatório do exercício 225522 – note que não é
possível determinar o ponto de intersecção da recta pp com o plano σ, pois este é
o que é pedido no enunciado (não é conhecido). De qualquer forma, o ponto de
intersecção da recta pp com o plano σ é um ponto que se situa na recta pp a 3 cm
(a distância entre os dois planos) do ponto II. 33.. Sobre pprr, a partir de IIrr, mediram-
-se os 3 cm (a distância entre os dois planos), obtendo um ponto II’’rr – II’’ será o
ponto de intersecção da recta pp com o plano σ. O ponto II’’rr situou-se sobre pprr de
forma a garantir que o plano σ (que contém o ponto II’’) se situe entre o eixo XX e o
plano ρ (como é pedido no enunciado). Note que IIෆrrෆIIෆ’’ෆrrෆ é, assim, a V.G. da distância
entre os dois planos. Por II’’rr conduziu-se uma recta ii’’rr, paralela à recta iirr (e perpen-
dicular a pprr) – ii’’ é a recta de intersecção do plano π com o plano σ. As rectas ii e ii’’
são necessariamente paralelas, pois são as rectas de intersecção de um plano
(o plano π) com dois planos paralelos (os planos ρ e σ). Em rebatimento, determi-
naram-se os traços da recta ii’’, sobre os traços homónimos do plano π (FF’’rr situa-se
sobre ffπrr
e HH’’rr situa-se sobre hhπrr
). Invertendo o rebatimento, determinaram-se as projecções de FF’’ (que é fixo, pois é um ponto da charneira)
e HH’’ – os traços do plano σ passam pelos traços homónimos da recta ii’’ e são paralelos aos traços homónimos do plano ρ (o plano σ é outro
plano de rampa).
257.
Em primeiro lugar representou-se o plano ρ, pelos seu traços, em função dos da-
dos. Um plano de rampa paralelo ao β1/3 é necessariamente ortogonal ao β2/4, pelo
que o plano ρ tem os seus traços coincidentes (planos ortogonais ao β2/4 têm os
seus traços coincidentes). Em seguida, procedeu-se à execução sequencial das
etapas do mmééttooddoo ggeerraall ddaa ddiissttâânncciiaa eennttrree ddooiiss ppllaannooss – tendo em conta que se
recorreu ao processo do rebatimento, trata-se de uma situação semelhante à do
exercício 225522, pelo que se aconselha o acompanhamento da resolução proposta
com a leitura do relatório daquele exercício. Note que a recta de intersecção do
plano de perfil π com o β1/3 (a recta ii’’) é uma recta de perfil ppaassssaannttee – está defini-
da por um ponto (o seu ponto de concorrência com o eixo XX) e por uma direcção
(faz ângulos de 45o com os planos de projecção e atravessa os 1o e 3o Diedros).
A recta ii’’, em rebatimento, faz ângulos de 45o com ffπrr
e hhπrr
e é nneecceessssaarriiaammeennttee
paralela à recta de intersecção de π com ρ (a recta ii), pois o plano ρ e o β1/3 são
paralelos e o plano π corta os dois planos segundo duas rectas paralelas.

95. 95
SOLUÇÕES
259.
261.
Em primeiro lugar representaram-se a recta hh e o ponto PP, pelas suas projecções,
em função dos dados. Uma vez que a distância de um ponto a uma recta é medida
perpendicularmente à recta, há que conduzir, pelo ponto, uma recta ppeerrppeennddiiccuullaarr
à recta hh. Tal procedimento pode efectuar-se com o recurso ao mmééttooddoo ggeerraall ppaarraa
aa ddeetteerrmmiinnaaççããoo ddaa ddiissttâânncciiaa ddee uumm ppoonnttoo aa uummaa rreeccttaa mas, atendendo a que a
recta hh é paralela ao Plano Horizontal de Projecção, pelo que a perpendicularidade
é directa em projecção horizontal, é possível conduzir, por PP, uma recta perpendi-
cular à recta hh de forma directa – a recta pp. Assim, conduziu-se pp11 por PP11, perpen-
dicular a hh11 – pp11 e hh11 são concorrentes em II11, que é a projecção horizontal do
ponto de concorrência das duas rectas. II22 situa-se sobre hh22, na linha de chamada
de II11 – pp22 fica definida por PP22 e II22. A recta pp, definida por PP e II, é a recta perpendi-
cular à recta hh que passa por PP. [PPII] é o segmento representativo da distância de PP
a hh, que não se projecta em V.G. em nenhum dos planos de projecção (é oblíquo a
ambos). Para determinar a V.G. de [PPII] recorreu-se a uma mudança do diedro de
projecção, na qual se transformou o segmento [PPII] num segmento de recta frontal
(de frente) – ver exercício 221166 e respectivo relatório.
260.
Por ddiissttâânncciiaa ddee uumm ppoonnttoo aa uummaa rreeccttaa entende-se o comprimento de um segmento de recta perpendicular à recta (concorrente com
esta), que tem um extremo no ponto dado e o outro no seu ponto de concorrência com a recta, ou seja, é a menor distância do ponto à recta,
medida numa perpendicular à recta que passa pelo ponto.
Em primeiro lugar representaram-se os dois planos, em função dos dados – o
plano ρ, passante, está definido pelo eixo XX e pelas projecções do ponto PP e o
plano σ está definido pelo seu traço frontal e pela sua orientação (é paralelo ao
plano ρ). Em seguida, procedeu-se à execução sequencial das etapas do mmééttooddoo
ggeerraall ddaa ddiissttâânncciiaa eennttrree ddooiiss ppllaannooss. 11.. Conduziu-se uma recta pp, qualquer,
ortogonal aos dois planos – a recta pp é uma recta de perfil. Por uma questão de
economia de traçados, optou-se por conduzir a recta pp pelo ponto PP, o ponto que
define o plano passante. 22.. Determinaram-se os pontos de intersecção da recta pp
com os planos ρ e σ. O ponto PP é, imediatamente, o ponto de intersecção da rec-
ta pp com o plano ρ. Para determinar o ponto de intersecção da recta pp com o pla-
no σ, uma vez que nem a recta pp nem o plano σ são projectantes, recorreu-se ao
mmééttooddoo ggeerraall ddaa iinntteerrsseeccççããoo eennttrree rreeccttaass ee ppllaannooss. Assim, conduziu-se, pela
recta pp, um plano π, auxiliar (π é um plano de perfil). Em seguida, determinou-se a
recta ii, a recta de intersecção dos planos π e σ. A recta ii está definida por um
ponto (o seu traço frontal, FF) e por uma direcção (é paralela a uma recta de perfil
do plano ρ – a recta ii’’, que é a recta de intersecção do plano π com o plano ρ,
pois qualquer plano corta dois planos paralelos segundo duas rectas paralelas).
A recta ii’’ é uma recta de perfil passante e está definida por dois pontos – o ponto
PP e o seu ponto de concorrência com o eixo XX. Não é possível determinar directa-
mente o ponto de concorrência das rectas pp e ii. Há que resolver o exercício com
o recurso a um processo geométrico auxiliar – o do rebatimento, por exemplo.
Rebateu-se o plano π para o Plano Frontal de Projecção – a charneira foi ffπ.
A recta iirr passa por FFrr e é paralela à recta ii’’rr (a recta ii’’rr está definida pelo seu
ponto de concorrência com o eixo XX, que é fixo, e por PPrr). Em rebatimento, desenhou-se pprr, perpendicular a iirr e ii’’rr e passando por PPrr, e
determinou-se o ponto de concorrência de pprr com iirr – IIrr. II é o ponto de intersecção de pp com σ e PP é o ponto de intersecção de pp com σ
(como acima se referiu). 33.. A distância entre os dois pontos é a distância entre os dois planos. PPෆrrෆIIෆrrෆ é, assim, a V.G. da distância entre os dois
pontos (e da distância entre os dois planos). Inverteu-se o rebatimento, obtendo as projecções de II. As projecções do segmento [PPII] são as
projecções de um segmento representativo da distância entre os dois planos.

96. 96
SOLUÇÕES
263.
Em primeiro lugar representaram-se a recta tt e o ponto MM, pelas suas projecções, em função
dos dados – a projecção frontal da recta tt é um ponto, o que se assinalou devidamente com
parêntesis. A distância de um ponto a uma recta é medida perpendicularmente à recta, pelo
que há que conduzir, pelo ponto, uma recta ppeerrppeennddiiccuullaarr à recta tt. A recta tt, de topo, é um
caso particular das rectas horizontais (de nível) – é paralela ao Plano Horizontal de Projecção,
pelo que a perpendicularidade é directa em projecção horizontal. Assim, à semelhança do
exercício 226611, conduziu-se a projecção horizontal da recta pp (a recta perpendicular à recta tt) –
pp11 passa por MM11 e é perpendicular a tt11. As rectas pp11 e tt11 são concorrentes em II11, que é a pro-
jecção horizontal do ponto de concorrência das duas rectas – II22 tem determinação directa,
pois a recta é projectante frontal e pp22 fica definida por MM22 e II22. A recta pp, definida por MM e II, é a
recta perpendicular à recta tt que passa por MM – a recta pp é uma recta frontal (de frente). [MMII] é
o segmento representativo da distância de MM a tt, que se projecta em V.G. no Plano Frontal de
Projecção, pois é paralelo a este. A V.G. de [PPII] está na sua projecção frontal e é MMෆ22ෆIIෆ22ෆ.
262.
Em primeiro lugar representaram-se a recta ff e o ponto PP, pelas respectivas projecções,
em função dos dados. A distância de um ponto a uma recta é medida perpendicularmente
à recta, pelo que há que conduzir, pelo ponto, uma recta ppeerrppeennddiiccuullaarr à recta ff. Tal como
no exercício anterior, apesar desse procedimento se poder efectuar com o recurso ao mméé--
ttooddoo ggeerraall ppaarraa aa ddeetteerrmmiinnaaççããoo ddaa ddiissttâânncciiaa ddee uumm ppoonnttoo aa uummaa rreeccttaa, atendendo a
que a recta ff é paralela ao Plano Frontal de Projecção e a perpendicularidade é directa em
projecção frontal, é possível conduzir, por PP, uma recta perpendicular à recta ff de forma
directa – a recta pp. Assim, conduziu-se pp22 por PP22, perpendicular a ff22 – pp22 e ff22 são concor-
rentes em II22, que é a projecção frontal do ponto de concorrência das duas rectas. II11 situa-se
sobre ff11, na linha de chamada de II22 – pp11 fica definida por PP11 e II11. A recta pp, definida por PP e
II, é a recta perpendicular à recta ff que passa por PP. [PPII] é o segmento representativo da
distância de PP a ff, que não se projecta em V.G. em nenhum dos planos de projecção (é
oblíquo a ambos). Para determinar a V.G. de [PPII] recorreu-se a uma mudança do diedro de
projecção, na qual se transformou o segmento [PPII] num segmento de recta frontal (de
frente) – ver exercício 221166 e respectivo relatório. Note que o ponto II tem cota negativa, que
se manteve na mudança do diedro de projecção efectuada – mantiveram-se as cotas e
mudaram os afastamentos.
264.
Em primeiro lugar representou-se o ponto AA, pelas suas projecções, em função dos da-
dos. A distância de um ponto a uma recta é medida perpendicularmente à recta, pelo
que há que conduzir, pelo ponto, uma recta ppeerrppeennddiiccuullaarr ao eixo XX – o eixo XX é uma
recta fronto-horizontal, que é simultaneamente um caso particular das rectas horizontais
(de nível) e das rectas frontais (de frente). Qualquer recta perpendicular a uma recta fron-
to-horizontal é nneecceessssaarriiaammeennttee uma recta de perfil, pois a perpendicularidade é direc-
ta em qualquer das projecções ou em ambas as projecções. Assim, conduziu-se, pelo
ponto AA, uma recta pp de perfil, perpendicular ao eixo XX – uma vez que as duas rectas
são concorrentes, a recta pp é uma recta de perfil passante (é concorrente com o eixo XX
no ponto II). A recta pp é a recta perpendicular ao eixo XX que passa por AA e está definida
por dois pontos – o ponto AA e o ponto II. [AAII] é o segmento representativo da distância
de AA ao eixo XX, que não se projecta em V.G. em nenhum dos planos de projecção (é ob-
líquo a ambos). Para determinar a V.G. de [AAII] recorreu-se ao rebatimento do plano π, o
plano de perfil que contém a recta pp. Efectuou-se o rebatimento do plano π para o Plano
Frontal de Projecção (a charneira foi ffπ) – ver exercício 221155 e respectivo relatório (note
que o ponto II é fixo, pois situa-se na charneira). AAෆrrෆIIෆrrෆ é a V.G. da distância do ponto AA ao
eixo XX.

97. 97
SOLUÇÕES
265.
Em primeiro lugar representaram-se a recta rr e o ponto PP, pelas respectivas projecções,
em função dos dados. A distância de um ponto a uma recta é medida perpendicular-
mente à recta, pelo que há que conduzir, pelo ponto PP, uma recta ppeerrppeennddiiccuullaarr à recta rr.
No entanto, ao contrário das situações anteriores, em que a recta era paralela a um dos
planos de projecção ou a ambos (sendo que a perpendicularidade era directa em pro-
jecções), nesta situação a perpendicularidade não é directa em nenhuma das projec-
ções, pois a recta não é paralela a qualquer dos planos de projecção. Assim sendo, o
processo de resolução mais linear consiste em resolver o problema a dduuaass ddiimmeenn--
ssõõeess, nnoo ppllaannoo ddeeffiinniiddoo ppeellaa rreeccttaa ee ppeelloo ppoonnttoo – para tal é necessário rebater o plano
definido pela recta e pelo ponto, pois em rebatimento (em VG.) a perpendicularidade é
directa. Assim, rebateu-se esse plano para o plano horizontal (de nível) ν que contém o
ponto PP – a charneira do rebatimento (recta ee) fica definida pelo ponto PP e pelo ponto
de intersecção da recta rr com o plano ν, que é o próprio ponto AA (note que AA e PP têm a
mesma cota). PPrr ≡ PP11 e AArr ≡ AA11, pois PP e AA são dois pontos da charneira. Já temos um
ponto para definir a recta rr em rebatimento (o ponto AArr). Recorreu-se a um outro ponto
(o seu traço horizontal – HH) da recta, para rebater a recta – rrrr fica definida por AArr e HHrr.
Note que HH se rebateu pelo triângulo do rebatimento, em função da sua cota em rela-
ção ao plano ν (a distância de HH ao plano ν). Em rebatimento (no plano definido pela
recta e pelo ponto), conduziu-se, por PPrr, uma perpendicular a rrrr, obtendo IIrr - PPෆrrෆIIෆrrෆ é a V.G. da distância de PP a rr. Inverteu-se o rebatimento,
com o recurso à perpendicular à charneira que passa por II (e que corresponde ao plano ortogonal à charneira que contém o arco do seu
rebatimento), obtendo II11 sobre rr11 e II 22, na mesma linha de chamada de II11, sobre rr22. A partir das projecções de II, obtiveram-se as projecções
de [PPII], que é o segmento representativo da distância de PP a rr.
Em primeiro lugar representaram-se a recta rr e o ponto PP, pelas respectivas projec-
ções, em função dos dados. A recta rr é passante, pelo que é concorrente com o eixo
XX – as suas projecções são concorrentes entre si no eixo XX. Note que, em função dos
dados, o ponto de concorrência da recta rr com o eixo XX é um ponto com abcissa nula.
A distância de um ponto a uma recta é medida perpendicularmente à recta, pelo que
há que conduzir, pelo ponto PP, uma recta ppeerrppeennddiiccuullaarr à recta rr. Tal como na situa-
ção anterior, a perpendicularidade não é directa em nenhuma das projecções, pois a
recta não é paralela a qualquer dos planos de projecção. Assim sendo, à semelhança
do exercício anterior, o processo de resolução mais linear consiste em resolver o
problema a duas dimensões, nnoo ppllaannoo ddeeffiinniiddoo ppeellaa rreeccttaa ee ppeelloo ppoonnttoo, pelo que se
aconselha o acompanhamento da resolução gráfica apresentada com a leitura do rela-
tório do exercício anterior. A charneira do rebatimento (recta ee) fica definida por PP e
por BB, que é o ponto de intersecção do plano ν com a recta rr. O ponto AA foi o ponto a
que se recorreu para rebater a recta rr.
267.
Em primeiro lugar representaram-se a recta rr e o ponto PP, pelas respectivas projec-
ções, em função dos dados. A recta rr é paralela ao β2/4, pelo que as suas projecções
são paralelas entre si. O ponto PP tem cota e afastamento nulos, pois é um ponto do
eixo XX. A distância de um ponto a uma recta é medida perpendicularmente à recta,
pelo que há que conduzir, pelo ponto PP, uma recta ppeerrppeennddiiccuullaarr à recta rr. Tal como
na situação do exercício 226655, a perpendicularidade não é directa em nenhuma das
projecções, pois a recta não é paralela a qualquer dos planos de projecção. Assim
sendo, à semelhança daquele exercício, o processo de resolução mais linear consiste
em resolver o problema a duas dimensões, nnoo ppllaannoo ddeeffiinniiddoo ppeellaa rreeccttaa ee ppeelloo ppoonn--
ttoo, pelo que se aconselha o acompanhamento da resolução gráfica apresentada com
a leitura do relatório do exercício 226655. Rebateu-se o plano definido pela recta e pelo
ponto para o Plano Frontal de Projecção – a charneira fica definida pelo ponto PP (que
é um ponto do Plano Frontal de Projecção, pois situa-se no eixo XX) e pelo traço frontal
da recta rr – FF. O ponto AA foi o ponto da recta rr a que se recorreu para rebater a recta.
266.

98. 98
SOLUÇÕES
268.
Em primeiro lugar representaram-se a recta mm e o ponto MM, pelas respectivas projec-
ções, em função dos dados. A recta mm é uma recta do β2/4, pelo que tem as suas
projecções coincidentes. O ponto MM, porque pertence ao β1/3 (o bissector dos die-
dros ímpares), tem coordenadas iguais e projecções simétricas em relação ao eixo
XX. A distância de um ponto a uma recta é medida perpendicularmente à recta, pelo
que há que conduzir, pelo ponto MM, uma recta ppeerrppeennddiiccuullaarr à recta mm. Tal como na
situação do exercício 226655, a perpendicularidade não é directa em nenhuma das pro-
jecções, pois a recta não é paralela a qualquer dos planos de projecção. Assim sen-
do, à semelhança daquele exercício, o processo de resolução mais linear consiste
em resolver o problema a duas dimensões, nnoo ppllaannoo ddeeffiinniiddoo ppeellaa rreeccttaa ee ppeelloo
ppoonnttoo, pelo que se aconselha o acompanhamento da resolução gráfica apresentada
com a leitura do relatório do exercício 226655. Rebateu-se o plano definido pela recta e
pelo ponto para o plano frontal (de frente) ϕ que passa por MM – a charneira fica defi-
nida pelo ponto MM e pelo ponto AA, que é o ponto de intersecção do plano ϕ com a
recta mm. O ponto BB foi o ponto da recta mm a que se recorreu para rebater a recta – BB
é o ponto de concorrência da recta com o eixo XX.
Em primeiro lugar representaram-se a recta rr e o ponto PP, pelas respectivas
projecções, em função dos dados. A recta rr é uma recta do β1/3, pelo que tem
as suas projecções simétricas em relação ao eixo XX. O ponto PP, porque per-
tence ao β1/3, tem coordenadas iguais e projecções simétricas em relação ao
eixo XX. A distância de um ponto a uma recta é medida perpendicularmente à
recta, pelo que há que conduzir, pelo ponto PP, uma recta ppeerrppeennddiiccuullaarr à
recta rr. Tal como na situação do exercício 226655, a perpendicularidade não é di-
recta em nenhuma das projecções, pois a recta não é paralela a qualquer dos
planos de projecção. Assim sendo, à semelhança daquele exercício, o pro-
cesso de resolução mais linear consiste em resolver o problema a duas di-
mensões, nnoo ppllaannoo ddeeffiinniiddoo ppeellaa rreeccttaa ee ppeelloo ppoonnttoo, pelo que se aconselha o
acompanhamento da resolução gráfica apresentada com a leitura do relatório
do exercício 226655. Rebateu-se o plano definido pela recta e pelo ponto para o
plano horizontal (de nível) ν que passa por PP – a charneira fica definida pelo
ponto PP e pelo ponto BB, que é o ponto de intersecção do plano ν com a recta
rr. O ponto AA foi o ponto da recta rr a que se recorreu para rebater a recta – AA é
o ponto de concorrência da recta com o eixo XX. Note que, uma vez que tanto
a recta rr como o ponto PP pertencem ao β1/3, o plano definido pela recta e pelo
ponto é o próprio β1/3 – o rebatimento efectuado foi o rebatimento do β1/3, pelo
que a charneira é uma recta fronto-horizontal (é a recta de intersecção do β1/3
com um plano horizontal – o plano ν).
269.
270.
Em primeiro lugar representaram-se a recta rr e o ponto PP, pelas respectivas pro-
jecções, em função dos dados. Note que a situação do presente exercício é
idêntica à do exercício 226688, pelo que se aconselha a leitura do respectivo relatório.

99. 99
SOLUÇÕES
271.
Em primeiro lugar representaram-se a recta pp e o ponto PP, pelas respectivas
projecções, em função dos dados. A distância de um ponto a uma recta é me-
dida perpendicularmente à recta, pelo que há que conduzir, pelo ponto PP,
uma recta ppeerrppeennddiiccuullaarr à recta pp. A recta pp não é paralela a nenhum dos
planos de projecção, pelo que a perpendicularidade não é directa em nenhu-
ma das projecções – há, então, que resolver o problema a duas dimensões,
nnoo ppllaannoo ddeeffiinniiddoo ppeellaa rreeccttaa ee ppeelloo ppoonnttoo. Para tal, é necessário rebater o
plano definido pela recta e pelo ponto, pois em rebatimento (em VG.) a per-
pendicularidade é directa. Assim, rebateu-se esse plano para o plano frontal
(de frente) ϕ que contém o ponto PP – a charneira do rebatimento (recta ee’’) fica
definida pelo ponto PP e pelo ponto CC, que é o ponto de intersecção da recta pp
com o plano ϕ. Note que a determinação das projecções do ponto CC se pro-
cessou com o recurso a um processo geométrico auxiliar, pois as projecções
da recta pp não verificam o Critério de Reversibilidade. Assim, a determinação
de CC11, a projecção horizontal de CC, é directa, pois o plano ϕ é projectante ho-
rizontal. Para determinar CC22, a projecção frontal de CC, recorreu-se ao rebati-
mento da recta pp, pelo rebatimento do plano de perfil que a contém – o plano
π. Rebateu-se o plano π para o Plano Frontal de Projecção – a charneira foi ffπ (recta ee). A recta pprr fica definida por AArr e por BBrr – em rebati-
mento, sobre pprr, determinou-se CCrr a partir do rebatimento de CC11. Invertendo o rebatimento, determinou-se CC22. A charneira do rebatimento
do plano definido pela recta pp e pelo ponto PP (que é um plano oblíquo) para o plano frontal (de frente) ϕ está agora totalmente definida – a
recta ee’’ passa por PP e por CC. PPrr ≡ PP22 e CCrr’’ ≡ CC22, pois PP e CC são dois pontos da charneira (recta ee’’) – note que CCrr’’ é o ponto CC rebatido pelo
segundo rebatimento da recta pp. Já temos um ponto para definir a recta pp em rebatimento (o ponto CCrr’’). Recorreu-se a um outro ponto da
recta (o ponto AA), para a rebater – pprr’’ fica definida por AArr’’ e CCrr’’. O ponto AA rebateu-se pelo triângulo do rebatimento, em função do seu afas-
tamento em relação ao plano ϕ (a distância de AA ao plano ϕ). Note que a recta pprr’’ é a recta pp rebatida pelo rebatimento do plano definido
pela recta e pelo ponto PP (o seu segundo rebatimento), tal como AArr’’ é o ponto AA rebatido no seu segundo rebatimento (o rebatimento do
plano definido pela recta pp e pelo ponto PP). Em rebatimento (no plano definido pela recta e pelo ponto), conduziu-se, por PPrr, uma perpendi-
cular a pprr’’, obtendo IIrr – PPෆrrෆIIෆrrෆ é a V.G. da distância de PP a pp. Inverteu-se o rebatimento, com o recurso à perpendicular à charneira que passa
por II (e que corresponde ao plano ortogonal à charneira que contém o arco do seu rebatimento), obtendo II11 sobre pp11. Para determinar II22,
uma vez que as projecções da recta pp não verificam o Critério de Reversibilidade, recorreu-se ao rebatimento da recta pp pelo rebatimento do
plano π – IIrr’’ é o ponto II rebatido pelo rebatimento do plano π. IIrr’’ determinou-se sobre pprr a partir de II11. Invertendo o rebatimento, determi-
nou-se II22 sobre pp22. A partir das projecções de II, obtiveram-se as projecções de [PPII], que é o segmento representativo da distância de PP a pp.
Em primeiro lugar representaram-se a recta pp e o ponto MM, pelas res-
pectivas projecções, em função dos dados. Note que a recta pp está
definida por um ponto (o ponto AA) e pela sua direcção (é dado o ângulo
que a recta faz com o Plano Horizontal de Projecção). A distância de
um ponto a uma recta é medida perpendicularmente à recta, pelo que
há que conduzir, pelo ponto MM, uma recta ppeerrppeennddiiccuullaarr à recta pp. A
recta pp não é paralela a nenhum dos planos de projecção, pelo que a
perpendicularidade não é directa em nenhuma das projecções – no en-
tanto, recorrendo a uma mudança do diedro de projecção, é possível
transformar a recta pp numa recta frontal (de frente), o que fará com que
a perpendicularidade passe a ser directa, e o ângulo que a recta faz
com o Plano Horizontal de Projecção passará a projectar-se em V.G.,
no novo plano de projecção. Assim, efectuaram-se os traçados neces-
sários a tal – substituiu-se o Plano Frontal de Projecção (ppllaannoo 22) por
um novo plano de projecção (ppllaannoo 44), paralelo à recta pp. O novo eixo
XX (o eixo XX’’) é a recta de intersecção do Plano Horizontal de Projecção
(ppllaannoo 11) com o ppllaannoo 44 e é paralelo a pp11. As projecções dos pontos MM
e AA no ppllaannoo 44 determinaram-se em função das suas cotas, que se
mantêm – pp44, a projecção da recta pp no ppllaannoo 44, passa por AA44 e faz,
com o eixo XX’’, um ângulo de 30o (o ângulo dado, que é o ângulo que a
recta pp faz com o Plano Horizontal de Projecção). Note que se garantiu
que o traço frontal da recta pp (no diedro de projecção inicial) tenha
cota positiva. No novo diedro de projecção, a recta pp é uma recta frontal (de frente), pois é paralela ao ppllaannoo 44, pelo que se trata da situação do
exercício 226622 – a perpendicularidade é directa no ppllaannoo 44. Assim, por MM44 conduziu-se uma perpendicular a pp44 (a recta rr44), obtendo II44 – II11 situa-
-se sobre pp11, na linha de chamada de II44. A projecção frontal de II, II22, determinou-se em função da sua cota (a distância de II44 ao eixo XX’’), que se
mantém. A partir das projecções de II no diedro de projecção inicial, desenharam-se as projecções do segmento [MMII], que é o segmento repre-
sentativo da distância de MM a pp – [MMII] não se projecta em V.G. em nenhum dos planos de projecção, pois é oblíquo a ambos. Assim, para de-
terminar a V.G. de MMෆIIෆ recorreu-se a outra mudança do diedro de projecção – substituiu-se uma vez mais o Plano Frontal de Projecção (ppllaannoo 22)
por um outro plano de projecção (o ppllaannoo 55), transformando o segmento [MMII] num segmento frontal (de frente). O novo eixo XX (o eixo XX’’’’) é a
recta de intersecção do Plano Horizontal de Projecção (ppllaannoo 11) com o ppllaannoo 55 e é paralelo a [MM11II11]. As projecções de MM e II no ppllaannoo 55 deter-
minaram-se em função das respectivas cotas, que se mantêm – o comprimento do segmento [MM55II55] é a V.G. da distância de MM a pp.
272.

100. 100
SOLUÇÕES
273.
Em primeiro lugar representaram-se a recta pp e o ponto PP, pelas respecti-
vas projecções, em função dos dados. Note que a recta pp está definida
por um ponto (o ponto AA) e pela sua direcção (é paralela ao β1/3). A dis-
tância de um ponto a uma recta é medida perpendicularmente à recta,
pelo que há que conduzir, pelo ponto PP, uma recta ppeerrppeennddiiccuullaarr à recta
pp. A recta pp não é paralela a nenhum dos planos de projecção, pelo que
a perpendicularidade não é directa em nenhuma das projecções – há, en-
tão, que resolver o problema a duas dimensões, nnoo ppllaannoo ddeeffiinniiddoo ppeellaa
rreeccttaa ee ppeelloo ppoonnttoo. Para tal é necessário rebater o plano definido pela
recta e pelo ponto, pois em rebatimento (em VG.) a perpendicularidade é
directa. Assim, rebateu-se esse plano para o próprio Plano Frontal de
Projecção (o ponto PP é um ponto do Plano Frontal de Projecção). A char-
neira do rebatimento (recta ee’’) fica definida pelo ponto PP e por FF, o traço
frontal da recta pp. Este determinou-se com o recurso a um processo geo-
métrico auxiliar, pois as projecções da recta pp não verificam o Critério de
Reversibilidade. Optou-se pelo rebatimento da recta pp, pelo rebatimento
do plano de perfil que a contém – o plano π. Rebateu-se o plano π para o
Plano Frontal de Projecção – a charneira foi ffπ (recta ee). A recta pprr passa
por AArr e faz, com os traços do plano π em rebatimento, ângulos de 45o
(ver exercício 3311 e respectivo relatório). Em rebatimento, determinou-se FFrr, sobre ffπrr
– invertendo o rebatimento, determinaram-se as projec-
ções de FF. A charneira do rebatimento do plano definido pela recta pp e pelo ponto PP (que é um plano oblíquo) para o Plano Frontal de Pro-
jecção está agora totalmente definida – a recta ee’’ passa por PP e por FF. PPrr ≡ PP22 e FFrr’’ ≡ FF22, pois PP e FF são dois pontos da charneira (recta ee’’) –
note que FFrr’’ é o ponto FF rebatido pelo segundo rebatimento da recta pp. Já temos um ponto para definir a recta pp em rebatimento (o ponto
FFrr’’). Recorreu-se a um outro ponto da recta (o ponto AA), para a rebater – pprr’’ fica definida por AArr’’ e FFrr’’. O ponto AA rebateu-se pelo triângulo do
rebatimento, em função do seu afastamento. Note que a recta pprr’’ é a recta pp rebatida pelo rebatimento do plano definido pela recta e pelo
ponto PP (o seu segundo rebatimento), tal como AArr’’ é o ponto AA rebatido no seu segundo rebatimento (o rebatimento do plano definido pela
recta pp e pelo ponto PP). Em rebatimento (no plano definido pela recta e pelo ponto), conduziu-se, por PPrr, uma perpendicular a pprr’’, obtendo
IIrr – PPෆrrෆIIෆrrෆ é a V.G. da distância de PP a pp. Inverteu-se o rebatimento, com o recurso à perpendicular à charneira que passa por II (e que corres-
ponde ao plano ortogonal à charneira que contém o arco do seu rebatimento), obtendo II11 sobre pp11. Para determinar II22, uma vez que as pro-
jecções da recta pp não verificam o Critério de Reversibilidade, recorreu-se ao rebatimento da recta pp pelo rebatimento do plano π – IIrr’’ é o
ponto II rebatido pelo rebatimento do plano π. IIrr’’ determinou-se sobre pprr a partir de II11. Invertendo o rebatimento, determinou-se II22 sobre pp22.
A partir das projecções de II, obtiveram-se as projecções de [PPII], que é o segmento representativo da distância de PP a pp.
Em primeiro lugar representaram-se a recta pp e o ponto PP, pelas respectivas projec-
ções, em função dos dados. Note que a recta pp é uma recta do β2/4, pelo que, ape-
sar de as suas projecções não verificarem o Critério de reversibilidade, é possível
representar qualquer ponto da recta de forma directa – todos os pontos da recta
pertencem ao β2/4, pelo que todos os pontos da recta têm as suas projecções coin-
cidentes. A distância de um ponto a uma recta é medida perpendicularmente à rec-
ta, pelo que há que conduzir, pelo ponto PP, uma recta ppeerrppeennddiiccuullaarr à recta pp. A
recta pp não é paralela a nenhum dos planos de projecção, pelo que a perpendicu-
laridade não é directa em nenhuma das projecções – há, então, que resolver o pro-
blema a duas dimensões, nnoo ppllaannoo ddeeffiinniiddoo ppeellaa rreeccttaa ee ppeelloo ppoonnttoo. Para tal é
necessário rebater o plano definido pela recta e pelo ponto, pois em rebatimento
(em VG.) a perpendicularidade é directa. Assim, rebateu-se esse plano para o plano
horizontal (de nível) ν que passa pelo ponto PP – a charneira do rebatimento (recta
ee) fica definida pelo ponto PP e pelo ponto AA, que é o ponto de intersecção do plano
ν com a recta pp (as projecções do ponto AA determinaram-se directamente, sem o
recurso ao rebatimento da recta pp, pois AA é um ponto do β2/4 – tem as suas projec-
ções coincidentes, como acima se referiu). PPrr ≡ PP11 e AArr ≡ AA11, pois PP e AA são dois
pontos da charneira (recta ee). Já temos um ponto para definir a recta pp em rebatimento (o ponto AArr). Recorreu-se a um outro ponto da recta
– o ponto BB, que é o ponto de concorrência da recta pp com o eixo XX (a recta pp, sendo uma recta de perfil do β2/4, é necessariamente uma
recta de perfil passante). O ponto BB rebateu-se pelo triângulo do rebatimento, em função da sua cota em relação ao plano ν (a distância de
BB ao plano ν). Em rebatimento (no plano definido pela recta e pelo ponto), conduziu-se, por PPrr, uma perpendicular a pprr, obtendo IIrr – PPෆrrෆIIෆrrෆ é a
V.G. da distância de PP a pp. Inverteu-se o rebatimento, com o recurso à perpendicular à charneira que passa por II (e que corresponde ao pla-
no ortogonal à charneira que contém o arco do seu rebatimento), obtendo II11 sobre pp11. Uma vez que II é um ponto da recta pp e, por conse-
guinte, um ponto do β2/4, sabe-se que tem as suas projecções coincidentes, o que nos permitiu determinar II22 directamente. A partir das
projecções de II, obtiveram-se as projecções de [PPII], que é o segmento representativo da distância de PP a pp.
274.

101. 101
SOLUÇÕES
275.
Em primeiro lugar representaram-se a recta pp e o ponto PP,
pelas respectivas projecções, em função dos dados. Note que
a recta pp está definida por um ponto (o ponto AA) e pela sua
direcção (é dado o ângulo que a recta faz com o Plano Hori-
zontal de Projecção). A situação deste exercício é idêntica à do
exercício 227722, pelo que se aconselha o acompanhamento da
resolução gráfica apresentada com a leitura do relatório daque-
le exercício. O segmento [PPII] é o segmento representativo da
distância de PP a pp – [PPII] não se projecta em V.G. em nenhum
dos planos de projecção, pois é oblíquo a ambos. Assim, para
determinar a V.G. da distância recorreu-se ao rebatimento do
plano projectante frontal do segmento para o plano horizontal
(de nível) ν que passa por II. A charneira do rebatimento é a
recta de intersecção do plano projectante frontal de [PPII]) com
o plano ν (o plano horizontal que passa por II) – é a recta de
topo (ee) que passa por II, pois II é um ponto que pertence aos
dois planos. O plano projectante frontal do segmento está defi-
nido pelo segmento e pela charneira. O segmento rebatido
sobre o plano horizontal (de nível) ν projecta-se em V.G. no Plano
Horizontal de Projecção, pois ν é paralelo a este. II11 ≡ IIrr, pois II
é um ponto da charneira. O rebatimento de PP processa-se num plano ortogonal à charneira – um plano frontal (de frente). Dessa forma, o arco do
rebatimento de PP projecta-se em V.G. no Plano Frontal de Projecção e o seu centro é o ponto de intersecção da charneira com o plano frontal (de
frente) que contém o arco do rebatimento de PP. Note que não se identificou nem o plano frontal (de frente) nem o centro do arco do rebatimento
de PP. O ponto PP, no seu rebatimento, mantém o seu afastamento, pelo que PPrr tem o afastamento de PP11. A V.G. da distância de PP a II (que é a
distância do ponto PP à recta pp) é o comprimento do segmento [PPrr IIrr], que está em V.G. no Plano Horizontal de Projecção.
276.
Por âânngguulloo eennttrree dduuaass rreeccttaass entende-se a amplitude de qualquer dos dois ângulos menores entre elas formados. Como um ângulo é uma
ssuuppeerrffíícciiee bbiiddiimmeennssiioonnaall, o ângulo entre duas rectas concorrentes está nneecceessssaarriiaammeennttee contido no plano definido pelas duas rectas.
277.
Duas rectas enviesadas não formam, entre si, nenhum ângulo de forma directa, pois não são complanares (o ângulo entre duas rectas, sen-
do uma superfície bidimensional, está contido nnoo ppllaannoo definido pelas duas rectas e duas rectas enviesadas não definem plano nenhum).
No entanto, o ângulo que duas rectas enviesadas formam entre si é igual (tem a mesma amplitude) ao ângulo que formam, entre si, duas
rectas quaisquer, concorrentes entre si e com as direcções das rectas dadas (duas rectas complanares). Assim, sendo dadas duas rectas
enviesadas quaisquer, rr e ss, para determinar o ângulo entre elas é necessário conduzir, por um ponto qualquer da recta rr (por exemplo),
uma recta ss’’, paralela à recta ss – o ângulo formado entre as rectas rr e ss’’ (que são necessariamente concorrentes) tem a mesma amplitude
do ângulo formado entre rr e ss.
278.
Em primeiro lugar representaram-se as rectas tt e hh, pelas respectivas projecções, em função
dos dados. As duas rectas são concorrentes, pelo que definem um plano – trata-se de um pla-
no horizontal (de nível). O ângulo formado entre as duas rectas está contido nesse plano, que é
paralelo ao Plano Horizontal de Projecção – o ângulo formado entre as rectas tt e hh projecta-se,
assim, em V.G. no Plano Horizontal de Projecção. O ângulo entre tt e hh é, assim, qualquer dos
dois ângulos agudos entre tt11 e hh11, que têm vértice em AA11 e que se projectam em V.G. no Plano
Horizontal de Projecção. Assinalou-se um dos ângulo a traço forte (as semi-rectas que limitam
o ângulo) e assinalou-se a V.G. da sua amplitude com αo.
Em primeiro lugar representou-se a recta ff, pelas suas projecções, em função dos dados. A recta ff e o
eixo XX são duas rectas eennvviieessaaddaass, pelo que não formam, entre si e de forma directa, nenhum ângulo
(não definem plano nenhum). No entanto, o ângulo que formam entre si indirectamente é igual ao
ângulo que duas rectas concorrentes paralelas às rectas dadas formam entre si – a recta ff e qualquer
outra recta paralela ao eixo XX e concorrente com a recta ff, por exemplo. A projecção horizontal da rec-
ta ff, ff11, é uma recta paralela ao eixo XX que é concorrente com a recta ff (no traço horizontal da recta ff,
que não se assinalou). Assim, o ângulo pretendido é igual ao ângulo formado entre a recta ff e a sua
projecção horizontal, ff11 – esse ângulo está contido num plano frontal (de frente), que é o plano frontal
(de frente) que contém a recta ff. O ângulo formado entre as duas rectas está contido nesse plano, que é paralelo ao Plano Frontal de Projecção
– o ângulo formado entre as rectas ff e ff11 projecta-se, assim, em V.G. no Plano Frontal de Projecção. O ângulo entre ff e ff11 é, assim, qualquer dos
dois ângulos agudos entre ff22 e o eixo XX (a projecção frontal da recta que é ff11 situa-se no eixo XX) e que se projectam em V.G. no Plano Frontal de
Projecção. Assinalou-se um dos ângulo a traço forte (as semi-rectas que limitam o ângulo) e assinalou-se a V.G. da sua amplitude com αo.
279.

102. 102
SOLUÇÕES
Em primeiro lugar representaram-se as rectas rr e gg, pelas suas projecções, em função
dos dados. As rectas rr e gg são concorrentes (no ponto PP), pelo que definem um plano
– o ângulo entre as duas rectas eessttáá ccoonnttiiddoo nnoo ppllaannoo ddeeffiinniiddoo ppeellaass dduuaass rreeccttaass e
tem vértice em PP. Uma vez que o plano definido pelas duas rectas não é paralelo a
nenhum dos planos de projecção, para determinar a V.G. do ângulo entre as duas rectas
é necessário o recurso a um processo geométrico auxiliar. Por uma questão de econo-
mia de traçados, optou-se por rebater o plano definido pelas duas rectas para o plano
frontal (de frente) ϕ que contém a recta gg – a charneira do rebatimento (recta ee) é a
recta de intersecção dos dois planos, pelo que é a própria recta gg. Assim sendo, a
recta gg roda sobre si própria, pelo que se tem imediatamente ggrr ≡ ee22 ≡ gg22. Sublinha-se
que seria igualmente económico, em termos de traçado, efectuar o rebatimento do
plano definido pelas duas rectas para o plano horizontal (de nível) que contém a recta
gg. Note que, caso não tivesse sido essa a opção, seria necessário determinar a char-
neira do rebatimento, o que se evitou com a situação referida. PPrr ≡ PP22 pois PP é um
ponto da charneira. Para rebater a recta rr é necessário o recurso a um ponto qualquer
da recta – o ponto MM, por exemplo. MM rebateu-se pelo triângulo do rebatimento, em
função da sua distância a ϕ (o afastamento de MM em relação a ϕ). A recta rrrr está definida
por PPrr e MMrr. A V.G. do ângulo entre rr e gg está em qualquer dos dois ângulos agudos entre ggrr e rrrr, com vértice em PPrr – identificou-se um dos
ângulos pelas semi-rectas que limitam o ângulo e assinalando a sua amplitude com αo.
281.
Em primeiro lugar representaram-se as rectas rr e pp, pelas suas projecções, em função
dos dados. As duas rectas são concorrentes (no ponto PP), pelo que definem um plano –
o ângulo entre as duas rectas eessttáá ccoonnttiiddoo nnoo ppllaannoo ddeeffiinniiddoo ppeellaass dduuaass rreeccttaass e tem
vértice em PP. Uma vez que o plano definido pelas duas rectas não é paralelo a nenhum
dos planos de projecção, para determinar a V.G. do ângulo entre as duas rectas é neces-
sário o recurso a um processo geométrico auxiliar. Por uma questão de economia de tra-
çados, optou-se por rebater o plano definido pelas duas rectas para o plano frontal (de
frente) ϕ que passa por QQ. Note que caso não tivesse sido essa a opção, seria necessá-
rio o recurso a outro processo geométrico auxiliar (nomeadamente o do rebatimento do
plano de perfil que contém a recta pp) para a determinação de um outro ponto da recta,
que não o ponto QQ. A charneira do rebatimento (recta ee) é a recta de intersecção dos
dois planos e está definida pelos pontos QQ e RR (os pontos de intersecção do plano ϕ
com as rectas pp e rr, respectivamente). QQrr ≡ QQ22 e RRrr ≡ RR22, pois QQ e RR são dois pontos da
charneira. Rebateu-se o ponto PP pelo triângulo do rebatimento, em função da sua distân-
cia a ϕ (o afastamento de PP em relação a ϕ) – rrrr fica definida por RRrr e PPrr e pprr fica definida
por QQrr e PPrr. A V.G. do ângulo entre rr e pp é qualquer dos dois ângulos agudos entre rrrr e
pprr, com vértice em PPrr – identificou-se um dos ângulos através das semi-rectas que limi-
tam o ângulo e assinalando a sua amplitude com αo. Note que é de evitar que o plano ϕ
passe por PP pois, nesse caso, só teríamos um ponto da charneira, pelo que a determina-
ção de um segundo ponto da charneira ou da sua direcção obrigaria ao recurso a racio-
cínios e/ou processos geométricos auxiliares, como acima se referiu.
Em primeiro lugar representaram-se as rectas rr e ss, pelas suas projecções, em
função dos dados. As duas rectas são concorrentes (no ponto BB), pelo que defi-
nem um plano – o ângulo entre as duas rectas eessttáá ccoonnttiiddoo nnoo ppllaannoo ddeeffiinniiddoo
ppeellaass dduuaass rreeccttaass e tem vértice em BB. Uma vez que o plano definido pelas duas
rectas não é paralelo a nenhum dos planos de projecção, para determinar a V.G.
do ângulo entre as duas rectas é necessário o recurso a um processo geométrico
auxiliar. Optou-se por rebater o plano definido pelas duas rectas para o plano fron-
tal (de frente) ϕ que passa por CC. A charneira do rebatimento (recta ee) é a recta de
intersecção dos dois planos e está definida pelos pontos CC e DD (os pontos de
intersecção do plano ϕ com as rectas ss e rr, respectivamente). CCrr ≡ CC22 e DDrr ≡ DD22,
pois CC e DD são dois pontos da charneira (são fixos – rodam sobre si próprios).
Rebateu-se o ponto BB pelo triângulo do rebatimento, em função da sua distância
a ϕ (o afastamento de BB em relação a ϕ) – rrrr fica definida por DDrr e BBrr e ssrr fica defi-
nida por CCrr e BBrr. A V.G. do ângulo entre rr e ss é qualquer dos dois ângulos agudos
entre rrrr e ssrr, com vértice em BBrr – identificou-se um dos ângulos através das semi-
-rectas que limitam o ângulo e assinalando a sua amplitude com αo.
280.
282.

103. 103
SOLUÇÕES
284.
Em primeiro lugar representaram-se as rectas hh e pp, pelas respectivas projec-
ções, em função dos dados. A recta pp está definida por um ponto (o ponto PP)
e por uma direcção (faz um ângulo de 60o com o Plano Horizontal de Projec-
ção). As rectas hh e pp são eennvviieessaaddaass, pelo que não formam nenhum ângulo
directamente. Para determinar o ângulo formado entre hh e pp conduziu-se, pelo
ponto PP da recta pp, uma recta hh’’, paralela à recta hh – as rectas pp e hh’’ são con-
correntes, pelo que definem um plano e o ângulo que as rectas pp e hh’’ formam
entre si está contido nesse plano (e tem vértice em PP). O plano definido pelas
duas rectas não é paralelo a nenhum dos planos de projecção, pelo que é ne-
cessário o recurso a um processo geométrico auxiliar para determinar a V.G.
do ângulo entre as duas rectas. Optou-se por rebater o plano definido pelas
duas rectas para o plano horizontal (de nível) ν que contém a recta hh’’, o que
se traduz numa grande economia de traçados. A charneira do rebatimento
(recta ee) é a recta de intersecção dos dois planos, pelo que é a própria recta
hh’’ – hh’’rr ≡ ee11 ≡ hh’’11, pois a recta hh roda sobre si própria. O ponto PP é fixo, pois
roda sobre si próprio (é um ponto da charneira). Para rebater a recta pp é ne-
cessário o recurso a um ponto qualquer da recta – o ponto AA, por exemplo.
Para determinar o ponto AA foi necessário o recurso a um processo geométrico
auxiliar – optou-se pelo rebatimento da recta pp, pelo rebatimento do plano de
perfil que a contém (o plano π). Rebateu-se o plano π para o Plano Frontal de Projecção – a charneira foi ffπ (recta ee). A recta pprr passa por PPrr
e faz um ângulo de 60° (o ângulo dado) com hhπrr
(note que se garantiu que o traço horizontal da recta pp, que não se assinalou, se situa no
SSPPHHAA – tem afastamento positivo). Em rebatimento, sobre pprr, determinou-se AArr. Invertendo o rebatimento, determinaram-se as projecções
de AA. Analisemos, agora, o rebatimento do plano definido pelas rectas pp e hh’’ – PPrr’’ ≡ PP11 pois PP é um ponto da charneira (PPrr’’ é o ponto PP no
seu segundo rebatimento – no rebatimento do plano definido pelas rectas pp e hh’’). O ponto AA rebateu-se pelo triângulo do rebatimento, em
função da sua cota em relação a ν (a distância de AA a ν), obtendo AArr’’. A recta pprr’’ está definida por PPrr’’ e por AArr’’. Note que a recta pprr’’ é a rec-
ta pp rebatida pelo rebatimento do plano definido pela recta e pelo ponto PP (o seu segundo rebatimento), tal como AArr’’ é o ponto AA rebatido
no seu segundo rebatimento (o rebatimento do plano definido pela recta pp e pelo ponto PP). A V.G. do ângulo entre rr e hh está em qualquer
dos dois ângulos agudos entre rrrr e hh’’rr, com vértice em PPrr’’ – identificou-se o ângulo através das semi-rectas que limitam o ângulo e assina-
lando a sua amplitude com αo.
Em primeiro lugar representaram-se as rectas rr e ff, pelas respectivas
projecções, em função dos dados. As projecções da recta rr (que é uma
recta passante) são concorrentes entre si num ponto do eixo XX (o ponto SS).
As rectas rr e ff são eennvviieessaaddaass, pelo que não formam nenhum ângulo di-
rectamente. Para determinar o ângulo formado entre rr e ff conduziu-se,
pelo ponto RR da recta rr, uma recta ff’’, paralela à recta ff – as rectas rr e ff’’
são concorrentes, pelo que definem um plano e o ângulo que as rectas
rr e ff’’ formam entre si está contido nesse plano (e tem vértice em RR).
O plano definido pelas duas rectas não é paralelo a nenhum dos planos
de projecção, pelo que é necessário o recurso a um processo geométri-
co auxiliar para determinar a V.G. do ângulo entre as duas rectas. Op-
tou-se por rebater o plano definido pelas duas rectas para o plano
frontal (de frente) ϕ que contém a recta ff’’, o que se traduz numa grande
economia de traçados. A charneira do rebatimento (recta ee) é a recta de
intersecção dos dois planos, pelo que é a própria recta ff’’ – ff’’rr ≡ ee22 ≡ ff’’22,
pois a recta ff’’ roda sobre si própria. RRrr ≡ RR22 pois RR é um ponto da char-
neira. Para rebater a recta rr é necessário o recurso a um ponto qualquer
da recta – o ponto SS, por exemplo. SS rebateu-se pelo triângulo do reba-
timento, em função da sua distância a ϕ (o afastamento de SS em relação
a ϕ). A recta rrrr está definida por RRrr e SSrr. A V.G. do ângulo entre rr e ff está
em qualquer dos dois ângulos agudos entre rrrr e ff’’rr, com vértice em RRrr –
identificou-se o ângulo através das semi-rectas que limitam o ângulo e
assinalando a sua amplitude com αo.
283.

104. 104
SOLUÇÕES
285.
Em primeiro lugar representou-se a recta mm, pelas suas projecções, em função dos dados. A
recta mm e o eixo XX são duas rectas eennvviieessaaddaass, pelo que não formam, entre si e de forma directa,
nenhum ângulo (não definem plano nenhum). No entanto, o ângulo que formam entre si indi-
rectamente é igual ao ângulo que duas rectas concorrentes paralelas às rectas dadas formam
entre si – a recta mm e qualquer outra recta paralela ao eixo XX e concorrente com a recta mm, por
exemplo (também poderia ser uma recta paralela à recta mm e concorrente com o eixo XX).
Optou-se por conduzir, pelo ponto PP, uma recta gg, fronto-horizontal, paralela ao eixo XX – o ân-
gulo formado entre a recta mm e a recta gg é igual (tem a mesma amplitude) ao ângulo formado
entre a recta mm e o eixo XX. As rectas mm e gg são concorrentes (no ponto PP), pelo que definem
um plano – o ângulo entre as duas rectas eessttáá ccoonnttiiddoo nnoo ppllaannoo ddeeffiinniiddoo ppeellaass dduuaass rreeccttaass
e tem vértice em PP. Uma vez que o plano definido pelas duas rectas não é paralelo a nenhum
dos planos de projecção, para determinar a V.G. do ângulo entre as duas rectas é necessário o
recurso a um processo geométrico auxiliar. Por uma questão de economia de traçados, optou-
-se por rebater o plano definido pelas duas rectas para o plano horizontal (de nível) ν que con-
tém a recta gg – a charneira do rebatimento (recta ee) é a recta de intersecção dos dois planos,
pelo que é a própria recta gg. Assim sendo, a recta gg roda sobre si própria, pelo que se tem
imediatamente ggrr ≡ ee11 ≡ gg11. Sublinha-se que seria igualmente económico, em termos de traçado,
efectuar o rebatimento do plano definido pelas duas rectas para o plano frontal (de frente) que
contém a recta gg. Note que, caso não tivesse sido essa a opção, seria necessário determinar a charneira do rebatimento, o que se evitou
com a situação referida. PPrr ≡ PP11 pois PP é um ponto da charneira. Para rebater a recta mm é necessário o recurso a um ponto qualquer da
recta – o seu traço horizontal, por exemplo. HH (o traço horizontal da recta mm) rebateu-se pelo triângulo do rebatimento, em função da sua
distância a ν (a cota de HH em relação a ν). A recta mmrr está definida por PPrr e HHrr. A V.G. do ângulo entre a recta mm e o eixo XX está em qualquer
dos dois ângulos agudos entre mmrr e ggrr, com vértice em PPrr – identificou-se um dos ângulos pelas semi-rectas que limitam o ângulo e assina-
lando a sua amplitude com αo.
Em primeiro lugar representaram-se os planos α e δ, pelos respectivos tra-
ços, em função dos dados. O plano α tem os seus traços simétricos em rela-
ção ao eixo XX, pois é ortogonal ao β1/3. O plano δ tem os seus traços
coincidentes, pois é ortogonal ao β2/4. O traço frontal de α (ffα) e o traço hori-
zontal de δ (hhδ) são duas rectas eennvviieessaaddaass, pelo que não formam, entre si e
de forma directa, nenhum ângulo (não definem plano nenhum). No entanto,
o ângulo que formam entre si indirectamente é igual ao ângulo que duas rec-
tas concorrentes paralelas às rectas dadas formam entre si – ffα e qualquer
outra recta paralela a hhδ e concorrente com ffα, por exemplo (também pode-
ria ser uma recta paralela a ffα e concorrente com hhδ). Optou-se por conduzir,
pelo ponto AA (que é o ponto de concorrência dos traços do plano α), uma
recta hh, paralela a hhδ (hh é uma recta horizontal com cota nula – é uma recta
do Plano Horizontal de Projecção). O ângulo formado entre a recta hh e ffα é
igual (tem a mesma amplitude) ao ângulo formado entre ffα e hhδ. As rectas hh
e ffα são concorrentes (no ponto AA), pelo que definem um plano – o ângulo
entre as duas rectas eessttáá ccoonnttiiddoo nnoo ppllaannoo ddeeffiinniiddoo ppeellaass dduuaass rreeccttaass e
tem vértice em AA. Uma vez que o plano definido pelas duas rectas não é pa-
ralelo a nenhum dos planos de projecção, para determinar a V.G. do ângulo
entre as duas rectas é necessário o recurso a um processo geométrico auxi-
liar. Por uma questão de economia de traçados, optou-se por rebater o plano definido pelas duas rectas para o Plano Frontal de Projecção (que é
o plano frontal que contém ffα) – a charneira do rebatimento (recta ee) é ffα, que roda sobre si próprio, pelo que se tem imediatamente ffα ≡ ᐉᐉ22 ≡ ffαrr
.
Sublinha-se que seria igualmente económico, em termos de traçado, efectuar o rebatimento do plano definido pelas duas rectas para o Plano
Horizontal de Projecção, uma vez que a recta hh é uma recta do Plano Horizontal de Projecção – nesse caso, seria a recta hh a rodar sobre si
própria. AArr ≡ AA22 pois AA é um ponto da charneira. Para rebater a recta hh é necessário o recurso a um ponto qualquer da recta – o ponto BB, que é
um ponto qualquer da recta hh. BB rebateu-se pelo triângulo do rebatimento, em função do seu afastamento. A recta hhrr está definida por AArr e BBrr.
A V.G. do ângulo entre ffα e hhδ está em qualquer dos dois ângulos agudos entre hhrr e ffαrr
, com vértice em AArr – identificou-se um dos ângulos
pelas semi-rectas que limitam o ângulo e assinalando a sua amplitude com θo.
286.

105. 105
SOLUÇÕES
287.
Em primeiro lugar representaram-se as rectas ff e pp pelas respectivas projecções,
em função dos dados. A recta pp está definida por um ponto e uma direcção (faz
um ângulo de 60o com o Plano Frontal de Projecção). Note que os dados nos
permitiram, apenas, desenhar ff11, a projecção horizontal da recta ff. Uma vez que
as rectas são concorrentes (é dado no enunciado), é possível determinar, de for-
ma directa, a projecção horizontal do ponto de concorrência (o ponto PP), mas
não a sua projecção frontal. Para tal recorreu-se ao rebatimento da recta pp, pelo
rebatimento do plano π, o plano de perfil que a contém. A recta pprr está definida
por AArr e pela sua direcção – faz um ângulo de 60° com ffπrr
, sendo que se garantiu
que o seu traço frontal tenha cota positiva (apesar de não se ter assinalado o tra-
ço frontal da recta, pois tal não é necessário). A partir de PP11 determinou-se PPrr,
sobre pprr – invertendo o rebatimento, determinou-se PP22, o que nos permitiu dese-
nhar ff22, passando por PP22 e fazendo, com o eixo XX, o ângulo pedido (60o de aber-
tura para a direita). As rectas pp e ff são concorrentes (no ponto PP), pelo que
definem um plano – o ângulo entre as duas rectas eessttáá ccoonnttiiddoo nnoo ppllaannoo ddeeffiinnii--
ddoo ppeellaass dduuaass rreeccttaass e tem vértice em PP. Uma vez que o plano definido pelas
duas rectas não é paralelo a nenhum dos planos de projecção, para determinar
a V.G. do ângulo entre as duas rectas é necessário o recurso a um processo
geométrico auxiliar. Por uma questão de economia de traçados, optou-se por re-
bater o plano definido pelas duas rectas para o plano frontal (de frente) ϕ que
contém a recta ff – a charneira do rebatimento (recta ee’’) é a recta de intersecção
dos dois planos, pelo que é a própria recta ff. Assim sendo, a recta ff roda sobre si
própria, pelo que se tem imediatamente ffrr ≡ ee’’22 ≡ ff22. PPrr’’ ≡ PP22 pois PP é um ponto
da charneira (PPrr’’ é o ponto PP rebatido pelo seu segundo rebatimento – pelo reba-
timento do plano definido por pp e ff). Para rebater a recta pp é necessário o recurso a um ponto qualquer da recta – o ponto AA, por exemplo
(caso se escolhesse um outro ponto, este teria de ser determinado previamente no rebatimento da recta pp pelo rebatimento do plano π). AA re-
bateu-se pelo triângulo do rebatimento, em função da sua distância a ϕ (o afastamento de AA em relação a ϕ). A recta pprr’’ está definida por PPrr’’ e
AArr’’ – AArr’’ e pprr’’ são, respectivamente, o ponto AA e a recta pp rebatidos no seu segundo rebatimento (o rebatimento do plano definido pelas rectas ff
e pp). A V.G. do ângulo entre as rectas pp e ff está em qualquer dos dois ângulos agudos entre pprr’’ e ffrr, com vértice em PPrr’’ – identificou-se um dos
ângulos pelas semi-rectas que limitam o ângulo e assinalando a sua amplitude com α°.
288.
Por âânngguulloo eennttrree uummaa rreeccttaa ee uumm ppllaannoo entende-se qualquer dos dois menores ângulos formados entre a recta e a sua projecção ortogonal
sobre o plano, ou seja, o ângulo formado entre a recta dada e a recta de intersecção do plano dado com o plano que lhe é ortogonal e que
contém a recta dada. O ângulo entre uma recta e um plano eessttáá ccoonnttiiddoo no plano que contém a recta dada e que é ortogonal ao plano dado.
289.
O mmééttooddoo ggeerraall ppaarraa aa ddeetteerrmmiinnaaççããoo ddoo âânngguulloo eennttrree uummaa rreeccttaa ee uumm ppllaannoo consiste na execução sequencial das seguintes etapas:
11.. determinar o ponto de intersecção da recta dada com o plano – ponto II; 22.. determinar a projecção ortogonal da recta sobre o plano, o
que se processa conduzindo, por um ponto PP qualquer da recta, uma recta pp ortogonal ao plano e determinando PP’’, o ponto de intersecção
daquela com o plano – a projecção ortogonal da recta sobre o plano fica definida por II e por PP’’; 33.. o ângulo formado entre a recta e o plano
é qualquer dos dois menores ângulos formados entre a recta e a sua projecção ortogonal no plano.
290.
Os dois processos para determinar a amplitude do ângulo entre uma recta e um plano são o mmééttooddoo ggeerraall ppaarraa aa ddeetteerrmmiinnaaççããoo ddoo âânngguu--
lloo eennttrree uummaa rreeccttaa ee uumm ppllaannoo e o mmééttooddoo ddoo âânngguulloo ccoommpplleemmeennttaarr. Apesar de os dois métodos serem universais (utilizáveis indepen-
dentemente da situação), o recurso a um ou a outro tem a ver, aappeennaass, com economia de traçados. De facto, dada a quantidade de
traçados a que o primeiro processo obriga em determinadas situações, é, nessas situações, bastante mais vantajoso o recurso ao segundo
processo. Essas situações são aquelas em que se pretende o ângulo entre uma recta qualquer e um ppllaannoo nnããoo pprroojjeeccttaannttee, pois a determi-
nação das sucessivas intersecções (do ponto de intersecção da recta dada com o plano dado e do ponto de intersecção do plano dado
com a recta que lhe é ortogonal e que passa por um ponto da recta dada) obriga ao recurso ao mmééttooddoo ggeerraall ddaa iinntteerrsseeccççããoo ddee rreeccttaass
ccoomm ppllaannooss vezes sucessivas, o que resulta num traçado muito denso e complexo, de difícil leitura e de execução bastante morosa. Assim,
nessas situações (ângulo entre uma recta qualquer e um plano não projectante) é mais conveniente o recurso ao mmééttooddoo ddoo âânngguulloo ccoomm--
pplleemmeennttaarr.

106. 106
SOLUÇÕES
291.
Em primeiro lugar representaram-se o plano ϕ, pelo seu traço horizontal, e a recta hh, pelas
suas projecções, em função dos dados. O ângulo entre uma recta e um plano está contido
no plano ortogonal ao plano dado e que contém a recta – é o ângulo entre a recta dada e a
recta de intersecção dos dois planos (o plano dado e o plano que lhe é ortogonal e con-
tém a recta). O plano ortogonal ao plano ϕ que contém a recta hh é um plano horizontal (de
nível), pelo que o ângulo entre a recta e o plano se projecta em V.G. no Plano Horizontal de
Projecção – note que não se identificou esse plano. A recta de intersecção do plano hori-
zontal (de nível) que contém a recta hh com o plano ϕ é uma recta fronto-horizontal (que
não se identificou) que tem a sua projecção horizontal sobre o traço horizontal do plano
frontal (de frente), pois este é projectante horizontal. Assim sendo, a V.G. do ângulo entre o
plano ϕ e a recta hh está em qualquer dos dois ângulos agudos entre hh11 e (hhϕ) – identificou-
-se um dos ângulos pelas semi-rectas que limitam o ângulo e assinalando a sua amplitude
com αo. Note que não se recorreu ao mmééttooddoo ggeerraall ppaarraa aa ddeetteerrmmiinnaaççããoo ddoo âânngguulloo eenn--
ttrree uummaa rreeccttaa ee uumm ppllaannoo de forma deliberada, em função do ângulo pedido estar contido
num plano paralelo a um dos planos de projecção (o que resulta numa situação de resolu-
ção imediata, conforme se expôs) – no entanto, caso se tivesse recorrido a esse processo
de resolução, ter-se-ia chegado à mesma conclusão com um pouco mais de traçado.
293.
Em primeiro lugar representou-se a recta ss, pelas suas projecções, em função dos dados. A recta ss,
porque é uma recta passante, tem as suas projecções concorrentes entre si num ponto do eixo
XX. O ângulo entre a recta ss e o Plano Frontal de Projecção está contido num plano ortogonal ao
Plano Frontal de Projecção que contém a recta ss – é o plano de topo que contém a recta ss (é o
plano projectante frontal da recta). O ângulo entre a recta e o Plano Frontal de Projecção é o ân-
gulo entre a recta e a sua projecção frontal (note que a projecção frontal da recta ss é, imediata-
mente, a projecção ortogonal da recta ss no Plano Frontal de Projecção). Como o plano que
contém o ângulo (que é o plano projectante frontal da recta ss) não é paralelo a nenhum dos pla-
nos de projecção, o ângulo não se projecta em V.G., pelo que é necessário o recurso a um pro-
cesso geométrico auxiliar. Optou-se por rebater o plano que contém o ângulo (o plano
projectante frontal da recta) para o Plano Frontal de Projecção. O plano que contém o ângulo
está definido pela recta ss e pela charneira, que é a recta de intersecção dos dois planos (a char-
neira é a própria projecção frontal da recta ss). O ponto de concorrência da recta ss com o eixo XX é
fixo, pois é um ponto da charneira. O ponto SS foi o ponto a que se recorreu para rebater a recta ss
– o ponto SS rebateu-se em função do seu afastamento. A recta ssrr está definida pelo ponto do eixo
XX (que é fixo) e por SSrr. A V.G. do ângulo entre a recta ss e o Plano Frontal de Projecção está em
qualquer dos dois ângulos agudos entre ssrr e ee22, com vértice no eixo XX – identificou-se um dos ân-
gulos pelas semi-rectas que limitam o ângulo e assinalando a sua amplitude com αo. Note mais uma vez que, dado o imediatismo da situa-
ção, não se recorreu ao mmééttooddoo ggeerraall ppaarraa aa ddeetteerrmmiinnaaççããoo ddoo âânngguulloo eennttrree uummaa rreeccttaa ee uumm ppllaannoo de forma deliberada – no entanto,
caso se tivesse recorrido a esse processo de resolução, ter-se-ia chegado à mesma conclusão com um pouco mais de traçado.
Em primeiro lugar representaram-se o plano ν, pelo seu traço frontal, e a recta rr, pelas
suas projecções, em função dos dados. A recta rr, porque é paralela ao β2/4, tem as
suas projecções paralelas entre si. O ângulo entre uma recta e um plano está contido
no plano ortogonal ao plano dado e que contém a recta – é o ângulo entre a recta dada
e a recta de intersecção dos dois planos (o plano dado e o plano que lhe é ortogonal e
contém a recta). O ângulo entre a recta rr e o plano ν está contido num plano vertical
que contém a recta rr – o plano ortogonal a ν que contém a recta rr (é o plano projectan-
te horizontal da recta rr). Como esse plano não é paralelo a nenhum dos planos de pro-
jecção, o ângulo não se projecta em V.G. em nenhum dos planos de projecção, pelo
que é necessário o recurso a um processo geométrico auxiliar. Optou-se por rebater o
plano vertical que contém a recta rr para o próprio plano horizontal (de nível) ν – ver
exercício 221144. O plano vertical está definido pela recta rr e pela charneira (recta ee), que é
a recta de intersecção dos dois planos. A charneira (recta ee), porque é a recta de inter-
secção dos dois planos, é imediatamente a projecção ortogonal da recta rr sobre o pla-
no ν, pelo que o ângulo entre a recta rr e o plano ν é o ângulo formado entre a recta rr e
a charneira do rebatimento (recta ee), que tem vértice no ponto II – o ponto de intersec-
ção de rr com ν. II é um ponto da charneira, pelo que é fixo (roda sobre si próprio), pelo que se tem imediatamente IIrr ≡ II11. O ponto AA foi o
ponto a que se recorreu para rebater a recta rr – AA rebateu-se em função da sua cota em relação a ν (a distância de AA a ν). A recta rrrr está de-
finida por IIrr e por AArr. A V.G. do ângulo entre o plano ν e a recta rr está em qualquer dos dois ângulos agudos entre rrrr e ee11, com vértice em IIrr
– identificou-se um dos ângulos pelas semi-rectas que limitam o ângulo e assinalando a sua amplitude com αo. Note que, dado o imediatis-
mo da situação, não se recorreu ao mmééttooddoo ggeerraall ppaarraa aa ddeetteerrmmiinnaaççããoo ddoo âânngguulloo eennttrree uummaa rreeccttaa ee uumm ppllaannoo de forma deliberada – no
entanto, caso se tivesse recorrido a esse processo de resolução, ter-se-ia chegado à mesma conclusão com um pouco mais de traçado.
292.

107. 107
SOLUÇÕES
294.
Em primeiro lugar representaram-se o plano ϕ, pelo seu traço horizontal, e a recta pp, pelas suas
projecções, em função dos dados. O ângulo entre uma recta e um plano frontal (de frente) é
igual (tem a mesma amplitude) ao ângulo entre a recta e o Plano Frontal de Projecção. Como se
referiu no relatório do exercício anterior, o ângulo entre uma recta e o Plano Frontal de Projec-
ção é o ângulo entre a recta e a sua projecção frontal (que é a projecção ortogonal da recta no
Plano Frontal de Projecção) – esse ângulo existe no plano projectante frontal da recta. Assim,
nesta situação, o ângulo entre a recta pp e o plano ϕ é igual (tem a mesma amplitude) ao ângulo
entre a recta pp e o Plano Frontal de Projecção (que é paralelo ao plano ϕ) e que é, afinal, o ân-
gulo entre a recta pp e a sua projecção frontal (pp22) – esse ângulo está contido no plano projec-
tante frontal da recta, que é o plano de perfil que contém a recta. Assim, por pp conduziu-se o
plano π – o plano de perfil que contém a recta (π é o plano ortogonal ao Plano Frontal de Projec-
ção que contém a recta pp). O ângulo pretendido é o ângulo entre a recta pp e ffπ, que é a recta de
intersecção do plano π (o plano ortogonal ao Plano Frontal de Projecção que contém a recta pp)
com o Plano Frontal de Projecção. Esse ângulo não se projecta em V.G., pelo que é necessário
o recurso a um processo geométrico auxiliar. Optou-se pelo rebatimento do plano π para o Pla-
no Horizontal de Projecção – a charneira foi hhπ, pelo que se tem imediatamente hhπ ≡ ee11 ≡ hhπrr
e ffπrr
está no eixo XX. A recta pprr está definida por AArr e por BBrr. A V.G. do ângulo entre a recta pp e o plano
ϕ está em qualquer dos dois ângulos agudos entre pprr e ffπrr
– identificou-se um dos ângulos pelas
semi-rectas que limitam o ângulo e assinalando a sua amplitude com αo. Note de novo que, dado o imediatismo da situação, não se recor-
reu ao mmééttooddoo ggeerraall ppaarraa aa ddeetteerrmmiinnaaççããoo ddoo âânngguulloo eennttrree uummaa rreeccttaa ee uumm ppllaannoo de forma deliberada – no entanto, caso se tivesse
recorrido a esse processo de resolução, ter-se-ia chegado à mesma conclusão com um pouco mais de traçado.
295.
Em primeiro lugar representou-se a recta pp, pelas
suas projecções, em função dos dados. A recta pp
é uma recta passante – o ponto AA é o ponto em
que a recta pp é concorrente com o eixo XX. A recta
pp é paralela ao plano α (que se representou
pelos seus traços, em função dos dados), pelo
que é paralela a uma recta do plano – a recta pp’’,
pertencente ao plano α e definida pelos seus tra-
ços, é a recta a que se recorreu para definir a rec-
ta pp. A recta pp está definida por um ponto (o
ponto AA) e por uma direcção (é paralela à recta
pp’’). As rectas pp e pp’’ são paralelas, pelo que
fazem, com o Plano Horizontal de Projecção, âânn--
gguullooss iigguuaaiiss (com a mesma amplitude). Assim,
não há necessidade de efectuar mais traçados no
sentido de determinar um outro ponto da recta pp,
por exemplo, uma vez que é possível determinar
imediatamente o ângulo que a recta pp’’ faz com o
Plano Horizontal de Projecção. O ângulo entre a
recta pp’’ e o Plano Horizontal de Projecção é, afi-
nal, o ângulo entre a recta pp’’ e a sua projecção
horizontal (pp’’11), que é a projecção ortogonal da
recta pp’’ no Plano Horizontal de Projecção. Esse ângulo está contido no plano projectante horizontal da recta pp’’, que é um plano de perfil,
que não é paralelo a nenhum dos planos de projecção, pelo que é necessário o recurso a um processo geométrico auxiliar. Optou-se por
recorrer a uma mudança do diedro de projecção – substituindo o Plano Frontal de Projecção (ppllaannoo 22) por um novo plano de projecção
(ppllaannoo 44) paralelo à recta pp’’, obtém-se um diedro de projecção no qual a recta pp’’ é frontal (de frente) e, por isso, o ângulo entre a recta e a
sua projecção horizontal projecta-se em V.G. no ppllaannoo 44. O novo eixo XX (o eixo XX’’) é a recta de intersecção do ppllaannoo 11 (o plano que se man-
teve) com o ppllaannoo 44 e é paralelo a pp’’11. A projecção da recta pp’’ no ppllaannoo 44 (pp’’44) passa por HH44 e por FF44 – HH44 e FF44 são as projecções no ppllaannoo
44 dos traços da recta pp’’ e determinaram-se em função das respectivas cotas, que se mantiveram. O ângulo entre a recta pp’’ e a sua projec-
ção horizontal (pp’’11) projecta-se, agora, em V.G. no ângulo entre pp’’44 e o eixo XX’’ e tem vértice em HH44. A V.G. do ângulo entre a recta pp e o Pla-
no Horizontal de Projecção está em qualquer dos dois ângulos agudos entre pp’’44 e o eixo XX’’ – identificou-se um dos ângulos pelas
semi-rectas que limitam o ângulo e assinalando a sua amplitude com θo. Note de novo que não se recorreu ao mmééttooddoo ggeerraall ppaarraa aa ddeetteerr--
mmiinnaaççããoo ddoo âânngguulloo eennttrree uummaa rreeccttaa ee uumm ppllaannoo – no entanto, caso se tivesse recorrido a esse processo de resolução, ter-se-ia chegado à
mesma conclusão com um pouco mais de traçado.

108. 108
SOLUÇÕES
296.
Em primeiro lugar, representaram-se o plano ϕ, pelo seu traço horizontal, e a recta rr, pelas
suas projecções, em função dos dados. A recta rr, porque é uma recta do β2/4, tem as suas
projecções coincidentes. O ângulo entre uma recta e um plano frontal (de frente) é igual (tem
a mesma amplitude) ao ângulo entre a recta e o Plano Frontal de Projecção. O ângulo entre
uma recta e o Plano Frontal de Projecção é o ângulo entre a recta e a sua projecção frontal
(que é a projecção ortogonal da recta no Plano Frontal de Projecção) – esse ângulo existe no
plano projectante frontal da recta. Assim, nesta situação, o ângulo entre a recta rr e o plano ϕ
é igual (tem a mesma amplitude) ao ângulo entre a recta rr e o Plano Frontal de Projecção
(que é paralelo ao plano ϕ) e que é, afinal, o ângulo entre a recta rr e a sua projecção frontal
(rr22) – esse ângulo está contido no plano projectante frontal da recta, que é um plano de topo.
Esse ângulo não se projecta em V.G., pois o plano projectante frontal da recta não é paralelo
a nenhum dos planos de projecção, pelo que é necessário o recurso a um processo geomé-
trico auxiliar. Optou-se pelo rebatimento do plano para o Plano Frontal de Projecção – a char-
neira é a recta ee, que é a própria projecção frontal da recta rr. A recta rr é uma recta passante – é concorrente com o eixo XX num ponto. Esse
ponto, porque é um ponto da charneira, é fixo. Para rebater a recta rr é necessário o recurso a um outro ponto qualquer da recta rr – o ponto
AA, por exemplo. O ponto AA rebateu-se em função do seu afastamento. A recta rrrr passa pelo ponto fixo do eixo XX e por AArr. A V.G. do ângulo
entre a recta rr e o plano ϕ está em qualquer dos dois ângulos agudos entre rrrr e ee22 – identificou-se um dos ângulos pelas semi-rectas que li-
mitam o ângulo e assinalando a sua amplitude com αo. Note que ainda não se recorreu ao mmééttooddoo ggeerraall ppaarraa aa ddeetteerrmmiinnaaççããoo ddoo âânngguulloo
eennttrree uummaa rreeccttaa ee uumm ppllaannoo em função do imediatismo das situações apresentadas – sublinha-se sempre que, caso se tivesse recorrido a
esse processo de resolução, ter-se-ia chegado à mesma conclusão com um pouco mais de traçado.
298.
Em primeiro lugar representaram-se o plano δ, pelos seus traços, e a recta hh, pelas
suas projecções, em função dos dados. O ângulo entre a recta hh e o plano δ está con-
tido num plano ortogonal ao plano δ que contém a recta hh – trata-se do plano horizon-
tal (de nível) que contém a recta hh. O ângulo entre a recta hh e o plano δ é o ângulo
entre a recta e a sua projecção ortogonal no plano δ – essa projecção é a recta de
intersecção do plano δ com o plano horizontal (de nível) que contém a recta hh (que é
o plano ortogonal ao plano δ que contém a recta hh). Essa recta terá a sua projecção
frontal coincidente com hh22 (pois o plano horizontal é projectante frontal) e terá a sua
projecção horizontal sobre hhδ (pois o plano δ é projectante horizontal). O ângulo entre
as duas rectas projecta-se em V.G. no Plano Horizontal de Projecção, pois o plano
que o contém (o plano horizontal que contém a recta hh) é paralelo ao Plano Horizontal
de Projecção. Assim, a projecção horizontal desse ângulo é, directamente, o ângulo
entre hh11 e hhδ. A V.G. do ângulo entre a recta hh e o plano δ está em qualquer dos dois
ângulos agudos entre hh11 e hhδ – identificou-se um dos ângulos pelas semi-rectas que
limitam o ângulo e assinalando a sua amplitude com αo. Note que não se recorreu ao
mmééttooddoo ggeerraall ppaarraa aa ddeetteerrmmiinnaaççããoo ddoo âânngguulloo eennttrree uummaa rreeccttaa ee uumm ppllaannoo em fun-
ção do ângulo pedido estar contido num plano paralelo a um dos planos de projecção
(o que resulta numa situação de resolução imediata, conforme se expôs) – sublinha-se
mais uma vez que, caso se tivesse recorrido a esse processo de resolução, ter-se-ia
chegado à mesma conclusão com um pouco mais de traçado.
Em primeiro lugar, representaram-se o plano θ, pelos seus traços, e a recta ff, pelas suas
projecções, em função dos dados. O ângulo entre a recta ff e o plano θ está contido num
plano ortogonal ao plano θ que contém a recta ff – trata-se do plano frontal (de frente) que
contém a recta ff. O ângulo entre a recta ff e o plano θ é o ângulo entre a recta e a sua pro-
jecção ortogonal no plano θ – essa projecção é a recta de intersecção do plano θ com o
plano frontal (de frente) que contém a recta ff (que é o plano ortogonal ao plano θ que con-
tém a recta ff). Essa recta terá a sua projecção horizontal coincidente com ff11 (pois o plano
frontal é projectante horizontal) e terá a sua projecção frontal sobre ffθ (pois o plano θ é pro-
jectante frontal). O ângulo entre as duas rectas projecta-se em V.G. no Plano Frontal de
Projecção, pois o plano que o contém (o plano frontal que contém a recta ff) é paralelo ao
Plano Frontal de Projecção. Assim, a projecção frontal desse ângulo é, directamente, o ân-
gulo entre ff22 e ffθ. A V.G. do ângulo entre a recta ff e o plano θ está em qualquer dos dois
ângulos agudos entre ff22 e ffθ – identificou-se um dos ângulos pelas semi-rectas que limitam
o ângulo e assinalando a sua amplitude com αo. Note que não se recorreu ao mmééttooddoo
ggeerraall ppaarraa aa ddeetteerrmmiinnaaççããoo ddoo âânngguulloo eennttrree uummaa rreeccttaa ee uumm ppllaannoo em função do ângulo
pedido estar contido num plano paralelo a um dos planos de projecção (o que resulta
numa situação de resolução imediata, conforme se expôs) – sublinha-se ainda que, caso
se tivesse recorrido a esse processo de resolução, ter-se-ia chegado à mesma conclusão
com um pouco mais de traçado.
297.

109. 109
SOLUÇÕES
299.
Em primeiro lugar representaram-se o plano θ, pelos seus
traços, e a recta hh, pelas suas projecções, em função dos
dados. Uma vez que se trata do ângulo entre uma recta e
um plano projectante (e o ângulo não está contido em ne-
nhum plano paralelo a qualquer dos planos de projecção,
como em situações anteriores), recorreu-se ao mmééttooddoo ggee--
rraall ppaarraa aa ddeetteerrmmiinnaaççããoo ddoo âânngguulloo eennttrree uummaa rreeccttaa ee uumm
ppllaannoo. 11.. Determinou-se o ponto II, o ponto de intersecção
da recta hh com o plano θ (II é o vértice do ângulo). O ponto
II teve determinação directa a partir da sua projecção fron-
tal, pois o plano θ é projectante frontal. 22.. Determinou-se a
projecção ortogonal da recta hh no plano θ. Para tal condu-
ziu-se, por um ponto PP, da recta hh, uma recta pp, ortogonal
ao plano θ, e determinou-se o ponto de intersecção da rec-
ta pp com o plano θ – o ponto PP’’ (o ponto PP’’ teve determina-
ção directa a partir da sua projecção frontal, pois o plano θ
é projectante frontal). PP’’ é a projecção ortogonal do ponto
PP no plano θ. A recta rr, definida por II e por PP’’, é a projec-
ção ortogonal da recta hh no plano θ. A recta pp é uma recta
frontal (de frente). 33.. O ângulo entre a recta hh e a recta rr é
igual (tem a mesma amplitude) ao ângulo entre a recta hh e
o plano θ. Este ângulo está contido no plano definido pelas
rectas hh e rr – é um plano oblíquo. Note que o plano con-
tém, também, a recta pp. O ângulo não se projecta em V.G., pelo que se recorreu ao rebatimento do plano definido pelas duas rectas para o
plano frontal (de frente) ϕ que contém a recta pp. A recta pp é a própria charneira, pois é a recta de intersecção dos dois planos. Tem-se imedia-
tamente PPrr ≡ PP22 e PP’’rr ≡ PP’’22, pois PP e PP’’ são dois pontos da charneira. Rebateu-se o ponto II pelo triângulo do rebatimento, em função da sua
distância ao plano ϕ (o afastamento de II em relação a ϕ). A recta hhrr fica definida por PPrr e IIrr e a recta rrrr fica definida por PP’’rr e por IIrr. O ângulo
entre a recta hh e o plano θ é qualquer dos ângulos agudos entre hhrr e rrrr, com vértice em IIrr – identificou-se um dos ângulos pelas semi-rectas
que limitam o ângulo e assinalando a sua amplitude com αo.
Em primeiro lugar representaram-se o plano γ, pelos seus traços, e a recta
rr, pelas suas projecções, em função dos dados. As projecções da recta rr
fazem, com o eixo XX, ângulos iguais e com o mesmo sentido de abertura,
pois a recta é paralela ao β1/3. Uma vez que se trata do ângulo entre uma
recta e um plano projectante, recorreu-se ao mmééttooddoo ggeerraall ppaarraa aa ddeetteerr--
mmiinnaaççããoo ddoo âânngguulloo eennttrree uummaa rreeccttaa ee uumm ppllaannoo. 11.. Determinou-se o
ponto II, o ponto de intersecção da recta hh com o plano θ (II é o vértice do
ângulo). O ponto II teve determinação directa a partir da sua projecção ho-
rizontal, pois o plano γ é projectante horizontal. 22.. Determinou-se a projec-
ção ortogonal da recta rr no plano γ. Para tal conduziu-se, pelo ponto AA da
recta rr, uma recta pp, ortogonal ao plano γ, e determinou-se o ponto de in-
tersecção da recta pp com o plano γ – o ponto AA’’ (o ponto AA’’ teve determi-
nação directa a partir da sua projecção horizontal, pois o plano γ é
projectante horizontal). AA’’ é a projecção ortogonal do ponto AA no plano γ.
A recta rr’’, definida por II e por AA’’, é a projecção ortogonal da recta rr no
plano γ. A recta pp é uma recta horizontal (de nível). 33.. O ângulo entre a
recta rr e a recta rr’’ é igual (tem a mesma amplitude) ao ângulo entre a rec-
ta rr e o plano γ. Este ângulo está contido no plano definido pelas rectas rr
e rr’’ – é um plano oblíquo. Note que o plano contém, também, a recta pp.
O ângulo não se projecta em V.G., pelo que se recorreu ao rebatimento
do plano definido pelas duas rectas para o plano horizontal (de nível) ν
que contém a recta pp. A recta pp é a própria charneira, pois é a recta de
intersecção dos dois planos. Tem-se imediatamente AArr ≡ AA11 e AA’’rr ≡ AA’’11,
pois AA e AA’’ são dois pontos da charneira. Rebateu-se o ponto II pelo triân-
gulo do rebatimento, em função da sua distância ao plano ν (a cota de II
em relação a ν). A recta rrrr fica definida por AArr e IIrr e a recta rr’’rr fica definida por AA’’rr e por IIrr. O ângulo entre a recta rr e o plano γ é qualquer
dos ângulos agudos entre rrrr e rr’’rr, com vértice em IIrr – identificou-se um dos ângulos pelas semi-rectas que limitam o ângulo e assinalando a
sua amplitude com αo.
300.

110. 110
SOLUÇÕES
301.
Em primeiro lugar representaram-se o plano α, pelos seus traços, e a
recta ff, pelas suas projecções, em função dos dados. O plano α é orto-
gonal ao β1/3, pelo que os seus traços são simétricos em relação ao eixo
XX. Uma vez que se trata do ângulo entre uma recta e um plano não pro-
jectante, recorreu-se ao mmééttooddoo ddoo âânngguulloo ccoommpplleemmeennttaarr. 11.. Pelo pon-
to PP, da recta, conduziu-se uma recta pp, ortogonal ao plano α. Note que,
uma vez que o ponto PP é um ponto do β1/3 e que o plano α é ortogonal
ao β1/3, a recta pp é uma recta do β1/3 (é uma recta passante, concorrente
com o eixo XX no ponto AA). 22.. O ângulo formado entre as duas rectas
está contido no plano definido pelas mesmas (que é um plano de topo),
e não se projecta em V.G. – recorreu-se ao rebatimento do plano defini-
do pelas duas rectas para o Plano Horizontal de Projecção. A charneira
foi hhθ. Rebateu-se o ponto PP, obtendo PPrr. O ponto AA é um ponto da
charneira, pelo que é fixo – roda sobre si próprio. O traço horizontal da
recta ff, o ponto HH, foi o ponto a que se recorreu para rebater a recta ff –
HH também é fixo, pois é também um ponto da charneira. A recta pprr fica
definida por PPrr e por AArr. A recta ffrr fica definida por PPrr e por HHrr. O ângulo
entre ff e pp é qualquer dos ângulos agudos entre ffrr e pprr, com vértice em
PPrr, e identificou-se com 90o–βo, pois é o ângulo complementar do ângu-
lo pretendido. 33.. O ângulo entre a recta ff e o plano α é o âânngguulloo ccoomm--
pplleemmeennttaarr do ângulo 90o–βo – assim, por PPrr conduziu-se uma
perpendicular a pprr. O ângulo pretendido é o ângulo entre esta perpendi-
cular e ffrr, e identificou-se com βo.
Em primeiro lugar representaram-se o plano α, pelos seus traços, e
a recta rr, pelas suas projecções, em função dos dados. As projec-
ções da recta rr fazem, com o eixo XX, ângulos iguais e com o mes-
mo sentido de abertura, pois a recta é paralela ao β1/3. Uma vez que
se trata do ângulo entre uma recta e um plano não projectante,
recorreu-se ao mmééttooddoo ddoo âânngguulloo ccoommpplleemmeennttaarr. 11.. Por um ponto
AA qualquer, da recta rr, conduziu-se uma recta pp, ortogonal ao plano.
22.. O ângulo formado entre as duas rectas está contido no plano de-
finido pelas mesmas e não se projecta em V.G. – recorreu-se ao
rebatimento do plano definido pelas duas rectas para o plano frontal
(de frente) ϕ que passa pelo ponto PP. A charneira é a recta ee, que é
a recta de intersecção dos dois planos e está definida pelos pontos
PP e BB. PP é o ponto de intersecção do plano ϕ com a recta rr e BB é o
ponto de intersecção do plano ϕ com a recta pp. Tem-se imediata-
mente PPrr ≡ PP22 e BBrr ≡ BB22, pois PP e BB são dois pontos da charneira.
Rebateu-se o ponto AA pelo triângulo do rebatimento, em função da
sua distância ao plano ϕ (o afastamento de AA em relação a ϕ).
A recta rrrr fica definida por AArr e PPrr e a recta pprr fica definida por AArr e
por BBrr. O ângulo entre rr e pp é qualquer dos ângulos agudos entre rrrr
e pprr, com vértice em AArr, e identificou-se com 90o–θo, pois é o âânngguu--
lloo ccoommpplleemmeennttaarr do ângulo pretendido. 33.. O ângulo entre a recta rr
e o plano α é o ângulo complementar do ângulo 90o–θo – assim,
por AArr conduziu-se uma perpendicular a rrrr. O ângulo pretendido é o
ângulo entre esta perpendicular e pprr, e identificou-se com θo.
302.

111. 111
SOLUÇÕES
303.
Em primeiro lugar representaram-se o plano δ, pelos seus traços, e a rec-
ta rr, pelas suas projecções, em função dos dados. A recta rr é paralela ao
β2/4, pelo que tem as suas projecções paralelas entre si. O plano δ é orto-
gonal ao β2/4, pelo que tem os seus traços coincidentes. Uma vez que se
trata do ângulo entre uma recta e um plano não projectante, recorreu-se
ao mmééttooddoo ddoo âânngguulloo ccoommpplleemmeennttaarr. 11.. Pelo ponto PP, da recta rr, condu-
ziu-se uma recta pp, ortogonal ao plano. 22.. O ângulo formado entre as
duas rectas está contido no plano definido pelas mesmas, e não se pro-
jecta em V.G. – recorreu-se ao rebatimento do plano definido pelas duas
rectas para um plano frontal (de frente) ϕ. A charneira é a recta ee, que é a
recta de intersecção dos dois planos e está definida pelos pontos AA e BB.
AA é o ponto de intersecção do plano ϕ com a recta rr e BB é o ponto de inter-
secção do plano ϕ com a recta pp. Tem-se imediatamente AArr ≡ AA22 e BBrr ≡ BB22,
pois AA e BB são dois pontos da charneira. Rebateu-se o ponto PP pelo triân-
gulo do rebatimento, em função da sua distância ao plano ϕ (o afasta-
mento de PP em relação a ϕ). A recta rrrr fica definida por AArr e PPrr e a recta pprr
fica definida por BBrr e por PPrr. O ângulo entre rr e pp é qualquer dos ângulos
agudos entre rrrr e pprr, com vértice em PPrr, e identificou-se com 90o–θo, pois é
o âânngguulloo ccoommpplleemmeennttaarr do ângulo pretendido. 33.. O ângulo entre a recta rr
e o plano δ é o ângulo complementar do ângulo 90o–θo – assim, por PPrr
conduziu-se uma perpendicular a rrrr. O ângulo pretendido é o ângulo
entre esta perpendicular e pprr, e identificou-se com θo.
Em primeiro lugar representaram-se o plano ρ, pelos seus traços, e a
recta rr, pelas suas projecções, em função dos dados. Uma vez que se
trata do ângulo entre uma recta e um plano não projectante, recorreu-se
ao mmééttooddoo ddoo âânngguulloo ccoommpplleemmeennttaarr. 11.. Pelo ponto AA, da recta rr, con-
duziu-se uma recta pp, ortogonal ao plano ρ – a recta pp é uma recta de
perfil definida por um ponto (o ponto AA) e por uma direcção (é ortogonal
ao plano ρ). 22.. O ângulo formado entre as duas rectas está contido no
plano definido pelas mesmas (que é um plano oblíquo), e não se pro-
jecta em V.G. – recorreu-se ao rebatimento do plano definido pelas duas
rectas para o Plano Horizontal de Projecção. A charneira desse rebati-
mento é a recta ee’’, que está definida pelos traços horizontais das duas
rectas. O traço horizontal da recta pp determinou-se com o recurso ao
rebatimento do plano de perfil (o plano π) que a contém. A recta ii é a
recta de intersecção do plano π com o plano ρ (é uma recta de perfil) e
está definida pelos seus traços nos planos de projecção, FF e HH. A recta
pp tem de ser perpendicular à recta ii, o que se resolveu também em re-
batimento. Rebateu-se o plano π para o Plano Frontal de Projecção –
a charneira foi ffπ (recta ee). A recta iirr está definida por FFrr e HHrr. A recta pp,
em rebatimento (a recta pprr) passa por AArr e é perpendicular a iirr. Está ga-
rantida a ortogonalidade entre a recta pp e o plano ρ. Em rebatimento,
determinou-se o traço horizontal da recta pp – HH’’. Invertendo o rebati-
mento, determinaram-se as projecções de HH’’. A charneira do rebatimen-
to do plano definido pelas rectas pp e rr (recta ee’’) está definida por HH’’
(traço horizontal da recta pp) e por HH’’’’ (traço horizontal da recta rr). Reba-
teu-se o ponto AA, pelo seu triângulo do rebatimento (em função da sua
cota), obtendo AArr’’ (o ponto AArr’’ é o ponto AA rebatido pelo seu segundo
rebatimento – o rebatimento do plano definido pelas rectas rr e pp). HH’’rr ≡ HH’’11 e HH’’’’rr ≡ HH’’’’11, pois HH’’ e HH’’’’ são dois pontos da charneira (rodam
sobre si próprios). A recta pprr’’ fica definida por AArr’’ e por HH’’rr (a recta pprr’’ é a recta pp rebatida pelo seu segundo rebatimento – o rebatimento do
plano definido pelas rectas rr e pp). A recta rrrr fica definida por AArr’’ e por HH’’’’rr. O ângulo entre rr e pp é qualquer dos ângulos agudos entre rrrr e pprr’’,
com vértice em AArr’’, e identificou-se com 90o–θo, pois é o ângulo complementar do ângulo pretendido. 33.. O ângulo entre a recta rr e o plano ρ
é o âânngguulloo ccoommpplleemmeennttaarr do ângulo 90o–θo – assim, por AArr’’ conduziu-se uma perpendicular a rrrr. O ângulo pretendido é o ângulo entre esta
perpendicular e pprr’’, e identificou-se com θo.
304.

112. 112
SOLUÇÕES
305.
Em primeiro lugar representaram-se o plano ρ, pelo seu traço horizontal
(o plano está definido pelo seu traço horizontal e pela sua orientação), e a
recta hh, pelas suas projecções, em função dos dados. Uma vez que se
trata do ângulo entre uma recta e um plano não projectante, recorreu-se
ao mmééttooddoo ddoo âânngguulloo ccoommpplleemmeennttaarr. 11.. Pelo ponto PP, da recta hh, condu-
ziu-se uma recta pp, ortogonal ao plano ρ – a recta pp é uma recta de perfil
definida por um ponto (o ponto PP) e por uma direcção (é ortogonal ao
plano ρ). 22.. O ângulo formado entre as duas rectas está contido no plano
definido pelas mesmas (que é um plano oblíquo), e não se projecta em
V.G. – recorreu-se ao rebatimento do plano definido pelas duas rectas para
o plano horizontal (de nível) ν que contém a recta hh. A charneira desse
rebatimento é a própria recta hh, que roda sobre si própria, pelo que se tem
imediatamente hhrr ≡ ee11 ≡ hh11. O ponto PP, porque é um ponto da charneira,
roda sobre si próprio, pelo que se tem imediatamente PPrr ≡ PP11. Já temos
um ponto para definir a recta pp em rebatimento – necessitamos de um ou-
tro ponto, que tem de ser determinado em rebatimento, rebatendo a recta
pelo rebatimento do plano de perfil que a contém. Rebateu-se o plano de
perfil (o plano π) que contém a recta pp para o Plano Frontal de Projecção
(a charneira foi a recta ee’’, que é ffπ). A recta ii é a recta de intersecção do
plano π com o plano ρ (é uma recta de perfil) e está definida pelo seu traço horizontal, HH, e pela sua direcção (faz um ângulo de 30o com o
Plano Horizontal de Projecção, que é um ângulo com a mesma amplitude do diedro formado entre o plano ρ e o Plano Horizontal de Projec-
ção). A recta pp tem de ser perpendicular à recta ii, o que se resolveu também em rebatimento. A recta iirr está definida por HHrr e pela sua direc-
ção – faz um ângulo de 30o com hhπrr
. Note que se garantiu, ao medir o ângulo de 30o, que o traço frontal da recta (que não se assinalou) se
situa no SSPPFFSS. A recta pp, em rebatimento (a recta pprr) passa por PPrr’’ e é perpendicular a iirr (PPrr’’ é o ponto PP rebatido pelo seu segundo rebati-
mento – o rebatimento do plano π). Está garantida a ortogonalidade entre a recta pp e o plano ρ. Em rebatimento, determinou-se um outro
ponto qualquer da recta pp – o ponto AA (note que AA e o ponto de concorrência das rectas ii e pp, pelo que é o ponto de intersecção da recta pp
com o plano ρ, mas poderia ser um outro ponto qualquer). Invertendo o rebatimento, determinaram-se as projecções de AA. Rebateu-se o
ponto AA, pelo seu triângulo do rebatimento (em função da sua cota em relação a ν – a distância de AA a ν), obtendo AArr’’ (o ponto AArr’’ é o pon-
to AA rebatido pelo seu segundo rebatimento – o rebatimento do plano definido pelas rectas hh e pp). A recta pprr’’ fica definida por AArr’’ e por PPrr (a
recta pprr’’ é a recta pp rebatida pelo seu segundo rebatimento – o rebatimento do plano definido pelas rectas hh e pp). O ângulo entre hh e pp é
qualquer dos ângulos agudos entre hhrr e pprr’’, com vértice em PPrr, e identificou-se com 90o–βo, pois é o ângulo complementar do ângulo pre-
tendido. 33.. O ângulo entre a recta hh e o plano ρ é o âânngguulloo ccoommpplleemmeennttaarr do ângulo 90o–βo – assim, por PPrr conduziu-se uma perpendicular
a hhrr. O ângulo pretendido é o ângulo entre esta perpendicular e pprr’’, e identificou-se com βo.
Em primeiro lugar representaram-se o plano α, pelos seus traços, e a recta
pp, pelas suas projecções, em função dos dados. Uma vez que se trata do
ângulo entre uma recta e um plano projectante, é possível recorrer ao mméé--
ttooddoo ggeerraall ppaarraa aa ddeetteerrmmiinnaaççããoo ddoo âânngguulloo eennttrree uummaa rreeccttaa ee uumm ppllaannoo.
No entanto, é necessário ter em conta que a determinação da projecção
ortogonal da recta pp sobre o plano α poderia obrigar a raciocínios particu-
lares, nomeadamente o rebatimento da recta pp, para determinar o ponto
de intersecção da recta pp com o plano α. Assim, dada a universalidade dos
dois processos, optou-se por recorrer ao mmééttooddoo ddoo âânngguulloo ccoommpplleemmeenn--
ttaarr. 11.. Pelo ponto AA, da recta pp, conduziu-se uma recta mm, ortogonal ao
plano. A recta mm é uma recta horizontal (de nível). 22.. O ângulo formado en-
tre as duas rectas está contido no plano definido pelas mesmas, e não se
projecta em V.G. – recorreu-se ao rebatimento do plano definido pelas
duas rectas para o plano frontal (de frente) ϕ que contém o ponto BB (com
vista a uma maior economia de traçados, pois de outra forma seríamos ob-
rigados a determinar outro ponto da recta pp, o que implicaria o recurso a
processos geométricos auxiliares). A charneira é a recta ee, que é a recta de
intersecção dos dois planos e está definida pelos pontos BB e CC. BB é o pon-
to de intersecção do plano ϕ com a recta pp e CC é o ponto de intersecção
do plano ϕ com a recta mm. Tem-se imediatamente BBrr ≡ BB22 e CCrr ≡ CC22, pois BB
e CC são dois pontos da charneira. Rebateu-se o ponto AA pelo triângulo do
rebatimento, em função da sua distância ao plano ϕ (o afastamento de AA
em relação a ϕ). A recta pprr fica definida por AArr e BBrr e a recta mmrr fica definida
por AArr e por CCrr. O ângulo entre pp e mm é qualquer dos ângulos agudos en-
tre pprr e mmrr, com vértice em AArr, e identificou-se com 90o–θo, pois é o âânngguulloo
ccoommpplleemmeennttaarr do ângulo pretendido. 33.. O ângulo entre a recta pp e o pla-
no α é o ângulo complementar do ângulo 90o–θo – assim, por AArr conduziu-
-se uma perpendicular a pprr. O ângulo pretendido é o ângulo entre esta
perpendicular e mmrr, e identificou-se com θo.
306.

113. 113
SOLUÇÕES
307.
Em primeiro lugar representaram-se o plano α, pelos seus traços, e a recta
pp, pelas suas projecções, em função dos dados. O plano α tem os seus tra-
ços simétricos em relação ao eixo XX, pois é um plano ortogonal ao β1/3.
Uma vez que se trata do ângulo entre uma recta e um plano não projectan-
te, recorreu-se ao mmééttooddoo ddoo âânngguulloo ccoommpplleemmeennttaarr. 11.. Pelo ponto BB, da
recta pp, conduziu-se uma recta mm, ortogonal ao plano α. 22.. O ângulo forma-
do entre as duas rectas está contido no plano definido pelas mesmas, e não
se projecta em V.G. – recorreu-se ao rebatimento do plano definido pelas
duas rectas para o plano frontal (de frente) ϕ que contém o ponto AA (com
vista a uma maior economia de traçados, pois de outra forma seríamos obri-
gados a determinar outro ponto da recta pp, o que implicaria o recurso a pro-
cessos geométricos auxiliares). A charneira é a recta ee, que é a recta de
intersecção dos dois planos e está definida pelos pontos AA e CC. AA é o ponto
de intersecção do plano ϕ com a recta pp e CC é o ponto de intersecção do
plano ϕ com a recta mm. Tem-se imediatamente AArr ≡ AA22 e CCrr ≡ CC22, pois AA e CC
são dois pontos da charneira. Rebateu-se o ponto BB pelo triângulo do reba-
timento, em função da sua distância ao plano ϕ (o afastamento de BB em re-
lação a ϕ). A recta pprr fica definida por AArr e BBrr e a recta mmrr fica definida por BBrr
e por CCrr. O ângulo entre pp e mm é qualquer dos ângulos agudos entre pprr e
mmrr, com vértice em BBrr, e identificou-se com 90°–θ°, pois é o âânngguulloo ccoommppllee--
mmeennttaarr do ângulo pretendido. 33.. O ângulo entre a recta pp e o plano α é o
ângulo complementar do ângulo 90°–θ° – assim, por BBrr conduziu-se uma
perpendicular a mmrr. O ângulo pretendido é o ângulo entre esta perpendicu-
lar e pprr, e identificou-se com θ°.
Em primeiro lugar representaram-se o plano ρ, pelos seus traços,
e a recta pp, pelas suas projecções, em função dos dados. Apesar
de ser possível, neste exercício, recorrer a qualquer dos dois pro-
cessos referidos (o mmééttooddoo ggeerraall ppaarraa aa ddeetteerrmmiinnaaççããoo ddoo âânn--
gguulloo eennttrree uummaa rreeccttaa ee uumm ppllaannoo e o mmééttooddoo ddoo âânngguulloo
ccoommpplleemmeennttaarr), dada a especificidade da situação optou-se por
uma resolução diferente e bastante mais simples. Esta consistiu,
em primeiro lugar, em efectuar uma mudança do diedro de pro-
jecção, transformando o plano ρ num plano de topo e a recta pp
numa recta frontal (de frente), o que redunda na situação do
exercício 229977. Assim, substituiu-se o Plano Frontal de Projecção
(ppllaannoo 22) por um novo plano de projecção (ppllaannoo 44), paralelo à
recta pp e ortogonal ao plano ρ. O novo eixo XX (o eixo XX’’) é a recta
de intersecção do ppllaannoo 11 com o ppllaannoo 44 e é paralelo a pp11
(e perpendicular a hhρ). A projecção da recta pp no ppllaannoo 44, pp44,
determinou-se a partir das projecções dos pontos AA e BB no ppllaa--
nnoo 44 – AA44 e BB44 determinaram-se em função das cotas de AA e BB,
que se mantiveram. Para determinar o traço do plano ρ no ppllaannoo
44 recorreu-se a um ponto CC, de ffρ – CC44 determinou-se em função
da cota de CC, que se manteve. Uma vez que, no novo diedro de
projecção, o plano ρ é projectante, ff44ρ passa por CC44 e é concor-
rente com hhρ no eixo XX’’. No novo diedro de projecção (formado
pelo ppllaannoo 11 e pelo ppllaannoo 44), a recta pp é uma recta frontal (de
frente) e o plano ρ é um plano de topo, pelo que se trata da situa-
ção exposta no relatório do exercício 229977. Assim, o ângulo entre
a recta pp e o plano ρ está contido num plano paralelo ao ppllaannoo 44 (o plano ortogonal ao plano ρ que contém a recta pp), pelo que se projecta
em V.G. no ppllaannoo 44 – é qualquer dos dois ângulos agudos entre pp44 e ff44ρ, e identificou-se com θo.
308.

114. 114
SOLUÇÕES
309.
Em primeiro lugar representaram-se o plano ρ, pelos seus traços (que
estão coincidentes no eixo XX) e pelo ponto AA, e a recta pp, pelas suas
projecções, em função dos dados. A recta pp está definida por um ponto
(o ponto PP) e por uma direcção (é dado o ângulo que a recta faz com o
Plano Frontal de Projecção). Tal como na situação anterior, o processo
de resolução mais simples consiste em efectuar uma mudança do die-
dro de projecção, transformando o plano ρ num plano de topo e a recta
pp numa recta frontal (de frente), o que redunda mais uma vez na situa-
ção do exercício 229977. Assim, substituiu-se o Plano Frontal de Projecção
(ppllaannoo 22) por um novo plano de projecção (ppllaannoo 44), paralelo à recta pp
e ortogonal ao plano ρ. O novo eixo XX (o eixo XX’’) é a recta de intersec-
ção do ppllaannoo 11 com o ppllaannoo 44 e é paralelo a pp11 (e perpendicular a hhρ).
A projecção da recta pp no ppllaannoo 44, pp44, determinou-se a partir da projec-
ção do ponto PP no ppllaannoo 44 (PP44), e a em função do ângulo que a recta pp
faz com o Plano Frontal de Projecção. PP44 determinou-se em função da
sua cota (que se manteve). A recta pp, fazendo um ângulo de 60° com o
Plano Frontal de Projecção, faz um ângulo de 30° (o ângulo comple-
mentar) com o Plano Horizontal de Projecção – esse é o ângulo que
nos permitiu desenhar pp44, a partir de PP44, pois esse ângulo projecta-se
em V.G. no ppllaannoo 44, no ângulo entre pp44 e o eixo XX’’. Note que se garan-
tiu, ao medir o ângulo, que a recta pp intersecta o Plano Horizontal de Projecção num ponto com afastamento negativo (um ponto do SSPPHHPP),
conforme é expressamente pedido no enunciado. Para determinar o traço do plano ρ no ppllaannoo 44 recorreu-se à projecção, no ppllaannoo 44, do
ponto AA, que é o ponto que define o plano – AA44 determinou-se em função da cota de AA, que se manteve. Uma vez que, no novo diedro de
projecção, o plano ρ é projectante, ff44ρ passa por AA44 e é concorrente com hhρ no eixo XX’’. No novo diedro de projecção (formado pelo ppllaannoo 11
e pelo ppllaannoo 44), a recta pp é uma recta frontal (de frente) e o plano ρ é um plano de topo, pelo que se trata da situação exposta no relatório
do exercício 229977. Assim, o ângulo entre a recta pp e o plano ρ está contido num plano paralelo ao ppllaannoo 44 (o plano ortogonal ao plano ρ que
contém a recta pp), pelo que se projecta em V.G. no ppllaannoo 44 – é qualquer dos dois ângulos agudos entre pp44 e ff44ρ, e identificou-se com αo.
Em primeiro lugar representaram-se o plano ρ, pelos seus
traços, que estão coincidentes no eixo XX (o plano está defini-
do pelo eixo XX e pela sua orientação), e a recta rr, pelas suas
projecções, em função dos dados. A recta rr tem as suas
projecções simétricas em relação ao eixo XX, pois trata-se de
uma recta do β1/3 – é uma recta passante, concorrente com
o eixo XX num ponto AA. Uma vez que se trata do ângulo entre
uma recta e um plano não projectante, recorreu-se ao mmééttoo--
ddoo ddoo âânngguulloo ccoommpplleemmeennttaarr. 11.. Por um ponto PP, qualquer,
da recta rr, conduziu-se uma recta pp, ortogonal ao plano ρ –
a recta pp é uma recta de perfil definida por um ponto (o pon-
to PP) e por uma direcção (é ortogonal ao plano ρ). 22.. O
ângulo formado entre as duas rectas está contido no plano
definido pelas mesmas (que é um plano oblíquo), e não se
projecta em V.G. – recorreu-se ao rebatimento do plano defi-
nido pelas duas rectas para o Plano Horizontal de Projec-
ção. A charneira desse rebatimento é a recta ee’’, que está
definida pelo ponto AA (o ponto de concorrência da recta rr
com o eixo XX) e pelo traço horizontal da recta pp. O traço
horizontal da recta pp determinou-se com o recurso ao rebati-
mento do plano de perfil (o plano π) que a contém. A recta pp’’
é a recta de intersecção do plano π com o plano ρ (é uma
recta de perfil) – a recta pp’’ é uma recta de perfil passante, e
está definida por um ponto (o seu ponto de concorrência
com o eixo XX) e por uma direcção (faz um ângulo de 60o
com o Plano Frontal de Projecção, que é um ângulo com a
mesma amplitude do diedro formado entre o plano ρ e o
Plano Horizontal de Projecção). A recta pp tem de ser per-
pendicular à recta pp’’, o que se resolveu também em rebati-
mento. Rebateu-se o plano π para o Plano Frontal de
Projecção – a charneira foi ffπ (recta ee). A recta pp’’rr está definida pelo seu ponto de concorrência com o eixo XX (que é fixo, pois é um ponto da
charneira) e pela sua direcção – a recta pp’’rr faz um ângulo de 60o com ffπrr
. Note que se garantiu, ao medir o ângulo de 60o, que a recta atravessa
os 1o e 3o Diedros, pois PP é um ponto do 1o Diedro e pp’’rr passa pelo quadrante no qual se situa PPrr. A recta pp, em rebatimento (a recta pprr) passa
por PPrr e é perpendicular a pp’’rr. Está garantida a ortogonalidade entre a recta pp e o plano ρ. Em rebatimento, determinou-se o traço horizontal da
recta pp – HH. Invertendo o rebatimento, determinaram-se as projecções de HH. A charneira do rebatimento do plano definido pelas rectas pp e rr
310.
(Continua na página seguinte)

115. 115
SOLUÇÕES
311.
Em primeiro lugar representou-se a recta rr, pelas suas projecções, em função dos
dados. Note que não se representaram os traços do β1/3, por tal não ser necessário
(o β1/3 é um plano que não carece de representação), mas que estão coincidentes
no eixo XX. A recta rr tem as suas projecções coincidentes, pois trata-se de uma recta
do β2/4 – é uma recta passante, concorrente com o eixo XX num ponto AA. Uma vez
que se trata do ângulo entre uma recta e um plano não projectante, recorreu-se ao
mmééttooddoo ddoo âânngguulloo ccoommpplleemmeennttaarr. 11.. Por um ponto PP, qualquer, da recta rr, condu-
ziu-se uma recta pp, ortogonal ao β1/3 – a recta pp é uma recta de perfil definida por um
ponto (o ponto PP) e por uma direcção (é ortogonal ao β1/3). Note que a recta pp é nnee--
cceessssaarriiaammeennttee uma recta de perfil do β2/4, pelo que é possível, em qualquer circuns-
tância, determinar quaisquer pontos da recta pp – todos os seus pontos têm as suas
projecções coincidentes. 22.. O ângulo formado entre as duas rectas está contido no
plano definido pelas mesmas (que é o próprio β2/4, pois as duas rectas são rectas do
β2/4), e não se projecta em V.G. – recorreu-se ao rebatimento do plano definido pelas
duas rectas (o β2/4) para o Plano Horizontal de Projecção. A charneira desse rebati-
mento é a recta ee, que é o próprio eixo XX. A recta pp, sendo uma recta de perfil do β2/4, é nneecceessssaarriiaammeennttee uma recta de perfil passante – é
concorrente com o eixo XX num ponto BB. AArr ≡ AA11 e BBrr ≡ BB11, pois AA e BB são dois pontos da charneira. Rebateu-se o ponto PP, pelo seu triângulo do
rebatimento, em função da sua cota, obtendo PPrr. A recta rrrr está definida por AArr e por PPrr. A recta pprr está definida por BBrr e por PPrr. O ângulo entre rr
e pp é qualquer dos ângulos agudos entre rrrr e pprr, com vértice em PPrr, e identificou-se com 90o–αo, pois é o ângulo complementar do ângulo pre-
tendido. 33.. O ângulo entre a recta rr e o β1/3 é o âânngguulloo ccoommpplleemmeennttaarr do ângulo 90o–αo – assim, por PPrr conduziu-se uma perpendicular a rrrr. O
ângulo pretendido é o ângulo entre esta perpendicular e pprr, e identificou-se com αo.
Em primeiro lugar representaram-se os dois planos, pelos respectivos traços, em função dos dados –
o plano γ representou-se pelos seus dois traços e o plano ϕ representou-se pelo seu traço horizontal.
O plano γ é projectante horizontal, pelo que hhγ tem necessariamente de passar por AA11, pois AA é um
ponto do plano. Em seguida, e uma vez que a recta de intersecção dos dois planos (a aresta do die-
dro) é uma recta vertical, constatou-se que o plano ortogonal à aresta do diedro é projectante (é um
plano horizontal) e tem determinação imediata, pelo que se recorreu ao 11oo PPrroocceessssoo. 11.. A aresta do
diedro já está identificada – é uma recta vertical. 22.. Recorreu-se a um plano auxiliar, ortogonal à ares-
ta do diedro – o próprio Plano Horizontal de Projecção (que é um plano horizontal com cota nula).
33.. Determinaram-se as rectas de intersecção do Plano Horizontal de Projecção (o plano auxiliar) com
os dois planos – estas são, imediatamente, os traços horizontais dos dois planos (hhγ e hhϕ), pelo que
já estão determinadas. 44.. O ângulo entre as duas rectas é o ângulo entre os dois planos. O ângulo
entre hhγ e hhϕ está contido no Plano Horizontal de Projecção e está em V.G. – é qualquer dos dois ân-
gulos agudos entre as duas rectas e identificou-se com αo. Salienta-se que não é estritamente neces-
sária a determinação da recta de intersecção dos dois planos para a resolução do exercício. Note
que, na etapa 11.. do 11oo PPrroocceessssoo, está explicitamente iiddeennttiiffiiccaarr a recta de intersecção dos dois pla-
nos e não ddeetteerrmmiinnaarr a recta de intersecção dos dois planos. De facto, a determinação da recta de
intersecção dos dois planos não é essencial à resolução do exercício – essencial é, sim, a sua identi-
ficação, o que nos permite conduzir um plano qualquer que lhe seja ortogonal.
314.
312.
Por âânngguulloo eennttrree ddooiiss ppllaannooss entende-se o rectilíneo do menor diedro formado entre os dois planos, ou seja, o ângulo formado entre as
rectas de intersecção dos dois planos com um terceiro plano, ortogonal à aresta do diedro.
313.
Os dois processos para determinar a amplitude do diedro entre dois planos distinguem-se sobretudo ao nível dos traçados a executar, sen-
do que ambos são processos universais (utilizáveis independentemente da situação). De qualquer forma, o recurso a um ou a outro tem a
ver, aappeennaass, com economia de traçados. Assim, sempre que o plano ortogonal à aresta do diedro entre os dois planos dados ffoorr pprroojjeeccttaannttee
ee ttiivveerr ddeetteerrmmiinnaaççããoo iimmeeddiiaattaa (têm de se verificar as duas situações), é aconselhável o recurso ao 11oo PPrroocceessssoo, em função da linearidade
dos raciocínios e de traçados decorrentes da utilização desse processo. Por oposição, sempre que o plano ortogonal à aresta do diedro for-
mado entre os dois planos dados nnããoo sseejjaa pprroojjeeccttaannttee oouu nnããoo tteennhhaa ddeetteerrmmiinnaaççããoo iimmeeddiiaattaa (ou ambas as situações), o recurso ao
11oo PPrroocceessssoo reveste-se de grande complexidade ao nível dos traçados e raciocínios, pelo que é aconselhável o recurso ao 22oo PPrroocceessssoo,
em função, precisamente, da linearidade de raciocínios e de traçados decorrentes da utilização deste processo.
(recta ee’’) está definida por HH (traço horizontal da recta pp) e pelo ponto AA (o ponto de concorrência da recta rr com o eixo XX). Rebateu-se o ponto
PP, pelo seu triângulo do rebatimento (em função da sua cota), obtendo PPrr’’ (o ponto PPrr’’ é o ponto PP rebatido pelo seu segundo rebatimento – o re-
batimento do plano definido pelas rectas rr e pp). A recta pprr’’ fica definida por PPrr’’ e por HHrr’’ (o ponto HHrr’’ e a recta pprr’’ são, respectivamente, o ponto HH
e a recta pp rebatidos pelo segundo rebatimento – o rebatimento do plano definido pelas rectas rr e pp). O ângulo entre rr e pp é qualquer dos ângu-
los agudos entre rrrr e pprr’’, com vértice em PPrr’’, e identificou-se com 90o–βo, pois é o ângulo complementar do ângulo pretendido. 33.. O ângulo entre
a recta rr e o plano ρ é o âânngguulloo ccoommpplleemmeennttaarr do ângulo 90o–βo – assim, por PPrr’’ conduziu-se uma perpendicular a pprr’’. O ângulo pretendido é o
ângulo entre esta perpendicular e rrrr, e identificou-se com βo.

116. 116
SOLUÇÕES
315.
Em primeiro lugar representou-se o plano δ, pelos seus traços, em
função dos dados – o plano δ tem os seus traços simétricos em re-
lação ao eixo XX, pois é ortogonal ao β1/3. Pretende-se a VG. da am-
plitude do diedro formado entre o plano δ e o Plano Horizontal de
Projecção – a recta de intersecção dos dois planos (a aresta do die-
dro) é uma recta horizontal (é o próprio traço horizontal do plano δ
– hhδ), pelo que o plano ortogonal à aresta do diedro é projectante
(é um plano vertical) e tem determinação imediata. Assim, é possível
recorrer ao 11oo PPrroocceessssoo. No entanto, optou-se por um outro racio-
cino, mais simples. O ângulo entre um plano oblíquo qualquer e o
Plano Horizontal de Projecção é igual (tem a mesma amplitude) ao
ângulo que as suas rectas de maior declive fazem com o Plano Ho-
rizontal de Projecção. Assim, o problema resume-se à determina-
ção do ângulo entre uma recta (uma recta dd, de maior declive do
plano δ) e o Plano Horizontal de Projecção. Determinaram-se as
projecções de uma recta dd, uma recta de maior declive do plano,
qualquer – a recta dd está definida pelos seus traços. O ângulo entre
a recta dd e o Plano Horizontal de Projecção está contido num plano
que contém a recta dd e é ortogonal ao Plano Horizontal de Projec-
ção – trata-se do plano projectante horizontal da recta dd. Assim, por
dd conduziu-se um plano vertical (o plano γ) – o ângulo entre a recta dd e o Plano Horizontal de Projecção é o ângulo entre a recta dd e a sua
projecção ortogonal no Plano Horizontal de Projecção (que é dd11, que é o próprio traço horizontal do plano γ – hhγ). Esse ângulo está contido
no plano γ e não se projecta em V.G. em nenhum dos planos de projecção, pelo que é necessário o recurso a um processo geométrico au-
xiliar. Optou-se pelo rebatimento do plano γ para o Plano Frontal de Projecção – a charneira foi ffγ. Rebateu-se a recta dd, rebatendo os seus
traços – ddrr está definida por FFrr e por HHrr. A V.G. da amplitude do diedro ângulo o plano δ e o Plano Horizontal de Projecção está em qualquer
dos dois ângulos agudos entre ddrr e hhγrr
, com vértice em HHrr – identificou-se um dos ângulos pelas semi-rectas que limitam o ângulo e assina-
lando a sua amplitude com αo.
Em primeiro lugar representou-se o plano α, pelos seus tra-
ços, em função dos dados – o plano α tem os seus traços
coincidentes, pois é ortogonal ao β2/4. Pretende-se a VG. da
amplitude do diedro formado entre o plano α e o Plano Frontal
de Projecção – a recta de intersecção dos dois planos (a ares-
ta do diedro) é uma recta frontal (é o próprio traço frontal do
plano α – ffα), pelo que o plano ortogonal à aresta do diedro é
projectante (é um plano de topo) e tem determinação imedia-
ta. Assim, é possível recorrer ao 11oo PPrroocceessssoo. No entanto, op-
tou-se por um outro raciocínio, mais simples. O ângulo entre
um plano oblíquo qualquer e o Plano Frontal de Projecção é
igual (tem a mesma amplitude) ao ângulo que as suas rectas
de maior inclinação fazem com o Plano Frontal de Projecção.
Assim, o problema resume-se à determinação do ângulo entre
uma recta (uma recta ii, de maior inclinação do plano α) e o
Plano Frontal de Projecção. Determinaram-se as projecções
de uma recta ii, uma recta de maior inclinação do plano, qual-
quer – a recta ii está definida pelos seus traços. O ângulo entre a recta ii e o Plano Frontal de Projecção está contido num plano que contém
a recta ii e é ortogonal ao Plano Frontal de Projecção – trata-se do plano projectante frontal da recta ii. Assim, por ii conduziu-se um plano de
topo (o plano θ) – o ângulo entre a recta ii e o Plano Frontal de Projecção é o ângulo entre a recta ii e a sua projecção ortogonal no Plano
Frontal de Projecção (que é ii22, que é o próprio traço frontal do plano θ – ffθ). Esse ângulo está contido no plano θ e não se projecta em V.G.
em nenhum dos planos de projecção, pelo que é necessário o recurso a um processo geométrico auxiliar. Optou-se pelo rebatimento do
plano θ para o Plano Horizontal de Projecção – a charneira foi hhθ. Rebateu-se a recta ii, rebatendo os seus traços – iirr está definida por FFrr e
por HHrr. A V.G. da amplitude do diedro ângulo o plano α e o Plano Frontal de Projecção está em qualquer dos dois ângulos agudos entre iirr e
ffθrr
, com vértice em FFrr – identificou-se um dos ângulos pelas semi-rectas que limitam o ângulo e assinalando a sua amplitude com γ o.
316.

117. 117
SOLUÇÕES
317.
Em primeiro lugar representaram-se os dois planos pelos respectivos traços, em
função dos dados – o plano λ está representado pelos seus dois traços e o plano
ϕ está representado pelo seu traço horizontal. A amplitude do diedro entre um
plano oblíquo qualquer e um plano frontal (de frente) é igual à amplitude do die-
dro formado entre esse plano oblíquo e o Plano Frontal de Projecção – o plano
frontal (de frente) e o Plano Frontal de Projecção são dois planos paralelos. As-
sim, efectuaram-se os traçados necessários à determinação da amplitude do die-
dro formado entre o plano λ e o Plano Frontal de Projecção, o que consiste na
situação do exercício anterior, pelo que se aconselha a leitura do respectivo rela-
tório. A V.G. da amplitude do diedro entre o plano λ e o Plano Frontal de Projec-
ção (que é igual à amplitude do diedro formado entre o plano λ e o plano ϕ) está
em qualquer dos dois ângulos agudos entre iirr e ffθrr
, com vértice em FFrr – identifi-
cou-se um dos ângulos pelas semi-rectas que limitam o ângulo e assinalando a
sua amplitude com α°.
319.
Em primeiro lugar representou-se o plano ρ pelos seus traços (que estão coincidentes com o eixo
XX) e pelas projecções do ponto AA, em função dos dados. A determinação do ângulo entre os dois
planos (o plano ρ e o Plano Frontal de Projecção) processou-se com o recurso ao 11oo PPrroocceessssoo,
pois a recta de intersecção dos dois planos é ffρ, que é fronto-horizontal, e o plano que lhe é orto-
gonal é projectante (é um plano de perfil) e tem determinação imediata. 11.. A aresta do diedro já
está identificada – é uma recta fronto-horizontal. 22.. Recorreu-se a um plano auxiliar, ortogonal à
aresta do diedro – o plano π (é um plano de perfil). Por uma questão de economia de traçados,
optou-se por conduzir o plano π (o plano de perfil ortogonal à aresta do diedro) pelo ponto AA. 33..
Determinaram-se as rectas de intersecção do plano π (o plano auxiliar) com os dois planos – ii (é
uma recta de perfil do plano ρ, pelo que é uma recta de perfil passante) e ffπ. 44.. O ângulo entre as
duas rectas tem a amplitude do diedro entre os dois planos. O ângulo entre ii e ffπ está contido no
plano de perfil, pelo que não se projecta em V.G. em nenhum dos planos de projecção. Assim, re-
correu-se ao rebatimento do plano π para o Plano Frontal de Projecção – a charneira foi ffπ. A recta
iirr fica definida por AArr e pelo seu ponto de concorrência com o eixo XX, que é fixo (a recta ii é uma
recta de perfil passante). A V.G. do diedro formado entre o plano ρ e o Plano Frontal de Projecção
está em qualquer dos dois ângulos agudos entre iirr e ffπrr
– identificou-se um dos ângulos pelas
semi-rectas que limitam o ângulo e assinalando a sua amplitude com αo.
Em primeiro lugar representaram-se os pontos AA e BB, pelas respectivas pro-
jecções, em função dos dados. Em seguida, determinaram-se os traços do
plano ρ conduzindo, por AA e BB (que são dois pontos do plano), uma recta do
plano (recta rr) – determinaram-se os traços da recta rr, pelos quais se condu-
ziram os traços homónimos do plano ρ. Pretende-se a amplitude do diedro
formado entre o plano ρ e o Plano Horizontal de Projecção – a recta de inter-
secção dos dois planos (a aresta do diedro) é uma recta fronto-horizontal (é
hhρ) e o plano que lhe é ortogonal é projectante (é um plano de perfil) e tem
determinação imediata, pelo que, à partida, o problema se pode resolver
com o recurso ao 11oo PPrroocceessssoo para a determinação do ângulo entre os dois
planos. No entanto, optou-se por uma resolução diferente – recorreu-se a
uma mudança do diedro de projecção, transformando o plano ρ num plano
projectante, o que faz com que o problema passe a ter uma resolução direc-
ta. Assim, substituiu-se o Plano Frontal de Projecção (ppllaannoo 22) por um novo
plano de projecção (ppllaannoo 44) ortogonal ao plano ρ, criando um novo diedro
de projecção – neste, o plano ρ é um plano de topo. O novo eixo XX (o eixo
XX’’) é perpendicular a hhρ e é a recta de intersecção do ppllaannoo 11 com o ppllaannoo
44. O traço do plano ρ no ppllaannoo 44 (ff44ρ) determinou-se a partir da projecção do
traço frontal da recta rr, FF, no ppllaannoo 44 – FF44 determinou-se em função da sua
cota, que se manteve. Uma vez que, no novo diedro de projecção, o plano ρ
é projectante frontal, ff44ρ passa por FF44 e é concorrente com hhρ no eixo XX’’. Tra-
ta-se, agora, de determinar a amplitude do diedro entre um plano de topo e o Plano Horizontal de Projecção, que está contido num plano
frontal (de frente). No novo diedro de projecção, esse plano frontal (de frente) pode ser o próprio ppllaannoo 44. A recta de intersecção do ppllaannoo 44
com o plano ρ é ff44ρ. A V.G. da amplitude do diedro entre o plano ρ e o Plano Horizontal de Projecção está em qualquer dos dois menores
ângulos entre ff44ρ e o eixo XX’’– identificou-se um dos ângulos pelas semi-rectas que limitam o ângulo e assinalando a sua amplitude com αo.
318.

118. 118
SOLUÇÕES
320.
Em primeiro lugar representaram-se os dois planos, pelos seus traços, em
função dos dados. Em seguida, e uma vez que a recta de intersecção dos
dois planos (a aresta do diedro) é uma recta oblíqua, o plano ortogonal à
aresta do diedro nnããoo éé pprroojjeeccttaannttee nneemm tteemm ddeetteerrmmiinnaaççããoo iimmeeddiiaattaa, pelo
que se recorreu ao 22oo PPrroocceessssoo. 11.. Por um ponto PP, qualquer, exterior aos
planos, conduziram-se duas rectas – uma recta pp, ortogonal ao plano γ, e
uma recta pp’’, ortogonal ao plano α. A recta pp é uma recta horizontal (de ní-
vel). 22.. O ângulo entre as rectas pp e pp’’ é o ângulo entre os planos α e γ.
Esse ângulo está contido no plano definido pelas duas rectas, que não é pa-
ralelo a nenhum dos planos de projecção, pelo que o ângulo não se projec-
ta em V.G. em nenhum dos planos de projecção. Assim, rebateu-se o plano
definido por pp e pp’’ para o plano horizontal (de nível) ν, que contém a recta pp
– pp é a charneira (que é a recta de intersecção dos dois planos), pelo que se
tem imediatamente pprr ≡ ee11 ≡ pp11 e PPrr ≡ PP11 (PP é um ponto da charneira). A rec-
ta pp’’ rebateu-se com o recurso a um ponto AA, da recta pp’’ (AA rebateu-se com
o recurso ao seu triângulo do rebatimento, em função da sua cota em rela-
ção a ν – a distância de AA a ν) – pp’’rr está definida por AArr e PPrr. A V.G. do ângu-
lo entre α e γ está em qualquer dos dois ângulos menores entre pprr e pp’’rr,
com vértice em PPrr – identificou-se um dos ângulos pelas semi-rectas que li-
mitam o ângulo e assinalando a sua amplitude com θo
Em primeiro lugar representaram-se os dois planos, pelos seus tra-
ços, em função dos dados. O plano δ tem os seus traços coinci-
dentes, pois é ortogonal ao β2/4. Em seguida, e uma vez que a recta
de intersecção dos dois planos (a aresta do diedro) é uma recta
oblíqua, o plano ortogonal à aresta do diedro nnããoo éé pprroojjeeccttaannttee
nneemm tteemm ddeetteerrmmiinnaaççããoo iimmeeddiiaattaa, pelo que se recorreu ao 22oo PPrroo--
cceessssoo. 11.. Por um ponto PP, qualquer, exterior aos planos, conduzi-
ram-se duas rectas – uma recta pp, ortogonal ao plano α, e uma
recta pp’’, ortogonal ao plano δ. A recta pp é uma recta frontal (de
frente). 22.. O ângulo entre as rectas pp e pp’’ é o ângulo entre os pla-
nos α e δ. Esse ângulo está contido no plano definido pelas duas
rectas, que não é paralelo a nenhum dos planos de projecção, pelo
que o ângulo não se projecta em V.G. em nenhum dos planos de
projecção. Assim, rebateu-se o plano definido por pp e pp’’ para o pla-
no frontal (de frente) ϕ que contém a recta pp – pp é a charneira (que é
a recta de intersecção dos dois planos), pelo que se tem imediata-
mente pprr ≡ ee22 ≡ pp22 e PPrr ≡ PP22 (PP é um ponto da charneira). A recta pp’’
rebateu-se com o recurso a um ponto qualquer da recta – o seu tra-
ço frontal, FF. FF rebateu-se com o recurso ao seu triângulo do rebati-
mento, em função do seu afastamento em relação a ϕ – a distância
de FF a ϕ. A recta pp’’rr está definida por FFrr e PPrr. A V.G. do ângulo entre
α e δ está em qualquer dos dois ângulos menores entre pprr e pp’’rr,
com vértice em PPrr – identificou-se um dos ângulos pelas semi-rectas
que limitam o ângulo e assinalando a sua amplitude com βo.
321.

119. 119
SOLUÇÕES
322.
Em primeiro lugar representaram-se os dois planos, pelos seus traços, em
função dos dados. O plano α, porque é ortogonal ao β1/3, tem os seus traços
simétricos em relação ao eixo XX. Em seguida, e uma vez que a recta de inter-
secção dos dois planos é uma recta oblíqua, o plano ortogonal à aresta do
diedro nnããoo éé pprroojjeeccttaannttee nneemm tteemm ddeetteerrmmiinnaaççããoo iimmeeddiiaattaa, pelo que se re-
correu ao 22oo PPrroocceessssoo. 11.. Por um ponto PP, qualquer, exterior aos planos,
conduziram-se duas rectas – uma recta pp, ortogonal ao plano α, e uma recta
pp’’, ortogonal ao plano δ. 22.. O ângulo entre as rectas pp e pp’’ é o ângulo entre
os planos α e δ. Esse ângulo está contido no plano definido pelas duas rec-
tas, que não é paralelo a nenhum dos planos de projecção, pelo que o ângu-
lo não se projecta em V.G. em nenhum dos planos de projecção. Assim,
rebateu-se o plano definido por pp e pp’’ para um plano frontal (de frente) ϕ.
A charneira é a recta ee, que está definida pelos pontos AA e BB – AA e BB são,
respectivamente, os pontos de intersecção de ϕ com as rectas pp e pp’’. AArr ≡ AA22
e BBrr ≡ BB22, pois AA e BB são dois pontos da charneira. O ponto PP rebateu-se
pelo seu triângulo do rebatimento, em função do seu afastamento em relação
a ϕ (a distância de PP a ϕ). A recta pprr está definida por AArr e PPrr e a recta pp’’rr está
definida por BBrr e PPrr. A V.G. da amplitude do diedro entre α e δ está em qual-
quer dos dois ângulos menores entre pprr e pp’’rr, com vértice em PPrr – identificou-
-se um dos ângulos pelas semi-rectas que limitam o ângulo e assinalando a
sua amplitude com θo.
324.
Em primeiro lugar representaram-se os dois planos, pelos seus traços,
em função dos dados. Em seguida, e uma vez que a recta de intersecção
dos dois planos (a aresta do diedro) é uma recta oblíqua, constatou-se
que o plano ortogonal à aresta do diedro nnããoo éé pprroojjeeccttaannttee nneemm tteemm ddee--
tteerrmmiinnaaççããoo iimmeeddiiaattaa, pelo que se recorreu ao 22oo PPrroocceessssoo. 11.. Por um
ponto PP, qualquer, exterior aos planos, conduziram-se duas rectas – uma
recta aa, ortogonal ao plano ρ, e uma recta bb, ortogonal ao plano θ. A rec-
ta bb é uma recta frontal (de frente). A recta aa é uma recta de perfil, que
está definida por um ponto (o ponto PP) e por uma direcção (é ortogonal
ao plano ρ). 22.. O ângulo entre as rectas aa e bb é o ângulo entre os planos
Em primeiro lugar representaram-se os dois planos, pelos seus
traços, em função dos dados. O plano α, porque é ortogonal ao
β1/3, tem os seus traços simétricos em relação ao eixo XX. O plano
φ, porque é ortogonal ao β2/4, tem os seus traços coincidentes.
Em seguida, e uma vez que a recta de intersecção dos dois pla-
nos (a aresta do diedro) é uma recta oblíqua, o plano ortogonal à
aresta do diedro nnããoo éé pprroojjeeccttaannttee nneemm tteemm ddeetteerrmmiinnaaççããoo
iimmeeddiiaattaa, pelo que se recorreu ao 22oo PPrroocceessssoo – esta situação é,
assim, idêntica à situação do exercício anterior, pelo que se acon-
selha o acompanhamento da resolução gráfica apresentada com
a leitura do relatório do exercício anterior. A recta pp’’, ortogonal ao
plano φ, tem as suas projecções paralelas entre si.
323.
(Continua na página seguinte)

120. 120
SOLUÇÕES
ρ e θ. Esse ângulo está contido no plano definido pelas duas rectas, que não é paralelo a nenhum dos planos de projecção, pelo que o ân-
gulo não se projecta em V.G. em nenhum dos planos de projecção. Assim, rebateu-se o plano definido por aa e bb para o plano frontal (de
frente) ϕ, que contém a recta bb – esta é a charneira (recta ee’’), pelo que se tem imediatamente bbrr ≡ ee’’22 ≡ bb22. Para rebater a recta aa necessita-
mos de um outro ponto da recta, para o que é necessário o recurso a um outro processo geométrico auxiliar. Optou-se pelo rebatimento do
plano π, o plano de perfil que contém a recta aa. A recta aa, porque é ortogonal ao plano ρ, tem de ser ortogonal às rectas de perfil do plano ρ
– a recta ii é a recta de intersecção do plano π com o plano ρ e é uma recta de perfil do plano ρ. A recta ii está definida pelos seus traços nos
planos de projecção (trata-se do caso geral da intersecção entre planos). Rebateu-se o plano π para o Plano Frontal de Projecção – a char-
neira foi ffπ (recta ee). A recta iirr está definida por FFrr e HHrr. A recta aarr passa por PPrr e é perpendicular a iirr – a ortogonalidade entre a recta aa e o
plano ρ já está garantida. Em rebatimento, determinou-se um outro ponto da recta aa – o ponto AA (que é o traço frontal da recta aa). Invertendo
o rebatimento, obtiveram-se as projecções do ponto AA (que é fixo, pois é um ponto da charneira). Para rebater a recta aa (no rebatimento do
plano definido pelas rectas aa e bb) já temos um ponto – PPrr’’ (PPrr’’ é o ponto PP rebatido pelo seu segundo rebatimento – o rebatimento do plano
definido pelas rectas aa e bb). PP é um ponto da charneira (recta ee’’), pelo que se tem imediatamente PPrr’’ ≡ PP22. O ponto AA rebateu-se pelo seu
triângulo do rebatimento, em função do seu afastamento em relação a ϕ (a distância de AA a ϕ) – AArr’’ é o ponto AA rebatido pelo seu segundo
rebatimento (o rebatimento do plano definido pelas rectas aa e bb). A recta aarr’’ está definida por AArr’’ e PPrr (a recta aarr’’ é a recta aa rebatida pelo
seu segundo rebatimento – o rebatimento do plano definido por aa e bb). A V.G. da amplitude do diedro entre ρ e θ está em qualquer dos dois
ângulos menores entre aarr’’ e bbrr, com vértice em PPrr’’ – identificou-se um dos ângulos pelas semi-rectas que limitam o ângulo e assinalando a
sua amplitude com αo.
325.
Em primeiro lugar representaram-se os dois planos,
pelos seus traços, em função dos dados. Os dois
planos, por serem ortogonais ao β1/3, têm os seus
traços simétricos em relação ao eixo XX. Em seguida,
e uma vez que a recta de intersecção dos dois pla-
nos (a aresta do diedro) é oblíqua (é uma recta de
perfil), o plano ortogonal à aresta do diedro nnããoo éé
pprroojjeeccttaannttee nneemm tteemm ddeetteerrmmiinnaaççããoo iimmeeddiiaattaa, pelo
que se recorreu ao 22oo PPrroocceessssoo. 11.. Por um ponto PP,
qualquer, exterior aos planos, conduziram-se duas
rectas – uma recta aa, ortogonal ao plano ρ, e uma
recta bb, ortogonal ao plano α. A recta aa é uma recta
de perfil, que está definida por um ponto (o ponto PP)
e por uma direcção (é ortogonal ao plano ρ). 22.. O ân-
gulo entre as rectas aa e bb é o ângulo entre os planos
α e ρ. Esse ângulo está contido no plano definido
pelas duas rectas, que não é paralelo a nenhum dos
planos de projecção, pelo que o ângulo não se pro-
jecta em V.G. em nenhum dos planos de projecção.
Assim, rebateu-se o plano definido por aa e bb para o
Plano Horizontal de Projecção. A charneira do rebati-
mento (recta ee’’) está definida pelos traços horizontais
das rectas aa e bb. O traço horizontal da recta bb é o
ponto BB, que se determinou imediatamente. O traço
horizontal da recta aa, que é de perfil, não tem deter-
minação imediata – é necessário o recurso a um
outro processo geométrico auxiliar. Optou-se pelo
rebatimento do plano π, o plano de perfil que contém a recta aa. A recta aa, porque é ortogonal ao plano ρ, tem de ser ortogonal às rectas de
perfil do plano ρ – a recta ii é a recta de intersecção do plano π com o plano ρ e é uma recta de perfil do plano ρ. A recta ii está definida pelos
seus traços nos planos de projecção (trata-se do caso geral da intersecção entre planos). Rebateu-se o plano π para o Plano Frontal de Pro-
jecção – a charneira foi ffπ (recta ee). A recta iirr está definida por FFrr e HHrr. A recta aarr passa por PPrr e é perpendicular a iirr – a ortogonalidade entre
a recta aa e o plano ρ já está garantida. Em rebatimento, determinou-se o traço horizontal da recta aa – o ponto AA. Invertendo o rebatimento,
obtiveram-se as projecções do ponto AA. A recta ee’’ (a charneira do rebatimento do plano definido pelas rectas aa e bb) está definida por AA e BB
– AArr’’ ≡ AA11 e BBrr ≡ BB11, pois AA e BB são dois pontos da charneira (AArr’’ é o ponto AA rebatido pelo seu segundo rebatimento – o rebatimento do pla-
no definido pelas rectas aa e bb). Rebateu-se o ponto PP, pelo seu triângulo do rebatimento (em função da sua cota) – PPrr’’ é o ponto PP rebatido
pelo seu segundo rebatimento (o rebatimento do plano definido pelas rectas aa e bb). A recta bbrr está definida por BBrr e por PPrr’’. A recta aarr’’ está
definida por AArr’’ e por PPrr’’ (aarr’’ é a recta aa rebatida pelo seu segundo rebatimento – o rebatimento do plano definido por aa e bb). A V.G. da am-
plitude do diedro entre α e ρ está em qualquer dos dois ângulos menores entre aarr’’ e bbrr, com vértice em PPrr’’ – identificou-se um dos ângulos
pelas semi-rectas que limitam o ângulo e assinalando a sua amplitude com θo.

121. 121
SOLUÇÕES
326.
Em primeiro lugar representaram-se os dois planos, em fun-
ção dos dados – o plano α está definido pelos seus traços e o
plano ρ está definido pelo eixo XX (onde se situam os seus tra-
ços, que estão coincidentes) e pelas projecções do ponto PP.
Em seguida, e uma vez que a recta de intersecção dos dois
planos (a aresta do diedro) é uma recta oblíqua, o plano orto-
gonal à aresta do diedro nnããoo éé pprroojjeeccttaannttee nneemm tteemm ddeetteerrmmii--
nnaaççããoo iimmeeddiiaattaa, pelo que se recorreu ao 22oo PPrroocceessssoo. 11.. Por
um ponto qualquer, conduziram-se duas rectas – uma recta pp,
ortogonal ao plano ρ, e uma recta pp’’, ortogonal ao plano α.
Por uma questão de economia de traçados, optou-se por con-
duzir as duas rectas pelo ponto PP, o ponto que define o plano
passante. A recta pp’’ é uma recta horizontal (de nível). A recta pp
é uma recta de perfil, que está definida por um ponto (o ponto PP)
e por uma direcção (é ortogonal ao plano ρ). 22.. O ângulo
entre as rectas pp e pp’’ é o ângulo entre os planos ρ e α. Esse
ângulo está contido no plano definido pelas duas rectas, que
não é paralelo a nenhum dos planos de projecção, pelo que o
ângulo não se projecta em V.G. em nenhum dos planos de
projecção. Assim, rebateu-se o plano definido por pp e pp’’ para o plano horizontal (de nível) ν, que contém a recta pp’’ – esta é a charneira (rec-
ta ee’’), pelo que se tem imediatamente pp’’rr ≡ ee’’11 ≡ pp’’11. Para rebater a recta pp necessitamos de um outro ponto da recta, para o que é necessá-
rio o recurso a um outro processo geométrico auxiliar. Optou-se pelo rebatimento do plano π, o plano de perfil que contém a recta pp. A recta
pp, porque é ortogonal ao plano ρ, tem de ser ortogonal às rectas de perfil do plano ρ – a recta aa é a recta de intersecção do plano π com o
plano ρ e é uma recta de perfil do plano ρ. A recta aa está definida por dois pontos – o ponto PP (que é um ponto comum aos dois planos) e
pelo seu ponto de concorrência com o eixo XX (a recta aa, porque é uma recta de perfil do plano ρ, é nneecceessssaarriiaammeennttee uma recta de perfil
passante). Rebateu-se o plano π para o Plano Frontal de Projecção – a charneira foi ffπ. A recta aarr está definida por PPrr e pelo seu ponto de
concorrência com o eixo XX, que é fixo (é um ponto da charneira – recta ee). A recta pprr passa por PPrr e é perpendicular a aarr – a ortogonalidade
entre a recta pp e o plano ρ já está garantida. Em rebatimento, determinou-se um outro ponto da recta pp – o ponto FF (que é o traço frontal da
recta pp). Invertendo o rebatimento, obtiveram-se as projecções do ponto FF (que é fixo, pois é um ponto da charneira). Para rebater a recta pp
(no rebatimento do plano definido pelas rectas pp e pp’’) já temos um ponto – PPrr11
(PPrr11
é o ponto PP rebatido pelo seu segundo rebatimento – o
rebatimento do plano definido pelas rectas pp e pp’’). PP é um ponto da charneira (recta ee’’), pelo que se tem imediatamente PPrr11
≡ PP11. O ponto FF
rebateu-se pelo seu triângulo do rebatimento, em função da sua cota em relação a ν (a distância de FF a ν) – FFrr11
é o ponto FF rebatido pelo
seu segundo rebatimento (o rebatimento do plano definido pelas rectas pp e pp’’). A recta pprr11
está definida por FFrr11
e PPrr11
(a recta pprr11
é a recta pp
rebatida pelo seu segundo rebatimento – o rebatimento do plano definido por pp e pp’’). A V.G. da amplitude do diedro entre ρ e α está em
qualquer dos dois ângulos menores entre pprr11
e pp’’rr, com vértice em PPrr11
– identificou-se um dos ângulos pelas semi-rectas que limitam o ân-
gulo e assinalando a sua amplitude com βo
Em primeiro lugar representaram-se os dois planos, pelos seus traços,
em função dos dados. O plano ρ é ortogonal ao β1/3, pelo que os seus
traços são simétricos em relação ao eixo XX. A recta de intersecção dos
dois planos é uma recta fronto-horizontal e o plano que lhe é ortogonal é
projectante (é um plano de perfil) e tem determinação imediata, pelo que
é possível recorrer ao 11oo PPrroocceessssoo para a determinação do ângulo entre
os dois planos. No entanto, optou-se por uma resolução diferente – recor-
reu-se a uma mudança do diedro de projecção, transformando os dois
planos em planos projectantes, o que faz com que o problema passe a
ter uma resolução directa. Assim, substituiu-se o Plano Frontal de Projec-
ção (ppllaannoo 22) por um novo plano de projecção (ppllaannoo 44) ortogonal aos
dois planos, criando um novo diedro de projecção – neste, os dois planos
são planos de topo. O novo eixo XX (o eixo XX’’) é perpendicular aos traços ho-
rizontais dos dois planos. O traço do plano ρ no ppllaannoo 44 (ff44ρ) determinou-se
a partir da projecção de um ponto AA, qualquer, de ffρ, no ppllaannoo 44 – AA44
determinou-se em função da sua cota, que se manteve. Uma vez que, no
novo diedro de projecção, o plano ρ é projectante frontal, ff44ρ passa por AA44
e é concorrente com hhρ no eixo XX’’. De forma idêntica, o traço do plano σ no
ppllaannoo 44 determinou-se com o recurso a um ponto BB, qualquer, de ffσ – BB44
determinou-se em função da sua cota, que se manteve (note que, por
uma questão de economia de traçados, se fez com que os dois pontos –
AA e BB – se situassem na mesma linha de chamada). Tal como o plano ρ,
no novo diedro de projecção o plano σ é projectante frontal, pelo que ff44σ passa por BB44 e é concorrente com hhσ no eixo XX’’. Trata-se, agora,
de determinar o ângulo entre dois planos de topo, que está contido num plano frontal (de frente) – no novo diedro de projecção, esse plano
frontal (de frente) pode ser o próprio ppllaannoo 44. As rectas de intersecção do ppllaannoo 44 com os planos ρ e σ são, respectivamente, ff44ρ e ff44σ – o
ângulo entre ff44ρ e ff44σ está em V.G. no ppllaannoo 44 e identificou-se com αo.
327.

122. 122
SOLUÇÕES
328.
Em primeiro lugar representou-se o plano δ, pelos seus
traços, em função dos dados. O β1/3 é um plano que não
carece de representação (embora se trate de um plano
passante, cujos traços estão coincidentes no eixo XX). Em
seguida, e uma vez que a recta de intersecção dos dois
planos (a aresta do diedro) é uma recta oblíqua, o plano
ortogonal à aresta do diedro nnããoo éé pprroojjeeccttaannttee nneemm tteemm
ddeetteerrmmiinnaaççããoo iimmeeddiiaattaa, pelo que se recorreu ao 22oo PPrroo--
cceessssoo. 11.. Por um ponto PP, qualquer, exterior aos planos,
conduziram-se duas rectas – uma recta aa, ortogonal ao
β1/3, e uma recta bb, ortogonal ao plano δ. A recta aa é uma
recta de perfil, que está definida por um ponto (o ponto PP)
e por uma direcção (é ortogonal ao β1/3). 22.. O ângulo en-
tre as rectas aa e bb é o ângulo entre o plano δ e o β1/3.
Esse ângulo está contido no plano definido pelas duas
rectas, que não é paralelo a nenhum dos planos de pro-
jecção, pelo que o ângulo não se projecta em V.G. em ne-
nhum dos planos de projecção. Assim, rebateu-se o
plano definido por aa e bb para o Plano Horizontal de Pro-
jecção. A charneira do rebatimento (recta ee’’) está definida
pelos traços horizontais das rectas aa e bb. O traço horizon-
tal da recta bb é o ponto BB, que se determinou imediata-
mente. O traço horizontal da recta aa, que é de perfil, não
tem determinação imediata – é necessário o recurso a um
outro processo geométrico auxiliar. Optou-se pelo rebatimento do plano π, o plano de perfil que contém a recta aa. A recta aa, porque é orto-
gonal ao β1/3, tem de ser ortogonal às rectas de perfil do β1/3 – a recta ii é a recta de intersecção do plano π com o β1/3 e é uma recta de perfil
do β1/3 (é uma recta de perfil passante que faz ângulos de 45o com os dois planos de projecção). A recta ii está definida por um ponto (o seu
ponto de concorrência com o eixo XX) e pela sua direcção (faz ângulos de 45o com os planos de projecção). Rebateu-se o plano π para o
Plano Frontal de Projecção – a charneira foi ffπ (recta ee). A recta iirr passa pelo seu ponto de concorrência com o eixo XX (que é fixo, pois é um
ponto da charneira) e faz ângulos de 45o com ffπrr
e com hhπrr
(note que a recta ii atravessa os 1o e 3o Diedros, pelo que a recta iirr tem de passar
pelo quadrante no qual se situa PPrr – PP é um ponto do 1o Diedro). A recta aarr passa por PPrr e é perpendicular a iirr – a ortogonalidade entre
a recta aa e o β1/3 já está garantida. Em rebatimento, determinou-se o traço horizontal da recta aa – o ponto AA. Invertendo o rebatimento,
obtiveram-se as projecções do ponto AA. A recta ee’’ (a charneira do rebatimento do plano definido pelas rectas aa e bb) está definida por AA e BB
– AArr’’ ≡ AA11 e BBrr ≡ BB11, pois AA e BB são dois pontos da charneira (AArr’’ é o ponto AA rebatido pelo seu segundo rebatimento – o rebatimento do plano
definido pelas rectas aa e bb). Rebateu-se o ponto PP, pelo seu triângulo do rebatimento (em função da sua cota) – PPrr’’ é o ponto PP rebatido
pelo seu segundo rebatimento (o rebatimento do plano definido pelas rectas aa e bb). A recta bbrr está definida por BBrr e por PPrr’’. A recta aarr’’ está
definida por AArr’’ e por PPrr’’ (aarr’’ é a recta aa rebatida pelo seu segundo rebatimento – o rebatimento do plano definido por aa e bb). A V.G. da am-
plitude do diedro entre o plano δ e o β1/3 está em qualquer dos dois ângulos menores entre aarr’’ e bbrr, com vértice em PPrr’’ – identificou-se um
dos ângulos pelas semi-rectas que limitam o ângulo e assinalando a sua amplitude com θo.
329.
Em primeiro lugar representou-se o plano δ, pelos seus traços, em fun-
ção dos dados. O β2/4 é um plano que não carece de representação (em-
bora se trate de um plano passante, cujos traços estão coincidentes no
eixo XX). Em seguida, e uma vez que a recta de intersecção dos dois pla-
nos (a aresta do diedro) é uma recta oblíqua, o plano ortogonal à aresta
do diedro nnããoo éé pprroojjeeccttaannttee nneemm tteemm ddeetteerrmmiinnaaççããoo iimmeeddiiaattaa, pelo que
se recorreu ao 22oo PPrroocceessssoo. 11.. Por um ponto PP, qualquer, exterior aos
planos, conduziram-se duas rectas – uma recta aa, ortogonal ao β2/4,
e uma recta bb, ortogonal ao plano δ. A recta aa é uma recta de perfil, que
está definida por um ponto (o ponto PP) e por uma direcção (é ortogonal
ao β2/4). 22.. O ângulo entre as rectas aa e bb é o ângulo entre o plano δ e o
β2/4. Esse ângulo está contido no plano definido pelas duas rectas, que
não é paralelo a nenhum dos planos de projecção, pelo que o ângulo
não se projecta em V.G. em nenhum dos planos de projecção. Assim, re-
bateu-se o plano definido por aa e bb para um plano horizontal (de nível) ν
qualquer. A charneira do rebatimento (recta ee’’) está definida pelos pontos
de intersecção do plano ν com as rectas aa e bb – AA e BB, respectivamente.
O ponto BB teve determinação imediata, ao contrário do ponto AA, uma vez
que as projecções da recta aa não verificam o Critério de Reversibilidade.
Para determinar a projecção horizontal do ponto AA é necessário o recur-
so a um outro processo geométrico auxiliar. Optou-se pelo rebatimento
do plano π, o plano de perfil que contém a recta aa. A recta aa, porque é
(Continua na página seguinte)

123. 123
SOLUÇÕES
330.
Em primeiro lugar representou-se o plano ρ, pelo eixo XX (com o qual os seus tra-
ços estão coincidentes) e pelas projecções do ponto PP, em função dos dados.
O β1/3 é um plano que não carece de representação (embora se trate de um outro
plano passante, cujos traços estão também coincidentes com o eixo XX). Em segui-
da, e uma vez que a recta de intersecção dos dois planos (a aresta do diedro) é
uma recta fronto-horizontal (é o próprio eixo XX), o plano ortogonal à aresta do die-
dro é projectante (é um plano de perfil) e tem determinação imediata, pelo que se
recorreu ao 11oo PPrroocceessssoo. 11.. A aresta do diedro já está identificada – é uma recta
fronto-horizontal (é o próprio eixo XX). 22.. Recorreu-se a um plano auxiliar, ortogonal à
aresta do diedro – o plano π (é um plano de perfil). Por uma questão de economia
de traçados, optou-se por conduzir o plano π pelo ponto PP. 33.. Determinaram-se as
rectas de intersecção do plano π (o plano auxiliar) com os dois planos – a recta aa
(é uma recta de perfil do plano ρ) e a recta bb (é uma recta de perfil do β1/3). A recta
aa é uma recta de perfil passante – está definida pelo seu ponto de concorrência
com o eixo XX e pelo ponto PP (que é um ponto comum ao plano π e ao plano ρ). A
recta bb é outra recta de perfil passante – está definida pelo seu ponto de concor-
rência com o eixo XX e pela sua direcção (faz ângulos de 45o com os dois planos de projecção). 44.. O ângulo entre as duas rectas é o ângulo en-
tre os dois planos. O ângulo entre aa e bb está contido no plano de perfil π, pelo que não se projecta em V.G. em nenhum dos planos de
projecção. Assim, recorreu-se ao rebatimento do plano π para o Plano Horizontal de Projecção – a charneira foi hhπ. A recta aarr fica definida pelo
seu ponto de concorrência com o eixo XX (que é fixo, pois é um ponto da charneira) e por PPrr. A recta bbrr fica definida pelo seu ponto de concor-
rência com o eixo XX (que é fixo, pois é um ponto da charneira) e faz ângulos de 45° com ffπrr
e com hhπrr
(note que a recta bb atravessa os 1o e
3o Diedros, pelo que a recta bbrr tem de passar pelo quadrante no qual se situa PPrr – PP é um ponto do 1o Diedro). A V.G. da amplitude do diedro
entre o plano ρ e o β1/3 está em qualquer dos dois ângulos menores entre aarr e bbrr – identificou-se um dos ângulos pelas semi-rectas que limitam
o ângulo e assinalando a sua amplitude com αo.
ortogonal ao β2/4, tem de ser ortogonal às rectas de perfil do β2/4 – a recta pp é a recta de intersecção do plano π com o β2/4 e é uma recta de
perfil do β2/4 (é uma recta de perfil passante que faz ângulos de 45° com os dois planos de projecção). A recta pp está definida por um ponto
(o seu ponto de concorrência com o eixo XX) e pela sua direcção (faz ângulos de 45° com os planos de projecção). Rebateu-se o plano π
para o Plano Frontal de Projecção – a charneira foi ffπ. A recta pprr passa pelo seu ponto de concorrência com o eixo XX (que é fixo, pois é um
ponto da charneira) e faz ângulos de 45o com ffπrr
e com hhπrr
(note que a recta pp atravessa os 2o e 4o Diedros, pelo que a recta pprr não pode
passar pelo quadrante no qual se situa PPrr – PP é um ponto do 1o Diedro). A recta aarr passa por PPrr e é perpendicular a pprr – a ortogonalidade
entre a recta aa e o β2/4 já está garantida. Em rebatimento, e a partir da projecção frontal de AA, determinou-se AArr – por casualidade, AA é o pró-
prio traço frontal da recta aa. Invertendo o rebatimento, obtiveram-se as projecções do ponto AA (que é fixo, pois é um ponto da charneira).
A recta ee’’ (a charneira do rebatimento do plano definido pelas rectas aa e bb) está definida por AA e BB – AArr11
≡ AA11 e BBrr ≡ BB11, pois AA e BB são dois
pontos da charneira (AArr11
é o ponto AA rebatido pelo seu segundo rebatimento – o rebatimento do plano definido pelas rectas aa e bb). Rebateu-
-se o ponto PP, pelo seu triângulo do rebatimento (em função da sua cota em relação a ν – a distância de PP a ν) – PPrr11
é o ponto PP rebatido
pelo seu segundo rebatimento (o rebatimento do plano definido pelas rectas aa e bb). A recta bbrr está definida por BBrr e por PPrr11
. A recta aarr11
está
definida por AArr11
e por PPrr11
(aarr11
é a recta aa rebatida pelo seu segundo rebatimento – o rebatimento do plano definido por aa e bb). A V.G. da am-
plitude do diedro entre o plano δ e o β2/4 está em qualquer dos dois ângulos menores entre aarr11
e bbrr, com vértice em PPrr11
– identificou-se um
dos ângulos pelas semi-rectas que limitam o ângulo e assinalando a sua amplitude com θ°.
(Continua na página seguinte)
Em primeiro lugar representou-se o plano α, indicando os seus tra-
ços (que estão coincidentes com o eixo XX) e determinando as pro-
jecções do ponto MM, e o ponto PP, pelas suas projecções. O ponto PP,
porque pertence ao β2/4, tem as suas coordenadas simétricas e as
suas projecções coincidentes. Em seguida, procedeu-se à execução
sequencial das etapas do mmééttooddoo ggeerraall ppaarraa aa ddeetteerrmmiinnaaççããoo ddaa
ddiissttâânncciiaa ddee uumm ppoonnttoo aa uumm ppllaannoo. 11.. Por PP conduziu-se uma recta
pp, ortogonal ao plano α – a recta pp é uma recta de perfil. 22.. Determi-
nou-se o ponto II, o ponto de intersecção da recta pp com o plano α.
Para resolver esta etapa recorreu-se a uma mudança do diedro de
projecção. Assim, optou-se por transformar o plano α num plano de
topo, para o que se substituiu o Plano Frontal de Projecção (ppllaannoo
22) por um outro plano de projecção (ppllaannoo 44), ortogonal ao plano α.
Manteve-se o Plano Horizontal de Projecção, pelo que se mantive-
ram as projecções horizontais, o traço horizontal do plano α e as co-
tas. O novo eixo XX (o eixo XX’’) é a recta de intersecção do ppllaannoo 11
com o ppllaannoo 44 e é perpendicular a hhα. Para determinar o traço do
plano α no ppllaannoo 44 recorreu-se ao ponto MM, que é o ponto que define
o plano. MM44 é a projecção de MM no ppllaannoo 44 e determinou-se em fun-
ção da sua cota, que se manteve. O traço do plano α no ppllaannoo 44 (ff44α
)
passa por MM44 (no novo diedro de projecção, o plano α é projectante
331.

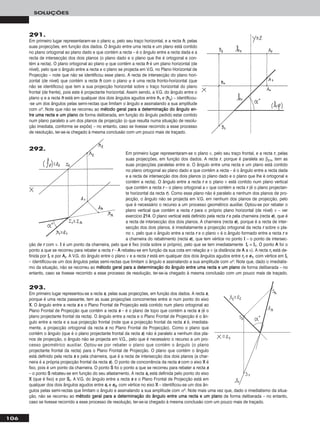
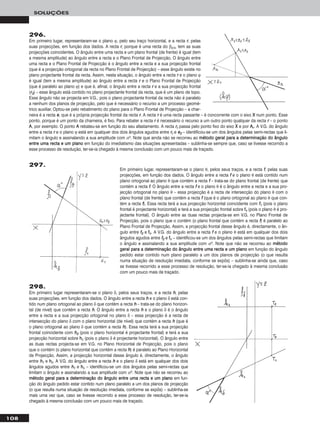
124. 124
SOLUÇÕES
frontal) e é concorrente com hhα no eixo XX’’. PP44 é a projecção de PP no ppllaannoo 44 e determinou-se, tal como MM44, em função da sua cota, que se
manteve (e que é negativa). No novo diedro de projecção (formado pelo ppllaannoo 11 e pelo ppllaannoo 44), o plano α é um plano de topo e a recta pp
(a recta ortogonal ao plano α que passa por PP) é uma recta frontal (note que o eixo XX é paralelo a pp11) com afastamento negativo (em função
da localização escolhida para o eixo XX’’, que se poderia ter localizado de forma a garantir que o afastamento da recta pp fosse positivo). As-
sim, por PP44 conduziu-se pp44, perpendicular a ff44α
– pp44 é a projecção da recta pp no ppllaannoo 44. O ponto II (o ponto de intersecção da recta pp com
o plano α) teve determinação directa, no novo diedro de projecção, a partir da sua projecção no ppllaannoo 44 – II44 é a projecção de II no ppllaannoo 44
e II11 determinou-se directamente. O exposto refere-se apenas à segunda etapa da determinação da distância do ponto PP ao plano α. 33.. A
distância de PP ao plano α é o comprimento do segmento de recta [PPII] – no diedro de projecção formado entre o ppllaannoo 11 e o ppllaannoo 44, o
segmento [PPII] é frontal (de frente), pelo que a V.G. da distância é PPෆ44ෆIIෆ44ෆ. A projecção frontal de II (no diedro de projecção inicial) determinou-
-se em função da sua cota, o que nos permitiu determinar as projecções do segmento [PPII] no diedro de projecção inicial – [PPII] é o segmento
representativo da distância de PP ao plano α.
332.
Em primeiro lugar representaram-se o ponto PP e a recta
rr, pelas respectivas projecções, em função dos dados.
Note que a recta rr, de perfil, está definida por um ponto
(o ponto AA) e pela sua direcção (é ortogonal ao β1/3, o
bissector dos diedros ímpares). Este problema é seme-
lhante ao do exercício 227711, pelo que se aconselha o
acompanhamento da resolução apresentada com a leitu-
ra do relatório daquele exercício. Note que a recta rrrr, a
recta rr em rebatimento, é perpendicular à recta iirr – a rec-
ta ii é a recta de intersecção do plano π (o plano de perfil
que contém a recta rr) com o β1/3 (a recta ii é uma recta de
perfil do β1/3). Trata-se portanto, de determinar uma recta
de perfil ortogonal ao β1/3, o que redunda numa situação
semelhante à do exercício 8855 (no qual era pedida uma
recta ortogonal ao β2/4), pelo que se aconselha a leitura
do respectivo relatório.
Em primeiro lugar representaram-se as rectas rr e ss, pelas respectivas
projecções. As projecções da recta rr fazem, com o eixo XX, ângulos
iguais e com o mesmo sentido de abertura, pois é uma recta paralela
ao β1/3. Note que esta situação (distância entre duas rectas paralelas),
não se tratando de um conteúdo do programa da disciplina, redunda,
no entanto, na ddiissttâânncciiaa ddee uumm ppoonnttoo aa uummaa rreeccttaa, pois a distância
entre duas rectas é a distância de qualquer ponto de uma das rectas à
outra recta (todos os pontos das duas rectas estão equidistantes da
outra recta). Assim, a distância entre duas rectas paralelas mede-se ne-
cessariamente numa recta perpendicular a ambas – tendo em conta
que as rectas são oblíquas (não são paralelas a nenhum dos planos de
projecção) pelo que a perpendicularidade não é directa, à semelhança
da situação do exercício 226655, é necessário resolver o exercício em
dduuaass ddiimmeennssõõeess, neste caso no ppllaannoo ddeeffiinniiddoo ppeellaass dduuaass rreeccttaass.
Para tal, é necessário rebater o plano definido pelas duas rectas para,
em rebatimento, se conduzir uma perpendicular às rectas. Rebateu-se
o plano definido pelas duas rectas (que é um plano de rampa) para o
Plano Horizontal de Projecção – a charneira do rebatimento (recta ee) está
definida pelos traços horizontais das duas rectas. HHrr ≡ HH11 e HH’’rr ≡ HH’’11,
pois HH e HH’’ são dois pontos da charneira. Já temos um ponto para defi-
333.
(Continua na página seguinte)

125. 125
SOLUÇÕES
334.
Em primeiro lugar representaram-se as rectas hh e pp pelas
respectivas projecções, em função dos dados. Note que
os dados nos permitiram, apenas, desenhar hh22, a projec-
ção frontal da recta hh. Uma vez que as rectas são concor-
rentes (é dado no enunciado), é possível determinar, de
forma directa, a projecção frontal do ponto de concorrên-
cia das duas rectas (o ponto BB), mas não a sua projecção
horizontal. Para tal recorreu-se ao rebatimento da recta pp,
pelo rebatimento do plano π, o plano de perfil que a con-
tém. A recta pprr está definida por FFrr e por HHrr. A partir de BB22
determinou-se BBrr, sobre pprr – invertendo o rebatimento, de-
terminou-se BB11, o que nos permitiu desenhar hh11, passando
por AA11 e por BB11. As rectas pp e hh são concorrentes (no pon-
to BB), pelo que definem um plano – o ângulo entre as duas
rectas eessttáá ccoonnttiiddoo nnoo ppllaannoo ddeeffiinniiddoo ppeellaass dduuaass rreeccttaass
e tem vértice em BB. Uma vez que o plano definido pelas
duas rectas não é paralelo a nenhum dos planos de pro-
jecção, para determinar a V.G. do ângulo entre as duas
rectas é necessário o recurso a um processo geométrico
auxiliar. Por uma questão de economia de traçados, optou-
-se por rebater o plano definido pelas duas rectas para o
plano horizontal (de nível) ν que contém a recta hh – a char-
neira do rebatimento (recta ee’’) é a recta de intersecção dos
dois planos, pelo que é a própria recta hh. Assim sendo, a
recta hh roda sobre si própria, pelo que se tem imediata-
mente hhrr ≡ ee’’11 ≡ hh11. BBrr’’ ≡ BB11 pois BB é um ponto da charnei-
ra (BBrr’’ é o ponto BB rebatido pelo seu segundo rebatimento
– pelo rebatimento do plano definido por pp e hh). Para reba-
ter a recta pp é necessário o recurso a um ponto qualquer
da recta – o seu traço horizontal, por exemplo. HH rebateu-
-se pelo triângulo do rebatimento, em função da sua distância a ν (a cota de HH em relação a ν). A recta pprr’’ está definida por BBrr’’ e HHrr’’ – HHrr’’ e pprr’’
são, respectivamente, o traço horizontal da recta pp e a própria recta pp, rebatidos no seu segundo rebatimento (o rebatimento do plano definido
pelas rectas hh e pp). A V.G. do ângulo entre as rectas pp e hh está em qualquer dos dois ângulos agudos entre pprr’’ e hhrr, com vértice em BBrr’’ – identi-
ficou-se um dos ângulos pelas semi-rectas que limitam o ângulo e assinalando a sua amplitude com αo.
nir cada uma das rectas em rebatimento. Para rebater a recta rr, por exemplo, é necessário o recurso a um outro ponto da recta – o ponto AA, por
exemplo. AA rebateu-se pelo triângulo do rebatimento, em função da sua cota. A recta rrrr passa por HH’’rr e por AArr (está definida por dois pontos).
A recta ssrr está definida por um ponto (HHrr) e por uma direcção (é paralela a rrrr, pois o paralelismo verifica-se no espaço, em projecções e em re-
batimento). Em rebatimento, conduziu-se uma perpendicular qualquer às rectas rebatidas – pprr – e determinaram-se os pontos de intersecção
desta com as rectas rebatidas – RRrr e SSrr. O comprimento do segmento de recta [RRrrSSrr] é a V.G. da distância entre as duas rectas. Invertendo o re-
batimento, conduzindo, por RRrr e SSrr, as perpendiculares à charneira que por eles passam (e que correspondem aos planos ortogonais à char-
neira que contêm os respectivos arcos do rebatimento) determinaram-se as projecções dos pontos RR e SS (sobre as projecções homónimas
das rectas rr e ss, respectivamente), bem como as projecções da recta pp (a perpendicular às duas rectas) e as projecções do segmento repre-
sentativo da distância (o segmento [RRSS]).
335. RReessoolluuççããoo
(Continua na página seguinte)

126. 126
SOLUÇÕES
336.
Em primeiro lugar representou-se a recta rr, pelas
suas projecções, em função dos dados. Em segui-
da, determinaram-se os traços dos planos α e β.
O traço horizontal do plano α, hhα passa por HH (o
traço horizontal da recta rr) e é perpendicular a rr11,
pois a recta rr é uma recta de maior declive do pla-
no α. O traço frontal do plano α, ffα, é concorrente
com hhα no eixo XX e passa por FF, o traço frontal da
recta rr. O traço frontal do plano β, ffβ passa por FF
(o traço frontal da recta rr) e é perpendicular a rr22,
pois a recta rr é uma recta de maior inclinação do
plano β. O traço horizontal do plano β, hhβ, é con-
corrente com ffβ no eixo XX e passa por HH, o traço
horizontal da recta rr. Em seguida, e uma vez que a
recta de intersecção dos dois planos é uma recta
oblíqua (é a própria recta rr), o plano ortogonal à
aresta do diedro nnããoo éé pprroojjeeccttaannttee nneemm tteemm ddee--
tteerrmmiinnaaççããoo iimmeeddiiaattaa, pelo que se recorreu ao
22oo PPrroocceessssoo – esta situação é, assim, idêntica à si-
tuação do exercício 332222, pelo que se aconselha o
acompanhamento da resolução gráfica apresenta-
da com a leitura do relatório daquele exercício.
337.
Em primeiro lugar representaram-se os dois planos, pelos
seus traços, em função dos dados. O plano β, porque é orto-
gonal ao β1/3, tem os seus traços simétricos em relação ao
eixo XX. O plano α, porque é ortogonal ao β2/4, tem os seus tra-
ços coincidentes. Note que a situação deste exercício é idênti-
ca à situação do exercício 332233, pelo que se aconselha o
acompanhamento da resolução gráfica apresentada com a lei-
tura do relatório daquele exercício.
Em primeiro lugar representou-se o plano β, pelos seus traços, bem como a recta rr, pelas suas projecções, em função dos dados. O plano β
tem os seus traços coincidentes, pois é ortogonal ao β2/4. A recta rr pertence ao plano β, pois tem os seus traços sobre os traços homónimos do
plano β. O ângulo entre a recta rr e o traço frontal de β está contido no próprio plano β (o ângulo entre duas rectas concorrentes está contido no
plano definido pelas duas rectas que, nesta situação, é o próprio plano β, pois ffβ e rr são duas rectas de β). O plano β não é paralelo a nenhum
dos planos de projecção, pelo que o ângulo não se projecta em V.G. em nenhum dos planos de projecção – é necessário o recurso a um pro-
cesso geométrico auxiliar. Por uma questão de economia de traçados, optou-se pelo rebatimento do plano β para o Plano Frontal de Projec-
ção – a charneira é ffβ, que é fixo, pois roda sobre si próprio. FFrr ≡ FF22, pois FF é um ponto da charneira. A recta rr rebateu-se a partir do seu
traço horizontal, HH – este rebateu-se pelo seu triângulo do rebatimento, e em função do seu afastamento. A V.G. do ângulo entre as rectas rr
e ffβ está em qualquer dos dois ângulos agudos entre rrrr e ffβrr
, com vértice em FFrr – identificou-se um dos ângulos pelas semi-rectas que limi-
tam o ângulo e assinalando a sua amplitude com αo.
335. RReellaattóórriioo

127. 127
SOLUÇÕES
338.
Em primeiro lugar representou-se o plano α, pelos seus traços, e os
pontos AA e CC, pelas suas projecções e pertencentes ao plano, em
função dos dados. O plano α é ortogonal ao β1/3, pelo que os seus
traços são simétricos em relação ao eixo XX. AA é um ponto de hhα,
que é uma recta horizontal (de nível) do plano com cota nula. AA e CC
situam-se no mesmo plano de perfil (situam-se na mesma recta de
perfil), pelo que têm a mesma abcissa e CC é um ponto de ffα, que é
uma recta frontal (de frente) do plano com afastamento nulo. Uma
vez que o quadrado [AABBCCDD] não se projecta em V.G. em nenhum
dos planos de projecção, para construir as suas projecções da
base da pirâmide, rebateu-se o plano α para o Plano Horizontal de
Projecção – a charneira foi hhα e tem-se imediatamente AArr ≡ AA11. Note
que, em termos de economia de traçados, seria indistinto o rebati-
mento para qualquer dos dois planos de projecção, pois o ponto CC
é um ponto do Plano Frontal de Projecção. O ponto CC foi o ponto
que nos permitiu rebater ffα. Em rebatimento, construiu-se o quadra-
do [AABBCCDD] em V.G. e determinou-se OOrr, o centro do quadrado em
rebatimento. Inverteu-se o rebatimento, com o recurso a rectas
frontais (de frente) do plano, obtendo-se as projecções de BB e DD
(ver exercício 118800) – note que se omitiram as notações referentes às
rectas frontais (de frente) que nos permitiram inverter o rebatimento
de BBrr e DDrr, com vista a não sobrecarregar visualmente a resolução
gráfica apresentada. A partir das projecções dos quatro vértices do
quadrado, desenharam-se as suas projecções (a traço leve, pois trata-se de um traçado auxiliar para o objectivo do exercício, que é as projecções
do sólido). As projecções de OO determinaram-se directamente a partir do desenho das projecções das diagonais do quadrado. Em seguida,
pelas projecções de OO conduziram-se as projecções homónimas de uma recta pp, ortogonal a α – a recta pp é a recta suporte do eixo da pirâmide.
Note que a recta pp é uma recta passante nesta situação particular. O vértice VV, da pirâmide, situa-se sobre pp, a 6 cm de OO. Como a recta pp é
oblíqua aos dois planos de projecção, o segmento [OOVV] não se projecta em V.G. em nenhum dos planos de projecção, pelo que é necessário o
recurso a um processo geométrico auxiliar. Optou-se por rebater o plano projectante horizontal da recta pp (o plano γ) para o Plano Horizontal de
Projecção – a charneira foi hhγ (recta ee’’). A recta pp rebateu-se com o recurso a dois dos seus pontos – o ponto OO e o seu ponto de concorrência
com o eixo XX (que é um ponto fixo, pois situa-se na charneira). A recta pprr fica definida por OOrr11
e pelo seu ponto de concorrência com o eixo XX
(note que OOrr11
é o ponto OO no seu segundo rebatimento – no rebatimento do plano γ). Sobre pprr, a partir de OOrr11
, mediram-se os 6 cm (a altura da
pirâmide), obtendo-se VVrr (garantindo que VV se situa no 1o Diedro). Inverteu-se o rebatimento de γ, obtendo-se as projecções de VV sobre as pro-
jecções homónimas da recta pp. A partir das projecções de todos os vértices do sólido, desenharam-se os seus contornos aparentes – o ccoonn--
ttoorrnnoo aappaarreennttee ffrroonnttaall é [AA22BB22VV22CC22DD22] e o ccoonnttoorrnnoo aappaarreennttee hhoorriizzoonnttaall é [AA11VV11BB11CC11DD11]. Em pprroojjeeccççããoo ffrroonnttaall, todos os vértices integram o
contorno aparente frontal. No entanto, a base do sólido é invisível, bem como a face lateral [BBCCVV] pelo que a aresta [BBCC] da base é a única
aresta invisível em projecção frontal (as restantes arestas são todas visíveis). Também em pprroojjeeccççããoo hhoorriizzoonnttaall se tem que todos os vértices
integram o contorno aparente horizontal. Também nesta projecção a base do sólido é invisível, bem como a face lateral [AABBVV] pelo que a
aresta [AABB] da base é a única aresta invisível em projecção horizontal (as restantes arestas são todas visíveis).
339.
Em primeiro lugar representou-se o plano δ, pelos seus traços, e o ponto OO, pelas suas projecções e pertencente ao plano, em função dos da-
dos. A recta hh, horizontal (de nível), pertencente ao plano e com 2 cm de cota, foi a recta auxiliar a que se recorreu para determinar as projec-
ções do ponto OO. O plano δ não é paralelo a nenhum dos planos de projecção, pelo que o pentágono não se projecta em V.G. em nenhum dos
planos de projecção – é necessário o recurso a um processo geométrico auxiliar. Optou-se por rebater o plano δ para o Plano Horizontal de
Projecção (a charneira é hhδ – hhδ ≡ ee11 ≡ hhδrr
). Para rebater o plano δ há que rebater o seu traço frontal, o que se processa rebatendo um dos seus
pontos – o ponto FF (traço frontal da recta hh), por exemplo. Para tal conduziu-se, por FF11, uma perpendicular à charneira (que corresponde ao
plano ortogonal à charneira que contém o arco do seu rebatimento). Os traços do plano δ são concorrentes num ponto fixo (um ponto do eixo
XX, que é um ponto da charneira). Com o recurso ao compasso, fazendo centro nesse ponto e raio até FF22, transportou-se essa distância até à
perpendicular à charneira que passa por FF11 e obteve-se FFrr – ffδrr
passa por FFrr e é concorrente com hhδrr
no eixo XX. A recta hhrr passa por FFrr e é para-
lela a hhδrr
(rectas horizontais de um plano são paralelas entre si e paralelas ao traço horizontal do plano, no espaço, em projecções e em rebati-
mento). Por OO11 conduziu-se uma perpendicular à charneira (que corresponde ao plano ortogonal à charneira que contém o arco do seu
rebatimento) e determinou-se OOrr sobre hhrr. Uma vez que a circunferência circunscrita ao pentágono é tangente a hhδ, com centro em OOrr dese-
nhou-se uma circunferência tangente a hhδrr
– o vértice AA do polígono, porque tem cota nula, é o ponto de tangência da circunferência com hhδrr
.
Em seguida, construiu-se o pentágono em V.G., em rebatimento. Para determinar as projecções do pentágono inverteu-se o rebatimento. AA é
um ponto da charneira, pelo que se tem imediatamente AArr ≡ AA11 – AA22 situa-se no eixo XX. A inversão do rebatimento dos pontos BB, CC, DD e EE
REPRESENTAÇÃO DE SÓLIDOS III
18
(Continua na página seguinte)

128. 128
SOLUÇÕES
processou-se com o recurso às rectas horizontais (de nível)
do plano que por eles passam, obtendo-se as suas projec-
ções (ver exercício 118822 e respectivo relatório) – note que se
omitiram as notações referentes às rectas horizontais (de ní-
vel) que nos permitiram inverter o rebatimento dos pontos,
com vista a não sobrecarregar visualmente a resolução gráfi-
ca apresentada. A partir das projecções dos cinco pontos,
desenharam-se as projecções do pentágono (a traço leve,
pois trata-se de um traçado auxiliar para o objectivo do exer-
cício, que é as projecções do sólido). Em seguida, pelas pro-
jecções de OO conduziram-se as projecções homónimas de
uma recta pp, ortogonal a δ – a recta pp é a recta suporte do
eixo da pirâmide. O vértice VV, da pirâmide, situa-se sobre pp,
a 8 cm (a altura da pirâmide) de OO. Como a recta pp é oblíqua
aos dois planos de projecção, o segmento [OOVV] não se pro-
jecta em V.G. em nenhum dos planos de projecção, pelo que
é necessário o recurso a um processo geométrico auxiliar.
Optou-se por rebater o plano projectante frontal da recta pp
(o plano γ) para o Plano Frontal de Projecção – a charneira foi
ffγ (recta ee’’). A recta pp rebateu-se com o recurso a dois dos
seus pontos – o ponto OO e o seu traço horizontal, HH. A recta pprr
fica definida por OOrr11
(OOrr11
é o ponto OO no seu segundo rebati-
mento – o rebatimento do plano γ) e por HHrr. Sobre pprr, a partir
de OOrr11
, mediram-se os 8 cm (a altura da pirâmide), obtendo-
se VVrr (garantindo que VV se situa no 1o Diedro). Inverteu-se o
rebatimento de γ, obtendo-se as projecções de VV sobre as
projecções homónimas da recta pp. A partir das projecções de
todos os vértices do sólido, desenharam-se os seus contor-
nos aparentes – o ccoonnttoorrnnoo aappaarreennttee ffrroonnttaall é [AA22VV22DD22EE22] e
o ccoonnttoorrnnoo aappaarreennttee hhoorriizzoonnttaall é [BB11VV11EE11DD11CC11]. Em pprroojjeecc--
ççããoo ffrroonnttaall, há dois vértices que não integram o contorno
aparente – CC e DD. Estes são os vértices de menor afastamento
do sólido, pelo que são invisíveis (bem como todas as ares-
tas que neles convergem). A base do sólido é invisível, bem
como as faces laterais [AABBVV], [BBCCVV] e [CCDDVV]. A aresta lateral [EEVV] é visível, pois separa duas faces visíveis em projecção frontal – as faces late-
rais [AAEEVV] e [DDEEVV]. Em pprroojjeeccççããoo hhoorriizzoonnttaall, o vértice AA é o único vértice que não integra o contorno aparente horizontal – este é invisível (por
ser o vértice de menor cota), bem como todas as arestas que nele convergem. Em projecção horizontal, a base do sólido é invisível, tal como
as faces laterais [AABBVV] e [AAEEVV]. As restantes faces laterais são visíveis, bem como as restantes arestas.
340.
Em primeiro lugar representaram-se os pontos AA e BB, pelas respectivas pro-
jecções, em função dos dados. O ponto AA é um ponto do Plano Frontal de
Projecção (AA tem afastamento nulo), pelo que é um ponto de ffα. O ponto BB é
um ponto do Plano Horizontal de Projecção (BB tem cota nula), pelo que é um
ponto de hhα. O plano α é ortogonal ao β2/4, pelo que tem os seus traços coinci-
dentes – estes estão coincidentes na recta que passa por AA22 e por BB11. O triân-
gulo [AABBCC] não se projecta em V.G. em nenhum dos planos de projecção
(o plano que o contém – o plano α – é oblíquo a ambos os planos de projec-
ção), pelo que é necessário o recurso a um processo geométrico auxiliar. Em
termos de economia de traçados, é indistinto o plano de projecção para o
qual se processe o rebatimento do plano α, pois temos um ponto de cada
plano de projecção. Optou-se pelo rebatimento do plano α para o Plano Hori-
zontal de Projecção – a charneira é hhα e BBrr ≡ BB11, pois BB é um ponto da char-
neira. É necessário rebater ffα, o que se processa rebatendo um dos seus
pontos – o ponto AA. Por AA11 conduziu-se uma perpendicular à charneira (que
corresponde ao plano ortogonal à charneira que contém o arco do seu rebati-
mento) – com o compasso, fazendo centro no ponto de concorrência dos tra-
ços do plano e raio até AA22, transportou-se essa distância para a perpendicular
à charneira que passa por AA11, obtendo AArr. O traço frontal do plano rebatido
(ffαrr
) passa por AArr e é concorrente com hhαrr
no eixo XX. A partir de AArr e BBrr cons-
truiu-se o triângulo [AABBCC] em V.G., em rebatimento e, com vista à determina-
ção das projecções da pirâmide, determinou-se também o seu centro –
o ponto OO. A inversão do rebatimento dos pontos OO e CC processou-se com
(Continua na página seguinte)

129. 129
SOLUÇÕES
Em primeiro lugar representou-se o plano α, pelos seus
traços, e o ponto OO, pelas suas projecções e pertencente
ao plano, em função dos dados. O plano α tem os seus
traços coincidentes, pois é ortogonal ao β2/4. A recta hh,
horizontal (de nível), pertencente ao plano e com 4 cm de
cota, foi a recta auxiliar a que se recorreu para determinar
as projecções do ponto OO. O plano α não é paralelo a ne-
nhum dos planos de projecção, pelo que o triângulo não
se projecta em V.G. em nenhum dos planos de projecção
– é necessário o recurso a um processo geométrico auxi-
liar. Optou-se por rebater o plano α para o Plano Horizon-
tal de Projecção (a charneira é hhα – hhα ≡ ee11 ≡ hhαrr
). Para
rebater o plano α há que rebater o seu traço frontal, o que
se processa rebatendo um dos seus pontos – o ponto FF
(traço frontal da recta hh), por exemplo. Para tal conduziu-
-se, por FF11, uma perpendicular à charneira (que corres-
ponde ao plano ortogonal à charneira que contém o arco
do seu rebatimento). Os traços do plano α são concorren-
tes num ponto fixo (um ponto do eixo XX, que é um ponto
da charneira). Com o recurso ao compasso, fazendo cen-
tro nesse ponto e raio até FF22, transportou-se essa distân-
cia até à perpendicular à charneira que passa por FF11 e
obteve-se FFrr – ffαrr
passa por FFrr e é concorrente com hhαrr
no
eixo XX. A recta hhrr passa por FFrr e é paralela a hhαrr
(rectas
horizontais de um plano são paralelas entre si e paralelas
ao traço horizontal do plano, no espaço, em projecções e
em rebatimento). Por OO11 conduziu-se uma perpendicular à
charneira (que corresponde ao plano ortogonal à charnei-
ra que contém o arco do seu rebatimento) e determinou-se OOrr sobre hhrr. Com o compasso, fazendo centro em OOrr e com 3,5 cm de raio,
desenhou-se a circunferência circunscrita ao triângulo e construiu-se o triângulo em V.G., em rebatimento, inscrito na circunferência e de
acordo com os dados – o lado [AABB] é horizontal (é paralelo a hhαrr
), sendo AA o vértice de maior afastamento e CC o vértice de menor cota
(o vértice que se situa mais próximo de hhαrr
). Em seguida, inverteu-se o rebatimento dos três vértices do triângulo, com o recurso às rectas
horizontais (de nível) do plano que por eles passam (ver exercício 118822 e respectivo relatório) – note que se omitiram as notações referentes
às rectas horizontais (de nível) que nos permitiram inverter o rebatimento dos pontos, com vista a não sobrecarregar visualmente a resolu-
ção gráfica apresentada. A partir das projecções dos três vértices do triângulo, desenharam-se as suas projecções (a traço leve, pois trata-
-se de um traçado auxiliar para o objectivo do exercício, que é as projecções do sólido). Em seguida, pelas projecções de OO conduziram-se
as projecções homónimas de uma recta pp, ortogonal a α – a recta pp é a recta suporte do eixo da pirâmide. O vértice VV, da pirâmide, porque
tem afastamento nulo, é o traço frontal da recta pp, o que nos permite determinar imediatamente as suas projecções, sem o recurso a qual-
quer outro rebatimento. A partir das projecções de todos os vértices do sólido, desenharam-se os seus contornos aparentes – o ccoonnttoorrnnoo
aappaarreennttee ffrroonnttaall é [BB22VV22CC22] e o ccoonnttoorrnnoo aappaarreennttee hhoorriizzoonnttaall é [AA11BB11VV11]. Em pprroojjeeccççããoo ffrroonnttaall, há um vértice que não integra o contorno
aparente – o vértice AA. Este é o vértice de maior afastamento do sólido, pelo que é visível (bem como todas as arestas que nele convergem).
A base do sólido é visível, bem como as faces laterais [AABBVV] e [AACCVV] (a face lateral [BBCCVV] é a única face invisível em projecção frontal). Em
pprroojjeeccççããoo hhoorriizzoonnttaall, há um vértice que não integra o contorno aparente – o vértice CC. Este é o vértice de menor cota do sólido, pelo que é
invisível (bem como todas as arestas que nele convergem). A face lateral [AABBVV] é a única face visível em projecção horizontal – a base e as
restantes faces são invisíveis.
341.
o recurso às rectas frontais (de frente) que por eles passam – ver exercício 118833 e respectivo relatório. A recta ff é a recta frontal (de frente)
que nos permitiu determinar as projecções de CC. A recta ff’’ é a recta frontal (de frente) que nos permitiu determinar as projecções de OO. A
partir das projecções dos três vértices do triângulo, desenharam-se as suas projecções (a traço leve, pois trata-se de um traçado auxiliar
para o objectivo do exercício, que é as projecções do sólido). Em seguida, pelas projecções de OO conduziram-se as projecções homónimas
de uma recta pp, ortogonal a α – a recta pp é a recta suporte do eixo da pirâmide. O vértice VV, da pirâmide, porque tem cota nula, é o traço ho-
rizontal da recta pp, o que nos permite determinar imediatamente as suas projecções, sem o recurso a qualquer outro rebatimento. A partir
das projecções de todos os vértices do sólido, desenharam-se os seus contornos aparentes – o ccoonnttoorrnnoo aappaarreennttee ffrroonnttaall é [BB22VV22CC22] e o
ccoonnttoorrnnoo aappaarreennttee hhoorriizzoonnttaall é [AA11BB11CC11VV11]. Em pprroojjeeccççããoo ffrroonnttaall, há um vértice que não integra o contorno aparente – o vértice AA. Este é
o vértice de menor afastamento do sólido, pelo que é invisível (bem como todas as arestas que nele convergem). A base do sólido é invisí-
vel, bem como as faces laterais [AABBVV] e [AACCVV]. Em pprroojjeeccççããoo hhoorriizzoonnttaall, todos os vértices integram o contorno aparente. No entanto, as
faces laterais [AABBVV] e [BBCCVV] são invisíveis, pelo que a aresta lateral [BBVV] (a aresta que separa aquelas faces) é invisível. Já a aresta [AACC] da
base é visível, pois separa duas faces visíveis em projecção horizontal – a base e a face lateral [AACCVV].

130. 130
SOLUÇÕES
Em primeiro lugar representaram-se os pontos OO e AA,
pelas respectivas projecções, em função dos dados, e
desenharam-se as projecções da recta rr. Em seguida, uma
vez que AA é o traço frontal da recta rr, foi possível desenhar
imediatamente ffψ, passando por AA22 e perpendicular a rr22.
Para determinar hhψ poder-se-ia determinar o traço horizon-
tal da recta rr, mas optou-se por conduzir, por OO, uma recta
frontal (de frente) ff, do plano (paralela a ffψ) – HH é o traço
horizontal da recta ff. O traço horizontal do plano, hhψ, passa
por HH11 e é concorrente com ffψ no eixo XX. O plano ψ não é
paralelo a nenhum dos planos de projecção, pelo que o
quadrado não se projecta em V.G. em nenhum dos planos
de projecção – é necessário o recurso a um processo geo-
métrico auxiliar. Uma vez que o ponto AA é um ponto do Pla-
no Frontal de Projecção, com vista a uma maior economia
de traçados, optou-se por rebater o plano ψ para o Plano
Frontal de Projecção (a charneira é ffψ – ffψ ≡ ee22 ≡ ffψrr
e tem-
-se imediatamente AArr ≡ AA22). Para rebater o plano ψ há que
rebater o seu traço horizontal, o que se processa rebaten-
do um dos seus pontos – o ponto HH (traço horizontal da
recta ff), por exemplo. Para tal conduziu-se, por HH22, uma
perpendicular à charneira (que corresponde ao plano orto-
gonal à charneira que contém o arco do seu rebatimento).
Os traços do plano ψ são concorrentes num ponto fixo
(um ponto do eixo XX, que é um ponto da charneira). Com
o recurso ao compasso, fazendo centro nesse ponto e
raio até HH11, transportou-se essa distância até à perpendi-
cular à charneira que passa por HH22 e obteve-se HHrr – hhψrr
passa por HHrr e é concorrente com ffψrr
no eixo XX. A recta ffrr
passa por HHrr e é paralela a ffψrr
. Conduzindo, por OO22, uma
perpendicular à charneira (que corresponde ao plano orto-
gonal à charneira que contém o seu arco do rebatimento) determinou-se OOrr sobre ffrr. A recta rrrr fica definida por AArr e por OOrr. Note que não se-
ria possível rebater o ponto OO exclusivamente através do rebatimento da recta rr, o que justifica o facto de se ter recorrido a uma recta frontal
(de frente) do plano, passando por OO. Com o compasso, fazendo centro em OOrr e raio até AArr, desenhou-se a circunferência circunscrita ao
quadrado e construiu-se o quadrado em V.G., em rebatimento, inscrito na circunferência. A inversão do rebatimento dos pontos BB e DD efec-
tuou-se com o recurso à recta frontal (de frente) ff, que passa por OO, pois os dois pontos pertencem à mesma recta. A inversão do rebati-
mento do ponto CC processou-se com o recurso a uma recta horizontal (de nível) do plano, passando por CC – note que se omitiram as
notações referentes à projecção frontal da recta horizontal (de nível) que nos permitiu inverter o rebatimento de CCrr, com vista a não sobre-
carregar visualmente a resolução gráfica apresentada. Omitiu-se a representação da projecção horizontal da recta horizontal (de nível), pois
CC é um ponto da recta rr e, assim, as projecções de CC situam-se sobre as projecções homónimas da recta rr. A partir das projecções dos
quatro pontos, desenharam-se as projecções do polígono (a traço leve, pois trata-se de um traçado auxiliar para o objectivo do exercício,
que é as projecções do sólido). O enunciado refere expressamente que o quadrado [AABBCCDD] é uma base de um prisma situado no 1o Diedro,
pelo que se infere que se trata da base inferior do sólido. Assim, em seguida conduziu-se, por CC, uma recta pp, ortogonal ao plano ψ – a recta pp é
a recta suporte da aresta lateral [CCCC’’] do prisma, que mede 5 cm (a altura do prisma). Como a recta pp é oblíqua aos dois planos de projec-
ção, o segmento [CCCC’’] não se projecta em V.G. em nenhum dos planos de projecção, pelo que é necessário o recurso a um processo geo-
métrico auxiliar. Optou-se por rebater o plano projectante horizontal da recta pp (o plano α) para o Plano Horizontal de Projecção – a
charneira foi hhα (recta ee’’). A recta pp rebateu-se com o recurso a dois dos seus pontos – o ponto CC e HH’’, o seu traço horizontal. A recta pprr fica
definida por CCrr11
e HH’’rr (note que CCrr11
é o ponto CC no seu segundo rebatimento – no rebatimento do plano α). Sobre pprr, a partir de CCrr11
, medi-
ram-se os 5 cm (a altura do prisma), obtendo-se CC’’rr (garantindo que CC’’ se situa no 1º Diedro). Inverteu-se o rebatimento de α, obtendo-se
as projecções de CC’’, sobre as projecções homónimas da recta pp. As projecções de AA’’, BB’’ e DD’’, os restantes vértices da base superior, deter-
minaram-se atendendo a que os lados do quadrado [AA’’BB’’CC’’DD’’] são paralelos aos lados correspondentes do quadrado [AABBCCDD] e que os
seus vértices estão sobre as rectas ortogonais a ψ (paralelas à recta pp) que contêm as respectivas arestas laterais. Assim, pelas projecções
de CC’’, conduziram-se as projecções da recta suporte do segmento [BB’’CC’’], até encontrarem as projecções homónimas da recta suporte da
aresta lateral [BBBB’’] – o ponto de concorrência das duas rectas é BB’’. Repetiu-se o processo para DD’’, a partir de CC’’, e ainda para AA’’, a partir de
BB’’ ou de DD’’. A partir das projecções de todos os vértices do sólido, desenharam-se os seus contornos aparentes – o ccoonnttoorrnnoo aappaarreennttee
ffrroonnttaall é [BB22CC22DD22DD’’22AA’’22BB’’22] e o ccoonnttoorrnnoo aappaarreennttee hhoorriizzoonnttaall é [AA11DD11CC11CC’’11BB’’11AA’’11]. Em pprroojjeeccççããoo ffrroonnttaall, existem dois vértices que não in-
tegram o contorno aparente – o vértice CC’’ (que é o vértice de maior afastamento, pelo que é visível bem como todas as arestas que nele
convergem) e o vértice AA (que é o vértice de menor afastamento, pelo que é invisível bem como todas as arestas que nele convergem). Em
pprroojjeeccççããoo hhoorriizzoonnttaall, também existem dois vértices que não integram o contorno aparente – o vértice DD’’ (que é o vértice de maior cota,
pelo que é visível bem como todas as arestas que nele convergem) e o vértice BB (que é o vértice de menor cota, pelo que é invisível bem
como todas as arestas que nele convergem). A base [AA’’BB’’CC’’DD’’] é visível em ambas as projecções e a base [AABBCCDD] é invisível em ambas as
projecções.
342.

131. 131
SOLUÇÕES
343.
Em primeiro lugar representou-se o plano λ, pelos seus
traços, e os pontos RR e SS, pelas suas projecções e perten-
centes ao plano, em função dos dados. O ponto RR é um
ponto de hhλ, pois tem cota nula. A recta hh, horizontal
(de nível), pertencente ao plano e com 3 cm de cota, foi a
recta auxiliar a que se recorreu para determinar as projec-
ções do ponto SS. O plano λ não é paralelo a nenhum dos
planos de projecção, pelo que o triângulo não se projecta
em V.G. em nenhum dos planos de projecção – é neces-
sário o recurso a um processo geométrico auxiliar. Com
vista a uma maior economia de traçados, e uma vez que o
ponto RR é um ponto do Plano Horizontal de Projecção,
optou-se por rebater o plano λ para o Plano Horizontal de
Projecção (a charneira é hhλ – hhλ ≡ ee11 ≡ hhλrr
e tem-se imedia-
tamente RRrr ≡ RR11). Para rebater o plano λ há que rebater o
seu traço frontal, o que se processa rebatendo um dos
seus pontos – o ponto FF (traço frontal da recta hh), por
exemplo. Para tal conduziu-se, por FF11, uma perpendicular
à charneira (que corresponde ao plano ortogonal à char-
neira que contém o arco do seu rebatimento). Os traços
do plano λ são concorrentes num ponto fixo (um ponto do
eixo XX, que é um ponto da charneira). Com o recurso ao
compasso, fazendo centro nesse ponto e raio até FF22,
transportou-se essa distância até à perpendicular à char-
neira que passa por FF11 e obteve-se FFrr – ffλrr
passa por FFrr e
é concorrente com hhλrr
no eixo XX. A recta hhrr passa por FFrr e é
paralela a hhλrr
. Por SS11 conduziu-se uma perpendicular à
charneira (que corresponde ao plano ortogonal à charneira
que contém o arco do seu rebatimento) e determinou-se SSrr sobre hhrr. A partir de RRrr e SSrr construiu-se o triângulo em V.G., em rebatimento,
obtendo TTrr. A inversão do rebatimento de TT processou-se com o recurso a uma recta frontal (de frente) do plano, passando por TT (recta ff). A partir
das projecções dos três pontos, desenharam-se as projecções do triângulo (a traço leve, pois trata-se de um traçado auxiliar para o objectivo do
exercício, que é as projecções do sólido). O enunciado refere expressamente que o triângulo [RR’’SS’’TT’’] é a base superior do prisma, pelo que se
infere que o triângulo [RRSSTT] é sua base inferior. Por outro lado, sabe-se que o vértice SS’’, da base superior, tem afastamento nulo – assim, em
seguida conduziu-se, por SS, uma recta pp, ortogonal ao plano λ (a recta pp é a recta suporte da aresta lateral [SSSS’’] do prisma). O ponto SS’’ é ime-
diatamente o traço frontal da recta pp. As projecções de RR’’ e TT’’, os restantes vértices da base superior, determinaram-se atendendo a que os
lados do triângulo [RR’’SS’’TT’’] são paralelos aos lados correspondentes do triângulo [RRSSTT] e que os seus vértices estão sobre as rectas ortogonais
a λ (paralelas à recta pp) que contêm as respectivas arestas laterais. Assim, pelas projecções de SS’’ conduziram-se as projecções da recta suporte
do segmento [RR’’SS’’], paralelas às projecções homónimas de [RRSS], até encontrarem as projecções homónimas da recta pp’’ (a recta suporte da
aresta lateral [RRRR’’]) – o ponto de concorrência das duas rectas é RR’’. Repetiu-se o processo para TT’’, a partir de SS’’ (a recta suporte da aresta
lateral [TTTT’’] é a recta pp’’’’). A partir das projecções de todos os vértices do sólido, desenharam-se os seus contornos aparentes – o ccoonnttoorrnnoo
aappaarreennttee ffrroonnttaall é [RR22SS22SS’’22TT’’22RR’’22] e o ccoonnttoorrnnoo aappaarreennttee hhoorriizzoonnttaall é [SS11TT11TT’’11RR’’11SS’’11]. Em pprroojjeeccççããoo ffrroonnttaall, existe um vértice que não
integra o contorno aparente – o vértice TT’’, que é o vértice de maior afastamento do sólido, pelo que é visível bem como todas as arestas que
nele convergem. Em pprroojjeeccççããoo hhoorriizzoonnttaall, também existe um vértice que não integra o contorno aparente – o vértice RR, que é o vértice de
menor cota, pelo que é invisível, bem como todas as arestas que nele convergem. A base [RRSSTT] é visível em projecção frontal e invisível em
projecção horizontal. A base [RR’’SS’’TT’’] é visível em projecção horizontal (a aresta [SS’’TT’’] da base é visível) e invisível em projecção frontal (a
aresta [RR’’SS’’] da base é invisível).
344.
Em primeiro lugar representou-se o plano γ, pelos seus traços, e o ponto OO, pelas suas projecções e pertencente ao plano, em função dos
dados. O plano γ tem os seus traços coincidentes, pois é ortogonal ao β2/4. A recta hh, horizontal (de nível), pertencente ao plano e com 3 cm
de cota, foi a recta auxiliar a que se recorreu para determinar as projecções do ponto OO. O plano γ não é paralelo a nenhum dos planos de
projecção, pelo que o triângulo não se projecta em V.G. em nenhum dos planos de projecção – é necessário o recurso a um processo geo-
métrico auxiliar. Optou-se por rebater o plano γ para o Plano Horizontal de Projecção (a charneira é hhγ – hhγ ≡ ee11 ≡ hhγrr
). Para rebater o plano γ
há que rebater o seu traço frontal, o que se processa rebatendo um dos seus pontos – o ponto FF (traço frontal da recta hh), por exemplo.
Para tal conduziu-se, por FF11, uma perpendicular à charneira – com o compasso, fazendo centro no ponto de concorrência dos traços do pla-
no (que é um ponto fixo) e raio até FF22, transportou-se essa distância até à perpendicular à charneira que passa por FF11, obtendo-se FFrr. O tra-
ço frontal do plano rebatido, ffγrr
, passa por FFrr e é concorrente com hhγrr
no eixo XX. A recta hhrr passa por FFrr e é paralela a hhγrr
(rectas horizontais
de um plano são paralelas entre si e paralelas ao traço horizontal do plano). Por OO11 conduziu-se uma perpendicular à charneira e determi-
nou-se OOrr sobre hhrr. Com o compasso, fazendo centro em OOrr e com 4 cm de raio, desenhou-se a circunferência circunscrita ao triângulo e
construiu-se o triângulo em V.G., em rebatimento, inscrito na circunferência e de acordo com os dados – o lado [AABB] é frontal (é paralelo a
ffγrr
), sendo AA o vértice de maior cota. Em seguida, inverteu-se o rebatimento dos três vértices do triângulo, com o recurso às rectas frontais
(de frente) do plano que por eles passam (ver exercício 118877 e respectivo relatório). A partir das projecções dos três vértices do triângulo,
desenharam-se as suas projecções (a traço leve, pois trata-se de um traçado auxiliar para o objectivo do exercício, que é as projecções do
(Continua na página seguinte)

132. 132
SOLUÇÕES
sólido) – note que o lado [AABB] é frontal
(paralelo a ffγ), o lado [BBCC] é horizontal
(paralelo a hhγ) e o lado [AACC] é de perfil.
Em seguida conduziu-se, por CC, uma recta
cc, ortogonal ao plano γ – a recta cc é a rec-
ta suporte da aresta lateral [CCCC’’] do pris-
ma, que mede 4 cm (a altura do prisma).
Como a recta cc é oblíqua aos dois planos
de projecção, o segmento [CCCC’’] não se
projecta em V.G. em nenhum dos planos
de projecção, pelo que é necessário o re-
curso a um processo geométrico auxiliar.
Optou-se por rebater o plano projectante
horizontal da recta cc (o plano α) para o
Plano Frontal de Projecção – a charneira
foi ffα (recta ee’’). A recta cc rebateu-se com o
recurso a dois dos seus pontos – o ponto
CC e FF’’, o seu traço frontal. A recta ccrr fica
definida por CCrr11
e FF’’rr (note que CCrr11
é o
ponto CC no seu segundo rebatimento – no
rebatimento do plano α). Sobre ccrr, a partir
de CCrr11
, mediram-se os 4 cm (a altura do
prisma), obtendo-se CC’’rr (garantindo que
CC’’ se situa no 1o Diedro). Inverteu-se o re-
batimento de α, obtendo-se as projecções
de CC’’ sobre as projecções homónimas da
recta cc. As projecções de AA’’ e BB’’, os ou-
tros dois vértices da base superior, deter-
minaram-se atendendo a que os lados do
triângulo [AA’’BB’’CC’’] são paralelos aos lados
correspondentes do triângulo [AABBCC] e que
os seus vértices estão sobre as rectas ortogonais a γ (paralelas à recta cc) que contêm as respectivas arestas laterais. Assim, pelas projec-
ções de CC’’ conduziram-se as projecções da recta suporte do segmento [BB’’CC’’], até encontrarem as projecções homónimas da recta bb (a rec-
ta suporte da aresta lateral [BBBB’’]) – o ponto de concorrência das duas rectas é BB’’. Repetiu-se o processo para AA’’ – pelas projecções de CC’’
conduziram-se as projecções da recta suporte do segmento [AA’’CC’’], até encontrarem as projecções homónimas da recta aa (a recta suporte
da aresta lateral [AAAA’’]) – o ponto de concorrência das duas rectas é AA’’. A partir das projecções de todos os vértices do sólido, desenharam-
se os seus contornos aparentes – o ccoonnttoorrnnoo aappaarreennttee ffrroonnttaall é [AA22AA’’22BB’’22BB22CC22] e o ccoonnttoorrnnoo aappaarreennttee hhoorriizzoonnttaall é [AA11BB11BB’’11CC’’11CC11]. Em
pprroojjeeccççããoo ffrroonnttaall, há um vértice que não integra o contorno aparente – o vértice CC’’, que é o vértice de menor afastamento do sólido, pelo
que é invisível bem como todas as arestas que nele convergem. Em pprroojjeeccççããoo hhoorriizzoonnttaall, também há um vértice que não integra o contor-
no aparente – o vértice AA’’, que é o vértice de maior cota do sólido, pelo que é visível bem como todas as arestas que nele convergem. A
base [AA’’BB’’CC’’] é visível em projecção horizontal e invisível em projecção frontal. A base [AABBCC] é visível em projecção frontal e invisível em
projecção horizontal – a aresta [AABB] da base é visível em projecção frontal e a aresta [BBCC] da base é invisível em projecção horizontal.
345.
Em primeiro lugar representou-se o plano α, pelos seus traços, e os pontos AA e BB, pertencentes ao plano α, pelas suas projecções, em fun-
ção dos dados. O ponto AA é um ponto de ffα, que é uma recta frontal (de frente) do plano com cota nula. O ponto BB é um ponto de hhα, que é
uma recta horizontal (de nível) do plano com cota nula. O plano α não é paralelo a nenhum dos planos de projecção, pelo que é necessário
o recurso a um processo geométrico auxiliar. Uma vez que o ponto AA é um ponto do Plano Frontal de Projecção e que o ponto BB é um pon-
to do Plano Horizontal de Projecção, ao nível da economia de traçados é indistinto efectuar o rebatimento do plano α para o Plano Frontal
de Projecção ou para o Plano Horizontal de Projecção. Optou-se por rebater o plano α para o Plano Horizontal de Projecção
(a charneira é hhα – hhα ≡ ee11 ≡ hhαrr
), pelo que se tem imediatamente BBrr ≡ BB11, pois BB é um ponto da charneira. Para rebater o plano α há que re-
bater o seu traço frontal, o que se processa rebatendo um dos seus pontos – o ponto AA, que é um ponto de ffα. Para tal conduziu-se, por AA11,
uma perpendicular à charneira – com o compasso, fazendo centro no ponto de concorrência dos traços do plano (que é um ponto fixo) e
raio até AA22, transportou-se essa distância até à perpendicular à charneira que passa por AA11, obtendo-se AArr. O traço frontal do plano rebatido,
ffαrr
, passa por AArr e é concorrente com hhαrr
no eixo XX. A partir de AArr e BBrr construiu-se o triângulo em V.G., em rebatimento. Para inverter o re-
batimento dos pontos CC e DD, recorreu-se à recta suporte do lado [CCDD] do quadrado – a recta ss. A recta ssrr passa por CCrr e DDrr e é paralela à
recta rrrr, que é a recta que passa por AArr e BBrr (a recta rr é a recta suporte do lado [AABB] do quadrado). As projecções da recta rr determinam-se
imediatamente – estão definidas pelas projecções homónimas de AA e BB. A recta ssrr é concorrente com hhαrr
no ponto HHrr – HH é o traço horizon-
tal da recta ss. As projecções de HH determinam-se imediatamente, pois HH é um ponto da charneira (é fixo). A recta ss fica definida por um pon-
to (HH) e por uma direcção (é paralela à recta rr), o que nos permitiu desenhar as projecções da recta ss – passam pelas projecções
homónimas de HH e são paralelas às projecções homónimas da recta rr. Conduzindo, por CCrr e DDrr, as perpendiculares à charneira que por
(Continua na página seguinte)

133. 133
SOLUÇÕES
eles passam (e que correspondem aos planos ortogonais à charneira que contêm os respectivos arcos do rebatimento), determinaram-se
as projecções de CC e DD, sobre as projecções homónimas da recta ss. A partir das projecções dos quatro vértices do quadrado, desenharam-
-se as suas projecções (a traço leve, pois trata-se de um traçado auxiliar para o objectivo do exercício, que é as projecções do sólido). Em
seguida conduziu-se, por AA, uma recta aa, ortogonal ao plano α – a recta aa é a recta suporte da aresta [AAAA’’] do cubo, cujo comprimento será
igual ao lado do quadrado [AArrBBrrCCrrDDrr]. Como a recta aa é oblíqua aos dois planos de projecção, o segmento [AAAA’’] não se projecta em V.G.
em nenhum dos planos de projecção, pelo que é necessário o recurso a um processo geométrico auxiliar. Optou-se por rebater o plano pro-
jectante horizontal da recta aa (o plano γ) para o Plano Frontal de Projecção – a charneira foi ffγ (recta ee’’). A recta aa rebateu-se com o recurso
a dois dos seus pontos – o ponto AA (que é o seu traço frontal) e um ponto PP, qualquer, da recta. A recta aarr fica definida por AArr11
e PPrr (note
que AArr11
é o ponto AA no seu segundo rebatimento – no rebatimento do plano γ). Transportou-se a medida do lado do quadrado [AArrBBrrCCrrDDrr]
para aarr, a partir de AArr11
, obtendo-se AA’’rr (garantindo que AA’’ se situa no 1o Diedro). Inverteu-se o rebatimento de γ, obtendo-se as projecções
de AA’’ sobre as projecções homónimas da recta aa. As projecções de BB’’, CC’’ e DD’’, os outros três vértices da face superior do cubo, determina-
ram-se atendendo a que os lados do quadrado [AA’’BB’’CC’’DD’’] são paralelos aos lados correspondentes do quadrado [AABBCCDD] e que os seus
vértices estão sobre as rectas ortogonais a α (paralelas à recta aa) que contêm as respectivas arestas. Assim, pelas projecções de AA’’ condu-
ziram-se as projecções da recta suporte do segmento [AA’’BB’’], até encontrarem as projecções homónimas da recta bb (a recta suporte da
aresta [BBBB’’]) – o ponto de concorrência das duas rectas é BB’’. Repetiu-se o processo para DD’’ – pelas projecções de AA’’ conduziram-se as
projecções da recta suporte do segmento [AA’’DD’’], até encontrarem as projecções homónimas da recta dd (a recta suporte da aresta [DDDD’’]) e o
ponto de concorrência das duas rectas é DD’’. Por fim, repetiu-se uma vez mais o processo descrito para CC’’ – pelas projecções de BB’’ (ou de DD’’)
conduziram-se as projecções da recta suporte do segmento [BB’’CC’’] (ou do segmento [CC’’DD’’]), até encontrarem as projecções homónimas da
recta cc (a recta suporte da aresta [CCCC’’]) e o ponto de concorrência das duas rectas é CC’’. A partir das projecções de todos os vértices do sólido,
desenharam-se os seus contornos aparentes – o ccoonnttoorrnnoo aappaarreennttee ffrroonnttaall é [BB22BB’’22AA’’22DD’’22DD22CC22] e o ccoonnttoorrnnoo aappaarreennttee hhoorriizzoonnttaall é
[AA11AA’’11BB’’11CC’’11CC11DD11]. Em pprroojjeeccççããoo ffrroonnttaall, existem dois vértices que não integram o contorno aparente – o vértice CC’’ (que é o vértice de
maior afastamento do cubo, pelo que é visível bem como todas as arestas que nele convergem) e o vértice AA (que é o vértice de menor
afastamento do cubo, pelo que é invisível bem como todas as arestas que nele convergem). Em pprroojjeeccççããoo hhoorriizzoonnttaall, também existem
dois vértices que não integram o contorno aparente – o vértice DD’’ (que é o vértice de maior cota do cubo, pelo que é visível bem como todas
as arestas que nele convergem) e o vértice BB (que é o vértice de menor cota do cubo, pelo que é invisível bem como todas as arestas que
nele convergem). A face [AA’’BB’’CC’’DD’’] é visível em ambas as projecções e a face [AABBCCDD] é invisível em ambas as projecções.

134. 134
SOLUÇÕES
346.
Em primeiro lugar representaram-se os pontos RR e TT, pelas
suas projecções, em função dos dados. Em seguida, dese-
nharam-se os traços do plano ρ – TT tem cota nula, pelo que
hhρ passa por TT1, e RR tem afastamento nulo, pelo que ffρ passa
por RR22. O quadrado não se projecta em V.G. em nenhum dos
planos de projecção – para construir as suas projecções é
necessário o recurso a um processo geométrico auxiliar. Uma
vez que o ponto RR é um ponto do Plano Frontal de Projecção
e que o ponto TT é um ponto do Plano Horizontal de Projec-
ção, ao nível da economia de traçados é indistinto efectuar o
rebatimento do plano ρ para o Plano Frontal de Projecção ou
para o Plano Horizontal de Projecção. Optou-se por rebater o
plano ρ para o Plano Horizontal de Projecção – a charneira foi
hhρ. TTrr ≡ TT11, pois TT é um ponto da charneira. Para rebater o
plano ρ há que rebater o seu traço frontal, o que se processa
rebatendo um dos seus pontos – o ponto RR (que é um ponto
de ffρ), por exemplo. Para tal conduziu-se, por RR, uma perpen-
dicular à charneira (que corresponde ao plano ortogonal à
charneira que contém o arco do seu rebatimento) – com o
compasso, fazendo centro em RR11 e raio até RR22 (o raio é a cota
de RR) transportou-se essa distância até ao eixo XX, o que nos
permitiu construir o triângulo do rebatimento de RR em V.G. e
determinar RRrr (ver exercício 118888). O traço frontal do plano ρ em
rebatimento, ffρrr
, passa por RRrr e é paralelo ao eixo XX (e a hhρrr
).
A partir de RRrr e TTrr construiu-se o quadrado em V.G., em reba-
timento, determinando SSrr e UUrr, bem como OOrr (OO é o centro da
circunferência circunscrita ao quadrado). Para inverter o reba-
timento de SSrr conduziu-se, por SSrr, uma recta ssrr, paralela à
recta rrrr – a recta rr é a recta que passa por RR e TT, cujas projec-
ções se determinaram imediatamente. O traço horizontal da
recta ss é fixo (é um ponto da charneira), pelo que as suas
projecções se determinaram imediatamente (note que não se
identificou o traço horizontal da recta ss, nem em projecções
nem em rebatimento, de forma a não sobrecarregar visual-
mente a resolução gráfica apresentada). A recta ss, em projecções, fica definida por um ponto (o seu traço horizontal) e por uma direcção (é
paralela à recta rr), o que nos permitiu desenhar imediatamente as suas projecções, paralelas às projecções homónimas da recta rr. Condu-
zindo, por SSrr, uma perpendicular à charneira (que corresponde ao plano ortogonal à charneira que contém o arco do seu rebatimento), de-
terminaram-se as projecções de SS sobre as projecções homónimas da recta ss. Repetiu-se o processo para o ponto UU – a recta mm é a recta
paralela à recta rr que passa por UU e está igualmente definida por um ponto e uma direcção (as projecções do ponto UU determinaram-se a
partir das projecções da recta mm). A partir das projecções dos quatro vértices do quadrado, desenharam-se as suas projecções (a traço
leve, pois trata-se de um traçado auxiliar para o objectivo do exercício, que é as projecções do sólido). As projecções do ponto OO determina-
ram-se a partir das duas diagonais do quadrado – OO22 é o ponto de concorrência das projecções frontais das duas diagonais do quadrado e
OO11 é o ponto de concorrência das projecções horizontais das duas diagonais do quadrado. Em seguida, pelas projecções de OO, conduzi-
ram-se as projecções de uma recta pp, ortogonal a ρ – a recta pp é a recta suporte do eixo da pirâmide e é uma rreeccttaa ddee ppeerrffiill. A recta pp está
definida por um ponto (o ponto OO) e pela sua direcção (é ortogonal a ρ). A recta pp é ortogonal às rectas de perfil do plano ρ. Para definir a
recta pp conduziu-se, pela recta, um plano de perfil π e determinou-se a recta de intersecção de π com ρ – recta ii (que está definida pelos
seus traços, FF e HH). A recta ii contém o ponto OO (que é um ponto dos dois planos) e a recta pp também – as duas rectas são perpendiculares
no ponto OO. Por outro lado, ο vértice VV, da pirâmide, situa-se sobre pp, a 8 cm de OO (a altura da pirâmide). Atendendo a que o segmento [OOVV]
não se projecta em V.G. em nenhum dos planos de projecção, é necessário o recurso a um outro processo geométrico auxiliar. Optou-se
pelo rebatimento do plano π para o Plano Frontal de Projecção – a charneira foi ffπ (recta ee’’). A recta iirr fica definida por FFrr e HHrr. Note que o
ponto OOrr11
tem também de se situar sobre iirr, pois OO é um ponto da recta ii (OOrr11
é o ponto OO no seu segundo rebatimento – no rebatimento do
plano π). A recta pprr passa por OOrr11
e é perpendicular a iirr em OOrr11
. Sobre pprr, a partir de OOrr11
, mediram-se os 8 cm, obtendo-se VVrr (garantindo
que VV se situa no 1o Diedro). Inverteu-se o rebatimento de π, obtendo-se as projecções de VV. A partir das projecções de todos os vértices do
sólido, desenharam-se os seus contornos aparentes – o ccoonnttoorrnnoo aappaarreennttee ffrroonnttaall é [SS22TT22UU22VV22] e o ccoonnttoorrnnoo aappaarreennttee hhoorriizzoonnttaall é
[RR11SS11VV11UU11]. Em pprroojjeeccççããoo ffrroonnttaall, há um vértice que não integra o contorno aparente – o vértice RR, que é o vértice de menor afastamento
do sólido, pelo que é invisível bem como todas as arestas que nele convergem. Em pprroojjeeccççããoo hhoorriizzoonnttaall, também há um vértice que não
integra o contorno aparente – o vértice TT, que é o vértice de menor cota do sólido, pelo que é invisível bem como todas as arestas que nele
convergem. A aresta lateral [TTVV] é visível em projecção frontal, pois separa duas faces visíveis em projecção frontal – as faces laterais [SSTTVV]
e [TTUUVV]. A aresta lateral [RRVV] é visível em projecção horizontal, pois separa duas faces visíveis em projecção horizontal – as faces laterais
[RRSSVV] e [RRUUVV].

135. 135
SOLUÇÕES
347.
Em primeiro lugar representou-se o plano ρ, pelos seus traços, em função dos dados – o plano ρ tem os seus traços simétricos em relação
ao eixo XX, pois é ortogonal ao β1/3. Os dados permitiram-nos, ainda, determinar as projecções de AA e BB – AA tem cota nula, pelo que é um
ponto de hhρ e BB tem afastamento nulo, pelo que é um ponto de ffρ. Os pontos AA e BB têm a mesma abcissa, pelo que se situam na mesma
linha de chamada. Uma vez que o triângulo não se projecta em V.G. em nenhum dos planos de projecção, para construir as suas projec-
ções é necessário o recurso a um processo geométrico auxiliar. Uma vez que o ponto AA é um ponto do Plano Horizontal de Projecção e que
o ponto BB é um ponto do Plano Frontal de Projecção, ao nível da economia de traçados é indistinto efectuar o rebatimento do plano ρ para
o Plano Frontal de Projecção ou para o Plano Horizontal de Projecção. Optou--se por rebater o plano ρ para o Plano Horizontal de Projec-
ção – a charneira foi hhρ. AArr ≡ AA11, pois AA é um ponto da charneira. Para rebater o plano ρ há que rebater o seu traço frontal, o que se proces-
sa rebatendo um dos seus pontos – o ponto BB (que é um ponto de ffρ), por exemplo. Para tal, conduziu-se, por BB, uma perpendicular à
charneira – com o compasso, fazendo centro em BB11 e raio até BB22 (a cota de BB) transportou-se essa distância até ao eixo XX, o que nos permi-
tiu construir o triângulo do rebatimento de BB em V.G. e determinar BBrr (ver exercício 118888). O traço frontal do plano ρ em rebatimento, ffρrr
, passa
por BBrr e é paralelo ao eixo XX (e a hhρrr
). A partir de AArr e BBrr construiu-se o triângulo em V.G., em rebatimento, determinando CCrr (garantindo que
CC é o vértice de menor abcissa, ou seja, o vértice que se situa mais à direita) e OOrr (OO é o centro do triângulo). Para inverter o rebatimento de
OOrr conduziu-se, por OOrr e por BBrr, uma recta rrrr – rrrr é concorrente com hhρrr
no ponto HHrr (HH é o traço horizontal da recta rr e BB é o seu traço fron-
tal). HH é um ponto da charneira, pelo que as suas projecções se determinaram imediatamente, o que nos permitiu, em seguida, determinar
as projecções da recta rr, passando pelas projecções homónimas de HH e BB. Conduzindo, por OOrr, uma perpendicular à charneira, determina-
ram-se as projecções de OO sobre as projecções homónimas de rr. CCrr situa-se na recta fronto-horizontal que passa por OOrr e cujas projecções
se determinaram a partir das projecções homónimas de OO – conduzindo, por CCrr, uma perpendicular à charneira, determinaram--se as pro-
jecções de CC sobre as projecções homónimas da recta fronto-horizontal. A partir das projecções dos três vértices do triângulo,
desenharam-se as suas projecções (a traço leve, pois trata-se de um traçado auxiliar para o objectivo do exercício, que é as projecções do
sólido). Em seguida, pelas projecções de OO conduziram-se as projecções de uma recta pp, ortogonal a ρ – a recta pp é a recta suporte do eixo
da pirâmide e é uma rreeccttaa ddee ppeerrffiill. A recta pp está definida por um ponto (o ponto OO) e pela sua direcção (é ortogonal a ρ). A recta pp é orto-
gonal às rectas de perfil do plano ρ. Para definir a recta pp conduziu-se, pela recta, um plano de perfil π e determinou-se a recta de intersec-
ção de π com ρ – recta ii (que está definida pelos seus traços, FF e HH’’). A recta ii contém o ponto OO (que é um ponto dos dois planos) e a
recta pp também – as duas rectas são perpendiculares no ponto OO. Por outro lado, ο vértice VV, da pirâmide, situa-se sobre pp, a 7 cm de OO
(a altura da pirâmide). Atendendo a que o segmento [OOVV] não se projecta em V.G. em nenhum dos planos de projecção, é necessário o
recurso a um outro processo geométrico auxiliar. Optou-se pelo rebatimento do plano π para o Plano Frontal de Projecção – a charneira foi
ffπ (recta ee’’). A recta iirr fica definida por FFrr e HH’’rr. Note que o ponto OOrr11
tem também de se situar sobre iirr, pois OO é um ponto da recta ii (OOrr11
é o
ponto OO no seu segundo rebatimento – no rebatimento do plano π). A recta pprr passa por OOrr11
e é perpendicular a iirr em OOrr11
. Sobre pprr, a partir
de OOrr11
, mediram-se os 7 cm, obtendo-se VVrr (garantindo que VV se situa no 1o Diedro). Inverteu-se o rebatimento de π, obtendo-se as projec-
ções de VV. A partir das projecções de todos os vértices do sólido, desenharam-se os seus contornos aparentes – o ccoonnttoorrnnoo aappaarreennttee ffrroonn--
ttaall é [AA22BB22VV22CC22] e o ccoonnttoorrnnoo aappaarreennttee hhoorriizzoonnttaall é [AA11BB11CC11VV11]. Em pprroojjeeccççããoo ffrroonnttaall, todos os vértices da pirâmide integram o contorno
aparente – no entanto, a base é invisível em projecção frontal, tal como a face lateral [BBCCVV]. Assim, em projecção frontal, apenas a aresta
[BBCC] da base é invisível (as restantes arestas são todas visíveis, pois situam-se na parte visível do sólido). Em pprroojjeeccççããoo hhoorriizzoonnttaall, todos
os vértices da pirâmide integram também o contorno aparente – no entanto, a base é invisível em projecção horizontal, tal como a face lateral
[AACCVV]. Assim, em projecção horizontal, apenas a aresta [AACC] da base é invisível (as restantes arestas são todas visíveis, pois situam-se na
parte visível do sólido).

136. 136
SOLUÇÕES
348.
Em primeiro lugar representou-se o plano ρ, pelos
seus traços, em função dos dados – o plano ρ tem
os seus traços simétricos em relação ao eixo XX,
pois é ortogonal ao β1/3. A recta rr é a recta do plano
a que se recorreu para determinar as projecções do
ponto QQ (a recta rr está definida pelos seus traços,
HH e FF). Uma vez que o triângulo não se projecta em
V.G. em nenhum dos planos de projecção, para
construir as suas projecções é necessário o recurso
a um processo geométrico auxiliar. Note que o ân-
gulo dado (o ângulo que um dos lados do triângulo
faz com hhρ) é um ângulo que eessttáá ccoonnttiiddoo no plano
(trata-se do ângulo entre duas rectas) e não tem
correspondência directa em projecções, pois o pla-
no ρ não é paralelo a nenhum dos planos de pro-
jecção. Ao nível da economia de traçados é
indistinto rebater o plano ρ para o Plano Frontal de
Projecção ou para o Plano Horizontal de Projecção.
Optou-se por rebater o plano ρ para o Plano Horizon-
tal de Projecção – a charneira foi hhρ. HHrr ≡ HH11, pois HH
(o traço horizontal da recta rr) é um ponto da char-
neira. Para rebater o plano ρ há que rebater o seu
traço frontal, o que se processa rebatendo um dos
seus pontos – o ponto FF (o traço frontal da recta rr),
por exemplo. Para tal, conduziu-se, por FF, uma per-
pendicular à charneira – com o compasso, fazendo
centro em FF11 e raio até FF22 (a cota de FF) transportou-
-se essa distância até ao eixo XX, o que nos permitiu
construir o triângulo do rebatimento de FF em V.G. e
determinar FFrr (ver exercício 118888). O traço frontal do
plano ρ em rebatimento, ffρrr
, passa por FFrr e é para-
lelo ao eixo XX (e a hhρrr
). Por FFrr e HHrr conduziu-se rrrr –
conduzindo, por QQ11, uma perpendicular à charneira
(que corresponde ao plano ortogonal à charneira
que contém o arco do seu rebatimento) determinou-se QQrr sobre rrrr. Com centro em QQrr, desenhou-se a circunferência circunscrita ao triângu-
lo e construiu-se o polígono, em V.G., inscrito na circunferência e de acordo com os dados. O ângulo que um lado do triângulo faz com hhρ
pode, agora, em rebatimento, ser medido em V.G. – o lado [AABB] é o lado do triângulo que faz, com hhρ, um ângulo de 20o e o vértice CC será,
assim, o vértice de menor cota do triângulo. Note que caso se tratasse da outra situação possível, em que CC seria o vértice de maior cota do
polígono, CC não se situaria no espaço do 1o Diedro, o que implica que a situação apresentada é a única solução do problema. Para inverter o
rebatimento de AArr e CCrr conduziu-se, pelos dois pontos, uma recta ssrr – ssrr é concorrente com hhρrr
em HH’’rr (HH’’ é o traço horizontal da recta ss) e é
concorrente com ffρrr
em FF’’rr (FF’’ é o traço frontal da recta ss). A recta ss é a recta suporte do lado [AACC] do triângulo. HH’’ é um ponto da charneira,
pelo que as suas projecções se determinaram imediatamente. As projecções de FF’’ determinaram-se conduzindo, por FF’’rr uma perpendicular
à charneira – FF’’ é um ponto de ffρ. A partir das projecções de FF’’ e HH’’, desenharam-se as projecções da recta ss. Conduzindo, por AArr e CCrr, as
perpendiculares à charneira que por eles passam, determinaram-se as projecções de AA e CC sobre as projecções homónimas de ss. Para in-
verter o rebatimento de BBrr conduziu-se, por AArr e BBrr, uma recta mmrr – mmrr é concorrente com ffρrr
em FF’’’’rr (FF’’’’ é o traço frontal da recta mm). A recta
mm é a recta suporte do lado [AABB] do triângulo. As projecções de FF’’’’ determinaram-se conduzindo, por FF’’’’rr uma perpendicular à charneira – FF’’’’
é um ponto de ffρ. A partir das projecções de AA e FF’’’’, desenharam-se as projecções da recta mm. Conduzindo, por BBrr, uma perpendicular à
charneira, determinaram-se as projecções de BB sobre as projecções homónimas de mm. A partir das projecções dos três vértices do triângu-
lo, desenharam-se as suas projecções (a traço leve, pois trata-se de um traçado auxiliar para o objectivo do exercício, que é as projecções
do sólido). Sobre a determinação das projecções de VV, o vértice da pirâmide, ver relatório do exercício anterior. A partir das projecções de
todos os vértices do sólido, desenharam-se os seus contornos aparentes – o ccoonnttoorrnnoo aappaarreennttee ffrroonnttaall é [AA22CC22BB22VV22] e o ccoonnttoorrnnoo aappaa--
rreennttee hhoorriizzoonnttaall é [AA11BB11CC11VV11]. Em pprroojjeeccççããoo ffrroonnttaall, todos os vértices da pirâmide integram o contorno aparente – no entanto, a base é in-
visível em projecção frontal, tal como a face lateral [AABBVV]. Assim, em projecção frontal, apenas a aresta [AABB] da base é invisível (as restantes
arestas são todas visíveis, pois situam-se na parte visível do sólido). Em pprroojjeeccççããoo hhoorriizzoonnttaall, todos os vértices da pirâmide integram tam-
bém o contorno aparente – no entanto, a base é invisível em projecção horizontal, tal como a face lateral [AACCVV]. Assim, em projecção hori-
zontal, apenas a aresta [AACC] da base é invisível (as restantes arestas são todas visíveis, pois situam-se na parte visível do sólido).

137. 137
SOLUÇÕES
349.
Em primeiro lugar representou-se o ponto AA, pelas suas projecções, em função dos dados. Os dados permitiram-nos, ainda, determinar as
projecções de BB – o lado [AABB] é fronto-horizontal e projecta-se em V.G. em ambos os planos de projecção. A recta gg é a recta fronto-hori-
zontal que passa por AA e BB. O plano está definido por um ponto (o ponto AA) e pela sua orientação (é dada a amplitude do diedro que o pla-
no faz com o Plano Horizontal de Projecção). O primeiro problema que o exercício nos coloca é a determinação dos traços do plano, o que
poderia ser resolvido com o recurso a uma recta de perfil do plano, passando por AA, e com o rebatimento do plano de perfil que contivesse
a recta. No entanto, optou-se por uma situação diferente – o recurso a uma mudança do diedro de projecção, transformando o plano ρ num
plano de topo. Assim, substituiu-se o Plano Frontal de Projecção (ppllaannoo 22) por um novo plano de projecção (ppllaannoo 44), ortogonal ao plano ρ
– o novo eixo XX (o eixo XX’’) é a recta de intersecção do ppllaannoo 11 (o Plano Horizontal de Projecção, que se manteve) com o ppllaannoo 44 e é per-
pendicular ao eixo XX. As projecções de AA e BB no ppllaannoo 44 determinaram-se em função da sua cota (que é a mesma), que se manteve, o que
nos permitiu, também, determinar a projecção da recta gg no ppllaannoo 44 – a recta gg, no novo diedro de projecção, é uma recta de topo, razão
pela qual se assinalou gg44 entre parêntesis. O plano ρ, no novo diedro de projecção, é um plano de topo e o diedro que o plano faz com o
Plano Horizontal de Projecção projecta-se em V.G. no ppllaannoo 44 – assim, o traço do plano ρ no ppllaannoo 44 (ff44ρ
) passa por AA44 (e por BB44) e faz,
com o eixo XX’’, um ângulo de 40o (o ângulo dado). Uma vez que os dois traços do planos são concorrentes no eixo XX’’, pelo ponto em que ff44ρ
intersecta o eixo XX conduziu-se uma paralela ao eixo XX inicial, que é hhρ. Em seguida, recorrendo a um ponto MM, do plano (e com afastamen-
to nulo no diedro de projecção inicial), determinou-se ffρ (o traço frontal do plano ρ no diedro de projecção inicial) – MM é um ponto de ffρ. O
triângulo não se projecta em V.G., pois o plano ρ não é paralelo a nenhum dos planos de projecção – é necessário o recurso a um processo
geométrico auxiliar. Aproveitando a mudança do diedro de projecção efectuada, procedeu-se ao rebatimento do plano ρ como plano projec-
tante (no novo diedro de projecção, o plano ρ é um plano de topo). A charneira foi hhρ (hhρ ≡ ee11 ≡ hhρrr
) que, no novo diedro de projecção, é
uma recta de topo – a projecção da charneira no ppllaannoo 44 é um ponto (ee44), que se assinalou devidamente entre parêntesis. Para rebater o
traço frontal do plano (ffρ) efectuou-se o rebatimento do ponto MM (que é um ponto de ffρ), pelo rebatimento do plano de topo (sugere-se que
o aluno ponha a folha de papel com o eixo XX’’ na horizontal, para melhor entendimento deste processo), obtendo MMrr – ffρrr
passa por MMrr e é
paralelo a hhρrr
. Também através do rebatimento do plano de topo se rebateram os pontos AA e BB. A partir de AArr e BBrr, construiu-se o triângulo
[AABBCC], em V.G., em rebatimento, e determinou-se ainda OOrr, o centro do triângulo. Para determinar as projecções de CC conduziu-se, por CCrr
uma recta rrrr – a recta rr é a recta suporte do lado [AACC] do triângulo. A recta rrrr é concorrente com hhρrr
em HHrr (HH é o traço horizontal da recta rr)
(Continua na página seguinte)

138. 138
SOLUÇÕES
350. RReessoolluuççããoo
e é concorrente com ffρrr
em FFrr (FF é o traço frontal da recta rr). HH é um ponto da charneira, pelo que as suas projecções se determinaram ime-
diatamente. As projecções de FF determinaram-se conduzindo, por FFrr, uma perpendicular à charneira – FF é um ponto de ffρ. A partir das pro-
jecções de FF e HH, desenharam-se as projecções da recta rr (note que as projecções da recta rr passam pelas projecções homónimas do
ponto AA, que é um ponto da recta – bastaria o traço horizontal da recta e o ponto AA para desenhar as projecções da recta). Conduzindo, por
CCrr, uma perpendicular à charneira, determinaram-se as projecções de CC sobre as projecções homónimas de rr. Para inverter o rebatimento
de OOrr conduziu-se, por OOrr, uma recta mmrr, fronto-horizontal – mmrr é concorrente com rrrr num ponto PPrr, cujas projecções se determinaram ime-
diatamente, sobre as projecções homónimas da recta rr. Pelas projecções de PP conduziram-se as projecções homónimas de mm. Conduzin-
do, por OOrr, uma perpendicular à charneira, determinaram-se as projecções de OO sobre as projecções homónimas de mm. A partir das
projecções dos três vértices do triângulo [AABBCC], desenharam-se as suas projecções (a traço leve, pois trata-se de um traçado auxiliar para o
objectivo do exercício, que é as projecções do sólido). O problema seguinte consiste em determinar as projecções do vértice DD (o quarto
vértice do tetraedro), pois não é conhecida a altura do sólido – apenas se sabe que as suas arestas têm todas o mesmo comprimento.
Assim, o ponto DD situa-se numa recta ortogonal ao plano ρ que passa por OO, estando equidistante dos outros três vértices do sólido. A recta
ortogonal ao plano ρ que passa por OO é uma recta de perfil (recta pp) e a aresta [CCDD] também é de perfil, pelo que é possível resolver o exer-
cício em rebatimento, recorrendo ao rebatimento do plano de perfil que contém as duas rectas (a recta pp e a recta suporte da aresta [CCDD]).
No entanto, atendendo à mudança do diedro de projecção efectuada, há que reconhecer que o ppllaannoo 44 é paralelo à aresta [CCDD], pelo que
esta se projecta em V.G. no ppllaannoo 44. Por outro lado, na mudança do diedro de projecção efectuada, o plano ρ é um plano de topo e a orto-
gonalidade entre a recta pp e o plano ρ também é directa. Assim, o processo mais simples consiste, efectivamente, em recorrer à mudança
do diedro de projecção, para concluir o exercício. Em primeiro lugar, determinaram-se as projecções de OO e CC no ppllaannoo 44, através das
linhas de chamada (perpendiculares ao eixo XX’’) que passam por OO11 e CC11 – OO44 e CC44 situam-se sobre ff44ρ
, pois no novo diedro de projecção, o
plano ρ é projectante frontal. A projecção da recta pp, no ppllaannoo 44, passa por OO44 e é perpendicular a ff44ρ
. Com o compasso, fazendo centro em
CC44 e com 6 cm de raio (a medida da aresta do tetraedro, que é a medida do lado do triângulo [AABBCC]), determinou-se DD44 sobre pp44. DD11 teve
determinação directa, a partir de DD44, e DD22 determinou-se através da cota de DD (que se manteve). A partir das projecções de todos os vértices
do sólido, desenharam-se os seus contornos aparentes – o ccoonnttoorrnnoo aappaarreennttee ffrroonnttaall é [AA22BB22DD22] e o ccoonnttoorrnnoo aappaarreennttee hhoorriizzoonnttaall é
[AA11CC11BB11DD11]. Em pprroojjeeccççããoo ffrroonnttaall, há um vértice que não integra o contorno aparente – o vértice CC, que é o vértice de menor afastamento
do sólido, pelo que é invisível bem como todas as arestas que nele convergem. Note que a face [AABBDD] é a única face visível em projecção
frontal. Em pprroojjeeccççããoo hhoorriizzoonnttaall, todos os vértices da pirâmide integram o contorno aparente – no entanto, a face [AABBCC] é invisível em pro-
jecção horizontal, tal como a face [AABBDD]. Assim, em projecção horizontal, apenas a aresta [AABB] é invisível.
(Relatório na página seguinte)

139. 139
SOLUÇÕES
350. RReellaattóórriioo
Em primeiro lugar representaram-se os pontos AA e BB, pelas suas projecções, em função dos dados. Em seguida, desenhou-se o traço hori-
zontal do plano ρ – BB tem cota nula, pelo que hhρ passa por BB1. Por AA e BB conduziu-se uma recta rr, do plano, e determinou-se o seu traço
frontal – ffρ passa por FF22. Uma vez que o quadrado não se projecta em V.G. em nenhum dos planos de projecção, para construir as suas pro-
jecções é necessário o recurso a um processo geométrico auxiliar. Uma vez que o ponto BB é um ponto do Plano Horizontal de Projecção,
ao nível da economia de traçados é preferível efectuar o rebatimento do plano ρ para o Plano Horizontal de Projecção (economiza-se o re-
batimento de um ponto). Rebateu-se o plano ρ para o Plano Horizontal de Projecção – a charneira foi hhρ. BBrr ≡ BB11, pois BB é um ponto da
charneira. Para rebater o plano ρ há que rebater o seu traço frontal, o que se processa rebatendo um dos seus pontos – o ponto FF (que é
um ponto de ffρ), por exemplo. Para tal, conduziu-se, por FF, uma perpendicular à charneira – com o compasso, fazendo centro em FF11 e raio
até FF22 (a cota de FF) transportou-se essa distância até ao eixo XX, o que nos permitiu construir o triângulo do rebatimento de FF em V.G. e de-
terminar FFrr (ver exercício 118888). O traço frontal do plano ρ em rebatimento, ffρrr
, passa por FFrr e é paralelo ao eixo XX (e a hhρrr
). A recta rrrr está de-
finida por BBrr e por FFrr. Conduzindo, por AA11, uma perpendicular à charneira, determinou-se AArr sobre rrrr. A partir de AArr e BBrr construiu-se o
quadrado em V.G., em rebatimento, determinando CCrr e DDrr. Para inverter o rebatimento de CCrr e DDrr conduziu-se, pelos dois pontos, uma recta
ssrr, paralela à recta rrrr. A recta ssrr é concorrente com ffρrr
no ponto FF’’rr (FF’’ é o traço frontal da recta ss). Note que o traço horizontal da recta ss se
situa fora dos limites do desenho. Conduzindo, por FF’’rr, uma perpendicular à charneira, determinaram-se as projecções de FF’’ – FF’’ é um pon-
to de ffρ. As projecções da recta ss determinaram-se imediatamente – passam pelas projecções homónimas de FF’’ e são paralelas às projec-
ções homónimas da recta rr (a recta ss está definida por um ponto e uma direcção). Conduzindo, por CCrr e DDrr, as perpendiculares à charneira
que por eles passam, determinaram-se as projecções de CC e DD sobre as projecções homónimas da recta ss. A partir das projecções dos
quatro vértices do quadrado, desenharam-se as suas projecções (a traço leve, pois trata-se de um traçado auxiliar para o objectivo do exer-
cício, que é as projecções do sólido). Em seguida, pelas projecções de AA conduziram-se as projecções de uma recta pp, ortogonal a ρ – a
recta pp é a recta suporte da aresta lateral [AAAA’’] e é uma rreeccttaa ddee ppeerrffiill (que está definida por um ponto – AA – e pela sua direcção – é orto-
gonal a ρ). A recta pp é ortogonal às rectas de perfil do plano ρ. Para definir a recta pp conduziu-se, pela recta, um plano de perfil π e
determinou-se a recta de intersecção de π com ρ – recta ii (que está definida pelos seus traços, FF’’’’ e HH). A recta ii contém o ponto AA (que é
um ponto dos dois planos) e a recta pp também – as duas rectas são perpendiculares no ponto AA. Por outro lado, ο vértice AA’’ situa-se sobre
pp, a 7 cm de AA (a altura do prisma). Atendendo a que o segmento [AAAA’’] não se projecta em V.G. em nenhum dos planos de projecção,
recorreu-se ao rebatimento do plano π para o Plano Frontal de Projecção – a charneira foi ffπ (recta ee’’). A recta iirr fica definida por FF’’’’rr e HHrr.
Note que o ponto AArr11
tem também de se situar sobre iirr, pois AA é um ponto da recta ii (AArr11
é o ponto AA no seu segundo rebatimento – no
rebatimento do plano π). A recta pprr passa por AArr11
e é perpendicular a iirr em AArr11
. Sobre pprr, a partir de AArr11
, mediram-se os 7 cm, obtendo-se
AA’’rr (garantindo que AA’’ se situa no 1o Diedro). Inverteu-se o rebatimento de π, obtendo-se as projecções de AA’’. A partir das projecções de AA’’
desenharam-se as projecções do quadrado [AA’’BB’’CC’’DD’’], cujos lados são paralelos aos lados correspondentes do quadrado [AABBCCDD] – BB’’, CC’’ e DD’’
estão nas rectas de perfil ortogonais a ρ que contêm BB, CC e DD, respectivamente. Assim, pelas projecções de AA’’ conduziram-se as projec-
ções homónimas da recta suporte do segmento [AA’’BB’’], até encontrarem as projecções homónimas da recta de perfil que contém a aresta
lateral [BBBB’’] – o ponto de concorrência das duas rectas é BB’’. Repetiu-se o processo para DD’’, a partir de AA’’, e ainda para CC’’, a partir de BB’’ ou
de DD’’. A partir das projecções de todos os vértices do sólido, desenharam-se os seus contornos aparentes – o ccoonnttoorrnnoo aappaarreennttee ffrroonnttaall é
[AA22BB22CC22CC’’22DD’’22AA’’22] e o ccoonnttoorrnnoo aappaarreennttee hhoorriizzoonnttaall é [AA11AA’’11BB’’11CC’’11CC11DD11]. Em pprroojjeeccççããoo ffrroonnttaall, existem dois vértices que não integram o
contorno aparente – o vértice BB’’ (que é o vértice de maior afastamento, pelo que é visível bem como todas as arestas que nele convergem)
e o vértice DD (que é o vértice de menor afastamento, pelo que é invisível bem como todas as arestas que nele convergem). Em pprroojjeeccççããoo
hhoorriizzoonnttaall, também existem dois vértices que não integram o contorno aparente – o vértice DD’’ (que é o vértice de maior cota, pelo que é
visível bem como todas as arestas que nele convergem) e o vértice BB (que é o vértice de menor cota, pelo que é invisível bem como todas
as arestas que nele convergem). Note que a base [AABBCCDD] é invisível em ambas as projecções e que a base [AA’’BB’’CC’’DD’’] é visível em ambas
as projecções. Em projecção horizontal, as faces laterais [CCCC’’DD’’DD] e [AAAA’’DD’’DD] são visíveis – no entanto, estas faces são invisíveis em projecção
frontal. Já as faces [AAAA’’BB’’BB] e [BBBB’’CC’’CC], são visíveis em projecção frontal e invisíveis em projecção horizontal.

140. 140
SOLUÇÕES
351.
Em primeiro lugar representaram-se os pontos RR e SS, pelas suas projec-
ções, em função dos dados. Por RR e SS conduziu-se uma recta rr, do plano,
e determinaram-se os seus traços nos planos de projecção – pelos traços
da recta conduziram-se os traços homónimos do plano ρ. Uma vez que o
triângulo não se projecta em V.G. em nenhum dos planos de projecção,
para construir as suas projecções é necessário o recurso a um processo
geométrico auxiliar. Optou-se por rebater o plano ρ para o Plano Horizontal
de Projecção – a charneira foi hhρ. HHrr ≡ HH11, pois HH (o traço horizontal da
recta rr) é um ponto da charneira. Para rebater o plano ρ há que rebater o
seu traço frontal, o que se processa rebatendo um dos seus pontos – o
ponto FF (o traço frontal da recta rr, que é um ponto de ffρ), por exemplo.
Para tal, conduziu-se, por FF, uma perpendicular à charneira – com o com-
passo, fazendo centro em FF11 e raio até FF22 (a cota de FF) transportou-se
essa distância até ao eixo XX, o que nos permitiu construir o triângulo do
rebatimento de FF em V.G. e determinar FFrr (ver exercício 118888). O traço frontal
do plano ρ em rebatimento, ffρrr
, passa por FFrr e é paralelo ao eixo XX (e a hhρrr
).
A recta rrrr está definida por HHrr e por FFrr. Conduzindo, por RR11 e por SS11, as
perpendiculares à charneira que por eles passam, determinaram-se RRrr e
SSrr sobre rrrr. A partir de RRrr e SSrr construiu-se o triângulo equilátero [RRrrSSrrTTrr]
em V.G., em rebatimento, determinando TTrr. Para inverter o rebatimento de
TTrr conduziu-se, pelo ponto, uma recta ssrr, paralela à recta rrrr. A recta ssrr é
concorrente com ffρrr
no ponto FF’’rr (FF’’ é o traço frontal da recta ss) e é con-
corrente com hhρrr
no ponto HH’’rr (HH’’ é o traço horizontal da recta ss). Condu-
zindo, por FF’’rr, uma perpendicular à charneira, determinaram-se as
projecções de FF’’ – FF’’ é um ponto de ffρ. HH’’rr ≡ HH’’11, pois HH’’ é um ponto da
charneira. As projecções da recta ss determinaram-se imediatamente –
passam pelas projecções homónimas de FF’’ e HH’’ (e são paralelas às pro-
jecções homónimas da recta rr). Conduzindo, por TTrr, uma perpendicular
à charneira, determinaram-se as projecções de TT sobre as projecções
homónimas da recta ss. A partir das projecções dos três vértices do triân-
gulo, desenharam-se as suas projecções (a traço leve, pois trata-se de
um traçado auxiliar para o objectivo do exercício, que é as projecções do
sólido). Em seguida, pelas projecções de RR conduziram-se as projecções de uma recta pp, ortogonal a ρ – a recta pp é a recta suporte da aresta
lateral [RRRR’’] e é uma rreeccttaa ddee ppeerrffiill (que está definida por um ponto – RR – e pela sua direcção – é ortogonal a ρ). A determinação das projec-
ções do ponto RR’’, o extremo superior da aresta lateral [RRRR’’] determinou-se conforme exposto no relatório do exercício anterior para o ponto AA’’.
O plano π é o plano de perfil que contém a recta pp. A recta ii (definida por FF’’’’ e por HH’’’’) é a recta de intersecção do plano π com o plano ρ.
Rebateu-se o plano π para o Plano Frontal de Projecção – iirr fica definida por FF’’’’rr e por HH’’’’rr (e passa por RRrr11
). A recta pprr é perpendicular a iirr em
RRrr11
. RR’’rr situa-se sobre pprr a 6 cm de RRrr11
(a altura do prisma). Invertendo o rebatimento, determinaram-se as projecções de RR’’. A partir das
projecções de RR’’ desenharam-se as projecções do triângulo [RR’’SS’’TT’’], cujos lados são paralelos aos lados correspondentes do triângulo [RRSSTT]
– SS’’ e TT’’ estão nas rectas de perfil ortogonais a ρ que contêm SS e TT, respectivamente. Assim, pelas projecções de RR’’ conduziram-se as projec-
ções homónimas da recta suporte do segmento [RR’’SS’’], até encontrarem as projecções homónimas da recta de perfil que contem a aresta lateral
[SSSS’’] – o ponto de concorrência das duas rectas é SS’’. Repetiu-se o processo para TT’’, a partir de RR’’. A partir das projecções de todos os vértices
do sólido, desenharam-se os seus contornos aparentes – o ccoonnttoorrnnoo aappaarreennttee ffrroonnttaall é [SS22SS’’22RR’’22TT’’22TT22] e o ccoonnttoorrnnoo aappaarreennttee hhoorriizzoonnttaall é
[RR11SS11SS’’11TT’’11TT11]. Em pprroojjeeccççããoo ffrroonnttaall, existe um vértice que não integra o contorno aparente – o vértice RR’’, que é o vértice de menor afasta-
mento, pelo que é invisível bem como todas as arestas que nele convergem. Em pprroojjeeccççããoo hhoorriizzoonnttaall, também existe um vértice que não inte-
gra o contorno aparente – o vértice RR’’, que é o vértice de maior cota, pelo que é visível bem como todas as arestas que nele convergem. Note
que a base [RRSSTT] é invisível em ambas as projecções e que a base [RR’’SS’’TT’’] é visível em ambas as projecções. Em projecção horizontal, as faces
laterais [RRRR’’SS’’SS] e [RRRR’’TT’’TT] são visíveis – no entanto, estas faces são invisíveis em projecção frontal. Já a face lateral [SSSS’’TT’’TT] é visível em
projecção frontal e invisível em projecção horizontal.
352.
Em primeiro lugar representou-se o plano ρ, pelos seus traços, em função dos dados. O plano ρ é ortogonal ao β1/3, pelo que os seus traços
são simétricos em relação ao eixo XX. Uma vez que a circunferência circunscrita ao rectângulo [AABBCCDD] é tangente aos dois planos de projec-
ção, sabe-se que a circunferência é tangente aos dois traços do plano. Por outro lado, uma vez que a diagonal [AACC] do plano é de perfil e que
AA tem cota nula, sabe-se que a circunferência será tangente a hhρ em AA. É possível, imediatamente, determinar as projecções de AA (que é um
ponto de hhρ). Por outro lado, atendendo a que CC será o outro extremo da diagonal, CC terá de ser o ponto em que a circunferência será tangente
a ffρ – este raciocínio permite-nos, imediatamente, determinar as projecções de CC (que é um ponto de ffρ com a mesma abcissa de AA). Só é pos-
sível desenhar a circunferência em V.G., com o recurso a um processo geométrico auxiliar, pois o plano ρ não é paralelo a nenhum dos planos
de projecção. Optou-se pelo rebatimento do plano ρ. Uma vez que o ponto AA é um ponto do Plano Horizontal de Projecção e que CC é um ponto
do Plano Frontal de Projecção, ao nível da economia de traçados é indistinto efectuar o rebatimento do plano ρ para o Plano Horizontal de Pro-
jecção ou para o Plano Frontal de Projecção. Optou-se por rebater o plano ρ para o Plano Horizontal de Projecção – a charneira foi hhρ. AArr ≡ AA11,
pois AA é um ponto da charneira. Para rebater o plano ρ há que rebater o seu traço frontal, o que se processa rebatendo um dos seus pontos –
o ponto CC, por exemplo. Para tal, conduziu-se, por CC, uma perpendicular à charneira – com o compasso, fazendo centro em CC11 e raio até CC22
(Continua na página seguinte)

141. 141
SOLUÇÕES
353.
Em primeiro lugar representou-se o plano ρ, pelos seus traços (que estão coincidentes no eixo XX) e pelo ponto AA. Uma vez que o triângulo
não se projecta em V.G. em nenhum dos planos de projecção, para construir as suas projecções é necessário o recurso a um processo
geométrico auxiliar. Optou-se pelo rebatimento do plano ρ para o Plano Horizontal de Projecção – a charneira foi hhρ (que é o próprio eixo XX).
O ponto AA rebateu-se pelo triângulo do rebatimento (ver exercício 119955 e respectivo relatório). Em rebatimento, construiu-se o triângulo equi-
látero [AABBCC] em V.G., em função dos dados. O ângulo que o lado [AABB] faz com o eixo XX é o âânngguulloo rreeaall, no espaço, e não em projecções,
pelo que só é possível medir esse ângulo em V.G., em rebatimento. Por AArr conduziu-se uma recta fazendo um ângulo de 45o com o eixo XX,
de forma a que BBrr se situe nessa recta à esquerda de AA e tenha cota inferior a AA – essa recta é rrrr, que é a recta suporte do lado [AABB] em
rebatimento. Sobre rrrr mediram-se os 5 cm (o lado do triângulo) e determinou-se BBrr, sobre rrrr. A partir de AArr e BBrr construiu-se o triângulo equi-
látero [AArrBBrrCCrr] em V.G., em rebatimento, e determinou-se OOrr, o centro do triângulo. Em seguida, inverteu-se o rebatimento do plano, inver-
tendo o rebatimento dos pontos CCrr e OOrr, com o recurso a rectas oblíquas do plano (que são rectas passantes). As projecções da recta rr
determinam-se imediatamente – passam pelas projecções homónimas do ponto AA e são concorrentes entre si no ponto de concorrência
(a cota de CC), transportou-se essa distância até ao eixo XX, o que nos
permitiu construir o triângulo do rebatimento de CC em V.G. e determinar
CCrr (ver exercício 118888). O traço frontal do plano ρ em rebatimento, ffρrr
,
passa por CCrr e é paralelo ao eixo XX (e a hhρrr
). Em rebatimento, deter-
minou-se o ponto médio de [AArrCCrr] (com o recurso à construção da
mediatriz de um segmento de recta) e, com centro nesse ponto e raio
até AArr (ou CCrr), desenhou-se a circunferência circunscrita ao rectângulo,
em V.G., em rebatimento (note que a circunferência é tangente a ffρrr
em CCrr e é tangente a hhρrr
em AArr). Em rebatimento, efectuou-se a cons-
trução do rectângulo, inscrito na circunferência, de acordo com os
dados. Tenha em conta que o ângulo dado (o ângulo que o lado [AABB]
do rectângulo faz com hhρ) é um ângulo que eessttáá ccoonnttiiddoo no plano
(trata-se do ângulo entre duas rectas) e não tem correspondência
directa em projecções, pois o plano ρ não é paralelo a nenhum dos
planos de projecção. O ângulo que [AABB] faz com hhρ pode, em rebati-
mento, ser medido em V.G. – com vértice em AArr, mediram-se os 25o
com hhρrr
, com abertura para a direita, garantindo que o vértice BB se si-
tua à direita de AA (note que BBrr tem de se situar sobre a circunferência).
A partir de BBrr, determinou-se DDrr, sobre a circunferência e no
extremo oposto do diâmetro que passa por BBrr. Para inverter o rebati-
mento de BBrr e DDrr conduziu-se, pelos dois pontos, uma recta rrrr (a recta rr
é a recta suporte da diagonal [BBDD]). A recta rrrr é concorrente com ffρrr
no
ponto FFrr (FF é o traço frontal da recta rr) e é concorrente com hhρrr
no ponto
HHrr (HH é o traço horizontal da recta rr). Conduzindo, por FFrr, uma perpen-
dicular à charneira, determinaram-se as projecções de FF – FF é um ponto
de ffρ. HHrr ≡ HH11, pois HH é um ponto da charneira. As projecções da recta
rr determinaram-se imediatamente – passam pelas projecções homóni-
mas de FF e HH. Conduzindo, por BBrr e DDrr, as perpendiculares à charneira
que por eles passam, determinaram-se as projecções de BB e DD sobre
as projecções homónimas da recta rr. A partir das projecções dos quatro
vértices do rectângulo, desenharam-se as suas projecções (a traço
leve, pois trata-se de um traçado auxiliar para o objectivo do exercício, que é as projecções do sólido). Em seguida, pelas projecções de AA
conduziram-se as projecções de uma recta pp, ortogonal a ρ – a recta pp é a recta suporte da aresta [AAAA’’] (sendo [AA’’BB’’CC’’DD’’] a face superior
do paralelepípedo) e é uma rreeccttaa ddee ppeerrffiill (que está definida por um ponto – AA – e pela sua direcção – é ortogonal a ρ). A determinação das
projecções do ponto AA’’, o extremo superior da aresta [AAAA’’] determinou-se conforme exposto no relatório do exercício 335500. O plano π é o plano
de perfil que contém a recta pp. A recta ii é a recta de intersecção do plano π com o plano ρ (note que a recta ii está definida por AA e por CC, que
são os seus traços nos planos de projecção – AA é o traço horizontal de ii e CC é o seu traço frontal). Rebateu-se o plano π para o Plano Frontal
de Projecção – iirr fica definida por AArr11
e por CCrr11
(note que AArr11
e CCrr11
são, respectivamente, os pontos AA e CC rebatidos pelo seu segundo rebati-
mento – o rebatimento do plano π). A recta pprr é perpendicular a iirr em AArr11
. AA’’rr situa-se sobre pprr a 4 cm de AArr11
(a altura do sólido). Invertendo o
rebatimento, determinaram-se as projecções de AA’’. A partir das projecções de AA’’ desenharam-se as projecções do rectângulo [AA’’BB’’CC’’DD’’], cujos
lados são paralelos aos lados correspondentes do rectângulo [AABBCCDD] – BB’’, CC’’ e DD’’ estão nas rectas de perfil ortogonais a ρ que contêm BB, CC e DD,
respectivamente (ver relatório do exercício 335500). A partir das projecções de todos os vértices do sólido, desenharam-se os seus contornos
aparentes – o ccoonnttoorrnnoo aappaarreennttee ffrroonnttaall é [AA22BB22BB’’22CC’’22DD’’22DD22] e o ccoonnttoorrnnoo aappaarreennttee hhoorriizzoonnttaall é [CC11DD11DD’’11AA’’11BB’’11BB11]. Em pprroojjeeccççããoo ffrroonnttaall,
existem dois vértices que não integram o contorno aparente – o vértice AA’’ (que é o vértice de maior afastamento, pelo que é visível bem como
todas as arestas que nele convergem) e o vértice CC (que é o vértice de menor afastamento, pelo que é invisível bem como todas as arestas
que nele convergem). Em pprroojjeeccççããoo hhoorriizzoonnttaall, também existem dois vértices que não integram o contorno aparente – o vértice CC’’ (que é
o vértice de maior cota, pelo que é visível bem como todas as arestas que nele convergem) e o vértice AA (que é o vértice de menor cota,
pelo que é invisível bem como todas as arestas que nele convergem). Note que a face [AABBCCDD] é invisível em ambas as projecções e que a
face [AA’’BB’’CC’’DD’’] é visível em ambas as projecções. Em projecção horizontal, as faces [CCCC’’DD’’DD] e [BBBB’’CC’’CC] são visíveis – no entanto, estas faces
são invisíveis em projecção frontal. Já as faces [AAAA’’BB’’BB] e [AAAA’’DD’’DD] são visíveis em projecção frontal e invisíveis em projecção horizontal.
(Continua na página seguinte)

142. 142
SOLUÇÕES
da recta rr com o eixo XX. Conduzindo, por BBrr, uma perpendicular à
charneira (que corresponde ao plano ortogonal à charneira que
contém o arco do seu rebatimento), determinaram-se as projecções
de BB sobre as projecções homónimas da recta rr. A recta ssrr é a recta
paralela à recta rrrr que passa por OOrr – as projecções da recta ss
determinaram-se imediatamente, paralelas às projecções homó-
nimas da recta rr. A recta ss está definida por um ponto (o seu ponto
de concorrência com o eixo XX, que é fixo) e por uma direcção
(é paralela à recta rr). Conduzindo, por OOrr, uma perpendicular à
charneira (que corresponde ao plano ortogonal à charneira que
contém o arco do seu rebatimento), determinaram-se as projecções
de OO sobre as projecções homónimas da recta ss. A recta mmrr é a
recta paralela às rectas rrrr e ssrr que passa por CCrr – as projecções da
recta mm determinaram-se imediatamente, paralelas às projecções
homónimas das rectas rr e ss. A recta mm está definida por um ponto
(o seu ponto de concorrência com o eixo XX, que é fixo) e por uma
direcção (é paralela às rectas rr e ss). Conduzindo, por CCrr, uma per-
pendicular à charneira (que corresponde ao plano ortogonal à char-
neira que contém o arco do seu rebatimento), determinaram-se as
projecções de CC sobre as projecções homónimas da recta mm.
A partir das projecções dos três vértices do triângulo, desenharam-
-se as suas projecções (a traço leve, pois trata-se de um traçado
auxiliar para o objectivo do exercício, que é as projecções do sólido).
Em seguida, pelas projecções de OO conduziram-se as projecções
de uma recta pp, ortogonal a ρ – a recta pp é a recta suporte do eixo da pirâmide e é uma rreeccttaa ddee ppeerrffiill (que está definida por um ponto – OO – e
pela sua direcção – é ortogonal a ρ). A recta pp é ortogonal às rectas de perfil do plano ρ. Para definir a recta pp conduziu-se, pela recta, um plano
de perfil π e determinou-se a recta de intersecção de π com ρ – recta ii (que está definida pelo ponto OO e pelo seu ponto de concorrência com o
eixo XX, pois trata-se de uma rreeccttaa ddee ppeerrffiill ppaassssaannttee). A recta ii contém o ponto OO (que é um ponto dos dois planos) e a recta pp também – as
duas rectas são perpendiculares no ponto OO. Por outro lado, ο vértice VV, da pirâmide, situa-se sobre pp e, uma vez que tem cota nula, será o traço
horizontal da recta pp. A determinação do traço horizontal da recta pp implica o recurso a um processo geométrico auxiliar. Optou-se pelo rebati-
mento do plano π para o Plano Frontal de Projecção – a charneira foi ffπ (recta ee’’). A recta iirr fica definida por OOrr11
e pelo seu ponto de concorrência
com o eixo XX, que é fixo, pois é um ponto da charneira (OOrr11
é o ponto OO no seu segundo rebatimento – no rebatimento do plano π). A recta pprr
passa por OOrr11
e é perpendicular a iirr em OOrr11
. Em rebatimento, determinou-se o traço horizontal da recta pp, que é VVrr – invertendo o rebatimento,
determinaram-se as projecções de VV. A partir das projecções de todos os vértices do sólido, desenharam-se os seus contornos aparentes – o
ccoonnttoorrnnoo aappaarreennttee ffrroonnttaall é [AA22VV22BB22CC22] e o ccoonnttoorrnnoo aappaarreennttee hhoorriizzoonnttaall é [AA11BB11CC11VV11]. Em pprroojjeeccççããoo ffrroonnttaall, todos os vértices do sólido
integram o contorno aparente frontal. No entanto, a base da pirâmide é invisível, bem como a face lateral [AABBVV], pelo que a única aresta invisí-
vel em projecção frontal é a aresta [AABB] da base. Em pprroojjeeccççããoo hhoorriizzoonnttaall, todos os vértices integram, igualmente, o contorno aparente hori-
zontal. No entanto, ao contrário da projecção frontal, a base é visível, bem como a face lateral [AACCVV] – as faces laterais [AABBVV] e [BBCCVV] são
ambas invisíveis em projecção horizontal, pelo que a aresta lateral [BBVV] é a única aresta invisível, em projecção horizontal. Note que a base do
sólido é visível em projecção horizontal e invisível em projecção frontal, pois o plano ρ é um plano em tensão.
354.
Em primeiro lugar representou-se o plano ρ, pelos seus traços (que estão coincidentes no eixo XX) e pelo ponto OO. Uma vez que o quadrado
não se projecta em V.G. em nenhum dos planos de projecção, para construir as suas projecções é necessário o recurso a um processo
geométrico auxiliar. Optou-se pelo rebatimento do plano ρ para o Plano Horizontal de Projecção – a charneira foi hhρ (que é o próprio eixo XX).
O ponto OO rebateu-se pelo triângulo do rebatimento (ver exercício 119955 e respectivo relatório). Em rebatimento, com o compasso, fazendo
centro em OOrr e com 4 cm de raio, desenhou-se a circunferência circunscrita ao quadrado e construiu-se o quadrado [AABBCCDD] em V.G., em
função dos dados. O ângulo que o lado [AABB] faz com o eixo XX é o âânngguulloo rreeaall, no espaço, e não em projecções, pelo que só é possível medir
esse ângulo em V.G., em rebatimento. A diagonal [AACC] faz um ângulo de 45o com o lado [AABB] que, por sua vez, faz um ângulo de 20o com o
eixo XX – a diagonal [AACC] faz, assim, um ângulo de 65o com o eixo XX (20o+45o = 65o). Este raciocínio permitiu-nos efectuar a construção do
quadrado, em rebatimento. Note que se garantiu que AA é o vértice de menor afastamento do quadrado (é o vértice mais próximo do eixo XX)
e que se situa à direita de BB. Em seguida, inverteu-se o rebatimento do plano, invertendo o rebatimento dos vértices do quadrado, com o re-
curso a rectas oblíquas do plano (que são rectas passantes). A recta rrrr é a recta suporte da diagonal [BBDD] do quadrado em rebatimento – note
que rrrr passa por OOrr. As projecções da recta rr determinam-se imediatamente – passam pelas projecções homónimas de OO e são concorrentes
entre si no ponto de concorrência da recta rr com o eixo XX. Conduzindo, por BBrr e DDrr, as perpendiculares à charneira que por eles passam (e
que correspondem aos planos ortogonais à charneira que contêm os respectivos arcos do rebatimento), determinaram-se as projecções de
BB e DD sobre as projecções homónimas da recta rr. A recta ssrr é a recta suporte do lado [AABB] do quadrado, em rebatimento. As projecções da
recta ss determinam-se imediatamente – passam pelas projecções homónimas de BB e são concorrentes entre si no ponto de concorrência da
recta ss com o eixo XX. Conduzindo, por AArr, uma perpendicular à charneira (que corresponde ao plano ortogonal à charneira que contém o
arco do seu rebatimento), determinaram-se as projecções de AA sobre as projecções homónimas da recta ss. A recta mmrr é a recta suporte do
lado [CCDD] do quadrado, em rebatimento – note que mmrr é paralela a ssrr. As projecções da recta mm determinam-se imediatamente – passam
(Continua na página seguinte)

143. 143
SOLUÇÕES
pelas projecções homónimas de DD e são paralelas às projecções homónimas da recta ss (a recta mm está definida por um ponto (o ponto DD) e
por uma direcção (é paralela à recta ss) – note que o ponto de concorrência da recta mm com o eixo XX se situa fora dos limites do desenho, mas
que já tínhamos as projecções do ponto DD. Conduzindo, por CCrr, uma perpendicular à charneira (que corresponde ao plano ortogonal à char-
neira que contém o arco do seu rebatimento), determinaram-se as projecções de CC sobre as projecções homónimas da recta mm. A partir das
projecções dos quatro vértices do quadrado, desenharam-se as suas projecções (a traço leve, pois trata-se de um traçado auxiliar para o ob-
jectivo do exercício, que é as projecções do sólido). Em seguida, pelas projecções de OO conduziram-se as projecções de uma recta pp, ortogo-
nal a ρ – a recta pp é a recta suporte do eixo da pirâmide e é uma rreeccttaa ddee ppeerrffiill (que está definida por um ponto – OO – e pela sua direcção – é
ortogonal a ρ). A recta pp é ortogonal às rectas de perfil do plano ρ. Para definir a recta pp conduziu-se, pela recta, um plano de perfil π e determi-
nou-se a recta de intersecção de π com ρ – recta ii (que está definida pelo ponto OO e pelo seu ponto de concorrência com o eixo XX, pois trata-se
de uma rreeccttaa ddee ppeerrffiill ppaassssaannttee). A recta ii contém o ponto OO (que é um ponto dos dois planos) e a recta pp também – as duas rectas são per-
pendiculares no ponto OO. Por outro lado, ο vértice VV, da pirâmide, situa-se sobre pp e, uma vez que tem afastamento nulo, será o traço frontal da
recta pp. A determinação do traço frontal da recta pp implica o recurso a um processo geométrico auxiliar. Optou-se pelo rebatimento do plano π
para o Plano Frontal de Projecção – a charneira foi ffπ (recta ee’’). A recta iirr fica definida por OOrr11
e pelo seu ponto de concorrência com o eixo XX,
que é fixo, pois é um ponto da charneira (OOrr11
é o ponto OO no seu segundo rebatimento – no rebatimento do plano π). A recta pprr passa por OOrr11
e
é perpendicular a iirr em OOrr11
. Em rebatimento, determinou-se o traço frontal da recta pp, que é VVrr – invertendo o rebatimento, determinaram-se as
projecções de VV. A partir das projecções de todos os vértices do sólido, desenharam-se os seus contornos aparentes – o ccoonnttoorrnnoo aappaarreennttee
ffrroonnttaall é [AA22BB22VV22DD22] e o ccoonnttoorrnnoo aappaarreennttee hhoorriizzoonnttaall é [AA11DD11CC11BB11VV11]. Em pprroojjeeccççããoo ffrroonnttaall, existe um único vértice que não integra o con-
torno aparente frontal – o vértice CC, que é o vértice de maior afastamento da pirâmide, pelo que é visível, bem como todas as arestas que nele
convergem. Note que a base da pirâmide é visível em projecção frontal, bem como as faces laterais [BBCCVV] e [CCDDVV]. Já as faces laterais [AADDVV]
e [AABBVV] são invisíveis, pelo que a única aresta invisível em projecção frontal é a aresta lateral [AAVV]. Em pprroojjeeccççããoo hhoorriizzoonnttaall, todos os vértices
da pirâmide integram o contorno aparente horizontal. No entanto, por oposição à projecção frontal, a base é invisível em projecção horizontal,
bem como a face lateral [AABBVV] – a aresta [AABB] da base é a única aresta invisível da pirâmide, em projecção horizontal. Note que as faces late-
rais [AADDVV], [CCDDVV] e [BBCCVV] são visíveis em projecção horizontal. Note que a base do sólido é invisível em projecção horizontal e visível em pro-
jecção frontal, pois o plano ρ é um plano em tensão.

144. 144
SOLUÇÕES
355.
Em primeiro lugar representou-se o plano ρ, pelos seus traços e pelo
ponto AA. Uma vez que o quadrado [AABBCCDD] não se projecta em V.G.
em nenhum dos planos de projecção (o plano ρ não é paralelo a
nenhum dos planos de projecção), para construir as suas projec-
ções é necessário o recurso a um processo geométrico auxiliar. Op-
tou-se pelo rebatimento do plano ρ para o Plano Frontal de
Projecção – a charneira foi ffρ (que é o próprio eixo XX). O ponto AA re-
bateu-se pelo triângulo do rebatimento. O ângulo que o lado [AABB]
faz com o eixo XX é o âânngguulloo rreeaall, no espaço, e não em projecções,
pelo que só é possível medir esse ângulo em V.G., em rebatimento.
Por AArr conduziu-se uma recta fazendo um ângulo de 30° com o eixo
XX, de forma a que BBrr se situe nessa recta à direita de AA e tenha afas-
tamento superior a AA – BBrr tem de estar mais distante do eixo XX do
que AArr. Sobre essa recta, a partir de AArr, mediram-se os 5 cm (a
aresta do cubo), obtendo BBrr. A partir de AArr e BBrr, construiu-se o qua-
drado [AABBCCDD] em V.G., em rebatimento. Inverteu-se o rebatimento
do plano ρ, com o recurso às rectas suportes dos lados [AADD] e [BBCC]
do quadrado, que são rectas passantes. A recta rrrr é, em rebatimen-
to, a recta suporte do lado [AADD] do quadrado – as projecções da rec-
ta rr determinaram--se imediatamente (passam pelas projecções
homónimas de AA e são concorrentes entre si no ponto de concorrên-
cia da recta rr com o eixo XX). Conduzindo, por DDrr, uma perpendicular
à charneira, determinaram-se as projecções de DD sobre as projec-
ções homónimas da recta rr. A recta ssrr é, em rebatimento, a recta
suporte do lado [BBCC] do quadrado (ssrr é paralela a rrrr) – as projecções
da recta ss determinaram-se imediatamente, paralelas às projecções
homónimas da recta rr. A recta rr está definida por um ponto (o seu
ponto de concorrência com o eixo XX, que é fixo) e por uma direcção
(é paralela à recta rr). Conduzindo, por BBrr e CCrr, as perpendiculares à
charneira que por eles passam, determinaram-se as projecções de BB
e CC sobre as projecções homónimas da recta ss. A partir das projecções dos quatro vértices do quadrado, desenharam-se as suas projecções
(a traço leve, pois trata-se de um traçado auxiliar para o objectivo do exercício, que é as projecções do sólido). Em seguida, pelas projecções
de AA conduziram-se as projecções de uma recta pp, ortogonal a ρ – a recta pp é a recta suporte da aresta [AAAA’’] (considerando que o quadrado
[AA’’BB’’CC’’DD’’] é a face superior o sólido) e é uma rreeccttaa ddee ppeerrffiill (que está definida por um ponto – AA – e pela sua direcção – é ortogonal a ρ). A
recta pp é ortogonal às rectas de perfil do plano ρ. Para definir a recta pp conduziu-se, pela recta, um plano de perfil π e determinou-se a recta de
intersecção de π com ρ – recta ii (que está definida pelo ponto AA e pelo seu ponto de concorrência com o eixo XX, pois trata-se de uma rreeccttaa ddee
ppeerrffiill ppaassssaannttee). A recta ii contém o ponto AA (que é um ponto dos dois planos) e a recta pp também – as duas rectas são perpendiculares no
ponto AA. Por outro lado, ο vértice AA’’ situa-se sobre pp, a 5 cm de AA (a aresta do cubo). Atendendo a que o segmento [AAAA’’] não se projecta em
V.G. em nenhum dos planos de projecção, recorreu-se ao rebatimento do plano π para o Plano Frontal de Projecção – a charneira foi ffπ (recta
ee’’). A recta iirr fica definida por AArr11
e pelo seu ponto de concorrência com o eixo XX, que é fixo, pois é um ponto da charneira (AArr11
é o ponto AA no
seu segundo rebatimento – no rebatimento do plano π). A recta pprr passa por AArr11
e é perpendicular a iirr em AArr11
. Sobre pprr, a partir de AArr11
, medi-
ram-se os 5 cm, obtendo-se AA’’rr (garantindo que AA’’ se situa no 1o Diedro). Inverteu-se o rebatimento de π, obtendo-se as projecções de AA’’. A
partir das projecções de AA’’ desenharam-se as projecções do quadrado [AA’’BB’’CC’’DD’’], cujos lados são paralelos aos lados correspondentes do
quadrado [AABBCCDD] – BB’’, CC’’ e DD’’ situam-se nas rectas de perfil ortogonais a ρ que contêm BB, CC e DD, respectivamente. Assim, pelas projecções de
AA’’ conduziram-se as projecções da recta suporte do segmento [AA’’BB’’], até encontrarem as projecções homónimas da recta de perfil que con-
tem a aresta [BBBB’’] – o ponto de concorrência das duas rectas é BB’’. Repetiu-se o processo para DD’’, a partir de AA’’, e para CC’’, a partir de BB’’ ou de
DD’’. A partir das projecções de todos os vértices do sólido, desenharam-se os seus contornos aparentes – o ccoonnttoorrnnoo aappaarreennttee ffrroonnttaall é
[AA22BB22BB’’22CC’’22DD’’22DD22] e o ccoonnttoorrnnoo aappaarreennttee hhoorriizzoonnttaall é [BB11CC11DD11DD’’11AA’’11BB’’11]. Em pprroojjeeccççããoo ffrroonnttaall, existem dois vértices que não integram o
contorno aparente – o vértice AA’’ (que é o vértice de menor afastamento do sólido, pelo que é invisível bem como todas as arestas que nele
convergem) e o vértice CC (que é o vértice de maior afastamento do sólido, pelo que é visível, bem como todas as arestas que nele convergem).
Em pprroojjeeccççããoo hhoorriizzoonnttaall, também existem dois vértices que não integram o contorno aparente – o vértice CC’’ (que é o vértice de maior cota do
sólido, pelo que é visível bem como todas as arestas que nele convergem) e o vértice AA (que é o vértice de menor cota do sólido, pelo que é
invisível bem como todas as arestas que nele convergem). Note que a face [AABBCCDD] é invisível em projecção horizontal e visível em projecção
frontal (o plano ρ é um plano em tensão), enquanto que a face [AA’’BB’’CC’’DD’’] é invisível em projecção frontal e visível em projecção horizontal.

145. 145
SOLUÇÕES
Em primeiro lugar representou-se o ponto OO, pelas suas projecções, em função dos dados – OO é um ponto do β1/3, pelo que as suas coorde-
nadas são iguais. Note que o β1/3 não carece de representação. Uma vez que o pentágono regular [AABBCCDDEE] não se projecta em V.G. em
nenhum dos planos de projecção (o β1/3 não é paralelo a nenhum dos planos de projecção), para construir as suas projecções é necessário o
recurso a um processo geométrico auxiliar. Optou-se pelo rebatimento do β1/3 para o Plano Frontal de Projecção – a charneira foi o próprio eixo XX.
O ponto OO rebateu-se pelo triângulo do rebatimento. Com centro em OOrr e 4 cm de raio, desenhou-se a circunferência circunscrita ao pentágono,
em rebatimento, e construiu-se o polígono, inscrito na circunferência, de acordo com os dados – o seu lado mais à esquerda é de perfil
(ou seja, é perpendicular ao eixo XX) Note que a ordem dos vértices é arbitrária, pois o enunciado é omisso. Para inverter o rebatimento do β1/3
recorreu-se a rectas do plano (poder-se-ia, também, ter recorrido ao triângulo do rebatimento, mas trata-se de um processo mais moroso e me-
nos rigoroso). A recta rrrr é, em rebatimento, uma recta do β1/3 que passa por OOrr, e que é paralela ao lado [AArrBBrr] do pentágono em rebatimento –
a recta rr é uma recta passante, cujas projecções se determinam imediatamente, pois são concorrentes entre si no ponto de concorrência da rec-
ta com o eixo XX e passam pelas projecções homónimas do ponto OO (a recta rr fica definida por dois pontos – o ponto OO e o seu ponto de con-
corrência com o eixo XX). Note que as projecções da recta rr são simétricas em relação ao eixo XX. A recta aarr é outra recta do β1/3 que passa por
AArr e BBrr – a recta aa é a recta suporte do lado [AABB] do pentágono e é necessariamente paralela à recta rr. As projecções da recta aa determinam-se
imediatamente, pois está definida por um ponto (o seu ponto de concorrência com o eixo XX) e por uma direcção (é paralela à recta rr). Condu-
zindo, por AArr e BBrr, as perpendiculares à charneira que por eles passam, determinaram-se as projecções de AA e BB sobre as projecções homóni-
mas da recta aa. A recta bbrr é, em rebatimento, a recta suporte da diagonal [CCEE] do pentágono (bbrr é paralela a rrrr e a aarr) – as projecções da recta
bb determinaram-se imediatamente, paralelas às projecções homónimas das rectas rr e aa. A recta bb está definida por um ponto (o seu ponto de
concorrência com o eixo XX, que é fixo) e por uma direcção (é paralela às rectas rr e aa). Conduzindo, por CCrr e EErr, as perpendiculares à charneira
que por eles passam, determinaram-se as projecções de CC e EE sobre as projecções homónimas da recta bb. A recta mmrr é, em rebatimento, a
recta fronto-horizontal do β1/3 que passa por DDrr – a recta mmrr é concorrente com a recta aarr no ponto PPrr. As projecções do ponto PP determinam-se
imediatamente, sobre as projecções homónimas da recta aa, com o recurso à perpendicular à charneira que passa por PPrr. Pelas projecções de
PP conduziram-se as projecções homónimas da recta mm – conduzindo, por DDrr, uma perpendicular à charneira, determinaram-se as projecções
de DD sobre as projecções homónimas da recta mm. A partir das projecções dos cinco vértices do pentágono, desenharam-se as suas projec-
ções (a traço leve, pois trata-se de um traçado auxiliar para o objectivo do exercício, que é as projecções do sólido). É dado que existe um
único vértice do prisma com cota nula. Uma vez que o prisma se situa no 1o Diedro, esse vértice será o vértice de menor cota do sólido – será o
vértice da base [AA’’BB’’CC’’DD’’EE’’] correspondente ao vértice EE (que é o vértice de menor cota da base [AABBCCDDEE]). Assim, pelas projecções de EE con-
duziram-se as projecções de uma recta pp, ortogonal a ρ – a recta pp é a recta suporte da aresta [EEEE’’] e é uma rreeccttaa ddee ppeerrffiill (que está definida
356.
(Continua na página seguinte)

146. 146
SOLUÇÕES
357.
Em primeiro lugar representou-se o plano γ, pelos seus traços, e os
pontos PP e QQ, pelas respectivas projecções, em função dos dados.
O plano γ é ortogonal ao β2/4, pelo que tem os seus traços coinciden-
tes. O ponto PP é um ponto do Plano Horizontal de Projecção (PP tem
cota nula), pelo que é um ponto de hhγ. A recta hh é a recta horizontal
(de nível) do plano, com 4 cm de cota, a que se recorreu para deter-
minar as projecções do ponto QQ. O triângulo [PPQQRR] não se projecta
em V.G. em nenhum dos planos de projecção (o plano que o con-
tém – o plano γ – é oblíquo a ambos os planos de projecção) pelo
que é necessário o recurso a um processo geométrico auxiliar. O
ponto PP é um ponto do Plano Horizontal de Projecção, pelo que,
atendendo a uma maior economia de traçados, se optou por reba-
ter o plano γ para o Plano Horizontal de Projecção – a charneira foi
hh e PPrr ≡ PP11, pois PP é um ponto da charneira. É necessário rebater ff,
o que se processa rebatendo um dos seus pontos – o ponto FF
(o traço frontal da recta hh). Por FF11 conduziu-se uma perpendicular à
charneira – com o compasso, fazendo centro no ponto de concorrên-
cia dos traços do plano e raio até FF22, transportou-se essa distância
para a perpendicular à charneira que passa por FF11, obtendo FFrr.
O traço frontal do plano rebatido (ffγrr
) passa por FFrr e é concorrente
com hhγrr
no eixo XX. Por FFrr conduziu-se a recta hhrr, paralela a hhγrr
. Con-
duzindo, por QQ11, uma perpendicular à charneira, determinou-se QQrr
sobre hhrr. A partir de PPrr e de QQrr, construiu-se o triângulo [PPQQRR] em
VG., em rebatimento e, com vista à determinação das projecções da pirâmide, determinou-se também o seu centro – o ponto OO. A inversão do
rebatimento dos pontos OO e RR processou-se com o recurso às rectas frontais (de frente) que por eles passam – ver exercício 118833 e respectivo
relatório. A recta ff é a recta frontal (de frente) que nos permitiu determinar as projecções de RR. A recta ff’’ é a recta frontal (de frente) que nos
permitiu determinar as projecções de OO. A partir das projecções dos três vértices do triângulo, desenharam-se as suas projecções (a traço leve,
pois trata-se de um traçado auxiliar para o objectivo do exercício, que é as projecções do sólido). Em seguida, pelas projecções de OO conduzi-
ram-se as projecções homónimas de uma recta pp, ortogonal a γ – a recta pp é a recta suporte do eixo da pirâmide. O vértice VV, da
pirâmide, porque tem afastamento nulo, é o traço frontal da recta pp, o que nos permite determinar imediatamente as suas projecções, sem o
recurso a qualquer outro rebatimento. A partir das projecções de todos os vértices do sólido, desenharam-se os seus contornos aparentes – o
ccoonnttoorrnnoo aappaarreennttee ffrroonnttaall é [PP22VV22QQ22] e o ccoonnttoorrnnoo aappaarreennttee hhoorriizzoonnttaall é [QQ11RR11VV11]. Em pprroojjeeccççããoo ffrroonnttaall, há um vértice que não integra o
contorno aparente – o vértice RR, que é o vértice de maior afastamento do sólido, pelo que é visível (bem como todas as arestas que nele con-
vergem). A base do sólido é visível, bem como as faces laterais [PPRRVV] e [QQRRVV] (a face lateral [PPQQVV] é a única face invisível em projecção frontal).
Em pprroojjeeccççããoo hhoorriizzoonnttaall, há um vértice que não integra o contorno aparente – o vértice PP, que é o vértice de menor cota do sólido, pelo que é
invisível (bem como todas as arestas que nele convergem). A base do sólido é invisível, bem como as faces laterais [PPRRVV] e [PPQQVV] (a face
lateral [QQRRVV] é a única face visível em projecção frontal). Note que o plano γ é um plano em tensão, o que justifica o facto de a base ser invi-
sível em projecção horizontal e ser visível em projecção frontal.
por um ponto – EE – e pela sua direcção – é ortogonal ao β1/3). A recta pp é ortogonal às rectas de perfil do β1/3. Para definir a recta pp conduziu-se,
pela recta, um plano de perfil π e determinou-se a recta de intersecção de π com ρ – recta ii (que está definida pelo ponto EE e pelo seu ponto de
concorrência com o eixo XX, pois trata-se de uma rreeccttaa ddee ppeerrffiill ppaassssaannttee). A recta ii contém o ponto EE (que é um ponto dos dois planos) e a rec-
ta pp também – as duas rectas são perpendiculares no ponto EE. Por outro lado, ο vértice EE’’ será o ponto da recta pp que tiver cota nula – será o tra-
ço horizontal da recta pp. A determinação do traço horizontal da recta pp requer o recurso a outro processo geométrico auxiliar. Optou-se pelo
rebatimento do plano π para o Plano Frontal de Projecção – a charneira foi ffπ (recta ee’’). A recta iirr fica definida por EErr11
e pelo seu ponto de concor-
rência com o eixo XX, que é fixo, pois é um ponto da charneira (EErr11
é o ponto EE no seu segundo rebatimento – no rebatimento do plano π). A recta
pprr passa por EErr11
e é perpendicular a iirr em EErr11
. EE’’rr é o traço horizontal da recta pp em rebatimento – invertendo o rebatimento, determinaram-se as
projecções do ponto EE’’. A partir das projecções de EE’’ desenharam-se as projecções do pentágono [AA’’BB’’CC’’DD’’EE’’], cujos lados são paralelos aos
lados correspondentes do pentágono [AABBCCDDEE] – AA’’, BB’’, CC’’ e DD’’ situam-se nas rectas de perfil ortogonais ao β1/3 que contêm AA, BB, CC e DD, respec-
tivamente. Assim, pelas projecções de EE’’ conduziram-se as projecções da recta suporte do segmento [EE’’DD’’], até encontrarem as projecções ho-
mónimas da recta de perfil que contem a aresta [DDDD’’] – o ponto de concorrência das duas rectas é DD’’. Repetiu-se o processo para AA’’, a partir de
EE’’, bem como para BB’’ (a partir de AA’’) e para CC’’ (a partir de BB’’). Note que, uma vez que o lado [CC’’DD’’] é de perfil, não seria possível determinar DD’’ a
partir de CC’’, sem o recurso a outro processo geométrico auxiliar. A partir das projecções de todos os vértices do sólido, desenharam-se os seus
contornos aparentes – o ccoonnttoorrnnoo aappaarreennttee ffrroonnttaall é [AA22BB22CC22CC’’22DD’’22EE’’22AA’’22] e o ccoonnttoorrnnoo aappaarreennttee hhoorriizzoonnttaall é [AA11EE11DD11CC11CC’’11BB’’11AA’’11]. Note que
a face lateral [CCCC’’DD’’DD] do prisma é de perfil, que é duplamente projectante, pelo que não há invisibilidades a assinalar nesta face – as arestas in-
visíveis estão ocultas por arestas visíveis. Ao nível dos restantes vértices do sólido, em pprroojjeeccççããoo ffrroonnttaall, existem dois vértices que não
integram o contorno aparente – o vértice EE (que é o vértice de menor afastamento do sólido, pelo que é invisível bem como todas as arestas que
nele convergem) e o vértice BB’’ (que é o vértice de maior afastamento do sólido, pelo que é visível, bem como todas as arestas que nele conver-
gem). Sem referir os vértices da face de perfil (pelas razões já indicadas), em pprroojjeeccççããoo hhoorriizzoonnttaall, também existem dois vértices que não inte-
gram o contorno aparente – o vértice BB (que é o vértice de maior cota do sólido, pelo que é visível bem como todas as arestas que nele
convergem) e o vértice EE’’ (que é o vértice de menor cota do sólido, pelo que é invisível bem como todas as arestas que nele convergem). Note
que a base [AABBCCDDEE] é visível em projecção horizontal e invisível em projecção frontal (o β1/3 é um plano em tensão), enquanto que a base
[AA’’BB’’CC’’DD’’EE’’] é visível em projecção frontal e invisível em projecção horizontal.

147. 147
SOLUÇÕES
358.
Em primeiro lugar representou-se o plano α, pelos seus
traços, em função dos dados. O plano α tem os seus
traços simétricos em relação ao eixo XX, pois é ortogonal
ao β1/3. O plano α é oblíquo aos dois planos de projec-
ção, pelo que o triângulo equilátero [AABBCC] não se
projecta em V.G. em nenhum dos planos de projecção
– é necessário o recurso a um processo geométrico
auxiliar. Optou-se pelo rebatimento do plano α para o
Plano Horizontal de Projecção. Note que, uma vez que
é dado que a circunferência circunscrita ao triângulo
[AABBCC] é tangente aos dois planos de projecção, sabe-
-se que a circunferência é tangente aos dois traços do
plano – este dado não nos permite, de forma directa,
determinar as projecções do centro da circunferência, o
ponto OO, pelo que é necessário, antes de mais, rebater
o plano. Para rebater o plano α há que rebater o seu
traço frontal, o que se processa rebatendo um dos seus
pontos – o ponto PP (que é um ponto qualquer de ffα).
Para tal, conduziu-se, por PP11, uma perpendicular à
charneira. Os traços do plano α são concorrentes num
ponto fixo (um ponto do eixo XX, que é um ponto da
charneira). Com o recurso ao compasso, fazendo cen-
tro nesse ponto e raio até PP22, transportou-se essa dis-
tância até à perpendicular à charneira que passa por PP11
e obteve-se PPrr – ffαrr
passa por PPrr e é concorrente com
hhαrr
no eixo XX. Em rebatimento, determinou-se o ponto
que está a 4 cm de ffαrr
e de hhαrr
– esse ponto é OOrr, que é
o centro da circunferência circunscrita ao triângulo, em
rebatimento. Com o compasso fazendo centro em OOrr e
com 4 cm de raio, desenhou-se a circunferência cir-
cunscrita ao triângulo, que é necessariamente tangente
a hhρrr
e a ffρrr
. Em seguida, procedeu-se à construção do
triângulo, de acordo com os dados – CC tem cota nula,
pelo que é um ponto de hhα, e o lado [AABB] é horizontal
(de nível), pelo que é paralelo a hhα. CCrr é, assim, o ponto
de tangência da circunferência a hhαrr
. O lado [AArrBBrr] tem de ser paralelo a hhαrr
, o que implica que um dos seus extremos (BBrr na resolução
apresentada) tem de se situar nneecceessssaarriiaammeennttee sobre ffαrr
(é o ponto de tangência da circunferência com ffαrr
). Em seguida, procedeu-se à in-
versão do rebatimento do plano α. O ponto CC é um ponto da charneira, pelo que as suas projecções se determinam imediatamente – CC11 ≡ CCrr
e CC22 situa-se no eixo XX. O ponto BB é um ponto de ffα, pelo que as suas projecções também se determinam imediatamente – conduzindo, por
BBrr, uma perpendicular à charneira, obtém-se BB11 no eixo XX e BB22 situa-se sobre ffα, na linha de chamada de BB11. A recta hh é a recta horizontal
(de nível) que é a recta suporte do lado [AABB] do triângulo – as projecções da recta hh determinam-se imediatamente (a recta hh está definida
por um ponto – o ponto BB e por uma direcção – é paralela a hhα). Conduzindo, por AArr, uma perpendicular à charneira, determinaram-se as
projecções de AA sobre as projecções homónimas da recta hh. A recta hh’’ é a recta horizontal (de nível) do plano a que se recorreu para inver-
ter o rebatimento de OO – hh’’rr passa por OOrr e é concorrente com ffαrr
em FFrr (FF é o traço frontal de hh’’). Conduzindo, por FFrr, uma perpendicular à
charneira, determinaram-se as projecções de FF (FF é um ponto de ffα). Pelas projecções de FF conduziram-se as projecções homónimas da
recta hh’’. Conduzindo, por OOrr, uma perpendicular à charneira, determinaram-se as projecções de OO sobre as projecções homónimas da rec-
ta hh’’. A partir das projecções dos três vértices do triângulo, desenharam-se as suas projecções (a traço leve, pois trata-se de um traçado au-
xiliar para o objectivo do exercício, que é as projecções do sólido). Atendendo a que um tetraedro toma a forma aparente de uma pirâmide
triangular regular, sabe-se que o eixo do sólido (relativo à face [AABBCC]) passa por OO e é ortogonal ao plano α – assim, pelas projecções de OO
conduziram-se as projecções homónimas de uma recta pp, ortogonal a α. A recta é necessariamente uma recta do β1/3 (é uma recta passan-
te). O quarto vértice do sólido, o vértice DD, situa-se sobre pp, equidistante de AA, de BB e de CC. Nenhuma das arestas [AADD], [BBDD] e [CCDD] se pro-
jecta em V.G., pelo que é necessário o recurso a um processo geométrico auxiliar. Optou-se pelo rebatimento do plano projectante
horizontal da recta pp – o plano γ. Note que o plano γ contém simultaneamente o eixo do sólido (relativo à face [AABBCC]) bem como a aresta
[CCDD], sendo esta que nos permitirá determinar o vértice DD do sólido. Rebateu-se o plano γ para o Plano Frontal de Projecção – a charneira
foi ffγ (recta ee’’) – rebatendo OO e AA. OOrr11
e AArr11
são os pontos OO e AA, rebatidos no seu segundo rebatimento (no rebatimento do plano γ). O pon-
to de concorrência da recta pp com o eixo XX é fixo (é um ponto da charneira) – pprr passa por esse ponto e por OOrr11
. Uma vez que as arestas do
sólido são todas iguais e que DDrr tem de se situar sobre pprr, com o compasso, fazendo centro em AArr11
e com raio AAෆrrෆBBෆrrෆ = BBෆrrෆCCෆrrෆ = AAෆrrෆCCෆrrෆ determi-
nou-se DDrr sobre pprr. Invertendo o rebatimento, determinaram-se as projecções de DD sobre as projecções homónimas da recta pp. A partir das
projecções de todos os vértices do sólido, desenharam--se os seus contornos aparentes – o ccoonnttoorrnnoo aappaarreennttee ffrroonnttaall é [AA22VV22CC22] e o ccoonn--
ttoorrnnoo aappaarreennttee hhoorriizzoonnttaall é [AA11BB11VV11]. Em pprroojjeeccççããoo ffrroonnttaall, há um vértice que não integra o contorno aparente – o vértice BB. Este é o vérti-
ce de menor afastamento do sólido, pelo que é invisível (bem como todas as arestas que nele convergem). A face [AABBCC] do sólido é invisível,
bem como as faces [AABBDD] e [BBCCDD] (a face [AACCDD] é a única face visível em projecção frontal). Em pprroojjeeccççããoo hhoorriizzoonnttaall, há um vértice que
não integra o contorno aparente – o vértice CC. Este é o vértice de menor cota do sólido, pelo que é invisível (bem como todas as arestas que
nele convergem). A face [AABBDD] é a única face visível em projecção horizontal – as restantes faces são invisíveis em projecção horizontal.

148. 148
SOLUÇÕES
359.
Em primeiro lugar representou-se a recta rr, pelas suas projecções, em função dos dados. Em seguida, determinaram-se os traços da recta rr nos
planos de projecção (FF é o traço frontal da recta rr e o ponto AA é o próprio traço horizontal da recta) pelos quais se conduziram os traços ho-
mónimos do plano α – hhα passa por AA11 e é perpendicular a rr11 (a recta rr é uma recta de maior declive do plano) e ffα passa por FF22 e é concor-
rente com hhα no eixo XX. O plano α é oblíquo aos dois planos de projecção, pelo que o triângulo equilátero [AABBCC] não se projecta em V.G.
em nenhum dos planos de projecção – é necessário o recurso a um processo geométrico auxiliar. Optou-se pelo rebatimento do plano α – uma
vez que o ponto AA é um ponto de hhα, com vista a uma maior economia de traçados, rebateu-se o plano α para o Plano Horizontal de Projecção
(a charneira foi hhα e tem-se imediatamente AArr ≡ AA11 pois AA é um ponto da charneira). Para rebater o plano α há que rebater o seu traço frontal, o
que se processa rebatendo um dos seus pontos – o ponto FF (o traço frontal da recta rr), por exemplo. Para tal conduziu-se, por FF11, uma perpen-
dicular à charneira. Os traços do plano α são concorrentes num ponto fixo (um ponto do eixo XX, que é um ponto da charneira). Com o recurso
ao compasso, fazendo centro nesse ponto e raio até FF22, transportou-se essa distância até à perpendicular à charneira que passa por FF11 e obteve-
-se FFrr – ffαrr
passa por FFrr e é concorrente com hhαrr
no eixo XX. A recta rrrr fica definida por AArr e por FFrr. A utilidade da recta rr para rebater o ponto OO é
nula, pelo que se recorreu a uma recta horizontal (de nível) hh, do plano, passando por OO – FF’’ é o traço frontal da recta hh. As rectas hh e rr são con-
correntes em OO. Conduzindo, por FF’’11, uma perpendicular à charneira, determinou-se FFrr sobre ffαrr
. Por FF’’rr conduziu-se hhrr, paralela a hhαrr
– OOrr é o
ponto de concorrência de hhrr com rrrr. Com o compasso, fazendo centro em OOrr e raio até AArr, desenhou-se a circunferência circunscrita ao triân-
gulo em V.G., em rebatimento, e construiu-se o triângulo em rebatimento. O lado [BBrrCCrr] é paralelo à recta hhrr, o que significa que está contido
noutra recta horizontal (de nível do plano. Inverteu-se o rebatimento desta recta (conforme exposto no relatório do exercício anterior), o que
nos permitiu determinar as projecções de BB e CC (ver exercício anterior e respectivo relatório). Note que se omitiram as notações referentes à
recta horizontal (de nível) que contém o lado [BBCC] do triângulo, bem como as referentes ao seu traço frontal, com vista a não sobrecarregar em
demasia a resolução gráfica apresentada. A partir das projecções dos três vértices do triângulo, desenharam-se as suas projecções (a traço
leve, pois trata-se de um traçado auxiliar para o objectivo do exercício, que é as projecções do sólido). Sobre a determinação do vértice DD
do tetraedro, ver exercício anterior e respectivo relatório. O plano γ é o plano vertical que contém a recta pp e o vértice AA do tetraedro. Reba-
teu-se o plano γ para o Plano Frontal de Projecção – a recta pp rebateu-se a partir do rebatimento de OO e de HH, o seu traço horizontal. A partir das
projecções de todos os vértices do sólido, desenharam-se os seus contornos aparentes – o ccoonnttoorrnnoo aappaarreennttee ffrroonnttaall é [AA22VV22BB22] e o ccoonnttoorrnnoo
aappaarreennttee hhoorriizzoonnttaall é [BB11CC11VV11]. Em pprroojjeeccççããoo ffrroonnttaall, há um vértice que não integra o contorno aparente – o vértice CC. Este é o vértice de
menor afastamento do sólido, pelo que é invisível (bem como todas as arestas que nele convergem). A face [AABBCC] do sólido é invisível, bem
como as faces [AACCDD] e [BBCCDD] (a face [AABBDD] é a única face visível em projecção frontal). Em pprroojjeeccççããoo hhoorriizzoonnttaall, há um vértice que não
integra o contorno aparente – o vértice AA. Este é o vértice de menor cota do sólido, pelo que é invisível (bem como todas as arestas que
nele convergem). A face [BBCCDD] é a única face visível em projecção horizontal – as restantes faces são invisíveis em projecção horizontal.

149. 149
SOLUÇÕES
360.
Em primeiro lugar representaram-se os pontos AA e BB, pelas suas
projecções, em função dos dados. AA é um ponto com cota nula,
pelo que é um ponto de hhρ, o que nos permitiu desenhar imediata-
mente hhρ. Para determinar o traço frontal do plano poder-se-ia con-
duzir, por AA e BB, uma recta do plano e determinar o seu traço
frontal, mas este situa-se fora dos limites do papel, pelo que se
optou por prosseguir com o exercício, mesmo sem determinar ffρ.
O plano ρ não é paralelo a nenhum dos planos de projecção, pelo
que o quadrado [AABBCCDD] não se projecta em VG. – é necessário o
recurso a um processo geométrico auxiliar. Optou-se pelo rebati-
mento do plano ρ. Uma vez que ffρ não é conhecido e que AA é um
ponto de hhρ, optou-se por rebater o plano ρ para o Plano Horizontal
de Projecção – a charneira foi hhρ e AArr ≡ AA11 pois AA é um ponto da
charneira. O ponto BB rebateu-se com o recurso ao seu triângulo do
rebatimento. A partir de AArr e BBrr, construiu-se o quadrado [AABBCCDD]
em V.G., em rebatimento. Para inverter o rebatimento, recorreu-se a
duas rectas do plano – as rectas suporte dos lados [AADD] e [BBCC] do
quadrado. A recta rrrr é, em rebatimento, a recta suporte do lado
[BBCC] do quadrado. A recta rrrr é concorrente com hhρrr
em HHrr (HH é o
traço horizontal da recta rr). HH é um ponto da charneira, pelo que é
fixo – as projecções de HH determinam-se imediatamente. A partir
das projecções de BB e HH, foi possível desenhar as projecções da
recta rr e determinar o seu traço frontal, FF. O traço frontal do plano,
ffρ, passa por FF22. Conduzindo, por FF11, uma perpendicular à charneira,
determinou-se FFrr sobre rrrr – ffρrr
passa por FFrr. Em seguida, conduziu-
-se, por CCrr, uma perpendicular à charneira e determinaram-se as
projecções de CC sobre as projecções homónimas da recta rr. Para
inverter o rebatimento de DDrr recorreu-se à recta ssrr – esta é, em
rebatimento, a recta suporte do lado [AADD] do quadrado. A recta ssrr
é concorrente com hhρrr
em AArr (AA é o próprio traço horizontal da recta ss) e é concorrente com ffρrr
em FF’’rr (FF’’ é o traço frontal da recta ss). Con-
duzindo, por FF’’rr, uma perpendicular à charneira, determinaram-se as projecções de FF’’ (FF’’ é um ponto de ffρ). As projecções da recta ss ficam
definidas pelas projecções de AA e FF’’. Conduzindo, por DDrr, uma perpendicular à charneira, determinaram-se as projecções de DD sobre as
projecções homónimas da recta ss. A partir das projecções dos quatro vértices do quadrado, desenharam-se as suas projecções (a traço
leve, pois trata-se de um traçado auxiliar para o objectivo do exercício, que é as projecções do sólido). Em seguida, efectuaram-se as cons-
truções necessárias à determinação das projecções dos vértices da face superior do cubo (a face [AA’’BB’’CC’’DD’’]), conforme exposto no relatório
do exercício 335522, pelo que se aconselha a leitura do respectivo relatório. A recta pp é a recta ortogonal ao plano ρ que passa por AA (é a recta
suporte da aresta [AAAA’’]). O plano π é o plano que contém a recta pp. A recta ii é a recta de intersecção do plano π com o plano ρ. FF’’’’ é o traço
frontal da recta ii e AA é o seu traço horizontal. As rectas pp e ii são perpendiculares em AA. AArr11
é o ponto AA rebatido pelo seu segundo rebatimento
– o rebatimento do plano π. O ponto AA’’rr é um ponto de pprr tal que AAෆ’’ෆrrෆAAෆrrෆ11
ෆ= AAෆrrෆBBෆrrෆ = AAෆrrෆDDෆrrෆ = BBෆrrෆCCෆrrෆ = CCෆrrෆDDෆrrෆ (que é a medida da aresta do cubo).
A partir das projecções de AA’’ desenharam-se as projecções do quadrado [AA’’BB’’CC’’DD’’], cujos lados são paralelos aos lados correspondentes
do quadrado [AABBCCDD]. A partir das projecções de todos os vértices do sólido, desenharam-se os seus contornos aparentes – o ccoonnttoorrnnoo
aappaarreennttee ffrroonnttaall é [AA22BB22BB’’22CC’’22DD’’22DD22] e o ccoonnttoorrnnoo aappaarreennttee hhoorriizzoonnttaall é [BB11CC11DD11DD’’11AA’’11BB’’11]. Em pprroojjeeccççããoo ffrroonnttaall, existem dois vértices
que não integram o contorno aparente – o vértice CC (que é o vértice de menor afastamento do sólido, pelo que é invisível bem como todas
as arestas que nele convergem) e o vértice AA’’ (que é o vértice de maior afastamento do sólido, pelo que é visível, bem como todas as ares-
tas que nele convergem). Em pprroojjeeccççããoo hhoorriizzoonnttaall, também existem dois vértices que não integram o contorno aparente – o vértice CC’’ (que
é o vértice de maior cota do sólido, pelo que é visível bem como todas as arestas que nele convergem) e o vértice AA (que é o vértice de me-
nor cota do sólido, pelo que é invisível bem como todas as arestas que nele convergem). Note que a face [AABBCCDD] é invisível em ambas as
projecções e a face [AA’’BB’’CC’’DD’’] é visível em ambas as projecções.
(Continua na página seguinte)
361.
Em primeiro lugar representou-se o plano ρ, pelos seus traços (que estão coincidentes no eixo XX), e o ponto OO, pela sua projecção horizontal (a
única que os dados do exercício nos permitem localizar de forma directa). O plano está definido pela sua orientação – é necessário, antes de
mais, definir totalmente o plano e determinar a projecção frontal do ponto OO. O diedro que o plano ρ faz com o Plano Horizontal de Projecção tem
a mesma amplitude que o ângulo que as rectas de perfil de ρ fazem com o Plano Horizontal de Projecção. Assim, conduziu-se, por OO, um plano
de perfil π – a recta ii é a recta de intersecção do plano π com o plano ρ. A recta ii é uma recta de perfil passante – está definida por um ponto (o
seu ponto de concorrência com o eixo XX) e por uma direcção (faz um ângulo de 30o com o Plano Horizontal de Projecção). Rebateu-se o plano
π para o Plano Frontal de Projecção – a charneira foi ffπ (recta ee). O ângulo que a recta ii faz com o Plano Horizontal de Projecção é igual (tem a
mesma amplitude) ao ângulo que a recta ii faz com hhπ e esse ângulo está em V.G. em rebatimento – em rebatimento, desenhou-se iirr, fazendo um
ângulo de 30o com hhπrr
e passando pelo seu ponto fixo (o ponto de concorrência com o eixo XX). Rebatendo o ponto OO a partir da sua projecção
horizontal, determinou-se OOrr sobre iirr – invertendo o rebatimento, determinou-se OO22. Note que o ponto OO é um ponto do 1o Diedro e se garantiu
que a recta iirr passa pelo quadrante em que OOrr se situa (o plano ρ atravessa os 1o e 3o Diedros). Em seguida, procedeu--se à construção do triân-
gulo [AABBCC] – este está contido no plano ρ, que não é paralelo a nenhum dos planos de projecção, pelo que não se projecta em V.G. nenhum

150. 150
SOLUÇÕES
dos planos de projecção. Nesse sentido, é necessário o recurso a um processo geométrico auxiliar – optou-se pelo rebatimento do plano ρ para
o Plano Horizontal de Projecção (a charneira foi hhρ, que é o próprio eixo XX). O ponto OO rebateu-se pelo seu triângulo do rebatimento, obtendo-se
OOrr11
(OOrr11
é o ponto OO rebatido no seu segundo rebatimento – no rebatimento do plano ρ). Com o compasso, fazendo centro em OOrr11
, desenhou-se
a circunferência circunscrita ao triângulo e construiu-se o triângulo em V.G., em rebatimento, de acordo com os dados (o lado [AABB] é fronto-hori-
zontal e CC é o vértice de maior cota do triângulo, ou seja, o vértice mais distante do eixo XX). Para inverter o rebatimento do plano ρ, recorreu-se a
rectas do plano (poder-se-ia, também, ter recorrido ao triângulo do rebatimento, mas trata-se de um processo mais moroso e menos rigoroso). A
recta rrrr é, em rebatimento, uma recta do plano ρ que passa por OOrr e que é paralela ao lado [AArrCCrr] do triângulo em rebatimento – a recta rr é uma
recta passante, cujas projecções se determinam imediatamente, pois são concorrentes entre si no ponto de concorrência da recta com o eixo XX
e passam pelas projecções homónimas do ponto OO (a recta rr fica definida por dois pontos – o ponto OO e o seu ponto de concorrência com o
eixo XX). A recta ssrr é outra recta do plano ρ e passa por AArr e CCrr – a recta ss é a recta suporte do lado [AACC] do triângulo e é necessariamente parale-
la à recta rr. As projecções da recta ss determinam-se imediatamente, pois está definida por um ponto (o seu ponto de concorrência com o eixo XX)
e por uma direcção (é paralela à recta rr). Conduzindo, por AArr e CCrr, as perpendiculares à charneira que por eles passam, determinaram-se as pro-
jecções de AA e CC sobre as projecções homónimas da recta ss. A recta mmrr é, em rebatimento, a recta fronto-horizontal que passa por AArr e é a recta
suporte do lado [AABB] do triângulo – as projecções da recta mm determinam-se imediatamente, passando pelas projecções homónimas do ponto AA
(a recta mm está definida por um ponto – AA – e por uma direcção – é fronto-horizontal). Conduzindo, por BBrr, uma perpendicular à charneira, deter-
minaram-se as projecções de BB sobre as projecções homónimas da recta mm. A partir das projecções dos três vértices do triângulo, desenharam-
-se as suas projecções (a traço leve, pois trata-se de um traçado auxiliar para o objectivo do exercício, que é as projecções do sólido). Em
seguida, pelas projecções de CC conduziram-se as projecções de uma recta pp, ortogonal a ρ – a recta pp é a recta suporte da aresta [CCCC’’] (consi-
derando que o triângulo [AA’’BB’’CC’’] é a base superior do sólido) e é uma rreeccttaa ddee ppeerrffiill (que está definida por um ponto – CC – e pela sua direcção
– é ortogonal a ρ). A recta pp é ortogonal às rectas de perfil do plano ρ.
Para definir a recta pp conduziu-se, pela recta, um plano de perfil π (é o
plano de perfil com o qual se iniciou o exercício) e determinou-se a
recta de intersecção de π com ρ – a recta ii (que é a recta inicialmente
determinada). A recta ii contém o ponto CC (que é um ponto dos dois
planos) e a recta pp também – as duas rectas são perpendiculares no
ponto CC. Por outro lado, ο vértice CC’’ situa-se sobre pp, a 6 cm de CC (a
altura do prisma). Atendendo a que o segmento [CCCC’’] não se projecta
em V.G. em nenhum dos planos de projecção, recorreu-se ao rebati-
mento já efectuado do plano π para o Plano Frontal de Projecção. A
recta iirr já estava definida e CCrr11
é um ponto de iirr (CCrr11
é o ponto CC no
seu segundo rebatimento – no rebatimento do plano π). A recta pprr é
perpendicular a iirr em CCrr11
. Sobre pprr, a partir de CCrr11
, mediram-se os 6
cm, obtendo-se CC’’rr (garantindo que CC’’ se situa no 1o Diedro). Inver-
teu-se o rebatimento de π, obtendo-se as projecções de CC’’. A partir
das projecções de CC’’ desenharam-se as projecções do triângulo
[AA’’BB’’CC’’], cujos lados são paralelos aos lados correspondentes do
triângulo [AABBCC] – ver exercício 335555 e respectivo re-
latório. A partir das projecções de todos os vérti-
ces do sólido, desenharam-se os seus contornos
aparentes – o ccoonnttoorrnnoo aappaarreennttee ffrroonnttaall é
[AA22BB22BB’’22CC’’22AA’’22] e o ccoonnttoorrnnoo aappaarreennttee hhoorriizzoonnttaall
é [BB11CC11AA11AA’’11BB’’11]. Em pprroojjeeccççããoo ffrroonnttaall, existe um
vértice que não integra o contorno aparente – o
vértice CC (que é o vértice de maior afastamento do
sólido, pelo que é visível bem como todas as ares-
tas que nele convergem). Em pprroojjeeccççããoo hhoorriizzoonn--
ttaall, também existe um vértice que não integra o
contorno aparente – o vértice CC’’ (que é o vértice
de maior cota do sólido, pelo que é visível bem
como todas as arestas que nele convergem). Note
que a base [AABBCC] é invisível em projecção hori-
zontal e visível em projecção frontal (o plano ρ é
um plano em tensão), enquanto que a base
[AA’’BB’’CC’’] é invisível em projecção frontal e visível
em projecção horizontal.
362.
Em primeiro lugar representou-se o plano α, pelo seu traço horizontal (o único que é dado) e o ponto AA, pelas suas projecções, em função dos
dados. O ponto AA é um ponto com cota nula, pelo que é um ponto de hhα. Os dados do enunciado não nos permitem desenhar ffα – note que o
ângulo dado (o ângulo entre os dois traços do plano) é o âânngguulloo rreeaall, que existe nnoo eessppaaççoo (ou, mais correctamente, que está contido no pla-
no α) e não tem correspondência directa em projecções, pois o plano α não é paralelo a nenhum dos planos de projecção. Trata-se, portanto,
de uma situação semelhante à do exercício 220033, pelo que se aconselha a leitura do respectivo relatório. O plano α não é paralelo a nenhum
dos planos de projecção, pelo que é necessário o recurso a um processo geométrico auxiliar. Rebateu-se o plano α para o Plano Horizontal de
Projecção, pois não se conhece o seu traço frontal (que seria a charneira, caso se efectuasse o rebatimento do plano α para o Plano Frontal de
(Continua na página seguinte)

151. 151
SOLUÇÕES
Projecção). Assim, a charneira foi hhα, pelo que se tem imediatamente AArr ≡ AA11, pois AA é um ponto da charneira. Em rebatimento, com vértice no
ponto de concorrência dos dois traços do plano (que é um ponto fixo, pois é um ponto da charneira) e a partir de hhαrr
, mediram-se os 70o (o ân-
gulo entre os dois traços do plano) em V.G., em rebatimento, o que nos permitiu desenhar ffαrr
. O vértice BB, do triângulo, tem afastamento nulo,
pelo que BB é um ponto de ffα – BBrr situa-se sobre ffαrr
, a 6 cm (a medida do lado do triângulo) de AArr. A partir de AArr e de BBrr construiu-se o triângulo
[AABBCC] em V.G., em rebatimento e determinou-se o ponto OOrr (o centro do triângulo, em rebatimento), com vista à determinação das projecções
da pirâmide. Para inverter o rebatimento, é necessário determinar ffα, o que se processa determinando as projecções de um dos seus pontos –
o ponto BB, neste caso, que é um ponto de ffα. Por BBrr conduziu-se uma perpendicular à charneira e determinou-se BB11 no eixo XX (BB é um ponto
com afastamento nulo). Com o compasso, fazendo centro no ponto de concorrência dos dois traços do plano (que é fixo) e raio até BBrr, dese-
nhou-se um arco de circunferência até à linha de chamada de BB11, onde se situa BB22 – ffα passa por BB22 e é concorrente com hhα no eixo XX. A inver-
são do rebatimento dos pontos CCrr e OOrr processou-se com o recurso às rectas horizontais (de nível) do plano α que por eles passam (e cujas
notações se omitiram). A partir das projecções dos três vértices do triângulo, desenharam-se as suas projecções (a traço leve, pois trata-se de
um traçado auxiliar para o objectivo do exercício, que é as projecções do sólido). Sobre a determinação do vértice da pirâmide, ver exercício
333399 e respectivo relatório. A recta pp, passando por OO, é a recta ortogonal ao plano α que contém o eixo da pirâmide. O plano γ é o plano pro-
jectante horizontal da recta pp. Rebateu-se o plano γ para o Plano Frontal de Projecção – a charneira foi ffγ (recta ee’’). A recta pp rebateu-se com o
recurso a dois dos seus pontos – OO e FF, o seu traço frontal (que é um ponto fixo, pois situa-se na charneira). OOrr11
é o ponto OO rebatido pelo seu se-
gundo rebatimento – o rebatimento do plano γ. A partir das projecções de todos os vértices do sólido, desenharam-se os seus contornos aparentes
– o ccoonnttoorrnnoo aappaarreennttee ffrroonnttaall é [AA22CC22VV22] e o ccoonnttoorrnnoo aappaarreennttee hhoorriizzoonnttaall é [AA11CC11VV11]. Em pprroojjeeccççããoo ffrroonnttaall, existe um vértice que não integra o
contorno aparente – o vértice BB (que é o vértice de menor afastamento do sólido, pelo que é invisível bem como todas as arestas que nele conver-
gem). Em pprroojjeeccççããoo hhoorriizzoonnttaall, também existe um vértice que não integra o contorno aparente – o vértice AA (que é o vértice de menor cota do sóli-
do, pelo que é invisível bem como todas as arestas que nele convergem). Note que a base [AABBCC] é invisível em ambas as projecções.
(Continua na página seguinte)
363.
Em primeiro lugar, representou-se o plano ρ, pelo seu traço frontal (o único que é conhecido), e o ponto AA, pela sua projecção frontal (a única
que os dados do exercício nos permitem localizar de forma directa). O plano está definido pela sua orientação – é necessário, antes de mais, de-
finir totalmente o plano e determinar a projecção horizontal do ponto AA. O diedro que o plano ρ faz com o Plano Horizontal de Projecção tem a
mesma amplitude que o ângulo que as rectas de perfil de ρ fazem com o Plano Horizontal de Projecção. Assim, conduziu-se, por AA, um plano de
perfil π – a recta ii é a recta de intersecção do plano π com o plano ρ. A recta ii é uma recta de perfil que está definida por um ponto (o seu traço
frontal FF) e por uma direcção (faz um ângulo de 30o com o Plano Horizontal de Projecção). Rebateu-se o plano π para o Plano Frontal de Projec-
ção – a charneira foi ffπ (recta ee). O ponto FF é um ponto fixo, pois situa-se na charneira. O ângulo que a recta ii faz com o Plano Horizontal de Pro-
jecção é igual (tem a mesma amplitude) ao ângulo que a recta ii faz com hhπ e esse ângulo está em V.G. em rebatimento – em rebatimento,
desenhou-se iirr, fazendo um ângulo de 30o com hhπrr
e passando pelo seu ponto fixo (FFrr). AA é o traço horizontal da recta ii, o que nos permitiu

152. 152
SOLUÇÕES
determinar imediatamente AArr. Invertendo o rebatimento, determinou-se AA11 – por AA11 conduziu-se hhρ. Note que o ponto AA é um ponto com afasta-
mento positivo, e é pedido expressamente que o traço horizontal do plano tenha afastamento positivo (AA é um ponto de hhρ pois tem cota nula).
Em seguida, procedeu-se à construção do triângulo [AABBCC] – este está contido no plano ρ, que não é paralelo a nenhum dos planos de projec-
ção, pelo que não se projecta em V.G. nenhum dos planos de projecção. Nesse sentido, é necessário o recurso a um processo geométrico auxi-
liar – optou-se pelo rebatimento do plano ρ para o Plano Frontal de Projecção (a charneira foi ffρ – recta ee’’). O triângulo do rebatimento de AA já
está em V.G. no triângulo [FFrrAA22AArr] – a hipotenusa do triângulo do rebatimento é, assim, [FFrrAArr], que já está em V.G., no rebatimento do plano π.
Assim, com o recurso ao compasso, fazendo centro em FFrr e raio até AArr, desenhou-se o arco do rebatimento de AA (pelo rebatimento do plano π)
e determinou-se AArr11
(AArr11
é o ponto AA rebatido pelo seu segundo rebatimento – o rebatimento do plano ρ). Note que o ângulo dado (o ângulo que
o lado [AABB] do quadrado faz com hhρ) é um ângulo que eessttáá ccoonnttiiddoo no plano (trata-se do ângulo entre duas rectas) e não tem correspondência
directa em projecções, pois o plano ρ não é paralelo a nenhum dos planos de projecção. Esse ângulo pode, em rebatimento, ser medido em
V.G. – o lado [AABB] faz, com hhρ, um ângulo de 30o e o vértice BB situa-se à direita de AA. Com vértice em AArr11
e a partir de hhρrr
, mediram-se os 30o, ob-
tendo a recta suporte do lado [AABB] em rebatimento – sobre essa recta mediram-se os 5 cm (o lado do quadrado) e determinou-se BBrr. A partir de
AArr11
e BBrr construiu-se o quadrado [AABBCCDD] em V.G, em rebatimento. Para inverter o rebatimento, recorreu-se a duas rectas do plano – as rectas
suporte dos lados [AADD] e [BBCC] do quadrado. A recta rrrr é, em rebatimento, a recta suporte do lado [AADD] do quadrado. A recta rrrr é concorrente
com hhρrr
em AArr11
(AA é o traço horizontal da recta rr) e é concorrente com ffρrr
em FF’’rr (FF’’ é o traço frontal da recta rr). FF’’ é um ponto da charneira, pelo
que é fixo – as projecções de FF’’ determinam-se imediatamente. As projecções de AA já são conhecidas. A partir das projecções de FF’’ e AA, foi pos-
sível desenhar as projecções da recta rr. Em seguida conduziu-se, por DDrr, uma perpendicular à charneira e determinaram-se as projecções de DD
sobre as projecções homónimas da recta rr. Para inverter o rebatimento de BBrr e CCrr recorreu-se à recta ssrr – esta é, em rebatimento, a recta suporte
do lado [BBCC] do quadrado. A recta ssrr é paralela à recta rrrr. A recta ssrr é concorrente com ffρrr
em FF’’’’rr (FF’’’’ é o traço frontal da recta ss). As projecções
de FF’’’’ determinaram-se imediatamente, pois é um ponto da charneira. As projecções da recta ss determinam-se imediatamente – passam pelas
projecções homónimas de FF’’’’ e são paralelas às projecções homónimas da recta rr (a recta ss está definida por um ponto e uma direcção). Con-
duzindo, por BBrr e CCrr, as perpendiculares à charneira que por eles passam, determinaram-se as projecções de BB e CC sobre as projecções homó-
nimas da recta ss. A partir das projecções dos quatro vértices do quadrado, desenharam-se as suas projecções (a traço leve, pois trata-se de um
traçado auxiliar para o objectivo do exercício, que é as projecções do sólido). Sobre a determinação das projecções do prisma, ver exercício 335500
e respectivo relatório. Com vista a uma maior economia de traçados, optou-se por conduzir a recta pp pelo ponto AA, uma vez que existe uma
quantidade significativa de traçados precedentes que nos permite economizar traçado. A recta pp é a recta ortogonal a ρ que passa por AA (é a
recta suporte da aresta lateral [AAAA’’] do prisma. A recta pp está definida por um ponto (o ponto AA) e por uma direcção (é ortogonal a ρ). A recta ii
(já determinada no início do exercício) é a recta
de intersecção do plano π com o plano ρ. Resol-
veu-se a questão da altura do prisma em rebati-
mento, no rebatimento previamente efectuado do
plano π – a recta pprr é perpendicular à recta iirr em
AArr. Sobre pprr, a partir de AArr, mediram-se os 8 cm
(a altura do prisma), obtendo AA’’rr. Invertendo o
rebatimento, determinaram-se as projecções de
AA’’ – a partir destas, determinaram-se as projec-
ções dos restantes vértices da base superior do
sólido (ver exercício 335500 e respectivo relatório).
A partir das projecções de todos os vértices do
sólido, desenharam-se os seus contornos apa-
rentes – o ccoonnttoorrnnoo aappaarreennttee ffrroonnttaall é
[AA22BB22BB’’22CC’’22DD’’22DD22] e o ccoonnttoorrnnoo aappaarreennttee hhoorrii--
zzoonnttaall é [CC11DD11DD’’11AA’’11BB’’11BB11]. Em pprroojjeeccççããoo
ffrroonnttaall, existem dois vértices que não integram
o contorno aparente – o vértice AA’’ (que é o vér-
tice de maior afastamento do sólido, pelo que é
visível bem como todas as arestas que nele
convergem) e o vértice CC (que é o vértice de
menor afastamento do sólido, pelo que é invisí-
vel bem como todas as arestas que nele con-
vergem). Em pprroojjeeccççããoo hhoorriizzoonnttaall, também
existem dois vértices que não integram o contor-
no aparente – o vértice CC’’ (que é o vértice de
maior cota do sólido, pelo que é visível bem
como todas as arestas que nele convergem) e o
vértice AA (que é o vértice de menor cota do sóli-
do, pelo que é invisível bem como todas as ares-
tas que nele convergem).

153. 153
SOLUÇÕES
364.
Por rreeccttaa ttaannggeennttee aa uummaa ssuuppeerrffíícciiee nnuumm ppoonnttoo entende-se uma recta tangente, nesse ponto, a qualquer curva que passa por esse ponto
e que está contida na superfície.
365.
Por ppllaannoo ttaannggeennttee aa uummaa ssuuppeerrffíícciiee nnuumm ppoonnttoo entende-se o lugar geométrico das rectas tangentes à superfície nesse ponto.
366.
Se o plano θ é tangente a uma superfície cónica num ponto, conclui-se que o plano θ é tangente à superfície ao longo da geratriz que con-
tém o ponto (a geratriz de contacto ou de tangência) e é igualmente tangente à directriz da superfície. Sabe-se, ainda, que o plano θ ccoonn--
ttéémm oo vvéérrttiiccee ddaa ssuuppeerrffíícciiee (qualquer geratriz de uma superfície cónica contém o vértice da superfície).
367.
A geratriz ao longo da qual um dado plano é tangente a uma superfície cónica chama-se ggeerraattrriizz ddee ccoonnttaaccttoo ou ggeerraattrriizz ddee ttaannggêênncciiaa.
368.
A afirmação é verdadeira. De facto, qualquer plano tangente a uma superfície cónica é tangente à superfície ao longo de uma geratriz –
qualquer plano tangente a uma superfície cónica contém, assim, uma geratriz da superfície (a geratriz de contacto ou de tangência). Uma
vez que todas as geratrizes contêm o vértice da superfície, qualquer plano tangente a uma superfície cónica contém necessariamente o vér-
tice da superfície (pois o vértice da superfície é um ponto da geratriz de contacto, ou de tangência, que, por sua vez, está contida no plano).
369.
Em primeiro lugar desenharam-se as projecções do cone, em função dos
dados. Para determinar as projecções do ponto PP determinou-se, previa-
mente, o lugar geométrico dos pontos da superfície lateral do cone que
têm 3 cm de cota. Para tal, recorreu-se a um plano horizontal (de nível) ν,
com 3 cm de cota, e determinou-se a circunferência resultante da inter-
secção desse plano com a superfície lateral do cone – o ponto MM é o ponto
de intersecção de ν com a geratriz mais à esquerda do contorno aparente
frontal. O ponto PP é o ponto dessa circunferência que tem 5 cm de afasta-
mento e se situa à esquerda do eixo do sólido. Em seguida, desenharam-
-se as projecções da geratriz gg, que contém o ponto PP – a geratriz gg é a
geratriz de contacto (ou de tangência) e é a geratriz ao longo da qual o
plano é tangente à superfície lateral do cone. A geratriz gg fica definida por
PP e por VV – HH, o traço horizontal da geratriz, é o ponto da geratriz que per-
tence à base do cone. A geratriz gg é, já, uma recta tangente à superfície
lateral do cone no ponto PP – já temos uma recta para definir o plano θ.
Necessitamos de outra recta. Recorreu-se à recta tt, outra recta tangente à
superfície no ponto PP. A recta tt é uma recta horizontal (de nível) e é a recta
de intersecção do plano θ com o plano ν (o plano auxiliar a que se recorreu
para determinar as projecções de PP). A recta tt está definida por um ponto
(o ponto PP) e uma direcção (é perpendicular ao raio da circunferência que
contém PP no ponto PP). Já temos duas rectas para definir o plano θ – a
geratriz gg e a recta tangente tt. Em seguida, determinaram-se os traços do
plano θ – hhθ, o traço horizontal de θ, passa por HH (traço horizontal de gg)
e é paralelo a tt (rectas horizontais de um plano são paralelas entre si e
paralelas ao traço horizontal do plano, que é uma recta horizontal do plano
com cota nula), estando definido por um ponto e uma direcção. O traço
frontal do plano, ffθ, passa por FF (o traço frontal da recta tt) e é concorrente
com hhθ no eixo XX – ffθ está definido por dois pontos. Note que hhθ é uma
recta tangente à base do cone em HH, pelo que é perpendicular ao raio da
base no ponto HH, tal como a recta tt é também perpendicular ao raio da
circunferência (que contém PP) em PP.
PLANOS TANGENTES ÀS SUPERFÍCIES CÓNICA E CILÍNDRICA
19

154. 154
SOLUÇÕES
370.
Em primeiro lugar desenharam-se as projecções do cone, em função dos dados.
A recta ff é a recta frontal (de frente) que contém o eixo do sólido. OO, o centro da
base do cone, é o traço horizontal da recta ff (o ponto de intersecção de ff com o
plano da base). O vértice VV, do cone, é o ponto da recta ff que tem 6 cm de cota
(que é a distância de VV ao plano da base). Para determinar as projecções do
ponto TT determinou-se, previamente, o lugar geométrico dos pontos da superfí-
cie lateral do cone que têm 3 cm de cota. Para tal, recorreu-se a um plano hori-
zontal (de nível) ν, com 3 cm de cota, e determinou-se a circunferência resultante
da intersecção desse plano com a superfície lateral do cone. Essa circunferência
tem centro no ponto QQ (que é o ponto de intersecção do eixo com o plano ν) e
raio QQෆ11ෆAAෆ11ෆ – o ponto AA é o ponto de intersecção de ν com a geratriz mais à direita
do contorno aparente frontal. O ponto TT é o ponto dessa circunferência que tem
4 cm de afastamento e que é visível em projecção horizontal (o outro ponto da
circunferência que também tem 4 cm de afastamento é invisível em projecção
horizontal). Em seguida, desenharam-se as projecções da geratriz gg, que contém
o ponto TT – a geratriz gg é a geratriz de contacto (ou de tangência) e é a geratriz
ao longo da qual o plano é tangente à superfície lateral do cone. A geratriz gg fica
definida por TT e por VV – HH, o traço horizontal da geratriz, é o ponto da geratriz
que pertence à base do cone. A geratriz gg é, já, uma recta tangente à superfície
lateral do cone no ponto TT – já temos uma recta para definir o plano θ. Necessita-
mos de outra recta. Recorreu-se à recta tt, outra recta tangente à superfície no
ponto TT. A recta tt é uma recta horizontal (de nível) e é a recta de intersecção do
plano θ com o plano ν (o plano auxiliar a que se recorreu para determinar as projecções de TT). A recta tt está definida por um ponto (o ponto TT)
e uma direcção (é perpendicular ao raio da circunferência que contém TT no ponto TT). Já temos duas rectas para definir o plano θ – a geratriz gg
e a recta tangente tt. Em seguida, determinaram-se os traços do plano θ – hhθ, o traço horizontal de θ, passa por HH (traço horizontal de gg) e é
paralelo a tt (rectas horizontais de um plano são paralelas entre si e paralelas ao traço horizontal do plano, que é uma recta horizontal do plano
com cota nula), estando definido por um ponto e uma direcção. O traço frontal do plano, ffθ, passa por FF (o traço frontal da recta tt) e é concor-
rente com hhθ no eixo XX – ffθ está definido por dois pontos. Note que hhθ é uma recta tangente à base do cone em HH, pelo que é perpendicular ao
raio da base no ponto HH, tal como a recta tt é também perpendicular ao raio da circunferência (que contém TT) em TT.
Em primeiro lugar desenharam-se as projecções do cone, em função dos dados.
O plano ν é o plano que contém a base do cone. A base do cone tem 4 cm de
raio, pois é tangente ao Plano Frontal de Projecção. O ponto AA é o ponto de maior
afastamento da base do cone – a geratriz gg fica definida por AA e VV. O ponto PP é o
ponto da geratriz gg que tem 4 cm de cota. A geratriz gg é a geratriz de contacto (ou
de tangência) e é a geratriz ao longo da qual o plano é tangente à superfície late-
ral do cone. A geratriz gg é, já, uma recta tangente à superfície lateral do cone no
ponto PP – já temos uma recta para definir o plano θ. Necessitamos de outra recta.
Recorreu-se à recta tt, uma recta tangente à base do cone no ponto AA – a recta tt é
uma outra recta tangente à superfície do cone. A recta tt é uma recta fronto-hori-
zontal e é a recta de intersecção do plano θ com o plano ν (o plano da base do
cone). A recta tt está definida por um ponto (o ponto AA) e uma direcção (é perpen-
dicular ao raio da base no ponto AA). Já temos duas rectas para definir o plano θ –
a geratriz gg e a recta tangente tt. Em seguida, determinaram-se os traços da gera-
triz gg nos planos de projecção. O plano θ está definido por uma recta oblíqua e
por uma recta fronto-horizontal, pelo que se trata necessariamente de um ppllaannoo
ddee rraammppaa. O traço horizontal do plano θ, hhθ, passa por HH (traço horizontal de gg) e
é paralelo a tt, estando definido por um ponto e uma direcção – hhθ é uma recta
fronto-horizontal do plano com cota nula. O traço frontal do plano, ffθ, passa por FF
(o traço frontal da geratriz gg) e é também paralelo à recta tt (está também definido
por um ponto e uma direcção) – ffθ é uma recta fronto-horizontal do plano com
afastamento nulo.
371.

155. 155
SOLUÇÕES
372.
Em primeiro lugar desenharam-se as projecções do cone, em função dos dados. O plano
ϕ é o plano frontal (de frente) que contém a base do cone. Para determinar as projecções
do ponto TT determinou-se, previamente, o lugar geométrico dos pontos da superfície late-
ral do cone que têm 5 cm de afastamento. Para tal, recorreu-se a um plano frontal (de
frente) ϕ1, com 5 cm de afastamento, e determinou-se a circunferência resultante da inter-
secção desse plano com a superfície lateral do cone – o ponto MM é o ponto de intersec-
ção de ϕ1 com a geratriz mais à direita do contorno aparente horizontal. O ponto TT é o
ponto dessa circunferência que tem 2 cm de cota e se situa à esquerda do eixo do sólido.
Em seguida, desenharam-se as projecções da geratriz gg, que contém o ponto TT – a gera-
triz gg é a geratriz de contacto (ou de tangência) e é a geratriz ao longo da qual o plano é
tangente à superfície lateral do cone. A geratriz gg fica definida por TT e por VV – AA é o ponto
da geratriz que pertence à base do cone. A geratriz gg é, já, uma recta tangente à superfí-
cie lateral do cone no ponto TT – já temos uma recta para definir o plano θ. Necessitamos
de outra recta. Recorreu-se à recta tt, uma recta tangente à base do cone no ponto AA – a
recta tt é uma outra recta tangente à superfície do cone. A recta tt é uma recta frontal (de
frente) e é a recta de intersecção do plano θ com o plano ϕ (o plano da base do cone). A
recta tt está definida por um ponto (o ponto AA) e uma direcção (é perpendicular ao raio da
base no ponto AA). Já temos duas rectas para definir o plano θ – a geratriz gg e a recta tt. HH é
o traço horizontal da recta tt. O traço horizontal da geratriz gg situa-se fora dos limites do
desenho. Assim, recorreu-se a uma outra recta do plano – a recta tt’’. A recta tt’’ é uma outra
recta do plano θ – é paralela à recta tt e passa por VV (que é um ponto do plano θ, pois
qualquer plano tangente a um cone contém o vértice do cone). Note que a recta tt’’ é con-
corrente com a geratriz gg em VV. HH’’ é o traço horizontal da recta tt’’. O traço horizontal do
plano θ, hhθ, passa por HH (traço horizontal de tt) e por HH’’ (traço horizontal da recta tt’’) – está
definido por dois pontos. O traço frontal do plano θ, ffθ, é concorrente com hhθ no eixo XX e é paralelo às rectas tt e tt’’ (rectas frontais de um plano
são paralelas entre si e paralelas ao traço frontal do plano, que é uma recta frontal do plano com afastamento nulo). Note que se poderia ter
determinado o traço frontal da geratriz gg, FF, que se situa nos limites do desenho, e, em seguida, desenhar imediatamente ffθ, passando por FF
e paralelo a tt – este procedimento evitaria o recurso à recta auxiliar tt’’, que acima se expôs.
373. RReessoolluuççããoo
(Relatório na página seguinte)

156. 156
SOLUÇÕES
373. RReellaattóórriioo
Em primeiro lugar desenharam-se as projecções do cone, em função dos dados. A recta rr tem as suas projecções paralelas entre si, pois é
paralela ao β2/4. O plano ϕ é o plano frontal (de frente) que contém a base do cone – OO, o centro da base, é o ponto de intersecção do plano
ϕ com a recta rr. O vértice do cone é o ponto da recta rr que dista 6 cm (a altura do cone) do plano ϕ – VV tem 8 cm de afastamento, pois o
plano ϕ tem 2 cm de afastamento (6 + 2 = 8). Para determinar as projecções do ponto AA determinou-se, previamente, o lugar geométrico
dos pontos da superfície lateral do cone que têm 4 cm de afastamento. Para tal, recorreu-se a um plano frontal (de frente) ϕ1, com 4 cm de
afastamento, e determinou-se a circunferência resultante da intersecção desse plano com a superfície lateral do cone. Essa circunferência tem
centro no ponto QQ (que é o ponto de intersecção do eixo com o plano ϕ1) e raio QQෆ22ෆNNෆ22ෆ – o ponto NN é o ponto de intersecção de ϕ1 com a ge-
ratriz mais à direita do contorno aparente horizontal. O ponto AA é o ponto dessa circunferência que tem 3,5 cm de cota e que é visível em
projecção frontal (o outro ponto da circunferência que também tem 3,5 cm de cota é invisível em projecção frontal). Em seguida, desenha-
ram-se as projecções da geratriz gg, que contém o ponto AA – a geratriz gg é a geratriz de contacto (ou de tangência) e é a geratriz ao longo da
qual o plano é tangente à superfície lateral do cone. A geratriz gg fica definida por AA e por VV – TT é o ponto da geratriz que pertence à base do
cone. A geratriz gg é, já, uma recta tangente à superfície lateral do cone no ponto AA – já temos uma recta para definir o plano θ. Necessita-
mos de outra recta. Recorreu-se à recta tt, outra recta tangente à superfície no ponto AA. A recta tt é uma recta frontal (de frente) e é a recta de
intersecção do plano θ com o plano ϕ1 (o plano auxiliar a que se recorreu para determinar as projecções de AA). A recta tt está definida por
um ponto (o ponto AA) e uma direcção (é perpendicular ao raio da circunferência que contém AA no ponto AA). Note que, à semelhança dos
exercícios anteriores, se poderia ter recorrido a uma recta tangente à base do cone no ponto TT. Já temos duas rectas para definir o plano θ –
a geratriz gg e a recta tt. HH é o traço horizontal da recta tt. O traço horizontal da geratriz gg situa-se fora dos limites do desenho. FF é o traço frontal
da geratriz gg. O traço frontal do plano θ, ffθ, passa por FF (traço frontal de gg) e é paralelo à recta tt (rectas frontais de um plano são paralelas
entre si e paralelas ao traço frontal do plano, que é uma recta frontal do plano com afastamento nulo) – está definido por um ponto e por
uma direcção. O traço horizontal do plano θ, hhθ, é concorrente com ffθ no eixo XX e passa por HH (traço horizontal da recta tt) – está definido
por dois pontos.
Em primeiro lugar representaram-se o cone e o ponto PP, pelas respec-
tivas projecções, em função dos dados. Em seguida, procedeu-se à
execução sequencial das etapas que nos conduzem à resolução do
problema. 11.. Por VV e PP conduziu-se uma recta (recta ii), que é a recta
de intersecção dos dois planos tangentes. 22.. Determinou-se o ponto
de intersecção da recta ii com o plano da base (que é o próprio Plano
Horizontal de Projecção) – é o traço horizontal da recta ii, que se identi-
ficou imediatamente com a letra HH. 33.. Por HH conduziram-se as rectas
tangentes à base do cone, que são imediatamente, os traços horizon-
tais dos dois planos tangentes (uma vez que o plano da base é o pró-
prio Plano Horizontal de Projecção, e só por isso). Cada um dos dois
planos tangentes já está definido por duas rectas – pelo seu traço hori-
zontal e pela recta ii. Note que as tangentes à base (os traços horizon-
tais dos planos) se determinaram através do processo rigoroso para a
determinação das rectas tangentes a uma circunferência que passam
por um ponto exterior que, neste caso, é HH11. Os pontos de tangência
são TT e TT’’. 44.. Determinaram-se as geratrizes de tangência (ou de con-
tacto), gg e gg’’ – gg está definida por VV e TT e gg’’ está definida por VV e TT’’.
55.. Cada um dos dois planos tangentes está definido por três rectas – o
plano θ1 está definido por hhθ11
, por ii e por gg e o plano θ2 está definido
por hhθ22
, por ii e por gg’’. Determinou-se FF o traço frontal da recta ii – ffθ11
passa por FF22 e é concorrente com hhθ11
no eixo XX (ffθ11
está definido por
dois pontos). O mesmo raciocínio não se pode aplicar à determinação
de ffθ22
, uma vez que o ponto de concorrência dos dois traços do plano
θ2 não se situa nos limites do desenho. Assim, recorreu-se a uma recta
auxiliar do plano θ2 – a recta ff, que é uma recta frontal (de frente) do
plano. A recta ff passa por VV (que é necessariamente um ponto do pla-
no θ2, pois qualquer plano tangente a um cone contém o seu vértice) e
o seu traço horizontal, HH’’, situa-se sobre hhθ22
. O traço frontal do plano
θ2, ffθ22
, passa pelo traço frontal da recta ii e é paralelo à recta ff (rectas
frontais de um plano são paralelas entre si e paralelas ao traço frontal
do plano, que é uma recta frontal do plano com afastamento nulo).
374.

157. 157
SOLUÇÕES
375.
Em primeiro lugar representaram-se o cone e o ponto PP, pelas
respectivas projecções, em função dos dados. Em seguida,
procedeu-se à execução sequencial das etapas que nos con-
duzem à resolução do problema. 11.. Por VV e PP conduziu-se
uma recta (recta ii), que é a recta de intersecção dos dois planos
tangentes. Note que a recta ii é uma recta frontal (de frente).
22.. Determinou-se o ponto de intersecção da recta ii com o plano
da base (que é o próprio Plano Horizontal de Projecção) – o
ponto II, que é o traço horizontal da recta ii e que se identificou
imediatamente com a letra HH. 33.. Por II conduziram-se as rectas
tangentes à base do cone, tt e tt’’ (que são imediatamente, os
traços horizontais dos dois planos tangentes, uma vez que o
plano da base é o próprio Plano Horizontal de Projecção).
Cada um dos dois planos tangentes já está definido por duas
rectas – pelo seu traço horizontal e pela recta ii. Note que as
tangentes à base (os traços horizontais dos planos) se deter-
minaram através do processo rigoroso para a determinação
das rectas tangentes a uma circunferência que passam por
um ponto exterior que, neste caso, é II11. Os pontos de tangên-
cia são TT e TT’’. 44.. Determinaram-se as geratrizes de tangência
(ou de contacto), gg e gg’’ – gg está definida por VV e TT e gg’’ está
definida por VV e TT’’. 55.. Cada um dos dois planos tangentes
está definido por três rectas – o plano θ1 está definido por hhθ11
,
por ii e por gg e o plano θ2 está definido por hhθ22
, por ii e por gg’’.
O traço frontal do plano θ1, ffθ11
, é concorrente com hhθ11
no eixo
XX e é paralelo à recta ii (rectas frontais de um plano são parale-
las entre si e paralelas ao traço frontal do plano, que é uma
recta frontal do plano com afastamento nulo) – ffθ11
está defini-
do por um ponto e uma direcção. O mesmo raciocínio se apli-
cou à determinação de ffθ22
, o traço frontal do plano θ2 – ffθ22
é
concorrente com hhθ22
no eixo XX e é paralelo à recta ii.
376.
Em primeiro lugar representaram-se o cone e o ponto GG, pelas res-
pectivas projecções, em função dos dados. O plano ν é o plano hori-
zontal (de nível) que contém a base do cone. Em seguida,
procedeu-se à execução sequencial das etapas que nos conduzem à
resolução do problema. 11.. Por VV e GG conduziu-se uma recta (recta ii),
que é a recta de intersecção dos dois planos tangentes. 22.. Determi-
nou-se o ponto de intersecção da recta ii com o plano da base – o
ponto II. 33.. Por II conduziram-se as rectas tangentes à base do cone,
tt e tt’’ (que são as rectas de intersecção dos dois planos tangentes
com o plano ν, o plano da base do cone). Tenha em conta que as
rectas tt e tt’’ são duas rectas horizontais (de nível). Cada um dos dois
planos tangentes já está definido por duas rectas – pela recta ii e por
uma das rectas tt e tt’’. Note que as tangentes à base se determinaram
através do processo rigoroso para a determinação das rectas tangen-
tes a uma circunferência que passam por um ponto exterior que, nes-
te caso, é II11. Os pontos de tangência são TT e TT’’. 44.. Determinaram-se
as geratrizes de tangência (ou de contacto), gg e gg’’ – gg está definida
por VV e TT e gg’’ está definida por VV e TT’’. 55.. Cada um dos dois planos
tangentes está definido por três rectas – o plano θ1 está definido pe-
las rectas ii, tt e gg e o plano θ2 está definido pelas rectas ii, tt’’ e gg’’.
Determinou-se HH, o traço horizontal da recta ii – note que o traço fron-
tal da recta ii se situa fora dos limites do desenho. O traço horizontal
do plano θ1, hhθ11
, passa por HH11 e é paralelo à recta tt (rectas horizon-
tais de um plano são paralelas entre si e paralelas ao traço horizontal
do plano, que é uma recta horizontal do plano com cota nula) – hhθ11
está definido por um ponto e uma direcção. Determinou-se FF, o traço
frontal da recta tt (que pertence ao plano θ1) – ffθ11
passa por FF22 e é
concorrente com hhθ11
no eixo XX, mas este ponto (o ponto de concorrência dos dois traços do plano θ1) situa-se fora dos limites do desenho.
Recorreu-se a uma outra recta do plano – a geratriz gg. FF’’’’ é o traço frontal da geratriz gg – ffθ11
passa por FF22 e por FF’’’’22 (está definido por dois pon-
tos). O traço horizontal do plano θ2, hhθ22
, passa pelo traço horizontal da recta ii e é paralelo à recta tt’’ – hhθ22
está definido por um ponto e uma
direcção. Determinou-se FF’’, o traço frontal da recta tt’’ (que pertence ao plano θ2) – ffθ22
passa por FF’’22 e é concorrente com hhθ22
no eixo XX.

158. 377.
Em primeiro lugar representaram-se o cone e o ponto AA, pelas respectivas
projecções, em função dos dados. O plano ϕ é o plano frontal (de frente) que
contém a base do cone. Em seguida, procedeu-se à execução sequencial
das etapas que nos conduzem à resolução do problema. 11.. Por VV e AA con-
duziu-se uma recta (recta ii), que é a recta de intersecção dos dois planos tan-
gentes – note que a recta ii é uma recta fronto-horizontal. 22.. Determinou-se o
ponto de intersecção da recta ii com o plano da base – o ponto II. A recta ii é
paralela ao plano da base, pelo que o ponto II ssee ssiittuuaa nnoo iinnffiinniittoo. 33.. Por II
(que se situa no infinito) conduziram-se as rectas tangentes à base do cone,
tt e tt’’ – as rectas tt e tt’’ são concorrentes com a recta ii num ponto do infinito,
pelo que são necessariamente paralelas à recta ii (são igualmente rectas fron-
to-horizontais). As rectas tt e tt’’ são as rectas de intersecção dos dois planos
tangentes com o plano ϕ, o plano da base do cone. Cada um dos dois pla-
nos tangentes já está definido por duas rectas – pela recta ii e por uma das
rectas tt e tt’’. Note que as tangentes à base se determinaram através do pro-
cesso rigoroso para a determinação das rectas tangentes a uma circunferên-
cia que são paralelas a uma recta dada que, neste caso, é a recta ii. Os
pontos de tangência são TT e TT’’. 44.. Determinaram-se as geratrizes de tangên-
cia (ou de contacto), gg e gg’’ – gg está definida por VV e TT e gg’’ está definida por VV
e TT’’. 55.. Cada um dos dois planos tangentes está definido por três rectas – o
plano θ1 está definido pelas rectas ii, tt e gg e o plano θ2 está definido pelas rec-
tas ii, tt’’ e gg’’. Note que se trata nneecceessssaarriiaammeennttee de ppllaannooss ddee rraammppaa – os
dois traços de ambos os planos são rectas fronto-horizontais. Determinaram-
-se os traços da geratriz gg, HH e FF, pelos quais se conduziram os traços homó-
nimos do plano θ1. Em seguida, determinaram-se os traços da geratriz gg’’, HH’’
e FF’’, pelos quais se conduziram os traços homónimos do plano θ2.
158
SOLUÇÕES
378.
Em primeiro lugar representaram-se o cone e o ponto PP, pelas
respectivas projecções, em função dos dados. Em seguida, pro-
cedeu-se à execução sequencial das etapas que nos conduzem
à resolução do problema. 11.. Por VV e PP conduziu-se uma recta
(recta ii), que é a recta de intersecção dos dois planos tangen-
tes. 22.. Determinou-se o ponto de intersecção da recta ii com o
plano da base (que é o próprio Plano Horizontal de Projecção) –
é o traço horizontal da recta ii, que se identificou imediatamente
com a letra HH. 33.. Por HH conduziram-se as rectas tangentes à
base do cone, que são imediatamente, os traços horizontais dos
dois planos tangentes (uma vez que o plano da base é o próprio
Plano Horizontal de Projecção). Cada um dos dois planos tan-
gentes já está definido por duas rectas – pelo seu traço horizon-
tal e pela recta ii. Note que as tangentes à base (os traços
horizontais dos planos) se determinaram através do processo
rigoroso para a determinação das rectas tangentes a uma cir-
cunferência que passam por um ponto exterior que, neste caso,
é HH11. Os pontos de tangência são TT e TT’’. 44.. Determinaram-se as
geratrizes de tangência (ou de contacto), gg e gg’’ – gg está definida
por VV e TT e gg’’ está definida por VV e TT’’. 55.. Cada um dos dois pla-
nos tangentes está definido por três rectas – o plano θ1 está de-
finido por hhθ11
, por ii e por gg e o plano θ2 está definido por hhθ22
,
por ii e por gg’’. Note que hhθ22
é uma recta fronto-horizontal com
cota nula, pelo que se conclui que o plano θ2 é um plano de
rampa (não poderá ser um plano frontal, pois contém uma recta
oblíqua). Determinou-se FF o traço frontal da recta ii – ffθ11
passa
por FF22 e é concorrente com hhθ11
no eixo XX (ffθ11
está definido por
dois pontos). Uma vez que o plano θ2 é um plano de rampa, ffθ22
é uma recta fronto-horizontal que passa por FF22.

159. 159
SOLUÇÕES
Em primeiro lugar representaram-se o cone e a recta rr, pelas respectivas
projecções, em função dos dados. A recta rr tem as suas projecções para-
lelas entre si, pois trata-se de uma recta paralela ao β2/4. Em seguida, pro-
cedeu-se à execução sequencial das etapas que nos conduzem à
resolução do problema. 11.. Por VV conduziu-se uma recta paralela à recta rr
(recta ii), que é a recta de intersecção dos dois planos tangentes. 22.. Deter-
minou-se o ponto de intersecção da recta ii com o plano da base (que é o
próprio Plano Horizontal de Projecção) – é o traço horizontal da recta ii,
que se identificou imediatamente com a letra HH. 33.. Por HH conduziram-se
as rectas tangentes à base do cone, que são imediatamente, os traços
horizontais dos dois planos tangentes (uma vez que o plano da base é o
próprio Plano Horizontal de Projecção, e só por isso). Cada um dos dois
planos tangentes já está definido por duas rectas – pelo seu traço hori-
zontal e pela recta ii. Note que as tangentes à base (os traços horizontais
dos planos) se determinaram através do processo rigoroso para a deter-
minação das rectas tangentes a uma circunferência que passam por um
ponto exterior que, neste caso, é HH11. Os pontos de tangência são TT e TT’’.
44.. Determinaram-se as geratrizes de tangência (ou de contacto), gg e gg’’ –
gg está definida por VV e TT e gg’’ está definida por VV e TT’’. 55.. Cada um dos
dois planos tangentes está definido por três rectas. Determinou-se FF, o
traço frontal da recta ii. O traço frontal do plano θ1, ffθ11
, passa por FF22 e é
concorrente com hhθ11
no eixo XX. O mesmo raciocínio não se pode aplicar à
determinação do traço frontal do plano θ2, pois o ponto de concorrência
dos dois traços do plano θ2 situa-se fora dos limites do desenho. Assim,
foi necessário o recurso a uma recta auxiliar do plano – a recta hh. A recta
hh é uma recta horizontal (de nível) do plano θ2, que é concorrente com a
geratriz gg’’ no ponto AA. A recta hh está definida por um ponto (o ponto AA) e
por uma direcção – é paralela a hhθ22
(pois rectas horizontais de um plano
são paralelas entre si e paralelas ao traço horizontal do plano, que é uma
recta horizontal do plano com cota nula). FF’’ é o traço frontal da recta hh – ffθ22
passa pelos traços frontais das rectas ii e hh (que são duas rectas do plano θ2),
estando assim definido por dois pontos.
379.
380.
Em primeiro lugar representaram-se o cone e a recta ff, pelas res-
pectivas projecções, em função dos dados. O vértice do cone, VV, é
o ponto da recta rr que tem 7 cm (a altura do cone) de afastamento
– é o ponto da recta rr que dista 7 cm do plano da base, que é o Pla-
no Frontal de Projecção. Em seguida, procedeu-se à execução se-
quencial das etapas que nos conduzem à resolução do problema.
11.. Por VV conduziu-se uma recta paralela à recta ff (recta ii), que é a
recta de intersecção dos dois planos tangentes (a recta ii é igual-
mente uma recta frontal). 22.. Determinou-se o ponto de intersecção
da recta ii com o plano da base – o ponto II. A recta ii é paralela ao
plano da base, pelo que o ponto II ssee ssiittuuaa nnoo iinnffiinniittoo. 33.. Por II (que
se situa no infinito) conduziram-se as rectas tangentes à base do
cone, que são imediatamente os traços frontais dos dois planos tan-
gentes – ffθ11
e ffθ22
. As rectas ffθ11
e ffθ22
são concorrentes com a recta ii
num ponto do infinito, pelo que são necessariamente paralelas à
recta ii. As rectas ffθ11
e ffθ22
são as rectas de intersecção dos dois pla-
nos tangentes com o Plano Frontal de Projecção, o plano que con-
tém a base do cone. Note que as tangentes à base se
determinaram através do processo rigoroso para a determinação
das rectas tangentes a uma circunferência que são paralelas a uma
recta dada que, neste caso, é a recta ii. Os pontos de tangência são
TT e TT’’. 44.. Determinaram-se as geratrizes de tangência (ou de con-
tacto), gg e gg’’ – gg está definida por VV e TT e gg’’ está definida por VV e TT’’.
55.. Cada um dos dois planos tangentes está definido por três rectas.
Determinou-se HH, o traço horizontal da recta ii. O traço horizontal do
plano θ1, hhθ11
, passa por HH11 e é concorrente com ffθ11
no eixo XX. Recor-
reu-se a um raciocínio idêntico para a determinação de hhθ22
– hhθ22
passa por HH11 e é concorrente com ffθ22
no eixo XX.

160. 160
SOLUÇÕES
381.
Em primeiro lugar representaram-se o cone e a recta hh, pelas respectivas
projecções, em função dos dados. O plano ν é o plano horizontal (de ní-
vel) que contém a base do cone. Em seguida, procedeu-se à execução
sequencial das etapas que nos conduzem à resolução do problema.
11.. Por VV conduziu-se uma recta paralela à recta hh (recta ii), que é a recta
de intersecção dos dois planos tangentes (a recta ii é igualmente uma rec-
ta horizontal). 22.. Determinou-se o ponto de intersecção da recta ii com o
plano da base – o ponto II. A recta ii é paralela ao plano da base, pelo que
o ponto II ssee ssiittuuaa nnoo iinnffiinniittoo. 33.. Por II (que se situa no infinito) conduzi-
ram-se as rectas tangentes à base do cone, tt e tt’’ – a rectas tt e tt’’ são con-
correntes com a recta ii num ponto do infinito, pelo que são
necessariamente paralelas à recta ii (são igualmente rectas horizontais). As
rectas tt e tt’’ são as rectas de intersecção dos dois planos tangentes com o
plano ν, o plano da base do cone. Cada um dos dois planos tangentes já
está definido por duas rectas – pela recta ii e por uma das rectas tt e tt’’.
Note que as tangentes à base se determinaram através do processo rigo-
roso para a determinação das rectas tangentes a uma circunferência que
são paralelas a uma recta dada que, neste caso, é a recta ii. Os pontos de
tangência são TT e TT’’. 44.. Determinaram-se as geratrizes de tangência (ou de
contacto), gg e gg’’ – gg está definida por VV e TT e gg’’ está definida por VV e TT’’.
55.. Cada um dos dois planos tangentes está definido por três rectas. Uma
vez que a recta ii (que é uma recta comum aos dois planos) é horizontal
(de nível), sabe-se imediatamente que os traços horizontais dos dois pla-
nos são paralelos à recta ii (rectas horizontais de um plano são paralelas
entre si e paralelas ao traço horizontal do plano, que é uma recta horizon-
tal do plano com cota nula). Determinou-se HH, o traço horizontal da gera-
triz gg. O traço horizontal do plano θ11, hhθ11
, passa por HH11 e é paralelo à recta
ii. Determinou-se FF, o traço frontal da recta ii. O traço frontal do plano θ11,
ffθ11
, passa por FF22 e é concorrente com hhθ11
no eixo XX. Determinou-se HH, o
traço horizontal da geratriz gg’’. O traço horizontal do plano θ22 passa por HH’’11
e é paralelo à recta ii – o traço frontal do plano, ffθ22
, passa por FF22 e é con-
corrente com hhθ22
no eixo XX.
382.
Em primeiro lugar representaram-se o cone e a recta mm, pelas respectivas
projecções, em função dos dados. O plano ν é o plano horizontal (de nível)
que contém a base do cone. Em seguida, procedeu-se à execução sequen-
cial das etapas que nos conduzem à resolução do problema. 11.. Por VV con-
duziu-se uma recta paralela à recta mm (recta ii), que é a recta de intersecção
dos dois planos tangentes – a recta ii é igualmente uma recta fronto-hori-
zontal. 22.. Determinou-se o ponto de intersecção da recta ii com o plano da
base – o ponto II. A recta ii é paralela ao plano da base, pelo que o ponto II
ssee ssiittuuaa nnoo iinnffiinniittoo. 33.. Por II (que se situa no infinito) conduziram-se as rec-
tas tangentes à base do cone, tt e tt’’ – as rectas tt e tt’’ são concorrentes com
a recta ii num ponto do infinito, pelo que são necessariamente paralelas à
recta ii (são igualmente rectas fronto-horizontais). As rectas tt e tt’’ são as rec-
tas de intersecção dos dois planos tangentes com o plano ν, o plano da
base do cone. Cada um dos dois planos tangentes já está definido por
duas rectas – pela recta ii e por uma das rectas tt e tt’’. Note que as tangentes
à base se determinaram através do processo rigoroso para a determinação
das rectas tangentes a uma circunferência que são paralelas a uma recta
dada que, neste caso, é a recta ii. Os pontos de tangência são TT e TT’’. 44..
Determinaram-se as geratrizes de tangência (ou de contacto), gg e gg’’ – gg
está definida por VV e TT e gg’’ está definida por VV e TT’’. Note que as geratrizes
gg e gg’’ são, ambas, de perfil. 55.. Cada um dos dois planos tangentes está
definido por três rectas – o plano θ1 está definido pelas rectas ii, tt e gg e o
plano θ2 está definido pelas rectas ii, tt’’ e gg’’. Note que se trata nneecceessssaarriiaa--
mmeennttee de ppllaannooss ddee rraammppaa – os dois traços de ambos os planos são rec-
tas fronto-horizontais. A determinação dos traços dos dois planos pode
passar pela determinação dos traços das geratrizes que, sendo de perfil,
(Continua na página seguinte)

161. 161
SOLUÇÕES
obrigar-nos-ia ao recurso a um qualquer processo geométrico auxiliar. Assim, optou-se por um outro raciocínio – o recurso a rectas auxilia-
res dos planos. A recta rr é uma recta auxiliar do plano θ1 – a recta rr é concorrente com a recta tt no ponto AA e é concorrente com a recta ii no
ponto BB (recorde que as rectas tt e ii são duas rectas do plano θ1). A recta rr está definida por dois pontos e é necessariamente uma recta do
plano θ1. Determinaram-se os traços da recta rr nos planos de projecção, HH e FF, pelos quais se conduziram os traços homónimos do plano
θ1. Recorreu-se a um raciocínio idêntico para o plano θ2 – a recta ss é a recta auxiliar do plano θ2 a que se recorreu (por uma questão de econo-
mia de traçados, optou-se por fazer a projecção frontal da recta ss coincidente com a projecção frontal da recta rr). A recta ss é concorrente
com a recta tt’’ no ponto CC e é concorrente com a recta ii no ponto BB (recorde que as rectas tt’’ e ii são duas rectas do plano θ2). A recta ss está
definida por dois pontos e é necessariamente uma recta do plano θ2. Determinaram-se os traços da recta ss nos planos de projecção, HH’’ e FF’’,
pelos quais se conduziram os traços homónimos do plano θ2. Sublinha-se que se poderia ter recorrido, por exemplo, ao rebatimento das ge-
ratrizes, através do rebatimento do plano de perfil que as contém, e determinar, em rebatimento, os traços das duas geratrizes nos planos
de projecção – invertendo o rebatimento, obter-se-iam as respectivas projecções, o que nos permitiria determinar os traços dos planos tan-
gentes. No entanto, este processo seria mais moroso do que o apresentado e teria mais traçado.
383.
Em primeiro lugar representaram-se o cone e a recta ff,
pelas respectivas projecções, em função dos dados.
A recta pp é a recta de perfil que contém o eixo do cone.
Os dados permitiram-nos determinar imediatamente VV22,
a projecção frontal do vértice do cone e, assim, concluir
a construção da sua projecção frontal. Para determinar
VV11 foi necessário o recurso a um processo geométrico
auxiliar – optou-se pelo rebatimento do plano π, o plano
de perfil que contém a recta pp. Rebateu-se o plano π
para o Plano Frontal de Projecção – a charneira foi ffπ.
A recta pprr (a recta pp em rebatimento) passa por OOrr e é
concorrente com o eixo XX num ponto fixo, que é o ponto
de concorrência dos dois traços do plano (a recta pp é
uma recta passante). A partir de VV22 transportou-se, para
o rebatimento, a cota de VV, obtendo VVrr – invertendo o re-
batimento, determinou-se VV11, o que nos permitiu concluir
a construção da projecção horizontal do cone. No que
respeita à recta ff, note que a sua localização foi total-
mente arbitrária, pois não é dado nenhum ponto da recta
ff. Tal facto, no entanto, não é relevante para o exercício,
pois a solução final será sempre a mesma, independen-
temente da situação da recta ff – a solução do problema
depende, unicamente, ddaa ddiirreeccççããoo da recta ff. Em segui-
da, procedeu-se à execução sequencial das etapas que
nos conduzem à resolução do problema. 11.. Por VV con-
duziu-se uma recta paralela à recta ff (a recta ii), que é a
recta de intersecção dos dois planos tangentes. Note
que a recta ii é igualmente uma recta frontal (de frente).
22.. Determinou-se o ponto de intersecção da recta ii com
o plano da base – o ponto II. 33.. Por II conduziram-se as
rectas tangentes à base do cone, tt e tt’’. Cada um dos
dois planos tangentes já está definido por duas rectas –
pela recta ii e por uma das duas rectas tt e tt’’. Note que as
tangentes à base se determinaram através do
processo rigoroso para a determinação das rectas tan-
gentes a uma circunferência que passam por um ponto exterior que, neste caso, é II11. Os pontos de tangência são TT e TT’’. 44.. Determinaram-se
as geratrizes de tangência (ou de contacto), gg e gg’’ – gg está definida por VV e TT e gg’’ está definida por VV e TT’’. 55.. Cada um dos dois planos tangentes
está definido por três rectas – o plano θ1 está definido por ii, tt e gg e o plano θ2 está definido por ii, tt’’ e gg’’. Determinou-se HH, o traço horizontal da
recta ii. O traço horizontal do plano θ1, hhθ11
, passa por HH11 e é paralelo à recta tt, pois a recta tt é uma recta horizontal (de nível) do plano θ1 (rectas
horizontais de um plano são paralelas entre si e paralelas ao traço horizontal do plano, que é uma recta horizontal do plano com cota nula).
O traço frontal do plano θ1, ffθ11
, é concorrente com hhθ11
no eixo XX e é paralelo à recta ii, pois a recta ii é uma recta frontal (de frente) do plano θ1
(rectas frontais de um plano são paralelas entre si e paralelas ao traço frontal do plano, que é uma recta frontal do plano com afastamento nulo).
De forma idêntica, o traço horizontal do plano θ2, hhθ22
, passa por HH11 e é paralelo à recta tt’’, pois a recta tt’’ é uma recta horizontal (de nível) do plano
θ2 – o traço frontal do plano θ2, ffθ22
, é concorrente com hhθ22
no eixo XX e é paralelo à recta ii, pois a recta ii é também uma recta frontal (de frente) do
plano θ2.
384.
Se o plano θ é tangente a uma superfície cilíndrica num ponto, conclui-se que o plano θ é tangente à superfície ao longo da geratriz que
contém o ponto (a geratriz de contacto ou de tangência) e é igualmente tangente à directriz da superfície. Sabe-se, ainda, que o plano θ
ccoonnttéémm aa ««ffaammíílliiaa»» ddee rreeccttaass ddaass ggeerraattrriizzeess ddaa ssuuppeerrffíícciiee (e do seu eixo).

162. 162
SOLUÇÕES
385.
A geratriz ao longo da qual um dado plano é tangente a uma superfície cilíndrica chama-se ggeerraattrriizz ddee ccoonnttaaccttoo ou ggeerraattrriizz ddee ttaannggêênncciiaa.
386.
A afirmação é verdadeira. De facto, qualquer plano tangente a uma superfície cilíndrica é tangente à superfície ao longo de uma geratriz –
qualquer plano tangente a uma superfície cilíndrica contém, assim, uma geratriz da superfície (a geratriz de contacto ou de tangência), pelo
que contém igualmente, uma infinidade de rectas paralelas a essa geratriz. Uma vez que todas as geratrizes de uma superfície cilíndrica são
paralelas entre si e paralelas ao eixo da superfície, qualquer plano tangente a uma superfície cilíndrica contém, assim, a «família» de rectas
do eixo da superfície, ou seja, verifica o CCrriittéérriioo ddee ppaarraalleelliissmmoo eennttrree ppllaannooss ee rreeccttaass em relação ao eixo da superfície (para que um plano
seja paralelo a uma recta, tem de conter a «família» de rectas a que essa recta pertence).
387.
Em primeiro lugar representou-se o cilindro, pelas suas projecções, em fun-
ção dos dados. O plano ν é o plano horizontal (de nível) que contém a base
superior do sólido. Para determinar as projecções do ponto PP determinou-
-se, previamente, o lugar geométrico dos pontos da superfície lateral do
cilindro que têm 2 cm de cota. Para tal, recorreu-se a um plano horizontal
(de nível) ν1, com 2 cm de cota, e determinou-se a circunferência resultante
da intersecção desse plano com a superfície lateral do cilindro – essa cir-
cunferência tem raio igual ao raio das bases e tem centro no ponto QQ, que é
o ponto de intersecção do plano ν1 com o eixo do sólido. O ponto PP é o
ponto dessa circunferência que tem 3 cm de afastamento e é visível em pro-
jecção horizontal (o outro ponto da circunferência que também tem 3 cm de
afastamento é invisível em projecção horizontal). Em seguida, conduziu-se,
por PP, uma geratriz gg, da superfície lateral do cilindro – a geratriz gg é a gera-
triz de contacto ou de tangência (é a geratriz ao longo da qual o plano θ é
tangente à superfície lateral do cilindro). A geratriz gg está definida por um
ponto (o ponto PP) e por uma direcção (é paralela ao eixo do cilindro). O
ponto HH é o traço horizontal da geratriz e é o ponto da geratriz que se situa
na base inferior do sólido. A geratriz gg é, já, uma recta tangente à superfície
lateral do cilindro no ponto PP – já temos uma recta para definir o plano θ.
Necessitamos de outra recta. Recorreu-se à recta tt, outra recta tangente à
superfície no ponto PP. A recta tt é uma recta horizontal (de nível) e é a recta
de intersecção do plano θ com o plano ν1 (o plano auxiliar a que se recorreu
para determinar as projecções de PP). A recta tt está definida por um ponto
(o ponto PP) e uma direcção (é perpendicular ao raio da circunferência que contém PP no ponto PP). Já temos duas rectas para definir o plano
θ – a geratriz gg e a recta tangente tt. O traço horizontal do plano θ, hhθ, passa por HH (o traço horizontal da geratriz gg) e é paralelo à recta tt,
pois tt é uma recta horizontal (de nível) do plano θ. Em seguida, determinou-se FF, o traço frontal da recta tt – o traço frontal do plano θ, ffθ,
passa por FF e é concorrente com hhθ no eixo XX.
388.
Em primeiro lugar representou-se o cilindro, pelas suas projecções, em função dos dados.
O plano ν é o plano horizontal (de nível) que contém a base inferior do sólido. O plano ν1 é
o plano horizontal (de nível) que contém a base superior do cilindro. Para determinar as
projecções do ponto MM recorreu-se a uma geratriz gg, do cilindro, com 3 cm de afastamento e
situada à esquerda do eixo do sólido – o ponto MM é o ponto da geratriz gg que tem 5 cm de
cota. Note que este raciocínio é exclusivo dos cilindros de revolução com geratrizes verti-
cais (que é o caso) ou de topo. A geratriz gg, porque contém o ponto MM, é a geratriz de
contacto ou de tangência (é a geratriz ao longo da qual o plano θ é tangente à superfície
lateral do cilindro). Já temos uma recta para definir o plano θ – falta-nos outra recta. O pon-
to AA é o ponto da geratriz gg que se situa na base inferior do cilindro. A recta tt é a recta tan-
gente à base inferior do sólido no ponto AA (tt é perpendicular ao raio da base no ponto AA) –
a recta tt está definida por um ponto e uma direcção. O plano θ está definido por duas rec-
tas concorrentes – a recta tt e a geratriz gg. HH é o traço horizontal da geratriz gg – hhθ passa
por HH11 e é paralelo à recta tt (rectas horizontais de um plano são paralelas entre si e parale-
las ao traço horizontal do plano, que é uma recta horizontal do plano com cota nula). O
traço frontal do plano θ, ffθ, é concorrente com hhθ no eixo XX e é paralelo à geratriz gg (a ge-
ratriz gg é uma recta vertical, que é uma caso particular das rectas frontais – rectas frontais
de um plano são paralelas entre si e paralelas ao traço frontal do plano, que é uma recta
frontal do plano com afastamento nulo). Note que, atendendo a que a geratriz gg é uma
recta vertical (projectante horizontal), era um dado adquirido que o plano θ seria necessa-
riamente um plano projectante horizontal. Note que este raciocínio permitir-nos-ia ter pou-
pado o recurso à recta tt, pois bastava garantir que o plano θ contivesse a geratriz gg e
fosse tangente ao cone, o que era possível garantir, directamente, em projecção horizontal.

163. 163
SOLUÇÕES
389.
Em primeiro lugar representou-se o cilindro, pelas suas projec-
ções, em função dos dados. O plano ϕ é o plano frontal (de frente)
que contém a base de maior afastamento do sólido. Para determi-
nar as projecções do ponto PP recorreu-se a uma geratriz gg, do ci-
lindro, com 6,5 cm de cota e situada à esquerda do eixo do sólido
– o ponto PP é o ponto da geratriz gg que tem 5 cm de afastamento.
Sublinha-se que este raciocínio é exclusivo dos cilindros de revo-
lução com geratrizes de topo (que é o caso) ou verticais (que é o
caso do exercício anterior). A geratriz gg, porque contém o ponto
PP, é a geratriz de contacto ou de tangência (é a geratriz ao longo
da qual o plano θ é tangente à superfície lateral do cilindro). Já
temos uma recta para definir o plano θ – falta-nos outra recta.
O ponto FF é o ponto da geratriz gg que se situa na base de menor
afastamento do cilindro (FF é o traço frontal da geratriz gg). A recta tt
é a recta tangente à base de menor afastamento do sólido em FF
(tt é perpendicular ao raio da base no ponto FF) – a recta tt é o pró-
prio traço frontal do plano θ. O plano θ está definido por duas rec-
tas concorrentes – a geratriz gg e o seu traço frontal (ffθ). O traço
horizontal do plano θ, hhθ, é concorrente com ffθ no eixo XX e é para-
lelo à geratriz gg (a geratriz gg é uma recta de topo, que é uma caso
particular das rectas horizontais – rectas horizontais de um plano
são paralelas entre si e paralelas ao traço horizontal do plano, que
é uma recta horizontal do plano com cota nula). Note que, aten-
dendo a que a geratriz gg é uma recta de topo (projectante frontal),
era um dado adquirido que o plano θ seria necessariamente um
plano projectante frontal.
390.
Em primeiro lugar representou-se o cilindro, pelas suas projec-
ções, em função dos dados. O plano ϕ é o plano frontal (de fren-
te) que contém a base de maior afastamento do sólido. O plano
ϕ1 é o plano frontal (de frente) que contém a base de menor afas-
tamento do sólido. Os pontos TT e TT’’ são os pontos de menor cota
das duas bases do sólido (da base de maior afastamento e da
base de menor afastamento, respectivamente). A geratriz gg está
definida por TT e TT’’ (e é paralela ao eixo do sólido). A geratriz gg é a
geratriz de contacto ou de tangência (é a geratriz ao longo da
qual o plano θ é tangente à superfície lateral do cilindro). A gera-
triz gg é, já, uma recta do plano θ – já temos uma recta para definir
o plano θ. Necessitamos de outra recta. Recorreu-se à recta tt, ou-
tra recta tangente à superfície – a recta tt é a recta tangente à base
de maior afastamento do cilindro no ponto TT. A recta tt é uma recta
fronto-horizontal e é a recta de intersecção do plano θ com o pla-
no ϕ (o plano da base de maior afastamento). A recta tt está defini-
da por um ponto (o ponto TT) e uma direcção (é perpendicular ao
raio da base no ponto TT). Já temos duas rectas para definir o pla-
no θ – a geratriz gg e a recta tangente tt. O plano está definido por
uma recta oblíqua (a geratriz gg) e por uma recta fronto-horizontal
(a recta tt), pelo que o plano θ é necessariamente um ppllaannoo ddee
rraammppaa. Determinaram-se os traços da geratriz gg nos planos de
projecção, pelos quais se conduziram os traços homónimos do
plano θ.

164. 164
SOLUÇÕES
391.
Em primeiro lugar representou-se o cilindro, pelas suas projec-
ções, em função dos dados. A recta rr tem as suas projecções
paralelas entre si, pois é paralela ao β2/4. O centro da base de
maior afastamento é o ponto da recta rr que dista 3 cm (o raio das
bases) do Plano Horizontal de Projecção – o ponto OO é o ponto da
recta rr que tem 3 cm de cota. O plano ϕ é o plano frontal (de frente)
que contém a base de maior afastamento do cilindro. O plano ϕ1 é
o plano frontal (de frente) que contém a base de menor afasta-
mento do cilindro. O plano ϕ1 dista 4 cm (a altura do cilindro) do
plano ϕ. O ponto OO’’ é o centro da base de menor afastamento do
cilindro e é o ponto de intersecção do plano ϕ1 com a recta rr. Para
determinar as projecções do ponto PP determinou-se, previamente,
o lugar geométrico dos pontos da superfície lateral do cilindro que
têm 5 cm de afastamento. Para tal, recorreu-se a um plano frontal
(de frente) ϕ2, com 5 cm de afastamento, e determinou-se a cir-
cunferência resultante da intersecção desse plano com a superfí-
cie lateral do cilindro – essa circunferência tem centro no ponto AA
(que é o ponto de intersecção do plano ϕ2 com o eixo do sólido) e
raio AAෆ22ෆMMෆ22ෆ (MM é o ponto em que o plano ϕ2 corta a geratriz [GGGG’’],
que é a geratriz mais à direita do contorno aparente horizontal). O
ponto PP é o ponto dessa circunferência que tem 2 cm de cota (é o
úúnniiccoo ponto dessa circunferência que tem 2 cm de cota). Note
que o raio dessa circunferência é igual ao raio das faces, pelo que
a determinação do ponto MM não foi fundamental. Em seguida con-
duziu-se, por PP, uma geratriz gg, da superfície lateral do cilindro – a
geratriz gg é a geratriz de contacto ou de tangência (é a geratriz ao
longo da qual o plano θ é tangente à superfície lateral do cilindro).
A geratriz gg está definida por um ponto (o ponto PP) e por uma
direcção (é paralela ao eixo do cilindro). O ponto HH é o traço horizontal da geratriz e é o ponto da geratriz que se situa na base de maior
afastamento do sólido. A geratriz gg é, já, uma recta tangente à superfície lateral do cilindro no ponto PP – já temos uma recta para definir o
plano θ. Necessitamos de outra recta. Recorreu-se à recta tt, outra recta tangente à superfície no ponto PP. A recta tt é uma recta fronto-hori-
zontal e é a recta de intersecção do plano θ com o plano ϕ2 (o plano auxiliar a que se recorreu para determinar as projecções de PP). A recta
tt está definida por um ponto (o ponto PP) e uma direcção (é perpendicular ao raio da circunferência que contém PP no ponto PP). Já temos
duas rectas para definir o plano θ – a geratriz gg e a recta tangente tt. O plano θ está definido por uma recta oblíqua (a geratriz gg) e por uma
recta fronto-horizontal (a recta tt), pelo que o plano θ é necessariamente um ppllaannoo ddee rraammppaa. Determinou-se o traço frontal da geratriz gg,
pelo qual se conduziu o traço frontal do plano θ. O traço horizontal do plano θ passa pelo traço horizontal da geratriz gg, já determinado.
392.
Em primeiro lugar representou-se o cilindro e o ponto AA, pelas respectivas
projecções, em função dos dados. Em seguida, procedeu-se à execução
sequencial das etapas que nos conduzem à resolução do problema. 11.. Por AA
conduziu-se uma recta paralela às geratrizes do cilindro (recta ii), que é a recta
de intersecção dos dois planos tangentes. A recta ii é uma recta vertical.
22.. Determinou-se o ponto de intersecção da recta ii com o plano da base de
referência (a base de menor cota), que é o próprio Plano Horizontal de Pro-
jecção. O ponto II é o próprio traço horizontal da recta ii, que se identificou
imediatamente com a letra HH. 33.. Por II conduziram-se as rectas tangentes à
base de referência do cilindro, que são imediatamente, os traços horizontais
dos dois planos tangentes (uma vez que o plano da base é o próprio Plano
Horizontal de Projecção). Cada um dos dois planos tangentes já está definido
por duas rectas – pelo seu traço horizontal e pela recta ii. Note que as tangentes
à base (os traços horizontais dos planos) se determinaram através do processo
rigoroso para a determinação das rectas tangentes a uma circunferência que
passam por um ponto exterior que, neste caso, é II11. Os pontos de tangência
são TT e TT’’. 44.. Determinaram-se as geratrizes de tangência (ou de contacto), gg
e gg’’, que são rectas verticais – gg passa por TT e gg’’ passa por TT’’. 55.. Cada um
dos dois planos tangentes está definido por três rectas (a recta ii, a respectiva
geratriz de contacto e o respectivo traço horizontal). Para determinar os traços
frontais dos dois planos, teve-se em consideração que as rectas verticais
(a recta ii e as geratrizes gg e gg’’) são casos particulares das rectas frontais
(de frente) – os traços frontais são, assim, rectas verticais (rectas frontais de
um plano são paralelas entre si e paralelas ao traço frontal do plano, que é
uma recta frontal do plano com afastamento nulo) e são concorrentes com os
respectivos traços horizontais no eixo XX.

165. 165
SOLUÇÕES
Em primeiro lugar representou-se o cilindro e o ponto GG,
pelas respectivas projecções, em função dos dados. O pla-
no ν é o plano horizontal (de nível) que contém a base infe-
rior do cilindro. O plano ν1 é o plano horizontal (de nível)
que contém a base superior do cilindro. Em seguida, pro-
cedeu-se à execução sequencial das etapas que nos con-
duzem à resolução do problema. 11.. Por GG conduziu-se uma
recta paralela às geratrizes do cilindro (recta ii), que é a recta
de intersecção dos dois planos tangentes. 22.. Determinou-
-se o ponto de intersecção da recta ii com o plano da base
de referência (a base de menor cota) – o ponto II. 33.. Por II
conduziram-se as rectas tangentes à base de referência do
cilindro (a base de menor cota) – tt e tt’’. As rectas tt e tt’’ são
rectas horizontais (de nível) e são as rectas de intersecção
dos dois planos tangentes com o plano da base de referên-
cia (a base de menor cota do cilindro). Cada um dos dois
planos tangentes já está definido por duas rectas – pela
recta ii e por uma das duas rectas tt e tt’’. Note que as tan-
gentes à base se determinaram através do processo rigoroso
para a determinação das rectas tangentes a uma circunfe-
rência que passam por um ponto exterior que, neste caso,
é II11. Os pontos de tangência são TT e TT’’. 44.. Determinaram-
-se as geratrizes de tangência (ou de contacto), gg e gg’’ – gg
passa por TT e é paralela ao eixo do cilindro, tal como gg’’
passa por TT’’ e é também paralela ao eixo do sólido.
55.. Cada um dos dois planos tangentes está definido por
três rectas (a recta ii, a respectiva geratriz de contacto e a respectiva tangente à base inferior). Determinaram-se os traços da recta ii nos pla-
nos de projecção – FF e HH. O traço horizontal do plano θ1 passa por HH11 e é paralelo à recta tt (rectas horizontais de um plano são paralelas
entre si e paralelas ao traço horizontal do plano, que é uma recta horizontal do plano com cota nula). De forma idêntica, o traço horizontal
do plano θ2 passa também por HH11 e é paralelo à recta tt’’. O traço frontal do plano θ2, ffθ22
, passa por FF22 e é concorrente com hhθ22
no eixo XX.
O mesmo raciocínio não se pode aplicar à determinação do traço frontal do plano θ1, pois o ponto de concorrência dos dois traços do plano
situa-se fora dos limites do desenho. Assim, determinou-se o traço frontal da geratriz gg (a geratriz que pertence ao plano θ1) – FF’’. O traço
frontal do plano θ1 passa pelos traços frontais de ii e gg (está definido por dois pontos).
393.
394.
Em primeiro lugar representou-se o cilindro e o ponto PP, pelas res-
pectivas projecções, em função dos dados. O plano ϕ é o plano
frontal (de frente) com 6 cm de afastamento que contém a base de
maior afastamento do cilindro. Em seguida, procedeu-se à execu-
ção sequencial das etapas que nos conduzem à resolução do pro-
blema. 11.. Por PP conduziu-se uma recta paralela às geratrizes do
cilindro (recta ii), que é a recta de intersecção dos dois planos tan-
gentes. A recta ii é uma recta horizontal (de nível). 22.. Determinou-se
o ponto de intersecção da recta ii com o plano da base de referên-
cia (a base de menor afastamento) – o ponto II (note que II é, ime-
diatamente, o traço frontal da recta ii). 33.. Por II conduziram-se as
rectas tangentes à base de referência do cilindro (a base de menor
afastamento) – estas são, imediatamente, os traços frontais dos
dois planos tangentes (ffθ11
e ffθ22
). Cada um dos dois planos tangen-
tes já está definido por duas rectas – pela recta ii e pelo respectivo
traço frontal. Note que as tangentes à base se determinaram atra-
vés do processo rigoroso para a determinação das rectas tangen-
tes a uma circunferência que passam por um ponto exterior que,
neste caso, é II22. Note ainda que ffθ22
é paralelo ao eixo XX (é uma recta
fronto-horizontal). Os pontos de tangência são TT e TT’’. 44.. Determina-
ram-se as geratrizes de tangência (ou de contacto), gg e gg’’ – gg passa
por TT e é paralela ao eixo do cilindro, tal como gg’’ passa por TT’’ e é
também paralela ao eixo do sólido. 55.. Cada um dos dois planos
tangentes está definido por três rectas (a recta ii, a respectiva geratriz
de contacto e o respectivo traço frontal). Uma vez que a recta ii é uma recta horizontal (de nível), o traço horizontal do plano θ1, hhθ11
, é paralelo à
recta ii (rectas horizontais de um plano são paralelas entre si e paralelas ao traço horizontal do plano, que é uma recta horizontal do plano com
cota nula) e é concorrente com ffθ11
no eixo XX. Já o plano θ2, pelo seu traço frontal, só pode ser um plano de rampa ou um plano horizontal
(de nível). As três rectas conhecidas no plano θ2 (as rectas ii, gg e ffθ22
) são rectas horizontais (de nível) ou os seus casos particulares, pelo que o
plano θ2 é nneecceessssaarriiaammeennttee um plano horizontal (de nível), razão pela qual se assinalou o seu traço frontal entre parêntesis.

166. 166
SOLUÇÕES
395.
Em primeiro lugar representou-se o cilindro e o ponto MM, pelas respectivas projecções, em função dos dados. O plano ϕ é o plano frontal
(de frente) que contém a base de menor afastamento do cilindro. O plano ϕ1 é o plano frontal (de frente) que contém a base de maior afas-
tamento do cilindro. Em seguida, procedeu-se à execução sequencial das etapas que nos conduzem à resolução do problema. 11.. Por MM
conduziu-se uma recta paralela às geratrizes do cilindro (recta ii), que é a recta de intersecção dos dois planos tangentes. 22.. Determinou-se
o ponto de intersecção da recta ii com o plano da base de referência (a base de menor afastamento) – o ponto II. 33.. Por II conduziram-se as
rectas tangentes à base de referência do cilindro (a base de menor afastamento) – as rectas tt e tt’’, que são as rectas de intersecção dos dois
planos tangentes com o plano ϕ (o plano da base de referência). Cada um dos dois planos tangentes já está definido por duas rectas – pela
recta ii e por uma das duas rectas tt e tt’’. Note que as tangentes à base se determinaram através do processo rigoroso para a determinação
das rectas tangentes a uma circunferência que passam por um ponto exterior que, neste caso, é II22. Os pontos de tangência são TT e TT’’. 44..
Determinaram-se as geratrizes de tangência (ou de contacto), gg e gg’’ – gg passa por TT e é paralela ao eixo do cilindro, tal como gg’’ passa por TT’’
e é também paralela ao eixo do sólido. 55.. Cada um dos dois planos tangentes está definido por três rectas (a recta ii, a respectiva geratriz de
contacto e a respectiva recta tangente à base de referência). Determinou-se o traço frontal da recta ii (o ponto FF) – o seu traço horizontal
situa-se fora dos limites do desenho. Por FF22 conduziram-se os traços frontais dos dois planos tangentes – ffθ11
é paralelo às recta tt (a recta tt é
uma recta frontal do plano θ1 e rectas frontais de um plano são paralelas entre si e paralelas ao traço frontal do plano, que é uma recta fron-
tal do plano com afastamento nulo), tal como ffθ22
é paralelo à recta tt’’ (que, por sua vez, é uma recta frontal do plano θ2). Note que os traços
frontais dos dois planos estão, ambos, definidos por um ponto e uma direcção. Determinou-se o traço horizontal da recta tt – o ponto HH. O
traço horizontal do plano θ1, hhθ11
, passa por HH11 e é concorrente com ffθ11
no eixo XX (hhθ11
está definido por dois pontos). Determinou-se o traço
horizontal da recta tt’’ – o ponto HH’’. O ponto de concorrência dos traços do plano θ2 situa-se fora dos limites do desenho, pelo que, ao con-
trário do exposto para hhθ11
, só temos um ponto para definir hhθ22
– falta-nos outro ponto ou uma direcção, pelo que é necessário o recurso a
uma recta auxiliar do plano. Recorreu-se a uma recta horizontal (de nível) hh, do Plano θ2, que passa por TT’’ – a recta hh está definida por dois
pontos (o ponto TT’’ e o seu traço frontal, FF’’, que se situa sobre ffθ22
). O traço horizontal do plano θ2 passa por HH’’11 e é paralelo à recta hh (rectas
horizontais de um plano são paralelas entre si e paralelas ao traço horizontal do plano, que é uma recta horizontal do plano com cota nula) – hhθ22
está definido por um ponto e uma direcção.

167. 167
SOLUÇÕES
396.
Em primeiro lugar representou-se o cilindro e o ponto PP, pelas respectivas projecções, em função dos dados. As projecções da recta rr
fazem, com o eixo XX, ângulos iguais e com o mesmo sentido de abertura, pois a recta é paralela ao β1/3. O centro da base inferior do cilindro
é o ponto da recta rr que dista 3 cm (o raio das bases) do Plano Frontal de Projecção – o ponto OO é o ponto da recta rr que tem 3 cm de afas-
tamento. O plano ν é o plano horizontal (de nível) que contém a base inferior do cilindro. O eixo do cilindro (que mede 6 cm) não se projecta
em V.G. em nenhum dos planos de projecção, pois a sua recta suporte (a recta rr) é oblíqua a ambos os planos de projecção. É necessário o
recurso a um processo geométrico auxiliar – optou-se pelo rebatimento do plano α, o plano projectante horizontal da recta rr. Rebateu-se o pla-
no α para o Plano Frontal de Projecção – a charneira foi ffα. A recta rrrr é a recta rr rebatida e está definida por OOrr e por AArr – a partir de OOrr, sobre rrrr,
mediram-se os 6 cm (o comprimento do eixo do sólido), obtendo OO’’rr (OO’’ é o centro da base superior do cilindro). Invertendo o rebatimento,
determinaram-se as projecções de OO’’ (sobre as projecções homónimas da recta rr) e concluiu-se a construção das duas projecções do sólido.
O plano ν1 é o plano horizontal (de nível) que contém a base superior do cilindro. Em seguida, procedeu-se à execução sequencial das eta-
pas que nos conduzem à resolução do problema. 11.. Por PP conduziu-se uma recta paralela às geratrizes do cilindro (recta ii), que é a recta de
intersecção dos dois planos tangentes. Note que, uma vez que a recta rr (a recta suporte do eixo do cilindro) é paralela ao β1/3, a recta ii pas-
sando por PP (que é um ponto do β1/3) e sendo paralela à recta rr, é nneecceessssaarriiaammeennttee uma recta do β1/3. 22.. Determinou-se o ponto de inter-
secção da recta ii com o plano da base de referência (a base de menor cota) – o ponto II. 33.. Por II conduziram-se as rectas tangentes à base
de referência do cilindro (a base de menor cota) – as rectas tt e tt’’, que são as rectas de intersecção dos dois planos tangentes com o plano ν
(o plano da base de referência). Cada um dos dois planos tangentes já está definido por duas rectas – pela recta ii e por uma das duas rec-
tas tt e tt’’. Note que as tangentes à base se determinaram através do processo rigoroso para a determinação das rectas tangentes a uma cir-
cunferência que passam por um ponto exterior que, neste caso, é II11. Os pontos de tangência são TT e TT’’. 44.. Determinaram-se as geratrizes
de tangência (ou de contacto), gg e gg’’ – gg passa por TT e é paralela ao eixo do cilindro, tal como gg’’ passa por TT’’ e é também paralela ao eixo
do sólido. 55.. Cada um dos dois planos tangentes está definido por três rectas (a recta ii, a respectiva geratriz de contacto e a respectiva rec-
ta tangente à base de referência). A recta ii, sendo uma recta do β1/3, é uma recta passante, pelo que o ponto em que a recta ii é concorrente
com o eixo XX é o ponto de concorrência dos dois traços de ambos os planos. Assim, por esse ponto conduziram-se, imediatamente, os tra-
ços horizontais dos dois planos tangentes – hhθ11
é paralelo à recta tt (a recta tt é uma recta horizontal do plano θ1 e rectas horizontais de um
plano são paralelas entre si e paralelas ao traço horizontal do plano, que é uma recta horizontal do plano com cota nula), tal como hhθ22
é pa-
ralelo à recta tt’’ (que, por sua vez, é uma recta horizontal do plano θ2). Note que os traços horizontais dos dois planos estão, ambos, defini-
dos por um ponto e uma direcção. Determinou-se o traço frontal da recta tt – o ponto FF. O traço frontal do plano θ1, ffθ11
, passa por FF22 e é
concorrente com hhθ11
no eixo XX (ffθ11
está definido por dois pontos). Determinou-se o traço frontal da recta tt’’ – o ponto FF’’. O traço frontal do
plano θ2, ffθ22
, passa por FF’’22 e é concorrente com hhθ22
no eixo XX (ffθ22
está definido por dois pontos).

168. 168
SOLUÇÕES
397.
Em primeiro lugar representou-se o cilindro e a recta rr,
pelas respectivas projecções, em função dos dados.
A recta rr tem as suas projecções simétricas em relação
ao eixo XX, pois é uma recta do β1/3. O plano ν é o plano
horizontal (de nível) que contém a base superior do sólido.
Em seguida, procedeu-se à execução sequencial das
etapas que nos conduzem à resolução do problema.
11.. Determinar a orientação dos planos tangentes, defi-
nindo um plano paralelo aos planos tangentes através
das duas «famílias» de rectas que se conhecem – a «fa-
mília» da recta dada (recta rr) e a «família» das geratrizes
do cilindro. Assim, por um ponto qualquer, há que con-
duzir uma recta paralela à recta rr e uma recta paralela às
geratrizes do cilindro. Optou-se, com vista a uma maior
economia de traçados, por escolher um ponto RR, da rec-
ta rr, como o ponto exterior ao cilindro. Assim, por RR con-
duziu-se uma recta ff, paralela às geratrizes do sólido
(que estão contidas em rectas frontais) – o plano defini-
do pelas rectas rr e ff (plano θ) é paralelo aos planos tan-
gentes. 22.. Determinou-se a recta de intersecção do
plano θ (o plano definido por rr e ff) com o plano da base
de referência (a base de menor cota) – hhθ (que é, imedia-
tamente, o traço horizontal do plano θ). Optou-se por determinar também o traço frontal do plano θ, ffθ, apesar de, à partida, não ser neces-
sário. 33.. Conduziram-se as rectas tangentes à base de referência do cilindro (a base de menor cota) que são paralelas a hhθ – estas são,
imediatamente, os traços horizontais dos planos tangentes (hhθ11
e hhθ22
). As tangentes à base de referência permitem-nos, ainda, determinar
os pontos de tangência, TT e TT’’. Note que as tangentes à base se determinaram através do processo rigoroso para a determinação das rec-
tas tangentes a uma circunferência que são paralelas a uma recta dada que, neste caso, é hhθ. 44.. Determinaram-se as geratrizes de contacto
(ou de tangência), gg e gg’’ – gg passa por TT e é paralela ao eixo do cilindro e gg’’ passa por TT’’ e é também paralela ao eixo do cilindro. 55.. Cada
um dos dois planos tangentes está definido por duas rectas (o respectivo traço horizontal e a respectiva geratriz de contacto) e pela sua
orientação (são, ambos, paralelos ao plano θ, cujos traços já conhecemos). Assim, a determinação do traço frontal de θ1 é imediata – ffθ11
é
concorrente com hhθ11
no eixo XX e é paralelo a ffθ (plano paralelos têm os seus traços homónimos paralelos entre si. Em relação ao plano θ2,
observa-se que o ponto de concorrência dos dois traços se situa fora dos limites do desenho, pelo que temos, apenas, a direcção de ffθ22
– é
paralelo a ffθ. Falta-nos um ponto. Recorreu-se a uma recta auxiliar do plano θ2 – a recta tt. A recta tt é uma recta horizontal (de nível) do plano θ2
– tt é concorrente com a geratriz gg’’ no ponto TT’’’’ (TT’’’’ é o ponto da geratriz gg’’ que pertence à base superior do cilindro) e é paralela a hhθ22
. Note
que a recta tt é outra recta do plano θ2 que é tangente à base superior do cilindro (no ponto TT’’’’) – tt é a recta de intersecção do plano θ2 com
o plano ν. Determinou-se FF, o traço frontal da recta tt – ffθ22
passa por FF22 e é paralelo a ffθ.
398.
Em primeiro lugar representou-se o cilindro e a recta hh, pe-
las respectivas projecções, em função dos dados. O plano ϕ
é o plano frontal (de frente) que contém a base de maior
afastamento do cilindro. Em seguida, procedeu-se à execu-
ção sequencial das etapas que nos conduzem à resolução
do problema. 11.. Determinar a orientação dos planos tangen-
tes, definindo um plano paralelo aos planos tangentes atra-
vés das duas «famílias» de rectas que se conhecem – a
«família» da recta dada (recta rr) e a «família» das geratrizes
do cilindro. Assim, por um ponto qualquer há que conduzir
uma recta paralela à recta hh e uma recta paralela às geratri-
zes do cilindro. Optou-se, com vista a uma maior economia
de traçados, por escolher o ponto PP, da recta hh, como o
ponto exterior ao cilindro. Assim, por PP conduziu-se uma
recta rr, paralela às geratrizes do sólido (a recta rr é uma recta
de topo) – o plano definido pelas rectas rr e hh (plano θ) é pa-
ralelo aos planos tangentes. 22.. Determinou-se a recta de in-
tersecção do plano θ (o plano definido por hh e rr) com o
plano da base de referência (a base de menor afastamento)
– a recta ii, que é uma recta fronto-horizontal (está definida
por FF e FF’’, os traços frontais das rectas rr e hh, respectivamen-
te). Tenha em conta que o plano definido pelas rectas rr e hh é
nneecceessssaarriiaammeennttee um plano horizontal (de nível) – os dois
planos tangentes serão, igualmente, planos horizontais
(Continua na página seguinte)

169. 169
SOLUÇÕES
(de nível). 33.. Conduziram-se as rectas tangentes à base de referência do cilindro (a base de menor afastamento) que são paralelas à recta ii – tt
e tt’’.. Estas são, imediatamente, os traços frontais dos planos tangentes (ffθ11
e ffθ22
). As tangentes à base de referência permitem-nos, ainda, deter-
minar os pontos de tangência, TT e TT’’. Note que as tangentes à base se determinaram através do processo rigoroso para a determinação das
rectas tangentes a uma circunferência que são paralelas a uma recta dada que, neste caso, é ii22. 44.. Determinaram-se as geratrizes de con-
tacto (ou de tangência), gg e gg’’ – gg passa por TT e é paralela ao eixo do cilindro e gg’’ passa por TT’’ e é também paralela ao eixo do cilindro.
55.. Cada um dos dois planos tangentes está definido por duas rectas (o respectivo traço frontal e a respectiva geratriz de contacto) e pela
sua orientação (são, ambos, paralelos ao plano θ, que é um plano horizontal). Assim, os planos θ1 e θ2, porque são ppllaannooss hhoorriizzoonnttaaiiss ((ddee
nníívveell)), não têm traço horizontal e estão definidos por um único traço (o seu traço frontal), razão pela qual os respectivos traços frontais se
encontram assinalados entre parêntesis.
399.
Em primeiro lugar representou-se o cilindro e a recta ff, pelas respectivas projecções, em função dos dados. O plano ν é o plano horizontal
(de nível) que contém a base inferior do sólido. O plano ν1 é o plano horizontal (de nível) que contém a base superior do sólido. Em seguida,
procedeu-se à execução sequencial das etapas que nos conduzem à resolução do problema. 11.. Determinar a orientação dos planos tan-
gentes, definindo um plano paralelo aos planos tangentes através das duas «famílias» de rectas que se conhecem – a «família» da recta
dada (recta ff) e a «família» das geratrizes do cilindro. Assim, por um ponto qualquer, há que conduzir uma recta paralela à recta ff e uma rec-
ta paralela às geratrizes do cilindro. Optou-se, com vista a uma maior economia de traçados, por escolher o ponto MM, da recta ff, como o
ponto exterior ao cilindro. Assim, por MM conduziu-se uma recta rr, paralela às geratrizes do sólido (que estão contidas em rectas frontais) – o
plano definido pelas rectas rr e ff (plano θ) é paralelo aos planos tangentes. 22.. Determinou-se a recta de intersecção do plano θ (o plano defi-
nido por rr e ff) com o plano da base de referência (a base de menor cota). Uma vez que o plano da base de referência é paralelo ao Plano
Horizontal de Projecção, e atendendo a que um dado plano corta dois planos paralelos segundo duas rectas paralelas, optou-se por deter-
minar imediatamente a recta de intersecção do plano θ com o Plano Horizontal de Projecção – hhθ (o traço horizontal do plano θ). A recta de
intersecção do plano θ com o plano ν (o plano da base de referência), apesar de não se ter determinado, é paralela a hhθ. Optou-se por
determinar também o traço frontal do plano θ, ffθ, apesar de, à partida, não ser necessário. 33.. Conduziram-se as rectas tangentes à base de
referência do cilindro (a base de menor cota) que são paralelas a hhθ – as rectas tt e tt’’. Estas são as rectas de intersecção dos dois planos
tangentes com o plano ν (o plano da base de referência). As tangentes à base de referência permitem-nos, ainda, determinar os pontos de
tangência, TTe TT’’. Note que as tangentes à base se determinaram através do processo rigoroso para a determinação das rectas tangentes a
uma circunferência que são paralelas a uma recta dada que, neste caso, é hhθ. 44.. Determinaram-se as geratrizes de contacto (ou de tangên-
cia), gg e gg’’ – gg passa por TT e é paralela ao eixo do cilindro e gg’’ passa por TT’’ e é também paralela ao eixo do cilindro. 55.. Cada um dos dois
planos tangentes está definido por duas rectas (a respectiva tangente à base inferior do cilindro e a respectiva geratriz de contacto) e pela
sua orientação (são, ambos, paralelos ao plano θ, cujos traços já conhecemos). Determinou-se HH’’’’, o traço horizontal da geratriz gg – hhθ11
, o
traço horizontal do plano θ1, passa por HH’’’’11 e é paralelo a hhθ e à recta tt (a recta tt é uma recta horizontal do plano θ1 e rectas horizontais de
um plano são paralelas entre si e paralelas ao traço horizontal do plano, que é uma recta horizontal do plano com cota nula). O traço frontal
do plano θ1, ffθ11
, é concorrente com hhθ11
no eixo XX e é paralelo a ffθ (planos paralelos têm os traços homónimos paralelos entre si). Determi-
nou-se HH’’’’’’, o traço horizontal da geratriz gg’’ – hhθ22
, o traço horizontal do plano θ2, passa por HH’’’’’’11 e é paralelo à recta tt’’ (a recta tt’’ é uma recta
horizontal do plano θ2) e a hhθ. O traço frontal do plano θ2, ffθ22
, é concorrente com hhθ22
no eixo XX e é paralelo a ffθ.

170. 170
SOLUÇÕES
400.
Em primeiro lugar representou-se o cilindro e a recta rr, pelas respectivas projecções, em função dos dados. O plano ϕ é o plano frontal (de
frente) que contém a base de menor afastamento do cilindro. O plano ϕ1 é o plano frontal (de frente) que contém a base de maior afasta-
mento do cilindro. A recta rr, porque é uma recta do β2/4, tem as suas projecções coincidentes. Note que, apesar de as projecções da recta rr
passarem pelas projecções frontais de OO e de OO’’ (que estão coincidentes), nenhum destes pontos pertence à recta rr, pois são pontos que
não pertencem ao β2/4. Em seguida, procedeu-se à execução sequencial das etapas que nos conduzem à resolução do problema. 11.. Deter-
minar a orientação dos planos tangentes, definindo um plano paralelo aos planos tangentes através das duas «famílias» de rectas que se
conhecem – a «família» da recta dada (recta rr) e a «família» das geratrizes do cilindro. Assim, por um ponto qualquer, há que conduzir uma
recta paralela à recta rr e uma recta paralela às geratrizes do cilindro. Uma vez que as geratrizes do cilindro são projectantes frontais (são
rectas de topo), teve-se em conta que a orientação dos plano tangentes é determinada directamente – é a orientação do plano projectante
frontal da recta rr. O plano θ é o plano projectante frontal da recta rr e é um plano de topo – note que o plano θ (definido pelos seus traços)
contém a recta rr e contém rectas de topo, pelo que é nneecceessssaarriiaammeennttee paralelo às geratrizes do cilindro. Este raciocínio é exclusivo das
situações em que as geratrizes do cilindro ou a recta dada são projectantes. 22.. Determinou-se a recta de intersecção do plano θ (o plano
paralelo aos planos tangentes) com o plano da base de referência (a base de menor afastamento). Note que, à semelhança do exercício
anterior, se optou por determinar a recta de intersecção do plano θ com o Plano Frontal de Projecção (ffθ) que é paralela à recta de intersecção
de θ com ϕ (o plano da base de referência). O plano θ já estava definido pelos seus traços, pelo que esta segunda etapa já estava concluída.
33.. Conduziram-se as rectas tangentes à base de referência do cilindro (a base de menor afastamento) que são paralelas a ffθ – tt e tt’’. As tan-
gentes à base de referência permitem-nos, ainda, determinar os pontos de tangência, TT e TT’’. Note que as tangentes à base se determinaram
através do processo rigoroso para a determinação das rectas tangentes a uma circunferência que são paralelas a uma recta dada que, neste
caso, é ffθ. 44.. Determinaram-se as geratrizes de contacto (ou de tangência), gg e gg’’ – gg passa por TT e é paralela ao eixo do cilindro e gg’’ passa
por TT’’ e é também paralela ao eixo do cilindro. As duas geratrizes são rectas de topo. 55.. Cada um dos dois planos tangentes está definido
por duas rectas (a respectiva tangente à base de referência e a respectiva geratriz de contacto) e pela sua orientação (são, ambos, paralelos
ao plano θ, que é um plano de topo). Assim, porque os planos θ1 e θ2 são ppllaannooss ddee ttooppoo (pprroojjeeccttaanntteess ffrroonnttaaiiss), os seus traços tiveram
determinação directa.

171. 171
SOLUÇÕES
401.
Em primeiro lugar representou-se o cilindro e a recta hh, pelas respectivas projecções, em função dos dados. As projecções das geratrizes do
cilindro fazem, com o eixo XX, ângulos iguais e com o mesmo sentido de abertura, porque as respectivas rectas suporte são paralelas ao β1/3.
O plano ν é o plano horizontal (de nível) que contém a base inferior do sólido. O plano ν1 é o plano horizontal (de nível) que contém a base
superior do sólido e dista 5 cm (a altura do cilindro) do plano ν. Em seguida, procedeu-se à execução sequencial das etapas que nos con-
duzem à resolução do problema. 11.. Determinar a orientação dos planos tangentes, definindo um plano paralelo aos planos tangentes atra-
vés das duas «famílias» de rectas que se conhecem – a «família» da recta dada (recta hh) e a «família» das geratrizes do cilindro. Assim, por
um ponto qualquer há que conduzir uma recta paralela à recta hh e uma recta paralela às geratrizes do cilindro. Optou-se, com vista a uma
maior economia de traçados, por escolher o ponto PP, da recta hh, como o ponto exterior ao cilindro. Assim, por PP conduziu-se uma recta rr,
paralela às geratrizes do sólido – o plano definido pelas rectas rr e hh (plano θ) é paralelo aos planos tangentes. 22.. Determinou-se a recta de
intersecção do plano θ (o plano definido por rr e hh) com o plano da base de referência (a base de menor cota) – recta ii. A recta ii é uma recta
horizontal (de nível) do plano θ e está definida por um ponto (o ponto II, que é o ponto de intersecção da recta rr com o plano ν) e uma direc-
ção (é paralela à recta hh, pois rectas horizontais de um plano são paralelas entre si). 33.. Conduziram-se as rectas tangentes à base de refe-
rência do cilindro (a base de menor cota) que são paralelas à recta ii – as rectas tt e tt’’. As rectas tt e tt’’ são rectas horizontais (de nível) e são
as rectas de intersecção dos dois planos tangentes com o plano ν (o plano da base de referência). As tangentes à base de referência permi-
tem-nos, ainda, determinar os pontos de tangência, TT e TT’’. Note que as tangentes à base se determinaram através do processo rigoroso
para a determinação das rectas tangentes a uma circunferência que são paralelas a uma recta dada que, neste caso, é ii11. 44.. Determinaram-
-se as geratrizes de contacto (ou de tangência), gg e gg’’ – gg passa por TT e é paralela ao eixo do cilindro e gg’’ passa por TT’’ e é também paralela
ao eixo do cilindro. 55.. Cada um dos dois planos tangentes está definido por duas rectas (a respectiva tangente à base de referência e a res-
pectiva geratriz de contacto) e pela sua orientação (são, ambos, paralelos ao plano θ). Determinou-se o traço horizontal da geratriz gg – HH.
Por HH11 conduziu-se hhθ11
, o traço horizontal do plano θ1, paralelo à recta tt (a recta tt é uma recta horizontal do plano θ1 e rectas horizontais de
um plano são paralelas entre si e paralelas ao traço horizontal do plano, que é uma recta horizontal do plano com cota nula) – hhθ11
está defi-
nido por um ponto e uma direcção. Em seguida, determinou-se FF, o traço frontal da recta tt – ffθ11
, o traço frontal do plano θ1, passa por FF22 e é
concorrente com hhθ11
no eixo XX (ffθ11
está definido por dois pontos). Determinou-se o traço horizontal da geratriz gg’’ – HH’’. Por HH’’11 conduziu-se
hhθ22
, o traço horizontal do plano θ2, paralelo à recta tt (a recta tt é uma recta horizontal do plano θ2) – hhθ22
está definido por um ponto e uma
direcção. Em seguida determinou-se FF’’, o traço frontal da recta tt’’ – ffθ22
, o traço frontal do plano θ2, passa por FF’’22 e é concorrente com hhθ22
no
eixo XX (ffθ22
está definido por dois pontos).

172. 172
SOLUÇÕES
402.
Em primeiro lugar representaram-se o cone e o ponto MM, pelas respectivas projecções, em função dos dados. Em seguida, procedeu-se à
execução sequencial das etapas que nos conduzem à resolução do problema. 11.. Por VV e MM conduziu-se uma recta (recta ii), que é a recta de
intersecção dos dois planos tangentes. A recta ii é uma rreeccttaa ddee ppeerrffiill. 22.. Determinou-se o ponto de intersecção da recta ii com o plano da
base (que é o próprio Plano Horizontal de Projecção) – esse ponto é o traço horizontal da recta ii, cuja determinação requer o recurso a um
processo geométrico auxiliar. Optou-se pelo rebatimento – rebateu-se o plano π (o plano de perfil que contém a recta ii) para o Plano Frontal
de Projecção (a charneira foi ffπ). A recta iirr (a recta ii rebatida) fica definida por VVrr e por MMrr – HHrr é o traço horizontal da recta ii em rebatimento.
Invertendo o rebatimento, determinaram-se as projecções de HH – HH é, assim, o ponto de intersecção da recta ii com o plano da base
(o Plano Horizontal de Projecção). 33.. Por HH conduziram-se as rectas tangentes à base do cone, que são imediatamente, os traços horizon-
tais dos dois planos tangentes (uma vez que o plano da base é o próprio Plano Horizontal de Projecção) – hhθ11
e hhθ22
. Cada um dos dois pla-
nos tangentes já está definido por duas rectas – pelo seu traço horizontal e pela recta ii. Note que as tangentes à base (os traços horizontais
dos planos) se determinaram através do processo rigoroso para a determinação das rectas tangentes a uma circunferência que passam por
um ponto exterior que, neste caso, é HH11. Os pontos de tangência são TT e TT’’. 44.. Determinaram-se as geratrizes de tangência (ou de contac-
to), gg e gg’’ – gg está definida por VV e TT e gg’’ está definida por VV e TT’’. 55.. Cada um dos dois planos tangentes está definido por três rectas – o plano θ1
está definido por hhθ11
, por ii e por gg e o plano θ2 está definido por hhθ22
, por ii e por gg’’. Determinou-se FF, o traço frontal da recta ii – o ponto FF deter-
minou-se previamente em rebatimento (no rebatimento anteriormente efectuado para determinar HH). O traço frontal do plano θ1, ffθ11
, passa por
FF22 e é concorrente com hhθ11
no eixo XX (ffθ11
está definido por dois pontos). Raciocínio idêntico aplicou-se ao plano θ2 – o seu traço frontal, ffθ22
,
passa por FF22 e é concorrente com hhθ22
no eixo XX.

173. 173
SOLUÇÕES
403.
Em primeiro lugar representou-se o cilindro e a recta mm, pelas respectivas projecções, em função dos dados. O plano ϕ é o plano frontal
(de frente) que contém a base de maior afastamento do sólido. O plano ϕ1 é o plano frontal (de frente) que contém a base de menor afasta-
mento do sólido e dista 6 cm (a altura do cilindro) do plano ϕ. Em seguida, procedeu-se à execução sequencial das etapas que nos condu-
zem à resolução do problema. 11.. Determinar a orientação dos planos tangentes, definindo um plano paralelo aos planos tangentes através
das duas «famílias» de rectas que se conhecem – a «família» da recta dada (recta mm) e a «família» das geratrizes do cilindro. Assim, por um
ponto qualquer, há que conduzir uma recta paralela à recta mm e uma recta paralela às geratrizes do cilindro. Optou-se, com vista a uma
maior economia de traçados, por não executar esta etapa, uma vez que o plano θ (o plano paralelo aos planos tangentes), sendo um plano
definido por uma recta oblíqua e por uma recta fronto-horizontal, será nneecceessssaarriiaammeennttee um ppllaannoo ddee rraammppaa. Os dois planos tangentes
serão, assim, ppllaannooss ddee rraammppaa. Uma vez que planos de rampa têm sempre os seus traços homónimos paralelos entre si, quer sejam ou
não paralelos, a determinação dos traços do plano θ é desnecessária. 22.. Determinar a recta de intersecção do plano θ com o plano da base
de referência (a base de maior afastamento). Optou-se, também, por não executar esta etapa, pois a recta de intersecção de um plano de
rampa (o plano θ) com um plano frontal (o plano ϕ) é nneecceessssaarriiaammeennttee uma recta fronto-horizontal – já é conhecida a direcção da recta ii,
mesmo sem efectivar a sua determinação. 33.. Conduziram-se as rectas tangentes à base de referência do cilindro (a base de maior afasta-
mento) que são paralelas à recta ii – as rectas tt e tt’’. As rectas tt e tt’’ são rectas fronto-horizontais e são as rectas de intersecção dos dois pla-
nos tangentes com o plano ϕ (o plano da base de referência). As tangentes à base de referência permitem-nos, ainda, determinar os pontos
de tangência, TT e TT’’. 44.. Determinaram-se as geratrizes de contacto (ou de tangência), gg e gg’’ – gg passa por TT e é paralela ao eixo do cilindro
e gg’’ passa por TT’’ e é também paralela ao eixo do cilindro. 55.. Cada um dos dois planos tangentes está definido por duas rectas (a respectiva
tangente à base de referência e a respectiva geratriz de contacto). Determinaram-se os traços da geratriz gg – HH e FF. Pelos traços de gg con-
duziram-se os traços homónimos do plano θ1 (que é um plano de rampa). Determinaram-se os traços da geratriz gg’’ – HH’’ e FF’’. Note que HH’’11
se situa fora dos limites do desenho. Pelos traços de gg’’ conduziram-se os traços homónimos do plano θ2 (que é um plano de rampa).
Note que, uma vez que HH’’11 se situa fora dos limites do desenho, hhθ22
também se situa fora dos limites do desenho, pelo que não foi possí-
vel desenhá-lo.

174. 174
SOLUÇÕES
404.
Em primeiro lugar representaram-se o cone e o ponto PP, pelas respectivas projecções, em função dos dados. O plano ν é o plano horizontal
(de nível) que contém a base do cone. Os dados relativos ao cone permitiram-nos, de forma imediata, representar a sua base, desenhar
a projecção horizontal da recta rr (a recta que contém o eixo do sólido) e determinar a projecção horizontal do vértice do sólido (tendo em
conta que a geratriz mais à direita do sólido é de perfil). A partir de VV11, concluiu-se a construção da projecção horizontal do cone. No entan-
to, não se sabe a cota de VV – uma vez que o eixo do cone não se projecta em V.G. em nenhum dos planos de projecção (é oblíquo a am-
bos), é necessário o recurso a um processo geométrico auxiliar, para a determinação do vértice VV, do cone. Optou-se pelo rebatimento do
plano projectante horizontal do eixo – o plano α. Rebateu-se o plano α para o Plano Frontal de Projecção – a charneira foi ffα (recta ee). Reba-
teu-se o ponto OO (o centro da base, que é um extremo do eixo) e a referência de VV – com o compasso, fazendo centro em OOrr e com 9 cm (o
comprimento do eixo) de raio, determinou-se VVrr. Invertendo o rebatimento, determinou-se VV22, o que nos permitiu concluir a construção da
projecção frontal do cone. Em seguida, procedeu-se à execução sequencial das etapas que nos conduzem à resolução do problema. 11.. Por
VV e PP conduziu-se uma recta (recta ii), que é a recta de intersecção dos dois planos tangentes. A recta ii é uma rreeccttaa ddee ppeerrffiill. 22.. Determi-
nou-se o ponto de intersecção da recta ii com o plano da base (o plano ν) – esse ponto é o ponto II, cuja determinação requer o recurso a
um processo geométrico auxiliar (note que é possível determinar, de forma imediata, II22, a projecção frontal de II). Optou-se pelo rebatimento
– rebateu-se o plano π (o plano de perfil que contém a recta ii) para o Plano Frontal de Projecção (a charneira foi ffπ – recta ee’’). A recta iirr
(a recta ii rebatida) fica definida por VVrr e por PPrr – IIrr determinou-se, sobre iirr, em função da sua cota. Invertendo o rebatimento, determinou-se II11.
II é, assim, o ponto de intersecção da recta ii com o plano da base (o plano ν). 33.. Por II conduziram-se as rectas tangentes à base do cone –
as rectas tt e tt’’. Note que as tangentes à base se determinaram através do processo rigoroso para a determinação das rectas tangentes a
uma circunferência que passam por um ponto exterior que, neste caso, é II11. Os pontos de tangência são TT e TT’’. A recta tt é uma recta horizontal
(de nível) e a recta tt’’ é uma recta de topo. Cada um dos dois planos tangentes já está definido por duas rectas – pela recta ii e por uma das rectas tt
e tt’’. 44.. Determinaram-se as geratrizes de tangência (ou de contacto), gg e gg’’ – gg está definida por VV e TT e gg’’ está definida por VV e TT’’. Note que a ge-
ratriz gg’’ é uma rreeccttaa ddee ppeerrffiill. 55.. Cada um dos dois planos tangentes está definido por três rectas – o plano θ1 está definido por ii, tt e gg e o plano θ2
está definido por ii, tt’’ e gg’’. Uma vez que a recta ii e a geratriz gg’’ são duas rectas de perfil do mesmo plano de perfil, no qual está contida, ainda, a
recta tt’’, conclui-se que o plano θ2 é o próprio plano π. Determinaram-se os traços da recta ii – HH é o traço horizontal de ii e FF é o seu traço fron-
tal (note que HH e FF se determinaram pre-
viamente em rebatimento, no rebatimento
anteriormente efectuado do plano π). O
traço horizontal do plano θ1 passa por HH11
e é paralelo à recta tt, que é uma recta ho-
rizontal do plano θ1 (rectas horizontais de
um plano são paralelas entre si e paralelas
ao traço horizontal do plano, que é uma
recta horizontal do plano com cota nula).
O ponto de concorrência dos dois traços
do plano situa-se fora dos limites do dese-
nho, tal como o traço frontal da recta tt.
Recorreu-se a uma outra recta do plano θ1
– a geratriz gg. FF’’ é o traço frontal da gera-
triz gg – ffθ11
passa por FF22 e por FF’’22.

175. 175
SOLUÇÕES
405.
Em primeiro lugar representaram-se o cone e a recta pp, pelas respectivas projecções, em função dos dados. A recta pp está definida por um
ponto (o ponto AA) e por uma direcção (a recta faz um ângulo de 60o com o Plano Horizontal de Projecção, sendo que o seu traço frontal tem
cota negativa). Em seguida, procedeu-se à execução sequencial das etapas que nos conduzem à resolução do problema. 11.. Por VV con-
duziu-se uma recta paralela à recta pp (a recta ii), que é a recta de intersecção dos dois planos tangentes. Note que a recta ii é igualmente
uma recta de perfil – é uma recta de perfil paralela à recta pp. 22.. Determinou-se o ponto de intersecção da recta ii com o plano da base – o
ponto II. Uma vez que se trata de uma recta de perfil, a determinação do ponto II carece do recurso a um processo geométrico auxiliar –
optou-se pelo rebatimento do plano π (o plano de perfil que contém a recta ii). No entanto, é possível determinar, de forma imediata, II22.
Tenha em conta que a solução do problema depende, unicamente, ddaa ddiirreeccççããoo da recta pp e não da sua localização. Assim, com vista a uma
maior economia de traçados, optou-se por determinar um ponto AA’’, pertencente ao plano π e com as mesmas coordenadas do ponto AA. Por AA’’
conduziu-se uma recta pp’’, paralela à recta pp – a recta pp’’ é, afinal, a projecção ortogonal da recta pp no plano π. Este procedimento permite-
-nos economizar um rebatimento – as duas situações pendentes do recurso a processos geométricos auxiliares (a determinação do ponto II
e o paralelismo entre a recta ii e a recta pp) resolvem-se com um único rebatimento. Rebateu-se o plano π para o Plano Frontal de Projecção
– a charneira foi ffπ. A recta pp’’rr é a recta pp’’ rebatida – passa por AA’’rr faz, com hhπrr
, um ângulo de 60o, sendo que o seu traço frontal (que não
se determinou) tem cota negativa (situa-se no SSPPFFII). A recta iirr, a recta ii rebatida, passa por VVrr e é paralela à recta pp’’rr. O ponto II determinou-
-se em rebatimento, a partir da sua projecção frontal – invertendo o rebatimento, determinou-se II11. 33.. Por II conduziram-se as rectas tangen-
tes à base do cone, tt e tt’’. Cada um dos dois planos tangentes já está definido por duas rectas – pela recta ii e por uma das duas rectas tt e tt’’.
Note que as tangentes à base se determinaram através do processo rigoroso para a determinação das rectas tangentes a uma circunferên-
cia que passam por um ponto exterior que, neste caso, é II11. Os pontos de tangência são TT e TT’’. 44.. Determinaram-se as geratrizes de tan-
gência (ou de contacto), gg e gg’’ – gg está definida por VV e TT e gg’’ está definida por VV e TT’’. 55.. Cada um dos dois planos tangentes está definido
por três rectas – o plano θ1 está definido por ii, tt e gg e o plano θ2 está definido por ii, tt’’ e gg’’. Determinaram-se os traços da recta ii – HH, o seu
traço horizontal, e FF, o seu traço frontal. Tenha em conta que os traços da recta ii se determinaram previamente em rebatimento, no rebati-
mento anteriormente efectuado no plano π. O traço horizontal do plano θ1, hhθ11
, passa por HH11 e é paralelo à recta tt, pois a recta tt é uma recta
horizontal (de nível) do plano θ1 (rectas horizontais de um plano são paralelas entre si e paralelas ao traço horizontal do plano, que é uma
recta horizontal do plano com cota nula). O traço frontal do plano θ1, ffθ11
, é concorrente com hhθ11
no eixo XX e passa por FF22. O traço horizontal
do plano θ2, hhθ22
, passa igualmente por HH11 e é paralelo à recta tt’’, pois a recta tt’’ é uma recta horizontal (de nível) do plano θ2. O traço frontal
do plano θ2, ffθ22
, é concorrente com hhθ22
no eixo XX e passa por FF22.

176. 176
SOLUÇÕES
406.
Em primeiro lugar representou-se o cilindro e o ponto PP, pelas respectivas projecções, em função dos dados. No que respeita ao cilindro, os
dados do enunciado permitiram-nos, apenas, concluir a construção da sua projecção horizontal – o ponto OO’’ (o centro da base superior) tem
abcissa nula e 3 cm de afastamento (o raio das bases, pois a base superior é tangente ao Plano Frontal de Projecção). É dado que as geratrizes
do sólido medem 9 cm – o eixo do cilindro tem o mesmo comprimento e não se projecta em V.G. em nenhum dos planos de projecção, pois não
é paralelo a nenhum dos planos de projecção. É necessário o recurso a um processo geométrico auxiliar – optou-se pelo rebatimento do plano
α, o plano projectante horizontal do eixo do cilindro. Rebateu-se o plano α para o Plano Frontal de Projecção – a charneira foi ffα. Rebateu-se o
ponto OO e a referência de OO’’ – com o compasso, fazendo centro em OOrr e com 9 cm de raio, determinou-se OO’’rr. Invertendo o rebatimento, deter-
minou-se OO’’22 e concluiu-se a construção da projecção frontal do cilindro. O plano ν é o plano horizontal (de nível) que contém a base superior
do cilindro. Em seguida, procedeu-se à execução sequencial das etapas que nos conduzem à resolução do problema. 11.. Por PP conduziu-se
uma recta paralela às geratrizes do cilindro (recta ii), que é a recta de intersecção dos dois planos tangentes. 22.. Determinou-se o ponto de inter-
secção da recta ii com o plano da base de referência (a base inferior) – o ponto II (que é, imediatamente, o traço horizontal da recta ii). 33.. Por II
conduziram-se as rectas tangentes à base de referência do cilindro (a base inferior) – tt e tt’’. As rectas tt e tt’’ são, imediatamente, os traços hori-
zontais dos dois planos tangentes. Cada um dos dois planos tangentes já está definido por duas rectas – pela recta ii e pelo respectivo traço
horizontal. Note que as tangentes à base se determinaram através do processo rigoroso para a determinação das rectas tangentes a uma cir-
cunferência que passam por um ponto exterior que, neste caso, é II11. Os pontos de tangência são TT e TT’’. 44.. Determinaram-se as geratrizes de
tangência (ou de contacto), gg e gg’’ – gg passa por TT e é paralela ao eixo do cilindro, tal como gg’’ passa por TT’’ e é também paralela ao eixo do
sólido. 55.. Cada um dos dois planos tangentes está definido por três rectas (a recta ii, a respectiva geratriz de contacto e o respectivo traço
horizontal). Determinou-se o traço frontal da recta ii – FF. O traço frontal do plano θ2 passa por FF22 e é concorrente com hhθ22
no eixo XX. De forma
idêntica, o traço frontal do plano θ1 passa também por FF22 e é concorrente com hhθ11
no eixo XX. O ponto de concorrência dos dois traços do
plano θ1, no entanto, situa-se fora dos limites do desenho, pelo que é necessário o recurso a uma recta auxiliar do plano. Recorreu-se ao traço
frontal da geratriz gg – FF’’. O traço frontal do plano θ1, ffθ11
, passa pelos traços frontais das duas rectas (gg e ii) – está definido por dois pontos.

177. 177
SOLUÇÕES
407.
Em primeiro lugar representou-se o cilindro e a recta ff, pelas respectivas projecções, em função dos dados. As geratrizes do cilindro estão
contidas em rectas horizontais (de nível). O plano ϕ é o plano frontal (de frente) que contém a base de menor afastamento do sólido. O pla-
no ϕ’ é o plano frontal (de frente) que contém a base de maior afastamento do sólido. Em seguida, procedeu-se à execução sequencial das
etapas que nos conduzem à resolução do problema. 11.. Determinar a orientação dos planos tangentes, definindo um plano paralelo aos pla-
nos tangentes através das duas «famílias» de rectas que se conhecem – a «família» da recta dada (recta ff) e a «família» das geratrizes do ci-
lindro. Assim, por um ponto qualquer, há que conduzir uma recta paralela à recta ff e uma recta paralela às geratrizes do cilindro. Optou-se,
com vista a uma maior economia de traçados, por escolher o ponto NN, da recta ff, como o ponto exterior ao cilindro. Assim, por NN conduziu-
-se uma recta hh, paralela às geratrizes do sólido – o plano definido pelas rectas ff e hh (plano θ) é paralelo aos planos tangentes. 22.. Determi-
nou-se a recta de intersecção do plano θ (o plano definido por ff e hh) com o plano da base de referência (a base de menor afastamento) –
recta ii. A recta ii é uma recta frontal (de frente) do plano θ e está definida por um ponto (o ponto II, que é o ponto de intersecção da recta hh
com o plano ϕ) e uma direcção (é paralela à recta ff, pois rectas frontais de um plano são paralelas entre si). 33.. Conduziram-se as rectas tan-
gentes à base de referência do cilindro (a base de menor afastamento) que são paralelas à recta ii – as rectas tt e tt’’. As rectas tt e tt’’ são rectas
frontais (de frente) e são as rectas de intersecção dos dois planos tangentes com o plano ϕ (o plano da base de referência). As tangentes à
base de referência permitem-nos, ainda, determinar os pontos de tangência, TT e TT’’. Note que as tangentes à base se determinaram através
do processo rigoroso para a determinação das rectas tangentes a uma circunferência que são paralelas a uma recta dada que, neste caso,
é ii22. 44.. Determinaram-se as geratrizes de contacto (ou de tangência), gg e gg’’ – gg passa por TT e é paralela ao eixo do cilindro e gg’’ passa por TT’’
e é também paralela ao eixo do cilindro. 55.. Cada um dos dois planos tangentes está definido por duas rectas (a respectiva tangente à base
de referência e a respectiva geratriz de contacto) e pela sua orientação (são, ambos, paralelos ao plano θ). Determinou-se o traço horizontal
da recta tt – HH. Por HH11 conduziu-se hhθ11
, o traço horizontal do plano θ1, paralelo à geratriz gg (a geratriz gg é uma recta horizontal do plano θ1 e
rectas horizontais de um plano são paralelas entre si e paralelas ao traço horizontal do plano, que é uma recta horizontal do plano com cota
nula) – hhθ11
está definido por um ponto e uma direcção. Em seguida, desenhou-se ffθ11
, concorrente com hhθ11
no eixo XX e paralelo à recta tt
(a recta tt é uma recta frontal do plano θ1 e rectas frontais de um plano são paralelas entre si e paralelas ao traço frontal do plano, que é uma
recta frontal do plano com afastamento nulo) – ffθ11
está definido por um ponto e uma direcção. Determinou-se o traço horizontal da recta tt’’ – HH’’.
Por HH’’11 conduziu-se hhθ22
, o traço horizontal do plano θ2, paralelo à geratriz gg’’ (a geratriz gg’’ é uma recta horizontal do plano θ2) – hhθ22
está defi-
nido por um ponto e uma direcção. Em seguida, desenhou-se ffθ22
, concorrente com hhθ22
no eixo XX e paralelo à recta tt’’ (a recta tt’’ é uma recta
frontal do plano θ2) – ffθ22
está definido por um ponto e uma direcção.

178. Em primeiro lugar representou-se a pirâmide, pelas suas projecções, e o plano secante
(o plano ν1), pelo seu traço frontal, em função dos dados. O plano ν é o plano horizontal (de
nível) que contém a base do sólido. Em seguida, atendendo a que o plano secante é paralelo
ao plano da base, sabe-se imediatamente que a figura da secção será um polígono seme-
lhante ao polígono da base, e com os seus lados paralelos aos lados correspondentes do
quadrado da base. Por outro lado, uma vez que o plano ν1 (o plano secante) é projectante
frontal, os vértices da figura da secção foram determinados a partir das suas projecções
frontais – tratou-se de determinar os pontos de intersecção das arestas laterais (que estão
contidas em rectas não projectantes) com um plano projectante frontal (o plano ν1). A partir
das projecções dos quatro vértices da figura da secção (aos quais não se atribuiu nenhum
nome, para simplificar a leitura da resolução gráfica apresentada), desenharam-se as projec-
ções da figura (que é um quadrado, tal como a base). Em projecção frontal, a figura da sec-
ção reduz-se a um segmento de recta, pois o plano secante é projectante frontal. Já em
projecção horizontal, o quadrado projecta-se em V.G. mas, atendendo a que não houve a
desagregação do sólido (é pedida a ffiigguurraa ddaa sseeccççããoo e não o ssóólliiddoo rreessuullttaannttee ddaa
sseeccççããoo) há que representar as suas invisibilidades. Uma vez que todas as faces laterais (nas
quais estão contidos os lados da ffiigguurraa ddaa sseeccççããoo) são invisíveis em projecção horizontal, a
ffiigguurraa ddaa sseeccççããoo é invisível em projecção horizontal, na sua totalidade (a figura está contida
na superfície do sólido que é invisível em projecção horizontal). Note que, em termos de
traçado, o sólido se representou a traço médio (é um dado) e o pretendido (a ffiigguurraa ddaa
sseeccççããoo) se representou a traço forte.
178
SOLUÇÕES
408.
Por sseeccççããoo ppllaannaa ddee uumm ppoolliieeddrroo entende-se o polígono formado pela intersecção de um plano (plano secante) com as faces de um poliedro.
409.
Por ssóólliiddoo ttrruunnccaaddoo (ou ssóólliiddoo rreessuullttaannttee ddaa sseeccççããoo) entende-se uumm oouuttrroo ssóólliiddoo, formado por uma parte do sólido seccionado – a parte
compreendida entre o plano secante e uma base ou o vértice. Por ffiigguurraa ddaa sseeccççããoo entende-se, apenas, o ppoollííggoonnoo (que é uma ffiigguurraa ppllaa--
nnaa) resultante da secção produzida no sólido pelo plano secante.
410.
Em primeiro lugar representou-se a pirâmide, pelas suas projecções, e o plano
secante (o plano ν), pelo seu traço frontal, em função dos dados. As projecções da
pirâmide desenharam-se a traço leve, pois trata-se de uma construção auxiliar para o
objectivo do exercício – o ssóólliiddoo rreessuullttaannttee ddaa sseeccççããoo. Em seguida, atendendo a
que o plano secante é paralelo ao plano da base, sabe-se imediatamente que a figu-
ra da secção será um quadrado (semelhante ao quadrado da base), e com os seus
lados paralelos aos lados correspondentes do quadrado da base. Por outro lado,
uma vez que o plano ν (o plano secante) é projectante frontal, os vértices da figura
da secção foram determinados a partir das suas projecções frontais – tratou-se de
determinar os pontos de intersecção das arestas laterais (que estão contidas em rec-
tas não projectantes) com um plano projectante frontal (o plano ν). A partir das pro-
jecções dos quatro vértices da figura da secção (AA’’, BB’’, CC’’ e DD’’), desenharam-se as
projecções da figura (o quadrado [AA’’BB’’CC’’DD’’]) e as projecções do ssóólliiddoo rreessuullttaannttee
ddaa sseeccççããoo (a parte da pirâmide compreendida entre o plano secante e a base infe-
rior). Note que se representou, a traço forte, o ssóólliiddoo rreessuullttaannttee ddaa sseeccççããoo, por ser
esse o pretendido – a parte do sólido que é desprezada (a parte compreendida entre
o plano secante e o vértice da pirâmide) representou-se a traço leve, pois trata-se de
uma construção auxiliar para atingir o objectivo do exercício. O sólido resultante da
secção é, no presente caso, um tronco da pirâmide dada – um sólido compreendido
entre o quadrado [AABBCCDD] (a sua base inferior) e o quadrado [AA’’BB’’CC’’DD’’] (a sua base
superior). Assim, representaram-se os contornos aparentes (horizontal e frontal)
desse novo sólido, bem como as respectivas invisibilidades. Por fim, atendendo a
que, em projecção horizontal, a ffiigguurraa ddaa sseeccççããoo é visível (a superfície da figura, ou
seja, a área do corte), identificou-se a figura a tracejado (em projecção horizontal).
SECÇÕES PLANAS
20
411.

179. 179
SOLUÇÕES
412.
Em primeiro lugar representou-se a pirâmide, pelas suas projecções,
e o plano secante (o plano ϕ1), pelo seu traço horizontal, em função
dos dados. O plano ϕ é o plano frontal (de frente) que contém a base
do sólido. As projecções da recta rr fazem, com o eixo XX, ângulos
iguais e com o mesmo sentido de abertura, pois a recta rr é paralela
ao β1/3. O vértice da pirâmide, o ponto VV, é o ponto da recta rr que dista
8 cm (a altura da pirâmide) do plano ϕ. Em seguida, atendendo a que
o plano secante é paralelo ao plano da base, sabe-se imediatamente
que a figura da secção será um polígono semelhante ao polígono da
base, e com os seus lados paralelos aos lados correspondentes do
triângulo da base. Por outro lado, uma vez que o plano ϕ1 (o plano
secante) é projectante horizontal, os vértices da figura da secção foram
determinados a partir das suas projecções horizontais – tratou-se de
determinar os pontos de intersecção das arestas laterais (que estão
contidas em rectas não projectantes) com um plano projectante hori-
zontal (o plano ϕ1). A partir das projecções dos três vértices da figura
da secção (AA’’, BB’’ e CC’’), desenharam-se as projecções da figura (o
triângulo [AA’’BB’’CC’’]). Em projecção horizontal, a figura da secção reduz-
-se a um segmento de recta, pois o plano secante é projectante hori-
zontal. Já em projecção frontal, o triângulo projecta-se em V.G. mas,
atendendo a que não houve a desagregação do sólido (é pedida a
ffiigguurraa ddaa sseeccççããoo e não o ssóólliiddoo rreessuullttaannttee ddaa sseeccççããoo) há que
representar as suas invisibilidades. Os lados [AA’’BB’’] e [AA’’CC’’] estão
contidos em faces visíveis (em projecção frontal) da pirâmide (as fa-
ces laterais [AABBVV] e [AACCVV], respectivamente), pelo que são visíveis.
Já o lado [BB’’CC’’] da figura, porque está contido numa face lateral invi-
sível (em projecção frontal) da pirâmide (a face lateral [BBCCVV]), é invisí-
vel em projecção frontal. Note que, em termos de traçado, o sólido se
representou a traço médio (é um dado) e o pretendido (a ffiigguurraa ddaa
sseeccççããoo) se representou a traço forte.
Em primeiro lugar representou-se a pirâmide, pelas suas
projecções, e o plano δ, pelos seus traços, em função dos
dados. Uma vez que o plano α (o plano que contém a base
da pirâmide) não é paralelo a nenhum dos planos de projec-
ção, a determinação das projecções do hexágono [AABBCCDDEEFF]
processou-se com o recurso a um processo geométrico auxi-
liar – o rebatimento do plano α para o Plano Horizontal de
Projecção (a charneira foi hhα). O hexágono foi construído pre-
viamente em V.G., em rebatimento, respeitando os dados –
dois dos lados do polígono são de topo (paralelos a hhα e a
hhαrr
). Invertendo o rebatimento, determinaram-se as projec-
ções do hexágono da base da pirâmide. O eixo do sólido
está contido numa recta frontal (de frente), passando por OO
(o centro do hexágono) e ortogonal ao plano α e projecta-se
em V.G. no Plano Frontal de Projecção, pois é paralelo a este.
As projecções da pirâmide desenharam-se a traço leve, pois
trata-se de uma construção auxiliar para o objectivo do exercí-
cio – o ssóólliiddoo rreessuullttaannttee ddaa sseeccççããoo. Em seguida, atendendo
a que o plano secante é paralelo ao plano da base, sabe-se
imediatamente que a figura da secção será um hexágono
(semelhante ao hexágono da base), e com os seus lados
paralelos aos lados correspondentes do hexágono da base.
Por outro lado, uma vez que o plano δ (o plano secante) é
projectante frontal, os vértices da figura da secção foram
determinados a partir das suas projecções frontais – tratou-se
de determinar os pontos de intersecção das arestas laterais
(que estão contidas em rectas não projectantes) com um plano
projectante frontal (o plano δ). A partir das projecções dos seis vértices da figura da secção (AA’’, BB’’, CC’’, DD’’, EE’’ e FF’’), desenharam-se as projec-
ções da figura (o hexágono [AA’’BB’’CC’’DD’’EE’’FF’’]) e as projecções do ssóólliiddoo rreessuullttaannttee ddaa sseeccççããoo (a parte da pirâmide compreendida entre o plano
413.
(Continua na página seguinte)

180. secante e a base inferior). Note que se representou, a traço forte, o ssóólliiddoo rreessuullttaannttee ddaa sseeccççããoo, por ser esse o pretendido – a parte do sólido
que é desprezada (a parte compreendida entre o plano secante e o vértice da pirâmide) representou-se a traço leve, pois trata-se de uma cons-
trução auxiliar para atingir o objectivo do exercício. O sólido resultante da secção é, no presente caso, um tronco da pirâmide dada – um sólido
compreendido entre o hexágono [AABBCCDDEEFF] (a sua base inferior) e o hexágono [AA’’BB’’CC’’DD’’EE’’FF’’] (a sua base superior). Assim, representaram-se
os contornos aparentes (horizontal e frontal) desse novo sólido, bem como as respectivas invisibilidades. Por fim, atendendo a que, em projec-
ção horizontal, a ffiigguurraa ddaa sseeccççããoo é visível (a superfície da figura, ou seja, a área do corte), identificou-se a figura a tracejado (em projecção
horizontal). A V.G. da ffiigguurraa ddaa sseeccççããoo determinou-se com o recurso ao rebatimento do plano δ (o plano secante) para o Plano Frontal de Pro-
jecção – a charneira foi ffδ.
180
SOLUÇÕES
414.
Em primeiro lugar representou-se a pirâmide, pelas suas projecções, e o plano α, pelos seus traços, em função dos dados. Note que a dis-
tância entre os planos γ (o plano que contém a base do sólido) e α (o plano secante) é medida ortogonalmente aos dois planos (trata-se da
ddiissttâânncciiaa eennttrree ddooiiss ppllaannooss ppaarraalleellooss) e não é medida no eixo XX, ao contrário da situação anterior, em que eram dadas as abcissas dos
pontos em que os dois planos cortavam o eixo XX. Uma vez que o plano γ (o plano que contém a base da pirâmide) não é paralelo a nenhum
dos planos de projecção, a determinação das projecções do quadrado [AABBCCDD] processou-se com o recurso a um processo geométrico
auxiliar – o rebatimento do plano γ para o Plano Frontal de Projecção (a charneira foi ffγ). O quadrado foi construído previamente em V.G., em
rebatimento, respeitando os dados – o ângulo que o lado [AABB] faz com ffγ existe nnoo eessppaaççoo e não tem correspondência em projecções.
Esse ângulo está contido nnoo ppllaannoo γ e só pode ser medido em V.G., em rebatimento – com vértice em AArr, a partir de ffγrr
, mediram-se os 60o,
garantindo que BBrr se situe sobre hhγrr
(BB tem cota nula). A partir de AArr e BBrr, construiu-se o quadrado em V.G., em rebatimento. Invertendo o
rebatimento, determinaram-se as projecções do quadrado da base da pirâmide. O eixo do sólido está contido numa recta horizontal (de nível)
ortogonal ao plano γ (passando por OO, o centro do quadrado) e projecta-se em V.G. no Plano Horizontal de Projecção, pois é paralelo a este.
As projecções da pirâmide desenharam-se a traço leve, pois trata-se de uma construção auxiliar para o objectivo do exercício – o ssóólliiddoo
rreessuullttaannttee ddaa sseeccççããoo. Em seguida, atendendo a que o plano secante é paralelo ao plano da base, sabe-se imediatamente que a figura da
secção será um quadrado (um polígono semelhante ao quadrado da base), com os seus lados paralelos aos lados correspondentes do
quadrado da base. Por outro lado, uma vez que o plano α (o plano secante) é projectante horizontal, os vértices da figura da secção foram
determinados a partir das suas projecções horizontais – tratou-se de determinar os pontos de intersecção das arestas laterais (que estão con-
tidas em rectas não projectantes) com um plano projectante horizontal (o plano α). A partir das projecções dos quatro vértices da figura da
secção (AA’’, BB’’, CC’’ e DD’’), desenharam-se as projecções da ffiigguurraa ddaa sseeccççããoo (o quadrado [AA’’BB’’CC’’DD’’]). Em projecção horizontal, a figura
reduz-se a um segmento de recta, pois o plano secante (o plano α) é projectante horizontal. Já em projecção frontal, sendo pedida a ffiigguurraa
ddaa sseeccççããoo e não o ssóólliiddoo rreessuullttaannttee ddaa sseeccççããoo (não houve desagregação do sólido), há que representar as invisibilidades existentes na
ffiigguurraa ddaa sseeccççããoo. Os lados [AA’’BB’’] e [AA’’DD’’] estão contidos em faces visíveis (em projecção frontal) da pirâmide (as faces laterais [AABBVV] e
[AADDVV], respectivamente), pelo que são visíveis. Já os lados [BB’’CC’’] e [CC’’DD’’] da figura, porque estão contidos em faces laterais invisíveis (em
projecção frontal) da pirâmide (as faces laterais [BBCCVV] e [CCDDVV], respectivamente), são invisíveis em projecção frontal. Note que, em termos
de traçado, o sólido se representou a traço médio (é um dado) e o pretendido (a ffiigguurraa ddaa sseeccççããoo) se representou a traço forte.

181. 181
SOLUÇÕES
Em primeiro lugar representou-se o triângulo equilátero [AABBCC], pelas suas projecções, e o plano ν’, pelo seu traço frontal, em função dos
dados. O plano ν é o plano horizontal (de nível) que contém o triângulo [AABBCC]. Os dados do exercício permitiram-nos concluir a construção
da projecção horizontal do tetraedro – a projecção horizontal do vértice DD (o quarto vértice do sólido) está coincidente com OO11 (a projecção
horizontal do centro do triângulo). Não é possível, de forma directa, determinar a cota de DD, pois não se sabe a altura de um tetraedro –
sabe-se, apenas, que todas as suas arestas têm o mesmo comprimento, sendo esse o raciocínio que suporta a construção das projecções
de um tetraedro. Assim, as arestas [AADD], [BBDD] e [CCDD] têm comprimento igual ao lado do triângulo [AABBCC], mas nenhuma delas se projecta
em V.G. – é necessário o recurso a um processo geométrico auxiliar. Optou-se pelo rebatimento do plano π, o plano de perfil que contém a
aresta [CCDD]. Rebateu-se o plano π para o Plano Frontal de Projecção (a charneira foi ffπ), obtendo CCrr e a referência de DDrr. Com o compasso,
fazendo centro em CCrr e raio igual à medida do lado do triângulo [AABBCC], determinou-se DDrr – invertendo o rebatimento, determinou-se a pro-
jecção frontal de DD e concluiu-se a construção da projecção frontal do sólido (as projecções do sólido representaram-se a traço leve, pois
trata-se de uma construção auxiliar para o objectivo do exercício – o ssóólliiddoo rreessuullttaannttee ddaa sseeccççããoo). Em seguida, atendendo a que o plano
secante é paralelo ao plano da base, sabe-se imediatamente que a figura da secção será um triângulo equilátero (um polígono semelhante
ao triângulo da base), com os seus lados paralelos aos lados correspondentes do triângulo da base. Por outro lado, uma vez que o plano ν’
(o plano secante) é projectante frontal, os vértices da figura da secção foram determinados a partir das suas projecções frontais – tratou-se
de determinar os pontos de intersecção das arestas laterais (que estão contidas em rectas não projectantes) com um plano projectante fron-
tal (o plano ν’). No entanto, o ponto CC’’, que é o ponto em que o plano ν’ corta a aresta [CCDD] (a aresta de perfil), não teve determinação ime-
diata a partir da sua projecção frontal (como os pontos AA’’ e BB’’), uma vez que não é possível determinar, de forma directa, as projecções de
pontos pertencentes a rectas de perfil – as projecções de uma recta de perfil não verificam o Critério de Reversibilidade, pelo que a condi-
ção para que um ponto pertença a uma recta é condição necessária, mas não suficiente. No entanto, atendendo a que a figura da secção (o
polígono [AA’’BB’’CC’’]) é um ttrriiâânngguulloo eeqquuiilláátteerroo, de lados paralelos aos lados correspondentes do triângulo da base, sabe-se que o lado
[AA’’CC’’] é paralelo ao lado [AACC], da base, tal como o lado [BB’’CC’’] é paralelo ao lado [BBCC], da base. Com esse raciocínio, conduziu-se, por AA’’11,
uma paralela a [AA11CC11], obtendo CC’’11 sobre [CC11DD11] – o ponto CC’’11, assim determinado, garante-nos também que [BB’’CC’’] é paralelo a [BBCC].
A partir das projecções dos três vértices da figura da secção (AA’’, BB’’ e CC’’), desenharam-se as projecções da figura (o triângulo equilátero
[AA’’BB’’CC’’]) e as projecções do ssóólliiddoo rreessuullttaannttee ddaa sseeccççããoo (a parte do tetraedro compreendida entre o plano secante e a face inferior). Note
que se representou, a traço forte, o ssóólliiddoo rreessuullttaannttee ddaa sseeccççããoo, por ser esse o pretendido – a parte do sólido que é desprezada (a parte
compreendida entre o plano secante e o vértice DD) representou-se a traço leve, pois trata-se de uma construção auxiliar para atingir o objec-
tivo do exercício. O sólido resultante da secção é um outro sólido – um sólido compreendido entre o triângulo [AABBCC] (a sua face inferior) e o
triângulo [AA’’BB’’CC’’] (a figura da secção). Assim, representaram-se os contornos aparentes (horizontal e frontal) desse novo sólido, bem como
as respectivas invisibilidades. Por fim, atendendo a que, em projecção horizontal, a ffiigguurraa ddaa sseeccççããoo é visível (a superfície da figura, ou
seja, a área do corte), identificou-se a figura a tracejado (em projecção horizontal).
415.

182. 182
SOLUÇÕES
416.
Em primeiro lugar representou-se a pirâmide, pelas suas projecções, e o plano ϕ’,
pelo seu traço horizontal, em função dos dados. O plano ϕ é o plano frontal (de
frente) que contém a base da pirâmide. Note que, atendendo a que a aresta lateral
[BBVV] é de perfil, se sabe que o vértice da pirâmide tem a abcissa de BB. Por outro
lado, sabendo que a aresta lateral [CCVV] é horizontal (de nível), conclui-se que VV tem
a cota de CC. Estes dois dados permitiram-nos localizar a projecção frontal de VV,
que, segundo o enunciado, tem afastamento nulo. Em seguida, atendendo a que o
plano secante é paralelo ao plano da base, sabe-se imediatamente que a figura da
secção será um quadrado (um polígono semelhante ao quadrado da base), com os
seus lados paralelos aos lados correspondentes do quadrado da base. Por outro
lado, uma vez que o plano ϕ’ (o plano secante) é projectante horizontal, os vértices
da figura da secção foram determinados a partir das suas projecções horizontais –
tratou-se de determinar os pontos de intersecção das arestas laterais (que estão con-
tidas em rectas não projectantes) com um plano projectante horizontal (o plano ϕ’).
No entanto, o ponto BB’’, que é o ponto em que o plano ϕ’ corta a aresta [BBVV]
(a aresta de perfil), não teve determinação imediata a partir da sua projecção frontal
(como os pontos AA’’, CC’’ e DD’’), uma vez que não é possível determinar, de forma
directa, as projecções de pontos pertencentes a rectas de perfil – as projecções de
uma recta de perfil não verificam o Critério de Reversibilidade, pelo que a condição
para que um ponto pertença a uma recta é condição necessária, mas não suficiente.
No entanto, atendendo a que a figura da secção (o polígono [AA’’BB’’CC’’DD’’]) é um qquuaa--
ddrraaddoo, de lados paralelos aos lados correspondentes do quadrado da base, sabe-
-se que o lado [AA’’BB’’] é paralelo ao lado [AABB], da base, tal como o lado [BB’’CC’’] é
paralelo ao lado [BBCC], da base. Com esse raciocínio, conduziu-se, por AA’’22, uma para-
lela a [AA22BB22], obtendo BB’’22 sobre [BB22VV22] – o ponto BB’’22, assim determinado, garante-nos também que [BB’’CC’’] é paralelo a [BBCC]. A partir das
projecções dos quatro vértices da figura da secção (AA’’, BB’’, CC’’ e DD’’), desenharam-se as projecções da ffiigguurraa ddaa sseeccççããoo (o quadrado
[AA’’BB’’CC’’DD’’]). Em projecção horizontal, a figura reduz-se a um segmento de recta, pois o plano secante (o plano ϕ’) é projectante horizontal.
Já em projecção frontal, sendo pedida a ffiigguurraa ddaa sseeccççããoo e não o ssóólliiddoo rreessuullttaannttee ddaa sseeccççããoo (não houve desagregação do sólido), há
que representar as invisibilidades existentes na ffiigguurraa ddaa sseeccççããoo. Os lados [AA’’BB’’], [AA’’DD’’] e [CC’’DD’’] estão contidos em faces invisíveis (em
projecção frontal) da pirâmide (as faces laterais [AABBVV], [AADDVV] e [CCDDVV], respectivamente), pelo que são invisíveis. Já o lado [BB’’CC’’] da figura,
porque está contido numa face lateral visível (em projecção frontal) da pirâmide (a face lateral [BBCCVV]), é visível em projecção frontal. Note que,
em termos de traçado, o sólido se representou a traço médio (é um dado) e o pretendido (a ffiigguurraa ddaa sseeccççããoo) se representou a traço forte.
417.
Em primeiro lugar representou-se o prisma, pelas suas projecções, e o plano secante, pelo
seu traço horizontal, em função dos dados. O plano ϕ é o plano que contém a base de
menor afastamento do prisma e o plano ϕ1 o plano que contém a sua base de maior afasta-
mento. O plano ϕ2 é o plano secante. Uma vez que o plano secante é paralelo aos planos
das bases, sabe-se imediatamente que a figura da secção será um polígono geometrica-
mente igual aos quadrados das bases, e com os seus lados paralelos aos lados correspon-
dentes daqueles. Por outro lado, uma vez que o plano ϕ2 (o plano secante) é projectante
horizontal, os vértices da figura da secção foram determinados a partir das suas projecções
horizontais – tratou-se de determinar os pontos de intersecção das arestas laterais (que estão
contidas em rectas projectantes frontais) com um plano projectante horizontal (o plano ϕ2).
A partir das projecções dos quatro vértices da figura da secção (aos quais não se atribuiu
nenhum nome, para simplificar a leitura da resolução gráfica apresentada), desenharam-se
as projecções da figura (que é um quadrado) e as projecções do ssóólliiddoo rreessuullttaannttee ddaa sseecc--
ççããoo (a parte do prisma compreendida entre o plano secante e a base inferior). Note que se
representou, a traço forte, o ssóólliiddoo rreessuullttaannttee ddaa sseeccççããoo, por ser esse o pretendido – a parte
do sólido que é desprezada (a parte compreendida entre o plano secante e a base de maior
afastamento) representou-se a traço leve, pois trata-se de uma construção auxiliar para atingir
o objectivo do exercício. O sólido resultante da secção é, no presente caso, um outro prisma
– um prisma quadrangular regular, com bases frontais (de frente), cuja base de menor
afastamento é o quadrado [RRSSTTUU] e com 3 cm de altura (a diferença entre os afastamentos
do plano ϕ e do plano ϕ2). Assim, representaram-se os contornos aparentes (horizontal e
frontal) desse novo sólido, bem como as respectivas invisibilidades. Por fim, atendendo a
que, em projecção frontal, a ffiigguurraa ddaa sseeccççããoo é visível (a superfície da figura, ou seja, a
área do corte), identificou-se a figura a tracejado (em projecção horizontal).

183. 183
SOLUÇÕES
Em primeiro lugar representou-se o prisma, pelas suas projecções, e o plano
secante, pelo seu traço frontal, em função dos dados. O plano ν é o plano
que contém a base inferior do prisma e o plano ν1 o plano que contém
a sua base superior. O plano ν2 é o plano secante. Uma vez que o plano
secante é paralelo aos planos das bases, sabe-se imediatamente que a figura
da secção será um polígono geometricamente igual aos pentágonos das
bases, e com os seus lados paralelos aos lados correspondentes daque-
les. Por outro lado, uma vez que o plano ν2 (o plano secante) é projectante
frontal, os vértices da figura da secção foram determinados a partir das
suas projecções frontais – tratou-se de determinar os pontos de intersec-
ção das arestas laterais (que estão contidas em rectas não projectantes)
com um plano projectante frontal (o plano ν2). A partir das projecções dos
cinco vértices da figura da secção (aos quais não se atribuiu nenhum
nome, para simplificar a leitura da resolução gráfica apresentada), dese-
nharam-se as projecções da ffiigguurraa ddaa sseeccççããoo (que é um pentágono regu-
lar). Em projecção frontal, a figura reduz-se a um segmento de recta, pois o
plano secante (o plano ν2) é projectante frontal. Já em projecção horizon-
tal, sendo pedida a ffiigguurraa ddaa sseeccççããoo e não o ssóólliiddoo rreessuullttaannttee ddaa sseeccççããoo
(não houve desagregação do sólido), há que representar as invisibilidades
existentes na ffiigguurraa ddaa sseeccççããoo. Os lados da figura que se situam nas faces
laterais [CCCC’’DD’’DD] e [DDDD’’EE’’EE] são invisíveis em projecção horizontal, em vir-
tude de aquelas faces serem invisíveis em projecção horizontal. Os outros
três lados da figura da secção são visíveis, por se situarem em faces late-
rais que são visíveis em projecção horizontal (as faces laterais [AAAA’’EE’’EE],
[AAAA’’BB’’BB] e [BBBB’’CC’’CC]). Note que, em termos de traçado, o sólido se repre-
sentou a traço médio (é um dado) e o pretendido (a ffiigguurraa ddaa sseeccççããoo) se
representou a traço forte.
418.
419.
Em primeiro lugar representou-se o prisma, pelas suas
projecções, e o plano α, pelos seus traços, em função
dos dados. O plano α dista 4 cm do plano θ – a distância
entre os dois planos é medida ortogonalmente aos dois
planos (trata-se da distância entre dois planos parale-
los). Uma vez que o plano θ (o plano que contém a base
inferior do prisma) não é paralelo a nenhum dos planos
de projecção, a determinação das projecções do qua-
drado [AABBCCDD] processou-se com o recurso a um pro-
cesso geométrico auxiliar – o rebatimento do plano θ
para o Plano Horizontal de Projecção (a charneira foi hhθ).
O quadrado foi construído previamente em V.G., em
rebatimento. Invertendo o rebatimento, determinaram-se
as projecções do quadrado da base inferior do prisma.
As arestas laterais do sólido estão contidas em rectas
frontais (de frente), passando pelos vértices da base
inferior e ortogonais ao plano θ. O plano θ’, representado
apenas pelo seu traço frontal (razão pela qual se encontra
assinalado entre parêntesis), é o plano que contém a
base superior do sólido – está a 7 cm (a altura do prisma)
do plano θ. Os vértices da base superior do prisma deter-
minaram-se a partir das suas projecções frontais – trata-
-se da intersecção de rectas não projectantes (as rectas
suporte das arestas laterais) com um plano projectante
frontal (o plano θ’). As projecções do prisma desenharam-
-se a traço leve, pois trata-se de uma construção auxiliar
para o objectivo do exercício – o ssóólliiddoo rreessuullttaannttee ddaa
sseeccççããoo. Em seguida, atendendo a que o plano secante
é paralelo aos planos das bases, sabe-se imediatamente
que a figura da secção será um quadrado (um polígono
geometricamente igual aos polígonos das bases), e com
os seus lados paralelos aos lados correspondentes dos quadrados das bases. Por outro lado, uma vez que o plano α (o plano secante)
é projectante frontal, à semelhança dos vértices da base superior, os vértices da figura da secção foram determinados a partir das suas
(Continua na página seguinte)

184. 420.
Em primeiro lugar representou-se o prisma, pelas suas projecções, e o plano γ, pelos seus traços, em função dos dados. Uma vez que o
plano α (o plano que contém a base mais à direita do prisma) não é paralelo a nenhum dos planos de projecção, a determinação das
projecções do triângulo [RRSSTT] processou-se com o recurso a um processo geométrico auxiliar – o rebatimento do plano α para o Plano
Frontal de Projecção (a charneira foi ffα). O triângulo foi construído previamente em V.G., em rebatimento, em função dos dados. Invertendo
o rebatimento, determinaram-se as projecções do triângulo [RRSSTT]. As arestas laterais do sólido estão contidas em rectas fronto-horizontais,
passando pelos vértices do triângulo [RRSSTT]. O plano α’, representado pelos seus traços, é o plano que contém a base mais à esquerda do
sólido – está a 6 cm (a altura do prisma) do plano α. Note que a distância entre os planos α e α’ se mediu ortogonalmente aos dois planos,
pois trata-se da ddiissttâânncciiaa eennttrree ddooiiss ppllaannooss ppaarraalleellooss. Os vértices da base mais à esquerda do prisma (o triângulo [RR’’SS’’TT’’]) determinaram-
-se a partir das suas projecções horizontais – trata-se da intersecção de rectas não projectantes (as rectas suporte das arestas laterais) com
um plano projectante horizontal (o plano α’). Uma vez que o plano secante é paralelo aos planos das bases, sabe-se imediatamente que a
figura da secção será um polígono geometricamente igual aos pentágonos das bases, e com os seus lados paralelos aos lados correspon-
dentes daqueles. Por outro lado, uma vez que o plano γ (o plano secante) é projectante horizontal, os vértices da figura da secção foram de-
terminados a partir das suas projecções horizontais – à semelhança do exposto para a determinação dos vértices da base [RR’’SS’’TT’’], tratou-se
de determinar os pontos de intersecção das arestas laterais (que estão contidas em rectas não projectantes) com um plano projectante
horizontal (o plano γ). A partir das projecções dos três vértices da figura da secção (AA, BB e CC), desenharam-se as projecções da ffiigguurraa ddaa
sseeccççããoo (que, nnoo eessppaaççoo, é um triângulo equilátero, se bem que apresente deformação em projecções). Em projecção horizontal, a figura
reduz-se a um segmento de recta, pois o plano secante (o plano γ) é projectante horizontal. Já em projecção frontal, sendo pedida a ffiigguurraa
ddaa sseeccççããoo e não o ssóólliiddoo rreessuullttaannttee ddaa sseeccççããoo (não houve desagregação do sólido), há que representar as invisibilidades existentes na
ffiigguurraa ddaa sseeccççããoo. Os lados [AABB] e [BBCC] da figura, que se situam nas faces laterais [RRRR’’SS’’SS] e [SSSS’’TT’’TT], respectivamente, são invisíveis em
projecção frontal, em virtude de aquelas faces serem invisíveis em projecção frontal. O lado [AACC] da figura da secção é visível, por se situar
numa face lateral que é visível em projecção frontal (a face lateral [RRRR’’TT’’TT]). Note que, em termos de traçado, o sólido se representou a traço
médio (é um dado) e o pretendido (a ffiigguurraa ddaa sseeccççããoo) se representou a traço forte.
184
SOLUÇÕES
projecções frontais – tratou-se de determinar os pontos de intersecção das arestas laterais (que estão contidas em rectas não projectantes)
com um plano projectante frontal (o plano α). A partir das projecções dos quatro vértices da figura da secção (MM, NN, OO e PP), desenharam-se
as projecções da figura (o quadrado [MMNNOOPP]) e as projecções do ssóólliiddoo rreessuullttaannttee ddaa sseeccççããoo (a parte do prisma compreendida entre o
plano secante e a base inferior). Note que se representou, a traço forte, o ssóólliiddoo rreessuullttaannttee ddaa sseeccççããoo, por ser esse o pretendido – a parte
do sólido que é desprezada (a parte compreendida entre o plano secante e a base superior) representou-se a traço leve, pois trata-se de
uma construção auxiliar para atingir o objectivo do exercício. O sólido resultante da secção é, no presente caso, um outro prisma – um prisma
quadrangular regular, com 4 cm de altura compreendido entre o quadrado [AABBCCDD] (a sua base inferior) e o quadrado [MMNNOOPP] (a sua base
superior). Assim, representaram-se os contornos aparentes (horizontal e frontal) desse novo sólido, bem como as respectivas invisibilidades.
Por fim, atendendo a que, em projecção horizontal, a ffiigguurraa ddaa sseeccççããoo é visível (a superfície da figura, ou seja, a área do corte), identificou-
-se a figura a tracejado (em projecção horizontal).

185. 185
SOLUÇÕES
421.
Em primeiro lugar representou-se o cubo, pelas suas pro-
jecções, e o plano α (o plano secante) pelos seus traços,
em função dos dados. O plano α dista 2 cm do plano θ – a
distância entre os dois planos é medida ortogonalmente
aos dois planos (trata-se da distância entre dois planos pa-
ralelos). Uma vez que o plano θ (o plano que contém a
face inferior do cubo) não é paralelo a nenhum dos planos
de projecção, a determinação das projecções do quadra-
do [AABBCCDD] processou-se com o recurso a um processo
geométrico auxiliar – o rebatimento do plano θ para o Plano
Horizontal de Projecção (a charneira foi hhθ). O quadrado foi
construído previamente em V.G., em rebatimento. Invertendo
o rebatimento, determinaram-se as projecções do quadrado
da face inferior do cubo. Sobre a determinação das projec-
ções do cubo, ver exercício 441199 e respectivo relatório
(trata-se de duas situações semelhantes, tanto ao nível dos
raciocínios como ao nível dos traçados). O plano θ’, repre-
sentado apenas pelo seu traço frontal (razão pela qual se
encontra assinalado entre parêntesis), é o plano que con-
tém a face superior do sólido (o quadrado [AA’’BB’’CC’’DD’’]) –
está a 5,5 cm (a medida da aresta do cubo) do plano θ.
Em seguida, atendendo a que o plano secante é paralelo
aos planos das bases, sabe-se imediatamente que a figura
da secção será um quadrado (um polígono geometrica-
mente igual aos polígonos das faces de topo do sólido), e
com os seus lados paralelos aos lados correspondentes
dos quadrados [AABBCCDD] e [AA’’BB’’CC’’DD’’]. Por outro lado, uma
vez que o plano α (o plano secante) é projectante frontal, à
semelhança dos vértices da face superior, os vértices da figura da secção foram determinados a partir das suas projecções frontais – tratou-
-se de determinar os pontos de intersecção das arestas frontais (de frente) com um plano projectante frontal (o plano α). A partir das projec-
ções dos quatro vértices da figura da secção (MM, NN, OO e PP), desenharam-se as projecções da ffiigguurraa ddaa sseeccççããoo (o quadrado [MMNNOOPP]). Em
projecção frontal, a figura reduz-se a um segmento de recta, pois o plano secante (o plano α) é projectante frontal. Já em projecção horizontal,
sendo pedida a ffiigguurraa ddaa sseeccççããoo e não o ssóólliiddoo rreessuullttaannttee ddaa sseeccççããoo (não houve desagregação do sólido), há que representar as invisibili-
dades existentes na ffiigguurraa ddaa sseeccççããoo. Os lados [MMNN] e [NNOO] da figura, que se situam nas faces [AAAA’’BB’’BB] e [BBBB’’CC’’CC] respectivamente, são
invisíveis em projecção horizontal, em virtude de aquelas faces serem invisíveis em projecção horizontal. Os lados [MMPP] e [OOPP] da figura da
secção são visíveis, por se situarem em faces visíveis em projecção horizontal (as faces [AAAA’’DD’’DD] e [CCCC’’DD’’DD], respectivamente). Note que, em
termos de traçado, o sólido se representou a traço médio (é um dado) e o pretendido (a ffiigguurraa ddaa sseeccççããoo) se representou a traço forte.
422.
Em primeiro lugar representou-se a pirâmide, pelas suas projecções, e o plano
secante, pelos seus traços, em função dos dados. A circunferência circunscrita
ao quadrado da base tem centro em OO e raio OOෆAAෆ, pois AA é um dos vértices
do quadrado. As projecções da pirâmide desenharam-se a traço leve, pois
trata-se de uma construção auxiliar para o objectivo do exercício – o ssóólliiddoo
rreessuullttaannttee ddaa sseeccççããoo. Uma vez que o plano secante é projectante frontal,
é possível concluir que o plano corta as quatro arestas laterais da pirâmide
e não corta a base – a ffiigguurraa ddaa sseeccççããoo tem, assim, quatro vértices
(é um quadrilátero). No entanto, uma vez que o plano secante nnããoo éé ppaarraalleelloo
ao plano da base, esse quadrilátero nnããoo sseerráá um quadrado. Os pontos em
que o plano corta as arestas laterais tiveram determinação directa a partir das
suas projecções frontais, pois trata-se da intersecção de rectas não projec-
tantes (as arestas laterais) com um plano projectante frontal (o plano α).
A partir das projecções dos quatro vértices da figura da secção (AA’’, BB’’, CC’’ e DD’’),
desenharam-se as projecções da figura (o quadrilátero [AA’’BB’’CC’’DD’’]) e as pro-
jecções do ssóólliiddoo rreessuullttaannttee ddaa sseeccççããoo (a parte da pirâmide compreendida
entre o plano secante e o vértice da pirâmide). Note que se representou, a
traço forte, o ssóólliiddoo rreessuullttaannttee ddaa sseeccççããoo, por ser esse o pretendido – a parte
do sólido que é desprezada (a parte compreendida entre o plano secante e a
base) representou-se a traço leve, pois trata-se de uma construção auxiliar
para atingir o objectivo do exercício. Representaram-se os contornos aparentes
(horizontal e frontal) do novo sólido (o sólido resultante da secção), bem
como as respectivas invisibilidades. Atendendo a que, em projecção horizontal,
a ffiigguurraa ddaa sseeccççããoo é visível (a superfície da figura, ou seja, a área do corte),
identificou-se a figura a tracejado (em projecção horizontal).

186. 186
SOLUÇÕES
424.
Em primeiro lugar representou-se a pirâmide, pelas
suas projecções, e o plano secante, pelos seus tra-
ços, em função dos dados. Note que, para a constru-
ção das projecções da pirâmide, se recorreu ao
rebatimento do plano de perfil π que contém a base
do sólido para, dessa forma, se determinarem as pro-
jecções do hexágono. Rebateu-se o plano π para o
Plano Frontal de Projecção – a charneira foi ffπ. A cir-
cunferência circunscrita ao hexágono é tangente
aos dois planos de projecção, pelo que tem 4 cm
de raio (em rebatimento, a circunferência é simulta-
neamente tangente a ffπrr
e a hhπrr
). A atribuição de
letras aos vértices foi arbitrária, pois o enunciado é
omisso. O eixo da pirâmide está contido numa recta
fronto-horizontal (ortogonal ao plano π) que passa
por OO e o seu comprimento (que corresponde à
altura da pirâmide) projecta-se em V.G. nos dois
planos de projecção – determinou-se VV, o vértice
da pirâmide, que se situa à direita do plano da base
(para ter abcissa negativa) e desenharam-se as
projecções do sólido (note que não existem invisibi-
lidades, pois as arestas invisíveis do sólido estão
ocultas por arestas visíveis). Em função dos dados,
o plano θ (o plano secante) contém necessariamente
o vértice superior da base da pirâmide (o vértice DD,
neste caso) – o plano secante corta, assim, a aresta
lateral [DDVV] no próprio ponto DD. Além disso, o plano θ
corta as restantes arestas laterais (o que se constata
atendendo a que se trata de um plano projectante
frontal), pelo que a figura da secção tem seis vértices – é um hexágono. No entanto, uma vez que o plano secante nnããoo éé ppaarraalleelloo ao plano da
base, esse hexágono nnããoo sseerráá um hexágono regular. Os pontos em que o plano corta as arestas da pirâmide tiveram determinação directa a
partir das suas projecções frontais, pois trata-se da intersecção de rectas não projectantes com um plano projectante frontal (o plano α). A partir
das projecções dos seis vértices da figura da secção (AA’’, BB’’, CC’’, DD, EE’’ e FF’’), desenharam-se as projecções da ffiigguurraa ddaa sseeccççããoo (o hexágono
423.
Em primeiro lugar representou-se a pirâmide, pelas suas projecções, e o plano
secante, pelos seus traços, em função dos dados. O vértice CC, da base, é o vértice
de maior abcissa, ou seja, é o vértice que se situa mais à esquerda. Uma vez que
se trata de um plano projectante frontal, é possível concluir que o plano secante
corta duas arestas da base (as arestas [AABB] e [BBCC]) e uma aresta lateral (a aresta
[BBVV]) – a ffiigguurraa ddaa sseeccççããoo tem, assim, três vértices (é um triângulo). No entanto,
uma vez que o plano secante nnããoo éé ppaarraalleelloo ao plano da base, esse triângulo nnããoo
sseerráá um triângulo equilátero. Os pontos em que o plano corta as arestas da pirâ-
mide tiveram determinação directa a partir das suas projecções frontais, pois trata-
-se da intersecção de rectas não projectantes com um plano projectante frontal
(o plano α). A partir das projecções dos três vértices da figura da secção (KK, LL e MM),
desenharam-se as projecções da ffiigguurraa ddaa sseeccççããoo (o triângulo [KKLLMM]). Em pro-
jecção frontal, a figura reduz-se a um segmento de recta, pois o plano secante
(o plano α) é projectante frontal. Já em projecção horizontal, sendo pedida a ffiigguurraa
ddaa sseeccççããoo e não o ssóólliiddoo rreessuullttaannttee ddaa sseeccççããoo (não houve desagregação do
sólido), há que representar as invisibilidades existentes na ffiigguurraa ddaa sseeccççããoo.
O lado [LLMM] da figura, que se situa na face [AABBVV], é invisível em projecção hori-
zontal, uma vez que aquela face é invisível em projecção horizontal. O lado [KKLL]
da figura da secção é visível, por se situar numa face visível em projecção horizon-
tal (a face [BBCCVV]). Já o lado [KKMM], da figura da secção, uma vez que se situa na
base (que é projectante horizontal) não admite a representação de qualquer invisi-
bilidade. Note que, em termos de traçado, o sólido se representou a traço médio
(é um dado) e o pretendido (a ffiigguurraa ddaa sseeccççããoo) se representou a traço forte.
(Continua na página seguinte)

187. 187
SOLUÇÕES
[AA’’BB’’CC’’DDEE’’FF’’]). Uma vez que não existe desagregação do sólido (é pedida a ffiigguurraa ddaa sseeccççããoo e não o ssóólliiddoo rreessuullttaannttee ddaa sseeccççããoo), há
que representar as invisibilidades da ffiigguurraa ddaa sseeccççããoo (se as houver). Em projecção frontal, a figura da secção reduz-se a um segmento de
recta, pois o plano secante é projectante frontal. Em projecção horizontal, as faces laterais visíveis são as faces [CCDDVV] e [DDEEVV] – as faces
laterais [AABBVV] e [AAFFVV] são invisíveis, em projecção horizontal, e as faces laterais [BBCCVV] e [EEFFVV] são projectantes horizontais. Assim, os
lados [CC’’DD] e [DDEE’’], da figura da secção, são visíveis em projecção horizontal (por estarem contidos em faces laterais visíveis) enquanto que
os lados [AA’’BB’’] e [AA’’FF’’], da figura da secção, são invisíveis em projecção horizontal (por estarem contidos em faces laterais invisíveis). Note
que a superfície da ffiigguurraa ddaa sseeccççããoo (a área do corte) nnããoo éé vviissíívveell em nenhuma das projecções, pois não há a desagregação do sólido,
pelo que não há lugar à execução de tracejado.
425.
Em primeiro lugar representou-se a pirâmide, pelas suas projecções, e o plano secante, pelos seus traços, em função dos dados. AA é o vér-
tice mais à direita do pentágono (o vértice de menor abcissa) e o lado [CCDD] (o lado oposto a AA) é vertical. O vértice da pirâmide tem 10 cm
de afastamento (dista 8 cm do plano ϕ, o plano da base, que tem 2 cm de afastamento) – VV22 ≡ CC22, pois os dois pontos situam-se na mesma
recta projectante frontal.
a) As projecções da pirâmide desenharam-se a traço leve, pois trata-se de uma construção auxiliar para o objectivo do exercício – o ssóólliiddoo
rreessuullttaannttee ddaa sseeccççããoo. Uma vez que o plano secante é projectante frontal, é possível concluir que o plano corta duas arestas da base (as
arestas [AABB] e [EEDD]) e duas arestas laterais (as arestas [AAVV] e [EEVV]) – a ffiigguurraa ddaa sseeccççããoo tem, assim, quatro vértices (é um quadrilátero).
Os pontos em que o plano corta as arestas tiveram determinação directa a partir das suas projecções frontais, pois trata-se da intersecção
de rectas não projectantes com um plano projectante frontal (o plano α). A partir das projecções dos quatro vértices da figura da secção
(RR, SS, TT e UU), desenharam-se as projecções da figura (o quadrilátero [RRSSTTUU]) e as projecções do ssóólliiddoo rreessuullttaannttee ddaa sseeccççããoo (a parte da
pirâmide compreendida entre o plano secante e o Plano Horizontal de Projecção). Note que se representou, a traço forte, o ssóólliiddoo rreessuullttaannttee
ddaa sseeccççããoo, por ser esse o pretendido – a parte do sólido que é desprezada (a parte compreendida entre o plano secante e o vértice) repre-
sentou-se a traço leve, pois trata-se de uma construção auxiliar para atingir o objectivo do exercício. Representaram-se os contornos apa-
rentes (horizontal e frontal) do novo sólido (o sólido resultante da secção), bem como as respectivas invisibilidades. Atendendo a que,
em projecção horizontal, a ffiigguurraa ddaa sseeccççããoo é visível (a superfície da figura, ou seja, a área do corte), identificou-se a figura a tracejado
(em projecção horizontal).
b) Para determinar a V.G. da figura da secção, é necessário o recurso a um processo geométrico auxiliar – a secção está contida no plano θ,
que não é paralelo a nenhum dos planos de projecção. Optou-se pelo rebatimento do plano θ para o Plano Horizontal de Projecção – a
charneira foi hhθ. A V.G. da figura da secção está no quadrilátero [RRrrSSrrTTrrUUrr].

188. 188
SOLUÇÕES
426.
Em primeiro lugar representou-se a pirâmide, pelas
suas projecções, e o plano secante, pelos seus tra-
ços, em função dos dados. A circunferência circuns-
crita ao hexágono [AABBCCDDEEFF] tem centro em OO e raio
OOෆAAෆ, pois AA é um dos vértices do polígono. Uma vez
que se trata de um plano projectante horizontal, é
possível concluir que o plano secante corta duas ares-
tas da base (as arestas [AABB] e [EEDD]) e três arestas
laterais (as arestas [AAVV], [FFVV] e [EEVV]) – a ffiigguurraa ddaa
sseeccççããoo tem, assim, cinco vértices (é um pentágono
irregular). Os pontos em que o plano corta as arestas
da pirâmide tiveram determinação directa a partir das
suas projecções horizontais, pois trata-se da intersec-
ção de rectas não projectantes com um plano projec-
tante horizontal (o plano π). A partir das projecções dos
cinco vértices da figura da secção (JJ, KK, LL, MM e NN),
desenharam-se as projecções da ffiigguurraa ddaa sseeccççããoo (o
pentágono irregular [JJKKLLMMNN]). Em projecção horizon-
tal, a figura reduz-se a um segmento de recta, pois o
plano secante (o plano π) é projectante horizontal. Já
em projecção frontal, sendo pedida a ffiigguurraa ddaa sseecc--
ççããoo e não o ssóólliiddoo rreessuullttaannttee ddaa sseeccççããoo (não houve
desagregação do sólido), há que representar as invisi-
bilidades existentes na ffiigguurraa ddaa sseeccççããoo. Os lados
[JJKK], [KKLL] e [LLMM] da figura, que se situam nas faces
laterais [AABBVV], [AAFFVV] e [EEFFVV], respectivamente, são
invisíveis em projecção frontal, uma vez que aquelas faces são invisíveis em projecção frontal. O lado [MMNN] da figura da secção é visível, por
se situar numa face visível em projecção horizontal (a face [EEDDVV]). Já o lado [JJNN], da figura da secção, uma vez que se situa na base (que é
projectante frontal) não admite a representação de qualquer invisibilidade. Note que, em termos de traçado, o sólido se representou a traço
médio (é um dado) e o pretendido (a ffiigguurraa ddaa sseeccççããoo) se representou a traço forte. Para determinar a V.G. da ffiigguurraa ddaa sseeccççããoo, recorreu-
-se ao rebatimento do plano π para o Plano Frontal de Projecção (a charneira foi ffπ).
427. RReellaattóórriioo
Em primeiro lugar representou-se o triângulo equilátero [AABBCC], pelas suas projecções, e o plano secante, pelos seus traços, em função dos
dados. O plano ϕ é o plano frontal (de frente) que contém o triângulo [AABBCC]. O ponto AA, porque é um ponto do β1/3, tem coordenadas iguais
e projecções simétricas em relação ao eixo XX. Os dados do exercício permitiram-nos concluir a construção da projecção frontal do tetraedro
– a projecção frontal do vértice DD (o quarto vértice do sólido) está coincidente com OO22 (a projecção frontal do centro do triângulo). Não é
possível, de forma directa, determinar o afastamento de DD, pois não se sabe a altura de um tetraedro – sabe-se, apenas, que todas as suas
arestas têm o mesmo comprimento, sendo esse o raciocínio que suporta a construção das projecções deste sólido. Assim, as arestas [AADD],
[BBDD] e [CCDD] têm comprimento igual ao lado do triângulo [AABBCC], mas nenhuma delas se projecta em V.G. – é necessário o recurso a um pro-
cesso geométrico auxiliar. Optou-se pelo rebatimento do plano θ, o plano de topo que contém a aresta [AADD]. Rebateu-se o plano θ para o
Plano Horizontal de Projecção (a charneira foi hhθ – recta ee), obtendo AArr e a referência de DDrr. Com o compasso, fazendo centro em AArr e raio
igual à medida do lado do triângulo [AABBCC], determinou-se DDrr – invertendo o rebatimento, determinou-se a projecção horizontal de DD e con-
cluiu-se a construção da projecção horizontal do sólido (as projecções do sólido representaram-se a traço leve, pois trata-se de uma cons-
trução auxiliar para o objectivo do exercício – o ssóólliiddoo rreessuullttaannttee ddaa sseeccççããoo).
a) Uma vez que o plano secante é projectante horizontal, é possível concluir que o plano corta quatro arestas do sólido (as arestas [AABB],
[BBCC], [CCDD] e [AADD]) – a ffiigguurraa ddaa sseeccççããoo tem, assim, quatro vértices (é um quadrilátero). Os pontos em que o plano corta as arestas tive-
ram determinação directa a partir das suas projecções horizontais, pois trata-se da intersecção de rectas não projectantes com um plano
projectante horizontal (o plano α). A partir das projecções dos quatro vértices da figura da secção (AA’’, CC’’, MM e NN), desenharam-se as pro-
jecções da figura (o quadrilátero [AA’’CC’’MMNN]) e as projecções do ssóólliiddoo rreessuullttaannttee ddaa sseeccççããoo (a parte do tetraedro compreendida entre o
plano secante e o Plano Frontal de Projecção). Note que se representou, a traço forte, o ssóólliiddoo rreessuullttaannttee ddaa sseeccççããoo, por ser esse o
pretendido – a parte do sólido que é desprezada (a parte compreendida entre o plano secante e a base) representou-se a traço leve, pois
trata-se de uma construção auxiliar para atingir o objectivo do exercício. Representaram-se os contornos aparentes (horizontal e frontal)
do novo sólido (o sólido resultante da secção), bem como as respectivas invisibilidades. Atendendo a que, em projecção frontal, a ffiigguurraa
ddaa sseeccççããoo é visível (a superfície da figura, ou seja, a área do corte), identificou-se a figura a tracejado (em projecção frontal).
b) Para determinar a V.G. da figura da secção, é necessário o recurso a um processo geométrico auxiliar – a secção está contida no plano
α, que não é paralelo a nenhum dos planos de projecção. Optou-se pelo rebatimento do plano α para o Plano Frontal de Projecção – a
charneira foi ffα (recta ee’’). A V.G. da figura da secção está no quadrilátero [AA’’rrCC’’rrMMrrNNrr].
(Continua na página seguinte)

189. 189
SOLUÇÕES
427. RReessoolluuççããoo
428.
Em primeiro lugar representou-se o prisma, pelas suas projecções,
e o plano secante, pelos seus traços, em função dos dados. O pla-
no ν é o plano que contém a base inferior do prisma e o plano ν1 o
plano que contém a sua base superior.
a) Uma vez que se trata de um plano projectante frontal, é possí-
vel concluir que o plano secante corta as quatro arestas laterais
do prisma, não cortando nenhuma aresta da base (o plano θ
não corta nenhuma das bases) – a figura da secção tem, assim,
quatro vértices (é um quadrilátero). No entanto, uma vez que o
plano secante nnããoo éé ppaarraalleelloo aos planos das bases, esse qua-
drilátero nnããoo sseerráá um quadrado. Os pontos em que o plano
corta as arestas laterais do prisma tiveram determinação directa
a partir das suas projecções frontais, pois trata-se da intersec-
ção de rectas não projectantes (as rectas suporte das arestas
laterais) com um plano projectante frontal (o plano θ). A partir
das projecções dos quatro vértices da figura da secção (MM, NN,
OO e PP), desenharam-se as projecções da ffiigguurraa ddaa sseeccççããoo (o
quadrilátero [MMNNOOPP]). Em projecção frontal, a figura reduz-se a
um segmento de recta, pois o plano secante (o plano θ) é pro-
jectante frontal. Já em projecção horizontal, sendo pedida a
ffiigguurraa ddaa sseeccççããoo e não o ssóólliiddoo rreessuullttaannttee ddaa sseeccççããoo (não
houve desagregação do sólido), há que representar as invisibili-
dades existentes na ffiigguurraa ddaa sseeccççããoo. Os lados [NNOO] e [OOPP]
da figura, que se situam nas faces laterais [BBBB’’CC’’CC] e [CCCC’’DD’’DD],
respectivamente, são invisíveis em projecção horizontal, uma
vez que aquelas faces são invisíveis em projecção horizontal. Os lados [MMNN] e [MMPP] da figura da secção são visíveis, por se situarem em fa-
ces visíveis em projecção horizontal (as faces [AAAA’’BB’’BB] e [AAAA’’DD’’DD], respectivamente). Note que, em termos de traçado, o sólido se repre-
sentou a traço médio (é um dado) e o pretendido (a ffiigguurraa ddaa sseeccççããoo) se representou a traço forte.
b) Para determinar a V.G. da figura da secção, é necessário o recurso a um processo geométrico auxiliar – a secção está contida no plano θ,
que não é paralelo a nenhum dos planos de projecção. Optou-se pelo rebatimento do plano θ para o Plano Frontal de Projecção – a char-
neira foi ffθ. A V.G. da figura da secção está no quadrilátero [MMrrNNrrOOrrPPrr].

190. 190
SOLUÇÕES
Em primeiro lugar representou-se o prisma, pelas suas projecções, e o plano secante, pelos
seus traços, em função dos dados. O vértice CC, do triângulo [AABBCC], é o vértice que se situa mais
à direita, por ser o vértice de menor abcissa do triângulo. Os planos das bases distam 5 cm (a
altura do prisma). As projecções do sólido representaram-se a traço leve, pois trata-se de uma
construção auxiliar para o objectivo do exercício – o ssóólliiddoo rreessuullttaannttee ddaa sseeccççããoo. O plano se-
cante passa necessariamente pelo vértice AA’’ da base de maior afastamento do sólido. Uma vez
que se trata de um plano projectante horizontal, é possível concluir que o plano secante corta
duas arestas laterais do sólido (as arestas [AAAA’’] e [BBBB’’]) e duas arestas da base de menor afas-
tamento (as arestas [BBCC] e [AACC]) – a figura da secção tem, assim, quatro vértices (é um quadri-
látero). Note que o plano secante corta a aresta lateral [AAAA’’] e a base de maior afastamento no
mesmo ponto – o vértice AA’’ da base de maior afastamento. Os pontos em que o plano corta as
arestas do prisma tiveram determinação directa a partir das suas projecções horizontais, pois
trata-se da intersecção de rectas com um plano projectante horizontal (o plano α). A partir das
projecções dos quatro vértices da figura da secção (AA’’, JJ, KK e LL), desenharam-se as projecções
da figura (o quadrilátero [AA’’JJKKMM]) e as projecções do ssóólliiddoo rreessuullttaannttee ddaa sseeccççããoo (a parte do
prisma que está compreendida entre o plano secante e o Plano Frontal de Projecção). Note que
se representou, a traço forte, o ssóólliiddoo rreessuullttaannttee ddaa sseeccççããoo, por ser esse o pretendido – a par-
te do sólido que é desprezada (a parte compreendida entre o plano secante e a base de maior
afastamento) representou-se a traço leve, pois trata-se de uma construção auxiliar para atingir o
objectivo do exercício. Representaram-se os contornos aparentes (horizontal e frontal) do novo
sólido (o sólido resultante da secção), bem como as respectivas invisibilidades. Atendendo a
que, em projecção frontal, a ffiigguurraa ddaa sseeccççããoo é visível (a superfície da figura, ou seja, a área do
corte), identificou-se a figura a tracejado (em projecção frontal).
430.
Em primeiro lugar representou-se o prisma, pelas suas
projecções, e o plano secante, pelos seus traços, em
função dos dados. Note que, para a construção das
projecções do prisma se recorreu ao rebatimento do
plano de perfil π que contém a base mais à direita do
sólido para, dessa forma, se determinarem as projec-
ções do pentágono [AABBCCDDEE]. Rebateu-se o plano π
para o Plano Frontal de Projecção – a charneira foi ffπ. A
circunferência circunscrita ao hexágono é tangente ao
Plano Horizontal de Projecção, pois tem 3 cm de raio
(em rebatimento, a circunferência é tangente a hhπrr
). As
arestas laterais do prisma estão contidas em rectas pa-
ralelas ao β1/3, pelo que as respectivas projecções fa-
zem, ambas, ângulos de 25° (a.e.) com o eixo XX. O
plano π’ é o plano que contém a base mais à esquerda
do sólido – o plano π’ dista 7 cm (a altura do prisma) do
plano π. Os vértices da base mais à esquerda do prisma
foram determinados através da intersecção de rectas
não projectantes (as rectas suporte das arestas laterais
do sólido) com um plano projectante (o plano π’). As
projecções do sólido representaram-se a traço leve,
pois trata-se de uma construção auxiliar para o objectivo
do exercício – o ssóólliiddoo rreessuullttaannttee ddaa sseeccççããoo. O ponto MM
é o ponto médio do eixo do sólido e determinou-se com
o recurso à construção da mediatriz do segmento [OOOO’’].
O plano α (o plano secante) corta as cinco arestas late-
rais do sólido (o que se constata atendendo a que se
trata de um plano projectante horizontal), não cortando
nenhuma das bases – a figura da secção tem cinco vér-
tices (é um pentágono). No entanto, uma vez que o plano
secante nnããoo éé ppaarraalleelloo aos planos das bases, esse pentágono nnããoo sseerráá um pentágono regular. Os pontos em que o plano corta as arestas
laterais do prisma tiveram determinação directa a partir das suas projecções horizontais, pois trata-se da intersecção de rectas não projec-
tantes com um plano projectante horizontal (o plano α). A partir das projecções dos cinco vértices da figura da secção (QQ, RR, SS, TT e UU), de-
senharam-se as projecções da figura da secção (o pentágono [QQRRSSTTUU]) e do ssóólliiddoo rreessuullttaannttee ddaa sseeccççããoo (a parte do prisma que está
compreendida entre o plano secante e o plano π – a base mais à direita). Note que se representou, a traço forte, o ssóólliiddoo rreessuullttaannttee ddaa
sseeccççããoo, por ser esse o pretendido – a parte do sólido que é desprezada (a parte compreendida entre o plano secante e a base mais à es-
querda) representou-se a traço leve, pois trata-se de uma construção auxiliar para atingir o objectivo do exercício. Representaram-se os con-
tornos aparentes (horizontal e frontal) do novo sólido (o sólido resultante da secção), bem como as respectivas invisibilidades. Atendendo a
que, em projecção frontal, a ffiigguurraa ddaa sseeccççããoo é visível (a superfície da figura, ou seja, a área do corte), identificou-se a figura a tracejado
(em projecção frontal).
429.

191. 431.
Em primeiro lugar representou-se o prisma, pelas suas
projecções, e o plano secante, pelos seus traços, em
função dos dados. Note que, para a construção das pro-
jecções do prisma, se recorreu ao rebatimento do plano
de perfil π que contém a base mais à direita do sólido
para, dessa forma, se determinarem as projecções do
quadrado [AABBCCDD]. Rebateu-se o plano π para o Plano
Frontal de Projecção – a charneira foi ffπ. As arestas late-
rais do prisma estão contidas em rectas fronto-horizontais
e o plano π’ é o plano que contém a base mais à esquer-
da do sólido – o plano π’ dista 8 cm (a altura do prisma)
do plano π. Os vértices da base mais à esquerda do pris-
ma foram determinados através da intersecção de rectas
não projectantes (as rectas suporte das arestas laterais
do sólido) com um plano projectante (o plano π’). O plano
γ (o plano secante) corta as quatro arestas laterais do sóli-
do (o que se constata atendendo a que se trata de um
plano projectante horizontal), não cortando nenhuma das
bases – a figura da secção tem quatro vértices (é um qua-
drilátero). No entanto, uma vez que o plano secante nnããoo
éé ppaarraalleelloo aos planos das bases, esse quadrilátero nnããoo
sseerráá um quadrado. Os pontos em que o plano corta as
arestas laterais do prisma tiveram determinação directa
a partir das suas projecções horizontais, pois trata-se da
intersecção de rectas não projectantes com um plano
projectante horizontal (o plano γ). A partir das projec-
ções dos quatro vértices da figura da secção (RR, SS, TT e
UU), desenharam-se as projecções da ffiigguurraa ddaa sseeccççããoo (o
quadrilátero [RRSSTTUU]). Note que o quadrilátero [RRSSTTUU],
eemm pprroojjeeccççããoo ffrroonnttaall, é um quadrado, mas, nnoo eessppaaççoo,
não o é – na deformação inerente à sua projecção fron-
tal, a figura transformou-se num quadrado mas, na realidade, nnããoo éé uumm qquuaaddrraaddoo. Tal facto deveu-se a um conjunto de factores, nomeada-
mente à posição do plano secante em relação aos planos das bases e ao Plano Frontal de Projecção – o diedro que o plano secante faz
com os planos das bases tem a mesma amplitude do diedro que o plano secante faz com o Plano Frontal de Projecção. Em projecção hori-
zontal, a figura reduz-se a um segmento de recta, pois o plano secante (o plano γ) é projectante horizontal. Já em projecção frontal, sendo
pedida a ffiigguurraa ddaa sseeccççããoo e não o ssóólliiddoo rreessuullttaannttee ddaa sseeccççããoo (não houve desagregação do sólido), há que representar as invisibilidades
existentes na ffiigguurraa ddaa sseeccççããoo. Os lados [RRSS] e [SSTT] da figura, que se situam nas faces laterais [AAAA’’BB’’BB] e [BBBB’’CC’’CC], respectivamente, são
invisíveis em projecção frontal, uma vez que aquelas faces são invisíveis em projecção frontal. Os lados [RRUU] e [TTUU] da figura da secção são
visíveis, por se situarem em faces do prisma que são visíveis em projecção frontal (as faces [AAAA’’DD’’DD] e [CCCC’’DD’’DD], respectivamente). Note
que, em termos de traçado, o sólido se representou a traço médio (é um dado) e o pretendido (a ffiigguurraa ddaa sseeccççããoo) se representou a traço
forte.
191
SOLUÇÕES
432. RReellaattóórriioo
Em primeiro lugar representou-se o cubo, pelas suas projecções, e o plano θ (o plano secante) pelos seus traços, em função dos dados.
O plano ν é o plano horizontal (de nível) que contém a face inferior do cubo (o quadrado [AABBCCDD]). O plano ν’ é o plano horizontal (de nível)
que contém a face superior do cubo (o quadrado [AA’’BB’’CC’’DD’’]). O plano ν’ dista 6 cm (a medida da aresta do cubo) do plano ν. Uma vez que
o plano secante é um plano projectante frontal, é possível concluir que o plano secante corta uma única aresta vertical do sólido (a arestas
[DDDD’’]), duas arestas da face inferior (as arestas [AADD] e [AABB]) e outras duas arestas da face superior (as arestas [AA’’BB’’] e [CC’’DD’’]) – a figura da
secção tem, assim, cinco vértices (é um pentágono). Os pontos em que o plano secante corta as arestas do cubo (os pontos MM, NN¸OO, PP e
QQ) tiveram determinação directa, a partir das suas projecções frontais, pois o plano secante é projectante frontal. A partir das projecções
dos cinco vértices da figura da secção, desenharam-se as projecções da ffiigguurraa ddaa sseeccççããoo (o pentágono [MMNNOOPPQQ]). Em projecção frontal,
a figura reduz-se a um segmento de recta, pois o plano secante (o plano θ) é projectante frontal. Já em projecção horizontal, sendo pedida
a ffiigguurraa ddaa sseeccççããoo e não o ssóólliiddoo rreessuullttaannttee ddaa sseeccççããoo (não houve desagregação do sólido), há que representar as invisibilidades exis-
tentes na ffiigguurraa ddaa sseeccççããoo. O lado [MMNN] da figura, que se situa na face [AABBCCDD], é invisível em projecção horizontal, em virtude de aquela
face ser invisível em projecção horizontal. O lado [PPQQ] da figura da secção é visível, por se situar numa face do sólido que é visível em pro-
jecção horizontal (a faces [AA’’BB’’CC’’DD’’]). Os lados [MMQQ], [NNOO] e [OOPP] da figura da secção, por se situarem em faces do sólido que estão conti-
das em planos projectantes horizontais, não admitem a representação de qualquer invisibilidade. Note que, em termos de traçado, o sólido
se representou a traço médio (é um dado) e o pretendido (a ffiigguurraa ddaa sseeccççããoo) se representou a traço forte.
(Continua na página seguinte)

192. 192
SOLUÇÕES
432. RReessoolluuççããoo
433.
Em primeiro lugar representou-se a pirâmide, pelas suas projecções, e o plano ρ (o plano
secante) pelos seus traços, em função dos dados. Ao contrário das situações anteriores,
em que era possível identificar imediatamente as arestas do sólido que eram cortadas pelo
plano secante, em virtude de os planos secantes serem projectantes, nesta situação esse
raciocínio não é possível – o plano secante nnããoo éé pprroojjeeccttaannttee. Assim, começou-se por ave-
riguar se o plano secante corta a base da pirâmide. A recta de intersecção do plano ρ
(o plano secante) com o plano da base é hhρ – hhρ é exterior à base (não corta a base), pelo
que o plano ρ não corta a base da pirâmide. O plano cortará, então, apenas as arestas late-
rais da pirâmide, pelo que a figura da secção terá três vértices – será um triângulo. No en-
tanto, uma vez que o plano secante não é paralelo ao plano da base, esse triângulo não
será um triângulo equilátero. Assim, efectuaram-se os traçados necessários à determinação
dos pontos em que o plano ρ corta as arestas laterais do sólido. Começou-se por determi-
nar o ponto de intersecção da aresta lateral [BBVV] com o plano ρ – para tal recorreu-se ao
método geral da intersecção de rectas com planos. O plano α, vertical, é o plano auxiliar a
que se recorreu – é um plano que contém a aresta lateral [BBVV] (α é o plano projectante hori-
zontal da aresta [BBVV]). A recta ii é a recta de intersecção de α com ρ – ii está definida pelos
seus traços (trata-se do caso geral da intersecção entre planos). BB’’ é o ponto de intersec-
ção da recta ii com a aresta [BBVV] – BB’’ é o ponto em que o plano ρ corta a aresta [BBVV]. Já te-
mos um ponto da figura da secção – o ponto BB’’. Em seguida, determinou-se a recta de
intersecção do plano que contém a face lateral [AABBVV] (o plano AABBVV) com o plano secante –
a recta ii’’. Para definir a recta ii’’ necessitamos de dois pontos ou um ponto e uma direcção.
Já temos um ponto – BB’’. BB’’ é um ponto que pertence ao plano ρ (pois pertence à recta ii,
que pertence ao plano ρ) e pertence ao plano AABBVV (pois pertence à recta BBVV, que pertence
ao plano AABBVV). Falta-nos outro ponto ou uma direcção. Desenhou-se a recta suporte da
aresta [AABB], da base – a recta AABB. A recta AABB é a recta de intersecção do plano AABBVV com o plano da base (o Plano Horizontal de Projecção).
A recta AABB e hhρ são complanares (hhρ é a recta de intersecção do plano ρ com o plano da base) e não são paralelas, pelo que são concor-
rentes – HH’’ é o ponto de concorrência. O ponto HH’’ é, assim, outro ponto comum aos dois planos (o plano AABBVV e o plano ρ). A recta ii’’ (a rec-
ta de intersecção do plano AABBVV com o plano ρ) fica definida por BB’’ e por HH’’. A recta ii’’ intersecta a aresta [AAVV] no ponto AA’’ – AA’’ é, assim,
outro ponto da figura da secção. Em seguida, determinou-se a recta de intersecção do plano que contém a face lateral [BBCCVV] (o plano BBCCVV)
com o plano secante – a recta ii’’’’. Para definir a recta ii’’’’ necessitamos de dois pontos ou um ponto e uma direcção. Já temos um ponto – BB’’.
BB’’ é um ponto que pertence ao plano ρ e pertence ao plano BBCCVV (pois pertence à recta BBVV, que pertence ao plano BBCCVV). Falta-nos outro
(Continua na página seguinte)

193. 193
SOLUÇÕES
ponto ou uma direcção. Desenhou-se a recta suporte da aresta [BBCC], da base – a recta BBCC. A recta BBCC é a recta de intersecção do plano
BBCCVV com o plano da base (o Plano Horizontal de Projecção). A recta BBCC e hhρ são complanares (hhρ é a recta de intersecção do plano ρ com
o plano da base) e não são paralelas, pelo que são concorrentes – HH’’’’ é o ponto de concorrência. O ponto HH’’’’ é, assim, outro ponto comum
aos dois planos (o plano BBCCVV e o plano ρ). A recta ii’’’’ (a recta de intersecção do plano BBCCVV com o plano ρ) fica definida por BB’’ e por HH’’’’.
A recta ii’’’’ intersecta a aresta [CCVV] no ponto CC’’ – CC’’ é, assim, outro ponto da figura da secção. A partir dos três vértices da figura da secção,
desenharam-se as suas projecções (a figura da secção é o triângulo [AA’’BB’’CC’’]). Sendo pedida a ffiigguurraa ddaa sseeccççããoo e não o ssóólliiddoo rreessuullttaannttee
ddaa sseeccççããoo (não houve desagregação do sólido), há que representar as invisibilidades existentes na ffiigguurraa ddaa sseeccççããoo – note que o plano
secante nnããoo éé pprroojjeeccttaannttee, pelo que nenhuma das duas projecções da figura da secção se reduz a um segmento de recta. Assim, pode ha-
ver invisibilidades em ambas as projecções. Os três lados do triângulo [AA’’BB’’CC’’] estão contidos nas três faces laterais da pirâmide – estas
são todas visíveis em projecção horizontal, pelo que, em projecção horizontal, a figura da secção é visível na sua totalidade. Já em projec-
ção frontal, os lados [AA’’BB’’] e [BB’’CC’’] da figura, que se situam nas faces laterais [AABBVV] e [BBCCVV], respectivamente, são invisíveis em projecção
frontal, uma vez que aquelas faces são invisíveis em projecção frontal. O lado [AA’’CC’’] da figura da secção é visível, por se situar numa face da
pirâmide que é visível em projecção frontal (a face [AACCVV]). Note que, em termos de traçado, o sólido se representou a traço médio (é um
dado) e o pretendido (a ffiigguurraa ddaa sseeccççããoo) se representou a traço forte.
434.
Em primeiro lugar representou-se a pirâmide, pelas suas projecções, e
o plano γ (o plano secante) pelos seus traços, em função dos dados.
O plano ϕ é o plano frontal (de frente) que contém a base da pirâmide.
Tal como a situação do exercício anterior, uma vez que o plano secan-
te nnããoo éé pprroojjeeccttaannttee, não é possível, de forma directa identificar as
arestas do sólido que são cortadas pelo plano secante, o que obriga a
procedimentos auxiliares e à análise, aresta a aresta, das arestas que
são cortadas pelo plano secante. Assim, começou-se por averiguar se
o plano secante corta a base da pirâmide. A recta de intersecção do
plano γ (o plano secante) com o plano da base é a recta ii – a recta ii é
uma recta frontal (de frente) do plano γ. A recta ii está definida por um
ponto (HH, o seu traço horizontal) e por uma direcção (é paralela a ffγ,
pois rectas frontais de um plano são paralelas entre si e paralelas ao
traço frontal do plano, que é uma recta frontal do plano com afasta-
mento nulo). A recta ii corta a base em dois pontos – os pontos QQ e RR
que são, respectivamente, os pontos em que o plano γ (o plano secan-
te) corta as arestas [AADD] e [CCDD] da base. Já temos dois pontos da
figura da secção. Para determinar o ponto de intersecção da aresta
lateral [AAVV] com o plano γ recorreu-se ao método geral da intersecção
de rectas com planos – o plano α, de topo, é o plano auxiliar a que se
recorreu. O plano α é um plano que contém a aresta lateral [AAVV] (α é o
plano projectante horizontal da aresta [AAVV]) – o plano α contém, tam-
bém, a aresta lateral [CCVV]. A recta ii’’ é a recta de intersecção de α com
γ – ii’’ está definida por um ponto (HH’’, o seu traço horizontal) e por uma
direcção (é uma recta frontal comum aos dois planos, pois os traços
frontais dos dois planos são paralelos entre si). A recta ii’’ intersecta a
aresta lateral [CCVV] no ponto SS e a aresta lateral [AAVV] no ponto UU – SS e
UU são, respectivamente, os pontos em que o plano γ corta as arestas
laterais [CCVV] e [AAVV] da pirâmide. Já temos mais dois pontos da figura
da secção. O plano γ corta a face lateral [AADDVV] segundo o segmento
[QQUU] e corta a face lateral [CCDDVV] segundo o segmento [RRSS], pelo que
não corta a aresta lateral [DDVV]. Em seguida, determinou-se a recta de intersecção do plano que contém a face lateral [AABBVV] (o plano AABBVV)
com o plano secante – a recta ii’’’’. Para definir a recta ii’’’’ necessitamos de dois pontos ou um ponto e uma direcção. Já temos um ponto – UU.
UU é um ponto que pertence ao plano γ (pois pertence à recta ii’’, que pertence ao plano γ) e pertence ao plano AABBVV (pois pertence à recta
AAVV, que pertence ao plano AABBVV). Falta-nos outro ponto ou uma direcção. Desenhou-se a recta suporte da aresta [AABB], da base – a recta AABB.
A recta AABB é a recta de intersecção do plano AABBVV com o plano da base (o plano ϕ). A recta ii é a recta de intersecção do plano γ (o plano
secante) com o plano da base (o plano ϕ). A recta AABB e a recta ii são complanares (estão ambas contidas no plano ϕ) e não são paralelas,
pelo que são concorrentes – II é o ponto de concorrência. O ponto II é, assim, outro ponto comum aos dois planos (o plano AABBVV e o plano γ).
A recta ii’’’’ (a recta de intersecção do plano AABBVV com o plano γ) fica definida por UU e por II. A recta ii’’’’ intersecta a aresta [BBVV] no ponto TT – TT é,
assim, outro ponto da figura da secção. Note que se omitiu a representação, em projecção horizontal, do ponto II e da recta ii, por estas não
serem necessárias à conclusão do exercício. Já temos cinco pontos da figura da secção – o plano secante não corta mais nenhuma aresta
da pirâmide, pelo que a figura da secção é um pentágono. A partir das projecções dos cinco vértices da figura da secção (QQ, RR, SS, TT e UU),
desenharam-se as projecções da figura da secção (o pentágono [QQRRSSTTUU]) e do ssóólliiddoo rreessuullttaannttee ddaa sseeccççããoo (a parte da pirâmide que está
compreendida entre o plano secante e o plano da base). Note que se representou, a traço forte, o ssóólliiddoo rreessuullttaannttee ddaa sseeccççããoo, por ser
esse o pretendido – a parte do sólido que é desprezada (a parte compreendida entre o plano secante e o vértice) representou-se a traço
leve, pois trata-se de uma construção auxiliar para atingir o objectivo do exercício. Representaram-se os contornos aparentes (horizontal e
frontal) do novo sólido (o sólido resultante da secção), bem como as respectivas invisibilidades. Atendendo a que a ffiigguurraa ddaa sseeccççããoo (a super-
fície da figura, ou seja, a área do corte) é visível em ambas as projecções, identificou-se a figura a tracejado (em ambas as projecções).

194. 194
SOLUÇÕES
435.
Em primeiro lugar representou-se a pirâ-
mide, pelas suas projecções, e o plano
α (o plano secante) pelos seus traços,
em função dos dados. O plano ϕ é o pla-
no frontal (de frente) que contém a base
da pirâmide. Para que a aresta lateral
[AAVV] seja horizontal (de nível), a posição
do pentágono tem de ser tal que o lado
oposto ao vértice AA é vertical (note que
AA tem de ser o vértice mais à esquerda
do pentágono, para ser o vértice de
maior abcissa). A aresta [AAVV], por ser
horizontal (paralela ao Plano Horizontal
de Projecção), projecta-se em V.G. em
projecção horizontal – com o compasso,
fazendo centro em AA11 e com 8 cm de
raio (o comprimento da aresta) determi-
nou-se VV11, sobre a recta suporte do
eixo. Tal como as situações dos exercí-
cios anteriores, uma vez que o plano se-
cante nnããoo éé pprroojjeeccttaannttee, não é
possível, de forma imediata identificar as
arestas do sólido que são cortadas pelo
plano secante, o que obriga a procedi-
mentos auxiliares e à análise, aresta a
aresta, das arestas que são cortadas
pelo plano secante. Assim, começou-se
por averiguar se o plano secante corta a
base da pirâmide. A recta de intersec-
ção do plano α (o plano secante) com o
plano da base é a recta ff – a recta ff é
uma recta frontal (de frente) do plano α.
A recta ff está definida por um ponto (HH, o seu traço horizontal) e por uma direcção (é paralela a ffα, pois rectas frontais de um plano são paralelas
entre si e paralelas ao traço frontal do plano, que é uma recta frontal do plano com afastamento nulo). A recta ff corta a base em dois pontos – os
pontos JJ e KK que são, respectivamente, os pontos em que o plano α (o plano secante) corta as arestas [DDEE] e [AABB] da base. Já temos dois pon-
tos da figura da secção. Para determinar o ponto de intersecção da aresta lateral [CCVV] com o plano α recorreu-se ao método geral da intersec-
ção de rectas com planos – o plano γ, vertical, é o plano auxiliar a que se recorreu. O plano γ é um plano que contém a aresta lateral [CCVV] (γ é o
plano projectante horizontal da aresta [CCVV]) – o plano γ contém, também, a aresta lateral [DDVV] (note que a face lateral [CCDDVV] da pirâmide está
contida num plano projectante horizontal, que é o próprio plano γ). A recta ii é a recta de intersecção de α com γ – ii está definida por dois pontos,
que são os seus traços (trata-se do caso geral da intersecção entre rectas e planos). A recta ii intersecta a aresta lateral [CCVV] no ponto MM e a
aresta lateral [DDVV] no ponto LL – MM e LL são, respectivamente, os pontos em que o plano α corta as arestas laterais [CCVV] e [DDVV] da pirâmide.
Já temos mais dois pontos da figura da secção. Em seguida, determinou-se a recta de intersecção do plano que contém a face lateral [BBCCVV] (o
plano BBCCVV) com o plano secante – a recta ii’’. Para definir a recta ii’’ necessitamos de dois pontos ou um ponto e uma direcção. Já temos um pon-
to – MM. MM é um ponto que pertence ao plano α (pois pertence à recta ii, que pertence ao plano α) e pertence ao plano BBCCVV (pois pertence à recta
CCVV, que pertence ao plano BBCCVV). Falta-nos outro ponto ou uma direcção. Desenhou-se a recta suporte da aresta [BBCC], da base – a recta BBCC. A
recta BBCC é a recta de intersecção do plano BBCCVV com o plano da base (o plano ϕ). A recta ff é a recta de intersecção do plano α (o plano secante)
com o plano da base (o plano ϕ). A recta BBCC e a recta ff são complanares (estão ambas contidas no plano ϕ) e não são paralelas, pelo que são
concorrentes – II é o ponto de concorrência. O ponto II é, assim, outro ponto comum aos dois planos (o plano BBCCVV e o plano α). A recta ii’’ (a rec-
ta de intersecção do plano BBCCVV com o plano α) fica definida por MM e por II. A recta ii’’ intersecta a aresta [BBVV] no ponto NN – NN é, assim, outro pon-
to da figura da secção. O plano α corta a face lateral [AABBVV] segundo o segmento [KKNN], corta a base segundo o segmento [JJKK] e corta a face
lateral [DDEEVV] segundo o segmento [JJLL], pelo que o plano α não corta as arestas laterais [AAVV] e [EEVV]. Já temos cinco pontos da figura da secção
– o plano secante não corta mais nenhuma aresta da pirâmide, pelo que a figura da secção é um pentágono. A partir das projecções dos cinco
vértices da figura da secção (JJ, KK, LL, MM e NN), desenharam-se as projecções da figura da secção (o pentágono [JJKKLLMMNN]) – note que o plano
secante não é paralelo ao plano da base, pelo que o pentágono [JJKKLLMMNN] não é um pentágono regular. Sendo pedida a ffiigguurraa ddaa sseeccççããoo e não
o ssóólliiddoo rreessuullttaannttee ddaa sseeccççããoo (não houve desagregação do sólido), há que representar as invisibilidades existentes na ffiigguurraa ddaa sseeccççããoo – note
que o plano secante nnããoo éé pprroojjeeccttaannttee, pelo que nenhuma das duas projecções da figura da secção se reduz a um segmento de recta. Assim,
pode haver invisibilidades em ambas as projecções. As cinco faces laterais da pirâmide são invisíveis em projecção frontal, pelo que os lados do
pentágono [JJKKLLMMNN] que estão contidos nas faces laterais são invisíveis em projecção frontal – os lados [JJLL], [LLMM], [MMNN] e [KKNN]. Em projecção
frontal, apenas o lado [JJKK] da figura da secção é visível, por estar contido na base (que é visível, em projecção frontal). Já em projecção horizon-
tal, os lados [KKNN] e [MMNN] da figura, que se situam nas faces laterais [AABBVV] e [BBCCVV], respectivamente, são visíveis em projecção horizontal, uma
vez que aquelas faces são visíveis em projecção horizontal. O lado [JJLL] da figura da secção é invisível em projecção horizontal, por se situar
numa face da pirâmide que é invisível em projecção horizontal (a face [DDEEVV]). Os lados [JJKK] e [LLMM], porque se situam em faces projectantes
horizontais do sólido (a face lateral [CCDDVV] e a base) não admitem a representação de quaisquer invisibilidades em projecção horizontal). Note
que, em termos de traçado, o sólido se representou a traço médio (é um dado) e o pretendido (a ffiigguurraa ddaa sseeccççããoo) se representou a traço forte.

195. 195
SOLUÇÕES
436.
Em primeiro lugar representou-se a pirâmide, pelas suas projecções, e o plano secante, pelos seus traços, em função dos dados. A partir da
projecção horizontal do eixo da pirâmide determinou-se VV11, a projecção horizontal do vértice do sólido – VV22 determinou-se em função da
altura da pirâmide (VV tem 9 cm de cota, pois a pirâmide tem 7 cm de altura e a base tem 2 cm de cota). As projecções do sólido desenha-
ram-se a traço leve, pois trata-se de um traçado auxiliar para o objectivo do exercício (que é o ssóólliiddoo rreessuullttaannttee ddaa sseeccççããoo).
a) Uma vez que o plano secante nnããoo éé pprroojjeeccttaannttee, não é possível, de forma imediata identificar as arestas do sólido que são cortadas pelo
plano secante, o que obriga a procedimentos auxiliares e à análise, aresta a aresta, das arestas que são cortadas pelo plano secante.
Assim, começou-se por averiguar se o plano secante corta a base da pirâmide. A recta de intersecção do plano ρ (o plano secante) com
o plano da base é a recta mm – a recta mm está definida por uma direcção (é fronto-horizontal, pois a recta de intersecção de um plano de
rampa com um plano horizontal é necessariamente fronto-horizontal) e por um ponto (o ponto II, que é o ponto de intersecção da recta rr,
uma recta do plano ρ, com o plano ν). A recta mm corta a base da pirâmide nos pontos PP e QQ – os pontos PP e QQ são, respectivamente, os
pontos em que o plano ρ (o plano secante) corta as arestas [BBCC] e [AACC] da base. Já temos dois pontos da figura da secção. Em seguida
determinou-se o ponto de intersecção da aresta lateral [BBVV] com o plano ρ – para tal recorreu-se ao método geral da intersecção de rec-
tas com planos (nem a aresta [BBVV] nem o plano ρ são projectantes). O plano α, vertical, é um plano auxiliar que contém a aresta [BBVV] (α
é o plano projectante horizontal da aresta [BBVV]). A recta ii é a recta de intersecção de α com ρ e está definida por dois pontos (os seus
traços, HH’’ e FF’’) – trata-se do caso geral da intersecção entre planos. A recta ii intersecta a aresta [BBVV] no ponto RR – RR é o ponto de inter-
secção da aresta [BBVV] com o plano secante. Já temos mais um ponto da figura da secção – o ponto RR. Em seguida, determinou-se o
ponto de intersecção da aresta lateral [AAVV] com o plano ρ – para tal recorreu-se mais uma vez ao método geral da intersecção de rectas
com planos. O plano θ, de topo, é um plano auxiliar que contém a aresta [AAVV] (θ é o plano projectante frontal da aresta [AAVV]). A recta ii’’ é
a recta de intersecção de θ com ρ e está definida por dois pontos (os seus traços, HH’’’’ e FF’’’’) – trata-se mais uma vez do caso geral da in-
tersecção entre planos. A recta ii’’ intersecta a aresta [AAVV] no ponto SS – SS é o ponto de intersecção da aresta [AAVV] com o plano secante.
Já temos mais um ponto da figura da secção – o ponto SS. O plano ρ corta a face lateral [BBCCVV] segundo o segmento [PPRR], corta a base
segundo o segmento [PPQQ] e corta a face lateral [AACCVV] segundo o segmento [QQSS], pelo que o plano ρ não corta a aresta lateral [CCVV].
(Continua na página seguinte)

196. 196
SOLUÇÕES
437.
Em primeiro lugar representou-se o
triângulo equilátero [AABBCC], pelas
suas projecções, e o plano secante,
pelos seus traços, em função dos
dados. O plano α tem os seus tra-
ços simétricos em relação ao eixo XX,
pois é ortogonal ao β1/3. Em função
dos dados, o lado [BBCC] do triângulo
é nneecceessssaarriiaammeennttee fronto-horizon-
tal. Os dados do exercício permiti-
ram-nos concluir a construção da
projecção horizontal do tetraedro –
a projecção horizontal do vértice DD
(o quarto vértice do sólido) está
coincidente com OO11 (a projecção
horizontal do centro do triângulo).
Não é possível, de forma directa,
determinar a cota de DD, pois não se
sabe a altura de um tetraedro –
sabe-se, apenas, que todas as
suas arestas têm o mesmo compri-
mento, sendo esse o raciocínio que
suporta a construção das projec-
ções deste sólido. Assim, as ares-
tas [AADD], [BBDD] e [CCDD] medem
todas 8 cm (a medida da aresta do
tetraedro), mas nenhuma delas se
projecta em V.G. – é necessário o
recurso a um processo geométrico
auxiliar. Optou-se pelo rebatimento
do plano π, o plano de perfil que
contém a aresta [AADD]. Rebateu-se
o plano π para o Plano Frontal de
Projecção (a charneira foi ffπ – recta
ee), obtendo AArr e a referência de DDrr.
Com o compasso, fazendo centro em AArr e com 8 cm de raio, determinou-se DDrr – invertendo o rebatimento, determinou-se a projecção fron-
tal de DD e concluiu-se a construção da projecção frontal do sólido (as projecções do sólido representaram-se a traço leve, pois trata-se de
uma construção auxiliar para o objectivo do exercício – o ssóólliiddoo rreessuullttaannttee ddaa sseeccççããoo). Uma vez que o plano secante nnããoo éé pprroojjeeccttaannttee,
não é possível, de forma imediata identificar as arestas do sólido que são cortadas pelo plano secante, o que obriga a procedimentos auxi-
liares e à análise, aresta a aresta, das arestas que são cortadas pelo plano secante. Assim, começou-se por averiguar se o plano secante
corta a face inferior do sólido (o triângulo [AABBCC]). A recta de intersecção do plano α (o plano secante) com o plano da face [AABBCC] é hhα – hhα
corta a face [AABBCC] do tetraedro nos pontos PP e QQ que são, respectivamente, os pontos em que o plano α (o plano secante) corta as arestas
[AABB] e [BBCC] da face inferior do sólido. Já temos dois pontos da figura da secção. Em seguida determinou-se o ponto de intersecção da
aresta [AADD] com o plano α – para tal recorreu-se ao método geral da intersecção de rectas com planos (nem a aresta [AADD] nem o plano α
são projectantes). O plano π, de perfil, é o plano que contém a aresta [AADD] (que é de perfil) – π é o plano projectante da aresta [AADD]. A recta
(Continua na página seguinte)
Já temos quatro pontos da figura da secção – o plano secante não corta mais nenhuma aresta da pirâmide, pelo que a figura da secção
é um quadrilátero. A partir das projecções dos quatro vértices da figura da secção (PP, QQ, RR e SS), desenharam-se as projecções da figura
da secção (o quadrilátero [PPQQRRSS]) e do ssóólliiddoo rreessuullttaannttee ddaa sseeccççããoo (a parte da pirâmide que está compreendida entre o plano secante
e os planos de projecção). Note que se representou, a traço forte, o ssóólliiddoo rreessuullttaannttee ddaa sseeccççããoo, por ser esse o pretendido – a parte do
sólido que é desprezada (a parte que se situa para cima do plano secante) representou-se a traço leve, pois trata-se de uma construção
auxiliar para atingir o objectivo do exercício. Representaram-se os contornos aparentes (horizontal e frontal) do novo sólido (o sólido
resultante da secção), bem como as respectivas invisibilidades. Atendendo a que a ffiigguurraa ddaa sseeccççããoo (a superfície da figura, ou seja, a
área do corte) é visível em ambas as projecções, identificou-se a figura a tracejado (em ambas as projecções).
b) Para determinar a V.G. da figura da secção, é necessário o recurso a um processo geométrico auxiliar – a secção está contida no plano
ρ, que não é paralelo a nenhum dos planos de projecção. Optou-se pelo rebatimento do plano ρ para o Plano Frontal de Projecção – a
charneira foi ffρ (ver exercício 117700 e respectivo relatório). O ponto que nos permitiu rebater hhρ foi HH, o traço horizontal da recta rr. A recta rrrr
fica definida por FFrr e por HHrr. O ponto IIrr determinou-se conduzindo, por II22, uma perpendicular à charneira – IIrr situa-se sobre rrrr. A recta mmrr
passa por IIrr e é paralela a ffρrr
(e a hhρrr
). PPrr e QQrr determinaram-se, sobre mmrr, conduzindo, por PP22 e QQ22, as perpendiculares à charneira que
por eles passam. A recta iirr está definida por FF’’rr (que é um ponto da charneira) e por HH’’rr – RRrr situa-se sobre iirr, na perpendicular à charnei-
ra que passa por RR22. A recta ii’’rr está definida por FF’’’’rr (que é um ponto da charneira) e por HH’’’’rr – SSrr situa-se sobre ii’’rr, na perpendicular à
charneira que passa por SS22. A V.G. da figura da secção está no quadrilátero [PPrrQQrrRRrrSSrr].

197. 197
SOLUÇÕES
(Continua na página seguinte)
ii é a recta de intersecção de π com α e está definida por dois pontos (os seus traços, HH e FF) – trata-se do caso geral da intersecção entre
planos. A recta ii é uma recta de perfil. A determinação do ponto em que a recta ii intersecta a aresta [AADD] tem de se processar com o recurso
a um processo geométrico auxiliar – recorreu-se ao rebatimento previamente efectuado do plano de perfil, rebatendo a recta ii. A recta iirr está
definida por FFrr e HHrr. A recta iirr intersecta a aresta [AArrDDrr] no ponto RRrr – invertendo o rebatimento, determinaram-se as projecções de RR. Já temos
mais um ponto da figura da secção. Em seguida, determinou-se a recta de intersecção do plano que contém a face [AACCDD] (o plano AACCDD) com
o plano secante – a recta hh. Para definir a recta hh necessitamos de dois pontos ou um ponto e uma direcção. Já temos um ponto – RR. RR é um
ponto que pertence ao plano α (pois pertence à recta ii, que pertence ao plano α) e pertence ao plano AACCDD (pois pertence à recta AADD, que
pertence ao plano AACCDD). Falta-nos outro ponto ou uma direcção. A recta de intersecção do plano AACCDD com o Plano Horizontal de Projecção
(a recta AACC) é uma recta horizontal (de nível) e é paralela a hhα (que é outra recta horizontal), pelo que já se conhece a direcção das rectas
horizontais (de nível) dos dois planos – a recta de intersecção dos dois planos é nneecceessssaarriiaammeennttee uma recta horizontal (de nível), paralela a
AACC e a hhα. A recta hh, passando por RR e paralela a hhα (e a [AACC]) é a recta de intersecção do plano α com o plano AACCDD. A recta hh intersecta a
aresta [CCDD] no ponto SS – SS é um outro ponto da figura da secção. O plano α corta a face [AABBDD] segundo o segmento [PPRR], corta a face
[AABBCC] segundo o segmento [PPQQ] e corta a face [BBCCDD] segundo o segmento [QQSS], pelo que o plano α não corta a aresta [BBDD]. Já temos
quatro pontos da figura da secção – o plano secante não corta mais nenhuma aresta do sólido, pelo que a figura da secção é um quadrilátero.
A partir das projecções dos quatro vértices da figura da secção (PP, QQ, RR e SS), desenharam-se as projecções da figura da secção (o quadrilá-
tero [PPQQRRSS]) e do ssóólliiddoo rreessuullttaannttee ddaa sseeccççããoo (a parte do tetraedro que está compreendida entre o plano secante e os planos de projec-
ção). Note que se representou, a traço forte, o ssóólliiddoo rreessuullttaannttee ddaa sseeccççããoo, por ser esse o pretendido – a parte do sólido que é
desprezada (a parte que se situa para cima do plano secante) representou-se a traço leve, pois trata-se de uma construção auxiliar para
atingir o objectivo do exercício. Representaram-se os contornos aparentes (horizontal e frontal) do novo sólido (o sólido resultante da sec-
ção), bem como as respectivas invisibilidades. Atendendo a que a ffiigguurraa ddaa sseeccççããoo (a superfície da figura, ou seja, a área do corte) é visível
em ambas as projecções, identificou-se a figura a tracejado (em ambas as projecções). Para determinar a V.G. da figura da secção, é neces-
sário o recurso a um processo geométrico auxiliar – a secção está contida no plano α, que não é paralelo a nenhum dos planos de projec-
ção. Optou-se pelo rebatimento do plano α para o Plano Horizontal de Projecção (ver exercício 116633 e respectivo relatório) – a charneira foi
hhα (recta ee’’). PPrr ≡ PP11 e QQrr ≡ QQ11, pois PP e QQ são pontos da charneira. O ponto que nos permitiu rebater ffα foi FF’’, o traço frontal da recta hh. A
recta hhrr fica definida por um ponto (FF’’rr) e por uma direcção (é paralela a hhαrr
). Conduzindo, por RR11 e SS11, as perpendiculares à charneira que
por eles passam, determinaram-se RRrr e SSrr sobre hhrr. A V.G. da figura da secção está no quadrilátero [PPrrQQrrRRrrSSrr].
438.
Em primeiro lugar representou-se o prisma, pelas suas projecções, e
o plano secante, pelos seus traços, em função dos dados. O plano α
(o plano secante) tem os seus traços coincidentes, pois é ortogonal
ao β2/4. O plano ν é o plano horizontal (de nível) que contém a base
inferior do sólido. A circunferência circunscrita ao quadrado [AABBCCDD]
da base inferior do prisma tem centro em OO e raio OOෆAAෆ, pois AA é um
dos vértices do polígono. As projecções das arestas laterais do prisma
são paralelas às projecções homónimas do eixo do sólido. O plano ν1
é o plano horizontal (de nível) que contém a base superior do sólido.
Os vértices da base superior foram determinados a partir das suas
projecções frontais – trata-se da intersecção de rectas não projectan-
tes (as rectas suporte das arestas laterais) com um plano projectante
frontal (o plano ν1). A base superior do prisma é o quadrado
[AA’’BB’’CC’’DD’’], cujos lados são paralelos aos lados correspondentes do
quadrado [AABBCCDD]. Uma vez que o plano secante nnããoo éé pprroojjeeccttaannttee,
não é possível, de forma imediata identificar as arestas do sólido que
são cortadas pelo plano secante, o que obriga a procedimentos auxi-
liares e à análise, aresta a aresta, das arestas que são cortadas pelo
plano secante. Assim, começou-se por averiguar se o plano secante
corta as bases do sólido. A recta ii é a recta de intersecção do plano α
com o plano ν – a recta ii é uma recta horizontal (de nível) do plano α e
está definida por um ponto (o seu traço frontal, FF) e por uma direcção
(é paralela a hhα, pois rectas horizontais de um plano são paralelas en-
tre si e paralelas ao traço horizontal do plano, que é uma recta hori-
zontal do plano com cota nula). A recta ii é exterior ao quadrado
[AABBCCDD], pelo que o plano α não corta a base inferior do sólido. A rec-
ta ii’’ é a recta de intersecção do plano α com o plano ν1 – é igualmente
uma recta horizontal (de nível) do plano α e está igualmente definida
por um ponto e uma direcção. A recta ii’’ corta o quadrado [AA’’BB’’CC’’DD’’]
nos pontos QQ e RR – QQ e RR são, respectivamente, os pontos em que o
plano α corta as arestas [AA’’BB’’] e [AA’’DD’’] da base superior do prisma. Já
temos dois pontos da figura da secção. Em seguida, determinou-se o ponto de intersecção da aresta lateral [CCCC’’] com o plano α – para tal
recorreu-se ao método geral da intersecção de rectas com planos (nem a aresta [CCCC’’] nem o plano α são projectantes). O plano δ, de topo, é o
plano auxiliar que contém a aresta [CCCC’’] (δ é o plano projectante frontal da aresta). A recta aa é a recta de intersecção do plano δ com o plano α –
a recta aa está definida por dois pontos (os seus traços, FF’’’’ e HH). RR é o ponto de intersecção da recta aa com a aresta [CCCC’’] – RR é o ponto em que o
plano secante (o plano α) corta a aresta [CCCC’’]. Já temos outro ponto da figura da secção – o ponto RR. Em seguida, determinou-se o ponto de

198. 198
SOLUÇÕES
439.
Em primeiro lugar representou-se o pris-
ma, pelas suas projecções, e o plano
secante, pelos seus traços, em função
dos dados. Atendendo a que uma das
faces laterais do sólido (a face de menor
cota) está contida num plano horizontal
(de nível), foi possível determinar a posi-
ção dos pentágonos das bases. O plano
ϕ é o plano frontal (de frente) que con-
tém a base de menor afastamento. O
plano ϕ’ é o plano frontal (de frente) que
contém a base de maior afastamento – o
plano ϕ’ dista 7 cm (a altura do prisma)
do plano ϕ. As projecções do sólido de-
senharam-se a traço leve, pois trata-se
de um traçado auxiliar para o objectivo
do exercício (que é o ssóólliiddoo rreessuullttaannttee
ddaa sseeccççããoo). Uma vez que o plano se-
cante nnããoo éé pprroojjeeccttaannttee, não é possível,
de forma imediata identificar as arestas
do sólido que são cortadas pelo plano
secante, o que obriga a procedimentos
auxiliares e à análise, aresta a aresta,
das arestas que são cortadas pelo plano
secante. Assim, começou-se por averi-
guar se o plano secante corta as bases
do prisma. Para tal há que determinar as
rectas de intersecção do plano ρ (o plano secante) com os planos ϕ e ϕ’ (os planos das bases). A recta de intersecção de um plano frontal
(de frente) com um plano de rampa é uma recta fronto-horizontal – já temos a direcção (falta-nos um ponto) Recorreu-se a uma recta rr, do
plano ρ (a recta rr é uma recta auxiliar e está definida por dois pontos, que são os seus traços). O plano ϕ (o plano que contém a base de
menor afastamento) corta a recta rr no ponto KK – a recta mm, fronto-horizontal e passando por KK, é a recta de intersecção de ϕ com ρ. A recta
mm corta a base de menor afastamento do prisma nos pontos PP e QQ – PP e QQ são, respectivamente, os pontos em que o plano ρ corta as ares-
tas [AAEE] e [AABB] da base. Já temos dois pontos da figura da secção. Note que não se determinou a recta de intersecção do plano ϕ’ (o plano
que contém a base de maior afastamento do prisma) com o plano ρ – essa recta, no entanto, é uma recta fronto-horizontal que se situa no
4o Diedro, pelo que é exterior à base [AA’’BB’’CC’’DD’’EE’’]. O plano ρ não corta a base de maior afastamento do prisma. Em seguida, para determi-
nar os pontos de intersecção das arestas laterais do prisma com o plano ρ recorreu-se ao método geral da intersecção de rectas com pla-
nos. O plano ν é um plano horizontal (de nível) auxiliar – é o plano que contém as arestas laterais [BBBB’’] e [EEEE’’] do prisma. A recta de
intersecção do plano ν com o plano ρ é a recta ii – a recta ii é uma recta fronto-horizontal, que está definida por uma direcção e por um ponto
(o ponto II, que é o ponto em que o plano ν corta a recta rr). A recta ii intersecta a aresta lateral [BBBB’’] no ponto SS e intersecta a aresta lateral
[EEEE’’] no ponto SS – RR e SS são, respectivamente, os pontos em que o plano ρ corta as arestas laterais [BBBB’’] e [EEEE’’]. Já temos mais dois pontos
intersecção da aresta lateral [DDDD’’] com o plano α, pelo mesmo processo. O plano θ, de topo, é o plano auxiliar que contém a aresta [DDDD’’] (θ é
o plano projectante frontal da aresta e é paralelo ao plano δ). A recta bb é a recta de intersecção do plano θ com o plano α – a recta bb está defi-
nida por um ponto (o seu traço frontal, que não se identificou para evitar sobrecarregar em demasia a resolução gráfica apresentada) e por
uma direcção (é paralela à recta aa). Recorde que qualquer plano corta dois planos paralelos segundo rectas paralelas – os planos δ e θ são pa-
ralelos, pelo que as rectas aa e bb (as rectas de intersecção do plano α com os planos δ e θ, respectivamente) são necessariamente paralelas. SS
é o ponto de intersecção da recta bb com a aresta [DDDD’’] – SS é o ponto em que o plano α corta a aresta [DDDD’’]. Já temos outro ponto da figura da
secção – o ponto SS. Em seguida, determinou-se o ponto de intersecção da aresta lateral [BBBB’’] com o plano α, pelo mesmo processo. O plano γ,
de topo, é o plano auxiliar que contém a aresta [BBBB’’] (γ é o plano projectante frontal da aresta e é paralelo aos planos δ e θ). A recta cc é a recta
de intersecção do plano γ com o plano α – a recta cc está definida por um ponto (o seu traço frontal, que não se identificou) e por uma direcção
(é paralela às rectas aa e bb). Recorde que qualquer plano corta dois planos paralelos segundo rectas paralelas – os planos δ, θ e γ são paralelos,
pelo que as rectas aa, bb e cc (as rectas de intersecção do plano α com os planos δ, θ e γ, respectivamente) são necessariamente paralelas. TT é o
ponto de intersecção da recta cc com a aresta [BBBB’’] – TT é o ponto em que o plano α corta a aresta [BBBB’’]. Já temos outro ponto da figura da sec-
ção – o ponto TT. O plano α corta a face lateral [AAAA’’BB’’BB] segundo o segmento [PPTT], corta a base superior segundo o segmento [PPQQ] e corta a
face lateral [AAAA’’DD’’DD] segundo o segmento [QQSS], pelo que o plano α não corta a aresta lateral [AAAA’’]. A figura da secção tem, assim, cinco vérti-
ces – os vértices PP, QQ, RR, SS e TT (é um pentágono). A partir dos cinco vértices da ffiigguurraa ddaa sseeccççããoo (o pentágono [PPQQRRSSTT]), desenharam-se as
suas projecções. Sendo pedida a ffiigguurraa ddaa sseeccççããoo e não o ssóólliiddoo rreessuullttaannttee ddaa sseeccççããoo (não houve desagregação do sólido), há que repre-
sentar as invisibilidades existentes na ffiigguurraa ddaa sseeccççããoo. Os lados [RRSS] e [RRTT] da figura da secção são invisíveis em projecção frontal, por se
situarem em faces laterais invisíveis em projecção frontal (as faces laterais [CCCC’’DD’’DD] e [BBBB’’CC’’CC], respectivamente). Os restantes lados da figura
da secção são visíveis, em projecção frontal, por se situarem em faces visíveis (em projecção frontal) ou em faces projectantes frontais (a base
superior). Os lados [RRSS] e [QQSS] da figura da secção são invisíveis em projecção horizontal, por se situarem em faces laterais invisíveis em pro-
jecção horizontal (as faces laterais [CCCC’’DD’’DD] e [AAAA’’DD’’DD], respectivamente). Os restantes lados da figura da secção são visíveis, em projecção
horizontal, por se situarem em faces visíveis em projecção horizontal.
(Continua na página seguinte)

199. 199
SOLUÇÕES
da figura da secção. O plano ν’ é outro plano horizontal (de nível) auxiliar – é o plano que contém as arestas laterais [CCCC’’] e [DDDD’’] do prisma
(note que o plano ν’ é o plano que contém a face lateral inferior do sólido). A recta de intersecção do plano ν’ com o plano ρ é a recta ii’’ – a
recta ii’’ é outra recta fronto-horizontal, que está também definida por uma direcção e por um ponto (o ponto II’’, que é o ponto em que o plano ν’
corta a recta rr). A recta ii’’ intersecta a aresta lateral [CCCC’’] no ponto TT e intersecta a aresta lateral [DDDD’’] no ponto UU – TT e UU são, respectiva-
mente, os pontos em que o plano ρ corta as arestas laterais [CCCC’’] e [DDDD’’]. Já temos mais dois pontos da figura da secção. Já temos seis
pontos da figura da secção – o plano secante não corta mais nenhuma aresta do prisma, pelo que a figura da secção é um hexágono (irre-
gular). A partir das projecções dos seis vértices da figura da secção (PP, QQ, RR, SS, TT e UU), desenharam-se as projecções da figura da secção
(o hexágono [PPQQRRSSTTUU]) e do ssóólliiddoo rreessuullttaannttee ddaa sseeccççããoo (a parte do prisma que está compreendida entre o plano secante e o Plano Hori-
zontal de Projecção). Note que se representou, a traço forte, o ssóólliiddoo rreessuullttaannttee ddaa sseeccççããoo, por ser esse o pretendido – a parte do sólido que
é desprezada (a parte que se situa para cima do plano secante) representou-se a traço leve, pois trata-se de uma construção auxiliar para
atingir o objectivo do exercício. Representaram-se os contornos aparentes (horizontal e frontal) do novo sólido (o sólido resultante da sec-
ção), bem como as respectivas invisibilidades. Atendendo a que a ffiigguurraa ddaa sseeccççããoo (a superfície da figura, ou seja, a área do corte) é visível
em ambas as projecções, identificou-se a figura a tracejado (em ambas as projecções).
440.
Em primeiro lugar representou-se o
cubo, pelas suas projecções, e o plano
secante, pelos seus traços, em função
dos dados. O plano ν é o plano hori-
zontal (de nível) que contém a face su-
perior do cubo. O plano α, porque é
ortogonal ao β1/3, tem os seus traços
simétricos em relação ao eixo XX. Por
outro lado, uma vez que o plano α
contém o ponto AA (que é um ponto do
Plano Horizontal de Projecção), sabe-
-se que hhα passa por AA11. As projec-
ções do sólido desenharam-se a traço
leve, pois trata-se de um traçado auxi-
liar para o objectivo do exercício (que
é o ssóólliiddoo rreessuullttaannttee ddaa sseeccççããoo).
O plano secante nnããoo éé pprroojjeeccttaannttee,
pelo que não é possível, de forma
imediata identificar as arestas do sóli-
do que são cortadas pelo plano se-
cante, o que obriga a procedimentos
auxiliares e à análise, aresta a aresta,
das arestas que são cortadas pelo pla-
no secante. Assim, começou-se por
averiguar se o plano secante corta as
faces horizontais (de nível) do cubo.
Para tal há que determinar as rectas
de intersecção do plano α (o plano se-
cante) com o Plano Horizontal de Pro-
jecção (que contém a face inferior do
cubo) e o plano ν (que contém a face superior do cubo). A recta de intersecção do plano α com o Plano Horizontal de Projecção é hhα – hhα é
tangente (rasante) ao quadrado [AABBCCDD] no ponto AA, pelo que o plano α corta a face [AABBCCDD] do cubo no ponto AA. Já temos um ponto da figura
da secção. A recta hh é a recta de intersecção do plano α com o plano ν – é uma recta horizontal, que está definida por um ponto (o seu traço
frontal, que é o ponto DD’’) e por uma direcção (é paralela a hhα, pois rectas horizontais de um plano são paralelas entre si e paralelas ao traço ho-
rizontal do plano, que é uma recta horizontal do plano com cota nula). A recta hh corta a face superior do cubo (o quadrado [AA’’BB’’CC’’DD’’]) nos
pontos BB’’ e DD’’ – BB’’ e DD’’ são mais dois pontos da secção. Já temos três pontos da secção – AA, BB’’ e DD’’. O plano α corta a face [AAAA’’BB’’BB] segun-
do o segmento [AABB’’] (que é uma diagonal dessa face). O plano α corta a face [AA’’BB’’CC’’DD’’] segundo o segmento [BB’’DD’’] (que é uma diagonal dessa
face). O plano α corta a face [AAAA’’DD’’DD] segundo o segmento [AADD’’] (que é uma diagonal dessa face). Conclui-se que o plano α não corta
mais nenhuma face do cubo – a figura da secção é o triângulo [AABB’’DD’’]. A partir das projecções dos três vértices da figura da secção, desenha-
ram-se as projecções da figura da secção e do ssóólliiddoo rreessuullttaannttee ddaa sseeccççããoo (a parte do cubo que está compreendida entre o plano secante e
os planos de projecção). Note que se representou, a traço forte, o ssóólliiddoo rreessuullttaannttee ddaa sseeccççããoo, por ser esse o pretendido – a parte do sólido
que é desprezada (a parte que se situa para cima do plano secante) representou-se a traço leve, pois trata-se de uma construção auxiliar para
atingir o objectivo do exercício. Representaram-se os contornos aparentes (horizontal e frontal) do novo sólido (o sólido resultante da secção),
bem como as respectivas invisibilidades. Atendendo a que a ffiigguurraa ddaa sseeccççããoo (a superfície da figura, ou seja, a área do corte) é visível em am-
bas as projecções, identificou-se a figura a tracejado (em ambas as projecções). Para determinar a V.G. da figura da secção, é necessário o
recurso a um processo geométrico auxiliar – a secção está contida no plano α, que não é paralelo a nenhum dos planos de projecção. Optou-se
pelo rebatimento do plano α para o Plano Horizontal de Projecção (ver exercício 116633 e respectivo relatório) – a charneira foi hhα (recta ee). AArr ≡ AA11,
pois AA é um ponto da charneira. O ponto que nos permitiu rebater ffα foi DD’’, o traço frontal da recta hh. A recta hhrr fica definida por um ponto (DD’’rr) e
por uma direcção (é paralela a hhαrr
). Conduzindo, por BB’’11 uma perpendicular à charneira, determinou-se BB’’rr sobre hhrr. A V.G. da figura da secção
está no triângulo [AArrBB’’rrDD’’rr]. Note que se trata de um ttrriiâânngguulloo eeqquuiilláátteerroo.

200. 200
SOLUÇÕES
441.
Em primeiro lugar representou-se o cubo pelas suas projecções, em função dos dados. O β1/3 é um plano que não carece de representa-
ção. O plano ϕ é o plano frontal (de frente) que contém a face de menor afastamento do cubo (o quadrado [AABBCCDD]). O plano ϕ’ dista 6 cm
(a aresta do cubo) do plano ϕ e é o plano frontal (de frente) que contém a face de maior afastamento do cubo (o quadrado [AA’’BB’’CC’’DD’’]).
O plano α é o plano projectante frontal que contém uma das faces do cubo – a aresta [AAAA’’] é a aresta projectante frontal que se situa no Plano
Horizontal de Projecção e é de topo (está contida em hhα). As projecções do sólido desenharam-se a traço leve, pois trata-se de um traçado
auxiliar para o objectivo do exercício (que é o ssóólliiddoo rreessuullttaannttee ddaa sseeccççããoo). O plano secante (o β1/3) nnããoo éé pprroojjeeccttaannttee, pelo que não é
possível, de forma imediata identificar as arestas do sólido que são cortadas pelo plano secante, o que obriga a procedimentos auxiliares e à
análise, aresta a aresta, das arestas que são cortadas pelo plano secante. Assim, começou-se por averiguar se o plano secante corta as fa-
ces frontais (de frente) do cubo. Para tal há que determinar as rectas de intersecção do β1/3 (o plano secante) com o plano ϕ (o plano que
contém a face de menor afastamento do cubo) e o plano ϕ’ (que contém a face de maior afastamento do cubo). A recta ii é a recta de inter-
secção do plano ϕ com o β1/3 – trata-se de uma recta fronto-horizontal. O plano ϕ é projectante horizontal, pelo que ii11 tem determinação
imediata – rectas do β1/3 têm as suas projecções simétricas em relação ao eixo XX, pelo que é possível, de forma imediata, determinar ii22 (tem
2 cm de cota). A recta ii corta o quadrado [AABBCCDD] nos pontos PP e QQ – PP e QQ são, respectivamente, os pontos em que o β1/3 corta as arestas
[AADD] e [AABB] da face [AABBCCDD] do cubo. Já temos dois pontos da figura da secção. A recta ii’’ é a recta de intersecção do plano ϕ’ com o β1/3 –
trata-se de outra recta fronto-horizontal. O plano ϕ’ é projectante horizontal, pelo que ii’’11 tem determinação imediata – rectas do β1/3 têm as
suas projecções simétricas em relação ao eixo XX, o que nos permite determinar ii’’22 (tem 8 cm de cota). A recta ii’’ corta o quadrado [AA’’BB’’CC’’DD’’]
nos pontos RR e SS – RR e SS são, respectivamente, os pontos em que o β1/3 corta as arestas [CC’’DD’’] e [BB’’CC’’] da face [AA’’BB’’CC’’DD’’] do cubo. Já te-
mos mais dois pontos da figura da secção. A recta aa é a recta de intersecção do plano α (o plano que contém a face [AAAA’’BB’’BB’’] do cubo) –
note que o plano α contém a aresta [BBBB’’]. O plano α é projectante frontal, pelo que aa22 tem determinação imediata – a recta aa, porque é uma
recta do β1/3, tem as suas projecções simétricas em relação ao eixo XX, o que nos permite desenhar imediatamente aa11. Note que a recta aa
passa nneecceessssaarriiaammeennttee pelo ponto QQ, pois QQ é um ponto do plano α (situa-se na aresta [AABB], que está contida no plano α) e é um ponto
do β1/3 (pois é o ponto em que o β1/3 corta a aresta [AABB]). A recta aa corta a aresta [BBBB’’] no ponto UU – UU é um outro ponto da secção. O plano δ
é o plano que contém a face [AAAA’’DD’’DD] do cubo (e contém a aresta [DDDD’’]) – o plano δ é um plano de topo. A recta bb é a recta de intersec-
ção do plano δ com o β1/3 – o plano δ é projectante frontal, pelo que bb22 tem determinação imediata e a recta bb, porque é uma recta do β1/3,
tem as suas projecções simétricas em relação ao eixo XX, o que nos permite desenhar imediatamente bb11. Note que a recta bb passa nneecceess--
ssaarriiaammeennttee pelo ponto PP, pois PP é um ponto do plano δ (situa-se na aresta [AADD], que está contida no plano δ) e é um ponto do β1/3 (pois é
o ponto em que o β1/3 corta a aresta [AADD]). A recta bb corta a aresta [DDDD’’] no ponto TT – TT é um outro ponto da secção. O β1/3 não corta mais
nenhuma face e/ou aresta do cubo – a figura da secção tem seis vértices e é, assim, o hexágono (irregular) [PPQQRRSSTTUU]. A partir das projec-
ções dos seis vértices da figura da secção, desenharam-se as suas projecções e as do ssóólliiddoo rreessuullttaannttee ddaa sseeccççããoo (a parte do cubo que
está compreendida entre o β1/3 e o Plano Horizontal de Projecção). Note que se representou, a traço forte, o ssóólliiddoo rreessuullttaannttee ddaa sseeccççããoo,
por ser esse o pretendido – a parte do sólido que é desprezada (a parte que se situa entre o β1/3 e o Plano Frontal de Projecção) represen-
tou-se a traço leve, pois trata-se de uma construção auxiliar para atingir o objectivo do exercício. Representaram-se os contornos aparen-
tes (horizontal e frontal) do novo sólido (o sólido resultante da secção), bem como as respectivas invisibilidades. Atendendo a que a ffiigguurraa
ddaa sseeccççããoo (a superfície da figura, ou seja, a área do corte) éé vviissíívveell aappeennaass eemm pprroojjeeccççããoo hhoorriizzoonnttaall, identificou-se a figura a tracejado
(em projecção horizontal). Note que o β1/3 é um plano em tensão, o que justifica o facto de a figura da secção não ser visível em ambas as
projecções.

201. 201
SOLUÇÕES
442.
Em primeiro lugar representou-se o prisma, pelas suas
projecções, e o plano secante, pelos seus traços, em
função dos dados. O plano ν é o plano horizontal (de ní-
vel) que contém a base superior do sólido e tem 5 cm (a
altura do prisma) de cota. Os vértices da base superior
foram determinados a partir das suas projecções fron-
tais – trata-se da intersecção de rectas não projectantes
(as rectas suporte das arestas laterais) com um plano
projectante frontal (o plano ν). A base superior do pris-
ma é o triângulo equilátero [AA’’BB’’CC’’], cujos lados são pa-
ralelos aos lados correspondentes do triângulo [AABBCC].
Uma vez que o plano secante nnããoo éé pprroojjeeccttaannttee, não é
possível, de forma imediata identificar as arestas do sóli-
do que são cortadas pelo plano secante, o que obriga a
procedimentos auxiliares e à análise, aresta a aresta,
das arestas que são cortadas pelo plano secante.
Assim, começou-se por averiguar se o plano secante
corta as bases do sólido. A recta de intersecção do pla-
no α (o plano secante) com o Plano Horizontal de Pro-
jecção (o plano que contém a base inferior do sólido) é
hhα – hhα é exterior à base [AABBCC], pelo que o plano α não
corta a base inferior do sólido. Optou-se por não deter-
minar graficamente a recta de intersecção do plano α (o
plano secante) com o plano ν (o plano que contém a
base superior do prisma), mas caso se tivesse determi-
nado constatar-se-ia que a recta seria exterior à base
[AA’’BB’’CC’’] – o plano α também não corta a base superior
do sólido. Assim, cortará as três arestas laterais, pelo que a figura da secção será um triângulo (terá três vértices). Em seguida, determinou-
se o ponto de intersecção da aresta lateral [AAAA’’] com o plano α – para tal recorreu-se ao método geral da intersecção de rectas com planos
(nem a aresta [AAAA’’] nem o plano α são projectantes). O plano δ, de topo, é o plano auxiliar que contém a aresta [AAAA’’] (δ é o plano projec-
tante frontal da aresta). A recta ii é a recta de intersecção do plano δ com o plano α – a recta ii está definida por dois pontos (os seus traços,
FF e HH). MM é o ponto de intersecção da recta ii com a aresta [AAAA’’] – MM é o ponto em que o plano secante (o plano α) corta a aresta [AAAA’’]. Já
temos um ponto da figura da secção – o ponto MM. Em seguida, determinou-se o ponto de intersecção da aresta lateral [CCCC’’] com o plano α,
pelo mesmo processo. O plano γ, de topo, é o plano auxiliar que contém a aresta [CCCC’’] (γ é o plano projectante frontal da aresta e é parale-
lo ao plano δ). Note que o plano γ está representado, apenas, pelo seu traço frontal, razão pela qual este se assinalou entre parêntesis. A
recta ii’’ é a recta de intersecção do plano γ com o plano α – a recta ii está definida por um ponto (o seu traço frontal, FF’’) e por uma direcção
(é paralela à recta ii). Recorde que qualquer plano corta dois planos paralelos segundo rectas paralelas – os planos δ e γ são paralelos, pelo
que as rectas ii e ii’’ (as rectas de intersecção do plano α com os planos δ e γ, respectivamente) são necessariamente paralelas. NN é o ponto
de intersecção da recta ii’’ com a aresta [CCCC’’] – NN é o ponto em que o plano α corta a aresta [CCCC’’]. Já temos outro ponto da figura da secção
– o ponto NN. Em seguida, determinou-se o ponto de intersecção da aresta lateral [BBBB’’] com o plano α, pelo mesmo processo. O plano θ, de
topo, é o plano auxiliar que contém a aresta [BBBB’’] (θ é o plano projectante frontal da aresta e é paralelo aos planos δ e γ). Note que o plano
θ está representado, apenas, pelo seu traço frontal, razão pela qual este se assinalou entre parêntesis. A recta ii’’’’ é a recta de intersecção
do plano θ com o plano α – a recta ii’’’’ está definida por um ponto (o seu traço frontal, FF’’’’) e por uma direcção (é paralela às rectas ii e ii’’). Re-
corde que qualquer plano corta dois planos paralelos segundo rectas paralelas – os planos δ, γ e θ são paralelos, pelo que as rectas ii, ii’’ e ii’’’’
(as rectas de intersecção do plano α com os planos δ, γ e θ, respectivamente) são necessariamente paralelas. OO é o ponto de intersecção da
recta ii’’’’ com a aresta [BBBB’’] – OO é o ponto em que o plano α corta a aresta [BBBB’’]. Já temos o terceiro ponto da figura da secção – o ponto OO.
A figura da secção é o triângulo [MMNNOO]. A partir dos três vértices da ffiigguurraa ddaa sseeccççããoo, desenharam-se as suas projecções. Sendo pedida a
ffiigguurraa ddaa sseeccççããoo e não o ssóólliiddoo rreessuullttaannttee ddaa sseeccççããoo (não houve desagregação do sólido), há que representar as invisibilidades existentes
na ffiigguurraa ddaa sseeccççããoo. O lado [NNOO] da figura da secção é invisível em projecção frontal, por estar contido numa face lateral invisível em pro-
jecção frontal – a face lateral [BBBB’’CC’’CC]. Os restantes lados da figura da secção são visíveis em projecção frontal, por estarem contidos em
faces visíveis (em projecção frontal). O lado [MMOO] da figura da secção é invisível em projecção horizontal, por estar contido numa face lateral
invisível em projecção horizontal – a face lateral [AAAA’’BB’’BB’’]. Os restantes lados da figura da secção são visíveis em projecção horizontal, por
estarem contidos em faces visíveis em projecção horizontal. Para determinar a V.G. da figura da secção, é necessário o recurso a um pro-
cesso geométrico auxiliar – a secção está contida no plano α, que não é paralelo a nenhum dos planos de projecção. Optou-se pelo rebati-
mento do plano α para o Plano Horizontal de Projecção (ver exercício 116633 e respectivo relatório) – a charneira foi hhα (recta ee). O ponto que
nos permitiu rebater ffα foi FF, o traço frontal da recta ii. HHrr ≡ HH11, pois HH é um ponto da charneira. A recta iirr fica definida por dois pontos FFrr e HHrr.
Conduzindo, por MM11, uma perpendicular à charneira, determinou-se MMrr sobre iirr. Para rebater o ponto NN rebateu-se a recta ii’’, à qual o ponto
pertence. Conduzindo, por FF’’11, uma perpendicular à charneira, determinou-se FF’’rr sobre ffαrr
– a recta ii’’rr está definida por um ponto (FF’’rr) e por
uma direcção (é paralela a iirr, pois o paralelismo entre rectas verifica-se no espaço, em projecções e em rebatimento). Conduzindo, por NN11,
uma perpendicular à charneira, determinou-se NNrr sobre ii’’rr. O processo repetiu-se para o ponto OO e a recta ii’’’’. Conduziu-se uma perpendicular
à charneira por FF’’’’11, determinando-se FF’’’’rr sobre ffαrr
– a recta ii’’’’rr passa por FF’’’’rr e é paralela a iirr e a ii’’rr. NNrr situa-se sobre ii’’’’rr , na perpendicular à
charneira que passa por NN11. A V.G. da figura da secção está no triângulo [MMrrNNrrOOrr].

202. 202
SOLUÇÕES
444.
Em primeiro lugar representou-se a pirâmide, pelas suas projecções, e o plano secante,
pelos seus traços, em função dos dados. O plano ν é o plano horizontal (de nível) que
contém a base da pirâmide. Para determinar o centro da circunferência circunscrita ao
hexágono da base, procedeu-se à construção de um triângulo equilátero a partir de AA e
BB – o terceiro vértice desse triângulo é OO, o centro da circunferência circunscrita ao hexá-
gono [AABBCCDDEEFF]. As projecções do sólido desenharam-se a traço leve, pois trata-se de
um traçado auxiliar para o objectivo do exercício (que é o ssóólliiddoo rreessuullttaannttee ddaa sseeccççããoo).
Uma vez que se trata de um plano projectante frontal, é possível concluir que o plano se-
cante não corta a base da pirâmide – o plano θ corta as seis arestas laterais da pirâmide,
pelo que a ffiigguurraa ddaa sseeccççããoo tem seis vértices (será um hexágono). Por outro lado, uma
vez que o plano secante não é paralelo ao plano da base, a figura da secção não será
um hexágono regular. O plano secante corta as arestas laterais [CCVV], [DDVV], [EEVV] e [FFVV]
nos pontos CC’’, DD’’, EE’’ e FF’’, respectivamente – estes pontos têm determinação imediata a
partir das suas projecções frontais, pois o plano secante é projectante frontal (trata-se da
intersecção de rectas não projectantes com um plano projectante). O plano secante cor-
ta as arestas laterais [AAVV] e [BBVV] (as arestas de perfil) nos pontos AA’’ e BB’’, respectivamen-
te – as projecções frontais destes pontos determinam-se imediatamente, o mesmo não
acontecendo com as suas projecções horizontais, pois as projecções de rectas de perfil
não verificam o Critério de reversibilidade. Os pontos AA’’ e BB’’ são, assim, os pontos «pro-
blemáticos» da secção. A determinação destes pontos processou-se com o recurso ao
mmééttooddoo ddooss ppllaannooss ppaarraalleellooss àà bbaassee. Conduziu-se um plano horizontal (de nível) ν1 –
um plano paralelo à base – pelos pontos AA’’ e BB’’. Em seguida, desenhou-se parte da sec-
ção produzida pelo plano ν1 na pirâmide, da qual AA’’ e BB’’ são dois vértices – o plano ν1
corta a aresta lateral [FFVV] no ponto MM e corta a aresta lateral [CCVV] no ponto NN. A figura da
secção produzida por ν1 na pirâmide será um hexágono regular, semelhante ao polígono
da base e com os seus lados paralelos aos lados correspondentes do hexágono
[AABBCCDDEEFF]. Assim, por MM11 conduziu-se uma paralela a [AA11FF11], obtendo AA’’11 sobre [AA11VV11]. Em seguida, por NN11 conduziu-se uma paralela a
[CC11BB11], obtendo BB’’11 sobre [BB11VV11]. Já temos as projecções horizontais de AA’’ e BB’’. A partir das projecções dos seis vértices da figura da sec-
ção (a secção produzida pelo plano θ na pirâmide), desenharam-se as suas projecções, representando-se as projecções do sólido pedido a
traço forte – o ssóólliiddoo rreessuullttaannttee ddaa sseeccççããoo (a parte compreendida entre o plano secante e a base). A parte desprezada da pirâmide (a parte
compreendida entre o plano secante e o vértice) representou-se a traço leve. Note que a superfície da figura da secção (a área do corte) é
visível em projecção horizontal, razão pela qual se identificou com tracejado. Sublinha-se que a determinação dos pontos AA’’ e BB’’ (os pontos
«problemáticos» da secção) se poderia ter processado com o recurso ao rebatimento do plano de perfil que contém as arestas [AAVV] e [BBVV].
443.
Em primeiro lugar representou-se a pirâmide, pelas suas projecções, e o plano secante, pelos
seus traços, em função dos dados. A circunferência circunscrita ao quadrado [AABBCCDD] tem cen-
tro em OO, que é o ponto médio do segmento [RRTT]. O plano ϕ é o plano frontal (de frente) que
contém a base da pirâmide. As projecções do sólido desenharam-se a traço leve, pois trata-se
de um traçado auxiliar para o objectivo do exercício (que é o ssóólliiddoo rreessuullttaannttee ddaa sseeccççããoo).
Uma vez que se trata de um plano projectante horizontal, é possível concluir que o plano secan-
te corta duas arestas da base (as arestas [RRSS] e [SSTT]) e três arestas laterais (as arestas [UUVV],
[RRVV] e [TTVV]) – a ffiigguurraa ddaa sseeccççããoo tem, assim, cinco vértices (é um pentágono irregular). O pla-
no secante corta as arestas [SSTT] e [RRSS] da base nos pontos AA e BB, respectivamente – estes
pontos têm determinação imediata a partir das suas projecções horizontais, pois o plano secan-
te é projectante horizontal (trata-se da intersecção de rectas não projectantes com um plano
projectante). O plano secante corta a aresta lateral [UUVV] no ponto EE – este ponto tem igualmente
determinação imediata a partir da sua projecção horizontal (e pelo mesmo motivo), pois o plano
secante é projectante horizontal. O plano α corta as arestas laterais [TTVV] e [RRVV] (as arestas de
perfil) nos pontos CC e DD, respectivamente – as projecções horizontais destes pontos determi-
nam-se imediatamente, o mesmo não acontecendo com as suas projecções frontais, pois as
projecções de rectas de perfil não verificam o Critério de reversibilidade. Os pontos CC e DD são,
assim, os pontos «problemáticos» da secção. A determinação destes pontos processou-se com
o recurso ao mmééttooddoo ddooss ppllaannooss ppaarraalleellooss àà bbaassee. Conduziu-se um plano frontal (de frente) ϕ1
– um plano paralelo à base – pelos pontos CC e DD. Em seguida, desenhou-se parte da secção
produzida pelo plano ϕ1 na pirâmide, da qual CC e DD são dois vértices – o plano ϕ1 corta a aresta
[UUVV] no ponto MM. A figura da secção produzida por ϕ1 na pirâmide será um quadrado, semelhante ao polígono da base e com os seus lados para-
lelos aos lados correspondentes do quadrado [AABBCCDD]. Assim, por MM22 conduziu-se uma paralela a [UU22TT22], obtendo CC22 sobre [TT22VV22]. Em seguida,
por MM22 conduziu-se uma paralela a [UU22RR22], obtendo DD22 sobre [RR22VV22]. Já temos as projecções frontais de CC e DD. A partir das projecções dos quatro
vértices da figura da secção (a secção produzida pelo plano α na pirâmide), desenharam-se as suas projecções, representando-se as projecções
do sólido pedido a traço forte – o ssóólliiddoo rreessuullttaannttee ddaa sseeccççããoo (a parte compreendida entre o plano secante e o vértice). A parte desprezada da
pirâmide (a parte compreendida entre o plano secante e a base) representou-se a traço leve. Note que a superfície da figura da secção (a área do
corte) é visível em projecção frontal, razão pela qual se identificou com tracejado. Sublinha-se que a determinação dos pontos CC e DD (os pontos
«problemáticos» da secção) se poderia ter processado com o recurso ao rebatimento do plano de perfil que contém as arestas [RRVV] e [TTVV].

203. 203
SOLUÇÕES
445.
Em primeiro lugar representou-se o triângulo equilátero [AABBCC], pelas suas projecções, e o plano secante, pelos seus traços, em função dos
dados. Os dados do exercício permitiram-nos concluir a construção da projecção horizontal do tetraedro – a projecção horizontal do vértice DD
(o quarto vértice do sólido) está coincidente com a projecção horizontal do centro do triângulo. Não é possível, de forma directa, determinar
a cota de DD, pois não se sabe a altura de um tetraedro – sabe-se, apenas, que todas as suas arestas têm o mesmo comprimento, sendo
esse o raciocínio que suporta a construção das projecções deste sólido. Assim, as arestas [AADD], [BBDD] e [CCDD] medem todas 6 cm (a medida
da aresta do tetraedro), mas nenhuma delas se projecta em V.G. – é necessário o recurso a um processo geométrico auxiliar. Optou-se pelo
rebatimento do plano π, o plano de perfil que contém a aresta [CCDD]. Rebateu-se o plano π para o Plano Frontal de Projecção (a charneira foi
ffπ – recta ee), obtendo CCrr e a referência de DDrr. Com o compasso, fazendo centro em CCrr e com 6 cm de raio, determinou-se DDrr – invertendo o
rebatimento, determinou-se a projecção frontal de DD e concluiu-se a construção da projecção frontal do sólido. Uma vez que o plano secante
nnããoo éé pprroojjeeccttaannttee, não é possível, de forma imediata identificar as arestas do sólido que são cortadas pelo plano secante, o que obriga a
procedimentos auxiliares e à análise, aresta a aresta, das arestas que são cortadas pelo plano secante. Assim, começou-se por averiguar se
o plano secante corta a face inferior do sólido (o triângulo [AABBCC]). A recta de intersecção do plano α (o plano secante) com o plano da face
[AABBCC] é hhα – hhα é exterior ao triângulo [AABBCC], pelo que o plano α não corta a face inferior do sólido. Em seguida determinou-se o ponto de
intersecção da aresta [CCDD] com o plano α – para tal recorreu-se ao método geral da intersecção de rectas com planos (nem a aresta [CCDD]
nem o plano α são projectantes). O plano π, de perfil, é o plano que contém a aresta [CCDD] (que é de perfil) – π é o plano projectante da
aresta [CCDD]. A recta ii é a recta de intersecção de π com α e está definida por dois pontos (os seus traços, HH e FF) – trata-se do caso geral da
intersecção entre planos. A recta ii é uma recta de perfil. A determinação do ponto em que a recta ii intersecta a aresta [CCDD] tem de se pro-
cessar com o recurso a um processo geométrico auxiliar – recorreu-se ao rebatimento previamente efectuado do plano de perfil, rebatendo
a recta ii. A recta iirr está definida por FFrr e HHrr. A recta iirr intersecta a aresta [CCrrDDrr] no ponto RRrr – invertendo o rebatimento, determinaram-se as
projecções de RR. Já temos um ponto da figura da secção. Note que, ao contrário das situações anteriores, não era conhecida nenhuma das
projecções deste ponto (que é um ponto «problemático» da secção, pois situa-se numa aresta de perfil) – assim, não seria possível o recur-
so ao método dos planos paralelos à base, pois não se saberia por onde conduzir o plano paralelo à base que nos iria permitir determinar o
ponto RR. Em seguida, determinou-se o ponto de intersecção da aresta [AADD] com o plano α – nem a aresta nem o plano são projectantes,
pelo que há que recorrer, de novo, ao método geral da intersecção entre rectas e planos. O plano γ, vertical, é o plano que contém a aresta
[AADD] – γ é o plano projectante horizontal da aresta [AADD]. A recta ii’’ é a recta de intersecção do plano γ com o plano α e está definida por
dois pontos (os seus traços, que não se identificaram para não sobrecarregar demasiado a resolução gráfica apresentada) – trata-se do
caso geral da intersecção entre planos. A recta ii intersecta a aresta [AADD] no ponto SS – já temos mais um ponto da figura da secção. Em se-
guida, determinou-se a recta de intersecção do plano que contém a face [AABBDD] (o plano AABBDD) com o plano secante – a recta ii’’’’. Para definir
a recta ii’’’’ necessitamos de dois pontos ou um ponto e uma direcção. O plano AABBDD é um plano passante, pelo que já temos um ponto co-
mum aos dois planos – o ponto de concorrência dos traços do plano α. O ponto SS é um outro ponto da recta ii’’’’, pois SS é um ponto que per-
tence ao plano α (pois pertence à recta ii’’, que pertence ao plano α) e pertence ao plano AACCDD (pois pertence à recta AADD, que pertence ao
plano AACCDD). Já temos dois pontos para definir a recta ii’’’’ – as projecções da recta ii’’’’ passam pelas projecções homónimas do ponto SS e são
concorrentes entre si no ponto de concorrência dos traços do plano α. A recta ii’’’’ intersecta a aresta [BBDD] no ponto TT – TT é um outro ponto
da figura da secção. Já temos três pontos da figura da secção – o plano secante não corta mais nenhuma aresta do sólido, pelo que a figu-
ra da secção é um triângulo. A partir das projecções dos três vértices da figura da secção (RR, SS e TT), desenharam-se as projecções da ffiigguu--
rraa ddaa sseeccççããoo (o triângulo [RRSSTT]). Sendo pedida a ffiigguurraa ddaa sseeccççããoo e não o ssóólliiddoo rreessuullttaannttee ddaa sseeccççããoo (não houve desagregação do
sólido), há que representar as invisibilidades existentes na ffiigguurraa ddaa sseeccççããoo. Os lados da figura da secção estão, todos, contidos nas faces
laterais do sólido que são visíveis em projecção horizontal – em projecção, a figura da secção é visível na sua totalidade. Já em projecção
frontal, o lado [SSTT] da figura da secção é invisível, por estar contido numa face invisível em projecção frontal (a face lateral [AABBVV]). Os res-
tantes lados da figura da secção são visíveis, em projecção frontal, por se situarem em faces visíveis (em projecção frontal).

204. 204
SOLUÇÕES
447.
Um plano produz uma secção ttrriiaanngguullaarr num cone sempre que contiver o vértice do cone e for secante à sua base. Nestes casos, o plano
corta a superfície lateral do cone segundo duas geratrizes, as quais contêm dois lados do triângulo.
448.
Se o plano produz uma secção hhiippeerrbbóólliiccaa no cone, sabe-se que o plano é paralelo a duas geratrizes da superfície e não contém o vértice
da superfície (caso contivesse o vértice, a secção seria triangular).
449.
Em primeiro lugar, se a secção é eellííppttiiccaa, sabe-se que o plano secante é oblíquo ao plano da base, não contendo o vértice do cone e não
sendo paralelo a qualquer das geratrizes da superfície. A secção será um sseeggmmeennttoo ddaa eelliippssee se o plano secante, verificando as condições
anteriores, cortar a base do sólido.
446.
Em primeiro lugar representou-se a pirâmide, pelas suas projecções, e o
plano ϕ, pelo seu traço horizontal, em função dos dados. O ponto AA, da
base, porque tem afastamento nulo, é um ponto de ffγ. O ponto BB, porque
tem cota nula, é necessariamente um ponto de hhγ. É dado que o lado
[AABB] tem as suas projecções paralelas entre si (está contido numa recta
paralela ao β2/4) – uma vez que [AA11BB11] está contido em hhγ, sabe-se que
[AA22BB22] tem de ser paralelo a hhγ. Uma vez que o plano γ (o plano que con-
tém a base da pirâmide) não é paralelo a nenhum dos planos de projec-
ção, a determinação das projecções do quadrado [AABBCCDD] processou-se
com o recurso a um processo geométrico auxiliar – o rebatimento do pla-
no γ para o Plano Frontal de Projecção (a charneira foi ffγ). O quadrado foi
construído previamente em V.G., em rebatimento – a partir de AArr e BBrr,
construiu-se o quadrado em V.G., em rebatimento. Invertendo o rebati-
mento, determinaram-se as projecções do quadrado da base da pirâmi-
de. Sabendo que a aresta lateral [AAVV] é de perfil e que a aresta lateral
[DDVV] é horizontal (de nível), sabe-se que VV tem a abcissa de AA e a cota de
DD, o que nos permitiu determinar VV22. A aresta lateral [DDVV] mede 8 cm, e
atendendo a que é paralela ao Plano Horizontal de Projecção (é horizon-
tal), projecta-se em V.G. no Plano Horizontal de Projecção – com o com-
passo, fazendo centro em DD11 e com 8 cm de raio (o comprimento da
aresta), determinou-se VV11 e conclui-se a construção das projecções da pi-
râmide. Uma vez que o plano secante é um plano projectante horizontal,
é possível concluir que corta a base da pirâmide (corta duas arestas da
base) e três das suas arestas laterais – o plano ϕ corta cinco arestas da
pirâmide, pelo que a ffiigguurraa ddaa sseeccççããoo tem cinco vértices (será um pentá-
gono irregular). O plano secante corta as arestas [CCDD] e [BBCC] da base
nos pontos MM e NN, respectivamente – estes pontos têm determinação
imediata a partir das suas projecções horizontais, pois o plano secante é
projectante horizontal (trata-se da intersecção de rectas não projectantes com um plano projectante). O plano secante corta as arestas laterais
[DDVV] e [BBVV] nos pontos PP e OO, respectivamente – estes pontos têm também determinação imediata a partir das suas projecções horizontais,
pois o plano secante é projectante horizontal (trata-se mais uma vez da intersecção de rectas não projectantes com um plano projectante). Por
fim, o plano secante corta a aresta lateral [AAVV] (a aresta de perfil) no ponto QQ – a projecção horizontal deste ponto determina-se imediatamente,
o mesmo não acontecendo com a sua projecção frontal, pois as projecções de rectas de perfil não verificam o Critério de Reversibilidade. O
ponto QQ é, assim, o ponto «problemático» da secção. A determinação deste ponto processou-se com o recurso ao mmééttooddoo ddooss ppllaannooss ppaarraa--
lleellooss àà bbaassee. Conduziu-se um plano vertical α – um plano paralelo à base – pelo ponto QQ. Em seguida, desenhou-se parte da secção produzi-
da pelo plano α na pirâmide, da qual QQ é um vértice – o plano α corta a aresta lateral [BBVV] no ponto KK. A figura da secção produzida por α na
pirâmide será um quadrado, semelhante ao polígono da base e com os seus lados paralelos aos lados correspondentes do quadrado [AABBCCDD].
Assim, por KK22 conduziu-se uma paralela a [AA22BB22], obtendo QQ22 sobre [AA22VV22]. A partir das projecções dos cinco vértices da figura da secção (MM,
NN, OO, PP e QQ), desenharam-se as projecções da ffiigguurraa ddaa sseeccççããoo (o pentágono [MMNNOOPPQQ]). Em projecção horizontal, a figura reduz-se a um
segmento de recta, pois o plano secante (o plano ϕ) é projectante horizontal. Já em projecção frontal, sendo pedida a ffiigguurraa ddaa sseeccççããoo e não
o ssóólliiddoo rreessuullttaannttee ddaa sseeccççããoo (não houve desagregação do sólido), há que representar as invisibilidades existentes na ffiigguurraa ddaa sseeccççããoo. Os
lados [PPMM], [NNOO] e [OOQQ] estão contidos em faces visíveis (em projecção frontal) da pirâmide (as faces laterais [CCDDVV], [BBCCVV] e [AABBVV], respecti-
vamente), pelo que são visíveis. Já o lado [PPQQ] da figura, porque está contido numa face lateral invisível (em projecção frontal) da pirâmide (a
face lateral [AADDVV]), é invisível em projecção frontal. Da mesma forma, o lado [MMNN] da figura da secção, porque está contido na base da pirâmi-
de (que é invisível em projecção frontal), é igualmente invisível. Recorde que, em termos de traçado, o sólido se representa a traço médio (é um
dado) e o pretendido (a ffiigguurraa ddaa sseeccççããoo) se representa a traço forte.

205. 205
SOLUÇÕES
450.
Se o plano α produz uma secção ppaarraabbóólliiccaa numa superfície cónica, sabe-se que o plano α é paralelo a uummaa úúnniiccaa ggeerraattrriizz da superfície
(e não contém o vértice da superfície, pois nesse caso a secção seria uma única recta – a própria geratriz à qual o plano α é paralelo). Por
outro lado, se o plano δ produz uma secção hhiippeerrbbóólliiccaa nessa superfície cónica, sabe-se que o plano δ é paralelo a dduuaass ggeerraattrriizzeess da su-
perfície (e não contém o vértice da superfície, pois nesse caso a secção seria triangular).
451.
Em primeiro lugar representou-se o cone, pelas suas projecções, e o
plano secante, pelos seus traços, em função dos dados. O plano ϕ é
o plano frontal (de frente) que contém a base do cone. Em seguida,
executaram-se sequencialmente as três etapas que nos permitem
identificar o tipo de secção que o plano θ produz no cone. 11. Condu-
ziu-se, pelo vértice do cone, um plano α, paralelo a θ. Uma vez que o
plano θ é um plano de topo (projectante frontal), o plano α será igual-
mente um plano de topo (projectante frontal), com os seus traços pa-
ralelos aos traços homónimos do plano θ. Sendo um plano
projectante frontal, para que o plano α contenha o vértice VV do cone,
basta que ffα passe por VV22. 22.. Determinou-se a recta de intersecção
do plano α com o plano da base do cone (o plano ϕ). O plano ϕ é
projectante horizontal, pelo que se tem imediatamente (hhϕ) ≡ ii11. O pla-
no α é projectante frontal, pelo que se tem imediatamente ffα ≡ ii22. A
recta ii é a recta de intersecção dos dois planos (é uma recta frontal).
33.. Analisou-se a posição da recta ii em relação à base do cone – a
recta ii é secante à base do cone, pelo que a secção que o plano θ
produz no cone é uma hhiippéérrbboollee (ou, mais correctamente, um ramo
de uma hipérbole, uma vez que se trata de um cone que está limitado
lateralmente por uummaa úúnniiccaa ffoollhhaa de uma superfície cónica).
Em primeiro lugar representou-se o cone, pelas suas projecções, e o plano secante,
pelos seus traços, em função dos dados. O plano α tem os seus traços coincidentes,
pois é ortogonal ao β2/4. O plano ν é o plano horizontal (de nível) que contém a base
do cone. É dado que as geratrizes do cone medem 6 cm – as únicas geratrizes que
se projectam em V.G. são as geratrizes frontais (de frente) do cone que, na presente
situação, são as geratrizes do contorno aparente frontal. Considerou-se a geratriz es-
querda do contorno aparente frontal – a geratriz [AAVV]. Com o compasso, fazendo
centro em AA22 e com 6 cm de raio (o comprimento das geratrizes), determinou-se VV22,
na linha de chamada de VV11. Em seguida executaram-se sequencialmente as três eta-
pas que nos permitem identificar o tipo de secção que o plano α produz no cone. 11.
Conduziu-se, pelo vértice do cone, um plano α1, paralelo a α. Para tal, e uma vez que
o plano α nnããoo éé uumm ppllaannoo pprroojjeeccttaannttee (o plano α1 também não será projectante), é
necessário conduzir, por VV, uma recta do plano α1, para que VV pertença ao plano
(condição para que um ponto pertença a um plano). Recorreu-se a uma recta hh, hori-
zontal (de nível), paralela às rectas horizontais (de nível) do plano α (as rectas hori-
zontais de α1 são necessariamente paralelas às rectas horizontais de α).
Determinou-se FF, o traço frontal da recta hh, pelo qual se conduziu ffα11
, paralelo a ffα –
hhα11
é paralelo a hh (e a hhα) e é concorrente com ffα11
no eixo XX. O plano α1, definido pe-
los seus traços (que também estão coincidentes), é paralelo a α e contém VV. 22.. De-
terminou-se a recta de intersecção do plano α1 com o plano da base do cone (o
plano horizontal ν) – recta ii. A recta ii é uma recta horizontal (de nível) do plano α1 e
está definida por um ponto (o seu traço frontal, FF’’) e por uma direcção (a direcção
das rectas horizontais de α1). 33.. Analisou-se a posição da recta ii em relação à base
do cone – ii é tangente à base do cone, pelo que a secção que o plano α produz no
cone é uma ppaarráábboollaa.
452.

206. 206
SOLUÇÕES
453.
Em primeiro lugar representou-se o cone, pelas suas projecções, e o plano
secante, pelos seus traços, em função dos dados. O plano ϕ é o plano
frontal (de frente) que contém a base do cone. Em seguida, executaram-
-se sequencialmente as três etapas que nos permitem identificar o tipo de
secção que o plano α produz no cone. 11. Conduziu-se, pelo vértice do
cone, um plano σ, paralelo a ρ. Para tal, e uma vez que o plano ρ nnããoo éé
uumm ppllaannoo pprroojjeeccttaannttee (o plano σ também não será projectante), é neces-
sário conduzir, por VV, uma recta do plano σ, para que VV pertença ao plano
(condição para que um ponto pertença a um plano). Recorreu-se a uma
recta ss, oblíqua, paralela a uma recta rr, obliqua, do plano ρ. Determina-
ram-se os traços da recta ss nos planos de projecção, pelos quais se con-
duziram os traços homónimos do plano σ. O plano σ, definido pelos seus
traços, é paralelo a ρ e contém VV. 22.. Determinou-se a recta de intersecção
do plano σ com o plano da base do cone (o plano frontal ϕ) – recta ii.
A recta ii é necessariamente uma recta fronto-horizontal (a recta de inter-
secção entre um plano de rampa e um plano frontal é fronto-horizontal) –
a recta ii está definida pela sua direcção e por um ponto (o ponto II, que é
o ponto de intersecção da recta ss com o plano ϕ). 33.. Analisou-se a posi-
ção da recta ii em relação à base do cone – ii é exterior à base do cone,
pelo que a secção que o plano ρ produz no cone é uma eelliippssee.
Em primeiro lugar representou-se o cone, pelas suas projec-
ções, e o plano secante, pelos seus traços, em função dos
dados. O plano θ é ortogonal ao β1/3, pelo que os seus traços
são simétricos em relação ao eixo XX. O plano ϕ é o plano
frontal (de frente) que contém a base do cone. A partir da
cota do vértice do cone, é possível identificar as geratrizes
horizontais (de nível) do sólido. A recta hh é a recta suporte da
geratriz [AAVV], que é a geratriz que faz o ângulo de 60o (a.e.)
com o Plano Frontal de Projecção (a outra geratriz horizontal,
que não se assinalou, faz necessariamente um ângulo de
abertura para a direita). Em seguida, executaram-se sequen-
cialmente as três etapas que nos permitem identificar o tipo
de secção que o plano θ produz no cone. 11. Conduziu-se,
pelo vértice do cone, um plano α, paralelo a θ. Para tal, e
uma vez que o plano θ nnããoo éé uumm ppllaannoo pprroojjeeccttaannttee (o plano
α também não será projectante), é necessário conduzir, por
VV, uma recta do plano α, para que VV pertença ao plano (con-
dição para que um ponto pertença a um plano). Recorreu-se
a uma recta horizontal (de nível), paralela às rectas horizon-
tais (de nível) do plano θ (as rectas horizontais de α são ne-
cessariamente paralelas às rectas horizontais de θ). A recta
horizontal (de nível) é a própria recta hh. Determinou-se FF, o
traço frontal da recta hh, pelo qual se conduziu ffα, paralelo a
ffθ – hhα é paralelo a hh (e a hhθ) e é concorrente com ffα no eixo XX.
O plano α, definido pelos seus traços (que também estão
coincidentes), é paralelo a θ e contém VV. 22.. Determinou-se a
recta de intersecção do plano α com o plano da base do
cone (o plano frontal ϕ) – recta ii. A recta ii é uma recta frontal
(de frente) do plano α e está definida por um ponto (o seu
traço horizontal, HH) e por uma direcção (a direcção das rec-
tas frontais de α). 33.. Analisou-se a posição da recta ii em rela-
ção à base do cone – ii é tangente à base do cone, pelo que
a secção que o plano θ produz no cone é uma ppaarráábboollaa.
454.

207. 207
SOLUÇÕES
455.
Em primeiro lugar representou-se o cone, pelas suas projecções, e o plano
secante, pelos seus traços, em função dos dados. Atendendo a que o plano θ
é projectante frontal, o ponto PP, porque pertence ao plano θ (é um ponto da
secção que o plano θ produz no cone) tem de ter a sua projecção frontal so-
bre o traço frontal do plano – PP22 é o ponto de ffθ que tem 2,5 cm de cota e é vi-
sível em ambas as projecções. Em seguida, desenhou-se a projecção frontal
da geratriz gg, a geratriz do cone que contém o ponto PP, passando por PP22 – TT
é o ponto da geratriz gg que pertence à base do cone. A projecção horizontal
da geratriz, gg11, fica definida por VV11 e por TT11 – PP11 situa-se sobre gg11. Note que o
ponto TT é o traço horizontal da geratriz, pois a base do cone situa-se no Plano
Horizontal de Projecção. A rreeccttaa ttaannggeennttee aa uumm ppoonnttoo ddee uummaa sseeccççããoo é a
recta de intersecção do plano secante com o plano tangente à superfície nesse
ponto. Assim, há que determinar os traços do plano tangente à superfície do
cone no ponto PP (ver exercício 336699 e respectivo relatório). A geratriz gg, que
contém o ponto PP, é a geratriz de contacto (ou de tangência) – é a geratriz ao
longo da qual o plano α (o plano tangente) é tangente à superfície lateral do
cone. A geratriz gg é, já, uma recta tangente à superfície lateral do cone no
ponto PP – já temos uma recta para definir o plano α. Necessitamos de outra
recta. Essa recta pode ser, imediatamente, o traço horizontal do plano α (hhα),
que é tangente à base do cone no ponto TT. O plano definido pela geratriz gg e
por hhα é o plano tangente à superfície no ponto PP. O traço frontal da geratriz gg
situa-se fora dos limites do desenho, pelo que se recorreu a uma recta auxiliar
do plano α – uma recta horizontal (de nível) hh, paralela a hhα e passando pelo
vértice do cone (hh é concorrente com a geratriz gg em VV). FF é o traço frontal da
recta hh. O traço frontal do plano α (o plano tangente à superfície no ponto PP),
ffα é concorrente com hhα no eixo XX e passa por FF22. O plano α, definido pelos
seus traços, é o plano tangente à superfície no ponto PP. A recta de intersecção do plano α (o plano tangente à superfície no ponto PP) com o
plano θ (o plano secante) é a recta tangente à secção no ponto PP. Já temos um ponto da recta – o ponto PP (o ponto PP é, já, um ponto que
pertence aos dois planos). Determinou-se HH’’, o ponto de concorrência dos traços horizontais dos dois planos – HH’’ é o traço horizontal da
recta de intersecção dos dois planos (a recta tangente à secção no ponto PP). A recta tt é a recta tangente à secção no ponto PP – a recta tt
está definida por dois pontos (PP e HH’’, o seu traço horizontal). Note que a recta tt e a geratriz gg são concorrentes no ponto PP.
456.
Em primeiro lugar representou-se o cone, pelas suas projecções, e o
plano secante, pelos seus traços, em função dos dados. O plano ρ tem
os seus traços simétricos em relação ao eixo XX, pois é ortogonal ao β1/3.
O plano ϕ é o plano frontal (de frente) que contém a base do cone. Os
dados permitiram-nos desenhar as projecções da geratriz gg – gg está defi-
nida por dois pontos (VV, o vértice do cone, e TT, o ponto da geratriz que se
situa na base do cone). O ponto PP, da secção, porque pertence à geratriz
gg, tem de ser o ponto de intersecção da geratriz gg com o plano ρ (o pla-
no secante) – é o ponto em que o plano ρ corta a geratriz gg. Uma vez que
se trata da intersecção entre uma recta não projectante (a geratriz gg) e
um plano não projectante (o plano ρ), recorreu-se ao método geral da in-
tersecção entre rectas e planos. O plano α é o plano auxiliar a que se re-
correu – é o plano projectante frontal da geratriz gg. A recta ii, definida
pelos seus traços (FF e HH), é a recta de intersecção do plano α com o pla-
no ρ (trata-se do caso geral da intersecção entre rectas e planos). A recta
ii intersecta a geratriz gg no ponto PP – PP é o ponto em que o plano ρ corta
a geratriz gg. A rreeccttaa ttaannggeennttee aa uumm ppoonnttoo ddee uummaa sseeccççããoo é a recta de
intersecção do plano secante com o plano tangente à superfície nesse
ponto. Assim, há que determinar os traços do plano tangente à superfície
do cone no ponto PP (ver exercício 336699 e respectivo relatório). A geratriz gg,
que contém o ponto PP, é a geratriz de contacto (ou de tangência) – é a
geratriz ao longo da qual o plano θ (o plano tangente) é tangente à su-
perfície lateral do cone. A geratriz gg é, já, uma recta tangente à superfície
lateral do cone no ponto PP – já temos uma recta para definir o plano θ.
Necessitamos de outra recta. Essa recta pode ser a recta tt’’, que é uma
recta tangente à base do cone no ponto TT. A recta tt’’ é a recta de intersec-
ção do plano tangente (o plano θ) com o plano da base do cone (o plano ϕ). A recta tt’’ é uma recta frontal (de frente) do plano θ. O plano defini-
do pela geratriz gg e pela recta tt’’ é o plano tangente à superfície no ponto PP. Determinou-se o traço frontal da geratriz gg – FF’’. O traço frontal do
plano θ, ffθ, passa por FF’’22 e é paralelo à recta tt’’ (rectas frontais de um plano são paralelas entre si e paralelas ao traço frontal do plano, que é
(Continua na página seguinte)

208. 208
SOLUÇÕES
458.
Em primeiro lugar representou-se o cone, pelas suas projecções, e o plano secante, pelos
seus traços, em função dos dados. O plano ϕ é o plano frontal (de frente) que contém a
base do cone. O plano θ (o plano secante) contém o vértice do cone, pelo que a secção
produzida pelo plano θ no sólido é um ttrriiâânngguulloo, de que VV é um vértice. A recta ii é a recta
de intersecção do plano θ (o plano secante) com o plano ϕ (o plano da base). A recta ii
corta a base do cone nos pontos AA e BB – a figura da secção produzida pelo plano θ no
cone é o triângulo [AABBVV]. A partir das projecções dos seus três vértices, desenharam-se
as projecções da ffiigguurraa ddaa sseeccççããoo. Em projecção frontal, a figura reduz-se a um segmen-
to de recta, pois o plano secante (o plano θ) é projectante frontal. Já em projecção hori-
zontal, sendo pedida a ffiigguurraa ddaa sseeccççããoo e não o ssóólliiddoo rreessuullttaannttee ddaa sseeccççããoo (não
houve desagregação do sólido), há que representar as invisibilidades existentes na ffiigguurraa
ddaa sseeccççããoo. O lado [BBVV] da figura, que se situa na parte invisível da superfície lateral do
cone, é invisível em projecção horizontal. O lado [AAVV] da figura da secção é visível, por se
situar na parte visível da superfície lateral do cone. Já o lado [AABB], da figura da secção,
uma vez que se situa na base (que é projectante horizontal) não admite a representação
de qualquer invisibilidade. Note que, em termos de traçado, o sólido se representou a tra-
ço médio (é um dado) e o pretendido (a ffiigguurraa ddaa sseeccççããoo) se representou a traço forte.
uma recta frontal do plano com afastamento nulo). Determinou-se o traço horizontal da recta tt’’ – HH’’. O traço horizontal do plano θ, hhθ, passa por
HH’’11 e é concorrente com ffθ no eixo XX. O plano θ, definido pelos seus traços, é o plano tangente à superfície no ponto PP. A recta de intersecção
do plano θ (o plano tangente à superfície no ponto PP) com o plano ρ (o plano secante) é a recta tangente à secção no ponto PP. Já temos um
ponto da recta – o ponto PP (o ponto PP é, já, um ponto que pertence aos dois planos). Determinaram-se HH’’’’ e FF’’’’, os traços da recta de intersec-
ção dos planos θ e ρ (trata-se do caso geral da intersecção entre planos), mas bastaria determinar apenas um deles. A recta tt é a recta tangente
à secção no ponto PP – a recta tt está definida por dois pontos (os seus traços) e passa nneecceessssaarriiaammeennttee pelo ponto PP (ou seja, está definida
por três dos seus pontos). Note que a recta tt e a geratriz gg são concorrentes no ponto PP.
457.
Em primeiro lugar representou-se o cone, pelas suas projecções, e o plano secante,
pelo seu traço frontal, em função dos dados. O plano ν é o plano horizontal (de ní-
vel) que contém a base do cone. O plano ν1 é o plano secante. As projecções do só-
lido desenharam-se a traço leve, pois trata-se de uma construção auxiliar para o
objectivo do exercício (que é o ssóólliiddoo rreessuullttaannttee ddaa sseeccççããoo). O plano secante é pa-
ralelo ao plano da base e não contém o vértice do cone, pelo que a secção produzi-
da pelo plano ν1 no cone é um ccíírrccuulloo. O centro do círculo é o ponto QQ, que é o
ponto em que o plano ν1 (o plano secante) corta o eixo do sólido. Para determinar o
raio do círculo, determinou-se o ponto em que o plano ν1 corta a geratriz mais à di-
reita do contorno aparente frontal – a geratriz [AAVV]. Note que foi necessário desenhar
a projecção horizontal da geratriz, pois esta não foi necessária à construção da pro-
jecção horizontal do sólido. O ponto MM é o ponto em que o plano ν1 corta a geratriz
[AAVV]. A figura da secção produzida pelo plano ν1 no cone é o círculo com centro em
QQ e raio QQෆMMෆ. Note que o círculo é nneecceessssaarriiaammeennttee tangente às duas geratrizes do
contorno aparente horizontal. Em seguida, desenharam-se as projecções do ssóólliiddoo
rreessuullttaannttee ddaa sseeccççããoo – o tronco do cone que está compreendido entre a figura da
secção e a base. A parte desprezada do cone (a parte compreendida entre o plano
secante e o vértice) representou-se a traço leve. Note que a superfície da figura da
secção (a área do corte) é visível em projecção horizontal, razão pela qual se identifi-
cou com tracejado.

209. 209
SOLUÇÕES
459.
Em primeiro lugar representou-se o cone, pelas suas projecções, e o plano secante,
pelos seus traços, em função dos dados. A recta rr é a recta suporte do eixo do sólido.
Uma vez que a geratriz mais à esquerda é de perfil (que é imediatamente, uma gera-
triz do contorno aparente horizontal), e atendendo a que a recta rr faz, em projecção
horizontal, um ângulo de 45o (a.e.), a outra geratriz do contorno aparente horizontal é
frontal (de frente) e contém o ponto de maior afastamento da base do cone. A projec-
ção frontal da recta rr