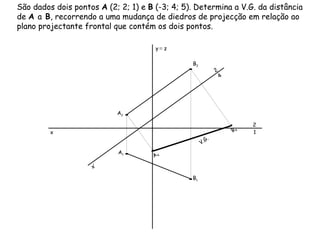
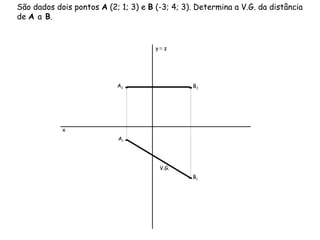
Este documento discute vários métodos para determinar a distância entre dois pontos em geometria descritiva, incluindo rebatimento de segmentos de reta para diferentes planos de projeção e mudança de diedros de projeção. Exemplos ilustram como aplicar esses métodos para calcular distâncias entre pontos especificados em coordenadas tridimensionais.

1. GEOMETRIA DESCRITIVA A 11.º Ano Problemas Métricos Distância entre Dois Pontos © antónio de campos, 2009

2. GENERALIDADES Os problemas métricos são situações que envolvem a determinação de alguma grandeza mensurável (distância ou ângulo). Por norma, trata-se da determinação da verdadeira grandeza . Para resolver estes problemas métricos é necessário a utilização dos métodos geométricos auxiliares, em particular o rebatimento e a mudança de diedro de projecção . Quando se refere à distância , entende-se que se trata da menor distância entre dois elementos.

3. Distância entre dois pontos, via rebatimento do Segmento de Recta para o Plano Frontal de Projecção Pretende-se a distância entre o ponto A e o ponto B do segmento de recta oblíquo [ AB ]. O processo do rebatimento é o mais rápido, havendo quatro variações. α f α h α A 2 A 1 B 1 B 2 B A h α f α A 2 B 2 A 1 B 1 ≡ e 2 ≡ f αr ≡ h αr (e 1 ) ≡ h αr ≡ e 2 ≡ f αr (e 1 ) A r B r V.G. A r B r V.G. x xz xy x

4. Distância entre dois pontos, via rebatimento do Segmento de Recta para o Plano Horizontal de Projecção Pretende-se a distância entre o ponto A e o ponto B do segmento de recta oblíquo [ AB ]. α f α h α A 2 A 1 B 1 B 2 B A h α f α A 2 B 2 A 1 B 1 ≡ e 1 ≡ h αr ≡ e 1 ≡ h αr A r B r V.G. A r B r V.G. f αr f αr ≡ e 2 ≡ e 2 x xz xy x

5. Distância entre dois pontos, via rebatimento do Segmento de Recta para o Plano Horizontal de Projecção Pretende-se a distância entre o ponto A e o ponto B do segmento de recta oblíquo [ AB ], via uma recta e (uma recta do plano) como charneira, rebatendo o plano projectante horizontal do segmento de recta. α f α h α A 2 A 1 B 1 B 2 B A h α f α A 2 B 2 A 1 B 1 ≡ e 1 ≡ e 1 A r B r V.G. A r B r V.G. ≡ e 2 ≡ e 2 x xz xy x

6. Distância entre dois pontos, via rebatimento do Segmento de Recta para um Plano Horizontal Pretende-se a distância entre o ponto A e o ponto B do segmento de recta oblíquo [ AB ], via uma recta e (uma recta do plano) como charneira, rebatendo o plano projectante horizontal do segmento de recta para um plano horizontal que passa por um dos pontos. α f α h α A 2 A 1 ≡ O 1 B 1 B 2 B ≡ B r A A 2 B 2 A 1 ≡ O 1 ≡ O r B 1 ≡ B r e 1 e A r V.G. A r V.G. ≡ e 2 υ ≡ e 1 (f υ ) ≡ e 2 (f υ ) ≡ e 2 O 2 O ≡ O r O 2 x xz xy x

7. São dados dois pontos A (2; 1; 3) e B (-3; 4; 3). Determina a V.G. da distância de A a B . V.G. x y ≡ z A 1 A 2 B 1 B 2

8. São dados dois pontos M (3; 1; 5) e N (-1; 4; 2). Determina a V.G. da distância de M a N , pelo o rebatimento do plano projectante horizontal do segmento [ MN ] para o plano horizontal que contém o ponto N . (f υ ) ≡ e 2 e 1 V.G. ≡ N r x y ≡ z M 1 M 2 N 1 N 2 M r

9. São dados dois pontos M (3; 1; 5) e N (-1; 4; 2). Determina a V.G. da distância de M a N , pelo o rebatimento do plano projectante frontal do segmento [ MN ] para o plano frontal que contém o ponto N . (h φ ) ≡ e 1 e 2 V.G. ≡ N r x y ≡ z M 1 M 2 N 1 N 2 M r

10. São dados dois pontos A (2; 2; 1) e B (-3; 4; 5). Determina a V.G. da distância de A a B , recorrendo a uma mudança de diedros de projecção em relação ao plano projectante frontal que contém os dois pontos. x’ V.G. y ≡ z A 1 A 2 B 1 B 2 x 2 1 2 4 A 4 B 4