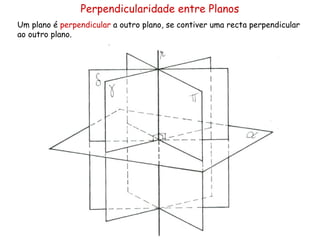
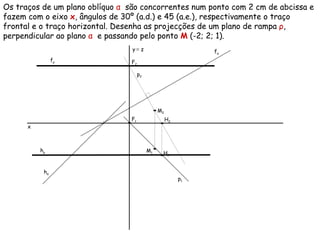
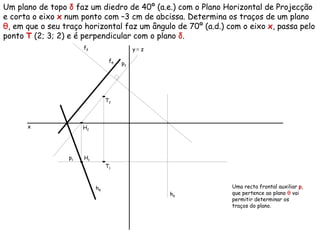
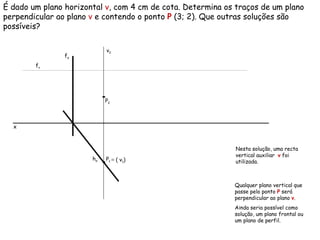
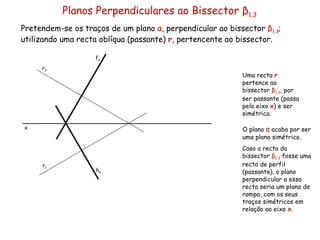
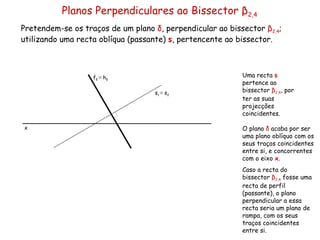
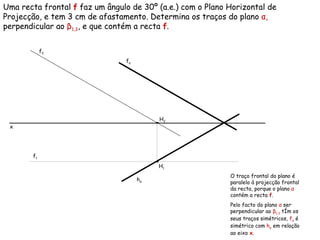
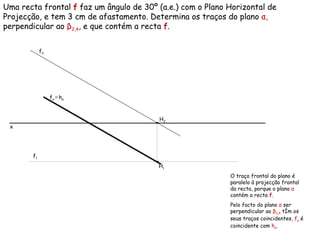
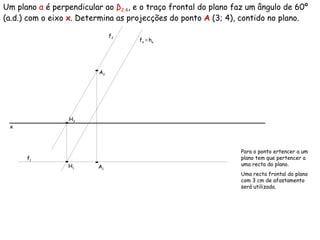
Este documento descreve os conceitos de perpendicularidade entre planos em geometria descritiva. Explica que um plano é perpendicular a outro se contiver uma reta perpendicular ao outro plano. Detalha como determinar os traços de planos perpendiculares a outros planos, bissectores e como encontrar as projeções de pontos contidos em planos perpendiculares.

1. GEOMETRIA DESCRITIVA A 11.º Ano Perpendicularidade entre Planos © antónio de campos, 2009

2. Perpendicularidade entre Planos Um plano é perpendicular a outro plano, se contiver uma recta perpendicular ao outro plano.

3. Planos Perpendiculares - Geral Pretendem-se os traços de um plano δ , perpendicular ao plano α e passando pelo ponto P . x f α p 1 P 1 P 2 p 2 Uma recta p que pertence ao plano δ é perpendicular ao plano α . h α f δ h δ Qualquer outro plano que contenha a recta p é perpendicular ao plano α . F 1 F 2 H 1 H 2

4. Os traços de um plano oblíquo α são concorrentes num ponto com 2 cm de abcissa e fazem com o eixo x , ângulos de 30º (a.d.) e 45 (a.e.), respectivamente o traço frontal e o traço horizontal. Desenha as projecções de um plano de rampa ρ , perpendicular ao plano α e passando pelo ponto M (-2; 2; 1). f α h α p 2 p 1 f ρ h ρ x y ≡ z M 1 M 2 H 1 H 2 F 2 F 1

5. Um plano de topo δ faz um diedro de 40º (a.e.) com o Plano Horizontal de Projecção e corta o eixo x num ponto com –3 cm de abcissa. Determina os traços de um plano θ , em que o seu traço horizontal faz um ângulo de 70º (a.d.) com o eixo x , passa pelo ponto T (2; 3; 2) e é perpendicular com o plano δ . f δ h δ p 2 p 1 Uma recta frontal auxiliar p , que pertence ao plano θ vai permitir determinar os traços do plano. h θ f θ x y ≡ z T 1 T 2 H 1 H 2

6. É dado um plano horizontal ν , com 4 cm de cota. Determina os traços de um plano perpendicular ao plano ν e contendo o ponto P (3; 2). Que outras soluções são possíveis? f ν Nesta solução, uma recta vertical auxiliar v foi utilizada. v 2 ≡ ( v 1 ) f α h α Qualquer plano vertical que passe pelo ponto P será perpendicular ao plano v . Ainda seria possível como solução, um plano frontal ou um plano de perfil. x P 1 P 2

7. Planos Perpendiculares aos Planos Bissectores A mesma regra geral é aplicada: de que um plano é perpendicular a outro plano, se contiver uma recta perpendicular ao outro plano. Com os bissectores é necessário ter em conta as características das rectas contidas nos bissectores. Os planos bissectores são planos de rampa (passante), e portanto contém rectas fronto-horizontais, rectas oblíquas (passantes) e rectas de perfil (passantes). No caso de rectas fronto-hrizontais, será sempre um plano de perfil que será perpendicular à recta. Assim os planos de perfil serão sempre perpendiculares aos bissectores.

8. Planos Perpendiculares ao Bissector β 1,3 Pretendem-se os traços de um plano α , perpendicular ao bissector β 1,3 ; utilizando uma recta oblíqua (passante) r , pertencente ao bissector. f α Uma recta r pertence ao bissector β 1,3 , por ser passante (passa pelo eixo x ) e ser simétrica. h α r 2 r 1 O plano α acaba por ser uma plano simétrico. Caso a recta do bissector β 1,3 fosse uma recta de perfil (passante), o plano perpendicular a essa recta seria um plano de rampa, com os seus traços simétricos em relação ao eixo x . x

9. Planos Perpendiculares ao Bissector β 2,4 Pretendem-se os traços de um plano δ , perpendicular ao bissector β 2,4 ; utilizando uma recta oblíqua (passante) s , pertencente ao bissector. f δ ≡ h δ Uma recta s pertence ao bissector β 2,4 , por ter as suas projecções coincidentes. s 1 ≡ s 2 O plano δ acaba por ser uma plano oblíquo com os seus traços coincidentes entre si, e concorrentes com o eixo x . Caso a recta do bissector β 2,4 fosse uma recta de perfil (passante), o plano perpendicular a essa recta seria um plano de rampa, com os seus traços coincidentes entre si. x

10. Uma recta frontal f faz um ângulo de 30º (a.e.) com o Plano Horizontal de Projecção, e tem 3 cm de afastamento. Determina os traços do plano α , perpendicular ao β 1,3 , e que contém a recta f . f 2 f 1 f α h α O traço frontal do plano é paralelo à projecção frontal da recta, porque o plano α contém a recta f . Pelo facto do plano α ser perpendicular ao β 1,3 têm os seus traços simétricos, f α é simétrico com h α em relação ao eixo x . x H 1 H 2

11. Uma recta frontal f faz um ângulo de 30º (a.e.) com o Plano Horizontal de Projecção, e tem 3 cm de afastamento. Determina os traços do plano α , perpendicular ao β 2,4 , e que contém a recta f . f 2 f 1 f α ≡ h α O traço frontal do plano é paralelo à projecção frontal da recta, porque o plano α contém a recta f . Pelo facto do plano α ser perpendicular ao β 2,4 têm os seus traços coincidentes, f α é coincidente com h α . x H 1 H 2

12. Um plano α é perpendicular ao β 2,4 , e o traço frontal do plano faz um ângulo de 60º (a.d.) com o eixo x . Determina as projecções do ponto A (3; 4), contido no plano. Para o ponto ertencer a um plano tem que pertencer a uma recta do plano. Uma recta frontal do plano com 3 cm de afastamento será utilizada. f α ≡ h α f 1 f 2 x A 1 A 2 H 1 H 2