1) O rebatimento permite obter uma representação mais conveniente de um objeto, rotacionando-o em torno de um eixo para uma posição favorável. 2) O rebatimento de planos consiste na rotação de um plano em torno de uma reta até coincidir com outro plano. 3) O documento fornece exemplos de rebatimento de planos verticais e de topo para os planos de projeção, mostrando como obter as vistas auxiliares.

1. GEOMETRIA DESCRITIVA A
10.º Ano
Métodos Geométricos Auxiliares I
Rebatimentos

2. GENERALIDADES
O rebatimento tem como objectivo permitir obter uma representação mais
conviniente de um determinado objecto, para assim poder resolver problemas e
situações que a representação inicial não nos permite.
O rebatimento consiste em rodar um objecto em torno de um eixo (ou
charneira, recta do plano que contém o objecto), para colocar o objecto numa
nova e mais favorável posição em relação aos planos de projecção, mantendo
os planos no mesmo lugar.
O processo de rebatimento é só para planos, pois consiste na rotação de um
plano em torno de uma das suas rectas, até coincidir com outro plano.
O rebatimento é semelhante à rotação, e é só válido para objectos uni ou
bidimensionais, enquanto a rotação permite também para casos com objectos
tridimensionais.

3. EXEMPLO DE REBATIMENTO
xz xz
Ar
A2 A2
Br
fα A fα ≡ e ≡ fαr A
B2 B2 Cr
α α
C2 C2
C C
B B
x x ≡ hαr
C1 C1
A1 A1
B1 B1
xy xy
hα hα

4. REBATIMENTO DE PLANOS VERTICAIS OU DE TOPO
Rebatimento de um plano vertical para o Plano Frontal de Projecção, sendo a
charneira do rebatimento o fα.
xz
fα ≡ e ≡ fαr α
A2
O
Ar A
k ≡ k1 ≡ k2
x ≡ hαr A1
hα
xy

5. Rebatimento de um plano vertical para o Plano Horizontal de Projecção, sendo
a charneira do rebatimento o hα.
xz
fα
α
A2
A
k ≡ k1 ≡ k2
A1 ≡ O
x
hα ≡ e ≡ hαr
xy
fαr
Ar

6. Rebatimento de um Plano Vertical para o Plano Frontal de
Projecção
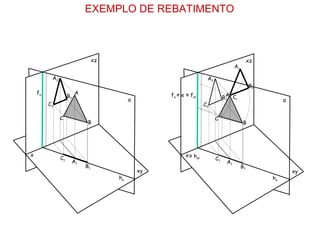
Pretende-se rebater o plano vertical α, que contém o triângulo [ABC], para obter
a V.G., através do rebatimento do plano α para o Plano Frontal de Projecção.
fα ≡ e2 ≡ fαr
Br B2
V.G.
Cr
C2
Ar
A2
(e1)
x ≡ hαr
A1
B1
C1
hα

7. Rebatimento de um Plano Vertical para um Plano Frontal
Pretende-se rebater o plano vertical α, que contém o triângulo [ABC], para obter
a V.G., através do rebatimento do plano α para um plano frontal φ.
e2
fα
Br B2
V.G.
Cr
C2
A2 ≡ Ar
x
(hφ) ≡ hαr A1 ≡ (e1)
B1
C1
hα

8. É dado um
segmento de
recta oblíquo y≡ z
[AB], sendo A fα ≡ e2 ≡ fαr
(4; 3; 4) e B (2;
1; 2).
A2 Ar
Determina a
V.G. do V.G.
segmento de B2
recta [AB], Br
rebatendo o seu
plano projectante
horizontal para o x ≡ hαr (e1)
B1
Plano Frontal de
Projecção.
A1
hα

9. É dado um
segmento de
recta oblíquo y≡ z
[AB], sendo A e2
fα
(4; 3; 4) e B (2;
1; 2).
A2 Ar
Determina a
V.G. do V.G.
segmento de
recta [AB], B2 ≡ Br
rebatendo o seu
plano projectante
horizontal para x
B1 ≡ (e1)
um plano frontal (hφ) ≡ hαr
que contém o
ponto B. A1
hα

10. É dado um plano
de topo δ que y≡ z
contém um
triângulo [PQR], fδ
sendo P (2; 4;
4), Q (-1; 3; 1) e
R (1; 3).
P2
Determina a R2
V.G. do triângulo
[PQR],
Q2
rebatendo o
plano δ para o (e2)
x ≡ fδr
Plano Horizontal R1 Rr
de Projecção.
V.G.
Q1 Qr
P1
Pr
hδ ≡ e1 ≡ hδr

11. É dado um triângulo
[ABC], contido num fα
plano vertical α, que e2
faz um diedro de 45º
(a.d.) com o Plano
C2 ≡ Cr B2 Br
Frontal de Projecção.
V.G.
A e B são dois pontos
do β1,3, sendo que A
tem 2 cm de cota e B
A2 ≡ Ar
tem 5 cm de
afastamento.
O lado [AC] é vertical, x
e o lado [BC] é
horizontal. A1 ≡ C1 ≡ (e1)
(hφ) ≡ hαr
Desenha as
projecções do triângulo
[ABC] e determina a
V.G. do triângulo, B1
rebatendo o plano α
para o plano frontal hα
que contém o lado
[AC].

12. Rebatimento de um Plano Vertical para o Plano Horizontal de
Projecção
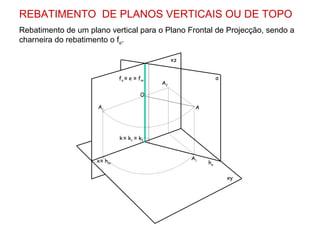
Pretende-se rebater o plano vertical α, que contém o triângulo [ABC], para obter a
V.G., através do rebatimento do plano α para o Plano Horizontal de Projecção.
fα
B2 h2
F2
C2
A2
F1
x ≡ e2
A1
Ar
hr
B1
Fr
C1
V.G.
hα ≡ e1 ≡ h1 ≡ hαr
fαr
Br Cr

13. Rebatimento de um Plano Vertical para um Plano Horizontal
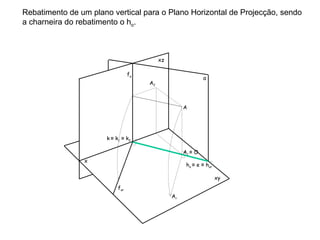
Pretende-se rebater o plano vertical α, que contém o triângulo [ABC], para obter a
V.G., através do rebatimento do plano α para um plano horizontal ν, que contém o
ponto A.
fα
B2
C2
(fν) ≡ e2
A2
x
A1 ≡ Ar
B1
V.G.
C1
Br Cr hα≡ e1

14. É dado um triângulo
[ABC], contido num fα
plano vertical α, que
faz um diedro de 45º
(a.d.) com o Plano
(fν) ≡ e2 C2 B2
Frontal de Projecção.
A e B são dois pontos
do β1,3, sendo que A
tem 2 cm de cota e B
A2
tem 5 cm de
afastamento.
O lado [AC] é vertical, x
e o lado [BC] é
horizontal. A1 ≡ C1 ≡ Cr
Determina a V.G. do
triângulo [ABC], V.G.
Ar
rebatendo o plano α
para o plano horizontal B1 ≡ Br
que contém o lado
h α ≡ e1
[BC].

15. É dado um plano y≡ z
fδ ≡ e2 ≡ f2 ≡ fδr
de topo δ que
contém um Pr
triângulo [PQR],
sendo P (2; 4; hδr
4), Q (-1; 3; 1) e fr
V.G.
R (1; 3).
P2 Rr
Determina a Qr
R2
Hr
V.G. do triângulo
[PQR],
rebatendo o Q2
plano δ para o
x ≡ e1 H2
Plano Frontal de R1
Projecção.
Q1
P1 H1
f1
hδ