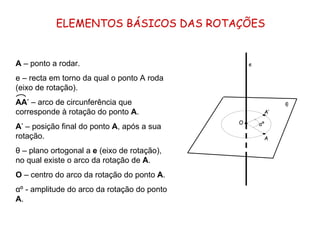
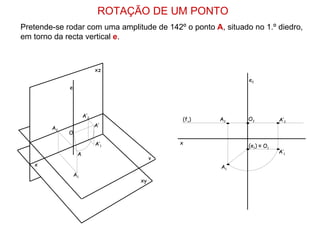
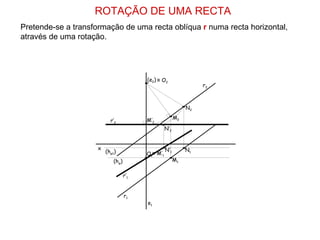
1) O documento descreve os elementos básicos e métodos de rotação em geometria descritiva, incluindo rotação de pontos, segmentos de reta e retas. 2) São apresentados vários exemplos de como aplicar rotações para transformar objetos geométricos em posições mais favoráveis e obter verdadeiras grandezas. 3) As rotações permitem representar objetos de forma mais conveniente para resolver problemas geométricos.

1. GEOMETRIA DESCRITIVA A
10.º Ano
Métodos Geométricos Auxiliares I
Rotações

2. GENERALIDADES
A rotação tem como objectivo permitir obter uma representação mais
conviniente de um determinado objecto, para assim poder resolver problemas e
situações que a representação inicial não nos permite.
A rotação consiste em rodar um objecto em torno de um eixo (ou charneira,
recta externa ao plano que contém o objecto), para colocar o objecto numa
nova e mais favorável posição em relação aos planos de projecção, mantendo
os planos no mesmo lugar.

3. ELEMENTOS BÁSICOS DAS ROTAÇÕES
A – ponto a rodar. e
e – recta em torno da qual o ponto A roda
(eixo de rotação).
AA’ – arco de circunferência que θ
corresponde à rotação do ponto A. A’
O αº
A’ – posição final do ponto A, após a sua
rotação. A
θ – plano ortogonal a e (eixo de rotação),
no qual existe o arco da rotação de A.
O – centro do arco da rotação do ponto A.
αº - amplitude do arco da rotação do ponto
A.

4. EXEMPLO DE ROTAÇÃO
xz xz
A’2
A’
A2 A2
e B’2
C’2 B’
A A
B2 B2
α C’ α
C2 C2
C C
B B
B’1 θ
A’1
C’1
x x
C1 C1
A1 A1
B1 B1
xy xy

5. ROTAÇÃO DE UM PONTO
Pretende-se rodar com uma amplitude de 142º o ponto A, situado no 1.º diedro,
em torno da recta vertical e.
xz
e2
e
A’2
(fν) A2 O2 A’2
A2 A’
O
A’1 x
(e1) ≡ O1
A A’1
ν
x A1
A1
xy

6. ROTAÇÃO DE UM SEGMENTO DE RECTA
Pretende-se rodar o segmento de recta [AB], com uma amplitude de 45º no
sentido dos ponteiros do relógio, em torno da recta de topo e.
xz A’2
φ1
φ
A’
B’2
Q A2 (e2) ≡ O2 ≡ Q2
B’
O
B B2
A
e
O1
x B’1 Q1
x (hφ1) B1
xy
(hφ) A1 A’1
e1

7. ROTAÇÃO DE UMA RECTA
Pretende-se a transformação de uma recta oblíqua r numa recta horizontal,
através de uma rotação.
(e2) ≡ O2
r2
N2
M’2 M2
r’2
N’2
x N’1 N1
(hφ1) O1≡ M’1
(hφ) M1
r’1
r1
e1

8. ROTAÇÃO DE UM SEGMENTO DE RECTA PARA OBTER
A SUA VERDADEIRA GRANDEZA
Pretende-se rodar o segmento de recta onlíquo [AB], para obter a V.G., através
da transformação do segmento de recta [AB] num segmento de recta frontal.
e2
(fν1) A2 A’2
(fν) P2 O2 ≡ P’2
(fν2) B2 B’2
x P’1
A’1 B1 B’1
P1
A1
(e1) ≡ O1

9. São dados os
pontos A (1; 1;
3) e B (-1; 3; 2). y≡ z
e2
Determina as
projecções do
ponto A, após
uma rotação de A2 O2
(fν) A’2
60º, no sentido
B2
dos ponteiros do
relógio, em torno
de uma recta
vertical que x A’1
contém o ponto
A1
B.
B1 ≡ (e1) ≡ O1

10. São dados os
pontos A (1; 1;
3) e B (-1; 3; 2). y≡ z
Determina as
B’2
projecções do
ponto B, após
uma rotação de A2 ≡ (e2) ≡ O2
90º, no sentido
B2
contrário dos
ponteiros do
relógio, em torno
de uma recta de x
topo que contém
A1
o ponto A.
O1
(hφ) B’1 B1
e1

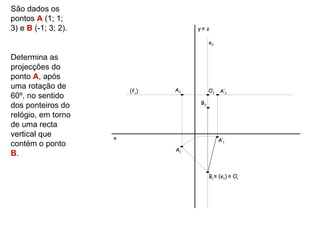
11. É dado um
segmento de
recta [PQ], y≡ z
sendo P (-2; 4;
v2
4) e Q (-4; 2; 1).
É dada uma
recta vertical v
(fν) P’2 R2 P2
que contém o
ponto A (1; 1; 2).
Determina as A2
projecções do (fν1) S2 Q’2 Q2
segmento de
recta [PQ], após x
uma rotação de A1 ≡ (v1) ≡ R1 ≡ S1
70º, no sentido
dos ponteiros do Q1
relógio, em torno
da recta v.
P1
P’1
Q’1

12. É dada uma
recta oblíqua r,
r2
que passa pelo
ponto A (1; 3).
As projecções da
recta r são
paralelas entre
(e2) ≡ O2 ≡ Q2 A2
si, e a sua
projecção frontal
faz um ângulo de P2
45º (a.d.) com o r’2 P’2 A’2
eixo x.
x
Q1 A’1
Transforma a (hφ1) A1
recta r numa
recta horizontal,
com o recurso a (hφ) O1≡ P’1 P1
uma rotação.
r’1 e1
r1

13. É dada uma
recta horizontal
h, com 3 cm de e2
cota, e faz um
ângulo de 30º
(a.e.) com o
Plano Frontal de
Projecção. h2 P2 O2
P’2 ≡ (h’2)
Transforma a
recta h numa
recta de topo,
com o recurso a
x
uma rotação.
P1
h1 P’1 (e1) ≡ O1
h’1

14. É dada uma
recta horizontal
h, com 3 cm de e2
cota, e faz um
ângulo de 30º
(a.e.) com o
Plano Frontal de
Projecção. h2 ≡ h’2 P2 O2 ≡ P’2
Transforma a
recta h numa
recta fronto-
horizontal, com o
x
recurso a uma
rotação.
h’1 P1 P’1
h1 (e1) ≡ O1

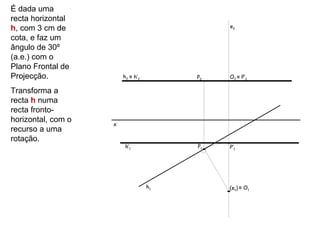
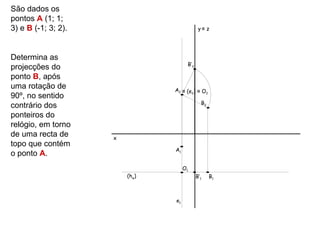
15. É dado um
segmento de
recta [PQ], y≡ z
sendo P (-2; 4;
4) e Q (-4; 2; 1).
Determina a
V.G. de PQ,
P2
transformando P’2 T’2 Q’2
[PQ] num
T2
segmento de
recta
Q2
horizontal, com (e2) ≡ O2 ≡ A2 ≡ B2
o recurso a uma
rotação. x
(hφ2) B1 Q’1 Q1
V.G.
(hφ) O1≡ T’1 T1
(hφ1) P’1 A1 P1
e1

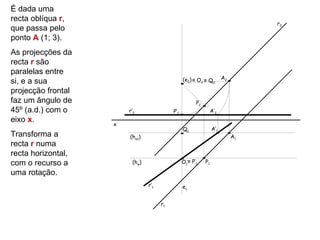
16. É dado um
segmento de
recta [AB],
situado no 1.º r2 r’2 e2
diedro, com 5 cm
de comprimento,
sendo A (3; 5) o (fν) A2 O2 ≡ A’2
seu extremo
superior.
A recta suporte
B’2
de [AB] é B2
(fν1)
passante e a sua
projecção frontal P’2
faz um ângulo de x P1 ≡ P2
45º (a.e.) com o B1
eixo x.
r’1
Desenha as A1
A’1 P’1
projecções do
segmento de r1
recta [AB], com o (e1) ≡ O1
recurso a uma
rotação.

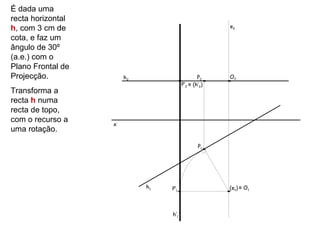
17. É dado um
segmento de
recta de perfil
[AB], sendo A (4; p1 ≡ p2
1) e B (2; 4).
Determina a V.G.
de AB,
B2
transformando p’2 B’2 A’2
[AB] num
segmento de
recta horizontal,
A2
com o recurso a
(e2) ≡ O2 ≡ Q2
uma rotação.
x
(hφ1) B’1 Q1 B1
V.G.
(hφ) O1 ≡ A’1 A1
e1
p’1