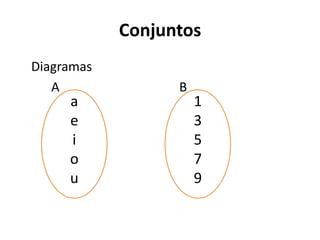
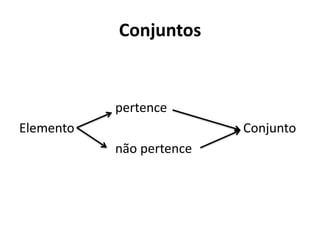
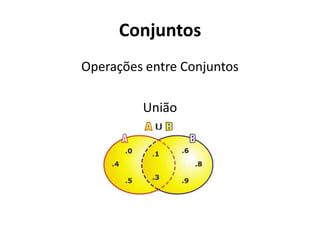
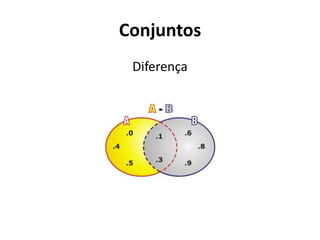
1) O documento apresenta os conceitos básicos de conjuntos, incluindo definições de pertencimento, subconjuntos, operações entre conjuntos e diagramas.
2) Em seguida, aborda os conjuntos numéricos como números naturais, inteiros, racionais, irracionais e reais.
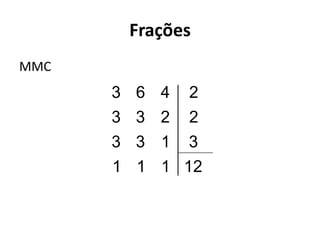
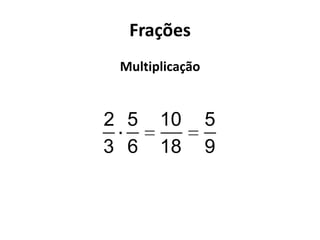
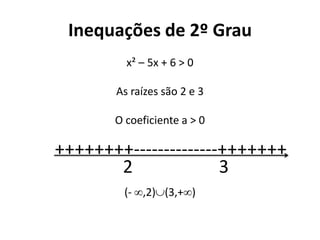
3) Por fim, introduz noções de intervalos, frações, equações do 1o e 2o grau e inequações.











![Intervalos
(2, 5] [3, 7)
(2, 5]
[3, 7)
(2, 5] [3, 7)
2 5
3 7
3 5](https://image.slidesharecdn.com/unidade1-130531164145-phpapp01/85/Unidade-1-16-320.jpg)