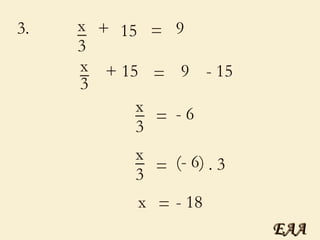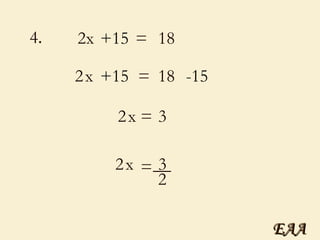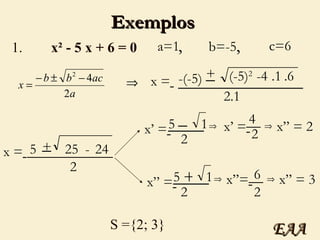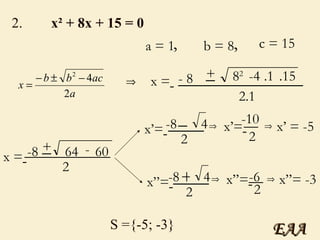1) A aula introduz o estudo de equações algébricas do 1o e 2o grau para alunos do 9o ano e 1o médio, revisando operações básicas e uso de letras na matemática. 2) Explica como resolver equações do 1o grau e introduz a fórmula de Bhaskara para equações do 2o grau. 3) Demonstra como calcular o discriminante e determinar o número de raízes reais de uma equação do 2o grau.

1. Aula de álgebra destinada a alunos do 9 o ano do ensino fundamental e revisão para alunos do 1 o do ensino médio do CEAL. O objetivo deste trabalho, é introduzir o estudo das equações de forma descontraída, chamando atenção para as operações fundamentais e o uso das letras no estudo da matemática. Observa se ainda a evolução do aluno no decorrer de sua formação. Professora Enoêmia.

2. Equações Algébricas operações algébricas como: adição, subtração, multiplicação, divisão e radiciação. Equações algébricas são equações nas quais a incógnita x está sujeita a EAA

3. Equação do primeiro grau = Os números reais a e b são os coeficientes da equação. (1 o membro) (2 o membro) a x + b 0 EAA

4. Resolução de equações 1. x + 8 = 15 x + 8 = 15 x = 7 - 8 2. x - 10 = 12 x = 12 + 10 x = 22 - 10 EAA

5. = 9 - 15 x = (- 6) 3. + + 15 = 9 . 3 = - 6 15 x = 18 - x _ 3 3 _ x x _ _ 3 3 EAA

6. 4 . 2x = 18 x = x = 3 2 __ 3 2 +15 +15 -15 2 x = 18 2 EAA

7. Equação do segundo grau a x² + b x + c = 0 Uma equação do segundo grau na incógnita x é da forma: Os números reais a , b e c são os coeficientes da equação. EAA

8. Exemplo: x² - 5 x + 6 = 0 Identificando os coeficientes: a x² + b x + c = 0 a = 1 b = -5 c = 6 EAA

9. Vamos completar a tabela 1 - 6 8 1 1 - 1 - 10 25 2 4 14 0 1 2 0 x² - 10 x + 25 = 0 x² - 6x + 8 = 0 2x² + 4x + 14 = 0 x² + 1 = 0 - x² + 2x = 0 EAA c b a Equação

10. Fórmula de Bháskara a x² + b x + c = 0 Bhaskara Acharya ( B. o Instruído ) viveu de 1 114 a 1 185 aprox . na India. { ( delta ) letra do alfabeto grego , usada para representar o valor da equação b² - 4ac }. EAA

11. = b² - 4ac é o discriminante da equação de 2 o grau ax 2 + bx + c = 0. onde a é o coeficiente de x 2 , b é o coeficiente de x e c o termo independente. EAA

12. Exemplos 3 x² - 3x + 6 = 0 a = 3 b = -3 c = 6 , , 1. Calcule o discriminante na equação. = b² - 4ac (-3) 2 -4 .3 .6 = 9 - 4. 18 = 9 - 72 = - 63 = EAA

13. x² + 6x + 9 = 0 a = 1 b = -6 c = 9 , , 2. Calcule o discriminante na equação. = b² - 4ac (-6) 2 - 4 . 1 .9 = 36 - 36 = 0 = EAA

14. x² + 2x - 3 = 0 a = 1 b = 2 c = -3 , , 3. Calcule o discriminante na equação. = b² - 4ac 2 2 - 4 . 2 .(-3) = 4 - 8. (-3) = 4 + 24 = 28 = EAA

15. Sendo = b² - 4ac e Dada a equação de 2 o grau ax 2 + bx + c = 0. temos, logo, EAA

16. Exemplos 1. x² - 5 x + 6 = 0 a=1 b=-5 c=6 , , x = -(-5) + (-5) 2 ______________ 2.1 _ -4 .1 .6 x = 5 + 25 ____________ 2 - 24 _ x’ = 5 1 2 _ ____ x’ = 4 2 __ x” = 2 S ={2; 3} x” = 5 1 2 + ____ x”= 6 2 __ x” = 3 EAA

17. 2. x² + 8x + 15 = 0 a = 1 b = 8 c = 15 , , x = - 8 + 8 2 ______________ 2.1 _ -4 .1 .15 x = -8 + 64 ____________ 2 - 60 _ x’= -8 4 2 _ ____ x’= -10 2 __ x’ = -5 S ={-5; -3} x”= -8 4 2 + ____ x”= -6 2 __ x”= -3 EAA

18. 3. x² + 6 x + 9 = 0 a = 1 b = 6 c = 9 , , x = - 6 + 6 2 ______________ 2.1 _ -4 .1 .9 x = -6 + 36 ____________ 2 - 36 _ x’= -6 0 2 _ ____ x’= -6 2 __ x’= -3 S ={-3} x”= -6 0 2 + ____ x”= -6 2 __ x”= -3 EAA

19. 4. 3 x² - x + 3 = 0 a = 3 b = -1 c = 3 , , x = - (-1) + (-1) 2 ______________ 2.3 _ -4 .3 .3 x = 1 + 1 ____________ 6 - 36 _ x= 1 -35 6 _ ______ S ={ } + x EAA

20. O discriminante há três possíveis situações: 1. Se há duas soluções reais e diferentes: e > 0 -b x’ = - _____ 2a -b x” = + 2a _____ EAA

21. x² - 5 x + 6 = 0 a=1 b=-5 c=6 , , x = -(-5) + (-5) 2 ______________ 2.1 _ -4 .1 .6 5 + 25 ____________ 2 - 24 _ x’ = 5 1 2 _ ____ x’ = 4 2 __ x’ = 2 A equação possui duas raízes diferentes. x” = 5 1 2 + ____ x” = 6 2 __ x” = 3 Logo, > 0 Exemplo x = EAA

22. x' = x” 2. Se há duas soluções reais iguais: = 0 EAA

23. x² + 6 x + 9 = 0 a = 1 b = 6 c = 9 , , x = - 6 + 6 2 ______________ 2.1 _ -4 .1 .9 -6 + 36 ____________ 2 - 36 _ x’= -6 0 2 _ ____ x’= -6 2 __ x’= -3 A equação possui duas raízes iguais. x”= -6 0 2 + ____ x”= -6 2 __ x”= -3 Logo, = 0 Exemplo x = EAA

24. não há solução real, pois não existe raiz logo, 3. Se < 0 quadrada real de número negativo. EAA

25. 3 x² - x + 3 = 0 a = 3 b = -1 c = 3 , , x = - (-1) + (-1) 2 ______________ 2.3 _ -4 .3 .3 x = 1 + 1 ____________ 6 - 36 _ x= 1 -35 6 _ ______ A equação não possui raízes reais. + x Logo, < 0 Exemplo EAA

26. Exemplos 3 x² - 3x + 6 = 0 a = 3 b = -3 c = 6 , , 1. Determine o número de raízes na equação. = b² - 4ac (-3) 2 -4 .3 .6 = 9 - 4. 18 = 9 - 72 = - 63 = A equação não possui raízes reais. EAA

27. x² + 6x + 9 = 0 a = 1 b = -6 c = 9 , , 2. Determine o número de raízes na equação. = b² - 4ac (-6) 2 - 4 . 1 .9 = 36 - 36 = 0 = A equação possui duas raízes iguais. EAA

28. x² + 2x - 3 = 0 a = 1 b = 2 c = -3 , , 3. Determine o número de raízes na equação. = b² - 4ac 2 2 - 4 . 2 .(-3) = 4 - 8. (-3) = 4 + 24 = 28 = A equação possui duas raízes diferentes. EAA

29. Resolva as equações. a) x² - 3x + 2 = 0 b) 2y² - 14y + 12 = 0 c) - x² + 7x – 10 = 0 d) 5x² - x + 7 = 0 e) 7x² - 3x = 4x + x² f) z² - 8z + 12 = 0 g) y² - 25 = 0 h) x² - 1/4 = 0 i) 5x² - 10x = 0 j) 5 + x² = 9 EAA