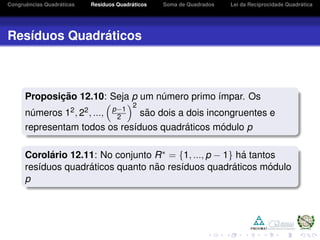
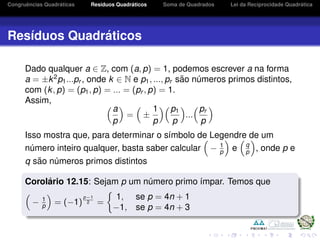
1. O documento discute congruências quadráticas, residuos quadráticos, soma de quadrados e a lei da reciprocidade quadrática. Apresenta definições, proposições e exemplos relacionados a esses tópicos. 2. É apresentada a definição de residuo quadrático módulo p e discutido como reconhecer se um número é ou não residuo quadrático módulo um dado primo p. Introduz o símbolo de Legendre. 3. É mostrado que um número natural ímpar c pode ser expresso como soma de quad

1. Sum´ario
CONGRU ˆENCIAS QUADR ´ATICAS
Luciana Santos da Silva Martino
lulismartino.blogspot.com.br
lulismartino@gmail.com
PROFMAT - Col´egio Pedro II
09 de dezembro de 2016

2. Congruˆencias Quadr´aticas Res´ıduos Quadr´aticos Soma de Quadrados Lei da Reciprocidade Quadr´atica
Sum´ario
1 Congruˆencias Quadr´aticas
2 Res´ıduos Quadr´aticos
3 Soma de Quadrados
4 Lei da Reciprocidade Quadr´atica

3. Congruˆencias Quadr´aticas Res´ıduos Quadr´aticos Soma de Quadrados Lei da Reciprocidade Quadr´atica
Outline
1 Congruˆencias Quadr´aticas
2 Res´ıduos Quadr´aticos
3 Soma de Quadrados
4 Lei da Reciprocidade Quadr´atica

4. Congruˆencias Quadr´aticas Res´ıduos Quadr´aticos Soma de Quadrados Lei da Reciprocidade Quadr´atica
Congruˆencias Quadr´aticas
Estamos interessados em resolver congruˆencias do tipo
AY2
+ BY + C ≡ 0 mod N
onde A, B, C ∈ Z e N > 1 ´e um natural tal que A ≡ 0 mod N
Pondo Z = 2AY + B, ∆ = B2 − 4AC e m = 4AN, resolver a
congruˆencia acima ´e equivalente a resolver o sistema de
congruˆencias
Z2
≡ ∆ mod m
2AY + B ≡ Z mod m

5. Congruˆencias Quadr´aticas Res´ıduos Quadr´aticos Soma de Quadrados Lei da Reciprocidade Quadr´atica
Congruˆencias Quadr´aticas
. Congruˆencias do tipo X2
≡ a mod n s˜ao mais simples de tratar
quando (a, n) = 1
Proposic¸ ˜ao 12.1: Seja (∆, m) = e2
l, onde l ´e livre de quadrados.
Escrevendo ∆ = ∆ e2
l e m = m e2
l, temos que a congruˆencia
Z2
≡ ∆ mod m admite soluc¸ ˜ao se, e somente se,
(∆ l, m ) = (l, m ) = 1 e a congruˆencia X2
≡ ∆ l mod m admite
soluc¸ ˜ao
Proposic¸ ˜ao 12.2: Seja n = pr1
1 ...prs
s a decomposic¸ ˜ao de n em fatores
primos. A congruˆencia X2
≡ a mod n admite soluc¸ ˜ao se, e somente
se, cada congruˆencia, separadamente, da fam´ılia
X2
≡ a mod pri
i , i = 1, ..., s
admitir soluc¸ ˜ao

6. Congruˆencias Quadr´aticas Res´ıduos Quadr´aticos Soma de Quadrados Lei da Reciprocidade Quadr´atica
Congruˆencias Quadr´aticas
Proposic¸ ˜ao 12.3: Sejam a, p, r ∈ Z, onde p ´e um n´umero primo ´ımpar e
r ≥ 2 tais que (a, p) = 1. A congruˆencia X2
≡ a mod pr
admite soluc¸ ˜ao se,
e somente se, a congruˆencia X2
≡ a mod p adimite soluc¸ ˜ao
Observe que congruˆencias do tipo X2
≡ a mod p nem sempre tem soluc¸ ˜ao.
A congruˆencia X2
≡ 2 mod 3 n˜ao possui nenhuma soluc¸ ˜ao
Proposic¸ ˜ao 12.4: Considere a congruˆencia
X2
≡ a mod 2r
onde a, r ∈ Z, com a ´ımpar e r ≥ 2. Temos que:
i) Se r = 2, a congruˆencia dmite soluc¸ ˜ao se, e somente se, a ≡ 1 mod 4 e,
nesse caso, ela admite duas soluc¸ ˜oes incongruentes
ii) Se r ≥ 3, a congruˆencia admite soluc¸ ˜ao se, e somente se, a ≡ 1 mod 8
Exemplo 12.5: Vamos resolver a congruˆencia quadr´atica
4Y2
+ 3Y + 5 ≡ 0 mod 2.52
.19

7. Congruˆencias Quadr´aticas Res´ıduos Quadr´aticos Soma de Quadrados Lei da Reciprocidade Quadr´atica
Outline
1 Congruˆencias Quadr´aticas
2 Res´ıduos Quadr´aticos
3 Soma de Quadrados
4 Lei da Reciprocidade Quadr´atica

8. Congruˆencias Quadr´aticas Res´ıduos Quadr´aticos Soma de Quadrados Lei da Reciprocidade Quadr´atica
Res´ıduos Quadr´aticos
Definic¸ ˜ao: Seja a um n´umero inteiro. Quando a congruˆencia
X2
≡ a mod p possui alguma soluc¸ ˜ao, diz-se que a ´e res´ıduo
quadr´atico m´odulo p, caso contr´ario diz-se que a n˜ao ´e res´ıduo
quadr´atico m´odulo p
2 n˜ao ´e res´ıduo quadr´atico m´odulo 3 (X2
≡ 2 mod 3)
todo n´umero natural a ´e res´ıduo quadr´atico m´odulo 2
(a congruˆencia X2
≡ a mod 2 tem soluc¸ ˜ao para todo a ∈ N)
Exemplo 10.27: Seja p um primo tal que p ≡ 1 mod 4. Tem-se
que
p − 1
2
!
2
≡ −1 mod p
Em particular, ∃a ∈ Z, com 0 < a ≤ p−1
2 , tal que a2
≡ −1 mod p
Assim, se p ´e um n´umero primo da forma 4n + 1, ent˜ao −1 ´e
res´ıduo quadr´atico m´odulo p

9. Congruˆencias Quadr´aticas Res´ıduos Quadr´aticos Soma de Quadrados Lei da Reciprocidade Quadr´atica
Res´ıduos Quadr´aticos
Teorema da Lei da Reciprocidade Quadr´atica
Algoritmo para reconhecer se um determinado inteiro a ´e ou
n˜ao ´e res´ıduo quadr´atico m´odulo p, para um dado primo p

10. Congruˆencias Quadr´aticas Res´ıduos Quadr´aticos Soma de Quadrados Lei da Reciprocidade Quadr´atica
Res´ıduos Quadr´aticos
Lema 12.6: Sejam p > 2 um n´umero primo e a ∈ Z tal que
(p, a) = 1. Se x0 ∈ R∗ = {1, ..., p − 1} ´e soluc¸ ˜ao da
congruˆencia X2 ≡ a mod p, ent˜ao (x0, p) = 1 e p − x0 tamb´em
´e soluc¸ ˜ao, n˜ao congruente a x0, e essas s˜ao as ´unicas
soluc¸ ˜oes em R∗
Proposic¸ ˜ao 12.7: Sejam p um n´umero primo e ´ımpar e a ∈ Z
tal que (a, p) = 1
i) Se X2 ≡ a mod p n˜ao tem soluc¸ ˜ao, ent˜ao a
p−1
2 ≡ −1 mod p
ii) Se X2 ≡ a mod p tem soluc¸ ˜ao, ent˜ao a
p−1
2 ≡ 1 mod p

11. Congruˆencias Quadr´aticas Res´ıduos Quadr´aticos Soma de Quadrados Lei da Reciprocidade Quadr´atica
Res´ıduos Quadr´aticos
Crit´erio de Euler
Teorema 12.8: Se p ´e um n´umero primo ´ımpar e a ∈ Z ´e tal
que (a, p) = 1, ent˜ao
i) p | a
p−1
2 − 1 se, e somente se, a ´e res´ıduo quadr´atico m´odulo
p
ii) p | a
p−1
2 + 1 se, e somente se, a n˜ao ´e res´ıduo quadr´atico
m´odulo p
Exemplo 12.9: Voltando ao Exemplo 7.20
47 divide um, e apenas um, dos n´umeros 223 − 1 ou 223 + 1
Temos que 47 | 223 − 1 pois X2 ≡ 2 mod 47 tem a soluc¸ ˜ao 7

12. Congruˆencias Quadr´aticas Res´ıduos Quadr´aticos Soma de Quadrados Lei da Reciprocidade Quadr´atica
Res´ıduos Quadr´aticos
Proposic¸ ˜ao 12.10: Seja p um n´umero primo ´ımpar. Os
n´umeros 12, 22, ..., p−1
2
2
s˜ao dois a dois incongruentes e
representam todos os res´ıduos quadr´aticos m´odulo p
Corol´ario 12.11: No conjunto R∗ = {1, ..., p − 1} h´a tantos
res´ıduos quadr´aticos quanto n˜ao res´ıduos quadr´aticos m´odulo
p

13. Congruˆencias Quadr´aticas Res´ıduos Quadr´aticos Soma de Quadrados Lei da Reciprocidade Quadr´atica
Res´ıduos Quadr´aticos
. Uma noc¸ ˜ao extremamente conveniente para lidar com
res´ıduos quadr´aticos
Definic¸ ˜ao: Se p ´e um n´umero primo e a ´e um inteiro tal que
p a, define-se o s´ımbolo de Legendre como
a
p =
1, se a ´e res´ıduo quadr´atico m´odulo p
−1, se a n˜ao ´e res´ıduo quadr´atico m´odulo p
. Se p a ent˜ao a2
p = 1. Em particular 1
p = 1
. Se a ´e ´ımpar ent˜ao a
2 = 1

14. Congruˆencias Quadr´aticas Res´ıduos Quadr´aticos Soma de Quadrados Lei da Reciprocidade Quadr´atica
Res´ıduos Quadr´aticos
. O s´ımbolo de Legendre possui as seguintes propriedades
Proposic¸ ˜ao 12.13: Sejam a, b ∈ Z e p um primo ´ımpar tal que
(a, p) = (b, p) = 1. Tem-se que
i) Se a ≡ b mod p, ent˜ao a
p = b
p
ii) a
p−1
2 ≡ a
p mod p
iii) a.b
p = a
p
b
p
Em particular, para todos m, k ∈ N tais que (m, p) = (k, p) = 1,
vale k2m
p = k2
p
m
p = m
p

15. Congruˆencias Quadr´aticas Res´ıduos Quadr´aticos Soma de Quadrados Lei da Reciprocidade Quadr´atica
Res´ıduos Quadr´aticos
Corol´ario 12.14: Sejam p um n´umero primo ´ımpar e a e b dois
n´umeros inteiros primos com p
i) Se a e b s˜ao ambos res´ıduos quadr´aticos ou n˜ao res´ıduos
quadr´aticos m´odulo p, ent˜ao ab ´e res´ıduo quadr´atico m´odulo p
ii) Se a ´e res´ıduo quadr´atico m´odulo p e b n˜ao ´e res´ıduo
quadr´atico m´odulo p, ent˜ao ab n˜ao ´e res´ıduo quadr´atico
m´odulo p

16. Congruˆencias Quadr´aticas Res´ıduos Quadr´aticos Soma de Quadrados Lei da Reciprocidade Quadr´atica
Res´ıduos Quadr´aticos
Dado qualquer a ∈ Z, com (a, p) = 1, podemos escrever a na forma
a = ±k2
p1...pr , onde k ∈ N e p1, ..., pr s˜ao n´umeros primos distintos,
com (k, p) = (p1, p) = ... = (pr , p) = 1.
Assim,
a
p
= ±
1
p
p1
p
...
pr
p
Isso mostra que, para determinar o s´ımbolo de Legendre de um
n´umero inteiro qualquer, basta saber calcular − 1
p e q
p , onde p e
q s˜ao n´umeros primos distintos
Corol´ario 12.15: Sejam p um n´umero primo ´ımpar. Temos que
− 1
p = (−1)
p−1
2 =
1, se p = 4n + 1
−1, se p = 4n + 3

17. Congruˆencias Quadr´aticas Res´ıduos Quadr´aticos Soma de Quadrados Lei da Reciprocidade Quadr´atica
Outline
1 Congruˆencias Quadr´aticas
2 Res´ıduos Quadr´aticos
3 Soma de Quadrados
4 Lei da Reciprocidade Quadr´atica

18. Congruˆencias Quadr´aticas Res´ıduos Quadr´aticos Soma de Quadrados Lei da Reciprocidade Quadr´atica
Soma de Quadrados
Teorema 12.16: Para um n´umero natural ´ımpar c s˜ao
equivalentes:
i) Existem n, m ∈ N, com (n, m) = 1 e de paridades distintas
tais que c = n2 + m2
ii) A congruˆencia X2 ≡ −1 mod c admite soluc¸ ˜ao em Z
iii) Os fatores primos de c s˜ao todos da forma 4k + 1
Corol´ario 12.17: Um n´umero natural ´e a hipotenusa de um
triˆangulo pitag´orico primitivo se, e somente se, ele s´o admite
divisores primos da forma 4k + 1.
Um n´umero natural ´e a hipotenusa de um triˆangulo pitag´orico
se, e somente se, ele ´e m´ultiplo de um primo da forma 4k + 1

19. Congruˆencias Quadr´aticas Res´ıduos Quadr´aticos Soma de Quadrados Lei da Reciprocidade Quadr´atica
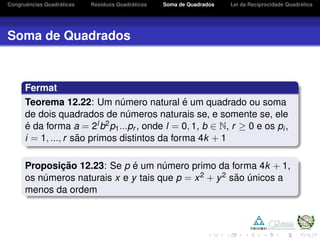
Soma de Quadrados
Corol´ario 12.18: Para um n´umero primo p > 2, s˜ao
equivalentes:
i) Existem n, m ∈ N, com (n, m) = 1 e de paridades distintas
tais que p = n2 + m2
ii) A congruˆencia X2 ≡ −1 mod c admite soluc¸ ˜ao em Z
iii) p ´e da forma 4k + 1
Lema 12.19: Quaiquer que sejam a, b, c, d ∈ Z, tem-se que:
i) (a2 + b2)(c2 + d2) = (ac − bd)2 + (ad + bc)2
ii) (2a + 1)2 + (2b + 1)2 = 2[(a + b + 1)2 + (b − a)2] e
(2a + 1, 2b + 1) = (a + b + 1, b − 1)

20. Congruˆencias Quadr´aticas Res´ıduos Quadr´aticos Soma de Quadrados Lei da Reciprocidade Quadr´atica
Soma de Quadrados
Corol´ario 12.20: Todo divisor de um n´umero da forma x2 + y2,
com (x, y) = 1, ´e da forma 2l(4k + 1), onde l = 0, 1
Exemplo 12.21: Existem infinitos primos da forma 8n + 5

21. Congruˆencias Quadr´aticas Res´ıduos Quadr´aticos Soma de Quadrados Lei da Reciprocidade Quadr´atica
Soma de Quadrados
Fermat
Teorema 12.22: Um n´umero natural ´e um quadrado ou soma
de dois quadrados de n´umeros naturais se, e somente se, ele
´e da forma a = 2lb2p1...pr , onde l = 0, 1, b ∈ N, r ≥ 0 e os pi,
i = 1, ..., r s˜ao primos distintos da forma 4k + 1
Proposic¸ ˜ao 12.23: Se p ´e um n´umero primo da forma 4k + 1,
os n´umeros naturais x e y tais que p = x2 + y2 s˜ao ´unicos a
menos da ordem

22. Congruˆencias Quadr´aticas Res´ıduos Quadr´aticos Soma de Quadrados Lei da Reciprocidade Quadr´atica
Outline
1 Congruˆencias Quadr´aticas
2 Res´ıduos Quadr´aticos
3 Soma de Quadrados
4 Lei da Reciprocidade Quadr´atica

23. Congruˆencias Quadr´aticas Res´ıduos Quadr´aticos Soma de Quadrados Lei da Reciprocidade Quadr´atica
Lei da Reciprocidade Quadr´atica
Lema de Gauss
Proposic¸ ˜ao 12.24: Sejam p e a dois n´umeros, com p primo ´ımpar e
(p, a) = 1. Sejam r1, ..., rp−1
2
os restos da divis˜ao por p dos n´umeros
a, 2a, ..., p−1
2 a, respectivamente. Se k ´e o n´umero dos ri que s˜ao
maiores do que p−1
2 , ent˜ao
a
p
= (−1)k
Proposic¸ ˜ao 12.25: Sejam p e a dois n´umeros naturais ´ımpares, com
p primo e (a, p) = 1. Pondo p = (p−1)
2 e κ = a
p + 2a
p + ... + p a
p ,
temos que
a
p
= (−1)κ

24. Congruˆencias Quadr´aticas Res´ıduos Quadr´aticos Soma de Quadrados Lei da Reciprocidade Quadr´atica
Lei da Reciprocidade Quadr´atica
Exemplo 12.26: Vamos mostrar que a equac¸ ˜ao diofantina
X2
− 13Y = 5 n˜ao possui soluc¸ ˜ao em n´umeros naturais
Corol´ario 12.27: Seja p um n´umero primo ´ımpar. Tem-se que
2
p = (−1)
p2−1
8 =
1, se p ≡ 1 ou p ≡ 7 mod 8
−1, se p ≡ 3 ou p ≡ 5 mod 8
Lema 12.28: Sejam p e q dois n´umeros primos ´ımpares distintos.
Tem-se que
q
p
+
2q
p
+...+
p−1
2 q
p
+
p
q
+
2p
q
+...+
q−1
2 p
q
=
p − 1
2
q − 1
2

25. Congruˆencias Quadr´aticas Res´ıduos Quadr´aticos Soma de Quadrados Lei da Reciprocidade Quadr´atica
Lei da Reciprocidade Quadr´atica
Lei da Reciprocidade Quadr´atica de Gauss
Teorema 12.29: Sejam p e q dois n´umeros primos ´ımpares
distintos. Tem-se que
p
q
q
p
= (−1)
p−1
2
q−1
2
Coroil´ario 12.31: Se p e q s˜ao dois n´umeros primos distintos,
tais que p ≡ 1 mod 4, ou q ≡ 1 mod 4, ent˜ao q ´e res´ıduo
quadr´atico m´odulo p se, e somente se, p ´e res´ıduo quadr´atico
m´odulo q

26. Congruˆencias Quadr´aticas Res´ıduos Quadr´aticos Soma de Quadrados Lei da Reciprocidade Quadr´atica
Lei da Reciprocidade Quadr´atica
A Lei de Reciprocidade Quadr´atica, juntamente com as
propriedades do s´ımbolo de Legendre contidas na Proposic¸ ˜ao
12.13 e nos Corol´arios 12.15 e 12.27, funciona como um
algoritmo para determinar se um n´umero ´e ou n˜ao ´e res´ıduo
qaudr´atico m´odulo um n´umero primo ´ımpar p
Exemplo 12.32: Vamos calcular 2561
241
Exemplo 12.33: Vamos calcular 3
p , onde p ´e um n´umero
primo maior do que 3
Exemplo 12.34: Vamos calcular 5
p , onde p ´e um n´umero
primo maior do que 5