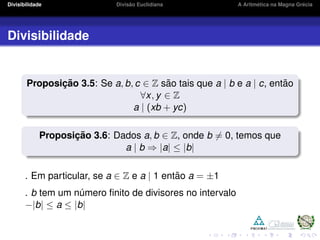
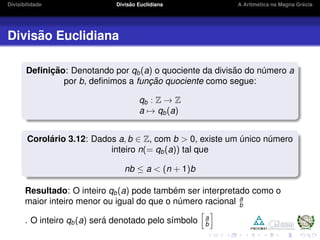
1) O documento discute conceitos de divisibilidade e divisão euclidiana em números inteiros. 2) A divisibilidade define quando um número divide outro deixando resto zero. A divisão euclidiana garante que sempre é possível dividir dois números inteiros com resto. 3) O texto apresenta proposições e definições formais sobre divisibilidade e quociente e resto da divisão euclidiana, além de exemplos ilustrativos.

1. Sum´ario
DIVIS ˜AO NOS INTEIROS
Luciana Santos da Silva Martino
lulismartino.blogspot.com.br
lulismartino@gmail.com
PROFMAT - Col´egio Pedro II
30 de setembro de 2016

2. Divisibilidade Divis˜ao Euclidiana A Aritm´etica na Magna Gr´ecia
Sum´ario
1 Divisibilidade
2 Divis˜ao Euclidiana
3 A Aritm´etica na Magna Gr´ecia

3. Divisibilidade Divis˜ao Euclidiana A Aritm´etica na Magna Gr´ecia
Outline
1 Divisibilidade
2 Divis˜ao Euclidiana
3 A Aritm´etica na Magna Gr´ecia

4. Divisibilidade Divis˜ao Euclidiana A Aritm´etica na Magna Gr´ecia
Divisibilidade
Quando n˜ao existir uma relac¸ ˜ao de divisibilidade entre dois
n´umeros inteiros, veremos que, ainda assim, ser´a poss´ıvel
efetuar uma “divis˜ao com resto pequeno” chamada de divis˜ao
euclidiana
Definic¸ ˜ao: Dados dois n´umeros inteiros a e b, diremos que a
divide b, escrevendo a|b, quando existir c ∈ Z tal que b = ca.
Nesse caso, diremos tamb´em que a ´e um divisor ou um fator
de b ou, ainda, que b ´e um m´ultiplo de a ou que b ´e divis´ıvel
por a.
A negac¸ ˜ao dessa sentenc¸a ´e representada por a b,
significando que n´umero inteiro c tal que b = ca

5. Divisibilidade Divis˜ao Euclidiana A Aritm´etica na Magna Gr´ecia
Divisibilidade
Proposic¸ ˜ao 3.2: Sejam a, b, c ∈ Z. Tem-se que:
i) 1 | a, a | a e a | 0
ii) 0 | a ⇔ a = 0 (∗)
iii) a | b ⇔ |a| | |b|
iv) se a | b e b | c ent˜ao a | c
Observe que a notac¸ ˜ao a | b n˜ao representa nenhuma operac¸ ˜ao em
Z, nem representa uma frac¸ ˜ao. Trata-se de uma sentenc¸a que diz ser
verdadeira que existe c inteiro tal que b = ca
(i) e (iii): todo n´umero inteiro a ´e divis´ıvel por ±1 e por ±a
(i): 0 tem infinitos divisores

6. Divisibilidade Divis˜ao Euclidiana A Aritm´etica na Magna Gr´ecia
Divisibilidade
Definic¸ ˜ao: Suponha que a | b e que a = 0. Seja c ∈ Z tal que
b = ca. O n´umero inteiro c, univocamente determinado, ´e chamado
de de quociente de b por a e ´e denotado por c = b
a
. b
a s´o est´a definido quando a = 0 e a | b
Proposic¸ ˜ao 3.3: Se a, b, c, d ∈ Z, ent˜ao
a | b e c | d ⇒ ac | bd
. Em particular, se a | b, ent˜ao ac | bc ∀c ∈ Z
Proposic¸ ˜ao 3.4: Sejam a, b, c ∈ Z tais que a | (b ± c). Ent˜ao
a | b ⇔ a | c

7. Divisibilidade Divis˜ao Euclidiana A Aritm´etica na Magna Gr´ecia
Divisibilidade
Proposic¸ ˜ao 3.5: Se a, b, c ∈ Z s˜ao tais que a | b e a | c, ent˜ao
∀x, y ∈ Z
a | (xb + yc)
Proposic¸ ˜ao 3.6: Dados a, b ∈ Z, onde b = 0, temos que
a | b ⇒ |a| ≤ |b|
. Em particular, se a ∈ Z e a | 1 ent˜ao a = ±1
. b tem um n´umero finito de divisores no intervalo
−|b| ≤ a ≤ |b|

8. Divisibilidade Divis˜ao Euclidiana A Aritm´etica na Magna Gr´ecia
Divisibilidade
A relac¸ ˜ao de divisibilidade em N ∪ {0} ´e uma relac¸ ˜ao de ordem
pois:
i) ´e reflexiva: ∀a ∈ N, a | a (Prop. 3.2(i))
ii) ´e transitiva: se a | b e b | c ent˜ao a | c (Prop. 3.2(iv))
iii) ´e antissim´etrica: se a | b e b | a, ent˜ao a = b (Prop. 3.6)
Entretanto a relac¸ ˜ao de divisibilidade n˜ao ´e uma relac¸ ˜ao de
ordem em Z pois n˜ao ´e antissim´etrica

9. Divisibilidade Divis˜ao Euclidiana A Aritm´etica na Magna Gr´ecia
Divisibilidade
Proposic¸ ˜ao 3.7: Sejam a, b ∈ Z e n ∈ N. Temos que
a − b | an − bn
Aplicac¸ ˜ao: Todo n´umero da forma 10n − 1, onde n ∈ N, ´e
divis´ıvel por 9
Proposic¸ ˜ao 3.8: Sejam a, b ∈ Z, e n ∈ N ∪ {0}. Temos que
a + b | a2n+1 + b2n+1
Proposic¸ ˜ao 3.9: Sejam a, b ∈ Z, e n ∈ N. Temos que
a + b | a2n − b2n

10. Divisibilidade Divis˜ao Euclidiana A Aritm´etica na Magna Gr´ecia
Outline
1 Divisibilidade
2 Divis˜ao Euclidiana
3 A Aritm´etica na Magna Gr´ecia

11. Divisibilidade Divis˜ao Euclidiana A Aritm´etica na Magna Gr´ecia
Divis˜ao Euclidiana
Euclides: ´E sempre poss´ıvel efetuar a divis˜ao de a por b com
resto
Divis˜ao Euclidiana
Teorema 3.10: Sejam a, b ∈ Z, com b = 0. Existem dois ´unicos
n´umeros inteiros q e r tais que a = bq + r, com 0 ≤ r < |b|
q: quociente da divis˜ao de a por b
r: resto da divis˜ao de a por b
Resultado: O resto da divis˜ao de a por b ´e zero ⇔ b | a

12. Divisibilidade Divis˜ao Euclidiana A Aritm´etica na Magna Gr´ecia
Divis˜ao Euclidiana
Definic¸ ˜ao: Denotando por qb(a) o quociente da divis˜ao do n´umero a
por b, definimos a func¸ ˜ao quociente como segue:
qb : Z → Z
a → qb(a)
Corol´ario 3.12: Dados a, b ∈ Z, com b > 0, existe um ´unico n´umero
inteiro n(= qb(a)) tal que
nb ≤ a < (n + 1)b
Resultado: O inteiro qb(a) pode tamb´em ser interpretado como o
maior inteiro menor ou igual do que o n´umero racional a
b
. O inteiro qb(a) ser´a denotado pelo s´ımbolo a
b

13. Divisibilidade Divis˜ao Euclidiana A Aritm´etica na Magna Gr´ecia
Divis˜ao Euclidiana
Definic¸ ˜ao: Denotando por rb(a) o resto da divis˜ao do n´umero a
por b, definimos a func¸ ˜ao resto como segue:
rb : Z → Z
a → rb(a)
Exemplo 3.13: r9(10n) = 1, qualquer que seja o n´umero
natural n

14. Divisibilidade Divis˜ao Euclidiana A Aritm´etica na Magna Gr´ecia
Divis˜ao Euclidiana
Exemplo 3.14: Dado um n´umero inteiro n ∈ Z qualquer, temos
duas possibilidades:
i) o resto da divis˜ao de n por 2 ´e 0, isto ´e, ∃q ∈ N : n = 2q
ii) o resto da divis˜ao de n por 2 ´e 1, isto ´e, ∃q ∈ N : n = 2q + 1
N´umeros inteiros
. n´umeros pares: n´umeros da forma 2q, para algum q ∈ Z
. n´umeros ´ımpares: n´umeros da forma 2q + 1, para algum
q ∈ Z

15. Divisibilidade Divis˜ao Euclidiana A Aritm´etica na Magna Gr´ecia
Divis˜ao Euclidiana
Exemplo 3.15: De um modo mais geral, fixado um n´umero
natural m ≥ 2, pode-se sempre escrever um n´umero qualquer
n, de modo ´unico, na forma n = mk + r, onde k, r ∈ Z e
0 ≤ r < m
. Todo n´umero inteiro pode ser escrito em uma , e somente
uma, das seguintes formas: 3k, 3k + 1 ou 3k + 2
. Todo n´umero inteiro pode ser escrito em uma , e somente
uma, das seguintes formas: 4k, 4k + 1, 4k + 2 ou 4k + 3

16. Divisibilidade Divis˜ao Euclidiana A Aritm´etica na Magna Gr´ecia
Divis˜ao Euclidiana
Exemplo 3.16: Dados a, n ∈ N, com a > 2 e ´ımpar, vamos
determinar a paridade de (an−1)
2
Exemplo 3.17: Vamos achar os m´ultiplos de 5 que se
encontram entre 1 e 253

17. Divisibilidade Divis˜ao Euclidiana A Aritm´etica na Magna Gr´ecia
Divis˜ao Euclidiana
Resultado: Dados a, c ∈ N, com a < c, o n´umero de m´ultiplos
n˜ao nulos de a menores ou iguais a c ´e igual ao quociente da
divis˜ao de c por a, isto ´e, igual a parte inteira c
a do n´umero
racional c
a
Proposic¸ ˜ao 3.18: Dados a, b, c ∈ Z, tais que 0 < a < b < c,
ent˜ao o n´umero dos m´ultiplos de a entre b e c ´e dado por:
i) c
a − b−1
a , se incluirmos b na contagem
ii) c
a − b
a , se excluirmos b da contagem

18. Divisibilidade Divis˜ao Euclidiana A Aritm´etica na Magna Gr´ecia
Outline
1 Divisibilidade
2 Divis˜ao Euclidiana
3 A Aritm´etica na Magna Gr´ecia