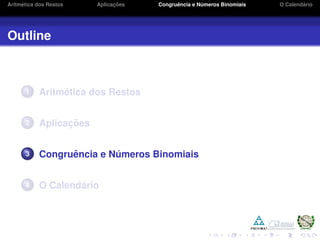
1. O documento discute aritmética dos restos, definindo congruência módulo m e propriedades como adição e multiplicação de números congruentes. É mostrado que a congruência forma uma relação de equivalência. 2. Aplicações incluem critérios de divisibilidade e a análise de padrões em sequências como números de Fibonacci. 3. O texto também abordará congruência e números binomiais.

1. Sum´ario
CONGRU ˆENCIAS
Luciana Santos da Silva Martino
lulismartino.blogspot.com.br
lulismartino@gmail.com
PROFMAT - Col´egio Pedro II
26 de novembro de 2016

2. Aritm´etica dos Restos Aplicac¸ ˜oes Congruˆencia e N´umeros Binomiais O Calend´ario
Sum´ario
1 Aritm´etica dos Restos
2 Aplicac¸ ˜oes
3 Congruˆencia e N´umeros Binomiais
4 O Calend´ario

3. Aritm´etica dos Restos Aplicac¸ ˜oes Congruˆencia e N´umeros Binomiais O Calend´ario
Outline
1 Aritm´etica dos Restos
2 Aplicac¸ ˜oes
3 Congruˆencia e N´umeros Binomiais
4 O Calend´ario

4. Aritm´etica dos Restos Aplicac¸ ˜oes Congruˆencia e N´umeros Binomiais O Calend´ario
Aritm´etica dos Restos
Gauss (1801): Disquisitiones Arithmeticae
Trata-se da realizac¸ ˜ao de uma aritm´etica com os restos da divis˜ao
euclidiana por um n´umero fixado
Definic¸ ˜ao: Seja m um n´umero natural. Diremos que dois n´umeros
inteiros a e b s˜ao congruentes m´odulo m se os restos de sua divis˜ao
euclidiana por m s˜ao iguais. Quando os inteiros a e b s˜ao
congruentes m´odulo m, escreve-se
a ≡ b mod m
Quando a relac¸ ˜ao a ≡ b mod m for falsa, diremos que a e b n˜ao s˜ao
congruentes, ou que s˜ao incongruentes, m´odulo m. Escreveremos
nesse caso a ≡ b mod m

5. Aritm´etica dos Restos Aplicac¸ ˜oes Congruˆencia e N´umeros Binomiais O Calend´ario
Aritm´etica dos Restos
. a ≡ b mod 1, quaisquer que sejam a, b ∈ Z: por isso
consideraremos sempre m > 1
A congruˆencia, m´odulo um inteiro fixado ´e uma relac¸ ˜ao de
equivalˆencia
Proposic¸ ˜ao 9.1: Seja m ∈ N. Para todos a, b, c ∈ Z tem-se que
(i) a ≡ a mod m
(i) se a ≡ b mod m, ent˜ao b ≡ a mod m
(iii) se a ≡ b mod m e b ≡ c mod m, ent˜ao a ≡ c mod m
Proposic¸ ˜ao 9.2: Suponha que a, b, m ∈ Z, com m > 1. Tem-se que
a ≡ b mod m se, e somente se, m | b − a

6. Aritm´etica dos Restos Aplicac¸ ˜oes Congruˆencia e N´umeros Binomiais O Calend´ario
Aritm´etica dos Restos
Note que todo n´umero inteiro ´e congruente m´odulo m ao seu
resto pela divis˜ao euclidiana por m e, portanto, ´e congruente
m´odulo m a um dos n´umeros 0, 1, ..., m − 1. Al´em disso, dois
desses n´umeros distintos n˜ao s˜ao congruentes m´odulo m.
Portanto, para achar o resto da divis˜ao de um n´umero a por m,
basta achar o n´umero natural r dentre os n´umeros 0, ..., m − 1
que seja congruente a a m´odulo m
Definic¸ ˜ao: Chamaremos de sistema completo de res´ıduos
m´odulo m a todo conjunto de n´umeros inteiros cujos restos
pela divis˜ao por m s˜ao os n´umeros 0, 1, ..., m − 1, sem
repetic¸ ˜oes e numa ordem qualquer
. Um sistema completo de res´ıduos m´odulo m possui m
elementos

7. Aritm´etica dos Restos Aplicac¸ ˜oes Congruˆencia e N´umeros Binomiais O Calend´ario
Aritm´etica dos Restos
. Se a1, ..., am s˜ao m n´umeros inteiros, dois a dois n˜ao congruentes m´odulo
m, ent˜ao eles formam um sistema completo de res´ıdulos m´odulo m
. Em particular, um conjunto formado por m inteiros consecutivos ´e um
sistema completo de res´ıduos m´odulo m
. Seja R um sistema completo de res´ıduos m´odulo m, ent˜ao a divis˜ao
euclidiana por m pode ser generalizada como segue:
Para todo a ∈ Z existem inteiros q e r univocamente determinados tais que
a = mq + r, com r ∈ R
Nessa situac¸ ˜ao dizemos tratar-se da divis˜ao com resto em R
A divis˜ao euclidiana corresponde ao caso em que R = {0, 1, ..., m − 1}
. Se tomarmos R = r ∈ Z; −m
2
≤ r < m
2
, que ´e um conjunto de m inteiros
consecutivos, a divis˜ao correspondente ser´a chamada de divis˜ao com menor
resto

8. Aritm´etica dos Restos Aplicac¸ ˜oes Congruˆencia e N´umeros Binomiais O Calend´ario
Aritm´etica dos Restos
A noc¸ ˜ao de congruˆencia ´e uma relac¸ ˜ao de equivalˆencia
compat´ıvel com as operac¸ ˜oes de adic¸ ˜ao e multiplicac¸ ˜ao nos
inteiros
Proposic¸ ˜ao 9.3: Sejam a, b, c, d, m ∈ Z, com m > 1
(i) Se a ≡ b mod m e c ≡ d mod m, ent˜ao
a + c ≡ b + d mod m
(ii) Se a ≡ b mod m e c ≡ d mod m, ent˜ao ac ≡ bd mod m
Corol´ario 9.4: Para todos n ∈ N, a, b ∈ Z, se a ≡ b mod m,
ent˜ao tem-se que an ≡ bn mod m

9. Aritm´etica dos Restos Aplicac¸ ˜oes Congruˆencia e N´umeros Binomiais O Calend´ario
Aritm´etica dos Restos
O Pequeno Teorema de Fermat: Se p ´e um n´umero primo e
a ∈ Z, ent˜ao
ap
≡ a mod p
Al´em disso, se p a, ent˜ao ap−1 ≡ 1 mod p
Exemplo 9.5: Sejam p um n´umero primo e a, b ∈ Z. Tem-se
que (a ± b)p ≡ ap ± bb mod p
Exemplo 9.6: Se a1, ..., ar ∈ Z e p ´e primo, ent˜ao
(a1 + ... + ar )p ≡ ap
1 + ... + ap
r mod p
Exemplo 9.7: Sejam a, b ∈ Z e p um n´umero primo. Vamos
mostrar que ap ≡ bp mod p ⇒ ap ≡ bp mod p2

10. Aritm´etica dos Restos Aplicac¸ ˜oes Congruˆencia e N´umeros Binomiais O Calend´ario
Aritm´etica dos Restos
Proposic¸ ˜ao 9.8: Sejam a, b, c, m ∈ Z, com m > 1. Tem-se que
a + c ≡ b + c mod m ⇔ a ≡ b mod m
A proposic¸ ˜ao acima nos diz que, para as congruˆencias, vale o
cancelamento com relac¸ ˜ao `a adic¸ ˜ao. Entretanto, n˜ao vale, em
geral, o cancelamento para a multiplicac¸ ˜ao
Exemplo 9.9: Como 6.9 − 6.5 = 24 e 8 | 24, temos que
6.9 ≡ 6.5 mod 8, e, no entanto, 9 ≡ 5 mod 8

11. Aritm´etica dos Restos Aplicac¸ ˜oes Congruˆencia e N´umeros Binomiais O Calend´ario
Aritm´etica dos Restos
A seguir um resultado relacionado ao cancelamento multiplicativo
Proposic¸ ˜ao 9.10: Sejam a, b, c, m ∈ Z. Temos que
ac ≡ bc mod m ⇔ a ≡ b mod
m
(c, m)
Corol´ario 9.11: Sejam a, b, c, m ∈ Z, com m > 1 e (c, m) = 1.
Temos que
ac ≡ bc mod m ⇔ a ≡ b mod m
Proposic¸ ˜ao 9.12: Sejam a, k, m ∈ Z, com m > 1 e (k, m) = 1. Se
a1, ..., am ´e um sistema completo de res´ıduos m´odulo m, ent˜ao
a + ka1, ..., a + kam tamb´em ´e um sistema completo de res´ıduos
m´odulo m

12. Aritm´etica dos Restos Aplicac¸ ˜oes Congruˆencia e N´umeros Binomiais O Calend´ario
Aritm´etica dos Restos
Proposic¸ ˜ao 9.13: Sejam a, b ∈ Z e m, n, m1, ..., mr inteiros
maiores do que 1. Temos que
i) se a ≡ b mod m e n | m, ent˜ao a ≡ b mod n
ii) a ≡ b mod mi, ∀i = 1, ..., r ⇔ a ≡ b mod [m1, ..., mr ]
iii) se a ≡ b mod m, ent˜ao (a, m) = (b, m)
Exemplo 9.14: Vamos achar o menor m´ultiplo positivo de 7
que deixa resto 1 quando dividido por 2, 3, 4, 5 e 6

13. Aritm´etica dos Restos Aplicac¸ ˜oes Congruˆencia e N´umeros Binomiais O Calend´ario
Aritm´etica dos Restos
Exemplo 9.15: Vamos achar o resto da divis˜ao de 23728 por 13
Exemplo 9.16: Vamos mostrar que 45 | 133n + 173n para todo
n´umero natural ´ımpar n
Exemplo 9.17: Vamos determinar o algarismo das unidades
de 777

14. Aritm´etica dos Restos Aplicac¸ ˜oes Congruˆencia e N´umeros Binomiais O Calend´ario
Outline
1 Aritm´etica dos Restos
2 Aplicac¸ ˜oes
3 Congruˆencia e N´umeros Binomiais
4 O Calend´ario

15. Aritm´etica dos Restos Aplicac¸ ˜oes Congruˆencia e N´umeros Binomiais O Calend´ario
Aplicac¸ ˜oes
Exemplo 9.18: Vamos mostrar que o n´umero de Mersenne
M83 = 283
− 1 n˜ao ´e primo, apesar de 83 ser primo
Exemplo 9.19: Vamos provar nesse exemplo o resultado de Euler
que afirma que o quinto n´umero de Fermat F5 = 225
+ 1 n˜ao ´e primo
Exemplo 9.20: Crit´erios de divisibilidade por 2, 5 e 10
Exemplo 9.21: Crit´erios de divisibilidade por 3 e 9
A regra dos noves fora: Para verificar se um dado n´umero ´e divis´ıvel
por 3 ou por 9, somam-se os seus algarismos, desprezando-se, ao
efetuar a soma, cada parcela igual a 9. Se o resultado final for zero,
ent˜ao o n´umero ´e divis´ıvel por 9. Se o resultado for um do
algarismos 0, 3 ou 6 ent˜ao o n´umero ´e divis´ıvel por 3

16. Aritm´etica dos Restos Aplicac¸ ˜oes Congruˆencia e N´umeros Binomiais O Calend´ario
Aplicac¸ ˜oes
Exemplo 9.22: Crit´erio de divisibilidade por 11
Exemplo 9.23: Prova dos nove
Exemplo 9.24 (Pietro Antonio Cataldi - 1588): Todo n´umero
da forma an = 22n(22n+1 − 1), onde n ∈ N, na sua
representac¸ ˜ao decimal, ou termina em 28 ou termina em a6,
onde a ´e um algarismo ´ımpar. Em particular, todo n´umero
perfeito termina de um desses modos

17. Aritm´etica dos Restos Aplicac¸ ˜oes Congruˆencia e N´umeros Binomiais O Calend´ario
Aplicac¸ ˜oes
Exemplo 9.25: Vamos mostrar que dado um n´umero natural
m ∈ N, existe um n´umero de Fibonacci un tal que m | un
. Existem infinitos n´umeros de Fibonacci divis´ıveis por m
. Dado um n´umero primo p qualquer, existe um n´umero de
Fibonacci divis´ıvel por p, ou seja, nas decomposic¸ ˜oes dos
n´umeros de Fibonacci em fatores primos aparecem todos os
n´umeros primos

18. Aritm´etica dos Restos Aplicac¸ ˜oes Congruˆencia e N´umeros Binomiais O Calend´ario
Aplicac¸ ˜oes
Exemplo 9.26: Seja m um n´umero natural. Definamos
Dm = {n ∈ N; m | un}
Do exemplo anterior, sabemos que Dm = ∅.
Seja m0 o menor elemento de Dm. Vamos mostrar que
Dm = m0N = {m0x; x ∈ N}
. Para achar os n´umeros de Fibonacci divis´ıveis por um
n´umero natural m, basta achar o primeiro deles um0
e tomar
todos os un para os quais n ∈ m0N

19. Aritm´etica dos Restos Aplicac¸ ˜oes Congruˆencia e N´umeros Binomiais O Calend´ario
Outline
1 Aritm´etica dos Restos
2 Aplicac¸ ˜oes
3 Congruˆencia e N´umeros Binomiais
4 O Calend´ario

20. Aritm´etica dos Restos Aplicac¸ ˜oes Congruˆencia e N´umeros Binomiais O Calend´ario
Congruˆencia e N´umeros Binomiais
Lema 9.27: Sejam p, m ∈ N, com p primo
(i) Tem-se que (pm)! = pmMm!, onde M ∈ N e
M ≡ [(p − 1)!]m mod p
(ii) Ep((mp)!) = m + Ep(m!)
Lema 9.28: Sejam a, p ∈ N, com p primo e r um n´umero inteiro
tal que 0 ≤ r < p. Ent˜ao
(i) Ep((pa + r)!) = Ep((pa)!)
(ii) Ep((pa − r)!) = Ep((pa)!) − [1 + Ep(a)]

21. Aritm´etica dos Restos Aplicac¸ ˜oes Congruˆencia e N´umeros Binomiais O Calend´ario
Congruˆencia e N´umeros Binomiais
Lema 9.29: Sejam m, n, p ∈ N, com p primo e n ≤ m e sejam
α, β ∈ N ∪ {0}, com α, β < p. Tem-se que:
(i)
mp
np
=
m
n
mod p
(ii)
mp + α
np + β
=
m
n
α
β
mod p
Teorema 9.30 (E. Lucas): Seja p um n´umero primo e sejam
m = m0 + m1p + m2p2
+ ... e n = n0 + n1p + n2p2
+ ... dois n´umeros
naturais representados relativamente `a base p. Tem-se que
m
n
=
m0
n0
m1
n1
m2
n2
... mod p

22. Aritm´etica dos Restos Aplicac¸ ˜oes Congruˆencia e N´umeros Binomiais O Calend´ario
Congruˆencia e N´umeros Binomiais
Lema 9.31: Sejam p um n´umero primo e α, β ∈ N, com α ≥ β.
Ent˜ao pα−β ´e a maior potˆencia de p que divide
pα
pβ
Teorema 9.32: Seja n ∈ N tal que
n
i
≡ 0 mod n, para
todo i tal que 0 < i < n, ent˜ao n ´e primo
. Mais um teste pouco eficiente de primalidade

23. Aritm´etica dos Restos Aplicac¸ ˜oes Congruˆencia e N´umeros Binomiais O Calend´ario
Outline
1 Aritm´etica dos Restos
2 Aplicac¸ ˜oes
3 Congruˆencia e N´umeros Binomiais
4 O Calend´ario

24. Aritm´etica dos Restos Aplicac¸ ˜oes Congruˆencia e N´umeros Binomiais O Calend´ario
O Calend´ario
. A f´ormula que estabeleceremos ter´a validade a partir do ano
de 1601
. O mˆes de fevereiro estar´a no fim da contagem dos meses, ou
seja, o mˆes 1 de um ano ser´a marc¸o, seguido de abril, etc, at´e
chegar aos meses 11 e 12 que s˜ao janeiro e fevereiro (do ano
seguinte)
. Uma data (d,m,A) ser´a constitu´ıda por trˆes n´umeros, onde d
representa o dia, m o mˆes, com a convenc¸ ˜ao acima
(marc¸o = 1), e A um ano posterior a 1600, ou seja, A ≥ 1601
. Os dias da semana ser˜ao enumerados como: domingo (1),
segunda (2), terc¸a (3), etc, e s´abado (7)

25. Aritm´etica dos Restos Aplicac¸ ˜oes Congruˆencia e N´umeros Binomiais O Calend´ario
O Calend´ario
. Para determinar o dia da semana s(d, m, A) da data (d, m, A)
procederemos por partes
. Determinaremos inicialmente uma f´ormula para s(1, 1, A), o
dia da semana do primeiro dia do mˆes 1 (marc¸o) do ano A,
posteriormente, acharemos uma f´ormula s(1, m, A), o dia da
semana do primeiro dia do mˆes m do ano A e finalmente a
f´ormula para s(d, m, A)

26. Aritm´etica dos Restos Aplicac¸ ˜oes Congruˆencia e N´umeros Binomiais O Calend´ario
O Calend´ario
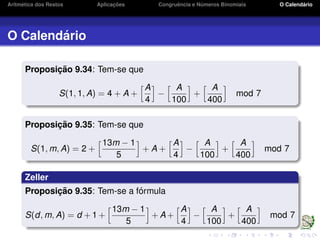
Proposic¸ ˜ao 9.33: Seja A > 1600. Ent˜ao no intervalo (1600, A]
i) o n´umero de anos m´ultiplos de 4 ´e
A
4
−
1600
4
=
A
4
− 400
ii) o n´umero de anos centen´arios que n˜ao s˜ao bissextos ´e
A
100
−
A
400
− 12
iii) o n´umero de anos bissextos ´e
b =
A
4
−
A
100
+
A
400
− 388

27. Aritm´etica dos Restos Aplicac¸ ˜oes Congruˆencia e N´umeros Binomiais O Calend´ario
O Calend´ario
Proposic¸ ˜ao 9.34: Tem-se que
S(1, 1, A) = 4 + A +
A
4
−
A
100
+
A
400
mod 7
Proposic¸ ˜ao 9.35: Tem-se que
S(1, m, A) = 2 +
13m − 1
5
+ A +
A
4
−
A
100
+
A
400
mod 7
Zeller
Proposic¸ ˜ao 9.35: Tem-se a f´ormula
S(d, m, A) = d + 1 +
13m − 1
5
+ A +
A
4
−
A
100
+
A
400
mod 7