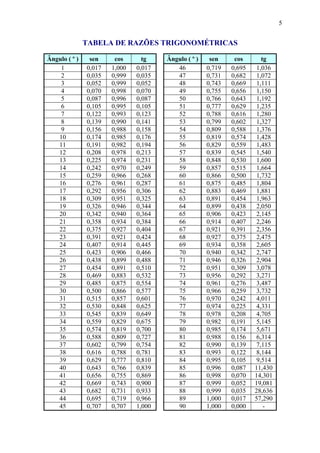
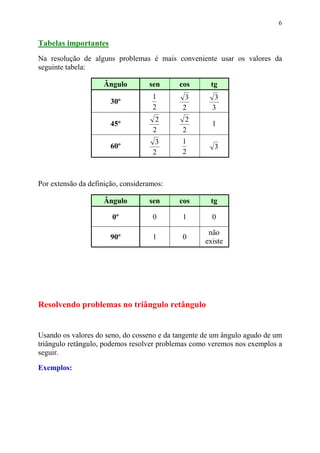
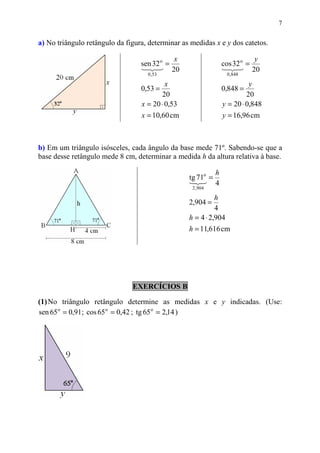
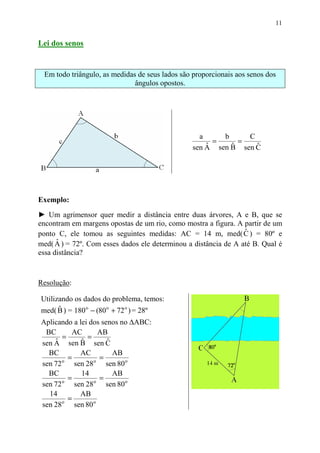
Este documento fornece informações sobre relações trigonométricas em triângulos retângulos e não retângulos. Ele define seno, cosseno e tangente para triângulos retângulos e apresenta uma tabela trigonométrica com esses valores para vários ângulos. Também mostra como resolver problemas usando essas relações trigonométricas e apresenta as leis do seno e do cosseno para triângulos não retângulos.

1. Relações trigonométricas nos triângulos
Profa. Dra. Denise Ortigosa Stolf
Sumário Página
Razões trigonométricas no triângulo retângulo .............................................................. 1
Seno .......................................................................................................................... 1
Cosseno .................................................................................................................... 2
Tangente ................................................................................................................... 2
Tabela trigonométrica ..................................................................................................... 4
Tabelas importantes.................................................................................................. 6
Resolvendo problemas no triângulo retângulo ............................................................... 6
Relações entre seno, cosseno e tangente......................................................................... 9
Relações trigonométricas em um triângulo qualquer ................................................... 10
Lei dos senos .......................................................................................................... 11
Lei dos cossenos ..................................................................................................... 12
Referências bibliográficas............................................................................................. 16

2. 1
Relações trigonométricas nos triângulos
Razões trigonométricas no triângulo retângulo
Um triângulo é uma figura geométrica plana, constituída por três lados e três
ângulos internos. Esses ângulos, tradicionalmente, são medidos numa unidade
de medida, denominada grau e, cada um deles tem medida entre 0o e 180o, de
modo que, em qualquer triângulo, a soma dessas medidas é 180o.
Num triângulo retângulo definimos as chamadas razões trigonométricas que são
relações entre os lados do triângulo e que têm a propriedade de determinar a
medida dos ângulos do triângulo, uma vez que seus lados sejam conhecidos.
Um triângulo é dito retângulo quando um de seus ângulos é reto, isto é, tem
medida igual a 90o. Os outros dois ângulos, evidentemente, são agudos.
No triângulo retângulo ABC, consideremos, por exemplo, o ângulo que tem
vértice em B, cuja medida α, em graus, é um número real que está no intervalo
]0,90[. Entre os lados do triângulo podemos estabelecer as seguintes razões:
Seno
Seno de α é a razão entre o comprimento do cateto oposto ao ângulo B e o
ˆ
comprimento da hipotenusa do triângulo. Indicando o seno de α por sen α,
AC
temos: sen α = .
BC
Dado um segmento AB , indicamos o comprimento de AB por AB, onde
AB = med( AB ).

3. 2
Cosseno
Cosseno de α é a razão entre o comprimento do cateto adjacente ao ângulo B e
ˆ
o comprimento da hipotenusa do triângulo. Indicando o cosseno de α por cos α,
AB
temos: cos α = .
BC
Tangente
Tangente de α é a razão entre os comprimentos do cateto oposto e do cateto
AC
adjacente ao ângulo B . Indicando a tangente de x por tg α, temos: tg α =
ˆ .
AB
sen α
Observação: De acordo com a definição, é fácil verificar que tg α = , para
cos α
todo α variando no intervalo ]0,90[.
Exemplo:
► No triângulo retângulo ABC, determine o valor do seno, cosseno e tangente
ˆ
do ângulo C .
Resolução:
Representando a medida da hipotenusa por x, calculamos esse valor aplicando o
teorema de Pitágoras no ∆ABC.
x 2 = 5 2 + 12 2 sen β =
CO
cos β =
CA
tg β =
CO
x 2 = 25 + 144 H H CA
5 12 5
x 2 = 169 sen β = cos β = tg β =
13 13 12
x = 169
x = 13

4. 3
EXERCÍCIOS A
(1) Considerando que 5 = 2,23 , determine o valor do seno, do cosseno e da
ˆ
tangente do ângulo B no triângulo retângulo ABC da figura abaixo.
(2) A figura seguinte é um triângulo eqüilátero ABC, onde cada ângulo interno
vale 60º. Traçando-se a altura AH , teremos um triângulo retângulo AHC.
l 3
Sabendo que h = (você já conhece essa fórmula), considere o triângulo
2
retângulo AHC e determine o valor de sen 60º, cos 60º e tg 60º, deixando esses
valores na forma de radical.

5. 4
(3) Usando a mesma figura e o mesmo triângulo retângulo AHC (do exercício
anterior), determine o valor de sen 30º, cos 30º e tg 30º, pois a altura AH
ˆ
coincide com a bissetriz do ângulo interno A , no triângulo eqüilátero (deixar a
resposta na forma de radical).
(4) No triângulo retângulo, determine o valor do seno, do cosseno e da tangente
do ângulo de 45º (deixar a resposta na forma de radical).
Tabela trigonométrica
Em muitos casos, para resolver problemas com triângulos retângulos é
necessário conhecer as razões trigonométricas dos ângulos agudos do triângulo.
Como a cada ângulo agudo está associado um único valor para o seno, para o
cosseno e para a tangente, podemos elaborar uma tabela que nos forneça esses
valores, evitando assim a necessidade de calculá-los a toda hora.
A tabela a seguir foi construída há séculos, e nos dá os valores do seno, do
cosseno e da tangente de ângulos de 1º até 89º, com aproximação até milésimos.
A maioria das calculadoras, hoje em dia, nos fornecem esses valores.

6. 5
TABELA DE RAZÕES TRIGONOMÉTRICAS
Ângulo ( º ) sen cos tg Ângulo ( º ) sen cos tg
1 0,017 1,000 0,017 46 0,719 0,695 1,036
2 0,035 0,999 0,035 47 0,731 0,682 1,072
3 0,052 0,999 0,052 48 0,743 0,669 1,111
4 0,070 0,998 0,070 49 0,755 0,656 1,150
5 0,087 0,996 0,087 50 0,766 0,643 1,192
6 0,105 0,995 0,105 51 0,777 0,629 1,235
7 0,122 0,993 0,123 52 0,788 0,616 1,280
8 0,139 0,990 0,141 53 0,799 0,602 1,327
9 0,156 0,988 0,158 54 0,809 0,588 1,376
10 0,174 0,985 0,176 55 0,819 0,574 1,428
11 0,191 0,982 0,194 56 0,829 0,559 1,483
12 0,208 0,978 0,213 57 0,839 0,545 1,540
13 0,225 0,974 0,231 58 0,848 0,530 1,600
14 0,242 0,970 0,249 59 0,857 0,515 1,664
15 0,259 0,966 0,268 60 0,866 0,500 1,732
16 0,276 0,961 0,287 61 0,875 0,485 1,804
17 0,292 0,956 0,306 62 0,883 0,469 1,881
18 0,309 0,951 0,325 63 0,891 0,454 1,963
19 0,326 0,946 0,344 64 0,899 0,438 2,050
20 0,342 0,940 0,364 65 0,906 0,423 2,145
21 0,358 0,934 0,384 66 0,914 0,407 2,246
22 0,375 0,927 0,404 67 0,921 0,391 2,356
23 0,391 0,921 0,424 68 0,927 0,375 2,475
24 0,407 0,914 0,445 69 0,934 0,358 2,605
25 0,423 0,906 0,466 70 0,940 0,342 2,747
26 0,438 0,899 0,488 71 0,946 0,326 2,904
27 0,454 0,891 0,510 72 0,951 0,309 3,078
28 0,469 0,883 0,532 73 0,956 0,292 3,271
29 0,485 0,875 0,554 74 0,961 0,276 3,487
30 0,500 0,866 0,577 75 0,966 0,259 3,732
31 0,515 0,857 0,601 76 0,970 0,242 4,011
32 0,530 0,848 0,625 77 0,974 0,225 4,331
33 0,545 0,839 0,649 78 0,978 0,208 4,705
34 0,559 0,829 0,675 79 0,982 0,191 5,145
35 0,574 0,819 0,700 80 0,985 0,174 5,671
36 0,588 0,809 0,727 81 0,988 0,156 6,314
37 0,602 0,799 0,754 82 0,990 0,139 7,115
38 0,616 0,788 0,781 83 0,993 0,122 8,144
39 0,629 0,777 0,810 84 0,995 0,105 9,514
40 0,643 0,766 0,839 85 0,996 0,087 11,430
41 0,656 0,755 0,869 86 0,998 0,070 14,301
42 0,669 0,743 0,900 87 0,999 0,052 19,081
43 0,682 0,731 0,933 88 0,999 0,035 28,636
44 0,695 0,719 0,966 89 1,000 0,017 57,290
45 0,707 0,707 1,000 90 1,000 0,000 -

7. 6
Tabelas importantes
Na resolução de alguns problemas é mais conveniente usar os valores da
seguinte tabela:
Ângulo sen cos tg
1 3 3
30º
2 2 3
2 2
45º 1
2 2
3 1
60º 3
2 2
Por extensão da definição, consideramos:
Ângulo sen cos tg
0º 0 1 0
não
90º 1 0
existe
Resolvendo problemas no triângulo retângulo
Usando os valores do seno, do cosseno e da tangente de um ângulo agudo de um
triângulo retângulo, podemos resolver problemas como veremos nos exemplos a
seguir.
Exemplos:

8. 7
a) No triângulo retângulo da figura, determinar as medidas x e y dos catetos.
x y
sen 32 o = cos 32 o =
123 20 123 20
0 ,53 0 ,848
x y
0,53 = 0,848 =
20 20
x = 20 ⋅ 0,53 y = 20 ⋅ 0,848
x = 10,60 cm y = 16,96 cm
b) Em um triângulo isósceles, cada ângulo da base mede 71º. Sabendo-se que a
base desse retângulo mede 8 cm, determinar a medida h da altura relativa à base.
h
tg 71o =
13 4
2
2 , 904
h
2,904 =
4
h = 4 ⋅ 2,904
h = 11,616 cm
EXERCÍCIOS B
(1) No triângulo retângulo determine as medidas x e y indicadas. (Use:
sen 65 o = 0,91; cos 65 o = 0,42 ; tg 65 o = 2,14 )

9. 8
(2) Considerando o triângulo retângulo ABC, determine as medidas a e b
indicadas.
(3) Na figura temos que PA = 18 cm. Nessas condições, calcule:
a) o comprimento r do raio da circunferência;
b) a distância x do ponto P ao centro O.
(4) A determinação feita por radares da altura de uma nuvem em relação ao solo
é importante para previsões meteorológicas e na orientação de aviões para que
evitem turbulências. Nessas condições, determine a altura das nuvens detectadas
pelos radares conforme o desenho seguinte.
(Use: sen 28 o = 0,47 ; cos 28 o = 0,88 ; tg 28 o = 0,53 )

10. 9
Relações entre seno, cosseno e tangente
As razões trigonométricas seno, cosseno e tangente se relacionam de várias
formas, como veremos a seguir:
1ª) sen 2 θ + cos 2 θ = 1 ( 0 o < θ < 90 o )
sen θ
2ª) tg θ = ( 0 o < θ < 90 o )
cos θ
Exemplo:
► Sabendo que sen α = 0,6 , determine o cos α e a tg α .
sen 2 α + cos 2 α = 1 tg α =
sen α
(0,6) 2 + cos 2 α = 1 cos α
0,6
0,36 + cos 2 α = 1 tg α =
0,8
cos 2 α = 1 − 0,36 tg α = 0,75
cos 2 α = 0,64
cos α = 0,64
64
cos α =
100
8
cos α =
10
cos α = 0,8
Então, cos α = 0,8 e tg α = 0,75 .

11. 10
EXERCÍCIOS C
2 2 17
(1) Sabendo que sen α = e cos α = , calcule o valor de tg α .
5 5
12
(2) No triângulo retângulo da figura, temos cos α = . Calcule:
13
a) o sen α e a tg α ;
b) a medida x da hipotenusa.
Relações trigonométricas em um triângulo qualquer
As relações trigonométricas estudadas até agora foram utilizadas em triângulos
retângulos. Vamos conhecer outras relações que valem para quaisquer
triângulos.

12. 11
Lei dos senos
Em todo triângulo, as medidas de seus lados são proporcionais aos senos dos
ângulos opostos.
a b C
= =
ˆ ˆ ˆ
sen A sen B sen C
Exemplo:
► Um agrimensor quer medir a distância entre duas árvores, A e B, que se
encontram em margens opostas de um rio, como mostra a figura. A partir de um
ˆ
ponto C, ele tomou as seguintes medidas: AC = 14 m, med( C ) = 80º e
ˆ
med( A ) = 72º. Com esses dados ele determinou a distância de A até B. Qual é
essa distância?
Resolução:
Utilizando os dados do problema, temos:
med( B ) = 180 o − (80 o + 72 o ) = 28º
ˆ
Aplicando a lei dos senos no ∆ABC:
BC AC AB
= =
ˆ ˆ
sen A sen B sen C ˆ
BC AC AB
o
= o
=
sen 72 sen 28 sen 80 o
BC 14 AB
= =
sen 72 o sen 28 o sen 80 o
14 AB
o
=
sen 28 sen 80 o

13. 12
Na tabela trigonométrica encontramos os valores de sen 28o e sen 80 o .
14 AB
=
0,469 0,985
0,469 AB = 14 ⋅ 0,985
13,79
AB =
0,469
AB = 29,4
Portanto, a distância entre as duas árvores é aproximadamente de 29,4 m.
Lei dos cossenos
Em todo triângulo, o quadrado da medida de um dos lados é igual à soma dos
quadrados das medidas dos outros dois lados menos duas vezes o produto das
medidas desses dois lados pelo cosseno do ângulo oposto ao primeiro lado.
a 2 = b 2 + c 2 − 2 ⋅ b ⋅ c ⋅ cos A
ˆ
b 2 = a 2 + c 2 − 2 ⋅ a ⋅ c ⋅ cos B
ˆ
c 2 = a 2 + b 2 − 2 ⋅ a ⋅ b ⋅ cos C
ˆ
Exemplo:

14. 13
► No triângulo ABC, as medidas de dois lados são 10 cm e 6 cm e o ângulo
formado por esses lados mede 50º. Qual é a medida do terceiro lado?
Resolução:
Como são dadas as medidas de dois lados e o
ângulo formado por eles, podemos aplicar a lei dos
cossenos.
a 2 = b 2 + c 2 − 2 ⋅ b ⋅ c ⋅ cos A
ˆ
a 2 = 6 2 + 10 2 − 2 ⋅ 6 ⋅10 ⋅ cos 50 o
Na tabela trigonométrica temos cos 50 o = 0,643
a 2 = 6 2 + 10 2 − 2 ⋅ 6 ⋅10 ⋅ cos 50 o
a 2 = 36 + 100 − 120 ⋅ 0,643
a 2 = 136 − 77,16
a 2 = 58,84
5884
a=
100
2 1471
a=
10
1471
a=
5
1471
Portanto, o terceiro lado mede cm.
5

15. 14
EXERCÍCIOS D
ˆ ˆ
(1) No triângulo ABC, o ângulo B mede 60º, o ângulo C mede 45º e o lado AB
mede 3 2 cm. Calcule a medida do lado AC.
(2) No triângulo RMP, determine o valor de x sabendo que: MP = 18 cm,
ˆ ˆ
med( M ) = 45º e med( P ) = 75º.

16. 15
(3) O ∆CNT possui dois lados que medem 4 cm e 3 3 cm. O ângulo formado
por esses lados mede 30º. Qual é a medida do lado oposto a esse ângulo?
ˆ
(4) Observe as medidas marcadas na figura e calcule a medida do ângulo A .

17. 16
Referências bibliográficas
ANDRINI, Álvaro; VASCONCELLOS, Maria José. Novo praticando
matemática. São Paulo: Brasil, 2002.
BIGODE, Antonio José Lopes. Matemática hoje é feita assim. São Paulo:
FTD, 2006.
DANTE, Luiz Roberto. Tudo é matemática. São Paulo: Ática, 2005.
E-CÁLCULO. Disponível em: <http://ecalculo.if.usp.br>. Acesso em: 9 de
outubro de 2008.
EDIÇÕES EDUCATIVAS DA EDITORA MODERNA. Projeto Araribá:
Matemática. São Paulo: Moderna, 2007.
GIOVANNI, José Ruy; GIOVANNI JUNIOR, José Ruy. Matemática: pensar e
descobrir. São Paulo: FTD, 2005.
GIOVANNI, José Ruy; CASTRUCCI; Benedito; GIOVANNI JUNIOR, José
Ruy. A conquista da matemática. São Paulo: FTD, 1998.
GUELLI, Oscar. Matemática em construção. São Paulo: Ática, 2004.
IMENES, Luiz Márcio; LELLIS, Marcelo Cestari. Matemática paratodos. São
Paulo: Scipione, 2006.
KLICK EDUCAÇÃO: O PORTAL DA EDUCAÇÃO. Disponível em:
<http://www.klickeducacao.com.br>. Acesso em: 9 de outubro de 2008.
MIANI, Marcos. Matemática no plural. São Paulo: IBEP, 2006.
MORI, Iracema; ONAGA, Dulce Onaga. Matemática: idéias e desafios. São
Paulo: Saraiva, 1997.
SÓ MATEMÁTICA. Disponível em: <http://www.somatematica.com.br>.
Acesso em: 21 de agosto de 2008.