O documento apresenta um curso sobre variáveis complexas que aborda:
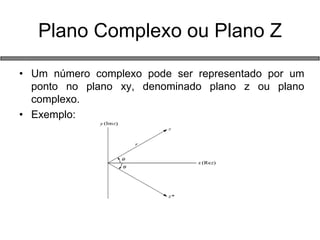
1) Números complexos, operações e representações geométricas;
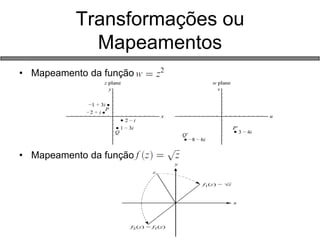
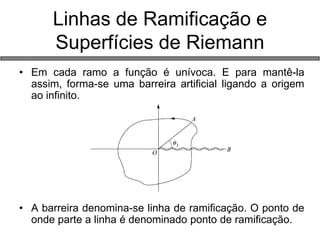
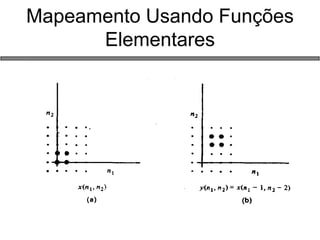
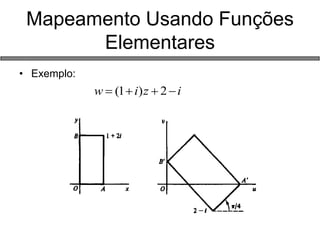
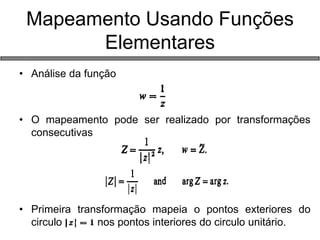
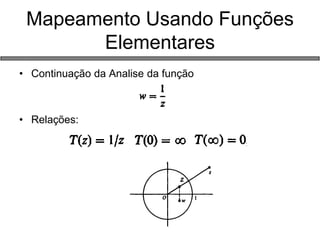
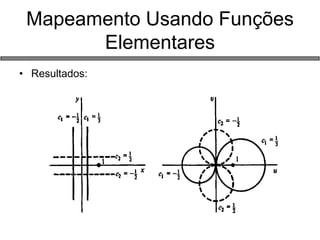
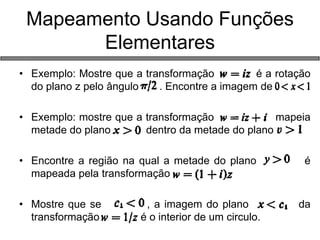
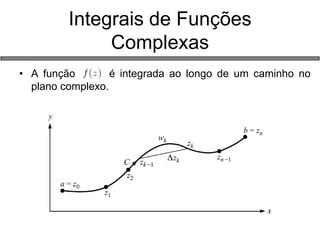
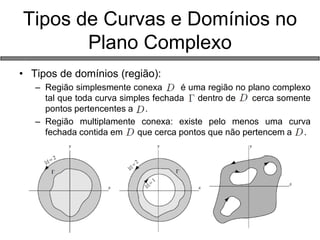
2) Funções de variáveis complexas, propriedades analíticas e mapeamentos;
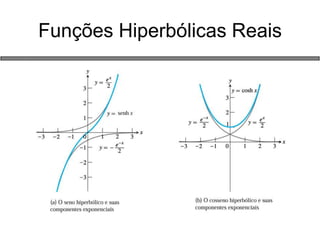
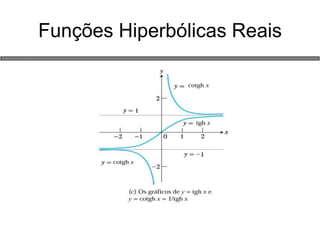
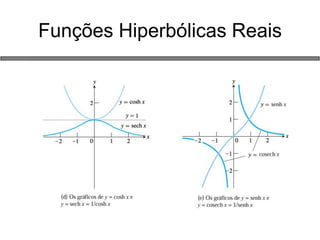
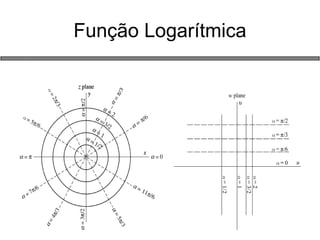
3) Funções elementares como exponencial, trigonométricas e logarítmica.