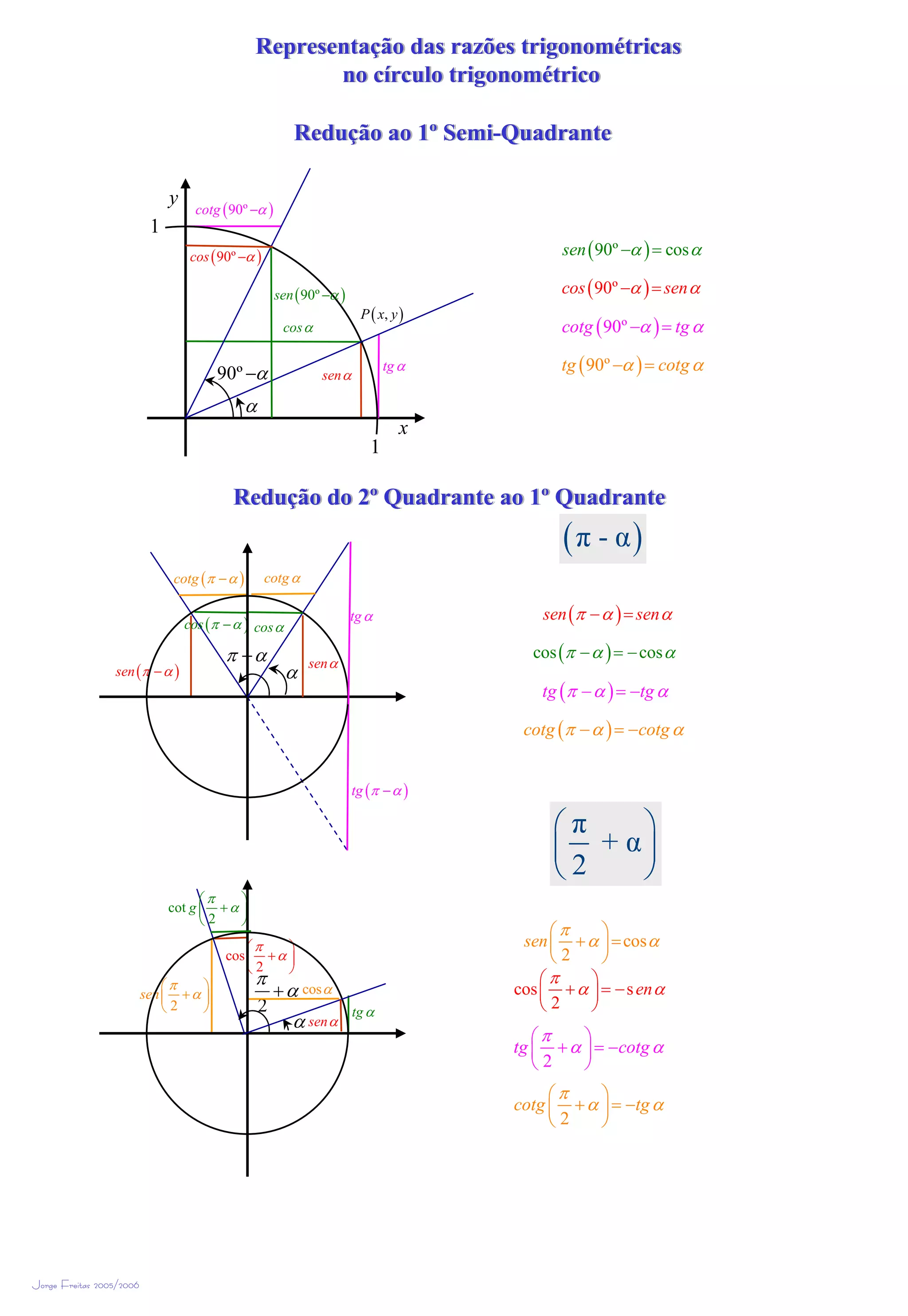
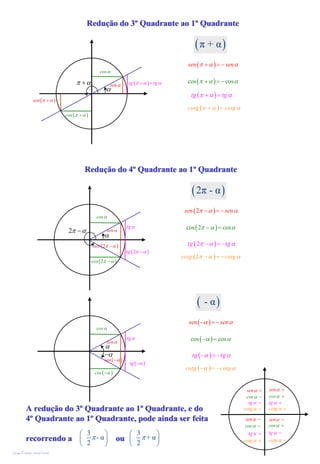
1) O documento descreve a representação das funções trigonométricas (seno, cosseno, tangente e cotangente) no círculo trigonométrico e como reduzir ângulos para o primeiro quadrante. 2) Ele explica como reduzir ângulos dos quadrantes 2, 3 e 4 para o primeiro quadrante usando propriedades trigonométricas como seno(π-α) = seno(α). 3) A redução dos quadrantes 3 e 4 também pode ser feita usando 2π±α.

1. Representação das razões trigonométricas
no círculo trigonométrico
Redução ao 1º Semi-Quadrante
y
cotg ( 90º −α )
1
cos ( 90º −α ) sen ( 90º −α ) = cos α
sen ( 90º −α ) cos ( 90º −α ) = sen α
P ( x, y )
cos α cotg ( 90º −α ) = tg α
90º −α tg α tg ( 90º −α ) = cotg α
sen α
α
x
1
Redução do 2º Quadrante ao 1º Quadrante
( π - α)
cotg (π − α ) cotg α
tg α sen (π − α ) = sen α
cos (π − α ) cos α
π −α cos (π − α ) = − cos α
sen α
sen (π − α ) α
tg (π − α ) = −tg α
cotg (π − α ) = −cotg α
tg (π − α )
⎛π ⎞
⎜ + α⎟
⎝2 ⎠
⎛π ⎞
cot g ⎜ + α ⎟
⎝2 ⎠
⎛π ⎞
⎛π ⎞ sen ⎜ + α ⎟ = cos α
cos ⎜ + α ⎟ ⎝ 2 ⎠
⎝2 ⎠
⎛π π ⎛π ⎞
cos ⎜ + α ⎟ = − s en α
⎞
sen ⎜ + α ⎟ + α cos α
⎝2 ⎠ 2 tg α ⎝2 ⎠
α sen α
⎛π ⎞
tg ⎜ + α ⎟ = −cotg α
⎝2 ⎠
⎛π ⎞
cotg ⎜ + α ⎟ = −tg α
⎝2 ⎠
Jorge Freitas 2005/2006

2. Redução do 3º Quadrante ao 1º Quadrante
( π + α)
sen (π + α ) = − sen α
cos α
π +α tg (π + α ) = tg α cos (π + α ) = − cos α
sen α
α
tg (π + α ) = tg α
sen (π + α )
cotg (π + α ) = cotg α
cos (π + α )
Redução do 4º Quadrante ao 1º Quadrante
( 2π - α )
sen ( 2π − α ) = − sen α
cos α
tg α cos ( 2π − α ) = cos α
2π − α sen α
α
sen ( 2π − α ) tg ( 2π − α ) = −tg α
tg ( 2π − α )
cotg ( 2π − α ) = − cotg α
cos ( 2π − α )
( - α)
sen ( −α ) = − sen α
cos α
sen α
tg α cos ( −α ) = cos α
α
−α tg ( −α ) = −tg α
sen ( −α )
tg ( −α )
cotg ( −α ) = − cotg α
cos ( −α )
sen α + sen α +
cos α − cos α +
tg α − tg α +
A redução do 3º Quadrante ao 1º Quadrante, e do cotg α − cotg α +
4º Quadrante ao 1º Quadrante, pode ainda ser feita sen α − sen α −
cos α − cos α +
⎛ 3 ⎞ ⎛ 3 ⎞ tg α + tg α −
recorrendo a ⎜ 2 π - α ⎟ ou ⎜ 2 π + α ⎟ cotg α + cotg α −
⎝ ⎠ ⎝ ⎠
Jorge Freitas 2005/2006