O documento discute algoritmos de recursividade, divisão e conquista, explicando conceitos fundamentais como fatorial, soma de números e algoritmos de busca binária. Ele também aborda métodos de ordenação como mergesort e quicksort, apresentando suas implementações e análises de complexidade. Através de exemplos e exercícios, o texto explora a eficácia e a natureza recursiva desses algoritmos.

1. An´alise de Algoritmos
Recursividade
Divisão e Conquista
– p. 1/71

2. Recursividade
Muitos problemas possuem a seguinte
propriedade: uma solução pode ser obtida através
da solução de instâncias menores do mesmo
problema. Dizemos que esses problemas têm
natureza recursiva.
Para resolver um tal problema podemos aplicar o
seguinte método:
– p. 2/71

3. Recursividade
se a instância em questão é pequena, resolva-a
diretamente
– p. 3/71

4. Recursividade
se a instância em questão é pequena, resolva-a
diretamente
senão,
reduza-a a instâncias menores do mesmo
problema,
resolva os problemas menores
recursivamente,
resolva o problema original.
– p. 3/71

5. Recursividade
se a instância em questão é pequena, resolva-a
diretamente
senão,
reduza-a a instâncias menores do mesmo
problema,
resolva os problemas menores
recursivamente,
resolva o problema original.
A aplicação desse método produz um algoritmo
recursivo. – p. 3/71

6. Fatorial
Fat(n) = n.(n − 1). . . . .2.1
– p. 4/71

7. Fatorial
Fat(n) = n. (n − 1). . . . .2.1
Fat(n − 1)
– p. 5/71

8. Fatorial
Fat(n) = n. (n − 1). . . . .2.1
Fat(n − 1)
Fat(n) = n.Fat(n − 1)
– p. 5/71

9. Fatorial
Fat(n) = n. (n − 1). . . . .2.1
Fat(n − 1)
Fat(n) = n.Fat(n − 1)
Fat(n) =



1 se n = 0,
n.Fat(n − 1) se n > 0
– p. 5/71

10. Fatorial - algoritmo
Algoritmo: Fat(n)
Entrada: Um inteiro n ≥ 0
Saída: n!
– p. 6/71

11. Fatorial - algoritmo
Algoritmo: Fat(n)
Entrada: Um inteiro n ≥ 0
Saída: n!
Início
Se n = 0 então retorne(1)
senão retorne(n.Fat(n − 1))
Fim
– p. 6/71

12. Fatorial - algoritmo
Algoritmo: Fat(n)
Entrada: Um inteiro n ≥ 0
Saída: n!
Início
Se n = 0 então retorne(1)
senão retorne(n.Fat(n − 1))
Fim
A condição de parada é fundamental!!!
– p. 6/71

13. Soma de n números
Algoritmo: Soma(n, A)
Entrada: Um inteiro n > 0 e um vetor A[1..n]
Saída: O valor A1 + A2 + · · · + An
– p. 7/71

14. Soma de n números
Algoritmo: Soma(n, A)
Entrada: Um inteiro n > 0 e um vetor A[1..n]
Saída: O valor A1 + A2 + · · · + An
Início
Se n = 1 então retorne(A1)
Senão retorne(An + Soma(n − 1, A))
Fim
– p. 7/71

15. Exercícios
1. Escreva um algoritmo recursivo para determinar
o (um) maior elemento de um vetor A[1..n] de
inteiros.
– p. 8/71

16. Busca binária – recursivo
– p. 9/71

17. Busca binária – recursivo
Algoritmo: Buscabin (l, r)
Entrada: Um par (l, r) representando A[l..r]
Saída: (“sim”, k) ou “não”
– p. 9/71

18. Busca binária – recursivo
Algoritmo: Buscabin (l, r)
Entrada: Um par (l, r) representando A[l..r]
Saída: (“sim”, k) ou “não”
Início
Se l > r então imprima “não”
– p. 9/71

19. Busca binária – recursivo
Algoritmo: Buscabin (l, r)
Entrada: Um par (l, r) representando A[l..r]
Saída: (“sim”, k) ou “não”
Início
Se l > r então imprima “não”
senão
k ← (l + r)/2 ;
Se x = Mk então imprima (“sim”, k)
– p. 9/71

20. Busca binária – recursivo
Algoritmo: Buscabin (l, r)
Entrada: Um par (l, r) representando A[l..r]
Saída: (“sim”, k) ou “não”
Início
Se l > r então imprima “não”
senão
k ← (l + r)/2 ;
Se x = Mk então imprima (“sim”, k)
senão se x > Mk então Buscabin (k + 1, r)
senão Buscabin (l, k − 1)
Fim
– p. 9/71

21. Busca binária – recursivo
Algoritmo: Buscabin (l, r)
Entrada: Um par (l, r) representando A[l..r]
Saída: (“sim”, k) ou “não”
Início
Se l > r então imprima “não”
senão
k ← (l + r)/2 ;
Se x = Mk então imprima (“sim”, k)
senão se x > Mk então Buscabin (k + 1, r)
senão Buscabin (l, k − 1)
Fim
Qual o tempo (pior caso) gasto pelo algoritmo?
– p. 9/71

22. Busca binária – recursivo
Algoritmo: Buscabin (l, r)
Entrada: Um par (l, r) representando A[l..r]
Saída: (“sim”, k) ou “não”
Início
Se l > r então imprima “não”
senão
k ← (l + r)/2 ;
Se x = Mk então imprima (“sim”, k)
senão se x > Mk então Buscabin (k + 1, r)
senão Buscabin (l, k − 1)
Fim
Qual o tempo (pior caso) gasto pelo algoritmo?
Resposta: O(log n)
– p. 9/71

23. An´alise de Algoritmos
Ordenação por intercalação
(Mergesort)
– p. 10/71

24. Ordenação por intercalação – mergesort
Algoritmo: Ordinter(l, r)
Entrada: Um par (l, r) representando A[l..r]
Saída: A[l..r] em ordem não decrescente
– p. 11/71

25. Ordenação por intercalação – mergesort
Algoritmo: Ordinter(l, r)
Entrada: Um par (l, r) representando A[l..r]
Saída: A[l..r] em ordem não decrescente
Início
Se l = r então retorne(Al)
– p. 11/71

26. Ordenação por intercalação – mergesort
Algoritmo: Ordinter(l, r)
Entrada: Um par (l, r) representando A[l..r]
Saída: A[l..r] em ordem não decrescente
Início
Se l = r então retorne(Al)
senão
k ← (l + r)/2 ;
L1 ← Ordinter(1, k); L2 ← Ordinter(k + 1, j);
L3 ← Intercala(L1, L2);
retorne(L3)
Fim
– p. 11/71

27. Ordenação por intercalação – mergesort
Algoritmo: Ordinter(l, r)
Entrada: Um par (l, r) representando A[l..r]
Saída: A[l..r] em ordem não decrescente
Início
Se l = r então retorne(Al)
senão
k ← (l + r)/2 ;
L1 ← Ordinter(1, k); L2 ← Ordinter(k + 1, j);
L3 ← Intercala(L1, L2);
retorne(L3)
Fim
Qual o tempo gasto pelo algoritmo?
– p. 11/71

28. Ordenação por intercalação – mergesort
O tempo gasto pelo mergesort pode ser descrito
pela recorrência
– p. 12/71

29. Ordenação por intercalação – mergesort
O tempo gasto pelo mergesort pode ser descrito
pela recorrência
T(n) = T( n/2 ) + T( n/2 ) + n, T(1) = 0
– p. 12/71

30. Ordenação por intercalação – mergesort
O tempo gasto pelo mergesort pode ser descrito
pela recorrência
T(n) = T( n/2 ) + T( n/2 ) + n, T(1) = 0
Uma forma mais imediata de resolvê-la é observar
que
T(n) ≤ 2T( n/2 ) + n
e aplicar o método master, o que resulta em
T(n) = O(n log n)
– p. 12/71

31. Exercícios
1. Escreva o algoritmo Intercala(L1, L2) para intercalar
dois vetores ordenados.
– p. 13/71

32. An´alise de Algoritmos
Ordenação por concatenação
(Quicksort)
– p. 14/71

33. Ordenação por concatenação – quicksort
Algoritmo: Ordconc(l, r)
Entrada: Um par (l, r) representando A[l..r]
Saída: A[l..r] em ordem não decrescente
– p. 15/71

34. Ordenação por concatenação – quicksort
Algoritmo: Ordconc(l, r)
Entrada: Um par (l, r) representando A[l..r]
Saída: A[l..r] em ordem não decrescente
Início
Se l < r então
j ← Partição(l, r);
Ordconc(1, j − 1);
Ordconc(j + 1, r);
Fim
– p. 15/71

35. Ordenação por concatenação – quicksort
Algoritmo: Ordconc(l, r)
Entrada: Um par (l, r) representando A[l..r]
Saída: A[l..r] em ordem não decrescente
Início
Se l < r então
j ← Partição(l, r);
Ordconc(1, j − 1);
Ordconc(j + 1, r);
Fim
Qual o tempo (pior caso) gasto pelo algoritmo?
– p. 15/71

36. Ordenação por concatenação – quicksort
Algoritmo: Ordconc(l, r)
Entrada: Um par (l, r) representando A[l..r]
Saída: A[l..r] em ordem não decrescente
Início
Se l < r então
j ← Partição(l, r);
Ordconc(1, j − 1);
Ordconc(j + 1, r);
Fim
Qual o tempo (pior caso) gasto pelo algoritmo?
Resposta: O(n2). Porém, o tempo médio é O(n log n)
– p. 15/71

37. Quicksort – partição
Algoritmo: Partição(l, r)
Entrada: (l, r) representando A[l..r]
Saída: Um valor j tal que A[l..j − 1] são menores do que Aj
que, por sua vez, é menor ou igual a A[j + 1..r].
– p. 16/71

38. Quicksort – partição
Algoritmo: Partição(l, r)
Entrada: (l, r) representando A[l..r]
Saída: Um valor j tal que A[l..j − 1] são menores do que Aj
que, por sua vez, é menor ou igual a A[j + 1..r].
Início
j ← l; k ← r;
– p. 16/71

39. Quicksort – partição
Algoritmo: Partição(l, r)
Entrada: (l, r) representando A[l..r]
Saída: Um valor j tal que A[l..j − 1] são menores do que Aj
que, por sua vez, é menor ou igual a A[j + 1..r].
Início
j ← l; k ← r;
Enquanto (j < k) faça
– p. 16/71

40. Quicksort – partição
Algoritmo: Partição(l, r)
Entrada: (l, r) representando A[l..r]
Saída: Um valor j tal que A[l..j − 1] são menores do que Aj
que, por sua vez, é menor ou igual a A[j + 1..r].
Início
j ← l; k ← r;
Enquanto (j < k) faça
Enquanto (j < k) e (Aj ≤ Ak) faça k ← k − 1;
Se j < k então { Troca(Mj, Mk); j ← j + 1 }
– p. 16/71

41. Quicksort – partição
Algoritmo: Partição(l, r)
Entrada: (l, r) representando A[l..r]
Saída: Um valor j tal que A[l..j − 1] são menores do que Aj
que, por sua vez, é menor ou igual a A[j + 1..r].
Início
j ← l; k ← r;
Enquanto (j < k) faça
Enquanto (j < k) e (Aj ≤ Ak) faça k ← k − 1;
Se j < k então { Troca(Mj, Mk); j ← j + 1 }
Enquanto (Aj < Ak) faça j ← j + 1;
Se j < k então { Troca(Mj, Mk); k ← k − 1 }
retorne(j)
Fim
– p. 16/71

42. Quicksort – partição
Algoritmo: Partição(l, r)
Entrada: (l, r) representando A[l..r]
Saída: Um valor j tal que A[l..j − 1] são menores do que Aj
que, por sua vez, é menor ou igual a A[j + 1..r].
Início
j ← l; k ← r;
Enquanto (j < k) faça
Enquanto (j < k) e (Aj ≤ Ak) faça k ← k − 1;
Se j < k então { Troca(Mj, Mk); j ← j + 1 }
Enquanto (Aj < Ak) faça j ← j + 1;
Se j < k então { Troca(Mj, Mk); k ← k − 1 }
retorne(j)
Fim
Qual o tempo (pior caso) gasto pelo algoritmo?
– p. 16/71

43. Quicksort – partição
Algoritmo: Partição(l, r)
Entrada: (l, r) representando A[l..r]
Saída: Um valor j tal que A[l..j − 1] são menores do que Aj
que, por sua vez, é menor ou igual a A[j + 1..r].
Início
j ← l; k ← r;
Enquanto (j < k) faça
Enquanto (j < k) e (Aj ≤ Ak) faça k ← k − 1;
Se j < k então { Troca(Mj, Mk); j ← j + 1 }
Enquanto (Aj < Ak) faça j ← j + 1;
Se j < k então { Troca(Mj, Mk); k ← k − 1 }
retorne(j)
Fim
Qual o tempo (pior caso) gasto pelo algoritmo? O(r − l).
– p. 16/71

44. Exercícios
1. Execute o algoritmo partição no caso em que
todos os elementos do vetor A[l..r] são iguais
entre si. O que voce observa? Qual o valor de j
que o algoritmo devolve?
2. Exiba uma instância de pior caso do algoritmo
partição?
– p. 17/71

45. An´alise de Algoritmos
Tempo médio do Quicksort
– p. 18/71

46. Tempo médio do quicksort
Teorema: O tempo médio gasto pelo quicksort para
ordenar um vetor A[1..n] é O(n log n), supondo que
cada uma das n! permutações dos n elementos de
A tem a mesma probabilidade de ocorrer como
entrada.
– p. 19/71

47. Tempo médio do quicksort
Teorema: O tempo médio gasto pelo quicksort para
ordenar um vetor A[1..n] é O(n log n), supondo que
cada uma das n! permutações dos n elementos de
A tem a mesma probabilidade de ocorrer como
entrada.
Dem.: A rapidez média T(n) em questão pode ser
expressa pela seguinte recorrência:
– p. 19/71

48. Tempo médio do quicksort
Teorema: O tempo médio gasto pelo quicksort para
ordenar um vetor A[1..n] é O(n log n), supondo que
cada uma das n! permutações dos n elementos de
A tem a mesma probabilidade de ocorrer como
entrada.
Dem.: A rapidez média T(n) em questão pode ser
expressa pela seguinte recorrência:
T(n) = n +
1
n
n−1
i=0
(T(i) + T((n − 1) − i))
– p. 19/71

49. Tempo médio do quicksort
T(n) = n +
1
n
n−1
i=0
(T(i) + T((n − 1) − i))
– p. 20/71

50. Tempo médio do quicksort
T(n) = n +
1
n
n−1
i=0
(T(i) + T((n − 1) − i))
T(n) = n +
2
n
n−1
i=0
T(i)
– p. 20/71

51. Tempo médio do quicksort
T(n) = n +
1
n
n−1
i=0
(T(i) + T((n − 1) − i))
T(n) = n +
2
n
n−1
i=0
T(i)
nT(n) = n2
+ 2
n−1
i=0
T(i)
– p. 20/71

52. Tempo médio do quicksort
nT(n) = n2
+ 2
n−1
i=0
T(i)
– p. 21/71

53. Tempo médio do quicksort
nT(n) = n2
+ 2
n−1
i=0
T(i)
(n − 1)T(n − 1) = (n − 1)2
+ 2
n−2
i=0
T(i)
– p. 21/71

54. Tempo médio do quicksort
nT(n) = n2
+ 2
n−1
i=0
T(i)
(n − 1)T(n − 1) = (n − 1)2
+ 2
n−2
i=0
T(i)
Subtraindo membro a membro as duas equações
acima, tem-se:
nT(n) − (n − 1)T(n − 1) = (2n − 1) + 2T(n − 1)
– p. 21/71

55. Tempo médio do quicksort
nT(n) − (n − 1)T(n − 1) = (2n − 1) + 2T(n − 1)
– p. 22/71

56. Tempo médio do quicksort
nT(n) − (n − 1)T(n − 1) = (2n − 1) + 2T(n − 1)
nT(n) = (n + 1)T(n − 1) + (2n − 1)
– p. 22/71

57. Tempo médio do quicksort
nT(n) − (n − 1)T(n − 1) = (2n − 1) + 2T(n − 1)
nT(n) = (n + 1)T(n − 1) + (2n − 1)
Dividindo ambos os membros por n(n + 1):
T(n)
n + 1
=
T(n − 1)
n
+
(2n − 1)
n(n + 1)
– p. 22/71

58. Tempo médio do quicksort
T(n)
n + 1
=
T(n − 1)
n
+
(2n − 1)
n(n + 1)
– p. 23/71

59. Tempo médio do quicksort
T(n)
n + 1
=
T(n − 1)
n
+
(2n − 1)
n(n + 1)
T(n)
n + 1
≤
2
n + 1
+
T(n − 1)
n
– p. 23/71

60. Tempo médio do quicksort
T(n)
n + 1
=
T(n − 1)
n
+
(2n − 1)
n(n + 1)
T(n)
n + 1
≤
2
n + 1
+
T(n − 1)
n
T(n)
n + 1
≤
2
n + 1
+
2
n
+
T(n − 2)
n − 1
– p. 23/71

61. Tempo médio do quicksort
T(n)
n + 1
=
T(n − 1)
n
+
(2n − 1)
n(n + 1)
T(n)
n + 1
≤
2
n + 1
+
T(n − 1)
n
T(n)
n + 1
≤
2
n + 1
+
2
n
+
T(n − 2)
n − 1
T(n)
n + 1
≤
2
n + 1
+
2
n
+
2
n − 1
+
T(n − 3)
n − 2
– p. 23/71

62. Tempo médio do quicksort
T(n)
n + 1
≤
2
n + 1
+
2
n
+
2
n − 1
+ · · · +
2
3
+
T(1)
2
– p. 24/71

63. Tempo médio do quicksort
T(n)
n + 1
≤
2
n + 1
+
2
n
+
2
n − 1
+ · · · +
2
3
+
T(1)
2
T(n)
n + 1
≤ 2
n+1
x=3
1
x
– p. 24/71

64. Tempo médio do quicksort
T(n)
n + 1
≤
2
n + 1
+
2
n
+
2
n − 1
+ · · · +
2
3
+
T(1)
2
T(n)
n + 1
≤ 2
n+1
x=3
1
x
T(n)
n + 1
≤ 2
n+1
x=2
dx
x
– p. 24/71

65. Tempo médio do quicksort
T(n)
n + 1
≤ 2
n+1
x=2
dx
x
– p. 25/71

66. Tempo médio do quicksort
T(n)
n + 1
≤ 2
n+1
x=2
dx
x
T(n)
n + 1
≤ 2 loge(n + 1)
– p. 25/71

67. Tempo médio do quicksort
T(n)
n + 1
≤ 2
n+1
x=2
dx
x
T(n)
n + 1
≤ 2 loge(n + 1)
T(n) ≤ 2(n + 1) loge(n + 1)
– p. 25/71

68. Tempo médio do quicksort
T(n)
n + 1
≤ 2
n+1
x=2
dx
x
T(n)
n + 1
≤ 2 loge(n + 1)
T(n) ≤ 2(n + 1) loge(n + 1)
T(n) = O(n log n)
– p. 25/71

69. An´alise de Algoritmos
Limite inferior para
a ordenação
– p. 26/71

70. Limite inferior para a ordenação
Algoritmos de ordenação como o bubblesort,
seleção, mergesort, quicksort, etc. são todos
algoritmos baseados em comparação. É
exatamente algoritmos desse tipo que
consideraremos nesta seção.
– p. 27/71

71. Limite inferior para a ordenação
Algoritmos de ordenação como o bubblesort,
seleção, mergesort, quicksort, etc. são todos
algoritmos baseados em comparação. É
exatamente algoritmos desse tipo que
consideraremos nesta seção.
Pergunta: Qual o número mínimo de comparações
que qualquer algoritmos de ordenação baseado
em comparações necessita para resolver o
problema da ordenação?
– p. 27/71

72. Limite inferior para a ordenação
A execução de qualquer algoritmo de ordenação
(baseado em comparações) pode ser representada
por uma árvore binária chamada “árvore de
decisão”.
– p. 28/71

73. Árvore de decisão
– p. 29/71

74. Árvore de decisão
Cada caminho da raiz até uma folha
corresponde a uma sequência de comparações
necessárias para se concluir uma ordem dos
elementos.
– p. 30/71

75. Árvore de decisão
Cada caminho da raiz até uma folha
corresponde a uma sequência de comparações
necessárias para se concluir uma ordem dos
elementos.
Cada uma das n! permutações de n elementos
pode ocorrer, e cada uma destas permutações
deve aparecer como folha em uma árvore de
decisão.
– p. 30/71

76. Árvore de decisão
Portanto, toda árvore de decisão que
representa um algoritmo de ordenação deve ter
pelo menos n! folhas.
– p. 31/71

77. Árvore de decisão
Portanto, toda árvore de decisão que
representa um algoritmo de ordenação deve ter
pelo menos n! folhas.
Baseado nestas observações, podemos mostrar
que:
– p. 31/71

78. Árvore de decisão
Portanto, toda árvore de decisão que
representa um algoritmo de ordenação deve ter
pelo menos n! folhas.
Baseado nestas observações, podemos mostrar
que:
Teorema: O problema da ordenação de n elementos
tem cota inferior Ω(n log n).
– p. 31/71

79. Árvore de decisão
Dem.: Considere um algoritmo R que resolve o
problema da ordenação.
– p. 32/71

80. Árvore de decisão
Dem.: Considere um algoritmo R que resolve o
problema da ordenação. Seja A a árvore de
decisão correspondente a R para uma entrada de
tamanho n.
– p. 32/71

81. Árvore de decisão
Dem.: Considere um algoritmo R que resolve o
problema da ordenação. Seja A a árvore de
decisão correspondente a R para uma entrada de
tamanho n. Então A possui pelo menos n! folhas.
– p. 32/71

82. Árvore de decisão
Dem.: Considere um algoritmo R que resolve o
problema da ordenação. Seja A a árvore de
decisão correspondente a R para uma entrada de
tamanho n. Então A possui pelo menos n! folhas.
Toda árvore binária com k folhas tem altura ≥ log k.
– p. 32/71

83. Árvore de decisão
Dem.: Considere um algoritmo R que resolve o
problema da ordenação. Seja A a árvore de
decisão correspondente a R para uma entrada de
tamanho n. Então A possui pelo menos n! folhas.
Toda árvore binária com k folhas tem altura ≥ log k.
Logo, A altura de A é ≥ log n!.
– p. 32/71

84. Árvore de decisão
Dem.: Considere um algoritmo R que resolve o
problema da ordenação. Seja A a árvore de
decisão correspondente a R para uma entrada de
tamanho n. Então A possui pelo menos n! folhas.
Toda árvore binária com k folhas tem altura ≥ log k.
Logo, A altura de A é ≥ log n!. Mas o tempo T(n)
gasto por R é dado pela altura de A.
– p. 32/71

85. Árvore de decisão
Dem.: Considere um algoritmo R que resolve o
problema da ordenação. Seja A a árvore de
decisão correspondente a R para uma entrada de
tamanho n. Então A possui pelo menos n! folhas.
Toda árvore binária com k folhas tem altura ≥ log k.
Logo, A altura de A é ≥ log n!. Mas o tempo T(n)
gasto por R é dado pela altura de A. Ou seja,
T(n) ≥ log n! = Θ(n log n).
– p. 32/71

86. Árvore de decisão
Dem.: Considere um algoritmo R que resolve o
problema da ordenação. Seja A a árvore de
decisão correspondente a R para uma entrada de
tamanho n. Então A possui pelo menos n! folhas.
Toda árvore binária com k folhas tem altura ≥ log k.
Logo, A altura de A é ≥ log n!. Mas o tempo T(n)
gasto por R é dado pela altura de A. Ou seja,
T(n) ≥ log n! = Θ(n log n). Portanto, o problema
da ordenação de n elementos tem cota inferior
Ω(n log n).
– p. 32/71

87. Exercícios
1. Mostre, através de uma árvore de decisão, que
o problema da busca (por comparações) de um
elemento em uma lista ordenada de n
elementos tem cota inferior Ω(log n).
– p. 33/71

88. An´alise de Algoritmos
Máximo e mínimo de um vetor
– p. 34/71

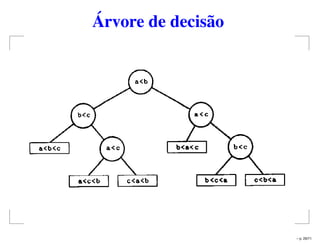
89. Máximo e mínimo de um vetor
Algoritmo: Maxmin(l, r)
Entrada: Um par (l, r) representando A[l..r]
Saída: Um par (Ai, Aj) contendo o maior e o menor valor
de A[l..r]
– p. 35/71

90. Máximo e mínimo de um vetor
Início
Se l = r então retorne(Al, Al)
– p. 36/71

91. Máximo e mínimo de um vetor
Início
Se l = r então retorne(Al, Al)
senão Se l = r − 1
então Se Al ≥ Ar então retorne(Al, Ar)
senão retorne(Ar, Al)
– p. 36/71

92. Máximo e mínimo de um vetor
Início
Se l = r então retorne(Al, Al)
senão Se l = r − 1
então Se Al ≥ Ar então retorne(Al, Ar)
senão retorne(Ar, Al)
senão k ← (l + r)/2 ;
(MaxL,MinL) ← Maxmin(l, k);
(MaxR,MinR) ← Maxmin(k + 1, r);
max ← maximo(MaxL,MaxR);
min ← minimo(MinL,MinR);
retorne(max,min)
Fim
– p. 36/71

93. Máximo e mínimo de um vetor
Início
Se l = r então retorne(Al, Al)
senão Se l = r − 1
então Se Al ≥ Ar então retorne(Al, Ar)
senão retorne(Ar, Al)
senão k ← (l + r)/2 ;
(MaxL,MinL) ← Maxmin(l, k);
(MaxR,MinR) ← Maxmin(k + 1, r);
max ← maximo(MaxL,MaxR);
min ← minimo(MinL,MinR);
retorne(max,min)
Fim
Qual o tempo (pior caso) gasto pelo algoritmo?
– p. 36/71

94. Tempo gasto pelo Maxmin
Seja T(n) o número de comparações feitas pelo
Maxmin para um vetor com n elementos.
– p. 37/71

95. Tempo gasto pelo Maxmin
Seja T(n) o número de comparações feitas pelo
Maxmin para um vetor com n elementos. Então
T(n) pode ser descrito pela seguinte recorrência:
– p. 37/71

96. Tempo gasto pelo Maxmin
Seja T(n) o número de comparações feitas pelo
Maxmin para um vetor com n elementos. Então
T(n) pode ser descrito pela seguinte recorrência:
T(1) = 0, T(2) = 1
– p. 37/71

97. Tempo gasto pelo Maxmin
Seja T(n) o número de comparações feitas pelo
Maxmin para um vetor com n elementos. Então
T(n) pode ser descrito pela seguinte recorrência:
T(1) = 0, T(2) = 1
T(n) = T ( n/2 ) + T ( n/2 ) + 2
– p. 37/71

98. Tempo gasto pelo Maxmin
Seja T(n) o número de comparações feitas pelo
Maxmin para um vetor com n elementos. Então
T(n) pode ser descrito pela seguinte recorrência:
T(1) = 0, T(2) = 1
T(n) = T ( n/2 ) + T ( n/2 ) + 2
Vamos mostrar que
T(n) ≤
3n
2
− 2
– p. 37/71

99. Tempo gasto pelo Maxmin
T(n) ≤
3n
2
− 2
– p. 38/71

100. Tempo gasto pelo Maxmin
T(n) ≤
3n
2
− 2
T(1) = 0 = 3.1
2 − 2
– p. 38/71

101. Tempo gasto pelo Maxmin
T(n) ≤
3n
2
− 2
T(1) = 0 = 3.1
2 − 2
T(2) = 1 = 3.2
2 − 2
– p. 38/71

102. Tempo gasto pelo Maxmin
T(n) ≤
3n
2
− 2
T(1) = 0 = 3.1
2 − 2
T(2) = 1 = 3.2
2 − 2
T(n) = T ( n/2 ) + T ( n/2 ) + 2
– p. 38/71

103. Tempo gasto pelo Maxmin
T(n) ≤
3n
2
− 2
T(1) = 0 = 3.1
2 − 2
T(2) = 1 = 3.2
2 − 2
T(n) = T ( n/2 ) + T ( n/2 ) + 2
≤ 3 n/2
2 − 2 + 3 n/2
2 − 2 + 2
– p. 38/71

104. Tempo gasto pelo Maxmin
T(n) ≤
3n
2
− 2
T(1) = 0 = 3.1
2 − 2
T(2) = 1 = 3.2
2 − 2
T(n) = T ( n/2 ) + T ( n/2 ) + 2
≤ 3 n/2
2 − 2 + 3 n/2
2 − 2 + 2
≤ 3 n/2
2 + 3 n/2
2 − 2
– p. 38/71

105. Tempo gasto pelo Maxmin
T(n) ≤
3n
2
− 2
T(1) = 0 = 3.1
2 − 2
T(2) = 1 = 3.2
2 − 2
T(n) = T ( n/2 ) + T ( n/2 ) + 2
≤ 3 n/2
2 − 2 + 3 n/2
2 − 2 + 2
≤ 3 n/2
2 + 3 n/2
2 − 2
Analisar os casos: n = 4k + i, para i = 0, 1, 2, 3.
– p. 38/71

106. Tempo gasto pelo Maxmin
T(n) ≤
3 n/2
2
+
3 n/2
2
− 2
n = 4k
– p. 39/71

107. Tempo gasto pelo Maxmin
T(n) ≤
3 n/2
2
+
3 n/2
2
− 2
n = 4k + 1
– p. 40/71

108. Tempo gasto pelo Maxmin
T(n) ≤
3 n/2
2
+
3 n/2
2
− 2
n = 4k + 2 e n = 4k + 3 (exercício).
– p. 41/71

109. Exercícios
1. Pode-se desenvolver um algoritmo não
recursivo para calcular o máximo e o mínimo de
uma lista baseado na seguinte idéia:
compara-se pares de elementos consecutivos
e, em seguida, compara-se o maior no par com
o máximo temporário e o menor no par com o
mínimo temporário. Escreva este algoritmo e
calcule o número de comparações realizadas.
2. Qual é um limite inferior para este problema?
– p. 42/71

110. An´alise de Algoritmos
Seleção do k-ésimo mínimo
– p. 43/71

111. Seleção do k-ésimo mínimo
Dado um vetor L[1 · · · n] com n elementos, escreva
um algoritmo para determinar o k-ésimo menor
elemento, para 1 ≤ k ≤ n.
– p. 44/71

112. Seleção do k-ésimo mínimo
Dado um vetor L[1 · · · n] com n elementos, escreva
um algoritmo para determinar o k-ésimo menor
elemento, para 1 ≤ k ≤ n.
Soluc¸ ˜ao: ordenar o vetor.
– p. 44/71

113. Seleção do k-ésimo mínimo
Dado um vetor L[1 · · · n] com n elementos, escreva
um algoritmo para determinar o k-ésimo menor
elemento, para 1 ≤ k ≤ n.
Soluc¸ ˜ao: ordenar o vetor. Tempo O(n log n).
– p. 44/71

114. Seleção do k-ésimo mínimo
Dado um vetor L[1 · · · n] com n elementos, escreva
um algoritmo para determinar o k-ésimo menor
elemento, para 1 ≤ k ≤ n.
Soluc¸ ˜ao: ordenar o vetor. Tempo O(n log n).
Utilizando a divisão e conquista, vamos projetar
um algoritmo linear.
– p. 44/71

115. Seleção do k-ésimo mínimo
Id´eia: dividir L em três sublistas L1, L2 e L3 de
acordo com um elemento m de L tais que:
L1 contenha todos os elementos menores do
que m;
L2 contenha todos os elementos iguais a m;
L3 contenha todos os elementos maiores do
que m.
– p. 45/71

116. Seleção do k-ésimo mínimo
Id´eia: dividir L em três sublistas L1, L2 e L3 de
acordo com um elemento m de L tais que:
L1 contenha todos os elementos menores do
que m;
L2 contenha todos os elementos iguais a m;
L3 contenha todos os elementos maiores do
que m.
Atenção especial à escolha de m.
– p. 45/71

117. Escolha de m
Divida L em |L|/5 listas de 5 elementos cada;
– p. 46/71

118. Escolha de m
Divida L em |L|/5 listas de 5 elementos cada;
Ordene separadamente cada uma dessas
listas;
– p. 46/71

119. Escolha de m
Divida L em |L|/5 listas de 5 elementos cada;
Ordene separadamente cada uma dessas
listas;
Seja M a lista das medianas das listas de 5
elementos.
– p. 46/71

120. Escolha de m
Divida L em |L|/5 listas de 5 elementos cada;
Ordene separadamente cada uma dessas
listas;
Seja M a lista das medianas das listas de 5
elementos.
m será a mediana de M.
– p. 46/71

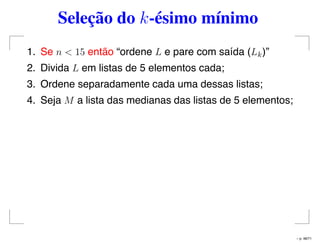
121. Seleção do k-ésimo mínimo
Algoritmo: Seleção(k, L)
Entrada: Um inteiro k e um vetor L[1..n]
Saída: O k-ésimo menor elemento de L
– p. 47/71

122. Seleção do k-ésimo mínimo
1. Se n < 15 então “ordene L e pare com saída (Lk)”
– p. 48/71

123. Seleção do k-ésimo mínimo
1. Se n < 15 então “ordene L e pare com saída (Lk)”
2. Divida L em listas de 5 elementos cada;
3. Ordene separadamente cada uma dessas listas;
4. Seja M a lista das medianas das listas de 5 elementos;
– p. 48/71

124. Seleção do k-ésimo mínimo
1. Se n < 15 então “ordene L e pare com saída (Lk)”
2. Divida L em listas de 5 elementos cada;
3. Ordene separadamente cada uma dessas listas;
4. Seja M a lista das medianas das listas de 5 elementos;
5. m ← Seleção( |M|/2 , M)
– p. 48/71

125. Seleção do k-ésimo mínimo
1. Se n < 15 então “ordene L e pare com saída (Lk)”
2. Divida L em listas de 5 elementos cada;
3. Ordene separadamente cada uma dessas listas;
4. Seja M a lista das medianas das listas de 5 elementos;
5. m ← Seleção( |M|/2 , M)
6. Sejam L1, L2 e L3 as sublistas dos elementos de L que
são menores, iguais e maiores do que m, respect.;
– p. 48/71

126. Seleção do k-ésimo mínimo
1. Se n < 15 então “ordene L e pare com saída (Lk)”
2. Divida L em listas de 5 elementos cada;
3. Ordene separadamente cada uma dessas listas;
4. Seja M a lista das medianas das listas de 5 elementos;
5. m ← Seleção( |M|/2 , M)
6. Sejam L1, L2 e L3 as sublistas dos elementos de L que
são menores, iguais e maiores do que m, respect.;
7. Se |L1| ≥ k então pare com saída Seleção(k, L1)
– p. 48/71

127. Seleção do k-ésimo mínimo
1. Se n < 15 então “ordene L e pare com saída (Lk)”
2. Divida L em listas de 5 elementos cada;
3. Ordene separadamente cada uma dessas listas;
4. Seja M a lista das medianas das listas de 5 elementos;
5. m ← Seleção( |M|/2 , M)
6. Sejam L1, L2 e L3 as sublistas dos elementos de L que
são menores, iguais e maiores do que m, respect.;
7. Se |L1| ≥ k então pare com saída Seleção(k, L1)
8. senão Se (|L1| + |L2|) ≥ k
– p. 48/71

128. Seleção do k-ésimo mínimo
1. Se n < 15 então “ordene L e pare com saída (Lk)”
2. Divida L em listas de 5 elementos cada;
3. Ordene separadamente cada uma dessas listas;
4. Seja M a lista das medianas das listas de 5 elementos;
5. m ← Seleção( |M|/2 , M)
6. Sejam L1, L2 e L3 as sublistas dos elementos de L que
são menores, iguais e maiores do que m, respect.;
7. Se |L1| ≥ k então pare com saída Seleção(k, L1)
8. senão Se (|L1| + |L2|) ≥ k
então pare com saída (m)
– p. 48/71

129. Seleção do k-ésimo mínimo
1. Se n < 15 então “ordene L e pare com saída (Lk)”
2. Divida L em listas de 5 elementos cada;
3. Ordene separadamente cada uma dessas listas;
4. Seja M a lista das medianas das listas de 5 elementos;
5. m ← Seleção( |M|/2 , M)
6. Sejam L1, L2 e L3 as sublistas dos elementos de L que
são menores, iguais e maiores do que m, respect.;
7. Se |L1| ≥ k então pare com saída Seleção(k, L1)
8. senão Se (|L1| + |L2|) ≥ k
então pare com saída (m)
senão pare com saída Seleção(k − |L1| − |L2|, L3)
– p. 48/71

130. Seleção do k-ésimo mínimo - Tempo
Seja T(n) o tempo gasto pelo algoritmo seleção
para determinar o k-ésimo mínimo em uma lista
com n elementos.
– p. 49/71

131. Seleção do k-ésimo mínimo - Tempo
Seja T(n) o tempo gasto pelo algoritmo seleção
para determinar o k-ésimo mínimo em uma lista
com n elementos.
O tempo de execução das linhas 1 a 4 é O(n).
– p. 49/71

132. Seleção do k-ésimo mínimo - Tempo
Seja T(n) o tempo gasto pelo algoritmo seleção
para determinar o k-ésimo mínimo em uma lista
com n elementos.
O tempo de execução das linhas 1 a 4 é O(n).
A lista M das medianas contém no máximo n/5
elementos, e a execução da linha 5 requer
tempo T(n/5).
– p. 49/71

133. Seleção do k-ésimo mínimo - Tempo
Seja T(n) o tempo gasto pelo algoritmo seleção
para determinar o k-ésimo mínimo em uma lista
com n elementos.
O tempo de execução das linhas 1 a 4 é O(n).
A lista M das medianas contém no máximo n/5
elementos, e a execução da linha 5 requer
tempo T(n/5).
A linha 6 também requer tempo O(n).
– p. 49/71

134. Seleção do k-ésimo mínimo - Tempo
Cada chamada recursiva nas linhas 7 e 8
requer tempo máximo T(3n/4).
– p. 50/71

135. Seleção do k-ésimo mínimo - Tempo
Cada chamada recursiva nas linhas 7 e 8
requer tempo máximo T(3n/4).
Podemos então expressar o tempo T(n) pela
seguinte recorrência:
T(n) ≤



cn para n < 15,
T(n/5) + T(3n/4) + cn para n ≥ 15
– p. 50/71

136. Seleção do k-ésimo mínimo - Tempo
Vamos mostrar, por indução em n que
T(n) ≤ 20cn
– p. 51/71

137. Seleção do k-ésimo mínimo - Tempo
Vamos mostrar, por indução em n que
T(n) ≤ 20cn
A afirmação é claramente verdadeira para n < 15.
– p. 51/71

138. Seleção do k-ésimo mínimo - Tempo
Vamos mostrar, por indução em n que
T(n) ≤ 20cn
A afirmação é claramente verdadeira para n < 15.
Vamos supor, por hipótese de indução, que ela é
válida para valores menores do que n, e vamos
provar sua validade para n.
– p. 51/71

139. Seleção do k-ésimo mínimo - Tempo
T(n) ≤ T(n/5) + T(3n/4) + cn
– p. 52/71

140. Seleção do k-ésimo mínimo - Tempo
T(n) ≤ T(n/5) + T(3n/4) + cn
≤ 20c(n/5) + 20c(3n/4) + cn
– p. 52/71

141. Seleção do k-ésimo mínimo - Tempo
T(n) ≤ T(n/5) + T(3n/4) + cn
≤ 20c(n/5) + 20c(3n/4) + cn
= 20c(n/5 + 3n/4) + cn
– p. 52/71

142. Seleção do k-ésimo mínimo - Tempo
T(n) ≤ T(n/5) + T(3n/4) + cn
≤ 20c(n/5) + 20c(3n/4) + cn
= 20c(n/5 + 3n/4) + cn
= 20c(19n/20) + cn
– p. 52/71

143. Seleção do k-ésimo mínimo - Tempo
T(n) ≤ T(n/5) + T(3n/4) + cn
≤ 20c(n/5) + 20c(3n/4) + cn
= 20c(n/5 + 3n/4) + cn
= 20c(19n/20) + cn
= 20cn
– p. 52/71

144. Exercícios
1. Calcule o tempo gasto pela seleção do k-ésimo
mínimo no caso em que as sublistas tenham:
(a) 7 elementos; (b) 3 elementos.
2. Suponha que ao invés de selecionar o k-ésimo
mínimo, queremos determinar os k-elementos
mínimos, mas sem a sua ordem relativa. Será
que isso pode ser feito em tempo O(n)?
3. Dado uma lista com n elementos, determine se
existe um elemento que aparece n/2 vezes ou
mais.
– p. 53/71

145. An´alise de Algoritmos
Multiplicação de matrizes
– p. 54/71

146. Multiplicação de matrizes
Sejam A e B duas matrizes n × n. A matriz
produto C = A.B é, por definição, uma matriz n × n
onde cada elemento cij é obtido por
cij =
n
k=1
aikbkj
Cada elemento cij requer, portanto, a realização de
n produtos. Como a matriz produto C possui n2
elementos cij, este algoritmo para calcular o
produto de duas matrizes tem rapidez O(n3
).
– p. 55/71

147. Multiplicação de matrizes
Veremos nesta seção o Algoritmos de Strassen,
um algoritmo para multiplicação de matrizes com
rapidez O(nlog 7
), que é aproximadamente n2,81
.
Para simplificar a apresentação, vamos supor que
n é uma potência de 2.
– p. 56/71

148. Multiplicação de matrizes
Particionamos A e B em submatrizes quadradas
de ordem (n/2) × (n/2). Então o produto A.B pode
ser calculado da seguinte forma:


C11 C12
C21 C22

 =


A11 A12
A21 A22

 ·


B11 B12
B21 B22


Ou equivalentemente,
Cij = Ai1B1j + Ai2B2j, i, j = 1, 2
– p. 57/71

149. Multiplicação de matrizes


C11 C12
C21 C22

 =


A11 A12
A21 A22

 ·


B11 B12
B21 B22


C11 = A11B11 + A12B21
C12 = A11B12 + A12B22
C21 = A21B11 + A22B21
C22 = A21B12 + A22B22
– p. 58/71

150. Multiplicação de matrizes
O cálculo das 4 matrizes Cij requer 8 produto de
matrizes. A idéia central do algoritmo de Strassen
é reduzir estes 8 produtos para 7. Isso é feito da
seguinte forma:
– p. 59/71

151. Multiplicação de matrizes
Calculamos inicialmente as matrizes
S1 = A11(B12 − B22)
S2 = (A11 + A12)B22
S3 = (A21 + A22)B11
S4 = A22(B21 − B11)
S5 = (A21 + A22)(B11 + B22)
S6 = (A12 − A22)(B21 + B22)
S7 = (A11 − A21)(B11 + B12)
– p. 60/71

152. Multiplicação de matrizes
As matrizes Cij podem ser calculadas da seguinte
forma:
C11 = S5 + S4 − S2 + S6
C12 = S1 + S2
C21 = S3 + S4
C22 = S5 + S1 − S3 + S7
– p. 61/71

153. Multiplicação de matrizes
As matrizes Cij podem ser calculadas da seguinte
forma:
C11 = S5 + S4 − S2 + S6
C12 = S1 + S2
C21 = S3 + S4
C22 = S5 + S1 − S3 + S7
O cálculo dos Cij desta forma requer 7 produtos de
e 18 soma de matrizes de ordem (n/2) × (n/2).
– p. 61/71

154. Multiplicação de matrizes
Portanto, o tempo gasto pelo algoritmo de Strassen
pode ser descrito pela recorrência
T(n) = 7T(n/2) + cn2
– p. 62/71

155. Multiplicação de matrizes
Portanto, o tempo gasto pelo algoritmo de Strassen
pode ser descrito pela recorrência
T(n) = 7T(n/2) + cn2
cuja solução pelo método master é
T(n) = Θ(nlog 7
)
– p. 62/71

156. Multiplicação de matrizes
Na prática, o algoritmo de Strassen não é mais
utilizado do que o algoritmo tradicional, por
algumas razões, tais como:
– p. 63/71

157. Multiplicação de matrizes
Na prática, o algoritmo de Strassen não é mais
utilizado do que o algoritmo tradicional, por
algumas razões, tais como:
O fator constante em Θ(nlog 7
) é alto;
As submatrizes adicionais e as chamadas
recursivas consomem espaço considerável.
– p. 63/71

158. Multiplicação de matrizes
Na prática, o algoritmo de Strassen não é mais
utilizado do que o algoritmo tradicional, por
algumas razões, tais como:
O fator constante em Θ(nlog 7
) é alto;
As submatrizes adicionais e as chamadas
recursivas consomem espaço considerável.
Testes empíricos mostram que o algoritmo de
Strassen começa a ser mais rápido que o
algoritmo tradicional quando n > 100.
– p. 63/71

159. An´alise de Algoritmos
Subsequência máxima
– p. 64/71

160. Subsequência máxima
Dada uma sequência (x1, x2, . . . , xn) de números
reais (positivos e negativos), encontre uma
subsequência (xi, xi+1, . . . , xj) (de elementos
consecutivos) tal que a soma dos números seja a
maior possível.
– p. 65/71

161. Subsequência máxima
Dada uma sequência (x1, x2, . . . , xn) de números
reais (positivos e negativos), encontre uma
subsequência (xi, xi+1, . . . , xj) (de elementos
consecutivos) tal que a soma dos números seja a
maior possível.
Por exemplo, na sequência
(2, −3, 1.5, −1, 3, −2, −3, 3)
a subsequência máxima é
– p. 65/71

162. Subsequência máxima
Dada uma sequência (x1, x2, . . . , xn) de números
reais (positivos e negativos), encontre uma
subsequência (xi, xi+1, . . . , xj) (de elementos
consecutivos) tal que a soma dos números seja a
maior possível.
Por exemplo, na sequência
(2, −3, 1.5, −1, 3, −2, −3, 3)
a subsequência máxima é (1.5, −1, 3).
– p. 65/71

163. Subsequência máxima
Pode haver mais de uma subsequência
máxima.
– p. 66/71

164. Subsequência máxima
Pode haver mais de uma subsequência
máxima.
Se todos os números são negativos, a
subsequência máxima é vazia, e a soma dos
seus elementos é zero.
– p. 66/71

165. Subsequência máxima
Pode haver mais de uma subsequência
máxima.
Se todos os números são negativos, a
subsequência máxima é vazia, e a soma dos
seus elementos é zero.
Queremos projetar um algoritmo que determima
uma subsequência máxima.
– p. 66/71

166. Subsequência máxima
Ajuda alguma coisa se:
dividirmos o problema? (divisão e conquista)
– p. 67/71

167. Subsequência máxima
Ajuda alguma coisa se:
dividirmos o problema? (divisão e conquista)
soubermos a subsequência máxima de
(x1, x2, . . . , xn−1)?
– p. 67/71

168. Subsequência máxima
Ajuda alguma coisa se:
dividirmos o problema? (divisão e conquista)
soubermos a subsequência máxima de
(x1, x2, . . . , xn−1)?
e se soubermos a subsequência máxima e o
sufixo máximo de (x1, x2, . . . , xn−1)?
– p. 67/71

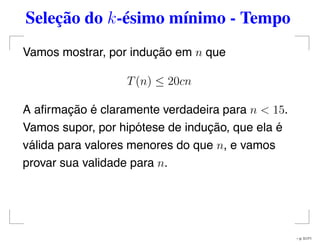
169. Subsequência máxima
Algoritmo: Subseq-Max(L)
Entrada: Um vetor x[1..n]
Saída: O valor da subsequência máxima
– p. 68/71

170. Subsequência máxima
Início
subseq-max ← 0; sufixo-max ← 0;
– p. 69/71

171. Subsequência máxima
Início
subseq-max ← 0; sufixo-max ← 0;
Para i = 1 até n faça
– p. 69/71

172. Subsequência máxima
Início
subseq-max ← 0; sufixo-max ← 0;
Para i = 1 até n faça
Se (xi+ sufixo-max > subseq-max)
– p. 69/71

173. Subsequência máxima
Início
subseq-max ← 0; sufixo-max ← 0;
Para i = 1 até n faça
Se (xi+ sufixo-max > subseq-max)
então sufixo-max ← sufixo-max +xi;
subseq-max ← sufixo-max
– p. 69/71

174. Subsequência máxima
Início
subseq-max ← 0; sufixo-max ← 0;
Para i = 1 até n faça
Se (xi+ sufixo-max > subseq-max)
então sufixo-max ← sufixo-max +xi;
subseq-max ← sufixo-max
senão se (xi+ sufixo-max > 0)
– p. 69/71

175. Subsequência máxima
Início
subseq-max ← 0; sufixo-max ← 0;
Para i = 1 até n faça
Se (xi+ sufixo-max > subseq-max)
então sufixo-max ← sufixo-max +xi;
subseq-max ← sufixo-max
senão se (xi+ sufixo-max > 0)
então sufixo-max ← sufixo-max +xi;
senão sufixo-max ← 0
Fim
– p. 69/71

176. Exercícios
1. Modifique o algoritmo para que ele determine
uma subsequência máxima.
– p. 70/71

177. Outros problemas
1. Par mais próximo.
– p. 71/71